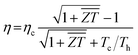Improved thermoelectric power factor and conversion efficiency of perovskite barium stannate

Abstract

In the pursuit of high thermoelectric conversion efficiency, both high operating temperature and high figure of merit ZT are desirable. Thermoelectric materials used in high-temperature power generation are still in great demand. Here we demonstrate the n-type doped barium stannate (BaSnO₃) behaves as a robust candidate, as a high-temperature thermoelectric material, due to its ultrahigh power factor and excellent structural and chemical stability. A systematic calculation focused on the geometric, electronic and thermoelectric transport properties of BaSnO₃ is performed by using density functional theory combined with Boltzmann transport theory. It can be noticed that the electrical conductivity of BaSnO₃ is improved dramatically when it is n-type doped, resulting from the small effective mass and extraordinary high mobility. The power factor maximum reaches 1.5 × 10⁻³ W m⁻¹ K⁻² at 1200 K with the optimal carrier concentration 1.6 × 10¹⁹ cm⁻³, which suggests the great potential of BaSnO₃ as an n-type high temperature thermoelectric material.

---

Introduction

Thermoelectric materials, which can directly convert heat to electricity, are of great interest in waste heat recovery, solid-state cooling and so on. The performance of thermoelectric materials is evaluated through the dimensionless figure of merit ZT, ZT = (S²σ/κ)T, where S, σ, κ and T are the Seebeck coefficient, the electrical conductivity, the thermal conductivity, and the absolute temperature, respectively. κ consists of lattice (κ_l) and electronic (κ_e) contributions. A high ZT value requires high power factor (S²σ) and low thermal conductivity (κ). In recent years, many efforts have been made with regard to reducing the thermal conductivity, such as by nanostructuring or introducing layered structures.^1,2 The strategies to maximize the power factor include optimal doping and band engineering.^3–6 However, it should be noted that optimizing all of features of thermoelectric coefficients at the same time is a challenging task due to their interdependent relationships.

Apart from the ZT value being used to evaluate the thermoelectric properties of a material, in a thermoelectric device, the conversion efficiency (η) is directly used to assess the performance, which is characterized by ZT and the Carnot efficiency η_c. A high Carnot limit, η_c = (T_h − T_c)/T_c, requires a large temperature difference between the hot side (T_h) and cold side (T_c) of the thermoelectric device. Thus, high temperature thermoelectric materials with good transport properties are highly desirable for power generating >1000 K. Oxide-based semiconductors are regarded as the candidates for high-temperature thermoelectric applications due to their thermal and chemical stability at high temperature.^7–9 The performance of the traditional oxide thermoelectric materials, such as p-type Na_xCoO₂,^10,11 Ca₃Co₄O₉,^12,13 BiCuSeO^14,15 and n-type SrTiO₃,^16,17 ZnO¹⁸ can be enhanced by heavy-element doping, band engineering and nanostructuring. Nevertheless, only the p-type layer structured oxide thermoelectrics Na_xCoO₂ and BiCuSeO exhibit high figures of merit approaching to 1,^10,15 which is closely related to their low κ. SrTiO₃ as a n-type solid thermoelectric material has been widely studied for many years due to the large Seebeck coefficient but limited by the low carrier mobility and high thermal conductivity.¹⁹ Therefore, exploring efficient ways to improve their electrical performance with stable low thermal conductivity is a promising strategy for oxide-based thermoelectric materials.

Fortunately, the carrier mobility and electrical conductivity of n-type doped BaSnO₃ can be dramatically enhanced due to the small effective mass (m*).^20–23 BaSnO₃, a typical perovskite-type compound, behaves as an excellent high-mobility electron transport material composed of abundant elements. The sample of BaSnO₃ doped with a few percent La has been reported of an unusually high electron mobility of 320 cm² V⁻¹ s⁻¹, which is the highest value reported in perovskite oxides.^20,21 The ultrahigh carrier mobility is ascribed to the small electron effective mass m* (0.06–0.21 m_e),^23–25 resulting from the light conduction band. The electrical conductivity is remarkably enhanced up to 10⁵ S m⁻¹ with the carrier concentration of 10²⁰ cm⁻³, showing a metal-like behavior.²⁶ Moreover, BaSnO₃ exhibits high thermal stability at high temperature exceed 1273 K, which is seven orders of magnitude more thermally stable in terms of the oxygen diffusion constant compared with SrTiO₃.^27,28 The thermal conductivity of pure BaSnO₃ is 9.68 W m⁻¹ K⁻¹ at room temperature,²⁹ which is smaller than the good oxide-based thermoelectric material SrTiO₃ (12 W m⁻¹ K⁻¹),³⁰ but higher than that of the layered structure, such as NaCo₂O₄ (2 W m⁻¹ K⁻¹), BiCuSeO (∼0.5 W m⁻¹ K⁻¹).^31,32 But it is in negative correlation with temperature and decreases to 3.2 W m⁻¹ K⁻¹ at 1262 K.²⁹ Furthermore, for the doped samples, dopants not only supply carriers to increase the electrical conductivity and optimize the power factor, but also deduce point defect scattering to suppress the lattice thermal conductivity. All these factors suggest the great potential of BaSnO₃ as a high temperature thermoelectric material by tuning carrier concentration.

In this work, we systematically investigated the geometric, electronic and thermoelectric properties of BaSnO₃ by employing the first principle calculations combined with Boltzmann transport theory. A comparison of the thermoelectric transport properties between n-type and p-type doped samples reveals that the n-type electrical conductivity is several order of magnitude higher than that of p-type one. The ultra-high n-type PF, 1.5 × 10⁻³ W m⁻¹ K⁻², is observed at 1200 K with carrier concentration of 1.6 × 10¹⁹ cm⁻³. This PF value is significantly higher than the highest value is standout among the oxide-based thermoelectric materials and even is comparable to those state-of-the-art thermoelectric materials such as Bi₂Te₃ and SnSe.^33,34

Computational details

The calculation of geometry optimization and electronic structure of BaSnO₃ is performed using the density functional theory (DFT) with project augmented wave (PAW)³⁵ potentials as implemented in the Vienna Ab initio Simulation Package (VASP) code.³⁶ For the exchange–correlation potential, we use the standard Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional³⁷ to obtain exact band gap. The kinetic energy cutoff of wave functions of 600 eV and a Monkhorst–Pack k-mesh of 6 × 6 × 6 are adopted to sample the Inreducible Brillouin Zone (IBZ) in the structure relaxation, with the energy convergence threshold set as 10⁻⁴ eV. Both the cell shape and volume are fully optimized and all atoms are allowed to relax until the maximal Hellmann–Feynman force acting on each atom is less than 0.001 eV Å⁻¹. The denser k-point mesh 15 × 15 × 15, 19 × 19 × 19 and 21 × 21 × 21 are test respectively to guarantee the convergence. Finally, a Monkhorst–Pack k-point mesh of 19 × 19 × 19 has been used to calculate the transport coefficients of BaSnO₃.

The electronic transport properties are obtained utilizing the semi-classical Boltzmann transport theory as implemented in the BoltzTrap code.³⁸ As the band structure is calculated at zero temperature, the effect of temperature T and Fermi level μ are introduced by using the broadening of Fermi distribution. In the phonon calculation, density functional perturbation theory with an atomic displacement of 0.005 Å is employed to determine the harmonic interatomic force constants (IFCs). Phonon frequencies are obtained from IFCs by using Phonopy package.³⁹ A 3 × 3 × 3 supercell of primitive cell containing 135 atoms with 6 × 6 × 6 k-point mesh is used to calculate harmonic and anharmonic IFCs. Convergence tests with systems composed of up to 4 × 4 × 4 unit cells showed no significant changes in phonon dispersion. The interactions up to third-nearest neighbors are considered when calculating the third order anharmonic IFCs. The lattice thermal conductivity is calculated by solving the phonon Boltzmann transport equation with the relaxation time approximation, as implemented in ShengBTE code.⁴⁰

Results and discussion

Geometrical and electronic structure

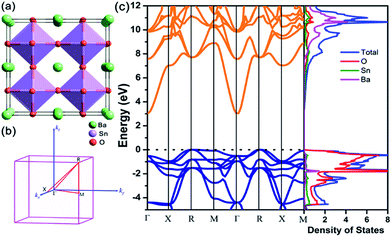
BaSnO₃ has an ideal cubic perovskite structure with space group Pm3̄m (no. 221) as shown in Fig. 1(a). After full relaxation, the lattice parameter a = 4.115 Å, which is in excellent agreement with experimental value (4.12 Å).⁴¹ Fig. 1(b) shows the Brillouin zone of cubic BaSnO₃. The thermoelectric transport properties are closely related to the electronic states near the Fermi level. As shown in Fig. 1(c), BaSnO₃ is an indirect semiconductor, with the conduction band minimum (CBM) and the valence band maximum (VBM) locating at Γ and R point respectively. The band gap calculated by HSE06 method is 3.0 eV, which is in excellent agreement with the experimental values (3.1 eV and 3.4 eV)^42,43 and more exact than the previous calculated values based on LDA (0.79 eV)⁴⁴ and GGA (1.4 eV) approximation.⁴⁵ BaSnO₃ possesses a large conduction band dispersion at Γ point, which originates from Sn 5s–O 2p antibonding orbital interactions, suggesting the small electron effective mass. By fitting the band structure around CBM using the equation, m* = ℏ²/(d²E/dk²), we calculated m* of BaSnO₃ 0.26 m_e. Moreover, the large dielectric constant contributes to remarkable low scattering rates.⁴⁶ According to the relationship of μ = eτ/m*, high mobility for n-type doped can be realized with small electron effective mass. Perovskites are favorable for attempts to introduce carriers through substitutional doping through substitution onto the Ba or Sn site. The extrinsic dopants introduce shallow donor states to the bottom of conduction band and move the Fermi level (E_f) away from the valance band, which are the source of high conductivity. In contrast, the flat valance band with heavy density-of-states effective mass indicates the high Seebeck coefficient for p-type BaSnO₃. To improve the thermoelectric performance of BaSnO₃, it is essential to balance both electrical conductivity and Seebeck coefficient.

Fig. 1 (a) The optimized crystal structure and (b) Brillouin zone of cubic BaSnO₃. (c) Electronic band structure and corresponding density of states based on HSE06 functional. The Fermi level is set at 0 eV.

Thermoelectric properties

By means of the semi-classical Boltzmann transport theory and invoking the parameters from the calculated electronic structure, the most important thermoelectric properties from electronic contribution of BaSnO₃ can be obtained and presented in Fig. 2. The Seebeck coefficient of n- and p-type doped BaSnO₃ as a function of carrier concentration at different temperature is shown in Fig. 2(a) and (b). The S decreases monotonically with increasing carrier concentration for both n- and p-type doped sample while increases gradually with the temperature rising. As aforementioned, the flat valance band with heavy density-of-states effective mass combined with the high valance DOS peak contributes to the larger Seebeck value of p-type doped BaSnO₃, comparing to the n-type doped sample. For example, at the same magnitude of hole and electron concentration, 1 × 10¹⁹ cm⁻³, the S of p-type doping sample is about four times higher than that of n-type doping one at 1200 K. Nevertheless, the S of the two cases possesses similar value at their respective optimal carrier concentration of ∼10²¹ cm⁻³ (p-type) and ∼10¹⁹ cm⁻³ (n-type) for maximal power factor. With the temperature rising, the susceptibility of Seebeck coefficient to temperature is degenerate. It comes very close to the two curves of 1000 K and 1200 K for the p-type doped sample.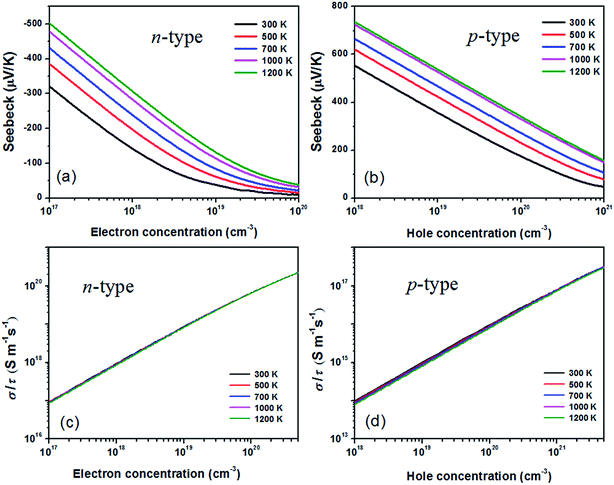

Fig. 2 The Seebeck coefficient (a) and (b), the ratio of σ to τ (c) and (d) as a function of n-type and p-type carrier concentration at different temperature.

In fact, only the ratio of electrical conductivity to relaxation time (σ/τ) is obtained directly from the BoltzTrap code. The value of σ/τ for n-type and p-type doped BaSnO₃ as functions of temperature and carrier concentration are displayed in Fig. 2(c) and (d). It can be found that σ/τ is almost temperature independent when the temperature increased from 300 K to 1200 K, in accordance with the temperature independence of carrier mobility. A remarkable increased σ/τ is achieved with the increase of carrier concentration at different temperature. The σ/τ − n relationship reveals over two orders of magnitude improvement within the range of electron and hole concentrations we considered. For the p-type doped sample, the heavy doping level (10²¹ cm⁻³) can bring the same magnitude enhancement of σ/τ, however, the value is significantly smaller than the n-type doping one. Generally, the electrical conductivity could be derived from the relation σ = enμ (n, carrier concentration; and μ, carrier mobility). The remarkable disparity in conductivity value between two doping types is attributed to the high carrier mobility of n-type doping, related to the large dispersive conduction band. For p-type system, the high DOS effective mass due to flat valance band reduces the mobility although it yields high Seebeck coefficient. Therefore, the trade-off between electrical conductivity and Seebeck coefficient results in the peak power factor (PF) and ZT value.

The constant relaxation time approximation is typically employed and the value of τ can be acquired by fitting it to the experimental results. Such method has been implemented to estimate the relaxation time in many other materials.^47,48 With the available experimental electrical conductivities of n-type and p-type doped BaSnO₃ adopted,^17,20 we determine the relaxation times are 9.8 × 10⁻¹⁵ s and 11.16 × 10⁻¹⁶ s for n-type and p-type system at room temperature, respectively. Furthermore, the electrical conductivities from experiment with different small carrier concentrations at room temperature give similar τ values, which indicates that τ is in weak dependence of the carrier concentration and the constant τ assumption is reasonable in small doping level. For the heavily doped samples, the temperature and carrier concentration dependence of τ is assumed in the typical electron–phonon form, τ = AT⁻¹n^−1/3 (τ in s, T in K, n in cm⁻³), where A is a constant. With the experimental data,²⁰ the yield A is 2.94 × 10⁻⁶ s K cm⁻¹. With the calculated τ, electrical conductivities as functions of carrier concentration are presented in Fig. 3(a) and (b). The σ of n-type doping increases rapidly from ∼10³ S m⁻¹ to ∼10⁶ S m⁻¹ as the carrier concentration increase from ∼10¹⁷ cm⁻³ to ∼10²⁰ cm⁻³, showing a transform from semiconductor to mental like behavior. The PF defined as S²σ, is usually used as a criterion in searching for new thermoelectric materials with high output power. The significantly enhanced σ satisfies the demonstration reported by Takada et al.⁴⁹ that the improvement of the electrical conductivity of the BaSnO₃ is very important to obtain a high power factor. The carrier concentration and temperature dependence of PF for n-type and p-type doping is shown in Fig. 3(c) and (d). The value of maximum PF corresponds to the optimal carrier concentration, resulting from the opposite dependence on carrier concentration between S and σ. Typically, the light electronic bands with small effective mass request low optimal carrier concentration (10¹⁹ to 10²⁰ cm⁻³), namely, a low content of dopants is enough to optimize the power factor. In contrast, for the heavy band materials, higher carrier concentrations are demanded to optimize the power factor. Consequently, at 1200 K, the PF values for n-type and p-type doped BaSnO₃ reach the maximum at carrier concentration of 1.6 × 10¹⁹ cm⁻³ and 2 × 10²¹ cm⁻³, respectively. Considering the similar Seebeck coefficient but great disparity of electrical conductivity for n- and p-type doped BaSnO₃ at optimal carrier concentration, the PF maximum of n-type is near four orders of magnitude higher than p-type one. Moreover, the PF increases with the rising of temperature. Thus a ultra-high optimal PF (1.5 × 10⁻³ W m⁻¹ K⁻²) of n-type doped BaSnO₃ is obtained, which is standout amongst the oxide-based thermoelectric materials, such as NaCo₂O₄ (ref. 50) and the doped CaMnO₃,⁵¹ indicating the great potential for n-type doped BaSnO₃ as a high temperature thermoelectric material. Our calculated PF values are in reasonable agreement with the experimental data. For example, at the carrier concentration of 7 × 10¹⁹ cm⁻³ for n-type doped samples, the calculated value of 0.63 × 10⁻³ W m⁻¹ K⁻² at 1000 K coincides with the experimented 0.45 × 10⁻³ W m⁻¹ K⁻² at 973 K. However, our simulated optimal PF value of 1.5 × 10⁻³ W m⁻¹ K⁻² indicates the thermoelectric performance of BaSnO₃ can be further improved and provides guidance of synergetic tuning optimum carrier concentration and higher temperature to experiment efforts.

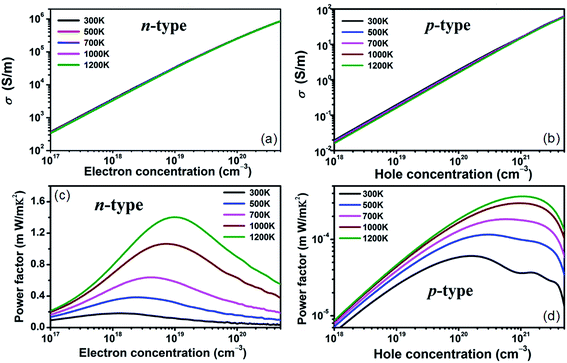Fig. 3 Calculated electrical conductivity (a) and (b) and power factor (c) and (d) as a function of n-type and p-type carrier concentration at different temperature.

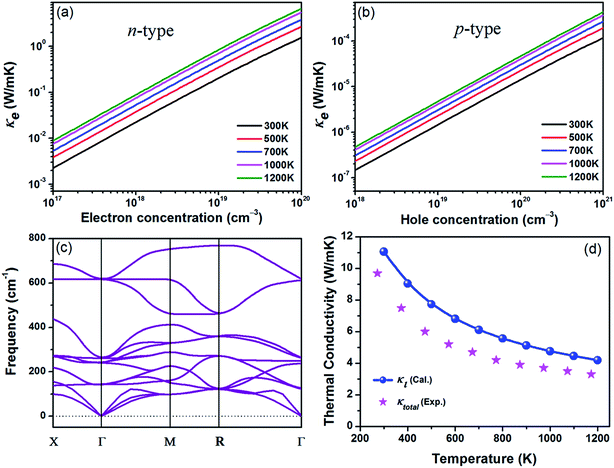
Next, we investigate the thermal transport properties of BaSnO₃. The electrical thermal conductivity κ_e is calculated from the electrical conductivity σ via the Wiedemann–Franz relationship κ_e = LσT, where L is the Lorenz number, which is approximately 2.44 × 10⁻⁸ W Ω K⁻². Consequently, the curves of κ_e versus carrier concentration exhibit the similar trends to σ, as shown in Fig. 4(a) and (b). In the degenerate semiconductor, the phonon conductivity is predominate part of the total thermal conductivity and thus the electronic contribution is negligible. The lattice thermal conductivity (κ_l) and the total thermal conductivity (κ_total) of the intrinsic BaSnO₃ at different temperature are shown in Fig. 4(d). The κ_l values estimated using ShengBTE code are slightly larger than the experimental value of κ_total, which originates from the following reason: in first principles approach only the phonon–phonon scattering is considered while in samples used for experimental measurement contain other types of scattering due to defects, impurities and dislocations which in turn reduce the thermal conductivity. The fitted line of κ_l follows the T⁻¹ relationship, indicating the phonon–phonon interaction plays the main role in the phonon mechanism. The decreased κ_l can be explained by the increased phonon–phonon scattering as temperature rising. To investigate the origin of the reduction of thermal conductivity, the phonon spectra of BaSnO₃ is calculated and plotted in Fig. 4(c). The heavy constituent elements contribute mainly to the lower frequency mode, leading to the low frequency optical branches overlapping with the acoustic modes. Thus, the optical branches share part of heat with the acoustic branches, which increase the chance of phonon scattering. The experiment reported κ_total decreases rapidly from 9.6 W m⁻¹ K⁻¹ to 3.2 W m⁻¹ K⁻¹ as temperature increases from 323 K to 1263 K.²⁹ Compared to the reported thermal conductivity of n-type doped Ba_1−xLa_xSnO₃, the thermal conductivities are quite similar at different doping levels,⁵² indicating the κ_total is independent with carrier concentration. As to the doped compound, the electronic contribution, κ_e is gradually enhanced due to the positive relationship to the carrier concentration. However, in thermoelectric materials, dopants not only supply carriers to optimize the power factor, but enhance the phonon scattering to reduce the contribution of κ_l. Thus, the compromise between κ_e and κ_l contributes to the doping level independence of κ_total.

Fig. 4 Electronic thermal conductivity as a function of carrier concentration at different temperature for n-type (a) and p-type (b) doped BaSnO₃. (c) Phonon dispersion of pure BaSnO₃. (d) Lattice thermal conductivity and total thermal conductivity.

With the electronic and thermal transport coefficients available, we now evaluate the thermoelectric performance of BaSnO₃ by ZT value and conversion efficiency. Considering the small power factor value of p-type doping is meaningless to practical application, only the ZT of n-type doped BaSnO₃ as a function of carrier concentration at different temperature is shown in Fig. 5. At low temperature (T < 700 K), the ZT is almost independent with the carrier concentration, possessing small values. However, there is a remarkable increase when the temperature elevates beyond 700 K. The ZT as a function of carrier concentration is in similar tendency to that of power factor. The maximal ZT value of 0.65 is obtained with the optimal electron doping concentration of 1.6 × 10¹⁹ cm⁻³ at 1200 K, which is higher than other well-known oxide thermoelectric materials in solid states.⁵³ The improved ZT value is originated from the significantly increased electrical conductivity with n-type doping as well as the high temperature stability. As known, in thermoelectric device application, not only a high ZT peak but the high ZT value over a wide temperature range is required.⁵⁴ The average ZT value of n-type doped BaSnO₃ is calculated to be ∼0.33 and ∼0.52 in the temperature of 300–1200 K and 900–1200 K, respectively. It is deduced that optimizing the ZT value by tuning the carrier concentration at high temperature makes BaSnO₃ to be a promising alternative in the great demanding for n-type thermoelectric materials nowadays. The main factor that degrade the ZT value at low temperature is the large thermal conductivity. Creating strong point-defect scattering by introducing dopants and enhancing phonon–phonon scattering by nanostructuring are effective ways to suppress the thermal conductivity. Furthermore, the quantum confinement effect of electronic carriers in the low-dimension can significantly enhance the thermo power. We predict the ZT value could be further boosted in the nanostructured BaSnO₃.

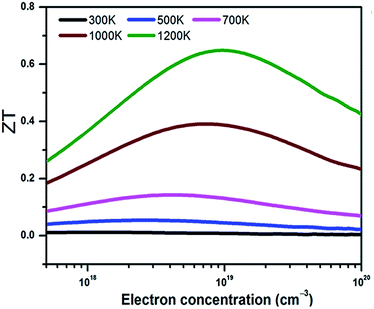Fig. 5 The ZT value of n-type doped BaSnO₃ single crystal as a function of carrier concentration at different temperature.

In practical application of thermoelectric device, the energy conversion efficiency is the direct index to assess the thermoelectric performance. The ideal maximum efficiency (η) characterizes the heat-electricity conversion ability of thermoelectric modules, which can be presented using the equation,⁵⁵

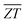where, T_c and T_h represent the temperature of cold side and hot resource of thermoelectric device. η_c = (T_h − T_c)/T_c is the Carnot efficiency. The dimensionless is the average figure of merit between the hot side and cold side thermoelectric materials of the module. To examine the practicability of BaSnO₃ in thermoelectric devices, the modules based on the n-type BaSnO₃ and four popular p-type materials are assembled (see Fig. S1 of ESI†). The high maximum conversion efficiency based on n-type BaSnO₃ and p-type half-Heusler FeNbSb under a high temperature difference of 900 K is achieved, suggesting the great potential of n-type BaSnO₃ for high temperature power generation.

Conclusions

We systematically investigated the geometric, electronic and thermoelectric properties of perovskite-type BaSnO₃ by the first-principle calculations combined with the semi-classical Boltzmann theory. The comparison of thermoelectric properties between n-type and p-type doped BaSnO₃ were performed. The results revel that the n-type doped system displays an ultra-high power factor of 1.5 × 10⁻³ W m⁻¹ K⁻² at 1200 K with optimal carrier concentration of 1.6 × 10¹⁹ cm⁻³. The excellent PF is attributed to the dramatically increased electrical conductivity, originating from the small effective mass of electron and extraordinary high mobility. The enhanced PF and ZT values serve as guides to related experiments in pointing out the importance of doping levels and operation temperature to optimize the thermoelectric performance of BaSnO₃. The lattice thermal conductivity can be suppressed by increasing temperature and introducing dopants. In addition, four types of thermoelectric modules formed by n-type BaSnO₃ and p-type thermoelectric materials were assembled.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21501177). We acknowledge the Supercomputing Center of Shenzhen and CNIC for providing the computer resources.

References

1. B. Poudel, Q. Hao, Y. Ma, Y. C. Lan, A. Minnich, B. Yu, X. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634–638.
2. L. D. Zhao, S. H. Lo, Y. S. Zhang, H. Sun, G. J. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
3. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557.
4. Y. Z. Pei, X. Y. Shi, A. LaLonde, H. Wang, L. D. Chen and G. J. Snyder, Nature, 2011, 473, 66–69.
5. Y. B. Luo, J. Y. Yang, M. Liu, Y. Xiao, L. W. Fu, W. X. Li, D. Zhang, M. Y. Zhang and Y. D. Cheng, J. Mater. Chem. A, 2015, 3, 1251–1257.
6. J. Li, Z. Ma and K. Wu, RSC Adv., 2017, 7, 8460–8466.
7. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
8. K. Koumoto, Y. F. Wang, R. Z. Zhang, A. Kosuga and R. Funahashi, Annu. Rev. Mater. Res., 2010, 40, 363–394.
9. G. K. Ren, J. L. Lan, C. C. Zeng, Y. C. Liu, B. Zhan, S. Butt, Y. H. Lin and C. W. Nan, JOM, 2015, 67, 211–221.
10. M. Lee, L. Viciu, L. Li, Y. Wang, M. L. Foo, S. Watauchi, R. A. Pascal Jr, R. J. Cava and N. P. Ong, Nat. Mater., 2006, 5, 537–540.
11. J. Sugiyama, J. H. Brewer, E. J. Ansaldo, H. Itahara, T. Tani, M. Mikami, Y. Mori, T. Sasaki, S. Hebert and A. Maignan, Phys. Rev. Lett., 2004, 92, 017602.
12. Y. Masuda, D. Nagahama, H. Itahara, T. Tani, W. S. Seo and K. Koumoto, J. Mater. Chem., 2003, 13, 1094–1099.
13. H. Ohta, K. Sugiura and K. Koumoto, Inorg. Chem., 2008, 47, 8429–8436.
14. Y. Liu, J. L. Lan, W. Xu, Y. C. Liu, Y. L. Pei, B. Cheng, D. B. Liu, Y. H. Lin and L. D. Zhao, Chem. Commun., 2013, 49, 8075–8077.
15. L. D. Zhao, J. Q. He, D. Berardan, Y. H. Lin, J. F. Li, C. W. Nan and N. Dragoe, Energy Environ. Sci., 2014, 7, 2900–2924.
16. H. Ohta, S. Kim, Y. Mune, T. Mizoguchi, K. Nomura, S. Ohta, T. Nomura, Y. Nakanishi, Y. Ikuhara, M. Hirano, H. Hosono and K. Koumoto, Nat. Mater., 2007, 6, 129–134.
17. W. S. Choi, H. K. Yoo and H. Ohta, Adv. Funct. Mater., 2015, 25, 799–804.
18. T. Tsubota, M. Ohtaki, K. Eguchi and H. Arai, J. Mater. Chem., 1997, 7, 85–90.
19. A. M. Dehkordi, S. Bhattacharya, T. Darroudi, J. W. Graff, U. Schwingenschloegl, H. N. Alshareef and T. M. Tritt, Chem. Mater., 2014, 26, 2478–2485.
20. H. J. Kim, U. Kim, T. H. Kim, J. Kim, H. M. Kim, B. G. Jeon, W. J. Lee, H. S. Mun, K. T. Hong, J. Yu, K. Char and K. H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165205.
21. H. J. Kim, U. Kim, H. M. Kim, T. H. Kim, H. S. Mun, B. G. Jeon, K. T. Hong, W. J. Lee, C. Ju, K. H. Kim and K. Char, Appl. Phys. Express, 2012, 5, 061102.
22. X. Luo, Y. S. Oh, A. Sirenko, P. Gao, T. Tyson, K. Char and S. W. Cheong, Appl. Phys. Lett., 2012, 100, 172112.
23. H. Mizoguchi, P. Chen, P. Boolchand, V. Ksenofontov, C. Felser, P. W. Barnes and P. M. Woodward, Chem. Mater., 2013, 25, 3858–3866.
24. H. R. Liu, J. H. Yang, H. J. Xiang, X. G. Gong and S. H. Wei, Appl. Phys. Lett., 2013, 102, 112109.
25. D. O. Scanlon, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 161201.
26. H. J. Kim, J. Kim, T. H. Kim, W. J. Lee, B. G. Jeon, J. Y. Park, W. S. Choi, D. W. Jeong, S. H. Lee, J. Yu, T. W. Noh and K. H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125204.
27. B. Ostrick, M. Fleischer, U. Lampe and H. Meixner, Sens. Actuators, B, 1997, 44, 601–606.
28. A. Bouhemadou and K. Haddadi, Solid State Sci., 2010, 12, 630–636.
29. T. Maekawa, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2006, 416, 214–217.
30. S. Ohta, T. Nomura, H. Ohta and K. Koumoto, J. Appl. Phys., 2005, 97, 034106.
31. K. Takahata, Y. Iguchi, D. Tanaka, T. Itoh and I. Terasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 12551.
32. F. Li, J. F. Li, L. D. Zhao, K. Xiang, Y. Liu, B. P. Zhang, Y. H. Lin, C. W. Nan and H. M. Zhu, Energy Environ. Sci., 2012, 5, 7188–7195.
33. M. Scheele, N. Oeschler, K. Meier, A. Kornowski, C. Klinke and H. Weller, Adv. Funct. Mater., 2009, 19, 3476–3483.
34. L. D. Zhao, G. J. Tan, S. Q. Hao, J. Q. He, Y. L. Pei, H. Chi, H. Wang, S. K. Gong, H. B. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144.
35. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
38. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
39. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
40. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
41. E. H. Mountstevens, J. P. Attfield and S. A. Redfern, J. Phys.: Condens. Matter, 2003, 15, 8315–8326.
42. H. Mizoguchi, H. W. Eng and P. M. Woodward, Inorg. Chem., 2004, 43, 1667–1680.
43. H. Mizoguchi, P. M. Woodward, C. H. Park and D. A. Keszler, J. Am. Chem. Soc., 2004, 126, 9796–9800.
44. D. Singh, D. Papaconstantopoulos, J. Julien and F. Cyrot-Lackmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9519–9523.
45. É. Bévillon, A. Chesnaud, Y. Wang, G. Dezanneau and G. Geneste, J. Phys.: Condens. Matter, 2008, 20, 145217.
46. T. N. Stanislavchuk, A. A. Sirenko, A. P. Litvinchuk, X. Luo and S. W. Cheong, J. Appl. Phys., 2012, 112, 044108.
47. G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146.
48. A. N. Gandi and U. Schwingenschloegl, Chem. Mater., 2014, 26, 6628–6637.
49. M. Takada, H. Taguchi, M. Kato and K. Hirota, J. Mater. Sci., 2015, 50, 476–481.
50. I. Terasaki, Y. Sasago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 685–687.
51. L. Bocher, M. Aguirre, D. Logvinovich, A. Shkabko, R. Robert, M. Trottmann and A. Weidenkaff, Inorg. Chem., 2008, 47, 8077–8085.
52. M. Yasukawa, T. Kono, K. Ueda, H. Yanagi, S. W. Kim and H. Hosono, Solid State Commun., 2013, 172, 49–53.
53. E. Guilmeau, P. Diaz-Chao, O. I. Lebedev, A. Recnik, M. C. Schafer, F. Delorme, F. Giovannelli, M. Kosir and S. Bernik, Inorg. Chem., 2017, 56, 480–487.
54. L. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu and V. P. Dravid, Science, 2016, 141–144.
55. D. Kraemer and G. Chen, Rev. Sci. Instrum., 2014, 85, 045107.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05193j

---