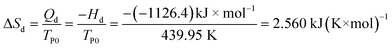DOI:
10.1039/C7RA05295B
(Paper)
RSC Adv., 2017,
7, 30747-30754
Thermal behavior and thermal safety of 6b-nitrohexahydro-2H-1,3,5-trioxacyclopenta[cd]-pentalene-2,4,6-triyltrinitrate
Received
10th May 2017
, Accepted 7th June 2017
First published on 13th June 2017
Abstract
6b-Nitrohexahydro-2H-1,3,5-trioxacyclopenta[cd]-pentalene-2,4,6-triyltrinitrate (NHTPN) is an energetic compound with interesting properties. Its thermal and kinetic behaviors were studied by differential scanning calorimetry (DSC), and its specific heat capacity (Cp) was determined by a continuous Cp mode of microcalorimetry (Micro-DSC III). In order to evaluate its thermal safety, the values (Te0 and Tp0) of Te and Tp corresponding to β → 0, critical temperature of thermal explosion (Tbe and Tbp), adiabatic time-to-explosion (tTIad), 50% drop height (H50) of impact sensitivity, critical temperature of hot-spot initiation (Tcr), thermal sensitivity probability density function [S(T)] vs. temperature (T) relation curves for NHTPN with radius of 1 m surrounded with ambient of 340 K, the peak temperature corresponding to the maximum value of S(T) vs. T relation curve (TS(T)max), safety degree (SD) and critical ambient temperature (Tacr) of thermal explosion of NHTPN were calculated respectively, by means of the onset temperature (Te) and maximum peak temperature (Tp) from the non-isothermal DSC curves of NHTPN at different heating rates (β), the apparent activation energy (EK and EO) and pre-exponential constant (AK) of thermal decomposition reaction obtained by Kissinger's method and Ozawa's method, Cp, density (ρ) and thermal conductivity (λ), the decomposition heat (Qd, taking half-explosion heat), Zhang–Hu–Xie–Li's formula, Smith's equation, Friedman's formula, Bruckman–Guillet's formula, Frank-Kamenetskii formula and Wang–Du's formulas.
1 Introduction
Nitric acid esters have long been recognized as one class of useful and promising functional group in the design and synthesis of energetic plasticizer, such as 1,2,3-propanetriol trinitrate (nitroglycerin), nitrocellulose, and pentaerythritol tetranitrate (PETN), which are used in propellants, explosives, and pyrotechnics.1–5 6b-Nitrohexahydro-2H-1,3,5-trioxacyclo-penta [cd]-pentalene-2,4,6-triyltrinitrate (NHTPN) is a new explosive with interesting properties. Its density is higher than 1.8 g cm−3 because of its symmetrical molecular structure. The detonation velocity of NHTPN is up to 8.0 km s−1 at maximal working density. It melts at ca. 115 °C and begins to decompose at ca. 150 °C with a linear heating rate of 10 K min−1. The apparent activation energy (Ea) of NHTPN is ca. 155 kJ mol−1, which is close to that of conventional explosives. Its oxygen balance and oxygen quotient are −12.97% and 82.35%, respectively. Moreover, NHTPN is an explosive sensitive to mechanical stimuli (2 J, 50 N).6
In this paper, using the original data of differential scanning calorimetry (DSC) and microcalorimetry, the self-accelerating decomposition temperature (TSADT), the critical temperature of thermal explosion (Tb) and the adiabatic time-to-explosion (tTIad)were estimated. The 50% drop height of impact sensitivity (H50), the critical temperature of hot-spot initiation caused by impact (Tcr), the safety degree (SD), the critical thermal explosion ambient temperature (Tacr) and thermal explosion probability (PTE) were obtained. Thus the thermal safety of NHTPN was evaluated which is useful for the evaluation on the process of the explosion from the thermal decomposition.
2 Experimental
2.1 Materials
The title compound (NHTPN) (structure see Fig. 1) used in this work was prepared and purified according to the literature method.6 The sample was kept in a vacuum desiccators before use. The structure of NHTPN was characterized by 1H and 13C NMR spectroscopy. 1H NMR (CD3OD, 500 MHz): δ = 5.72 ppm (s, 3H, H2a, H4a, H6a); 6.70 ppm (s, 3H, H2, H4 and H6). 13C NMR (CD3OD, 125 MHz): δ = 91.9 ppm (C2a, C4a, C6a); 105.7 ppm (C6b); 107.6 ppm (C2, C4, C6).
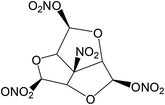 |
| | Fig. 1 Structure of NHTPN. | |
2.2 Thermal decomposition conditions
The DSC experiments for the title compound were performed using a Model TA 910S differential scanning calorimeter. The heating rates used were 2, 5, 10, 15 and 20 °C min−1 from ambient temperature to 500 °C under a nitrogen atmosphere at a flow rate of 60 mL min−1. DSC curves obtained under the same conditions overlapped with each other, indicating that the reproducibility of the tests was satisfactory.
2.3 Determination of the specific heat capacity
The specific heat capacity of the title compound was determined by a continuous Cp mode within 283–353 K at a heating rate of 0.15 K min−1 on a Micro-DSC III apparatus (Seteram, France) with the sample mass of 450 mg. The Micro-calorimeter was calibrated with α-Al2O3 (calcined), its math expression was Cp/J−1 g−1 K−1 = 0.1839 + 1.9966 × 10−3T within 283 K–353 K and the standard molar heat capacity CΘp,m (α − Al2O3) at 298.15 K was determined as 79.44 J mol−1 K−1 which is in an excellent agreement with the value of 79.02 J mol−1 K−1 reported in the literature.7
3 Results and discussion
3.1 Standard enthalpy of combustion
The standard enthalpy of combustion of NHTPN, ΔcHθm (NHTPN, s, 298.15 K), is referred to the combustion enthalpy change of the following ideal combustion reaction at 298.15 K and 100 kPa.| |
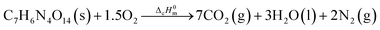 | (1) |
The standard enthalpy of combustion of NHTPN ΔcHθm is calculated by the following equations:
| | |
ΔcHθm (NHTPN, s, 298.15 K) = ΔcU (NHTPN, s, 298.15 K) + ΔnRT
| (2) |
| | |
Δn = ng (products) − ng (reactants)
| (3) |
where Δ
cU = −(
Qc) = −(2992.61 ± 111.04) kJ mol
−1,
6 ng is the total amount in mole of gases present as products or as reactants, Δ
n = 7 + 2 − 1.5 = 7.5,
R = 8.314 J K
−1 mol
−1,
T = 298.15 K. The result is – (2974.02 ± 111.04) kJ mol
−1.
3.2 Standard enthalpy of formation
The standard enthalpy of formation of NHTPN, ΔfHθm (NHTPN, s, and 298.15 K), is calculated by Hess's law according to thermochemical eqn (4).| | |
ΔfHθm (NHTPN, s, 298.15 K) = 7ΔfHθm (CO2, g, 298.15 K) + 3ΔfHθm (H2O, l, 298.15 K) − ΔcHθm (NHTPN, s, 298.15 K)
| (4) |
when ΔfHθm (CO2, g, 298.15 K) = (−393.51 ± 0.13) kJ mol−1, ΔfHθm (H2O, l, 298.15 K) = (−285.83 ± 0.042) kJ mol−1, the result obtained is – (638.04 ± 111.04) kJ mol−1.
3.3 Explosion properties
By substituting the values of a, b, c and d in CaHbNcOd = C7H6N4O14, ρ = 1.884 g cm−3, ΔfHθm = −638.04 kJ mol−1 into Kamlet–Jacobs eqn (5)–(9),8 the values of D of 8.720 km s−1, P of 34.65 GPa, N of 0.0284 mol g−1, Mg of 33.53 g mol−1, Q of 6086.2 J g−1 are obtained, showing that NHTPN has explosion performance level approaching that of PETN (ρ = 1.780 g cm−3,9 ΔfHθm = −538.48 kJ mol−1. C5H8N4O12 → 2N2 + 4H2O + 4CO2 + C, D = 8.461 km s−1, P = 32.06 GPa from eqn (5) and (6), D = 8.708 km s−1, P = 33.25 GPa from eqn (11) and (12)).| | |
D = 1.01(NM1/2Q1/2)1/2(1 + 1.30ρ)
| (5) |
| |
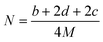 | (7) |
| |
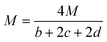 | (8) |
| |
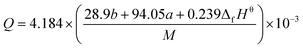 | (9) |
where D is detonation velocity (km s−1), P detonation pressure (GPa), N moles of gases detonation products per gram of explosive, M average molecular weight of gaseous products, Q chemical energy of detonation (J g−1), ρ density of explosives (g cm−3), and ΔfHθ standard enthalpy of formation.
By substituting the values of xN2 = 2, xH2O = 3, xCO2 = 5, xCO = 1, xH2 = 0, xO2 = 0, xC = 1, M = 370.143 g mol−1 from reaction formula (10) and ρ = 1.884 g cm−3 into empirical nitrogen equivalent eqn (11) and (12) (ref. 9) for predicting the D and P of C–H–N–O explosives, the values of D of 8.859 km s−1, P of 35.45 GPa are obtained.
| | |
C7H6N4O14(s) → 5CO2 + 3H2O + 2N2 + CO + C
| (10) |
| |
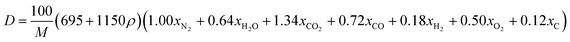 | (11) |
where 695 and 1150 are constants; 1.00, 0.64, 1.34, 0.72, 0.18, 0.50, 0.12 are the nitrogen equivalent coefficient of gaseous detonation products N
2, H
2O, CO
2, CO, H
2, O
2, C of explosive.
And
| |
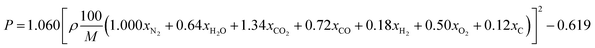 | (12) |
where 1.060 and 0.619 are constants.
3.4 The thermal behavior of NHTPN
A typical DSC curves at a heating rate of 10 °C min−1 for NHTPN is shown in Fig. 2. DSC curve consists of one endothermic peak and one exothermic peak. The endothermic peak at 114.55 °C is the phase change from solid to liquid. The exothermic peak is the decomposition reaction of NHTPN, and the peak temperature is 185.50 °C and the onset temperature is 165.12 °C.
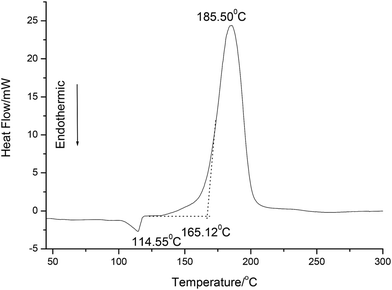 |
| | Fig. 2 DSC curve for NHTPN at a heating rate of 10 °C min−1. | |
3.5 Heat-temperature quotient for the exothermic decomposition process of NHTPN
The exothermic peak in Fig. 2 is caused by the decomposition reaction. Heat-temperature quotient of the process equals to
where the heat of decomposition reaction Qd is defined as Qd = 0.5 Q, i.e. Qd, taking half-chemical energy (heat) of detonation. For NHTPN, Qd = 0.5Q = 3043.1 J g−1. TP0 is the peak temperature Tp corresponding to β → 0.
3.6 Analysis of kinetic data for the exothermic main decomposition reaction of NHTPN
To obtain the kinetic parameters (the apparent activation energy (Ea) and pre-exponential constant (A)) of the exothermic main decomposition reaction for the title compound, two isoconversional methods [eqn (13) and (14)] are employed.
Differential methods. Kissinger equation10| |
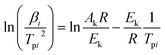 | (13) |
Integral methods. Ozawa equation11| |
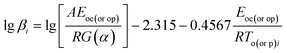 | (14) |
where α is the conversion degree, T the absolute temperature, E the apparent activation energy, β the heating rate, R the gas constant, Tp the peak temperature of DSC curve, A the pre-exponential factor.From the original data in Table 1, EK obtained by Kissinger's method10 is determined to be 199.48 kJ mol−1. The pre-exponential constant (A) is 1020.95 s−1. The linear correlation coefficient (rk) is 0.9965. The value of Eo obtained by Ozawa's method11 is 196.90 kJ mol−1. The value of r0 is 0.9968. The value of Eeo obtained by Tei vs. βi relation is 197.02 kJ mol−1. The value of reo is 0.9816.
Table 1 Maximum peak temperature (Tp) and onset temperature (Te) of the exothermic decomposition reaction for NHTPN determined by the DSC curves at various heating rates (β)
| β/(K min−1) |
2 |
5 |
10 |
15 |
20 |
| Tp/K |
446.31 |
454.40 |
458.65 |
462.79 |
466.05 |
| Te/K |
426.44 |
429.93 |
438.27 |
439.94 |
442.47 |
By substituting the experimental data, βi, Ti and αi, i = 1,2,…n, listed in Table 2 from DSC curves in Fig. 2 into eqn (15) which is known as Arrhenius-type's integral isoconversional non-linear method (NL-INT method) of solving Eα, the values of Eα satisfying the minimum value of eqn (15) for any given value of α are obtained and shown in Table 2 and Fig. 3. The average value of Eα in the α range of 0.20 to 0.80 in Fig. 2 is in good agreement with the calculated values obtained by Kissinger's method and Ozawa's method. The E values calculated using eqn (15) are used to check the validity of activation energy by the other methods.
| |
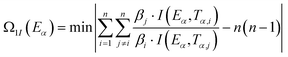 | (15) |
where,
I(
Eα,
Tα) integral is obtained taking Senum–Yang approximation calculation for approximation of 3
rd degree:
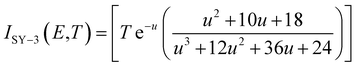
, where,
u =
E/
RT.
Table 2 Data of NHTPN determined by DSC at different heating rates and apparent activation energies (Ea) of thermal decomposition obtained by NL-INT method
| α (%) |
Ti/°C |
Eα/kJ mol−1 |
min |
| 2 °C min−1 |
5 °C min−1 |
10 °C min−1 |
15 °C min−1 |
20 °C min−1 |
| 0.000 |
398.95 |
401.15 |
404.48 |
406.15 |
414.82 |
178.20 |
|
| 0.025 |
421.54 |
426.23 |
428.8 |
429.09 |
433.23 |
310.53 |
0.9906 |
| 0.050 |
426.32 |
432.36 |
436.04 |
437.13 |
441.08 |
249.62 |
0.3722 |
| 0.075 |
429.08 |
435.57 |
439.9 |
441.45 |
445.28 |
228.32 |
0.2098 |
| 0.100 |
431.04 |
437.74 |
442.43 |
444.3 |
447.96 |
219.08 |
0.1330 |
| 0.125 |
432.6 |
439.38 |
444.3 |
446.4 |
449.95 |
214.16 |
0.09445 |
| 0.150 |
433.9 |
440.72 |
445.81 |
448.08 |
451.53 |
211.18 |
0.07032 |
| 0.175 |
435.03 |
441.86 |
447.09 |
449.48 |
452.88 |
209.05 |
0.05740 |
| 0.200 |
436.04 |
442.87 |
448.21 |
450.71 |
454.06 |
207.51 |
0.04780 |
| 0.225 |
436.95 |
443.78 |
449.22 |
451.79 |
455.13 |
206.19 |
0.04368 |
| 0.250 |
437.78 |
444.62 |
450.14 |
452.77 |
456.1 |
205.11 |
0.04057 |
| 0.275 |
438.56 |
445.4 |
450.98 |
453.67 |
456.99 |
204.37 |
0.03831 |
| 0.300 |
439.29 |
446.13 |
451.77 |
454.51 |
457.83 |
203.64 |
0.03720 |
| 0.325 |
439.98 |
446.83 |
452.51 |
455.31 |
458.63 |
202.93 |
0.03616 |
| 0.350 |
440.64 |
447.5 |
453.22 |
456.07 |
459.39 |
202.32 |
0.03540 |
| 0.375 |
441.28 |
448.15 |
453.89 |
456.79 |
460.11 |
201.96 |
0.03488 |
| 0.400 |
441.9 |
448.78 |
454.55 |
457.49 |
460.82 |
201.50 |
0.03512 |
| 0.425 |
442.49 |
449.39 |
455.18 |
458.17 |
461.5 |
201.01 |
0.03453 |
| 0.450 |
443.08 |
449.99 |
455.81 |
458.84 |
462.16 |
200.67 |
0.03365 |
| 0.475 |
443.66 |
450.58 |
456.43 |
459.48 |
462.81 |
200.41 |
0.03401 |
| 0.500 |
444.22 |
451.16 |
457.04 |
460.12 |
463.46 |
199.93 |
0.03412 |
| 0.525 |
444.78 |
451.73 |
457.65 |
460.75 |
464.1 |
199.53 |
0.03452 |
| 0.550 |
445.34 |
452.31 |
458.25 |
461.38 |
464.73 |
199.25 |
0.03406 |
| 0.575 |
445.9 |
452.88 |
458.86 |
462 |
465.36 |
198.97 |
0.03441 |
| 0.600 |
446.46 |
453.45 |
459.46 |
462.63 |
465.99 |
198.66 |
0.03436 |
| 0.625 |
447.02 |
454.03 |
460.08 |
463.26 |
466.63 |
198.30 |
0.03439 |
| 0.650 |
447.59 |
454.61 |
460.7 |
463.89 |
467.28 |
197.96 |
0.03542 |
| 0.675 |
448.16 |
455.19 |
461.33 |
464.54 |
467.94 |
197.46 |
0.03599 |
| 0.700 |
448.75 |
455.79 |
461.97 |
465.2 |
468.61 |
197.11 |
0.03658 |
| 0.725 |
449.35 |
456.41 |
462.64 |
465.89 |
469.31 |
196.56 |
0.03683 |
| 0.750 |
449.96 |
457.04 |
463.33 |
466.61 |
470.03 |
195.87 |
0.03670 |
| 0.775 |
450.6 |
457.69 |
464.05 |
467.37 |
470.8 |
195.00 |
0.03786 |
| 0.800 |
451.28 |
458.37 |
464.81 |
468.18 |
471.62 |
194.03 |
0.03985 |
| 0.825 |
451.99 |
459.08 |
465.64 |
469.07 |
472.51 |
192.60 |
0.04211 |
| 0.850 |
452.76 |
459.85 |
466.55 |
470.09 |
473.53 |
190.51 |
0.04616 |
| 0.875 |
453.6 |
460.69 |
467.6 |
471.28 |
474.72 |
187.45 |
0.05297 |
| 0.900 |
454.55 |
461.63 |
468.87 |
472.8 |
476.22 |
182.45 |
0.06698 |
| 0.925 |
455.69 |
462.75 |
470.59 |
475.07 |
478.4 |
173.03 |
0.10284 |
| 0.950 |
457.2 |
464.2 |
473.63 |
480.02 |
482.83 |
149.07 |
0.26368 |
| 0.975 |
459.71 |
466.53 |
483.54 |
494.25 |
495.87 |
97.70 |
0.80034 |
| 1.000 |
483.75 |
486.65 |
520.82 |
527.15 |
541.48 |
65.97 |
1.79787 |
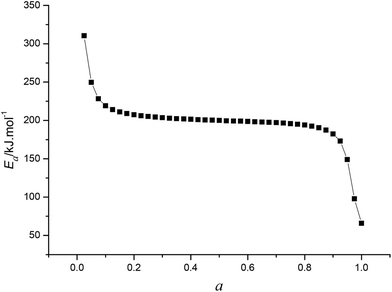 |
| | Fig. 3 The Eα ∼ α curve obtained by Qzawa's method. | |
The data (β, Ti, αi, i = 1, 2,…) in the range of α = 0.20–0.80 and 41 kinetic model functions12 were input to eqn (16) to obtain the values of E and A from a single non-isothermal DSC curve.
| |
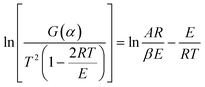 | (16) |
where
G(
α) is the integral model function,
T the temperature (K) at time
t,
α the conversion degree,
R the gas constant.
The kinetic parameters obtained by the logical choice method13 were presented in Table 3. Their values of E are very close to each other. The values of Ea and A obtained from a single non-isothermal DSC curves are in good agreement with the calculated values obtained by Kissinger's method and Ozawa's method. Therefore, we conclude that the reaction mechanism of exothermic main decomposition process of the compound is classified as G(α) = −ln(1 − α), f(α) = 1 − α. Substituting f(α) with 1 − α, E with 199.12 kJ mol−1 and A with 1018.89 s−1 in eqn (17):
| |
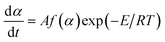 | (17) |
the kinetic equation of exothermic decomposition reaction for NHTPN may be described as
| | |
dα/dt = 1018.89(1 − α)e−2.3950×104/T
| (18) |
Table 3 Kinetic parameters obtained for thermal decomposition process of the NHTPNa
| Method |
β/(K min−1) |
E/(kJ mol−1) |
lg(A0/s−1) |
rlcc |
Qv |
| Note: rlcc is the linear correlation coefficient; Qv is the variance. |
| Ordinary-integral |
2 |
205.00 |
21.57 |
0.9993 |
0.0185 |
| 5 |
207.77 |
21.91 |
0.9991 |
0.0215 |
| 10 |
198.92 |
20.86 |
0.9990 |
0.0242 |
| 15 |
190.92 |
19.95 |
0.9993 |
0.0168 |
| 20 |
192.99 |
20.15 |
0.9991 |
0.0215 |
| Mean |
|
199.12 |
18.89 |
|
|
| Kissinger |
|
199.48 |
20.95 |
0.9965 |
|
| Flynn-Wall Ozawa |
|
196.90 |
|
0.9968 |
|
3.7 Self-accelerating decomposition temperature TSADT
Setting Te as the onset temperature and Tp as the peak temperature, and defining Te0 or p0 as the value of T(e0 or p0)i corresponding to β → 0 and Te0 as the self-accelerating decomposition temperature TSADT, we have| | |
Te or p = Te0 or p0 + bβi + cβi2 + dβi3, i = 1,2,…L
| (19) |
and
Submitting the original data: βi, Tei, Tpi, i = 1,2,…5 in Table 1 into eqn (19), the values of Te0 of 422.06 K and Tp0 of 439.95 K are obtained. The value of TSADT of 422.06 K is obtained by eqn (20).
3.8 The critical temperature of thermal explosion (Tb)
The critical temperature of thermal explosion (Tb) is an important parameter of evaluating the safety and elucidating transition tendency from thermal decomposition to thermal explosion for small-scale energetic materials (EMs).
For NHTPN, the values of Tb obtained by Zhang–Hu–Xie–Li equation [eqn (21)] taken from14 using the values of Te0 (=422.06 K) and Tp0 (=439.95 K) and the value of Eoe (=197.02 kJ mol−1) and Eop (=196.90 kJ mol−1) are 429.86 and 448.44 K, respectively:
| |
 | (21) |
The values of Tb obtained by eqn (23) (ref. 15) based on Berthelot's equation using the values of be0 (=0.1338) and bp0 (=0.1213) obtained by eqn (22) and Te0 (=422.06 K), and Tp0 (=439.95 K) obtained by eqn (19) via data in Table 1 are 429.53 and 448.19 K, respectively.
| |
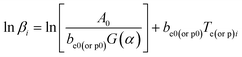 | (22) |
| |
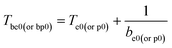 | (23) |
In comparison with PETN with Tbp = 459.29 K, lower value of Tb shows that the transition from thermal decomposition to thermal explosion is easy to take place.
3.9 Thermodynamic parameters of activation reaction
The entropy of activation (ΔS≠), enthalpy of activation (ΔH≠), and Gibbs free energy of activation (ΔG≠) corresponding to T = Tp0 = 439.95 K, E = Ek = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = Ak = 1020.95 s−1 obtained by eqn (24)–(26) are 144.60 J mol−1 K−1, 195.82 kJ mol−1 and 132.20 kJ mol−1, respectively. The positive value of ΔG≠ indicates that the exothermic decomposition reaction for NHTPN must proceed under the heating condition.
480 J mol−1, A = Ak = 1020.95 s−1 obtained by eqn (24)–(26) are 144.60 J mol−1 K−1, 195.82 kJ mol−1 and 132.20 kJ mol−1, respectively. The positive value of ΔG≠ indicates that the exothermic decomposition reaction for NHTPN must proceed under the heating condition.| |
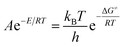 | (24) |
where kB is the Boltzmann constant (1.3807 × 10−23 J K−1) and h is the Planck constant (6.626 × 10−34 J s).
3.10 The specific heat capacity of NHTPN
Fig. 4 shows the determination results of NHTPN using a continuous specific heat capacity mode of the Micro-DSC III apparatus. We can see that specific heat capacity of NHTPN presents a good linear equation relationship with temperature in the determining temperature range. Specific heat capacity equation is shown as:| | |
Cp(NHTPN J g−1 K−1) = −6.918054 × 10−2 + 3.676170 × 10−3T(283.1 K < T < 323.2 K)
| (27) |
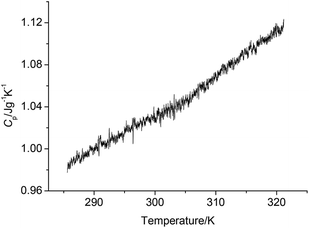 |
| | Fig. 4 Determination results of the continuous specific heat capacity Cp of NHTPN. | |
The specific heat capacity of NHTPN is 1.027 J g−1 K−1 at 298.15 K. The standard molar heat capacity of NHTPN is 380.14 J mol−1 K−1 at 298.15 K.
3.11 Thermodynamic functions of NHTPN
The enthalpy change, the entropy change and the Gibbs free energy change for NHTPN are calculated by eqn (28) to (30) within 283 K and 353 K, taking 298.15 K as the benchmark. The results are listed in Table 4.| |
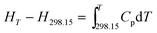 | (28) |
| |
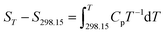 | (29) |
| |
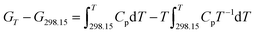 | (30) |
where Cp as eqn (27) expressed.
Table 4 The enthalpy change, the entropy change and the Gibbs free energy change for NHTPN within 283 K and 353 K, taking 298.15 K
| T/K |
HT – H298.15 K/(J g−1) |
ST – S298.15 K/(J K−1 g−1) |
GT – G298.15 K/(J g−1) |
| 283.15 |
−14.99 |
−0.052 |
10.14 |
| 288.15 |
−10.09 |
−0.034 |
6.85 |
| 293.15 |
−5.09 |
−0.017 |
3.47 |
| 298.15 |
|
|
|
| 303.15 |
5.189 |
0.017 |
−3.55 |
| 308.15 |
10.459 |
0.034 |
−7.19 |
| 313.15 |
15.82 |
0.052 |
−10.92 |
| 318.15 |
21.27 |
0.069 |
−14.73 |
| 323.15 |
26.82 |
0.086 |
−18.63 |
| 328.15 |
32.46 |
0.104 |
−22.61 |
| 333.15 |
38.19 |
0.121 |
−26.68 |
| 338.15 |
44.02 |
0.138 |
−30.84 |
| 343.15 |
49.93124 |
0.156 |
−35.08 |
| 348.15 |
55.93868 |
0.173 |
−39.41 |
| 353.15 |
62.03802 |
0.190 |
−43.83 |
3.12 The determination of the adiabatic time-to-explosion
The adiabatic time-to-explosion (tTIad, s) of energetic materials is the time of energetic material thermal decomposition transiting to explosion under the adiabatic conditions, and is an important parameter for assessing the thermal stability and the safety of energetic materials. The estimation formulae of calculating the adiabatic time-to explosion (t) of energetic materials used are Smith's eqn (31)–(33) taken from ref. 16.| |
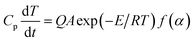 | (31) |
| |
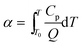 | (32) |
| |
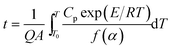 | (33) |
where Cp is the specific heat capacity (J g−1 K−1); f(α) is the differential mechanism function; E is the apparent activation energy; A is the pre-exponential constant; Q is the heat of decomposition; R is the gas constant (8.314 J mol−1 K−1) and α is the conversion degree.
By substituting the original data of Cp = 1.027 J g−1 K−1. f(α) = 1 − α, E = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = 1020.95 s−1, Qd = 3043.1 J g−1, R = 8.314 J mol−1 K−1, the integral upper limit T = Tb = 448.44 K and the lower limit T0 = Te0 = 422.06 K into eqn (33), the value of t of 13.80 s is obtained.
480 J mol−1, A = 1020.95 s−1, Qd = 3043.1 J g−1, R = 8.314 J mol−1 K−1, the integral upper limit T = Tb = 448.44 K and the lower limit T0 = Te0 = 422.06 K into eqn (33), the value of t of 13.80 s is obtained.
3.13 The critical temperature of hot-spot initiation (Tcr)
The inner of EMs can create a local hot-spot when the EMs accepted energy and the EMs will explore from thermal decomposition when the hot-spot temperature reaches to the explosive temperature. The critical temperature of hot-spot initiation (Tcr) is an important parameter for evaluating the thermal safety of EMs.
By submitting the density ρ = 1.884 g cm−3 of NHTPN, specific heat capacity Cp = 1.027 J g−1 K−1. Thermal conductivity λ = 22.50 × 10−4 J cm−1 s−1 K−1, heat of decomposition Qd = 3043.1 J g−1, kinetic parameters E = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1 and A = 1020.95 s−1, Troom = 293.15 K, R = 8.314 J mol−1 K−1, hot-spot critical radius a = 10−3 cm and time interval t − t0 = 10−4 s (ref. 15) to Bruckman–Guillet's first-order estimation equation [eqn (34)],17,18 the value of Tcr,hot spot of 314.18 °C is obtained.
480 J mol−1 and A = 1020.95 s−1, Troom = 293.15 K, R = 8.314 J mol−1 K−1, hot-spot critical radius a = 10−3 cm and time interval t − t0 = 10−4 s (ref. 15) to Bruckman–Guillet's first-order estimation equation [eqn (34)],17,18 the value of Tcr,hot spot of 314.18 °C is obtained.
| |
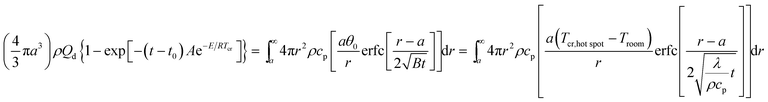 | (34) |
3.14 50% drop height (H50) of impact sensitivity
The impact sensitivity is an important parameter for evaluating the security and reliability of EMs and can be characterized by 50% drop height (H50). Using data of λ = 22.50 × 10−4 J cm−1 s−1 K−1, ρ = 1.884 g cm−3, Qd = 3043.1 J g−1, E = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, and A = 1020.95 s−1, the H50 of NHTPN was estimated as 13.13 cm by Friedman's formula (eqn (35)).19,20 This value shows that it has impact sensitivity level approaching those of PETN (16 cm) and tetryl (17 cm)
480 J mol−1, and A = 1020.95 s−1, the H50 of NHTPN was estimated as 13.13 cm by Friedman's formula (eqn (35)).19,20 This value shows that it has impact sensitivity level approaching those of PETN (16 cm) and tetryl (17 cm)| |
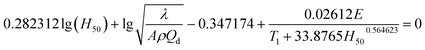 | (35) |
3.15 Critical thermal explosion ambient temperature Tacr, thermal sensitivity probability density function S(T), safety degree SD and thermal explosion probability PTE
To explore the heat-resistance ability of NHTPN, the values of Tacr, S(T) vs. T relation, SD and PTE are calculated by Frank-Kamenetskii formula (36) (ref. 21) and Wang–Du's formulas (36)–(42).22,23 In formulas (36)–(40), Tacr is the critical thermal explosion ambient temperature in K; E is the activation energy in J mol−1; A is the pre-exponential constant in s−1; R is the gas constant in 8.314 J K−1 mol−1; λ is the thermal conductivity in W m−1 K−1; δ is the Frank-Kamenetskii parameter (FK); δcr is the criticality of thermal explosion of exothermic system; r is the characteristic measurement of reactant in m; Qd is the decomposition heat in J kg−1; ρ is the density in kg m−3; μT is the average value of temperature, K; σδ is the standard deviation of FK parameter; σT is the standard deviation of ambient temperature; T is the surrounding temperature; S(T) is the thermal sensitivity probability density function; SD is the safety degree; PTE is the thermal explosion probability.
By substituting the values of r = 1 m, Qd = 3043.1 × 103 J kg−1, E = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = 1020.95 s−1, ρ = 1.884 × 103 kg m−3, λ = 0.2250 W m−1 K−1, ambient temperature Ta = 340 K, σδ = 10 K into eqn (36)–(42), the S(T) vs. T relation curves for infinite plate, infinite cylindrical and spheroidic NHTPN in Fig. 5 and determination results of the thermal sensitivity of the NHTPN in Table 5 are obtained, showing that the accelerating tendency from adiabatic decomposition to explosion of large scale NHTPN and the thermal safety of NHTPN with different shape decreases in the order of sphere > infinite cylinder > infinite plate.
480 J mol−1, A = 1020.95 s−1, ρ = 1.884 × 103 kg m−3, λ = 0.2250 W m−1 K−1, ambient temperature Ta = 340 K, σδ = 10 K into eqn (36)–(42), the S(T) vs. T relation curves for infinite plate, infinite cylindrical and spheroidic NHTPN in Fig. 5 and determination results of the thermal sensitivity of the NHTPN in Table 5 are obtained, showing that the accelerating tendency from adiabatic decomposition to explosion of large scale NHTPN and the thermal safety of NHTPN with different shape decreases in the order of sphere > infinite cylinder > infinite plate.
| |
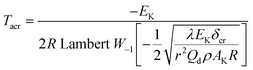 | (36) |
| |
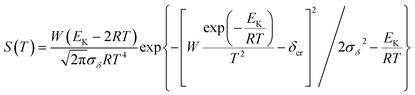 | (37) |
where
| |
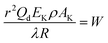 | (38) |
| |
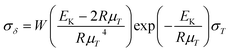 | (39) |
| |
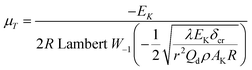 | (40) |
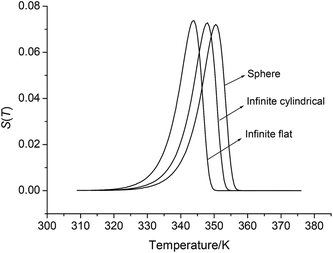 |
| | Fig. 5 S(T) vs. T relation curves for spheroidic, infinite cylindrical and infinite platelike NHTP. | |
Table 5 Determination results of the thermal sensitivity of the NHTPNa
| Shape types of reactant |
W/K2 |
Tarc/K |
σT/K |
TS(T)max/K |
S(T)TP |
SD/% |
PTE/% |
| 1 is the sphere; 2 is the infinite cylindrical; 3 is the infinite flat. |
| 1 |
5.45 × 1035 |
345.76 |
6.47 |
350.49 |
0.07214 |
52.53 |
47.46 |
| 2 |
5.45 × 1035 |
343.17 |
3.96 |
347.89 |
0.07280 |
47.10 |
52.90 |
| 3 |
5.45 × 1035 |
339.06 |
1.78 |
343.76 |
0.07388 |
37.27 |
62.73 |
SD is obtained by eqn (41)
| |
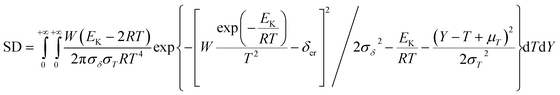 | (41) |
The thermal explosion probability (PTE) is expressed as eqn (42)
4 Conclusions
(1) Using Tbp as criterions, the heat-resistance abilities and the transition resistance from thermal decomposition to thermal explosion of NHTPN and PETN decrease in the order of PETN > NHTPN.
(2) The value of Gibbs free energy of activation (ΔG≠) of 132.20 kJ mol−1 of NHTPN corresponding to T = Tp0 = 439.95 K, E = Ek = 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = Ak = 1020.95 s−1 is close to the one of ΔG≠ of 134.11 kJ mol−1 of PETN corresponding to T = Tp0 = 443.93 K, E = Ek = 112
480 J mol−1, A = Ak = 1020.95 s−1 is close to the one of ΔG≠ of 134.11 kJ mol−1 of PETN corresponding to T = Tp0 = 443.93 K, E = Ek = 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 J mol−1, A = Ak = 1010.40 s−1.
300 J mol−1, A = Ak = 1010.40 s−1.
(3) NHTPN is sensitive to impact and shock, and has impact sensitivity level approaching those of PETN and tetryl.
(4) The thermal safety of large scale NHTPN with different shape decreases in the order of sphere > infinite cylinder > infinite plate.
(5) NHTPN has explosion performance level approaching that of PETN and can be used as a main ingredient of composite explosive.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (21673182), the Backbone Teacher of Chinese University Sustentation Fund of the Ministry of Education P. R. China, the Education Committee Foundation of Shaanxi Province (6JK172) and the Provincial Natural Foundation of Shaanxi (2005B15).
References
- Y. J. Luo and J. R. Liu, Chin. J. Energ. Mater., 2007, 15(4), 407–410 CAS.
- J. R. Liu, Y. J. Luo and Y. Yang, Chin. J. Energ. Mater., 2008, 16(1), 94–99 CAS.
- Y. P. Ji, P. R. Li, W. Wang, Y. Lan and F. Ding, Chin. J. Explos. Propellants, 2005, 28(4), 47–51 CAS.
- F. Q. Bi, B. Z. Wang, X. Z. Fan, C. Xu, Z. X. Ge, Q. Liu and G. F. Zhang, Chin. J. Struct. Chem., 2012, 3, 415–419 Search PubMed.
- D. E. Chavez, M. A. Hiskey and D. L. Naud, Angew. Chem., Int. Ed., 2008, 47, 8307–8314 CrossRef CAS PubMed.
- S. Cudziło, M. Nita, A. Chołuj, M. Szala and W. Danikiewicz, Propellants, Explos., Pyrotech., 2012, 37, 261–266 CrossRef.
- D. A. Ditmars, S. Ishihara and S. S. Chang, J. Res. Natl. Bur. Stand., 1982, 87, 159–163 CrossRef CAS.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1966, 48(1), 23–25 CrossRef.
- R. Z. Hu, E. G. Yao, H. X. Ma, H. Zhang, H. X. Gao, L. Han, F. Q. Zhao, Y. Luo and H. A. Zhao, Chin. J. Energ. Mater., 2015, 23(12), 1243–1244 Search PubMed , in Chinese.
- H. E. Kissinger, Anal. Chem., 1957, 29(11), 1702–1706 CrossRef CAS.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38(11), 1881–1886 CrossRef CAS.
- R. Z. Hu, S. L. Gao, F. Q. Zhao, Q. Z. Shi, T. L. Zhang and J. J. Zhang, Thermal analysis kinetics, Science Press, Beijing, 2008, pp. 151–155 Search PubMed.
- R. Z. Hu, Z. Q. Yang and Y. J. Liang, Thermochim. Acta, 1988, 123, 135–151 CrossRef.
- T. L. Zhang, R. Z. Hu, Y. Xie and F. P. Li, Thermochim. Acta, 1994, 244(2), 171–176 CAS.
- R. Z. Hu, F. Q. Zhao, H. X. Gao and J. R. Song, Fundamentals and Application of Calorimetry, Science Press, Beijing, 2010, pp. 342–405 Search PubMed.
- L. C. Smith, Thermochim. Acta, 1975, 13(1), 1–6 CrossRef CAS.
- M. H. Friedman, Trans. Faraday Soc., 1963, 59, 1865–1873 RSC.
- H. J. Bruckman and J. E. Guillet, Can. J. Chem., 1968, 41, 3221–3228 CrossRef.
- M. H. Friedman, A Correlation of Impact Sensitivities by Means of the Hot Model, 9th (international) Symposium on Combustion, Academic Press Inc., New York, 1963, p. 294–302 Search PubMed.
- R. Z. Hu, F. Q. Zhao, H. X. Gao, H. Zhang, H. A. Zhao, X. J. Wang, X. L. Zhang, Y. Feng and H. X. Ma, Chin. J. Energ. Mater., 2009, 17(3), 252–254 Search PubMed , in Chinese.
- D. A. Frank-Kamenetskii, J. Phys. Chem., 1939, 13(6), 738–755 CAS.
- P. Wang, Study on Thermal Safety and Ignition Reliability of Exothermic System [D], Beijing Institute of Technology, Beijing, China, 2008 Search PubMed.
- P. Wang and Z. M. Du, Energy Mater., 2007, 15(6), 633–636 CAS.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Rui Liua,
Tie-Zheng Jia,
Jing-Chen Renb,
Qi Guob,
Bo-Zhou Wangc and
Rong-Zu Huc
*a,
Rui Liua,
Tie-Zheng Jia,
Jing-Chen Renb,
Qi Guob,
Bo-Zhou Wangc and
Rong-Zu Huc
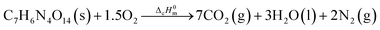
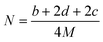
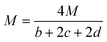
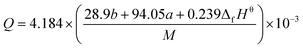
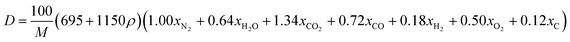
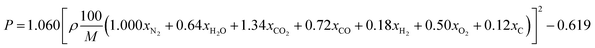
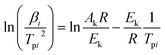
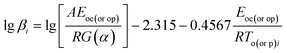
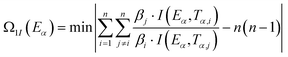
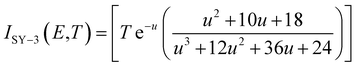 , where, u = E/RT.
, where, u = E/RT.
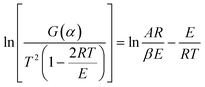
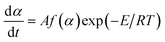

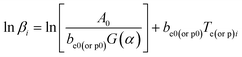
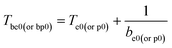
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = Ak = 1020.95 s−1 obtained by eqn (24)–(26) are 144.60 J mol−1 K−1, 195.82 kJ mol−1 and 132.20 kJ mol−1, respectively. The positive value of ΔG≠ indicates that the exothermic decomposition reaction for NHTPN must proceed under the heating condition.
480 J mol−1, A = Ak = 1020.95 s−1 obtained by eqn (24)–(26) are 144.60 J mol−1 K−1, 195.82 kJ mol−1 and 132.20 kJ mol−1, respectively. The positive value of ΔG≠ indicates that the exothermic decomposition reaction for NHTPN must proceed under the heating condition.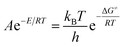
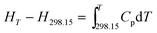
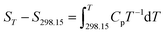
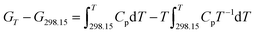
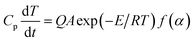
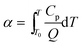
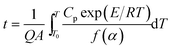
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = 1020.95 s−1, Qd = 3043.1 J g−1, R = 8.314 J mol−1 K−1, the integral upper limit T = Tb = 448.44 K and the lower limit T0 = Te0 = 422.06 K into eqn (33), the value of t of 13.80 s is obtained.
480 J mol−1, A = 1020.95 s−1, Qd = 3043.1 J g−1, R = 8.314 J mol−1 K−1, the integral upper limit T = Tb = 448.44 K and the lower limit T0 = Te0 = 422.06 K into eqn (33), the value of t of 13.80 s is obtained.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1 and A = 1020.95 s−1, Troom = 293.15 K, R = 8.314 J mol−1 K−1, hot-spot critical radius a = 10−3 cm and time interval t − t0 = 10−4 s (ref. 15) to Bruckman–Guillet's first-order estimation equation [eqn (34)],17,18 the value of Tcr,hot spot of 314.18 °C is obtained.
480 J mol−1 and A = 1020.95 s−1, Troom = 293.15 K, R = 8.314 J mol−1 K−1, hot-spot critical radius a = 10−3 cm and time interval t − t0 = 10−4 s (ref. 15) to Bruckman–Guillet's first-order estimation equation [eqn (34)],17,18 the value of Tcr,hot spot of 314.18 °C is obtained.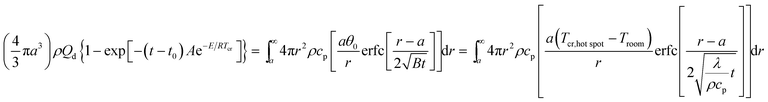
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, and A = 1020.95 s−1, the H50 of NHTPN was estimated as 13.13 cm by Friedman's formula (eqn (35)).19,20 This value shows that it has impact sensitivity level approaching those of PETN (16 cm) and tetryl (17 cm)
480 J mol−1, and A = 1020.95 s−1, the H50 of NHTPN was estimated as 13.13 cm by Friedman's formula (eqn (35)).19,20 This value shows that it has impact sensitivity level approaching those of PETN (16 cm) and tetryl (17 cm)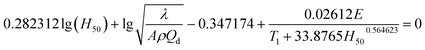
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = 1020.95 s−1, ρ = 1.884 × 103 kg m−3, λ = 0.2250 W m−1 K−1, ambient temperature Ta = 340 K, σδ = 10 K into eqn (36)–(42), the S(T) vs. T relation curves for infinite plate, infinite cylindrical and spheroidic NHTPN in Fig. 5 and determination results of the thermal sensitivity of the NHTPN in Table 5 are obtained, showing that the accelerating tendency from adiabatic decomposition to explosion of large scale NHTPN and the thermal safety of NHTPN with different shape decreases in the order of sphere > infinite cylinder > infinite plate.
480 J mol−1, A = 1020.95 s−1, ρ = 1.884 × 103 kg m−3, λ = 0.2250 W m−1 K−1, ambient temperature Ta = 340 K, σδ = 10 K into eqn (36)–(42), the S(T) vs. T relation curves for infinite plate, infinite cylindrical and spheroidic NHTPN in Fig. 5 and determination results of the thermal sensitivity of the NHTPN in Table 5 are obtained, showing that the accelerating tendency from adiabatic decomposition to explosion of large scale NHTPN and the thermal safety of NHTPN with different shape decreases in the order of sphere > infinite cylinder > infinite plate.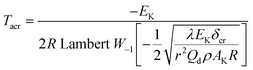
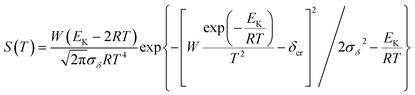
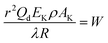
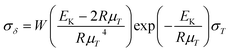
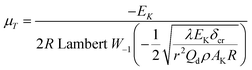
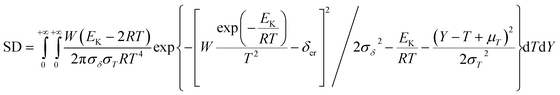
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 J mol−1, A = Ak = 1020.95 s−1 is close to the one of ΔG≠ of 134.11 kJ mol−1 of PETN corresponding to T = Tp0 = 443.93 K, E = Ek = 112
480 J mol−1, A = Ak = 1020.95 s−1 is close to the one of ΔG≠ of 134.11 kJ mol−1 of PETN corresponding to T = Tp0 = 443.93 K, E = Ek = 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 J mol−1, A = Ak = 1010.40 s−1.
300 J mol−1, A = Ak = 1010.40 s−1.