Open Access Article
Open Access ArticleReactions of hydroxyl radicals with benzoic acid and benzoate†
Chongchong Wua,
Alex De Visscherab and
Ian Donald Gates *a
*a
aDepartment of Chemical and Petroleum Engineering, University of Calgary, Canada. E-mail: ian.gates@ucalgary.ca; Tel: +1-403-220-5752
bDepartment of Chemical and Materials Engineering, Concordia University, Montreal, QC, Canada
First published on 19th July 2017
Abstract
Density functional theory was used to study the mechanism and kinetics of benzoic acid with hydroxyl radicals in both gas and aqueous phases as well as benzoate with hydroxyl radicals in the aqueous phase at the M06-2X/6-311+G(d,p) level of theory. The results show that all reaction pathways involved the formation of pre-reactive complexes which in turn alter reaction energy barriers. The reaction rate constants, calculated based on classical transitional theory, followed the order of meta addition > para addition > ortho addition for the reaction of benzoic acid and hydroxyl radicals in both gas and aqueous media. The energy barrier analysis reveals that the ortho adducts were also less vulnerable to subsequent reaction. In addition, the rate constants for the addition reactions were highest for benzoate in the aqueous phase, followed by benzoic acid in the aqueous phase, then by benzoic acid in the gas phase, consistent with electrostatic potential analysis. However, the rate constants of hydrogen abstraction in the aqueous phase were much lower than that in the gas phase and thus, gas phase reactions are preferred. The incorporation of one explicit water molecule, for addition reactions between benzoic acid and hydroxyl radicals, lowered reaction rates in the aqueous phase by increasing the bond length between the oxygen and reacting carbon in the benzene ring.
1. Introduction
Water produced from mining operations, in particular, oil sands mining operations, contains solids, salts, and other organic compounds such as benzene, phenols, naphthenic acids (NAs) which are toxic to wildlife.1,2 Despite the small amount of aromatic alkanoic acids such as benzoic acid (BA) in NAs, they increase the toxicity and recalcitrance of NAs in wastewater.3 In addition, BA is a common recalcitrant contaminant which exists in domestic wastewater as well as other industrial wastewater, making it imperative to remove BA from waste water.4,5Ultrasound is effective for breaking down organic compounds in water.6 When water is treated by ultrasonic waves, cavitation within the water leads to generation and collapse of micro bubbles that result in high temperatures in a small region where organic compounds are degraded through pyrolysis. In addition, organic compounds will also be oxidized by hydroxyl radicals (˙OH) generated by the cavitation bubbles during ultrasonic treatment.7–9 Furthermore, BA can be removed during electrochemical oxidation, photochemical oxidation, Fenton oxidation, and ozonation.10,11 These methods involve the reaction of BA with hydroxyl radicals in the liquid phase. Moreover, BA could also react with hydroxyl radicals inside the bubble under ultrasound irradiation.12 BA is a weak acid with a pKa of 4.2 and it can exist in the form of benzoate (BZ) in the aqueous phase.13 Therefore, the reaction between BZ and hydroxyl radicals can also take place in the oxidation process under neutral and alkaline pH.
Quantum chemical reaction computation using density functional theory is a powerful tool to understand mechanisms. These methods enable the calculation of optimized geometries for reactants and products, assessment of intermediate and transition states, and estimation of reaction kinetics for different reaction pathways with reasonable accuracy.14 Theoretical studies of the mechanism and kinetics of BA reacting with hydroxyl radicals are important to improve techniques to remove BA completely from wastewater. The distribution of the intermediates is crucial to the detoxification of BA.15 San et al. studied the transition states of photo degradation of BA in liquid phase.16 Minakata et al. analyzed the lowest unoccupied molecular orbital and singly occupied molecular orbital of hydroxyl radical addition to BZ at ortho, meta, and para positions in the aqueous phase.17 Li et al. investigated the effects of OH substitution on the rates and mechanisms of decarboxylation of BA.18 Chuchev et al. conducted a detailed theoretical study of the decarboxylation reaction for BA ortho-derivatives.19 Wang et al. calculated the catalytic decarboxylation mechanism of BA.20 These studies are useful but do not examine uncatalyzed reaction mechanism and kinetics of BA with hydroxyl radicals in both gas and aqueous phases. Existing studies do not consider the difference between ortho and meta carbons on the side of carboxyl group and opposite the carboxyl group. In addition, these studies did not consider pre-reactive complexes, which can alter the kinetics of OH reactions dramatically. Furthermore, there are few theoretical studies that compare rate constants differences between BA and BZ in the aqueous phase.
The objective of this paper is to employ density functional theory to study the transition states of six different pathways of BA with hydroxyl radicals both in gas and aqueous phases, BZ with hydroxyl radicals in the aqueous phase, and estimate the energy barrier and reaction rate constants to determine the possible distribution of intermediates including the potential effect of pre-reactive complexes. Moreover, the influence of an individual explicit water molecule on rate constants was investigated.
2. Computational methods
The evolution of the reactions between BA and hydroxyl radicals was evaluated by using the Gaussian09 molecular modelling package.21 Restricted and unrestricted density functional theory (DFT) was adopted for closed and open shell systems separately. The M06-2X method was reported to be appropriate for calculating hydroxyl radical reactions and predicting optimized geometries and vibrational frequencies.22,23 6-311+G(d,p) is a widely used basis set by researchers for radical reaction calculation.24,25 Considering accuracy and computational costs, M06-2X/6-311+G(d,p) was chosen as the method and basis set for the optimizations, electronic, and vibrational properties calculations both in the gas and aqueous phases in this study. After optimization of the reactants and products, the transition state, saddle point in the potential energy surface, was optimized by a quasi-Newton synchronous transit (QST3) calculation followed by the Berny optimization method calculation.26,27 Frequency analyses were conducted to confirm the transition state by one imaginary frequency and obtain zero-point corrected energies as well as free energies. Intrinsic reaction coordinate (IRC) calculations were conducted to ensure that the transition states connected the original reactants and products.28,29 Comparison of the calculated rate constants with experimental data also provided confidence that the pre-reactant complexes and transition states determined were adequate. The implicit solvation model based on density (SMD) was adopted to investigate the effects of water solvent on the reaction (the dielectric constant was taken to be 78.3553 for water).30–32 The relative energy and rate constants were calculated at 298.15 K, and 1 atm. The single-point energies were further refined employing coupled cluster theory at the level of CCSD(T)/6-311++G(d,p).33,34 The study on incorporating one water molecule around the carboxylic group of BZ and BA followed the same methods as described above.3. Results and discussion
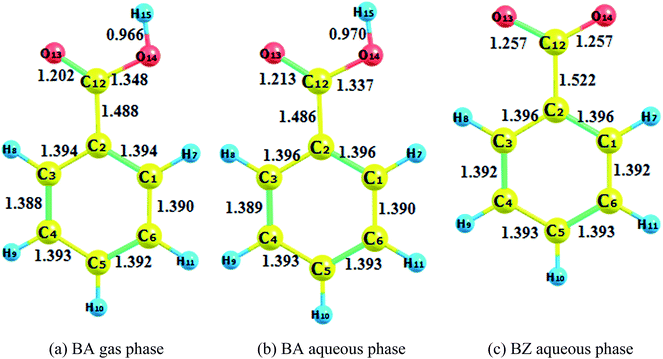
3.1 Reaction pathways
Due to the existence of unpaired electrons, the hydroxyl radical is an electrophilic radical.35 When reacting with BA, there are five possible reaction pathways: ortho-addition (o-add), para-addition (p-add), meta-addition (m-add), ipso-addition (ipso-add), and hydrogen-abstraction (H-abs), respectively. On the other hand, o-add, p-add, m-add, and ipso-add are the four reaction pathways between BZ and hydroxyl radicals, as shown in Scheme 1. The optimized structures of the reactants are depicted in Fig. 1, indicating that the geometry of BA and BZ were planar. In addition, the bond length of the optimized structures of BA in the gas and liquid phases were almost the same. However, it is noteworthy that the structure of BA was not symmetric, and the reaction of o-add and m-add could happen at two different sites of the benzene ring, leading to seven different reaction pathways. Furthermore, it is demonstrated that the reaction rate constant of ipso-add is negligible compared to other reaction pathways considering the significant steric effect of the carboxylic group,36 and this pathway was excluded in the present study. Thus, the six reaction pathways for BA with hydroxyl radicals were calculated both in the gas and aqueous phases. The addition opposite the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group was denoted as o-add and m-add on ortho and meta positions, respectively, whereas the additions on the side of C
O group was denoted as o-add and m-add on ortho and meta positions, respectively, whereas the additions on the side of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group was denoted as o2-add and m2-add, separately. Due to the symmetric structures of BZ, the reaction between BZ and hydroxyl radicals were calculated only for the ortho, meta, and para positions.
O group was denoted as o2-add and m2-add, separately. Due to the symmetric structures of BZ, the reaction between BZ and hydroxyl radicals were calculated only for the ortho, meta, and para positions.
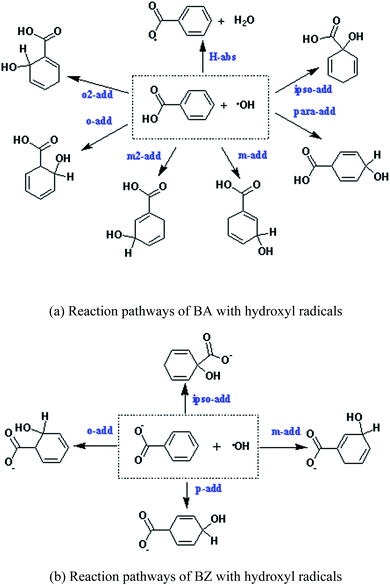 | ||
| Scheme 1 Reaction pathways of BA and BZ with hydroxyl radicals. (a) Reaction pathways of BA with hydroxyl radicals. (b) Reaction pathways of BZ with hydroxyl radicals. | ||
The optimization of adducts in the gas and aqueous phases are depicted in Fig. S1–S3.† When hydroxyl radicals reacted with BA through addition reaction, the π bonds of the aromatic rings were broken, and the carbon–carbon lengths were altered. In the process of hydrogen abstraction reactions, the O–H bond broke and hydrogen was abstracted to hydroxyl radicals to form a new O–H bond, leading to the formation of a water molecule. On the other hand, it was deduced that the length of the newly formed carbon–oxygen bond was below 1.45 Å in the gas phase for all addition reaction pathways, which was the same reported by the addition of hydroxyl radicals to phenol.37 When comparing the bond lengths in the gas phase and aqueous phase, the bond length was prolonged for the reaction taking place in the aqueous phase. In addition, the bond length of BZ products was longer than that of BA products.
3.2 Pre-reactant complexes and transition states
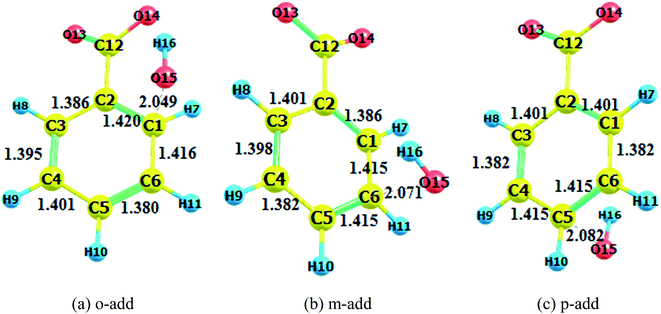
Pre-reactive complexes have been identified in many radical-molecule reactions as the precursors for reaction,38 however, it has not been reported for reactions of BA and hydroxyl radicals thus far. From the calculations, when hydroxyl radicals approached BA, weakly bonded pre-reactive complexes were formed due to van der Waals interactions and long range coulombic interactions. The optimized pre-reactive structures for the gas phase and liquid medium reactions for BA and BZ are drawn in Fig. S4 to S6,† separately. For the addition reaction, the OH radicals interacted with the benzene ring, forming the O–H⋯π hydrogen bond complex, whereas for the hydrogen abstraction reaction, the OH radical approached the hydrogen atom of the carboxyl group, leading to a O14–H15⋯O16 hydrogen bond complex. Interestingly, the orientation of hydroxyl radicals for the ortho site reaction was different from meta and para site reactions. The hydroxyl radicals were positioned above the benzene ring plane for the reactions that occurred at meta and para sites, whereas they were almost in the same plane for the o-add and o2-add reactions. In addition, the o-add had a longer distance between the hydroxyl radical and benzoic ring compared with the m-add and p-add reactions. The above phenomena could be caused by steric hindrance of the carboxyl as well as the hydrogen bond formation between hydroxyl radicals and carboxyl group, hindering the approach of OH radicals to benzoic acids.The transition states in the gas and liquid phases are shown in Fig. 2 to 4. They were confirmed by a single imaginary frequency as well as the IRC analysis. There were remarkable changes between the structures of pre-reactive complexes and transition states. The main structural changes were located around the reacting carbon and oxygen. For the o-add reaction pathway, it was observed that the C2–C1, C1–C6, C3–C4, and C5–C4 bonds elongated whereas the C2–C3 and C5–C6 bond lengths shortened. The same trends were also found in other hydroxyl radical addition reactions both in the gas and aqueous phases. In other words, when the hydroxyl radicals reacted with a particular carbon in the benzene ring, the bond length of the reacting carbon with adjacent carbons increased as well as the length of the bonds between the carbon opposite the reacting carbon on the aromatic ring with its neighboring carbons. The remaining two carbon–carbon bonds in the aromatic rings were shortened. This is explained by the electron density transfer of the aromatic ring.
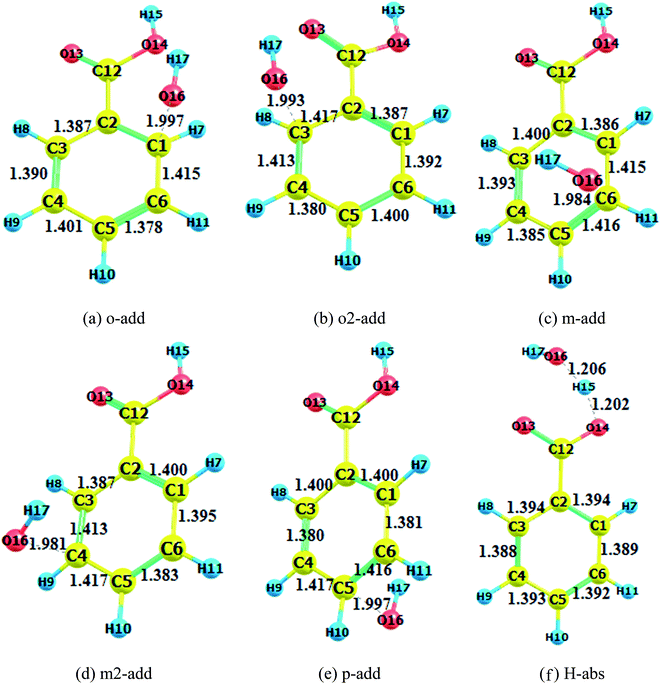 | ||
| Fig. 2 Transition state optimization (BA gas phase). (a) o-add. (b) o2-add. (c) m-add. (d) m2-add. (e) p-add. (f) H-abs. | ||
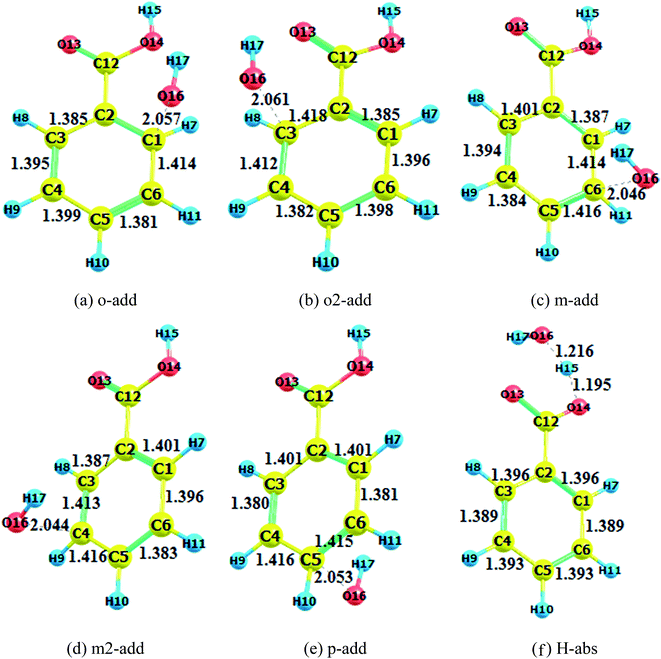 | ||
| Fig. 3 Transition state optimization (BA aqueous phase). (a) o-add. (b) o2-add. (c) m-add. (d) m2-add. (e) p-add. (f) H-abs. | ||
Comparing the transition states of hydroxyl radical addition to BA in gas phase versus aqueous phase, it is obvious that the transition states of the distances of oxygen and reacting carbon in the aqueous phase was longer than that in the gas phase, which could possibly be due to the formation of hydrogen bonds between BA and water, therefore, hindering the approach of hydroxyl radicals to benzene rings. However, it is worth noting that the bond length of oxygen and the reacting carbon for BZ o-add was shorter than BA o-add, and the difference was caused by the larger steric effects of the carboxylic group than the carboxylic anion. As for the hydrogen abstraction reaction, the bond between O14 and H15 was broken, and H15 was attracted to hydroxyl radicals, generating water and a benzoic acid free radical as products.
3.3 Energetics of the reaction paths
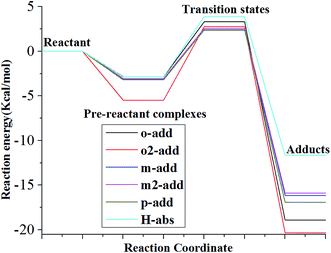
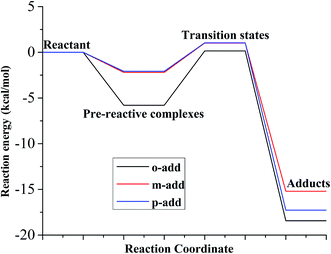
The reaction energies for the six different reaction paths with reactants, pre-reactive complexes, transition state, and products were calculated and presented in Fig. 5 and Table S1† for the gas phase. The results show that the energy of pre-reactive complexes was lower than the energy of reactant, which would influence the energy barriers for the reaction. It has also been detected in previous research that pre-reactive complexes are critical to the reaction path since they would influence energy barrier and the energy partitioning of the products.39,40 The reaction energy barriers from pre-reactive complexes to transition states in the gas phase followed the order of o2-add > H-abs > o-add > m2-add > m-add > p-add, indicating that the addition of hydroxyl radicals on the same side as the carboxyl group was more difficult than on the opposite side for this step reaction, which might be caused by steric effects. It is remarkable that the energy of H-abs product was higher than addition reaction products for the gas phase reaction, indicating its instability and relative ease to proceed to the next step reaction, whereas the products of o-add and o2-add were the most stable among the six reaction pathways.The relative energy for the reaction between BA and hydroxyl radicals in the aqueous phase is displayed in Fig. 6 and Table S2.† Compared with the reaction path in the liquid and gas phases, it was deduced that the reactants needed to overcome smaller energy barriers for the reaction from pre-reactive complexes to transition states. The reaction energy barriers for the reaction from pre-reactive complexes to transition states in the aqueous medium was highest for H-abs. In addition, the energy barrier for H-abs in the aqueous phase was much higher than in the gas phase, which was possibly caused by hydrogen bonding formation between the carboxylic group and water molecules. Therefore, the reaction in the gas phase was preferable for H-abs reaction compared to the aqueous phase reaction. According to the energy, o2-add products were most stable among the six different reaction pathways, making them less vulnerable to subsequent reaction.
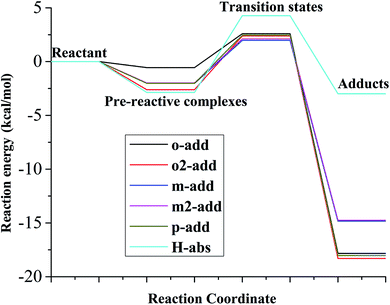
As for the reaction energy between BZ and hydroxyl radicals, displayed in Fig. 7 and Table S3,† the energy barrier from pre-reactive complexes to transitions states followed the order of o-add > m-add > p-add with p-add transition state having the longest bond length among the addition reactions. This is explained because the p-add transition state was the earliest transition state among the addition reaction pathways from pre-reactive complexes for the reaction between BZ and hydroxyl radicals.39 In addition, the product of o-add had the lowest energy among all the products, which was the same for the reaction between BA and hydroxyl radicals in the gas and aqueous phases, indicating that the ortho position was not susceptible for the following reactions.
Furthermore, the 〈s2〉 values of the open shell systems for all the reaction pathways in the gas and aqueous phases are summarized in Tables S4–S6† to analyze spin contamination. Spin contamination is measured by analyzing the deviation of the 〈s2〉 values to the exact values (0.75 for a doublet).41 It is deduced that the variation were within 10% for all the species, implying that spin contamination had insignificant influences on the reaction pathways.42
3.4 Reaction rate constants
The reaction rate constants for the elementary reaction were calculated by using transition state theory. Due to the formation of pre-reactive complex, the main reactant pathway is expressed as:
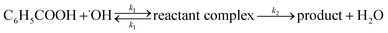 | (1) |
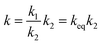 | (2) |
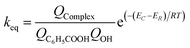 | (3) |
 | (4) |
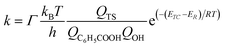 | (5) |
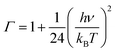 | (6) |
The reaction rate constants in the gas and aqueous phases are listed in Table 1. As shown, the reaction rate constants of m-add, m2-add, p-add were higher than o-add and o2-add for the reaction between BA and hydroxyl radicals both in the gas and aqueous phases. There are three possible reasons to explain the phenomena, one is that the carboxyl group is an electron withdrawing group and it would decrease the electron density on the benzene ring through a resonance withdrawing effect at the ortho and para positions. Another reason is the steric influence at the ortho positions of the carboxyl group that impedes the approach of hydroxyl radicals. The formation of hydrogen bonds between hydroxyl radicals and hydrogen in the carboxyl group is another possible factor that would inhibit the ortho position reaction. For the gas phase reaction, the overall rate constant followed the order of H-abs > (m-add + m2-add) > para addition > ortho addition (o-add + o2-add). The reason why the rate constant for H-abs was highest is that benzene ring is capable of withdrawing electron density from carboxyl group by induction, making the hydrogen on the carboxyl group more active and reacting with hydroxyl group to form water.48 The H-abs rate constant in the gas phase (8.61 × 10−11 cm3 per molecule per s) was higher than in the aqueous phase (6.30 × 10−13 cm3 per molecule per s−1), implying that the optimum reaction medium should be in gas phase or inside the cavitation bubble when targeting the decarboxylation reaction. Furthermore, the tunneling factors of H-abs were much higher than all the addition reaction pathways both in the gas and aqueous phases.
| Reaction path | BA gas phase | BA aqueous phase | BZ aqueous phase | |||
|---|---|---|---|---|---|---|
| k | Γ | k | Γ | k | Γ | |
| a Note: units for gas phase rate constants and aqueous phase rate constants are cm3 per molecule per s−1, and M−1 s−1, respectively. | ||||||
| o-add | 4.19 × 10−12 | 1.343 | 1.67 × 108 | 1.227 | 9.73 × 108 | 1.186 |
| o2-add | 4.81 × 10−12 | 1.363 | 1.32 × 108 | 1.223 | 9.73 × 108 | 1.186 |
| m-add | 1.14 × 10−11 | 1.278 | 2.94 × 108 | 1.165 | 8.98 × 108 | 1.122 |
| m2-add | 9.71 × 10−12 | 1.281 | 2.16 × 108 | 1.166 | 8.98 × 108 | 1.122 |
| p-add | 1.21 × 10−11 | 1.303 | 2.11 × 108 | 1.212 | 9.21 × 108 | 1.138 |
| H-abs | 8.61 × 10−11 | 3.009 | 1.05 × 107 | 3.087 | ||
Except for H-abs, the rate constants of the other five reaction pathways in the aqueous phase were much higher than in the gas phase. Furthermore, the hydrogen abstraction rates of benzoic acid were much higher than for phenol (1.60 × 10−16 cm3 per molecule per s),49 since benzoic acid has an electronic withdrawing group, while phenol contains an electron donor group.50 San et al. calculated the reaction rate constants of benzoic acid with hydroxyl radical reaction in the aqueous phase, and the reaction rates were 8.38 × 10−11, 4.20 × 10−8, 1.65 × 10−20, 5.08 × 10−24 cm3 per molecule per s for meta addition reaction, ortho addition reaction, para addition reaction, and H-abs, respectively.16 The reaction rates calculated were different due to the discovery of pre-reactive complexes as well as the different calculation levels. The overall rate constant of the six reaction pathways computed at 298 K, 1 atm in the aqueous medium was 1.03 × 109 M−1 s−1. Assuming an uncertainty of 0.4 kcal mol−1 on the calculated energy levels, the expected uncertainty on the calculated rate constants was about a factor of 2, which was in the range of the previous reported experimental value (2.1 ± 0.3 × 109 and 1.8 × 109 M−1 s−1),51,52 indicating the reliability of the calculations reported here. Moreover, the rate constants for the BA aqueous phase reaction was (m-add + m2-add) > (o-add + o2-add) > p-add, which followed the same trend with other experimental results.53
The rate constant for the reaction between BZ and hydroxyl radicals was approximately 4.66 × 109 M−1 s−1, which corresponds well with the experimental value of 5.9 × 109 M−1 s−1.54 Furthermore, the rate constant for the reaction between BZ and hydroxyl radicals was higher than that between BA and hydroxyl radicals, implying that transferring BA to BZ could promote the addition reaction. Therefore, the alkaline pH is more favorable for the degradation of BA in waste water. In addition, the rate constant followed the order of BZ aqueous phase > BA aqueous phase > BA gas phase. To further explain the trends, electrostatic potential analysis were carried out to display charge distributions three dimensionally by M06-2X method using 6-311+G(d,p) basis set, shown in Fig. 8. It is worth noting that BZ in the aqueous phase had the biggest negative electrostatic potential, followed by BA in the aqueous phase, then by BA in the gas phase, consistent with the rate constants results. Hydroxyl radicals have strong electrophilic character and tend to react at negative regions, therefore, the electrostatic potential analysis results can help explain the lower energy barrier and higher rate constants for addition reactions in the aqueous phase than in the gas phase, further confirming the accuracy of the rate constants results.
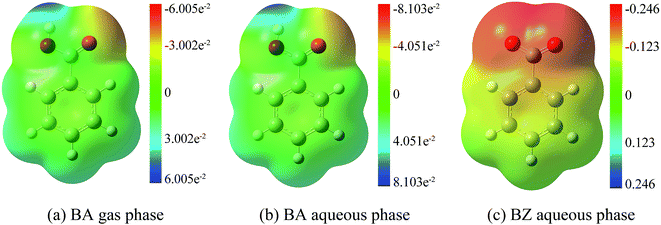 | ||
| Fig. 8 Electrostatic potential analysis. (a) BA gas phase. (b) BA aqueous phase. (c) BZ aqueous phase. | ||
After a single-point energy calculation at CCSD (T)/6-311++G(d,p) level of theory, the rate constants of all the reaction pathways were recalculated (Table S7†). Compared with rate constants obtained by M06-2X method, it was deduced that the rate constants predicted by CCSD (T) method has obvious deviation from the experimental data. On the other hand, the CCSD (T) method is computationally more expensive than the M06-2X method. Therefore, the rates constants in this study were calculated by using the M06-2X method.
3.5 Influence of explicit water molecule
In the aqueous phase, water molecules form a hydrogen bond with the carboxylic group of BA and BZ that might influence energy barriers. However, one of the significant drawbacks of being implicit SMD is that it does not completely account for hydrogen bonding interactions.55 To investigate the impact of solvation on transition states structures and rate constants, one explicit water molecule was incorporated around the carboxylic group of BA and BZ. Due to the addition of water molecule to BZ, the structures of the reactants are not symmetric, therefore, there are five different reaction pathways between BZ and hydroxyl radicals. The structures for the pre-reactant complexes, transition states, and products were optimized, and rate constants of the six reaction pathways between BA and hydroxyl radicals, and five reaction pathways between BZ and hydroxyl radicals, were calculated.The transition states with the addition of one explicit water molecule for BA and BZ are depicted in Fig. S7 and S8,† respectively. It was deduced that the carbon–carbon length in the benzene ring of the transition states was essentially the same compared to the cases without one water molecule for both BA and BZ. The main difference was found in the variation in bond length between oxygen and the reacting carbon in benzene ring. Compared to the case without the explicit water molecule, bond lengths of the reacting carbons and oxygens were elongated for all the addition reactions between BA and hydroxyl radicals. On the other hand, they were longer for o-add and o2-add, and shorter for m-add, m2-add, and p-add for the addition reactions between BZ and hydroxyl radicals. As for the rate constants, listed in Table 2, they were different from the case without a water molecule, which was possibly caused by electron redistribution on the benzene ring. The most substantial variation was the rate constant for H-abs, only accounting for 16% of that for implicit water molecule. Furthermore, the rate constants of H-abs was much smaller than for addition reaction. Therefore, the formation of hydrogen bonds between the carboxylic group and water molecules negatively influenced the rate constant for H-abs, and reaction medium should choose the gas phase or inside the bubble for the H-abs pathway. In addition, it should be noted that the joint use of implicit solvation model and one explicit water molecule may not accurately reproduce the boundary conditions between the solute and bulk, and it also requires the evaluation of entropic effects with the explicit water molecule.56
| Reaction path | BA aqueous phase | BZ aqueous phase | ||
|---|---|---|---|---|
| K (M−1 s−1) | Γ | K (M−1 s−1) | Γ | |
| o-add | 1.01 × 108 | 1.215 | 3.85 × 108 | 1.188 |
| o2-add | 1.46 × 108 | 1.210 | 3.07 × 108 | 1.181 |
| m-add | 3.29 × 108 | 1.158 | 3.72 × 108 | 1.124 |
| m2-add | 3.19 × 108 | 1.160 | 4.87 × 108 | 1.125 |
| p-add | 1.09 × 108 | 1.199 | 2.79 × 108 | 1.139 |
| H-abs | 1.68 × 106 | 3.128 | ||
4. Conclusions
An extensive theoretical study was conducted on the six possible reaction pathways of benzoic acid with hydroxyl radicals both in the gas phase and aqueous medium and benzoate with hydroxyl radicals in the aqueous phase. The pre-reactive complexes identified affect the energy barriers. The rate constants calculated were 1.28 × 10−10 cm3 per molecule per s and 1.03 × 109 M−1 s−1 for the reaction between benzoic acid and hydroxyl radicals in the gas and aqueous phases, respectively, and 4.66 × 109 M−1 s−1 for the reaction between benzoate and hydroxyl radicals in the aqueous phase, whereas they were 1.00 × 109 M−1 s−1 and 1.83 × 109 M−1 s−1 for benzoic acid and benzoate with one explicit water molecule, respectively. The rate constant of hydrogen abstraction was higher by a factor of 137 in the gas phase than that in the liquid medium, however, the rate constants of addition reactions were much lower in the gas phase. Moreover, the energy barrier for hydrogen abstraction in the aqueous phase was higher than that in the gas phase. The incorporation of one water molecule was found to influence rate constants for both benzoic acid and benzoate in the aqueous medium.Acknowledgements
Financial support for the study provided by the Department of Chemical and Petroleum Engineering, University of Calgary, is acknowledged. The authors also acknowledge simulation support from Westgrid, and suggestions from Professor Sathish Ponnurangam.References
- C. Wang, N. Klamerth, R. Huang, H. Elnakar and M. Gamal El-Din, Environ. Sci. Technol., 2016, 50, 4238–4247 CrossRef CAS PubMed.
- Z. Shu, C. Li, M. Belosevic, J. R. Bolton and M. G. El-Din, Environ. Sci. Technol., 2014, 48, 9692–9701 CrossRef CAS PubMed.
- R. J. Johnson, B. E. Smith, P. A. Sutton, T. J. McGenity, S. J. Rowland and C. Whitby, ISME J., 2011, 5, 486–496 CrossRef CAS PubMed.
- S. Enami, M. R. Hoffmann and A. J. Colussi, Phys. Chem. Chem. Phys., 2016, 18, 31505–31512 RSC.
- H. S. Wahab, J. Mol. Model., 2012, 18, 2709–2716 CrossRef CAS PubMed.
- O. M. Perrone, F. M. Colombari, J. S. Rossi, M. M. S. Moretti, S. E. Bordignon, C. D. C. C. Nunes and R. Da-Silva, Bioresour. Technol., 2016, 218, 69–76 CrossRef CAS PubMed.
- M. Lin, X. A. Ning, T. An, J. Zhang, C. Chen, Y. Ke and J. Liu, J. Hazard. Mater., 2016, 307, 7–16 CrossRef CAS PubMed.
- A. De Visscher, Ultrason. Sonochem., 2003, 10, 157–165 CrossRef CAS PubMed.
- N. S. M. Yusof, B. Babgi, Y. Alghamdi, M. Aksu, J. Madhavan and M. Ashokkumar, Ultrason. Sonochem., 2016, 29, 568–576 CrossRef CAS PubMed.
- R. Oliveira, D. Geraldo and F. Bento, Electrochim. Acta, 2014, 135, 19–26 CrossRef CAS.
- X. Huang, X. Li, B. Pan, H. Li, Y. Zhang and B. Xie, Water Res., 2015, 73, 9–16 CrossRef CAS PubMed.
- R. Singla, M. Ashokkumar and F. Grieser, Res. Chem. Intermed., 2004, 30, 723–733 CrossRef CAS.
- B. Nair, Int. J. Toxicol., 2000, 20, 23–50 Search PubMed.
- J. Raúl Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, J. Am. Chem. Soc., 2001, 123, 2018–2024 CrossRef PubMed.
- Y. Li, B. Wen, W. Ma, C. Chen and J. Zhao, Environ. Sci. Technol., 2012, 46, 5093–5099 CrossRef CAS PubMed.
- N. San, M. Kılıç, Z. Tuiebakhova and Z. Çınar, J. Adv. Oxid. Technol., 2007, 10, 43–50 CAS.
- D. Minakata, W. Song, S. P. Mezyk and W. J. Cooper, Phys. Chem. Chem. Phys., 2015, 17, 11796–11812 RSC.
- J. Li and T. B. Brill, J. Phys. Chem. A, 2003, 107, 2667–2673 CrossRef CAS.
- K. Chuchev and J. J. BelBruno, J. Mol. Struct.: THEOCHEM, 2007, 807, 1–9 CrossRef CAS.
- M. F. Wang, Z. J. Zuo, R. P. Ren, Z. H. Gao and W. Huang, Energy Fuels, 2016, 30, 2833–2840 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- C. Bian, Y. Li, S. Wang and X. Jing, Int. J. Quantum Chem., 2017, 117 DOI:10.1002/qua.25342.
- M. R. Dash and B. Rajakumar, Atmos. Environ., 2013, 79, 161–171 CrossRef CAS.
- T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225–232 CrossRef CAS.
- Ö. Farkas and H. B. Schlegel, J. Mol. Struct.: THEOCHEM, 2003, 666, 31–39 CrossRef.
- H. B. Xie, C. Li, N. He, C. Wang, S. Zhang and J. Chen, Environ. Sci. Technol., 2014, 48, 1700–1706 CrossRef CAS PubMed.
- Q. Zhao, F. Y. Liu, W. Wang, C. Li, J. Lu and W. Wang, Phys. Chem. Chem. Phys., 2017, 19, 15073–15083 RSC.
- H. Sabet-Sarvestani, H. Eshghi and M. Izadyar, RSC Adv., 2017, 7, 1701–1710 RSC.
- P. L. Bhoorasingh and R. H. West, Phys. Chem. Chem. Phys., 2015, 17, 32173–32182 RSC.
- T. Papp, L. Kollár and T. Kégl, Chem. Phys. Lett., 2013, 588, 51–56 CrossRef CAS.
- M. Tiwari and P. C. Mishra, RSC Adv., 2016, 6, 86650–86662 RSC.
- L. Kazmierczak, D. Swiatla-Wojcik and M. Wolszczak, RSC Adv., 2017, 7, 8800–8807 RSC.
- G. Kaur and Vikas, RSC Adv., 2015, 5, 50989–50998 RSC.
- G. Kaur and Vikas, RSC Adv., 2015, 5, 82587–82604 RSC.
- M. E. Medina, C. Iuga and J. R. Álvarez-Idaboy, RSC Adv., 2014, 4, 52920–52932 RSC.
- D. Minakata, K. Li, P. Westerhoff and J. Crittenden, Environ. Sci. Technol., 2009, 43, 6220–6227 CrossRef CAS PubMed.
- P. Wu, J. Li, S. Li and F. M. Tao, Sci. China: Chem., 2012, 55, 270–276 CrossRef CAS.
- J. Raúl Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, J. Am. Chem. Soc., 2001, 123, 2018–2024 CrossRef PubMed.
- V. H. Uc, J. R. Alvarez-Idaboy, A. Galano, I. García-Cruz and A. Vivier-Bunge, J. Phys. Chem. A, 2006, 110, 10155–10162 CrossRef CAS PubMed.
- I. Degirmenci and M. L. Coote, J. Phys. Chem. A, 2016, 120, 1750–1755 CrossRef CAS PubMed.
- A. S. Menon and L. Radom, J. Phys. Chem. A, 2008, 112, 13225–13230 CrossRef CAS PubMed.
- R. Kaur and Vikas, RSC Adv., 2016, 6, 29080–29098 RSC.
- L. Chen, W. Wang, W. Wang, C. Li, F. Liu and J. Lü, RSC Adv., 2015, 5, 28044–28053 RSC.
- J. M. Anglada, J. Am. Chem. Soc., 2004, 126, 9809–9820 CrossRef CAS PubMed.
- A. Reisi-Vanani, L. Shahrokh and S. N. Kokhdan, Comput. Theor. Chem., 2015, 1051, 72–78 CrossRef CAS.
- H. Zhou, D. Song, C. Zhong and G. Ye, Sci. Rep., 2016, 6, 38473 CrossRef CAS PubMed.
- S. Hoseinpour and A. Reisi-Vanani, Prog. React. Kinet. Mech., 2016, 41, 301–308 CrossRef CAS.
- J. DeRuiter, Carboxylic acid structure and chemistry: part 1. principles of drug action I, Auburn university, Alabama, 2005, pp. 1–10 Search PubMed.
- P. B. Jayathilaka, G. C. Pathiraja, A. Bandara, N. D. Subasinghe and N. Nanayakkara, Can. J. Chem., 2014, 92, 809–813 CrossRef CAS.
- M. Bellardita, V. Augugliaro, V. Loddo, B. Megna, G. Palmisano, L. Palmisano and M. A. Puma, Appl. Catal., A, 2012, 441, 79–89 CrossRef.
- L. M. Dorfman, I. A. Taub and D. A. Harter, J. Chem. Phys., 1964, 41, 2954–2955 CrossRef CAS.
- L. Ashton, G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 91, 1631–1633 RSC.
- R. Wander, P. Neta and L. M. Dorfman, J. Phys. Chem., 1968, 72, 2946–2949 CrossRef CAS.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886 CrossRef CAS.
- B. Thapa and H. B. Schlegel, J. Phys. Chem. A, 2016, 120, 5726–5735 CrossRef CAS PubMed.
- S. C. Kamerlin, M. Haranczyk and A. Warshel, ChemPhysChem, 2009, 10, 1125–1134 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05488b |
| This journal is © The Royal Society of Chemistry 2017 |