Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlled shaping of lipid vesicles in a microfluidic diffusion chamber†
M. Mally *a,
B. Božiča,
S. Vrhovec Hartmana,
U. Klančnika,
M. Murab,
S. Svetinaab and
J. Derganc*a
*a,
B. Božiča,
S. Vrhovec Hartmana,
U. Klančnika,
M. Murab,
S. Svetinaab and
J. Derganc*a
aInstitute of Biophysics, Faculty of Medicine, University of Ljubljana, Ljubljana, Slovenia. E-mail: mojca.mally@mf.uni-lj.si; jure.derganc@mf.uni-lj.si
bJožef Stefan Institute, Ljubljana, Slovenia
First published on 21st July 2017
Abstract
Synthetic lipid vesicles represent an important model system for studying membrane processes, which often depend on membrane shape, but controlled shaping of vesicles remains a challenging experimental task. Here, we present a novel method for shaping giant lipid vesicles by independently regulating osmotic conditions and the concentration of membrane-shaping molecules, which intercalate into the membrane and drive membrane bending. The method is based on the microfluidic diffusion chamber, where the solution around the vesicles can be repeatedly exchanged solely by diffusion, without any hydrodynamic flow that could deform the membrane. By using lipopolysaccharide (LPS) as a vesicle shape-modifying molecule, we demonstrate controlled and reversible transformations across three shape classes, from invaginated to evaginated vesicles. We show that extensive shape transformations can lead to shapes that are assumed to comprise narrow membrane necks that hinder equilibration of the membrane and the vesicle interior. All the observed shapes are in good agreement with the predictions of the area-difference-elasticity model applied to the vesicles that were denser than their surrounding solution. Our results validate the microfluidic diffusion chamber as a universal framework for membrane shaping that could also pave the way towards controlled fabrication of synthetic membranes resembling cell-compartments with large surface-to-volume ratios.
Introduction
Lipid vesicles have long served as a versatile in vitro model system for biological membranes and provide a valuable insight into membrane-related processes. As emphasized by a recent themed issue of Physical Chemistry Chemical Physics, these model systems are also increasingly used for biochemical compartmentalization in biomimetic applications.1 Current applications of synthetic membranes are predominantly limited to spherical vesicles, and there are not many methods for controlled shaping of flaccid vesicles with larger area-to-volume ratios, resembling cellular organelles.One of the main challenges in membrane shaping stems from their inherent soft-matter nature. Membranes are relatively large structures, self-assembled by nonspecific hydrophobic interactions; mechanically, the membranes are almost non-stretchable but they are very easy to bend. Spherical lipid vesicles are therefore practically non-deformable, whereas flaccid vesicles are extremely soft, undergo noticeable thermal fluctuations and can warp under the slightest hydrodynamic flow. The transformations in vesicle shape have been demonstrated in a number of studies by applying different methods for influencing the vesicle morphology, for example by mechanical manipulation (by micropipettes,2 axial straining of the vesicles,3 flow and shear forces4…), osmotic or temperature changes,5–9 or by membrane-interacting molecules,10,11 yet none of these techniques provides a universal well-controlled system for flaccid vesicle shaping: any mechanical manipulation may significantly increase the membrane lateral tension and cause unwanted and/or irreversible transformations of vesicle shapes; osmotic or temperature changes affect a variety of parameters at once, making it difficult to deduce the predominant mechanism for the shape transformation, while membrane-interacting molecules are added by micropipette ejection into the vicinity of vesicles, causing more or less significant hydrodynamic currents. The shape transitions have been observed even without an external stimulus, with the hypotheses that they could be a consequence of the lipid molecules dissolving from the membrane into the surrounding solution,12 or of the release of the lipids from the membrane folds that are below optical resolution.13 Such spontaneous transformations led from concave to convex shapes and/or vice versa, with the direction of changes not possible to control or predict in the beginning of the experiment.
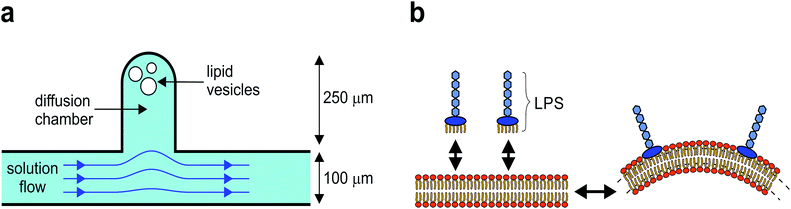
Here, we present a novel method for controlled shaping of giant flaccid lipid vesicles, i.e. the cell-size vesicles with non-tensed membranes. The method is based on the microfluidic diffusion chamber, where the solution can be exchanged solely by diffusion, without any hydrodynamic flow that could deform the membrane (Fig. 1a).14 In this approach, several parameters can be controlled independently. Spherical vesicles are first transferred into the diffusion chamber by optical tweezers, then they are osmotically deflated to become more flaccid, and finally, their shape is manipulated by adjusting the concentration of membrane-shaping molecules in the solution. Specifically, we use lipopolysaccharide (LPS) as a membrane-shaping molecule.
LPS is a main component of Gram negative bacteria outer membranes and is in the research focus as a target for novel antibiotics.15 During bacterial infection, LPS molecules are binding specifically to the receptors in the cell membrane, triggering a strong immune response.16 However, because a LPS molecule is composed of a large soluble oligosaccharide part coupled to a lipid part with six hydrophobic tails, LPS partitions non-specifically from the solution into the outer membrane leaflet and thus drives membrane bending by the bilayer-couple mechanism (Fig. 1b), whereas it does not flip to the inner side.11,17
In the designed experimental setup the vesicles were made to be heavier than the surrounding solution for easier handling. The intercalation of LPS molecules into the membranes of flaccid vesicles was controlled by regulating the LPS concentration in the bulk solution. The changes of vesicle shape were monitored with brightfield video microscopy. The observed shape changes were then compared to a detailed theoretical model, for which the contributions of membrane bending, relative stretching of the membrane leaflets, gravitational effects, and the mixing of the native lipid molecules with the intercalating LPS molecules in the membrane are taken into consideration. We find that moderate shape changes across three shape-classes are well controlled and follow the theoretical predictions of the area-difference-elasticity (ADE) model for equilibrium shapes.18–20 Larger shape transformations often result in vesicle protrusions with thin necks that hinder the transport of volume and membrane surface area, but are still reversible and can be described within the ADE model. The properties and the extent of LPS partitioning into the vesicle membrane are estimated from comparing the theoretical predictions to the measurements. The presented microfluidic diffusion chamber provides a robust universal platform for vesicle shaping where the experimental conditions can be readily and controllably altered and the monitored parameters regulated independently.
Materials and methods
Microfluidic system
The microfluidic device is fabricated by standard soft-lithography techniques.14 The microfluidic chip is designed with the main microchannel having an entrance reservoir on one end and a waste reservoir connected to the other end. The flow rate in the microchannel is controlled by changing the vertical position of the waste reservoir. The solution in the microchannel is easily exchanged by several consecutive washes of the entrance reservoir using a standard pipette. The microfluidic diffusion chamber is designed as a 250 micrometers long and 100 micrometers wide cavity, extending from the main channel (Fig. 1a).Microscopy and optical tweezers
In the experiment we used an inverted microscope (Nikon Eclipse Ti), equipped with Tweez optical tweezers (Aresis, Slovenia). In this multi-trap laser tweezers system, the laser beam of 1064 nm is AOD-controlled which enables software control of the power and position of the optical traps. The microscope is equipped with 20× objective for a large field view, and with 60× water immersion objective (NIR APO NA 1.0) for operating the optical tweezers. Microscope image was recorded by a Pixelink PL-B741U CCD camera. The recorded images were analyzed with ImageJ.21Vesicle preparation and materials
Phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) for the vesicle preparation was purchased from Avanti Polar Lipids and used without further purification. Giant vesicles were made by a slightly modified method of electroformation22 at room temperature. In the procedure the lipids are dissolved in a mixture of chloroform and methanol (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) with a total lipid concentration of 1 mg ml−1. Approximately 20 μl of the lipid solution is spread on two platinum electrodes and dried in vacuum for 2 hours. Electrodes with lipid film are placed into a plastic 2 ml microcentrifuge tube, which is filled with 2 ml sucrose solution (0.22 M). An alternating electric field, 10 Hz/8 V, is applied to the electrodes for 2 hours. The frequency and the voltage are then gradually reduced, first to 5 Hz/4 V for 15 minutes, then to 2.5 Hz/2 V for 15 minutes and then to the final values of 1 Hz/1 V for 30 minutes. The contents of the chamber is poured out and gently mixed with 2 ml glucose (0.22 M), which is also used for rinsing the electrodes. The density of the sucrose is higher than of the isoosmolar glucose solution (the difference being Δρ = 16 g l−1),23 which causes the vesicles to sink to the substrate. This makes them easier to handle in the experimental procedures, where a good focus and contrast of the vesicle image can be obtained. The vesicles were used one to four days after the preparation.
1, v/v) with a total lipid concentration of 1 mg ml−1. Approximately 20 μl of the lipid solution is spread on two platinum electrodes and dried in vacuum for 2 hours. Electrodes with lipid film are placed into a plastic 2 ml microcentrifuge tube, which is filled with 2 ml sucrose solution (0.22 M). An alternating electric field, 10 Hz/8 V, is applied to the electrodes for 2 hours. The frequency and the voltage are then gradually reduced, first to 5 Hz/4 V for 15 minutes, then to 2.5 Hz/2 V for 15 minutes and then to the final values of 1 Hz/1 V for 30 minutes. The contents of the chamber is poured out and gently mixed with 2 ml glucose (0.22 M), which is also used for rinsing the electrodes. The density of the sucrose is higher than of the isoosmolar glucose solution (the difference being Δρ = 16 g l−1),23 which causes the vesicles to sink to the substrate. This makes them easier to handle in the experimental procedures, where a good focus and contrast of the vesicle image can be obtained. The vesicles were used one to four days after the preparation.
In the experiment we used lipopolysaccharide (LPS) from E. coli O55:B5 by Sigma Co. (St. Louis, USA). The provider declares the molecular mass to be between 10 and 20 kDa; the concentration of LPS is therefore stated as the mass concentration (cLPS in μg ml−1). The LPS concentrations applied in the experiments were in the interval between 0.1 and 10 μg ml−1, which is below the reported critical micelle concentrations of intermediate chain length LPS (13–16 μg ml−1).24
Experimental protocol
After the flow was established in a microfluidic device, a suspension of 0.22 M glucose with vesicles was introduced into the entrance reservoir. The flow rate in the main channel was slowed down in order to monitor the passing vesicles. A small number of suitable vesicles without visible membrane protrusions were selected, trapped by optical tweezers, and then slowly repositioned from the main channel into the flow-free region in a diffusion chamber. Then the suspension in the entrance reservoir was exchanged with glucose solution of lower osmolarity (0.19 M) to cause the osmotic swelling of the vesicles and to accurately determine the radius (R0) and the surface area (A) of a spherical vesicle. Next, the suspension in the entrance reservoir was exchanged with glucose solution of higher osmolarity (0.26 M) causing the vesicles in a diffusion chamber to deflate. The flow rate in the main channel was increased and kept at its maximum value. Another exchange was made, adding the LPS solution at a chosen concentration (cLPS from 0.1 to 10 μg ml−1 in 0.26 M glucose) into the microfluidic system, and the vesicles in the chamber responded to the LPS insertion by morphological transformations (Fig. 1b); they were recorded for later analysis. Afterwards the characteristics of the vesicle response to LPS and the reversibility of the process were studied by removing the LPS from the system by washing the channels with pure glucose solution of the same osmolarity (0.26 M).Model of the LPS diffusion in the microfluidic chamber
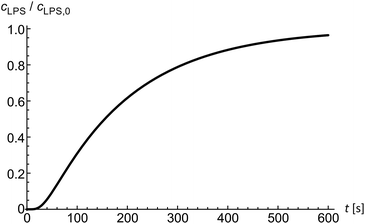
Diffusion of solutes into the diffusion chamber is modeled by a one-dimensional diffusion equation and by setting the boundary conditions to meet the exponential decrease of the flow–velocity profile at the entrance of the microfluidic chamber.14 Below the critical micelle concentrations24 we assume LPS to be in monomeric form. In the first approximation, the diffusion coefficient of a solute can be obtained from the comparison of the Einstein–Stokes radii with another molecule of a known Einstein–Stokes radius and a known diffusion coefficient. By comparing the sizes of LPS and hemoglobin molecules, the mean LPS diffusion coefficient was estimated to be DLPS ≈ 150 μm2 s−1. The diffusion equation is solved numerically to obtain the LPS concentration in dependence on time and position inside the microfluidic chamber (Fig. 2) at a given LPS concentration in the bulk solution.Theoretical framework
Equilibrium vesicle shapes under gravity
To set the ground for analyzing the vesicle response to the intercalating molecules we first outline and discuss the theory of the flaccid vesicle mechanics. The mechanical properties of a non-tensed lipid membrane are described by the ADE model,18–20 which expresses its elastic energy as:
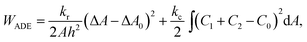 | (1) |
The equilibrium shapes of free-floating vesicles correspond to the minima of the membrane elastic energy (eqn (1)). But a vesicle containing a solution that is denser than the surrounding solution, as is the case in our experiments, sinks to the substrate due to gravity, and attains a shape that is different from the one of a free-floating vesicle. To obtain its exact equilibrium configuration, a corresponding gravitational energy term has to be included:25
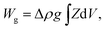 | (2) |
The gravity-modified equilibrium vesicle shapes are calculated by minimizing the sum of WADE (eqn (1)) and Wg (eqn (2)). The procedure is described in detail in (ESI, Section 1†). Briefly, the vesicle shapes correspond to solutions of the Euler–Lagrange differential equations, obtained by variation of the total vesicle energy (ESI, eqn (SI11)–(SI13)†). In contrast to the free-floating vesicles, where the equilibrium shapes do not depend on the vesicle size, the shapes of vesicles under gravity depend on their dimensions. At a given Δρ and at a given ratio between the nonlocal and local bending constants (q = kr/kc), the equilibrium shapes depend on four independent parameters: ΔA0, C0, the radius of a spherical vesicle (R0) with the surface area A = 4πR02, and the vesicle relative volume v, which describes the fullness of the vesicle (v = 3V/(4πR03)). The parameters ΔA0 and C0 both influence the intrinsic symmetry of the membrane and its consequent tendency to bend; it can be shown that both parameters can be combined into a single dimensionless parameter26–29 that we denote as the transmembrane asymmetry, TMA, to emphasize its origin:
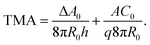 | (3) |
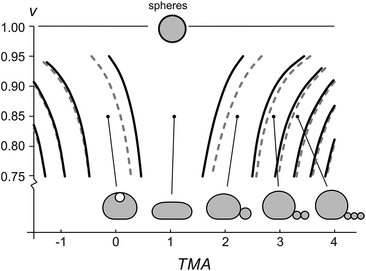
The shapes with different number of beads in the protrusion can be categorized into different shape classes. The transitions between the shape classes (marked by curves in Fig. 3) are calculated by comparing the energies of adjacent classes and finding the values of TMA and v, at which the total energies of both shapes are equal, whereas the details of the shape transformation and the energy barriers between the transitions were not analyzed. The transitions depend on vesicle size – the larger the vesicle, the more it is affected by the gravity and the larger TMA changes are needed to transform it. Noteworthy, the diagram (Fig. 3) schematically illustrates that the fuller the vesicle (the more its shape resembles a sphere), the higher the change in TMA that is required for triggering a formation of a bead-like protrusion. When the vesicle is full (v = 1) it can only have a spherical shape. When the relative volume is decreased as in our experiment, a small increase in TMA is sufficient for the vesicles to form one or more beads. Importantly, with the growing number of beads in the protrusion the relative volume of the mother vesicle is increasing as well. When the shape of the mother vesicle approaches the sphere, its position in the phase diagram approaches that of a free-floating vesicle.
Accurate calculations of the shapes with bead-like protrusions are numerically demanding. However, the mother vesicle sitting on a substrate can be approximated by a simpler model of a spherical dome with a flat bottom10 (ESI, Fig. SI1†). We have calculated the predictions for the radii of the vesicles and the beads in their protrusions according to both models and compared the results: specifically, we find that for a typical vesicle (R0 = 8 μm, v = 0.85), the calculated radii of the first bead, determined accurately and by the dome-model, differ for about 2%, and that the difference in calculated radii of the beads decreases with each consecutive bead, formed in the protrusion.
The effect of LPS intercalation on the transmembrane asymmetry
In general, intercalation of LPS molecules into the membrane affects its TMA through both the spontaneous curvature C0 and the preferred area difference ΔA0 and both parameters are proportional to the number of intercalated molecules (ESI, Section 3†). The preferred area difference can be conveyed in the fraction of the membrane surface occupied by LPS, denoted as ϕ = NLPSALPS/A, where NLPS is the number of intercalated LPS molecules and ALPS is the surface area of one LPS molecule. The preferred area difference ΔA0 is directly proportional to the number of intercalated molecules:| ΔA0 = ΔA00 + NLPSALPS = ΔA00 + ϕA, | (4) |
The spontaneous curvature of the membrane can be written as 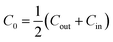 , where Cout and Cin are the spontaneous curvatures of the outer and the inner membrane leaflets, respectively;18 the estimate on the spontaneous curvature of each leaflet can be obtained from the area fractions and the intrinsic curvatures of the leaflet constituents. Considering that LPS intercalates into the outer leaflet only, the membrane spontaneous curvature can be expressed as:
, where Cout and Cin are the spontaneous curvatures of the outer and the inner membrane leaflets, respectively;18 the estimate on the spontaneous curvature of each leaflet can be obtained from the area fractions and the intrinsic curvatures of the leaflet constituents. Considering that LPS intercalates into the outer leaflet only, the membrane spontaneous curvature can be expressed as:
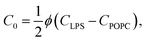 | (5) |
Taking eqn (4) and (5) and inserting them into eqn (3), the influence of LPS on TMA can be written as:
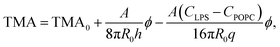 | (6) |
Equilibrium partitioning of LPS into the membrane
As the LPS molecules partition from the bulk solution into the outer membrane leaflet, the surface ratio of LPS molecules in the membrane ϕ is increasing,11 which changes the free energy of the system (lipid membrane with intercalated LPS molecules and the surrounding LPS solution).In general the system's chemical potential depends on the membrane's elastic energy, which changes due to insertion of hydrophobic molecules.10,34 In our case we have to take into account the elastic energy (eqn (1)) and gravitational energy (eqn (2)) and also (a) the entropic mixing of LPS molecules with POPC molecules, expressed in the approximation for low molar ratios of LPS in the membrane (the ideal gas limit), (b) the interactions between the intercalated LPS molecules and the lipid molecules in the membrane, and (c) the free energy of LPS molecules in the solution.35 These contributions to the free energy (F) can be expressed by the sequence of terms as:
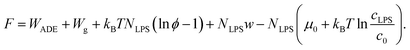 | (7) |
By joining the parameters that describe the partitioning of LPS molecules from the surrounding solution into the membrane, we can conveniently define the partition coefficient for LPS as 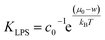 . The equilibrium partitioning of the LPS molecules into the membrane corresponds to the minimum of the free energy:
. The equilibrium partitioning of the LPS molecules into the membrane corresponds to the minimum of the free energy:
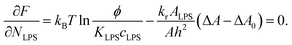 | (8) |
From here, the equilibrium surface ratio of LPS in the outer membrane can be expressed:
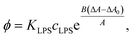 | (9) |
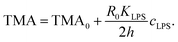 | (10) |
Results and discussion
Osmotic deflation
In our experimental procedure the vesicles in an osmotically swollen state are transferred into the diffusion chamber by optical tweezers. Their initial radii (R0) are measured. LPS binding to such vesicles does not cause visible changes in their morphology. With the aim of monitoring the shape transformations of the vesicles, they are osmotically deflated before adding LPS. Even in the absence of LPS, in the process of osmotic deflation most of the vesicles acquire shapes with bead-like protrusions on one or the other side of the membrane, and only a small number of vesicles become flaccid.14 This indicates that the vesicles made by the electroformation procedure may vary considerably in their initial TMA. We find that only moderate osmotic changes result in equilibrated and reasonably flaccid vesicles, and therefore typically use an osmolarity change from 0.22 Osm to 0.26 Osm, which results in vesicles with relative volumes of about 0.85. At the given relative volumes and the influence of gravity, the vesicles are in theory oblate in shape,25,28 which was also observed in our experiments.Shape transformations induced by small changes of LPS concentration
The shape of flaccid vesicles is controlled by regulating the concentration of LPS in the solution with a constant osmolarity. Solutions with different LPS concentrations were prepared in advance and sequentially introduced in the main channel, from where LPS molecules diffuse into the chamber with the observed vesicles. LPS partitions from the solution into the outer leaflet and induces membrane evaginations, while the changes in the vesicle volume or surface area are negligible.11 Fig. 4a and Movie 1 (ESI†) show a sequence of two controlled shape transformations. When the concentration of LPS was first changed from 0.185 to 0.22 μg ml−1, the vesicle shape changed from an invaginated vesicle shape to a discoid one, and after the concentration was changed from 0.22 to 0.25 μg ml−1 the shape transformed from a discoid to an evaginated shape, thus illustrating a vesicle shape being led across three shape-classes (as presented in Fig. 3). Importantly, the process is completely reversible since a decrease of the LPS concentration transforms the vesicle back to the initial shape. Of note, thermal undulations of the flaccid vesicle are present at all times, but the transitions from one shape-class to another are clearly noticeable (ESI, Movie 1†). This is in agreement with the theory which predicts discontinuous shape transitions.20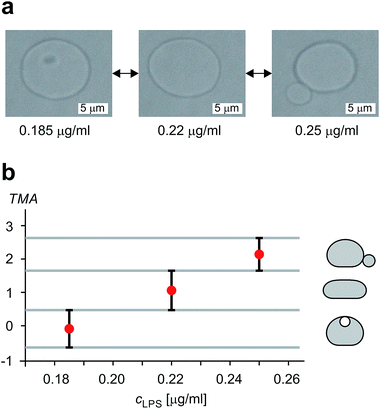 | ||
| Fig. 4 Illustration of controlled shape transformations. (a) Equilibrium shapes of a vesicle are shown at three sequentially interchanged LPS concentrations, illustrating the shape dependence on cLPS for the observed vesicle (R0 = 6 μm): the vesicle with one bead on the inner side of the membrane (at cLPS = 0.185 μg ml−1 LPS), the flaccid vesicle (at cLPS = 0.22 μg ml−1) and the vesicle with a bead on the outer side of the membrane (at cLPS = 0.25 μg ml−1). The vesicle reversibly responds to the concentration changes in both directions (Movie 1, ESI†). The relative volume of the vesicle is 0.85. (b) The experimentally determined transmembrane asymmetry (TMA) for the same three shapes as in the example above. Denoted by red dots at chosen cLPS values, the respective TMA value is estimated as the middle TMA value of the corresponding shape interval in the phase diagram (Fig. 3). The width of this interval is taken as a measurement uncertainty in determining the TMA value (denoted by the error bars). The horizontal grey lines represent the values of TMA corresponding to the transitions from one shape-class to another. | ||
The shapes of a vesicle in this experiment are then compared to theoretically calculated shapes in the phase diagram (Fig. 3) to obtain an estimate for the TMA value of each observed shape and depict the dependence of experimentally determined TMA on LPS concentration (Fig. 4b). For each shape a middle TMA value is taken from a corresponding TMA interval (Fig. 3) and at respective LPS concentration it is denoted by a red dot (Fig. 4b). We can thus determine the number of LPS molecules that intercalate at each LPS concentration by using eqn (10). We find that a concentration increase on the order of 0.03 μg ml−1 is needed for a transition from one shape-class to another (Fig. 4b). As the change of TMA is on the order of 1, we find that the surface area of the outer leaflet changes for approximately 0.1% of the total vesicle surface area, which is in agreement with previous reports8 and corresponds to approximately 700 LPS molecules per μm2 of the membrane (ALPS ≈ 1.5 nm2).11,36 In addition, assuming that at small concentrations the partitioning of LPS from the solution into the membrane follows a linear law, ϕ = KLPScLPS, we find the estimate of the partition coefficient for LPS to be KLPS ≈ 0.025 ml μg−1 (Fig. 4b). While each of the three equilibrium shapes is marked by a red dot in the middle of the respective TMA interval, the real TMA value can lie anywhere within that interval and the related measurement uncertainty in KLPS determination can be estimated as ΔKLPS ≈ ±0.0125 ml μg−1.
Extensive shape transformations induced by large changes of LPS concentration
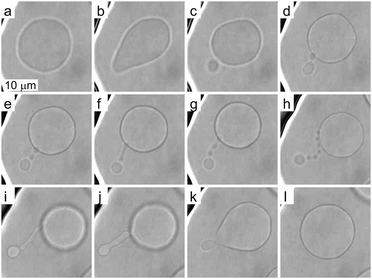
To investigate more extensive shape transformations, we applied larger LPS concentration changes in the main channel and monitored the vesicle response during the gradual LPS concentration increase in the chamber (Fig. 2). Fig. 5 and Movie 2 (ESI†) present a response of a flaccid vesicle during LPS concentration increasing to a final value of 1 μg ml−1 in the main channel (a similar response is obtained for all final concentrations up to 10 μg ml−1). First, the vesicle undergoes intense fluctuations and then a protrusion in a form of bead starts to appear on the outer side of the membrane. For different vesicles the time intervals to this point in vesicle shape evolution are different, in concord with the vesicles possessing different initial values of TMA. Of note, although the inhomogeneity of inclusions in the membrane might affect the vesicle shape through contributing to its TMA,37 this contribution is negligible at given LPS concentration gradients in the vicinity of the vesicle: the first bead formation was not conditioned by the vesicle orientation (the exposure to the chamber entrance). Afterwards we typically observe the formation of a string-of-beads between the mother vesicle and the first-formed bead (Fig. 5a–h and ESI, Movie 2†). In most cases, the first bead remains the largest and has an approximately constant radius, whereas the beads, that are formed later, all have more or less equal, smaller radii. Due to conservation of the volume and the surface area of the vesicle, the diameters of the small beads in the string decrease as their number is increasing (Fig. 5). When the vesicle shape transitions between adjacent shape-classes, typically the beads in a string elongate and transform into dumbbell-like shapes before one more spherical bead in the string is formed (Fig. 5e–g and ESI, Movie 2†). The time-intervals of the passages through these intermediate shapes are relatively short.Upon depletion of LPS from the solution we observed that even large shape transformations are reversible: the beads are “eaten up” by the mother vesicle either one by one or by merging first into a tube and then with the mother vesicle (Fig. 5h–l and ESI, Movie 2†). In some cases the depletion of LPS resulted in the formation of the inner protrusion in the form of equally sized beads (not shown).38 When repeating the cycles of LPS addition and subsequent depletion, the formation of outer and inner strings-of-beads was observed, correspondingly, in each cycle. Of note, the final TMA appeared higher than the initial one, which indicates that the intercalation of LPS molecules into the outer leaflet could accelerate the flipping of the lipid molecules from the inner to the outer leaflet.39
These observations are expected to be interpreted within the ADE model. However, the occurrence of the first, larger bead is not in accord with the theory, which predicts all the beads in the protrusion to have the same radii33 (ESI, Section 1†). This implies that the neck between this bead and the rest of the bead-string is so narrow that it significantly hinders the exchange of the membrane and the interior solution. Therefore when this occurred in the experiments, we have assumed that the neck of this bead has closed, and we deducted its volume and the surface area from the main vesicle and then independently analyzed the behavior of the rest of the vesicle (ESI, Section 2†). The experimental measurements of the radii of this first-formed, largest bead (Rl), radii of the mother vesicles (Rv), and of the small beads in the string (Rn) agree well with the radii, calculated by the dome-model (Fig. 6).
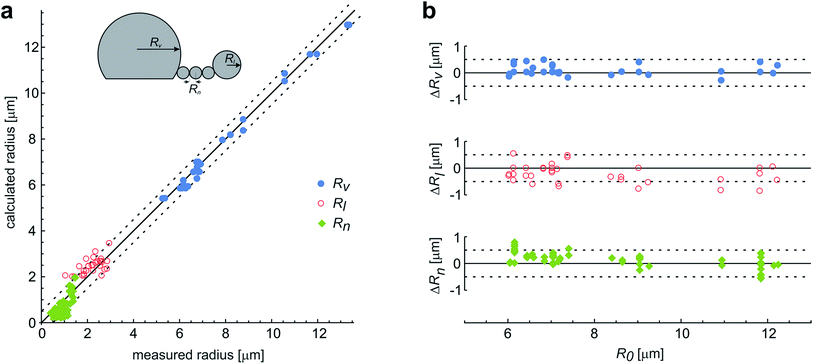 | ||
| Fig. 6 The comparison of the measured and the calculated radii of the vesicles with protrusions. (a) The results represent the measurements on 29 single vesicles, with each vesicle involved in up to three experiments with different LPS concentrations. The vesicles formed the protrusions due to the LPS partitioning (illustrated in the upper left corner). Most often, the protrusion from the main vesicle (with a radius Rv) was a string of equally sized beads (with radius Rn), except for the first-formed bead, which remained larger and constant in size (Rl). The measurements are compared to the calculated predictions on the vesicle and bead sizes, made on the basis of the initial radius of a spherical vesicle (R0) within a dome-model (ESI, Section 2†). (b) For the same vesicles the differences between the calculated and the measured radii of the vesicle and the beads in the protrusion are shown with respect to the initial radius of the respective osmotically swollen vesicle (R0). The differences are within the limits of the estimated measurement error, which is around 0.5 μm (as indicated by the dashed lines). | ||
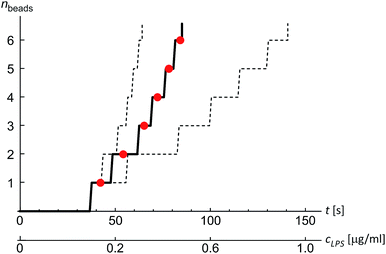
Finally, we analyzed the time evolution of the number of beads in a protrusion (n(t), Fig. 7) by assuming that the concentration of LPS around the vesicles increases gradually as LPS diffuses from the main channel into the diffusion chamber, which was modeled as described in the previous section (Fig. 2). The TMA values in dependence on time were then calculated (eqn (10)) and the corresponding number of beads in the protrusion was determined by finding the vesicle configuration with a minimal total energy. The slope of the “staircase” describing the dynamics of the formation of beads (Fig. 7) depends crucially on the partition coefficient, which was taken as the only free parameter for model fitting. Within the interval of LPS concentrations from 1 to 5 ml μg−1, the average value of the partition coefficient was found to have an average value KLPS ≈ 0.01 ml μg−1, with the obtained values scattered for a factor of 3. The average KLPS value is lower than that obtained from the analysis of equilibrated shapes at lower LPS concentrations (Fig. 4), presented in the previous section, but it is still within the estimated measurement errors. As these measurements are made during the ongoing transformations, it is possible that the differences arise because our model is not well-suited to describe the dynamics of the bead formation as it does not account for the energy barriers that have to be crossed when each new bead in the string is formed. Presumably the bead formation in the experiment is slower than the one estimated from our model and our fitting procedure therefore underestimates the partition coefficient value.
As a side note, eqn (9) predicts that at a given concentration of LPS in the bulk, more LPS can intercalate into a flaccid vesicle that is able to relax the tension in the outer leaflet by adjusting its shape, than into a tensed spherical vesicle. At small ratios of LPS in the membrane (ϕ) that were analyzed in our experiments, this difference is only slight – about 10% larger ϕ is predicted in totally relaxed membrane compared to the insertion into the spherical membrane and the linear relation between ϕ and cLPS is a reasonable approximation. On the other hand, in cases of hydrophobic molecules inserting into the membrane with a higher partition coefficient than the estimated KLPS, the exponential term of ϕ (eqn (9)) may no longer be neglected as it expresses an important characteristic of the partitioning into the membranes.
Conclusions
Our results validate the microfluidic diffusion chamber as a versatile universal framework for manipulation and shaping of flaccid giant lipid vesicles, a model system mimicking non-tensed cellular membranes. In particular, we showed controlled and reversible shape transformations by independently modifying the vesicle relative volume and the transmembrane asymmetry (TMA) due to intercalation of LPS molecules into the outer leaflet. We find that the gravity-extended area difference elasticity model, schematically presented in the phase diagram (Fig. 3), is in good agreement with the observed shape transformations (Fig. 4) and the measurements of the vesicle and bead sizes (Fig. 6). Based on the combined models of possible equilibrium vesicle shapes under gravity, of LPS diffusion into the microfluidic chamber and of LPS partitioning from the solution into the membrane, we described the dynamics of the formation of beads in the protrusion (Fig. 7). We observed that in most cases the first-formed bead remains the largest in the forming string of otherwise equally sized beads. This configuration indicates that in the induced response of the vesicle to the TMA increase the necks between the beads can close up and hinder the exchange of the membrane and the interior solution between the adjacent beads. A good control of neck formation is thus essential for any extensive shaping of membranes.In agreement with a number of previous studies, TMA proved to be a crucial parameter for membrane shaping. While the TMA value can be regulated by LPS addition or depletion, there are aspects of TMA regulation that are more difficult to manipulate. For example, electro-formation method produces vesicles that may possess very different initial TMA values, leading to different shape transformation dynamics even at the same experimental conditions (such as vesicle size or LPS concentration in the main channel). In addition, it has been shown that other mechanisms than the regulation of TMA are needed to obtain complex membrane compartments with large surface-to-volume ratios.40 To find new design schemes, one should turn to the mechanisms used by the cells for shaping their organelles, such as employing non-isotropic self-assembling scaffolding molecules or inducing adhesion between the flat membrane parts. If needed, the microfluidic diffusion chamber method can be readily extended by other approaches for membrane shaping, such as the temperature control, or integrated with techniques for the lab-on-a-chip. Finding the right recipe should be greatly facilitated also by theoretical modeling of possible paths that lead from a spherical vesicle to a compartment with a large surface-to-volume ratio.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The study was supported by Slovenian Research Agency through Grant P1-0055.References
- P. A. Beales and B. Ciani, Phys. Chem. Chem. Phys., 2015, 17, 15487 RSC.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094 CrossRef CAS PubMed.
- D. Kuchnir Fygenson, J. F. Marko and A. Libchaber, Phys. Rev. Lett., 1997, 79, 4497 CrossRef.
- D. Abreu, M. Levant, V. Steinberg and U. Seifert, Adv. Colloid Interface Sci., 2014, 208, 129 CrossRef CAS PubMed.
- E. Boroske, M. Elwenspoek and W. Helfrich, Biophys. J., 1981, 34, 95 CrossRef CAS PubMed.
- K. Berndl, J. Käs, R. Lipowsky, E. Sackmann and U. Seifert, EPL, 1990, 13, 659 CrossRef.
- J. Käs and E. Sackmann, Biophys. J., 1991, 60, 825 CrossRef.
- P. G. Petrov, J. B. Lee and H.-G. Döbereiner, EPL, 1999, 48, 435 CrossRef CAS.
- Y. Sakuma and M. Imai, Life, 2015, 5, 651 CrossRef PubMed.
- J. Kovačič, B. Božič and S. Svetina, Biophys. Chem., 2010, 152, 46 CrossRef PubMed.
- J. M. Alam and M. Yamazaki, Chem. Phys. Lipids, 2011, 164, 166 CrossRef CAS PubMed.
- J. Majhenc, B. Božič, S. Svetina and B. Žekš, Biochim. Biophys. Acta, Biomembr., 2004, 1664, 257 CrossRef CAS PubMed.
- A. Sakashita, N. Urakami, P. Ziherl and M. Imai, Soft Matter, 2012, 8, 8569 RSC.
- S. Vrhovec, M. Mally, B. Kavčič and J. Derganc, Lab Chip, 2011, 11, 4200 RSC.
- H. Dong, Q. Xiang, Y. Gu, Z. Wang, N. G. Paterson, P. J. Stansfeld, C. He, Y. Zhang, W. Wang and C. Dong, Nature, 2014, 511, 52 CrossRef CAS PubMed.
- C. R. H. Raetz and C. Whitfield, Annu. Rev. Biochem., 2002, 71, 635 CrossRef CAS PubMed.
- M. P. Sheetz and S. J. Singer, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 4457 CrossRef CAS.
- S. Svetina, M. Brumen and B. Žekš, Stud. Biophys., 1985, 110, 177 CAS.
- V. Heinrich, S. Svetina and B. Žekš, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3112 CrossRef CAS.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
- M. I. Angelova, S. Soléau, P. Méléard, J. F. Faucon and P. Bothorel, Prog. Colloid Polym. Sci., 1992, 89, 127 CAS.
- A. V. Wolf, M. G. Brown and P. G. Prentiss, in CRC Handbook of Chemistry and Physics, ed. R. C. Weast, CRC Press, Inc., Boca Raton, Florida, 59th edn, 1979, Section D, vol. 277, p. 308 Search PubMed.
- L. Yu, M. Tan, B. Ho, J. L. Ding and T. Wohland, Anal. Chim. Acta, 2006, 556, 216 CrossRef CAS PubMed.
- M. Kraus, U. Seifert and R. Lipowsky, Europhys. Lett., 1995, 32, 431 CrossRef CAS.
- S. Svetina and B. Žekš, in Biophysics of membrane transport, ed. J. Kuczela and S. Przestalski, Agricultural University of Wroclaw, Poland, 1992, vol. 2, pp. 116–140 Search PubMed.
- S. Svetina and B. Žekš, in Handbook of nonmedical applications of liposomes, ed. D. D. Lasič and Y. Berenholz, CRC Press, Inc., Boca Raton, Florida, 1996, vol. 1, pp. 13–42 Search PubMed.
- H.-G. Döbereiner, E. Evans, M. Kraus, U. Seifert and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4458 CrossRef.
- P. G. Petrov, J. B. Lee and H.-G. Döbereiner, EPL, 1999, 48, 435 CrossRef CAS.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101 CrossRef CAS PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182 CrossRef CAS.
- H. J. Deuling and W. Helfrich, Biophys. J., 1976, 16, 861 CrossRef CAS PubMed.
- B. Božič, G. Gomišček, V. Kralj-Iglič, S. Svetina and B. Žekš, Eur. Biophys. J., 2002, 31, 487 CrossRef PubMed.
- M. Mally, P. Peterlin and S. Svetina, J. Phys. Chem. B, 2013, 117, 12086 CrossRef CAS PubMed.
- T. L. Hill, An introduction to statistical thermodynamics, Dover Publications, New York, 1986 Search PubMed.
- S. Jo, E. L. Wu, D. Stuhlsatz, J. B. Klauda, G. Widmalm and W. Im, Methods Mol. Biol., 2015, 1273, 391 CAS.
- B. Božič, V. Kralj-Iglič and S. Svetina, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2006, 73, 041915–41921 CrossRef PubMed.
- M. Vitek, MSc thesis, University of Ljubljana, 2013.
- R. M. Raphael, R. E. Waugh, S. Svetina and B. Žekš, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2001, 64, 051913 CrossRef CAS PubMed.
- J. Derganc, B. Božič and R. Romih, PLoS One, 2011, 6, e26824 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The stationary shapes of vesicles under gravity. Accurate determination of the shape (ESI, Section 1). Simplified calculations by the dome-model (ESI, Section 2). Spontaneous curvature of the membrane with intercalated LPS molecules (ESI, Section 3). Movie 1: reversible shape alterations between the equilibrium shapes of a vesicle at very low LPS concentrations. Movie 2: reversible transformation of the membrane shape at high LPS concentrations. See DOI: 10.1039/c7ra05584f |
| This journal is © The Royal Society of Chemistry 2017 |