Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A facile method to fabricate hybrid hydrogels with mechanical toughness using a novel multifunctional cross-linker†
Jiangbo Li,
Hanchao Liu,
Chao Wang and
Guangsu Huang *
*
College of Polymer Science and Engineering, Sichuan University, Chengdu 610041, Sichuan, China. E-mail: Guangsu-huang@hotmail.com
First published on 13th July 2017
Abstract
Introducing both chemical and physical cross-links into a polymer network has emerged as a prevalent strategy to toughen hydrogels. However, most of these hybrid hydrogels are prepared in a multi-step route with more than one polymer or cross-linker, which is sophisticated and time consuming. Here, we report on a facile fabrication by in situ polymerization of acrylamide with a single multifunctional cross-linker. Compressive and tensile tests show the obtained hydrogels exhibit superior mechanical toughness. They can be stretched up to 1900% with a maximal fracture stress of nearly 500 kPa and be compressed by 90%. More impressively, the hydrogels can be fully recovered under compression. Rheological measurements suggest the co-existence of physical and chemical cross-links. Finally, an effective energy dissipation mechanism is observed and discussed. We conclude that the reversible physical cross-links originated from entanglement provide a mechanism of energy dissipation while the chemical cross-links ensure the structural integrity, which could be responsible for the improved mechanical properties.
1. Introduction
Hydrogels, which possess the properties of solids and liquids simultaneously, have a powerful development potentiality in many areas, including the pharmaceutical,1 medical,2 and engineering3 fields. However, hydrogels prepared by the traditional way often exhibit poor mechanical performance, including brittleness, low extensibility and irreversible deformation, which has severely constrained the scope of their applications.4 Tremendous efforts have been devoted to overcome these limitations.4–8 A general approach of improving the mechanical strength is to introduce an energy dissipation mechanism under large deformation and to maintain its original configurations after deformation. For example, a double-network hydrogel,8–10 which is a recognized tough and robust hydrogel, employs a sacrificial rigid network to dissipate energy and a loose network to maintain its shape and enlarges the damage zone before catastrophic failure. Another successful example is nanocomposite hydrogel whose elongation at break can reach 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000%.11–13 Its energy dissipation is due to the detachment of the polymer chains from nano-particles where the reversible cross-linking of polymer chains through nanoparticles is responsible for its structural integrity after deformation. Such strong and tough hydrogels also include slide-ring gels,14 triblock copolymers,15 tetra-PEG gels16 and macromolecular microsphere composite hydrogels.17,18
000%.11–13 Its energy dissipation is due to the detachment of the polymer chains from nano-particles where the reversible cross-linking of polymer chains through nanoparticles is responsible for its structural integrity after deformation. Such strong and tough hydrogels also include slide-ring gels,14 triblock copolymers,15 tetra-PEG gels16 and macromolecular microsphere composite hydrogels.17,18
More recently, a prevalent strategy to toughen hydrogels is introducing both covalent and physical cross-links into the polymer network. When these hybrid gels are deformed, the weak physical cross-links, derived from hydrogen bonding,19,20 electrostatic interactions,21,22 hydrophobic interactions,23,24 crystallization,25 inclusion complexation26 or interpolymer complexation,27 can break and dissipate energy. Therefore, the macroscopic rupture is delayed and the fracture toughness is increased. Moreover, due to the high elasticity given by the covalent cross-links, hydrogels still can recover to their original state after deformation. For example, Suo et al. developed a kind of alginate/PAM hybrid gels with a remarkable fracture toughness of ∼9000 J m−2 and notch insensitive properties, which is comprised of a Ca2+ cross-linked alginate network and a covalently cross-linked PAAm network.28 Okay et al. coupled the hydrophobic interactions into the covalent network to prepare a hybrid hydrogel, as a consequence, the resultant sample achieves greater improvement in mechanical property than that of the single covalent cross-linked hydrogels does.23 However, in spite of their unprecedented mechanical strength and excellent fatigue resistance, there are still concerns over the complicated fabrication process and few researches have worked on the possibility for building hybrid hydrogels through a single cross-linker and polymer.
Herein we propose, on the basis of general principle, a simple approach to synthesize a robust and tough hydrogel with both of the chemical and physical cross-linking networks. The entanglements between dangling chains have contributed to its energy dissipation while the covalent bonds stabilize the shape of the hydrogel. Due to its unique hybrid networks, the hydrogels have displayed superior mechanical toughness and apparent viscoelastic properties. The elongation at break during stretching can be over 1900%, meanwhile, they can recover to their original state after a compression ratio of 90%. Unlike those hybrid hydrogels reported previously,28–31 our hydrogels are fabricated in a simple way based on acrylamide where a multifunctional cross-linker is constructed and used. The multifunctional cross-linker contains a nucleus of melamine ring and several arms with controlled double bonds. It is suggested, hydrogels with different mechanical properties can be obtained by regulating the number of double bonds in the cross-linker. Moreover, as physical links are, in general, dependent on the strain, our hydrogels have shown different recovery capabilities between stretch and compression. Overall, we think we have put forward a new convenient method for the design of tough hydrogels.
2. Experimental section
2.1 Materials
Acrylamide (AM, Chengdu Kelong Chemical Reagent Factory, China, AR), melamine (Chengdu Kelong Chemical Reagent Factory, China), allyl glycidyl ether (AGE, Chengdu Best Reagent, China), tetramethylethylenediamine (TMEDA, Tianjin Bodi chemical industry LTD, China, AR), N,N′-methylenebisacrylamide (MBA, Tianjin Bodi chemical industry LTD, China, AR.), ethyl alcohol (Chengdu Kelong Chemical Reagent Factory, China, AR). The above chemicals are used as received. Water used in this study is ion-exchanged water unless otherwise mentioned.2.2 Synthesis of the multifunctional cross-linker (AGE-M)
To a 100 mL glass reactor equipped with a stirrer and a heating jacket, are added 1 g of melamine, 100 mL of deionized water, and a predetermined amount of allyl glycidyl ether (AGE). The molar ratio of AGE to melamine is 3 to 18. The mixture is heated while being stirred to 75 °C and kept at this temperature until the reaction is completed. The extent of reaction is followed by measuring the epoxy number with a dioxane solution of hydrochloric acid. The final products for the NMR characterizations are obtained by freeze drying the aqueous solution. The cross-linkers are labelled as AGEx-M where x is the molar ratio of AGE to melamine.2.3 Synthesis of the hydrogels
The MF hydrogels are prepared by free radical polymerization of AGE-M and acrylamide (AM) monomer with TMEDA as an accelerator at 25 °C. During the synthesis of hydrogels, the solutions of AGEx-M are used directly. Typically, AM (15 g), AGEx-M (the solution of which varying from 0.5 g to 2 g) and TMEDA (20 μL) are dissolved in 50 mL of deionized water. Then they are bubbled with N2 for 15 min to remove the dissolved oxygen. For hydrogel used for tensile test, the solution is poured to a mold consisting of a 1 mm silicone spacer sandwiched by two parallel glass plates, while for hydrogel used for compression test, the solution is transferred to a glass tube with inner diameter of 5 mm, respectively. Afterwards, 2 mL of freshly prepared solutions of KPS (1.5 × 10−4 mol) is added to initiate the reaction at 25 °C. After 24 h of polymerization, the as-prepared hydrogels are taken out.2.4 Scanning electron microscopy (SEM) measurement
Water-swollen hydrogel slices (1 mm–10 mm–10 mm) are flash frozen in liquid nitrogen for 5 min and immediately lyophilized for 48 h. Specimen cross-sections are subjected to Au-sputter coating and viewed with a field emission scanning electron microscope (SEM, FEI Quanta S-4800 FE-SEM) at an accelerated electron energy of 5 kV.2.5 Rheological measurements
Frequency sweep and creep experiments are used to investigate the viscoelastic properties of MF hydrogels. All the rheological measurements are done on a TA AR 2000 rheometer equipped with a Peltier plate for temperature control. A 40 mm parallel-plate geometry and a gap of 0.5 mm are used for all experiments which are done at 25 °C. A solvent trap is used to prevent water evaporation during the measurements. The reactions are conducted in the rheometer at 25 °C for up to about 3 h. After 3 h, frequency sweep measurements are carried out over the frequency range 0.1 to 100 Hz and a deformation amplitude γ0 = 0.01 is selected to ensure that the oscillatory deformation is within the linear regime. Creep experiments (constant stress) are done with an applied shear stress of 100 Pa for 10 min followed by 30 min of recovery.2.6 Compressing test
Compressing test is operated on a Instron 3360 electronic universal testing machine (Instron Corporation, MA, USA) in compressive mode at a constant speed of 5 mm min−1. The as-prepared hydrogels are cut into cylindrical shape with a height of 50 mm. The tests are carried out at 25 °C and repeated for at least 5 times for each sample.2.7 Tensile test
Tensile test is also performed on a Instron 3360 electronic universal testing machine (Instron Corporation, MA, USA). The as-prepared samples are cut into a dumbbell shape as standardized JISK6251-7 sizes (length 35 mm, width 2 mm, gauge length 12 mm) with a gel cutting machine (DumbBell Co., Ltd.). Both ends of the dumbbell-shaped samples are clamped and stretched at a constant velocity of 100 mm min−1, by which the stress–strain curves are recorded. Each sample is repeated for 5 times.3. Results and discussion
3.1 Preparation and characterization of the MF hydrogels
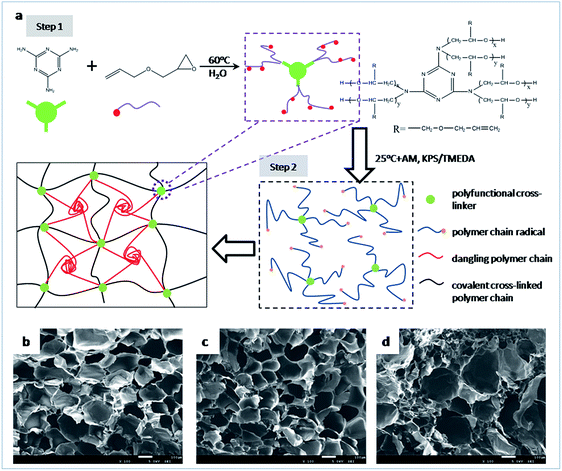
A schematic illustration of the preparation process and structure model of the high performance hydrogels is shown in Fig. 1a. First, a series of multifunctional cross-linkers bearing various amounts of unsaturated bonds are synthesized from melamine and allyl glycidyl ether (AGE) by ring-opening reaction. Since the poor solubility of melamine in water, a dilute concentration (1 g mL−1) of melamine is selected. Once the mixture is heated to 75 °C, melamine can be dissolved completely in few minutes under stirring. Then the reaction of melamine and AGE is quickly reacted due to its high effectiveness, and soon the mixture becomes pale yellow. The reaction is carried out for 6 h to ensure it reacted completely. The resultant products can be regarded to have a star-shaped structure where a melamine ring exists in its centre around which there are a few oligomers with double bonds. Obviously, the higher molar ratio of AGE to melamine in the recipe, the more double bonds combined to each melamine molecule. Thus, cross-linkers with different functionalities can be obtained by regulating the molar ratio of AGE to melamine. The prepared cross-linkers are labeled as AGEx-M where x represents the molar ratio of AGE to melamine in each cross-linker molecule. Details of their structures are characterized by NMR and shown in ESI.†Second, the MF hydrogels are fabricated by free radical polymerization of AM using AGEx-Ms as cross-linking agents under a redox system at room temperature. When TMEDA meets with the initiator KPS, AM polymerization is initiated. The acrylamide radical can initiate the double bonds in AGEx-M to result in AGEx-M radicals. Subsequently, long polymer chain radicals are generated when chain propagation occurs on AGEx-M radicals. These polymer chain radicals can either initiate another AGEx-Ms or be terminated by other free radicals. As a consequence, the former leads to covalent bridges between two AGEx-Ms while the latter results in dangling polymer chains. Moreover, dynamic physical links can also be established by entanglement between dangling polyacrylamide chains due to the strong intermolecular interaction. In this way, hydrogels consisting of chemical and physical cross-links are successfully constructed. The hydrogels are designated as MFx-y-z where x denotes that AGEx-M is used, y is the content of cross-linker as a weight percentage of water and z represents the molar concentration of monomer in the hydrogel preparation, respectively. For example, MF9-0.1-4 means that the MF hydrogel is prepared by AGE9-M whose content is 0.1 wt% at an AM molar concentration of 4 mol L−1. As a reference, the ordinary hydrogels (OR-gel) with single chemical networks are synthesized by MBA as cross-linker, and labeled as OR-0.1-4.
SEM images are used to reflect the three-dimensional network structure of fully swollen hydrogels in Fig. 1. By contrast, the pores existing in MF hydrogels are more uniform and regular than those in the OR hydrogel, which indicates networks in MF hydrogels are more homogeneous. The phenomena can be attributed to the diffusion of free dangling polymer chains.32,33 As they move preferably to the large porous regions where covalent cross-links are lower, the networks become more homogeneous. Moreover, a more compact microstructure can be obtained if the value of x is increased, which can be seen from the images of Fig. 1b and c.
3.2 Mechanical properties of the MF hydrogels
As vividly shown in Fig. 2, the resultant MF hydrogels display the predominant properties of softness, resilience, toughness, and complete transparency. They can be bent, knotted, compressed or stretched dozens of times and recover. To quantitatively investigate the mechanical properties of the MF hydrogels, a set of mechanical tests are performed. | ||
| Fig. 2 The MF hydrogels could withstand (a) ultrastretching, (b) knotting, (c) compression, and (d) maintain their shapes for weeks in a urea solution at a high temperature of 85 °C. | ||
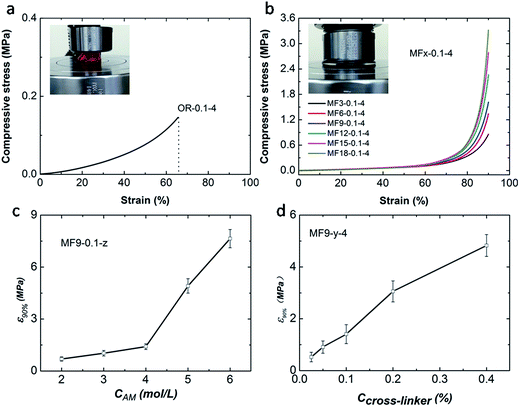
Compressive experimental results show that the as-prepared MF hydrogels are extremely strong and tough. All the MF hydrogels can be compressed to a 10% height of the original cylinder samples without fracture (Fig. 3b). Compared with MF hydrogels, the OR hydrogel breaks easily at a low deformation of about 60% as shown in Fig. 3a. Fig. 3b also illustrates that the number of vinyl groups in the cross-linker plays an important role in the strength of MF hydrogels. As the value of x increases from 3 to 18, the compressive stress at a strain of 90% increases from 0.86 MPa to 3.31 MPa, suggesting that the strength is raised. Moreover, the concentration of acylamide monomers (CAm) and AGEx-M (Ccross-linker) also have a great influence on the strength of MF hydrogels (Fig. 3c and d). Obviously, with a higher CAm and Ccross-linker, a denser and stronger cross-linking network is established.
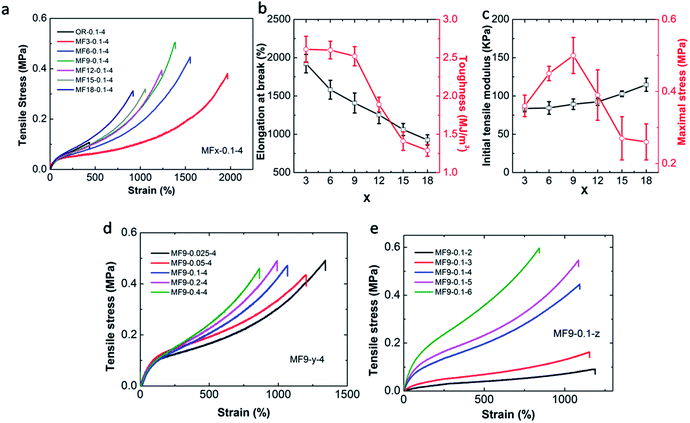
Tensile results show that the OR hydrogel is the weakest for it is quite brittle and fractured at a very low elongation which is only 440% with a tensile strength of 100 kPa (Fig. 4a). Conversely, the MF hydrogels are ultra stretchable. It is surprising that the MF3-0.05-4 hydrogel can achieve a fracture strain of 1900%. Its fracture strength is 0.38 MPa and the toughness, as defined by the area under the stress–strain curve, is 2.61 MJ m−3, all of which are much higher than the OR hydrogel.
Under the same condition, increasing the value of x will result in the following phenomena: (1) the elongation at break decreases from 1900% to 900%. (2) The maximum value of toughness declines from 2.61 MJ m−3 to 1.29 MJ m−3. (3) The strength of the hydrogels gets enhanced. The same trend can also be found when the cross-linker increases from 0.025% to 0.4% (Fig. 4d). Reasonably, we can conclude that MF hydrogel becomes stiffer and more brittle with the increase in the number of vinyl groups or the content of the cross-linker. It is perplexing that tensile modulus measured in the initial part just shows little dependency on x or the cross-linker content. The unexpected observation is also reported by Shi et al.34 However, when the CAm changes from 3 mol L−1 to 6 mol L−1, the mechanical strength varies greatly as strain–stress curves for the MF hydrogels separate with each other quickly at the beginning (Fig. 4e).
3.3 Deformation recoverability of the MF hydrogels
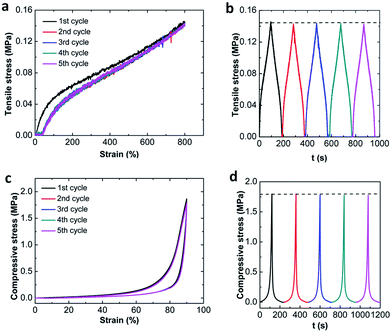
The deformation recoverability is studied by cyclic tests. Fig. 5 shows the five consecutive loading–unloading compression and tensile cycles of MF hydrogels up to a constant terminal strain below the failure without waiting, where MF9 is used as an example. During compression, very impressively, the five cycle hysteresis loops are almost completely overlapped with each other. No apparent decrease in the stress at the strain of 90% is detected in the stress–time curves on the cycle loading–unloading tests (Fig. 5a). Moreover, no residual strain is generated after unloading. These results suggest that the MF hydrogels can recover immediately and have excellent deformation recoverability under compression. In addition, an area between the loading–unloading curves can be also observed which means there is an effective energy dissipation mechanism existing in the MF hydrogels. However, in the course of tensioning, the behavior appears a little different. Only the first cycle has an obvious hysteresis loop and it becomes negligible for the following four cycles since they are nearly elastic and closely follow the path of the first unloading. Besides, a residual strain (about 40%) can be observed when the load is removed. Similar behavior can be reported by the filled rubbers or tough hydrogels such as double-network (DN)35 and nanocomposite (NC)36 hydrogels, where it is called “Mullins effect”. And, it is more like the DN hydrogels since the residual strain in our MF hydrogels is also permanent. Though the hysteresis energy disappears after the first loading, the terminal stress doesn't decay with the increase of loading cycles. Thus, no new fracture is generated and the MF hydrogels show absolute resilience during the following cycles.3.4 Viscoelastic properties of MF hydrogels
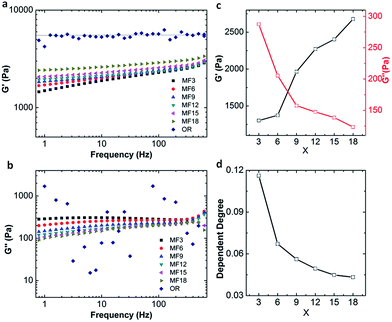
It is evident that the MF hydrogels show superior mechanical properties, particularly toughness, high stretchability and excellent fatigue resistance. As mentioned in 3.1, a network of MF hydrogels is constructed by both of the chemical cross-linking and linear dangling chains. And the entanglement of dangling chains has provided dynamic cross-links. The existence of chemical cross-links is confirmed by soaking the MF hydrogels in a urea solution which is a dissociator disrupting hydrogen bonds since MF hydrogels are stable and can maintain their shapes for weeks at a high temperature of 85 °C (Fig. 2d). Further, we investigate the rheological properties of the hydrogels as they can reflect molecular motions in polymer sensitively.A variety of storage moduli G′ and loss moduli G′′ of the hydrogels as a function of angular frequency are detected by frequency sweep measurements on rheometer. Results shown in Fig. 6a indicate that G′ of MF hydrogels is obviously dependent on frequency where it slightly increases as the augment of frequency. On the contrary, the OR hydrogel keeps almost constant in the whole frequency range, demonstrating its G′ is completely irrelevant with frequency. According to the extreme power law equation,37 the storage modulus in the low frequency region is responsive to frequency in an entanglement gel network or other physical networks (1), and less dependent in the perfect gel networks or chemical networks (2).
| G′ ∝ ω2 | (1) |
| G′ ∝ ω0 | (2) |
The index in the equation is defined as the dependent index for G′ vs. frequency and can be calculated to estimate the structure of a polymer network. In our MF hydrogels, the dependent degree is around 0.04–0.12 between 0 and 2, which demonstrates the existence of both covalent and physical cross-linking.
Loss modulus of the hydrogels is also obtained and displayed in Fig. 6c and values (about several hundred Pa) of G′′ can be obtained for all the MF hydrogels. As to OR gel, the loss modulus is erratic and random in the whole frequency range. This is due to the rheometer sensitivity limit to determine δ at oscillates around zero, suggesting G′′ is very low in OR gels as reported by Giasson et al.38 Because loss modulus represents the energy dissipation capacity during deformation, our MF hydrogels have stronger capacities in energy dissipation than the OR hydrogel. On the basis of the results, we can present that the MF hydrogels are viscoelastic while the OR hydrogels are almost absolutely elastic. Nevertheless, it must be pointed out that, in all the MF hydrogels, chemical cross-linking still dominates, for the dependence degree is closer to 0 and G′ (about 2000 Pa) is much higher than G′′ (about 200 Pa) as shown in Fig. 6. In frequency sweep tests, the modulus of OR hydrogel is much higher than that of all the MF hydrogels, which is different from the results in tensile tests. We attribute this incongruence to the different degree of deformation in the two tests.
In more detail, for the MF hydrogels, with the increase of x, G′ increases while G′′ decreases, and at a higher value of x, the fact that G′ is less dependent on the frequency confirms a more chemical cross-linked network with fewer dangling chains is formed. One possibility is that, as the number of vinyl groups increases, two AGEx-M radicals are much easier to meet with each other, and as a result, more covalent bridges are formed. Thus, the physical cross-links originated from the free dangling polymer chains are diminished.
3.5 Creep tests confirm viscoelastic properties
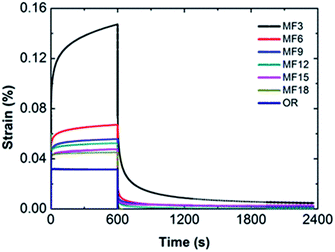
To further testify the results from rheological measurement and clarify the architectures of hydrogels, creep-recovery experiments are employed. As is shown in Fig. 7, the shapes of creep-recovery curves are different in the MF hydrogel and OR hydrogel. Once a constant stress is applied, an instantaneous deformation appears in both of the two kinds of hydrogels. However, the strain increases steadily over time in the MF hydrogel, showing a time-dependent trend. On the contrary, it keeps exactly the same and is almost time-independent in the OR hydrogel. Such disparity can also be discovered when the stress is removed, since a delayed recovery takes place in the MF hydrogel, while the OR hydrogel recovers instantly and completely. The creep curves suggest that structure arrangements exist in the MF hydrogels, while the OR hydrogel doesn't have such capability. And such structure arrangements prove the existence of free dangling polymer chain in the MF hydrogels.By comparison of different MF hydrogels, the maximum value γ reached at the end of the loading phase decreases with the value of x. Moreover, after cessation of shear stress, MF3 needs the longest time to reach a plateau value and exhibits a more obvious permanent strain which is a little different from other hydrogels. This suggests the presence of a predominant viscous deformation in MF3, showing a partly viscoelastic fluid-like behavior. As a consequence of lower degree of crosslinking, the slippage of the dangling chains can hardly be rearranged to its initial state. Accordingly, a permanent deformation remains after the unloading phase. In contrast, at a higher degree of cross-linking, such disentanglement presents in a smaller quantity and is restricted in a more complete chemical network, thus the gels exhibit a fast recovery rate and a lower permanent strain.
Burger's model can be introduced to analyze quantitatively the creep curves during the loading step. It is obtained by combination of three different elements in series: a spring with shear modulus G1, a Kelvin–Voigt element (a spring with shear modulus G2 and a dash pot with viscosity η2 arranged in parallel) and a dash pot with viscosity η3. According to this equation, the compliance J(t) is the sum of an instantaneous elastic response, J1 = 1/G1, a viscoelastic (delayed elastic) component, J2 = 1/G2(1 − exp(−t/λ2)), and unrecovered viscous flow, J3 = t/η3.
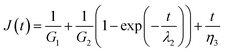 | (3) |
Data fitting isn't performed on the OR hydrogel as no noticeable creep region is found. From Table 1 it is clearly found that the elastic component G1 arises as the value of x goes up indicating that the cross-linking degree is enhanced. This agrees with the result of frequency sweep tests. The viscoelastic components, the value G2 and η have similar trends. Since the viscous η is correlated with the internal frictions between macromolecular chains, it suggesting the resistance to the polymer chains of slipping and stretching under stress. Therefore, for a lager value of x, the maximum value γ of MF hydrogels gets smaller. We may conclude that MF18 should have the largest content of dangling chains which is inconsistent with the results of frequency sweep tests on G′′. However, as the dangling chains are restricted in a chemical network, their slipping and stretching should condition that the chemical network is stretched. As a result, the resistance needed can be divided into two parts. One is the internal frictions during the slipping of polymer chains, the other owes to the deformation of a chemical network. Thus, more resistance is needed as x grows. The influence of η2 with respect to G2 can be displayed by the retardation time λ2 which goes down with the value of x. Overall, the MF hydrogels demonstrate to be viscoelastic materials and they vary in the content of entanglement of dangling chains which play an important role in the their properties.
| Sample name | G1 (Pa) | G2 (Pa) | η2 (Pa s) | λ2 (s) | η3 (Pa s) | R2 |
|---|---|---|---|---|---|---|
| MF3 | 1286.8 | 2427.2 | 4.0 × 104 | 16.4 | 1.8 × 104 | 0.989 |
| MF6 | 2130.3 | 7716.1 | 1.1 × 105 | 13.7 | 6.8 × 104 | 0.985 |
| MF9 | 2278.4 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.6 262.6 |
1.8 × 105 | 13.4 | 1.1 × 105 | 0.984 |
| MF12 | 2378.9 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985.6 985.6 |
2.1 × 105 | 11.7 | 1.6 × 105 | 0.983 |
| MF15 | 2400.7 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421.5 421.5 |
2.5 × 105 | 11.2 | 1.7 × 105 | 0.985 |
| MF18 | 2475.2 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761.9 761.9 |
2.2 × 105 | 7.4 | 3.3 × 105 | 0.976 |
3.6 Energy dissipation and the strengthening mechanism of MF hydrogels
To investigate the energy dissipation in detail, another cyclic loading–unloading test is conducted on the optimal hydrogel with successive strain increment (Fig. 8). It is clear that new damage is generated with the increase of the maximum strain, which can be revealed by the increment of energy dissipation in compressive procedure and the emergence of new hysteresis loop in tensile tests. From Fig. 5c and 8a, we can find the damage is recoverable during compression since all loading curves overlap together. However, under stretching, the damage seems irreversible and a permanent deformation can be observed. As the end stretch increases, each successive loading curve can be divided into two parts. One is elastic without any damage, while the other is damaged again. As a result, the permanent residual strain is dependent on the maximum strain which can be seen in Fig. 8b. Such different behaviors in compressive and tensile tests have also been observed in other tough hydrogels. One example is nanomicelle (NM) cross-linked hydrogels reported by Sun et al.39 These NM hydrogels could recover partially with a small residual strain upon unloading during stretching, meanwhile, they can recover to their original dimensions without losing toughness under compression. Their hysteresis energy dissipation roots from the deformation and dislocation of micelles under stress. However, most of the tough hydrogels exhibit the same deformation resilience during tension and compression. For example, the DN hydrogels35 behave elastically during the second loading with limited hysteresis in both cases. Their energy dissipation is attributed to the fracture of covalent bonds, thus the damage zone in the first cycle can barely recover. In NC hydrogels12 based on physical adsorption of polymers onto nanoparticles, the energy dissipation is due to the detachment of the polymer chains from nanoparticles which is reversible. After a certain time, the energy lost in the first cycle can be fully recovered. In our MF hydrogels, the energy dissipation is presumably due to chain entanglement which is responsible for their different behaviors in compressive and tensile tests.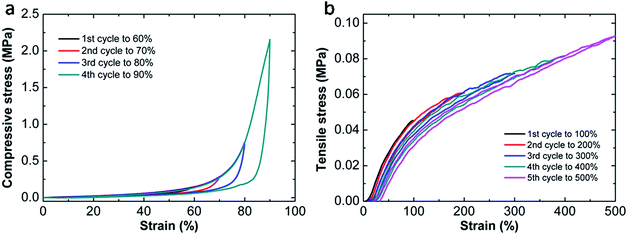 | ||
| Fig. 8 Cyclic loading–unloading curves with successive strain increment on the optimal hydrogel MF9-0.1-4 during compressive (a) and tensile tests (b). | ||
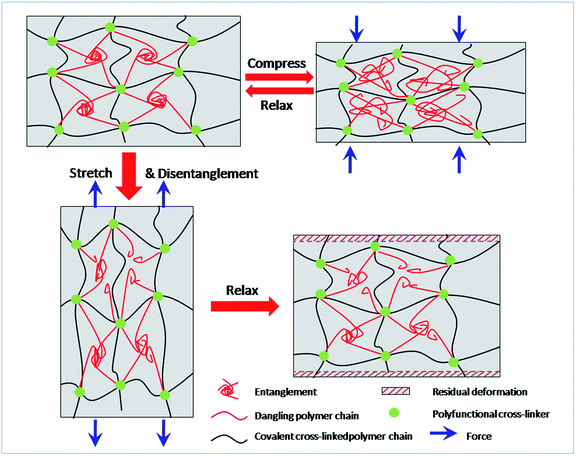
For decades, it has been recognized that chain entanglement between polymer chains and networks inside a hydrogel can significantly increase the mechanical properties of the hydrogel.40,41 When the MF hydrogels are subjected to tensile or compressive force, the slippage of entangled polymer chains is responsible for the energy dissipation and contributes to the improvement in mechanical toughness. Under compression, these sliding chains are still interpenetrated with each other. As a result, the network can reform and be recovered after unloading. On the other hand, they become isolated due to the large strain during stretching. Moreover, covalent bonds may also break under this degree of deformation which makes the residual strain become permanent. So the dissociated polymer chains can hardly entangle again. Thus energy dissipated in stretching is irreversible. Based on the discussion above, a brief sketch (Fig. 9) is proposed to illustrate the different changes of networks under compression and stretch.
4. Conclusion
We have demonstrated a new type of acrylamide-based hybrid hydrogels which is mechanically tough by fabricating a hybrid network with both of the covalent and physical links. Following the design strategy, a novel star-shaped cross-linker with multi-functionality is used. Both of syntheses of the cross-linker and hydrogel are easy and simple. The hydrogels are viscoelastic with splendid mechanical properties. They can be fully recovered and show superior fatigue resistance under compression. Specifically, as the active double bonds in the cross-linker can be controlled, a series of hydrogels with different mechanical properties can be obtained. Overall, owing to their advantages in mechanical property and preparation, we believe our MF hydrogels have very wide application foreground.Acknowledgements
This research was supported by the State Key Scientific Special Project (2016ZX05011-004) of China.References
- P. Gupta, K. Vermani and S. Garg, Drug Discovery Today, 2002, 7, 569–579 CrossRef CAS PubMed
.
- M. Verhulsel, M. Vignes, S. Descroix, L. Malaquin, D. M. Vignjevic and J. L. Viovy, Biomaterials, 2014, 35, 1816–1832 CrossRef CAS PubMed
.
- N. A. Chekina, V. N. Pavlyuchenko, V. F. Danilichev, N. A. Ushakov, S. A. Novikov and S. S. Ivanchev, Polym. Adv. Technol., 2006, 17, 872–877 CrossRef CAS
.
- S. Naficy, H. R. Brown, J. M. Razal, G. M. Spinks and P. G. Whitten, Aust. J. Chem., 2011, 64, 1007–1025 CrossRef CAS
.
- G. Gao, G. Du, Y. Cheng and J. Fu, J. Mater. Chem. B, 2014, 2, 1539–1548 RSC
.
- Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485–487 CrossRef CAS
.
- J. Hu, T. Kurokawa, T. Nakajima, T. L. Sun, T. Suekama, Z. L. Wu and J. P. Gong, Macromolecules, 2012, 45, 9445–9451 CrossRef CAS
.
- T. C. Suekama, J. Hu, T. Kurokawa, J. P. Gong and S. H. Gehrke, ACS Macro Lett., 2013, 2, 137–140 CrossRef CAS
.
- Y. Tanaka, J. P. Gong and Y. Osada, Prog. Polym. Sci., 2005, 30, 1–9 CrossRef CAS
.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC
.
- M. Kokabi, M. Sirousazar and Z. M. Hassan, European polymer journal, 2007, 43, 773–781 CrossRef CAS
.
- K. Haraguchi, Curr. Opin. Solid State Mater. Sci., 2007, 11, 47–54 CrossRef CAS
.
- M. Zhu, Y. Liu, B. Sun, W. Zhang, X. Liu, H. Yu and H. J. P. Adler, Macromol. Rapid Commun., 2006, 27, 1023–1028 CrossRef CAS
.
- K. Ito, Polym. J., 2007, 39, 489 CrossRef CAS
.
- K. J. Henderson, T. C. Zhou, K. J. Otim and K. R. Shull, Macromolecules, 2010, 43, 6193–6201 CrossRef CAS
.
- K. Fujii, H. Asai, T. Ueki, T. Sakai, S. Imaizumi, U. I. Chung and M. Shibayama, Soft Matter, 2012, 8, 1756–1759 RSC
.
- T. Huang, H. G. Xu, K. X. Jiao, L. P. Zhu, H. R. Brown and H. L. Wang, Adv. Mater., 2007, 19, 1622–1626 CrossRef CAS
.
- F. K. Shi, X. P. Wang, R. H. Guo, M. Zhong and X. M. Xie, J. Mater. Chem. B, 2015, 3, 1187–1192 RSC
.
- M. Guo, L. M. Pitet, H. M. Wyss, M. Vos, P. Y. Dankers and E. W. Meijer, J. Am. Chem. Soc., 2014, 136, 6969–6977 CrossRef CAS PubMed
.
- Q. Chen, L. Zhu, H. Chen, H. Yan, L. Huang, J. Yang and J. Zheng, Adv. Funct. Mater., 2015, 25, 1598–1607 CrossRef CAS
.
- J. Li, Z. Suo and J. J. Vlassak, J. Mater. Chem. B, 2014, 2, 6708–6713 RSC
.
- J. Yang, L. H. Deng, C. R. Han, J. F. Duan, M. G. Ma, X. M. Zhang and R. C. Sun, Soft Matter, 2013, 9, 1220–1230 RSC
.
- D. C. Tuncaboylu, M. Sari, W. Oppermann and O. Okay, Macromolecules, 2011, 44, 4997–5005 CrossRef CAS
.
- D. C. Tuncaboylu, A. Argun, M. Sahin, M. Sari and O. Okay, Polymer, 2012, 53, 5513–5522 CrossRef CAS
.
- L. Zhang, J. Zhao, J. Zhu, C. He and H. Wang, Soft Matter, 2012, 8, 10439–10447 RSC
.
- T. Kakuta, Y. Takashima and A. Harada, Macromolecules, 2012, 46, 4575–4579 CrossRef
.
- S. Naficy, J. M. Razal, P. G. Whitten, G. G. Wallace and G. M. Spinks, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 423–430 CrossRef CAS
.
- J. Y. Sun, X. Zhao, W. R. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney and Z. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed
.
- K. J. Jeong and A. Panitch, Biomacromolecules, 2009, 10, 1090–1099 CrossRef CAS PubMed
.
- B. Liu, A. K. Lewis and W. Shen, Biomacromolecules, 2009, 10, 3182–3187 CrossRef CAS PubMed
.
- J. Hao and R. A. Weiss, Polymer, 2013, 54, 2174–2182 CrossRef CAS
.
- M. Antonietti and H. Sillescu, Macromolecules, 1985, 18, 1162–1166 CrossRef CAS
.
- M. Yamaguchi, S. Ono and K. Okamoto, Mater. Sci. Eng., B, 2009, 162, 189–194 CrossRef CAS
.
- F. K. Shi, X. P. Wang, R. H. Guo, M. Zhong and X. M. Xie, J. Mater. Chem. B, 2015, 3, 1187–1192 RSC
.
- R. E. Webber, C. Creton, H. R. Brown and J. P. Gong, Macromolecules, 2007, 40, 2919–2927 CrossRef CAS
.
- S. Rose, A. Dizeux, T. Narita, D. Hourdet and A. Marcellan, Macromolecules, 2013, 46, 4095–4104 CrossRef CAS
.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed
.
- D. Calvet, J. Y. Wong and S. Giasson, Macromolecules, 2004, 37, 7762–7771 CrossRef CAS
.
- Y. N. Sun, G. R. Gao, G. L. Du, Y. J. Cheng and J. Fu, ACS Macro Lett., 2014, 3, 496–500 CrossRef CAS
.
- M. Huang, H. Furukawa, Y. Tanaka, T. Nakajima, Y. Osada and J. P. Gong, Macromolecules, 2007, 40, 6658–6664 CrossRef CAS
.
- L. W. Xia, R. Xie, X. J. Ju, W. Wang, Q. Chen and L. Y. Chu, Nat. Commun., 2013, 4, 2226 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05645a |
| This journal is © The Royal Society of Chemistry 2017 |