Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical insights into C–C bond formation through isonitrile insertion into a Cp*Ti complex†
Ming-Ran Du‡
a,
Xiang-Biao Zhang *a,
Sheng-Meng Si‡a,
Feng Yang‡a and
Lei Wang*b
*a,
Sheng-Meng Si‡a,
Feng Yang‡a and
Lei Wang*b
aSchool of Chemical Engineering, Anhui University of Science and Technology, Huainan 232001, People's Republic of China. E-mail: xbzhang_theochem@yahoo.com
bDepartment of Chemistry, Huaibei Normal University, Huaibei, Anhui 235000, People's Republic of China. E-mail: leiwang@chnu.edu.cn
First published on 11th July 2017
Abstract
The migratory insertion of isonitriles into the metal–C bond is important for constructing C–C bonds in organic and pharmaceutical syntheses. We examine the reaction of Cp*(Cl)Ti(diene) with isonitriles using density functional theory calculations. At room temperature, the bis-insertion reaction occurs easily for N-tert-butyl (tBu), methyl (Me), ethyl (Et), 2,6-dimethylphenyl (Ar), and N-1-adamantyl (1-Ad)-substituted isonitriles. The elementary reactions include the isomerisation of Cp*(Cl)Ti(diene), migratory insertion of the first isonitrile into a Ti–C bond, C–C reductive elimination, β-H elimination, migratory insertion of the second isonitrile into a Ti–H bond, and C–C reductive coupling. Two reliable fragmentation mechanisms are suggested for the bis-insertion products. For the bulkier tBuNC, ArNC, and 1-AdNC, the β-H elimination reaction pathway is dominant. For the smaller MeNC and EtNC, the γ-H elimination reaction pathway competes with the β-H elimination. For ArNC, the isomerisation reaction pathway to a newly predicted “σ complex” is kinetically favourable.
Introduction
Ti complexes have displayed powerful and tunable reactivities, in addition to other advantages such as the abundance of Ti in the earth and its low toxicity and cost.1–11 Tonks et al. reported the [py2TiCl2NPh]2-catalysed synthesis of α,β-unsaturated imines and α-(iminomethyl)cyclopropanes through multi-component reactions, which couple alkynes, alkenes, and diazenes and show substrate control selectivity.1d Xie et al. developed a methodology for the efficient synthesis of mono/bicyclic guanidines catalysed by a Ti-amide, and obtained chiral guanidines.2c Xia and Li et al. described an efficient method to synthesise substituted piperazines through Ti(NMe2)4-mediated C–C bond formation, and explored the reaction mechanism using density functional theory (DFT).3d Other researchers have reported Ti alkoxyimido (Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–OR) complexes and their reactivities towards internal alkynes;4c Ti hydrazides and their reactivities towards CO2, CS2, isocyanates, and organic nitriles;5b,5c and a dimeric Ti complex with terminal Ti
N–OR) complexes and their reactivities towards internal alkynes;4c Ti hydrazides and their reactivities towards CO2, CS2, isocyanates, and organic nitriles;5b,5c and a dimeric Ti complex with terminal Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O with reactivity towards CO2.6a Meanwhile, isonitriles could react with radicals, electrophiles, and nucleophiles with several advantages compared to the isoelectronic CO.12–18 For example, the isonitrile reactions do not have to be performed under pressure, and the reactivities can be easily modulated by introducing substituents of different sizes and electron-donating/withdrawing properties onto the nitrogen.
O with reactivity towards CO2.6a Meanwhile, isonitriles could react with radicals, electrophiles, and nucleophiles with several advantages compared to the isoelectronic CO.12–18 For example, the isonitrile reactions do not have to be performed under pressure, and the reactivities can be easily modulated by introducing substituents of different sizes and electron-donating/withdrawing properties onto the nitrogen.
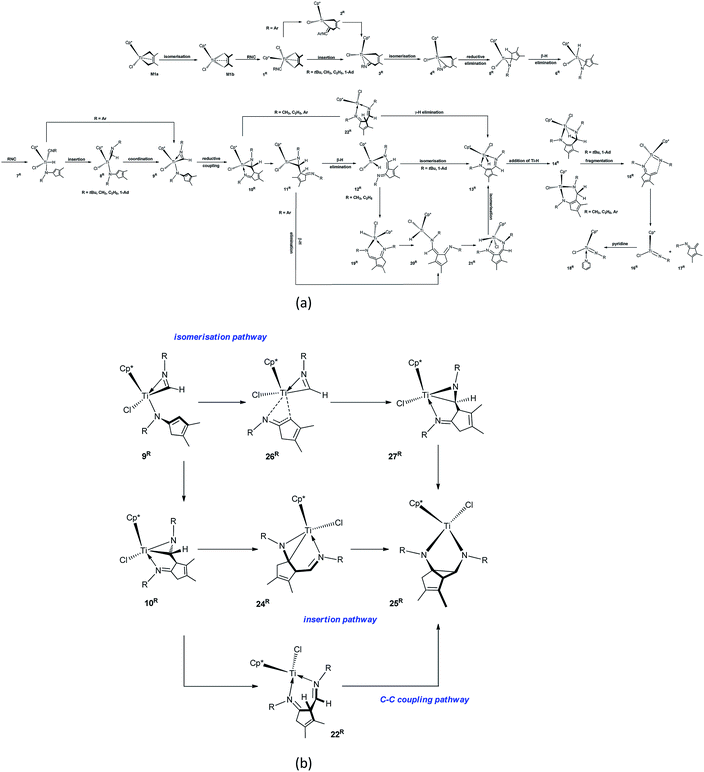
Complex nitrogen-containing cyclic compounds are prevalent in natural products and pharmaceuticals.19,20 For their synthesis, C–C bond formation reactions mediated by transition metals are the most important transformations.21–25 Currently, the migratory insertion of isonitriles into metal–C bonds is a potentially important method for forming C–C bonds.26–29 The resulting iminoacyl and metallaaziridine complexes are versatile intermediates in numerous transition metal-promoted stoichiometric and catalytic transformations. Xie et al. reported the migratory insertion of isonitriles into Ta–C bonds. They pointed out that alkyl and aryl isonitriles have different reactivity patterns, and the reaction products depend on the type and stoichiometry of the isonitriles.27a,27b Norton et al. described the migratory insertion of isonitriles into Zr–C bonds, and revealed the reversibility of the migratory insertion of tert-butyl (tBu) isonitrile.27d In particular, the migratory insertion of isonitrile into titanacyclobutane complexes bearing two Cp* allows the stereocontrolled synthesis of valuable cyclobutanimines.30 Recently, Norton et al. reported the reaction of Cp*(Cl)M(2,3-dimethylbutadiene) (M = Ti, M1a; M = Hf, 1a) with isonitriles.31 M1a can react with N-tBu- and N-1-adamantyl (1-Ad)-substituted isonitriles at room temperature to form the bis-insertion product titanaaziridines. At elevated temperatures in benzene with pyridine, the titanaaziridine fragments to afford the complex cyclic compound of α-methylene cyclopent-3-enimine. The proposed mechanism for the reaction of M1a with N-tBu-substituted isonitrile (tBuNC) is shown in Scheme 1. However, for the reaction of 1a with N-2,6-dimethylphenyl (Ar)-substituted isonitrile (ArNC), diazahafnacyclopentane with the Ar groups is the final product, and the bis-insertion product of the isonitrile (the Hf analogue of titanaaziridine) is regarded as an intermediate instead. The work of Norton et al. not only expands the application of Ti complexes for C–C bond formation through the migratory insertion of isonitriles into Ti–C bond, but also provides a new method for synthesising complex cyclic compounds with potential bioactivity.
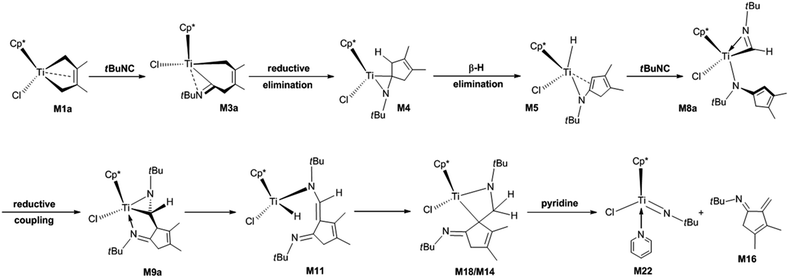 | ||
| Scheme 1 Proposed mechanism for the formation of N-tBu-substituted α-methylene cyclopentenimine via the four-membered titanacycle. | ||
However, several important aspects about the reaction of M1a with isonitriles remain poorly understood: (1) the detailed mechanisms for the formation of titanaaziridines via bis-insertion and their fragmentations; (2) the effects of substituent groups on the nitrogen of isonitrile, in terms of the reaction mechanisms; (3) whether diazatitanacyclopentane, the Ti analogue of diazahafnacyclopentane, can be generated; and (4) if yes, which isonitriles should be used for this purpose. Herein, we used DFT calculations to theoretically examine the reactions of M1a with various isonitriles, in the hope of helping chemists explore new methods to form C–C bonds and synthesise new substances. Isonitriles bearing tBu, methyl (Me), ethyl (Et), Ar, and 1-Ad groups were used as substrates to reveal their steric and electronic effects on the reaction mechanism and products. The substituent Et is more electron-donating than Me; tBu, Ar and 1-Ad are bulkier than Me and Et; and tBuNC, ArNC, and 1-AdNC have been experimentally adopted by Norton et al.31
Computational details
All calculations were performed using the Gaussian 09 program package.32 Molecular structures were optimised by the B3LYP/BS1 method.32a,33,34 Solvent effects were taken into account by invoking the PCM solvation model using n-pentane and benzene,35 which were experimentally used as solvents for crystallisation and reaction medium, respectively.31 In the basis sets (BS1), the Ti and Cl atoms are described by the LANL2DZ basis sets improved with a set of f- or d-polarisation functions (α = 1.506 for Ti, α = 0.640 for Cl) with effective core potentials (ECPs),36–40 while the other atoms are represented with the 6-311+G(d,p) basis sets, except for atoms on the tBu, Me, Et, Ar, and 1-Ad substituent groups which are described by 6-31G basis sets.41–43 As shown in ESI,† this theoretical model has been proven to be reliable, as it gives results in good agreement with experimental data. Meanwhile, frequency calculations were performed to confirm that the calculated species are minima (no imaginary frequency) or transition states (one and only one imaginary frequency), and to provide thermodynamic corrections at 1 atm and 298.15 K. Moreover, intrinsic reaction coordinate (IRC) calculations were carried out to ensure that the obtained transition states are correctly connected to the identified intermediates.44 Finally, more accurate energies were calculated using the 6-311G(d,p) instead of the 6-31G basis sets in the BS1 (BS5). In order to take the dispersion effects into account, the B3LYP-D3/BS5//B3LYP/BS1 calculations on the optimum reaction pathways and important species were carried out at the same time.32b,45 Natural bond orbital (NBO) analysis was performed at the stationary points, and the Wiberg bond indices (WBIs) and interaction energies between the Ti centre and other molecular moieties were computed by the NBO program as implemented in the G09 package.32a Corrected Gibbs free energies were used to describe the energetic profiles of the reactions.Results and discussion
Mechanism of the reaction of M1a with tBuNC
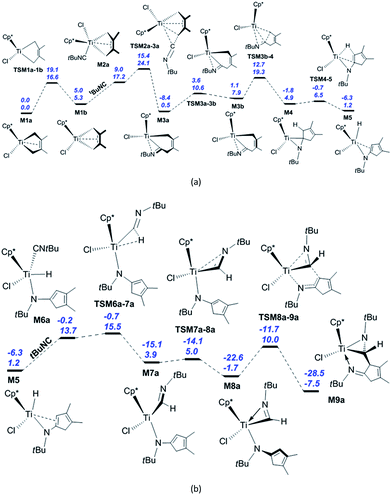
We begin with the reaction of M1a with tBuNC, whose calculated reaction pathway is shown in Scheme 1. The coordination of the isonitrile to M1a and its subsequent migratory insertion into the Ti–C bond [Scheme S1(a)†] require an energy of 29.6 kcal mol−1, which is too high for the reaction to occur. Instead, M1a is converted to M1b via TSM1a–1b, with the energy barrier of 16.6 kcal mol−1 and endergonic by 5.3 kcal mol−1 [Fig. 1(a)]. The dispersion-corrected energy barrier is 19.1 kcal mol−1, which is larger than the uncorrected value. Therefore, the dispersion effects increase the energy barrier of the isomerisation from M1a to M1b. M1a and M1b both feature the coordinated C2–C3 π-double bond, as evidenced by the lengths of Ti–C2 and Ti–C3 (2.35 and 2.35 Å in M1a, 2.38 and 2.38 Å in M1b, respectively; see Fig. S1†). The C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 π-bond coordination to Ti is further confirmed by the WBIs of Ti–C2 (0.29 for M1a and 0.28 for M1b) and Ti–C3 (0.29 for M1a and 0.28 for M1b). The interaction energies between the C2
C3 π-bond coordination to Ti is further confirmed by the WBIs of Ti–C2 (0.29 for M1a and 0.28 for M1b) and Ti–C3 (0.29 for M1a and 0.28 for M1b). The interaction energies between the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 π orbitals and the valence orbitals on Ti are calculated to be 52.2 kcal mol−1 for M1a and 54.4 kcal mol−1 for M1b, respectively. The isonitrile coordinates to M1b with the carbon atom end-on, a process that is endergonic by 11.9 kcal mol−1 due to the entropy reduction (−42.0 cal mol−1 K−1). After the dispersion corrections, this endergonicity is reduced to 4.0 kcal mol−1. Therefore, the dispersion effects significantly influence the isonitrile coordination. In M2a, the lengths of Ti–C1 (2.27 Å) and Ti–C4 (2.53 Å) are longer than that (2.15 Å) in M1b, and the structure of M2a is consistent with the coordinated C2–C3 π-bond (Ti–C2 = 2.29 Å, Ti–C3 = 2.41 Å). The calculated WBIs of Ti–C2 and Ti–C3 (0.42 and 0.24) confirm the C2–C3 π-bond coordination to the Ti centre in M2a. The subsequent migratory insertion of the isonitrile into the neighbouring Ti–C bond requires 6.9 kcal mol−1 to afford M3a with an exergonicity of 16.7 kcal mol−1. The dispersion effects decrease the energy barrier of the isonitrile insertion into the Ti–C bond by 0.5 kcal mol−1 and increase the exergonicity by 0.7 kcal mol−1. This energy requirement is much lower, and the endergonicity is larger compared to those of a similar insertion into the PdIII–C bond reported by Yan et al. (15.4 and 7.7 kcal mol−1, respectively).26c However, the reported activation energy for the PdIII complex is much lower than that for the migratory insertion of isonitrile into Ti–C bond in M2b [23.4 kcal mol−1; see Scheme S1(a)†]. Obviously, the energy required for isonitrile insertion into the metal–C bond varies greatly with the metal complex and the configuration. The energy barrier for the migratory insertion of isonitrile into the Ti
C3 π orbitals and the valence orbitals on Ti are calculated to be 52.2 kcal mol−1 for M1a and 54.4 kcal mol−1 for M1b, respectively. The isonitrile coordinates to M1b with the carbon atom end-on, a process that is endergonic by 11.9 kcal mol−1 due to the entropy reduction (−42.0 cal mol−1 K−1). After the dispersion corrections, this endergonicity is reduced to 4.0 kcal mol−1. Therefore, the dispersion effects significantly influence the isonitrile coordination. In M2a, the lengths of Ti–C1 (2.27 Å) and Ti–C4 (2.53 Å) are longer than that (2.15 Å) in M1b, and the structure of M2a is consistent with the coordinated C2–C3 π-bond (Ti–C2 = 2.29 Å, Ti–C3 = 2.41 Å). The calculated WBIs of Ti–C2 and Ti–C3 (0.42 and 0.24) confirm the C2–C3 π-bond coordination to the Ti centre in M2a. The subsequent migratory insertion of the isonitrile into the neighbouring Ti–C bond requires 6.9 kcal mol−1 to afford M3a with an exergonicity of 16.7 kcal mol−1. The dispersion effects decrease the energy barrier of the isonitrile insertion into the Ti–C bond by 0.5 kcal mol−1 and increase the exergonicity by 0.7 kcal mol−1. This energy requirement is much lower, and the endergonicity is larger compared to those of a similar insertion into the PdIII–C bond reported by Yan et al. (15.4 and 7.7 kcal mol−1, respectively).26c However, the reported activation energy for the PdIII complex is much lower than that for the migratory insertion of isonitrile into Ti–C bond in M2b [23.4 kcal mol−1; see Scheme S1(a)†]. Obviously, the energy required for isonitrile insertion into the metal–C bond varies greatly with the metal complex and the configuration. The energy barrier for the migratory insertion of isonitrile into the Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond reported by Clot and Mountford et al. is larger than our calculated value (14.0 vs. 6.9 kcal mol−1).5c The reversibility of the migratory insertion of the isonitrile into Ti–C bond is consistent with that of tBuNC into the Zr–C bond.27d In TSM2a–3a, the C5–C4 σ-bond (1.92 Å) is formed, the Ti–C4 distance (2.47 Å) is shortened, and C5 changes from sp to sp2 hybridisation, accompanied by the bending of the Ti–C5–N1 structure. In M3a, the N atom is coordinated to the Ti centre (Ti–N1 = 2.06 Å), and the C2–C3 π-double bond is repelled from the Ti centre to create a 14-valence electron configuration. The calculated WBIs of Ti–C2 and Ti–C3 (0.03 and 0.05, respectively) are so small that the interaction between the Ti centre and the C2–C3 π-double bond can be ignored, and C5–N1 is a characteristic double bond (WBI = 1.72). The calculated interaction energy between the empty d orbital on the Ti centre and the lone pair on the nitrogen is about 97 kcal mol−1, and the WBI of Ti–N1 is 0.62. While the distorted five-membered titanacyle is converted to a six-membered one, ring tension is released so that the system is exergonic by 16.7 kcal mol−1. Overcoming the energy barrier of 10.1 kcal mol−1, M3a is converted to an isomer M3b (Ti–C1 = 2.21 Å) via TSM3a–3b. The increased ring tension leads to the endergonicity of 7.4 kcal mol−1. After considering the dispersion effects, the energy barrier of this isomerisation increases by 1.9 kcal mol−1 and the endergonicity increases by 2.1 kcal mol−1. The reductive elimination from M3b produces the titanaaziridine M4 (Ti–C1 = 2.43 Å, C5–C1 = 1.50 Å) through TSM3b–4 (Ti–C1 = 2.36 Å, C5–C1 = 1.97 Å). This process involves breaking the Ti–C1 bond and forming the C5–C1 bond, with the energy barrier and exergonicity of 11.4 and 3.0 kcal mol−1, respectively. It is easily found that dispersion effects have a marginal influence on this process. In M4 there is a strong agostic interaction between the Ti centre and C1–H1 bond, as evidenced by the lengths of Ti–H1 (1.98 Å) and C1–H1 (1.17 Å). The calculated WBI of Ti and H1 is 0.19, and the interaction energy between valence orbitals on Ti and C1–H1 σ orbitals is 70.9 kcal mol−1. The subsequent β-H elimination via TSM4–5 requires a relatively lower energy of 1.6 kcal mol−1 (Ti–C5 = 2.26 Å, Ti–C1 = 2.36 Å, Ti–H1 = 1.72 Å, and C1–H1 = 1.51 Å) to furnish the Ti hydride M5 (Ti–C5 = 2.42 Å, Ti–C1 = 2.62 Å) with an exergonicity of 3.7 kcal mol−1. The small energy barrier and the exergonicity stem from the conjugation with another π-double bond. In TSM4–5, the Ti–C5 and Ti–N1 bonds are lengthened, the length of Ti–C1 is shorter than that in M4, and the C5–C1 single bond is changed to a π-double bond. In M5, the lengths of Ti–C5 and Ti–C1 indicate that there is a weak interaction between the Ti centre and the C5–C1 π-double bond. The coordination of a second isonitrile to M5 generates M6a (Ti–C7 = 2.14 Å, Ti–H1 = 1.68 Å) with an endergonicity of 12.5 kcal mol−1 [Fig. 1(b)]. After the dispersion corrections, the endergonicity is decreased
to 6.1 kcal mol−1. In M6a, the C5–C1 π-double bond is repelled from the Ti centre to maintain a 14-valence electron configuration. Then, the migratory insertion of the isonitrile into the Ti–H bond generates M7a via TSM6a–7a (Ti–C7 = 2.06 Å, Ti–H1 = 1.71 Å, and C7–H1 = 1.66 Å) with an energy barrier of only 1.8 kcal mol−1, and the system is exergonic by 9.8 kcal mol−1. The dispersion effects increase the exergonicity of the system by 5.1 kcal mol−1. Compared to M6a, the bond parameters of TSM6a–7a imply that it is an early transition state. Through the N coordination, M7a is easily converted to the 14-valence electron complex M8a via TSM7a–8a, overcoming a negligible energy barrier of 1.1 kcal mol−1. The exergonicity (5.6 kcal mol−1) originates from the higher stability of M8a compared to M7a. The dispersion corrections lead to an increase of the exergonicity by 1.9 kcal mol−1. Subsequently, M8a undergoes the C–C reductive coupling to afford the titanaaziridine M9a via TSM8a–9a (Ti–N1 = 2.15 Å, and C7–C1 = 2.10 Å), a process that requires 11.7 kcal mol−1 and releases 5.8 kcal mol−1 in energy. The dispersion-corrected energy barrier is 10.9 kcal mol−1, which is 0.8 kcal mol−1 less than the uncorrected value.
N bond reported by Clot and Mountford et al. is larger than our calculated value (14.0 vs. 6.9 kcal mol−1).5c The reversibility of the migratory insertion of the isonitrile into Ti–C bond is consistent with that of tBuNC into the Zr–C bond.27d In TSM2a–3a, the C5–C4 σ-bond (1.92 Å) is formed, the Ti–C4 distance (2.47 Å) is shortened, and C5 changes from sp to sp2 hybridisation, accompanied by the bending of the Ti–C5–N1 structure. In M3a, the N atom is coordinated to the Ti centre (Ti–N1 = 2.06 Å), and the C2–C3 π-double bond is repelled from the Ti centre to create a 14-valence electron configuration. The calculated WBIs of Ti–C2 and Ti–C3 (0.03 and 0.05, respectively) are so small that the interaction between the Ti centre and the C2–C3 π-double bond can be ignored, and C5–N1 is a characteristic double bond (WBI = 1.72). The calculated interaction energy between the empty d orbital on the Ti centre and the lone pair on the nitrogen is about 97 kcal mol−1, and the WBI of Ti–N1 is 0.62. While the distorted five-membered titanacyle is converted to a six-membered one, ring tension is released so that the system is exergonic by 16.7 kcal mol−1. Overcoming the energy barrier of 10.1 kcal mol−1, M3a is converted to an isomer M3b (Ti–C1 = 2.21 Å) via TSM3a–3b. The increased ring tension leads to the endergonicity of 7.4 kcal mol−1. After considering the dispersion effects, the energy barrier of this isomerisation increases by 1.9 kcal mol−1 and the endergonicity increases by 2.1 kcal mol−1. The reductive elimination from M3b produces the titanaaziridine M4 (Ti–C1 = 2.43 Å, C5–C1 = 1.50 Å) through TSM3b–4 (Ti–C1 = 2.36 Å, C5–C1 = 1.97 Å). This process involves breaking the Ti–C1 bond and forming the C5–C1 bond, with the energy barrier and exergonicity of 11.4 and 3.0 kcal mol−1, respectively. It is easily found that dispersion effects have a marginal influence on this process. In M4 there is a strong agostic interaction between the Ti centre and C1–H1 bond, as evidenced by the lengths of Ti–H1 (1.98 Å) and C1–H1 (1.17 Å). The calculated WBI of Ti and H1 is 0.19, and the interaction energy between valence orbitals on Ti and C1–H1 σ orbitals is 70.9 kcal mol−1. The subsequent β-H elimination via TSM4–5 requires a relatively lower energy of 1.6 kcal mol−1 (Ti–C5 = 2.26 Å, Ti–C1 = 2.36 Å, Ti–H1 = 1.72 Å, and C1–H1 = 1.51 Å) to furnish the Ti hydride M5 (Ti–C5 = 2.42 Å, Ti–C1 = 2.62 Å) with an exergonicity of 3.7 kcal mol−1. The small energy barrier and the exergonicity stem from the conjugation with another π-double bond. In TSM4–5, the Ti–C5 and Ti–N1 bonds are lengthened, the length of Ti–C1 is shorter than that in M4, and the C5–C1 single bond is changed to a π-double bond. In M5, the lengths of Ti–C5 and Ti–C1 indicate that there is a weak interaction between the Ti centre and the C5–C1 π-double bond. The coordination of a second isonitrile to M5 generates M6a (Ti–C7 = 2.14 Å, Ti–H1 = 1.68 Å) with an endergonicity of 12.5 kcal mol−1 [Fig. 1(b)]. After the dispersion corrections, the endergonicity is decreased
to 6.1 kcal mol−1. In M6a, the C5–C1 π-double bond is repelled from the Ti centre to maintain a 14-valence electron configuration. Then, the migratory insertion of the isonitrile into the Ti–H bond generates M7a via TSM6a–7a (Ti–C7 = 2.06 Å, Ti–H1 = 1.71 Å, and C7–H1 = 1.66 Å) with an energy barrier of only 1.8 kcal mol−1, and the system is exergonic by 9.8 kcal mol−1. The dispersion effects increase the exergonicity of the system by 5.1 kcal mol−1. Compared to M6a, the bond parameters of TSM6a–7a imply that it is an early transition state. Through the N coordination, M7a is easily converted to the 14-valence electron complex M8a via TSM7a–8a, overcoming a negligible energy barrier of 1.1 kcal mol−1. The exergonicity (5.6 kcal mol−1) originates from the higher stability of M8a compared to M7a. The dispersion corrections lead to an increase of the exergonicity by 1.9 kcal mol−1. Subsequently, M8a undergoes the C–C reductive coupling to afford the titanaaziridine M9a via TSM8a–9a (Ti–N1 = 2.15 Å, and C7–C1 = 2.10 Å), a process that requires 11.7 kcal mol−1 and releases 5.8 kcal mol−1 in energy. The dispersion-corrected energy barrier is 10.9 kcal mol−1, which is 0.8 kcal mol−1 less than the uncorrected value.
Among the elementary reaction steps, the coordination of the isonitrile, migratory insertion of the isonitrile into Ti–C bond, isomerisation of the six-membered titanacycle, C–C reductive elimination, and C–C reductive coupling require relatively higher energies. With the formation of M9a, the reaction is exergonic by 7.5 kcal mol−1. Three steps, namely the isomerisation of M1a to M1b, the coordination of the first isonitrile, and its subsequent migratory insertion into the Ti–C bond determine the apparent activation energy of the whole reaction, which is 24.1 kcal mol−1. Considering the dispersion effects, the exergonicity for the formation of M9a is increased to 28.5 kcal mol−1. Owing to the much reduced endergonicity for the isonitrile coordination, the isomerisation of M1a to M1b becomes the sole elementary reaction for determining the reaction rate. This feature is consistent with the fact that no intermediates (M3a, M4, M5 or M8a) have been found experimentally.31 The coordination of the second isonitrile to M3a and its subsequent migratory insertion to generate bis(iminoacyl)titanacycle M7b require the energy of 39.1 kcal mol−1 [Scheme S1(b)†], which is too high under typical experimental conditions. Indeed, products related to the titanacycle M7b were not found experimentally, although two relevant enantiomers including M9a were experimentally isolated as green powders.31 The calculated activation energy for the migratory insertion of the isonitrile into the Ti–C bond in M6b (16.6 kcal mol−1) is comparable to the reported value for the PdIII system.26c
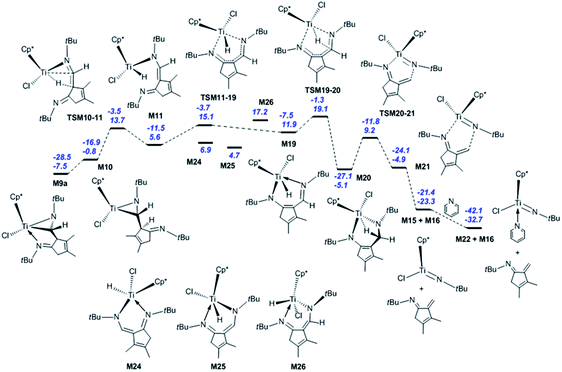
Next, the fragmentation of M9a into the Ti imido complex M15 and N-tBu-substituted α-methylene cyclopentenimine M16 is studied. Initially, the dissociation of Ti–N(ketimine) bond in M9a affords M10 (Fig. 2) with the endergonicity of 6.7 kcal mol−1, whereas N(ketimine) denotes the nitrogen atom in the ketimine. After the dispersion corrections, the endergonicity is increased to 11.6 kcal mol−1. Then, the β-H elimination produces the Ti hydride complex M11 (Ti–N1 = 3.56 Å, Ti–N2 = 1.93 Å, and Ti–H2 = 1.67 Å) with a 12-valence electron configuration via TSM10–11 (Ti–H2 = 1.75 Å, C1–H2 = 1.49 Å). This process requires 14.5 kcal mol−1 and is endergonic by 6.4 kcal mol−1. The dispersion-corrected energy barrier and endergonicity both decrease by about 1 kcal mol−1 relative to the uncorrected values. In TSM10–11, the C1–H2 bond is almost broken and the Ti–H2 bond is almost formed. In the product M11, the length of Ti–N1 indicates that there is no interaction between the Ti centre and the N(ketimine) atom. In the work by Norton et al., a four-membered titanacycle (M14 or M18) is supposed to be an intermediate in the fragmentation reaction of M9a.31 Indeed, M14 is the relatively stable species in this study (with an energy of −1.6 kcal mol−1 referred to M1a and 2 molecules of tBuNC), and it easily fragments to form the target products with an energy barrier of 8.7 kcal mol−1 [Fig. S2(a)†]. The reaction pathway to the four-membered titanacycle M14 via a zwitterionic intermediate M13 (generated by the addition of Ti–H across the double bond in M11) requires a high energy (at least 35.4 kcal mol−1), due to the charge separation in M13. Another reaction pathway to form M18 through an intermediate M17 (produced by the hydrogen transfer to Cp* in the metal hydride M11) needs to overcome an energy barrier of at least 40.1 kcal mol−1. The apparent energy barriers of these two routes are too high, thus the corresponding reactions cannot proceed under experimental conditions. Thus, our attempts to find a feasible fragmentation pathway for M11 via four-membered titanacycle intermediate failed. The proposed fragmentation mechanism for M9a is shown in Scheme 2(a). Along the β-H elimination reaction pathway, M11 isomerises into M19 (Ti–N1 = 2.13 Å, Ti–N2 = 2.15 Å, Ti–H2 = 1.63 Å, and C7–N2 = 1.32 Å) via TSM11–19 (Ti–N1 = 2.40 Å, Ti–N2 = 1.97 Å), overcoming an energy barrier of 9.5 kcal mol−1 and with an endergonicity of 6.3 kcal mol−1 (Fig. 2). Considering the dispersion effects, the energy barrier and endergonicity decrease by 1.7 and 2.3 kcal mol−1, respectively. In this process, the N1 atom, i.e., N(ketimine), gradually approaches the Ti centre. In M19, the Ti–N2 bond is slightly longer than the Ti–N1 bond, and the structure of six-membered titanacycle is stabilised by electron delocalisation. Then, M19 undergoes the addition of Ti–H across the azaallyl double bond, and is thus converted to M20 (Ti–N2 = 1.86 Å, Ti–H2 = 2.17 Å, and C7–N2 = 1.49 Å) via TSM19–20 (Ti–N2 = 1.89 Å, Ti–H2 = 1.70 Å, C7–H2 = 1.89 Å, and C7–N2 = 1.41 Å), with an energy barrier of 7.2 kcal mol−1 and the exergonicity of 17.0 kcal mol−1. The dispersion-corrected energy barrier is reduced to 6.2 kcal mol−1, and the exergonicity is increased to 19.6 kcal mol−1. In TSM19–20, the C7–H2 distance is much longer than that of the usual C–H bond, and the Ti–H2 and C7–N2 bonds in TSM19–20 are slightly longer than those in M19. In M20, the length of Ti–H2 implies the existence of a strong agostic interaction between the Ti centre and the C7–H2 σ bond, and the interaction energy is calculated to be 42.3 kcal mol−1. M20 is lower in energy than the four-membered titanacycles M14 and M18. Therefore, the conversion of M11 to M20 via M19 is kinetically and thermodynamically more favourable, with an energy barrier of 13.5 kcal mol−1 and the exergonicity of 10.7 kcal mol−1. M20 fragments to M15 and M16 via TSM20–21 (Ti–N1 = 2.26 Å, C7–N2 = 2.07 Å, and Ti–H2 = 2.18 Å). In this step, the system overcomes an energy barrier of 14.3 kcal mol−1 and releases 18.2 kcal mol−1 in energy. The large exergonicity is mainly ascribed to increased entropy (65.2 cal mol−1 K−1). Our calculated results are similar to the reported energy barrier (11.3 kcal mol−1) and exergonicity (17.7 kcal mol−1) for the fragmentation of the titanacycle produced through the cycloaddition reaction of Ti alkoxyimido complex and ketone.46 In sharp contrast to the large exergonicity, after the dispersion corrections this fragmentation step becomes endergonic by 5.7 kcal mol−1, and the energy barrier increases by 1.0 kcal mol−1. The structure of TSM20–21 is stabilised by a strong agostic interaction between the Ti centre and the C7–H2 σ bond. The formed M15 is trapped by a pyridine to generate M22, with an exergonicity of 9.4 kcal mol−1. Considering the dispersion corrections, the exergonicity is increased to 20.7 kcal mol−1. In this reaction mechanism, the β-H elimination and fragmentation of six-membered titanacycle have higher energy barriers; and the addition of Ti–H and the trapping of the Ti imido complex by pyridine release more energies. This reaction pathway requires the apparent activation energy of 27.2 kcal mol−1 (after the dispersion corrections), thus it is kinetically feasible under the experimental conditions, and the large exergonicity of 13.6 kcal mol−1 (after the dispersion corrections) makes the fragmentation thermodynamically favourable and irreversible. Because the reaction was experimentally carried out in benzene, we re-calculated the overall energetic profile of the reaction using benzene as solvent. The results are almost the same as that in n-pentane (Table S1†), because both n-pentane and benzene are nonpolar solvents. In the γ-H elimination reaction pathway, M9a is converted to M23 with the Ti–C bond breaking via TSM9a–23, overcoming an energy barrier of 24.7 kcal mol−1 [Fig. S2(b)†], and the process is endergonic by 21.3 kcal mol−1. Then, M23 undergoes γ-H elimination and is converted to M19 via TSM23–19, and this step has an energy barrier of 13.6 kcal mol−1 and is exergonic by 1.9 kcal mol−1. The required apparent activation energy for this fragmentation pathway (34.9 kcal mol−1) is larger than that of the β-H elimination reaction pathway discussed above (26.7 kcal mol−1 without dispersion correction), thus the γ-H elimination reaction pathway is kinetically unfavourable for the titanaaziridine with the tBu groups. The direct conversion of M11 to M20 through the addition of Ti–H across the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond requires an energy of 19.3 kcal mol−1, which is larger than 13.3 kcal mol−1 for the conversion from M11 to M20 via M19 (Fig. 2), thus this possibility is also ruled out. In addition, three stationary points (M24, M25, and M26) were localised; however, none of them is located on the optimum reaction pathway.
C double bond requires an energy of 19.3 kcal mol−1, which is larger than 13.3 kcal mol−1 for the conversion from M11 to M20 via M19 (Fig. 2), thus this possibility is also ruled out. In addition, three stationary points (M24, M25, and M26) were localised; however, none of them is located on the optimum reaction pathway.
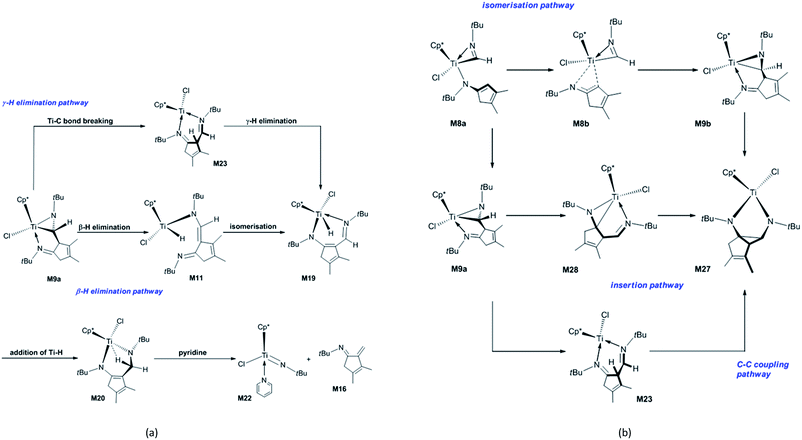 | ||
| Scheme 2 Proposed mechanisms for (a) the fragmentation of the titanaaziridine M9a and (b) forming diazatitanacyclopentane M27. | ||
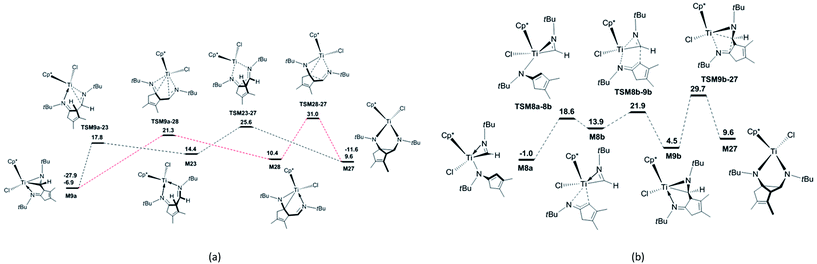
In order to explore the possible formation of the diazatitanacyclopentane M27, three reaction mechanisms are considered [Scheme 2(b)]. (1) In the insertion reaction pathway, the intermediate M28 is 17.3 kcal mol−1 higher in energy than M9a [Fig. 3(a)]. M28 undergoes the insertion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N into the Ti–C bond via TSM28–27 to generate M27, with an energy barrier of 20.6 kcal mol−1 and exergonic by 0.8 kcal mol−1. (2) In the C–C coupling reaction pathway, through the C–C coupling, M23 is converted to M27, overcoming an energy of 11.2 kcal mol−1 and exergonic by 4.8 kcal mol−1. (3) In the isomerisation reaction pathway, M8a firstly isomerises into M8b via TSM8a–8b, with an energy barrier of 19.6 kcal mol−1 and endergonic by 14.9 kcal mol−1 [Fig. 3(b)]. Then, M8b undergoes C–C reductive coupling to give M9b (an isomer of M9a) via TSM8b–9b. This step requires an energy of 8.0 kcal mol−1, and is exergonic by 9.4 kcal mol−1. Through the insertion of C
N into the Ti–C bond via TSM28–27 to generate M27, with an energy barrier of 20.6 kcal mol−1 and exergonic by 0.8 kcal mol−1. (2) In the C–C coupling reaction pathway, through the C–C coupling, M23 is converted to M27, overcoming an energy of 11.2 kcal mol−1 and exergonic by 4.8 kcal mol−1. (3) In the isomerisation reaction pathway, M8a firstly isomerises into M8b via TSM8a–8b, with an energy barrier of 19.6 kcal mol−1 and endergonic by 14.9 kcal mol−1 [Fig. 3(b)]. Then, M8b undergoes C–C reductive coupling to give M9b (an isomer of M9a) via TSM8b–9b. This step requires an energy of 8.0 kcal mol−1, and is exergonic by 9.4 kcal mol−1. Through the insertion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N into the Ti–C bond, M9b is converted to the target compound M27 via TSM9b–27, with an energy barrier of 25.2 kcal mol−1 and the endergonicity of 5.1 kcal mol−1. In contrast, the C–C coupling reaction pathway is more favourable, but it still requires a high apparent activation energy of 32.5 kcal mol−1, with an endergonicity of 16.5 kcal mol−1 referred to M9a. The analyses above show that for tBuNC, the formation of diazatitanacyclopentane M27 is kinetically and thermodynamically unfavourable.
N into the Ti–C bond, M9b is converted to the target compound M27 via TSM9b–27, with an energy barrier of 25.2 kcal mol−1 and the endergonicity of 5.1 kcal mol−1. In contrast, the C–C coupling reaction pathway is more favourable, but it still requires a high apparent activation energy of 32.5 kcal mol−1, with an endergonicity of 16.5 kcal mol−1 referred to M9a. The analyses above show that for tBuNC, the formation of diazatitanacyclopentane M27 is kinetically and thermodynamically unfavourable.
Effects of substituent groups on reaction mechanisms and products
In order to reveal the steric and electronic effects of isonitrile N-substituent groups on the mechanisms and products, the energetic profiles of the reactions using MeNC, EtNC, ArNC, and 1-AdNC instead of tBuNC were calculated (Fig. S3–S10†). The reaction pathways are shown in Scheme 3, and the results are summarised in Tables 1 and 2.| Mol. | ΔG | ||||
|---|---|---|---|---|---|
| tBu | Me | Et | Ar | 1-Ad | |
| a (1) TSA–B denotes a transition state connected species A and B; (2) 23R is an isomer of 13R; (3) solvent: benzene. | |||||
| 1R | 17.1 | 16.7 | 16.7 | 17.6 | 17.0 |
| TS1R–3R (for R = Ar, TS1R–2R) | 24.4 | 21.0 | 20.9 | 21.7 | 24.6 |
| 2R | 12.4 | ||||
| TS2R–3R | 12.9 | ||||
| 3R | 1.0 | −3.1 | −2.3 | 5.0 | 1.5 |
| TS3R–4R | 10.8 | 3.9 | 8.9 | ||
| 4R | 8.0 | 0.9 | 2.3 | 6.4 | 9.0 |
| TS4R–5R | 19.5 | 10.2 | 11.3 | 14.7 | 19.9 |
| 5R | 5.2 | −4.9 | −3.5 | −1.5 | 5.4 |
| TS5R–6R | 6.8 | −3.7 | 0.3 | ||
| 6R | 1.4 | −10.1 | −4.1 | ||
| 7R | 14.1 | −3.7 | 8.0 | ||
| TS7R–8R (for R=Ar, TS7R–9R) | 15.9 | −1.8 | 8.1 | ||
| 8R | 4.5 | −11.2 | |||
| TS8R–9R | 5.5 | −8.1 | |||
| 9R | −1.0 | −21.8 | −17.5 | 0.1 | −1.0 |
| TS9R–10R | 10.7 | −10.9 | 12.8 | ||
| 10R | −6.9 | −31.0 | −25.2 | −6.1 | −5.7 |
| 11R | −0.1 | −15.4 | −12.2 | −5.0 | 3.0 |
| TS11R–12R (for R = Ar, TS11R–20R) | 14.5 | 1.3 | 3.8 | 11.3 | 15.2 |
| 12R | 6.5 | −9.1 | −6.2 | 7.1 | |
| TS12R–13R (for R = Me, Et, TS12R–19R) | 15.7 | −9.9 | 17.8 | ||
| 13R | 12.6 | −22.8 | −17.2 | 4.9 | 15.0 |
| TS13R–14R | 19.8 | −10.1 | −4.3 | 16.4 | 21.8 |
| 14R | −4.8 | −40.6 | −36.7 | −13.7 | −2.5 |
| TS14R–15R | 9.9 | −19.7 | 0.3 | ||
| 15R | −4.1 | −34.2 | −10.3 | ||
| 16R + 17R | −23.6 | −33.2 | −35.8 | ||
| 18R + 17R | −32.2 | −42.2 | −40.9 | −43.0 | −31.5 |
| 19R | 7.6 | −31.7 | −25.4 | ||
| 20R | −12.1 | −9.9 | −2.9 | ||
| 21R | 18.0 | −20.4 | −16.7 | −7.3 | |
| TS21R–13R | −20.7 | −13.7 | 5.8 | ||
| TS10R–22R | 17.8 | −10.5 | −4.7 | ||
| 22R | 14.4 | −14.3 | −11.9 | 16.9 | |
| TS22R–13R (for R = Et, Ar, TS22R–23R) | 28.0 | 0.1 | 4.4 | 26.4 | |
| 23R | −16.4 | 0.6 | |||
| TS23R–14R | 16.7 | ||||
| Mol. | ΔG | ||||
|---|---|---|---|---|---|
| tBu | Me | Et | Ar | 1-Ad | |
| a (1) TSA–B denotes a transition state connected species A and B; (2) 26ISR is an isomer of 26R; (3) solvent: benzene. | |||||
| 10R | −6.9 | −31.0 | −25.2 | −6.1 | −5.7 |
| TS10R–24R | 21.3 | −9.8 | −1.8 | 18.9 | 23.1 |
| 24R | 10.4 | −22.1 | −16.4 | −5.4 | 10.9 |
| TS24R–25R | 31.0 | −9.6 | −6.0 | 9.4 | 32.6 |
| 25R | 8.9 | −28.2 | −23.2 | −13.7 | 11.1 |
| TS10R–22R | 17.8 | −10.5 | −4.7 | 19.4 | |
| 22R | 14.4 | −14.3 | −11.9 | 16.9 | 19.2 |
| TS22R–25R | 25.6 | −6.8 | −2.3 | 21.9 | 28.1 |
| 9R | −1.0 | −21.8 | −17.5 | 0.1 | −1.0 |
| TS9R–26R (R = Ar, TS9R–26ISR) | 18.6 | −11.6 | −6.5 | 3.1 | 20.0 |
| 26ISR | 1.6 | ||||
| TS26ISR–26R | 14.5 | ||||
| 26R | 13.9 | −12.8 | −7.7 | 7.0 | 15.5 |
| TS26R–27R | 21.9 | −5.7 | −0.9 | 15.6 | 23.5 |
| 27R | 4.5 | −23.7 | −19.4 | −9.1 | 5.8 |
| TS27R–25R | 29.7 | −13.4 | −8.7 | 3.9 | 30.9 |
For the bis-insertion reaction of MeNC, we found the following results from Table 1. (1) The isonitrile coordinates to M1b and Ti hydride 6Me [Scheme 3(a)], endergonic by 11.7 and 6.4 kcal mol−1, respectively. The endergonicity is less than that in the case of tBuNC. Although the Me group is less electron-donating than the tBu group, the smaller size of the former leads to less repulsion between the substituents relative to the latter. The reduced repulsion causes less energy increase for the MeNC-coordinated complexes (1Me and 7Me). The entropy change caused by the coordination of tBuNC to M8a is only 6.6 cal mol−1 K−1 larger than that caused by the coordination of MeNC to 6Me (−36.5 cal mol−1 K−1 for tBuNC and −29.9 cal mol−1 K−1 for MeNC). (2) The isonitrile migratory insertion into the Ti–C bond, the isomerisation of Ti complex, C–C reductive elimination, β-H elimination, and C–C reductive coupling require less energies for MeNC than for tBuNC (4.3 vs. 7.3, 7.0 vs. 9.8, 9.3 vs. 11.5, 1.2 vs. 1.6, and 10.9 vs. 11.7 kcal mol−1, respectively). The bulkier groups make the structures of transition states more congested than that of the reactants, thus the activation energies of elementary reactions are larger for tBuNC than for MeNC. The MeNC migratory insertion into the Ti–H bond needs to overcome almost the same energy barrier as that for tBuNC (1.9 vs. 1.8 kcal mol−1). These elementary reactions are either much more exergonic or endergonic relative to that for tBuNC, except for the isonitrile insertion into the Ti–H bond that has a smaller exergonicity (7.5 vs. 9.6 kcal mol−1). The N coordination in 8Me is very exergonic (10.6 kcal mol−1). These differences are mainly attributed to the distinct steric effects of the Me and tBu groups on the intermediates. (3) Without considering the dispersion corrections, the overall bis-insertion reaction of MeNC requires 21.0 kcal mol−1, which is smaller than that of tBuNC, and releases more energy (31.0 kcal mol−1). In the β-H elimination reaction pathway, the energy required for dissociating the Ti–N(ketimine) bond in 10Me is much larger than that in 10tBu (15.6 vs. 6.8 kcal mol−1). Overcoming an energy barrier of 16.7 kcal mol−1, 11Me undergoes the β-H elimination to afford the Ti hydride 12Me via TS11Me–12Me with an endergonicity of 6.3 kcal mol−1. In TS11Me–12Me, the length of Ti–H2 (1.76 Å; Fig. S11†) is marginally longer than that in TSM10–11 (1.75 Å), and that of C1–H2 (1.47 Å) is shorter than that in TSM10–11 (1.50 Å). 12Me is easily converted to the six-membered titanacycle 19Me through the rotation of the Cp*TiClH segment about the Ti–N2 σ-bond, and the re-coordination of the N(ketimine) atom to the Ti centre. The energy barrier in this step is negligible, and the system is highly exergonic (22.6 kcal mol−1) mainly due to the coordination of the N(ketimine). The electron delocalisation stabilises the nearly planar six-membered structure of 19Me. The dissociation of the Ti–N(ketimine) bond in 19Me generates 20Me with an endergonicity of 19.6 kcal mol−1. Through the rotation of Cp*TiClH segment about the N2–C7 bond and re-coordination of the N(ketimine) atom to the Ti centre, 20Me is converted to 21Me with an exergonicity of 8.3 kcal mol−1. 21Me rapidly isomerises to 13Me, slightly exergonic by 2.4 kcal mol−1. Subsequent addition of Ti–H requires an energy of 12.7 kcal mol−1 and is exergonic by 17.8 kcal mol−1, both values are larger than those in the case of tBuNC. Unlike M20, there is no agostic interaction between the Ti centre and the C7–H2 bond in 14Me, since the weaker repulsion between the Cp* and Me groups on nitrogen makes the six-membered titanacycle more planar. The lengths of Ti–H2 and C7–H2 indicate that TS13Me–14Me is an early transition state. Overcoming an energy barrier of 20.9 kcal mol−1, 14Me fragments to form the Ti imido complex 16Me and N-Me-substituted α-methylene cyclopentenimine 17Me, with the endergonicity of 7.4 kcal mol−1. This endergonicity is in sharp contrast to the large exergonicity for M20, which is ascribed to increased electronic energy due to the formation of the intermediate 15Me featuring the coordinated N(ketimine) atom. The lengths of Ti–N1 and C7–N2 in 15Me are shorter than those in M21 (2.24 vs. 2.58 Å and 3.18 vs. 3.32 Å, respectively), indicating that the increase of entropy during the fragmentation of 14Me is less than that in the case of M20 (5.3 vs. 10.5 cal mol−1 K−1). In the absence of pyridine, the final reaction product with MeNC is possibly the titanacycle 14Me. Clearly, the dissociation of the Ti–N(ketimine) bond and the subsequent β-H elimination determine the apparent activation energy barrier of the reaction. After the dispersion corrections, this β-H elimination reaction pathway to 14M requires the energy of 32.6 kcal mol−1 and is exergonic by 10.5 kcal mol−1 with reference to 10Me (Fig. S4†). In the γ-H elimination reaction pathway, compared to that for tBuNC, the breaking of Ti–C bond requires less energy and is less endergonic (20.5 vs. 16.7 kcal mol−1) for MeNC. The length of Ti–C bond in 10Me is longer than that in M9a (2.120 vs. 2.095 Å), indicating that the Ti–C bond in 10Me is stronger than that in M9a. Also, the γ-H elimination requires slightly more energy (14.4 kcal mol−1) and releases a large amount of energy (8.5 kcal mol−1). Considering the dispersion effects, the overall γ-H elimination reaction pathway needs to overcome an energy of 32.3 kcal mol−1 (Fig. S4†). Given the small difference in the apparent activation energies (0.3 kcal mol−1) and the calculation errors, these two fragmentation pathways for 10Me compete with each other. Compared to the case of M9a, the fragmentation of 10Me needs to overcome a higher energy barrier and releases less energy. For the formation of the diazatitanacyclopentane 25Me, among three suggested reaction pathways [Scheme 3(b)], the insertion reaction pathway is kinetically most favourable (Table 2). However, this reaction is thermodynamically unfavourable compared to the formation of N-Me-substituted α-methylene cyclopentenimine.
Conclusions for the substrate EtNC are the same as those for MeNC. When the Me group is replaced by Et, the required energy for the migratory insertion of the first isonitrile (EtNC) into Ti–C is slightly reduced (4.2 vs. 4.3 kcal mol−1; Table 1), but the system is less exergonic (19.0 vs. 19.8 kcal mol−1). It is well known that the Et group is larger in size but also more electron-donating than the Me group. Their combined effect is a slight reduction of the activation energy for EtNC insertion into Ti–C bond compared to MeNC insertion. The C–C reductive elimination from 4Et affords 5Et, overcoming an energy barrier of 9.0 kcal mol−1 and exergonic by 5.8 kcal mol−1. The more electron-donating Et group leads to a reduction of 0.3 kcal mol−1 for the energy barrier of C–C reductive elimination compared to MeNC. It can be inferred that, without considering the dispersion corrections, the formation of the titanaaziridine 10Et requires an energy of 20.9 kcal mol−1 and exergonic by 25.2 kcal mol−1. Compared to the fragmentation of 10Me, (1) the dissociation of the Ti–N(ketimine) bond and β-H elimination in the β-H elimination reaction pathway, and the dissociation of Ti–C bond in the γ-H elimination reaction pathway are both less endergonic; (2) the coordination of the N(ketimine) atom in the β-H elimination reaction pathway and the γ-H elimination are less exergonic; and (3) the required energy for β-H elimination decreases by 0.7 kcal mol−1. In the transition state for β-H elimination, there is the formation of an azaallyl structure. A more electron-donating group connected to the forming azaallyl double bond is beneficial to β-H elimination. (4) The dissociation of the Ti–C bond and the addition of Ti–H are much less affected. However, the γ-H elimination requires more energy (16.3 vs. 14.4 kcal mol−1), and the addition of Ti–H is more exergonic (19.5 vs. 17.8 kcal mol−1). These differences can be ascribed to the more severe congestions in TS10Et–22Et and 13Et than in the corresponding 10Et and 14Et. In addition, due to the stronger electron-donating capacity of the Et group, the electron-richer Ti centre in 22Et retards γ-H elimination. It is obvious that after the dispersion corrections, the β-H elimination reaction pathway to titanacycle 14Et requires an energy of 30.8 kcal mol−1, the γ-H elimination reaction pathway has an energy barrier of 30.0 kcal mol−1, and the system is exergonic by 12.3 kcal mol−1 with reference to 10Et [Fig. S6(c)†]. Compared to the case of 10Me, formation of 14Et requires less apparent activation energy and has higher exergonicity. In contrast, the C–C coupling reaction pathway is kinetically more favourable for forming the diazatitanacyclopentane 25Et. Compared to the case of M9a, in the C–C coupling reaction pathway, the elementary reactions require less energy, the breaking of Ti–C bond is less endergonic, and the C–C coupling is more exergonic. Herein, the fragmentation pathway of 27Et, which includes β-H elimination, rotation of Cp*ClH segment, addition of Ti–H across azaallyl double bond, and other elementary reaction steps was also explored, in order to obtain theoretical insights into the fragmentation of the analogues with other substituent groups. The calculated apparent activation energy barrier is more than 31 kcal mol−1 with reference to 10Et (Fig. S12†). As a consequence, the fragmentation of 27Et is unfavourable compared to that of 10Et.
The energy barrier for the insertion of ArNC into the Ti–C bond is slightly reduced compared to that of EtNC (4.1 vs. 4.2 kcal mol−1), which is ascribed to the fact that the conjugation with the Ar group stabilises the transition state of insertion. The formed 2Ar is a N-uncoordinated six-membered titanacycle. This is related to the reduced N-coordination ability of the ArNC moiety. The isomerisation of N-coordinated titanacycle 3Ar requires less energy (3.9 kcal mol−1) and is less endergonic (1.4 kcal mol−1) compared to the values calculated for tBuNC and MeNC. The C–C reductive elimination from 4Ar overcomes an energy barrier of 8.3 kcal mol−1 to form 5Ar, and this step is exergonic by 7.9 kcal mol−1. The required energy is less than those in the cases of tBuNC (11.5 kcal mol−1), MeNC (9.3 kcal mol−1), and EtNC (9.0 kcal mol−1). The reduced activation energy barriers are related to the expanded conjugation of the π electrons in transition states. The insertion of ArNC into the Ti–H bond occurs rapidly to directly afford the N(ketimine)-coordinated 9Ar, with the exergonicity of 7.9 kcal mol−1. The direct formation of 9Ar is related to the more electron-deficient Ti centre for ArNC relative to tBu and EtNC. The required energy for C–C reductive coupling is 1.8 kcal mol−1 higher than that of MeNC, and 1.0 kcal mol−1 lower than that of tBuNC. In the β-H elimination reaction pathway, the dissociation of Ti–N(ketimine) requires much less energy (1.1 kcal mol−1) compared to the cases of tBuNC, MeNC, and EtNC. 11Ar is a stable intermediate due to π electron delocalisation. Subsequent β-H elimination directly leads to the formation of 20Ar, overcoming the energy barrier of 16.3 kcal mol−1 and endergonic by 2.1 kcal mol−1. 21Ar isomerises into 13Ar, requiring more energy (13.1 kcal mol−1) and being more endergonic (12.2 kcal mol−1). The strong repulsion between the Cp* and Ar groups and the conjugation of system make the isomerisation difficult. The addition of the Ti–H bond requires 4.3 kcal mol−1 more energy in ArNC than in tBuNC, because the Ti–H bond is stronger in the case of ArNC. Similar to the cases of MeNC and EtNC, there is no agostic structure in the Ti–H bond addition product 14Ar. Because π-electron delocalisation stabilises the transition state in the fragmentation of 14Ar, this step requires less energy (14.0 kcal mol−1) for ArNC than for tBuNC and MeNC. TS22Ar–13Ar, a transition state for γ-H elimination from 22Ar, is higher in energy by 32.5 kcal mol−1 than 10Ar, indicating that the γ-H elimination reaction pathway requires too much energy to occur. For the formation of the diazatitanacyclopentane 25Ar, it can be found that the isomerisation reaction pathway is kinetically the most favourable, in which 9Ar isomerises into 26Ar with the endergonicity of 6.9 kcal mol−1. The endergonicity is smaller than those in the cases of tBuNC, MeNC, and EtNC. The C–C reductive coupling requires 8.6 kcal mol−1 in energy and is much more exergonic for ArNC (16.1 kcal mol−1) than for tBuNC (9.4 kcal mol−1), MeNC (10.9 kcal mol−1), and EtNC (11.7 kcal mol−1). The insertion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N requires the energy of 13.0 kcal mol−1, with the exergonicity of 4.6 kcal mol−1. Apparently, for ArNC, after including the dispersion effects, the formation of α-methylene cyclopentenimine needs to overcome an energy barrier of 24.2 kcal mol−1 and is exergonic by 55.9 kcal mol−1 (Fig. S7 and S8†), and the formation of diazatitanacyclopentane requires 22.5 kcal mol−1 and is exergonic by 41.9 kcal mol−1 [Fig. S7–S9(b)†]. We theoretically predicted the possibility of generating a new “σ complex” (25Ar), because its formation is kinetically favourable. Experimentally, the diazahafnacyclopentane with the Ar groups has been observed and characterised by X-ray crystallography.31 In 25Ar, the lengths of Ti–C7 (2.45 Å) and Ti–C5 (2.49 Å) indicate that there is a C–C⋯Ti agostic interaction,47 and the length of the C7–C5 bond (1.57 Å) is longer than those of C7–C1 and C5–C1 bonds (1.52 and 1.53 Å). The lengths of Ti–C7 and Ti–C5 are shorter than the reported lengths of the corresponding Hf–C (2.49 and 2.53 Å), and the C7–C5 bond is longer than the corresponding C–C bond (1.55 Å) in diazahafnacyclopentane.31 These differences can be ascribed to the stronger C–C⋯Ti agostic interaction in diazatitanacyclopentane than that in the Hf counterpart. The calculated WBIs of Ti–C7 and Ti–C5 in 25Ar are 0.15 and 0.13, respectively, and the C–C⋯Ti interaction energy was calculated to be 44.8 kcal mol−1.
N requires the energy of 13.0 kcal mol−1, with the exergonicity of 4.6 kcal mol−1. Apparently, for ArNC, after including the dispersion effects, the formation of α-methylene cyclopentenimine needs to overcome an energy barrier of 24.2 kcal mol−1 and is exergonic by 55.9 kcal mol−1 (Fig. S7 and S8†), and the formation of diazatitanacyclopentane requires 22.5 kcal mol−1 and is exergonic by 41.9 kcal mol−1 [Fig. S7–S9(b)†]. We theoretically predicted the possibility of generating a new “σ complex” (25Ar), because its formation is kinetically favourable. Experimentally, the diazahafnacyclopentane with the Ar groups has been observed and characterised by X-ray crystallography.31 In 25Ar, the lengths of Ti–C7 (2.45 Å) and Ti–C5 (2.49 Å) indicate that there is a C–C⋯Ti agostic interaction,47 and the length of the C7–C5 bond (1.57 Å) is longer than those of C7–C1 and C5–C1 bonds (1.52 and 1.53 Å). The lengths of Ti–C7 and Ti–C5 are shorter than the reported lengths of the corresponding Hf–C (2.49 and 2.53 Å), and the C7–C5 bond is longer than the corresponding C–C bond (1.55 Å) in diazahafnacyclopentane.31 These differences can be ascribed to the stronger C–C⋯Ti agostic interaction in diazatitanacyclopentane than that in the Hf counterpart. The calculated WBIs of Ti–C7 and Ti–C5 in 25Ar are 0.15 and 0.13, respectively, and the C–C⋯Ti interaction energy was calculated to be 44.8 kcal mol−1.
The obtained conclusions for 1-AdNC are the same as those for tBuNC. From Fig. S10,† it can be inferred that considering the dispersion corrections, forming the bis-insertion product 101-Ad requires an energy of 19.1 kcal mol−1 and is exergonic by 30.2 kcal mol−1. In fact, 101-Ad has been experimentally isolated.31 The fragmentation of 101-Ad into the Ti complex 181-Ad and 1-Ad-substituted α-methylene cyclopentenimine 171-Ad via the β-H elimination reaction pathway requires 27.7 kcal mol−1 and releases 11.9 kcal mol−1 in energy with reference to 101-Ad.
The mechanisms of the reactions of M1a with tBuNC, MeNC, EtNC, ArNC, and 1-AdNC are summarised in Scheme S2.† As shown in Scheme S2(a),† in the β-H reaction pathways for tBuNC and 1-AdNC, there are no intermediates like 19R, 20R, and 21R (R = Me and Et), because the bulky tBu and 1-Ad groups hinder the rotation of the Cp*TiClH segment. The β-H elimination reaction pathway for ArNC does not produce intermediates like 12Me and 19Me for MeNC and 12Et and 19Et for EtNC. This is related to the combined effects of the bulkier ArNC moiety and its reduced N-coordination ability. The γ-H elimination reaction pathway for tBuNC, ArNC, and 1-AdNC is unfavourable, because the strong repulsion between the Cp* and tBu, Ar, or 1-Ad group makes the transition state for γ-H elimination higher in energy. For ArNC, the formation of 25Ar (σ complex) via the isomerisation reaction pathway is favourable, due to the fact that the π electron delocalisation lowers the activation energy barrier of the reaction and stabilises the product 25Ar.
Conclusions
The migratory insertion of isonitrile into metal–carbon bond is becoming a potentially important method for constructing C–C bonds in organic and pharmaceutical syntheses. In this work, we theoretically studied the reaction of Cp*(Cl)Ti(2,3-dimethylbutadiene) with different isonitriles using DFT calculations. For tBuNC, MeNC, EtNC, ArNC, and 1-AdNC, the bis-insertion reaction of isonitrile all easily occurs at room temperature. After the dispersion corrections, the isomerisation of Cp*(Cl)Ti(2,3-dimethylbutadiene) determines the apparent activation energies of the bis-insertion reactions of the studied isonitriles, which is 19.1 kcal mol−1. The bis-insertion reactions with the bulky tBuNC and 1-AdNC release less energy in comparison to those with the smaller MeNC and EtNC, and the exergonicity of the bis-insertion of electron-withdrawing ArNC is similar to that of the bulky tBuNC and 1-AdNC. The elementary reactions include isomerisation of Cp*(Cl)Ti(2,3-dimethylbutadiene), isonitrile coordination, isonitrile migratory insertion into the Ti–C and Ti–H bonds, isomerisation of six-membered titanacycle, C–C reductive elimination, β-H elimination, and C–C reductive coupling. The fused three-five metallabicyclic bis-insertion product titanaazidine can be experimentally observed, except that the product with the Ar groups is rapidly converted to diazatitanacyclopentane. In the presence of pyridine, the titanaazidines fragment into Ti imido complex and α-methylene cyclopentenimine for tBuNC, ArNC, and 1-AdNC. For isonitriles with bulky substitution groups such as tBu and 1-Ad, the fragmentation of titanaazidines requires >27 kcal mol−1 and is exergonic by >11 kcal mol−1. For the small MeNC and EtNC, considered the dispersion effects, the titanaazidines are converted to six-membered titanacycles, with a higher energy barrier of >30 kcal mol−1 and an exergonicity of <13 kcal mol−1. In the case of ArNC, the fragmentation of titanaazidines requires the largest amount of energy (33.5 kcal mol−1) and releases the largest amount of energy (24.7 kcal mol−1), and the diazatitanacyclopentane with the Ar groups is an important intermediate. For the bulky tBuNC, ArNC, and 1-AdNC, the β-H elimination reaction pathway is responsible for the fragmentation of titanaazidines. The associated elementary reactions include dissociation of Ti–N(ketimine) bond, β-H elimination, isomerisation of Ti complex, addition of Ti–H bond, and fragmentation of titanacycle. For the small-sized MeNC and EtNC, the γ-H elimination reaction pathway competes with the β-H elimination reaction pathway. The former includes rotation of the Cp*TiClH segment and γ-H elimination. It is found that ArNC can be used to generate the diazatitanacyclopentane via the isomerisation reaction path, in which the system undergoes isomerisation of Ti complex, C–C reductive coupling, and insertion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond. The results presented here are expected to be useful for chemists to synthesise new substances via the reaction of Ti complex and isonitriles. A theoretical study of the reaction of Cp*(Cl)Hf(diene) with isonitriles is underway.
N bond. The results presented here are expected to be useful for chemists to synthesise new substances via the reaction of Ti complex and isonitriles. A theoretical study of the reaction of Cp*(Cl)Hf(diene) with isonitriles is underway.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are grateful for the financial support from The Natural Sciences Foundation of Anhui Province (1608085MB42), Scientific Research Foundation of Anhui University of Science and Technology (ZY538), Beijing National Laboratory for Molecular Sciences (1G129), and The Undergraduate Innovation and Entrepreneurship Training Program (201610361242). We thank professors Song Wang and Zhao Xi at Jilin University (JLU) for calculation resource support.Notes and references
- (a) A. L. dom and T. J. McDaniel, Acc. Chem. Res., 2015, 48, 2822–2833 CrossRef PubMed; (b) J. Majer, P. Kwiatkowski and J. Jurczak, Org. Lett., 2011, 13, 5944–5947 CrossRef CAS PubMed; (c) A. Millán, L. Á. De Cienfuegos, D. Miguel, A. G. Campaña and J. M. Cuerva, Org. Lett., 2012, 14, 5984–5987 CrossRef PubMed; (d) Z. W. Davis-Gilbert, L. J. Yao and I. A. Tonks, J. Am. Chem. Soc., 2016, 138, 14570–14573 CrossRef CAS PubMed; (e) B. Wu, M. W. Bezpalko, B. B. Foxman and C. M. Thomas, Chem. Sci., 2016, 6, 2044–2049 RSC.
- (a) Z. Chen, J. Liu, H. Pei, W. Liu, Y. Chen, J. Wu, W. Li and Y. Li, Org. Lett., 2015, 17, 3406–3409 CrossRef CAS PubMed; (b) C.-C. Chang, F. Jin, L.-Y. Jang, J.-F. Lee and S. Cheng, Catal. Sci. Technol., 2016, 6, 7631–7642 RSC; (c) H. Shen, Y. Wang and Z. Xie, Org. Lett., 2011, 13, 4562–4565 CrossRef CAS PubMed; (d) D. Hollmann, K. Grabow, J. Jiao, M. Kessler, A. Spannenberg, T. Beweries, U. Bentrup and A. Brückner, Chem.–Eur. J., 2013, 19, 13705–13713 CrossRef CAS PubMed; (e) J. A. Suttil and D. S. McGuinness, Organometallics, 2012, 31, 7004–7010 CrossRef CAS.
- (a) A. Rosales, J. Muñoz-Bascón, C. López-Sánchez, M. Álvarez-Corral, M. Muñoz-Dorado, I. Rodríguez-García and J. E. Oltra, J. Org. Chem., 2012, 77, 4171–4176 CrossRef CAS PubMed; (b) L. Becker, P. Arndt, A. Spannenberg, H. Jiao and U. Rosenthal, Angew. Chem., 2015, 127, 5614–5617 CrossRef; (c) I. R. Márquez, D. Miguel, A. Millán, M. L. Marcos and L. Á. de Cienfuegos, J. Org. Chem., 2014, 79, 1529–1541 CrossRef PubMed; (d) Z. Chen, J. Wu, Y. Chen, L. Li, Y. Xia, Y. Li, W. Liu, T. Lei, L. Yang, D. Gao and W. Li, Organometallics, 2012, 31, 6005–6013 CrossRef CAS; (e) H. A. Spinney, C. R. Clough and C. C. Cummins, Dalton Trans., 2015, 44, 6784–6796 RSC.
- (a) Q. L. Lu, Q. Q. Luo, Y. D. Li and S. G. Huang, Phys. Chem. Chem. Phys., 2015, 17, 20897–20902 RSC; (b) M. Sumimoto, Y. Kawashima, K. Hori and H. Fujimoto, Phys. Chem. Chem. Phys., 2015, 17, 6478–6483 RSC; (c) A. D. Schwarz, A. Nova, E. Clot and P. Mountford, Chem. Commun., 2011, 47, 4926–4928 RSC; (d) A. C. Behrle, J. R. Levin, J. E. Kim, J. M. Drewett, C. L. Barnes, E. J. Schelter and J. R. Walensky, Dalton Trans., 2015, 44, 2693–2702 RSC; (e) T. A. Manz, RSC Adv., 2015, 5, 48246–48254 RSC.
- (a) R. Robinson, D. S. McGuinness and B. F. Yates, ACS Catal., 2013, 3, 3006–3015 CrossRef CAS; (b) P. J. Tiong, A. Nova, L. R. Groom, A. D. Schwarz, J. D. Selby, A. D. Schofield, E. Clot and P. Mountford, Organometallics, 2011, 30, 1182–1201 CrossRef CAS; (c) A. D. Schofield, A. Nova, J. D. Selby, A. D. Schwarz, E. Clot and P. Mountford, Chem.–Eur. J., 2011, 17, 265–285 CrossRef CAS PubMed; (d) C. Prieto, J. A. G. Delgado, J. F. Arteaga, M. Jaraíz, J. L. López-Pérez and A. F. Barrero, Org. Biomol. Chem., 2015, 3, 3462–3469 RSC; (e) K. Nomura, S. Patamma, H. Matsuda, S. Katao, K. Tsutsumi and H. Fukuda, RSC Adv., 2015, 5, 64503–64513 RSC.
- (a) K. Kim, S. H. Choi, D. Ahn, Y. Kim, J. Y. Ryu, J. Lee and Y. Kim, RSC Adv., 2016, 6, 97800–97807 RSC; (b) S. Basu, P. S. Kandiyal, R. S. Ampapathway and T. K. Chakraborty, RSC Adv., 2013, 3, 13630–13634 RSC; (c) D. A. Smith and O. V. Ozerov, Chem. Commun., 2011, 47, 10779–10781 RSC; (d) C. Paniagua, M. E. G. Mosquera, T. Cuenca and G. Jiménez, Organometallics, 2011, 30, 2993–3000 CrossRef CAS; (e) A. C. T. Kuate, S. K. Mohapatra, C. G. Daniliuc, P. G. Jones and M. Tamm, Organometallics, 2012, 31, 8544–8555 CrossRef.
- (a) A. Millán, A. Martín-Lasanta, D. Miguel, L. Á. de Cienfuegos and J. M. Cuerva, Chem. Commun., 2011, 47, 10470–10472 RSC; (b) J. A. Sutti, M. F. Shaw, D. S. McGuinness, M. G. Gardiner and S. J. Evans, Dalton Trans., 2013, 42, 9129–9138 RSC; (c) A. Rosales, J. Muñoz-Bascón, V. M. Morales-Alcázar, J. A. Castilla-Alcalá and J. E. Oltra, RSC Adv., 2012, 2, 12922–12925 RSC; (d) M. Lein, J. A. Harrison and A. J. Nielson, Dalton Trans., 2011, 40, 10731–10741 RSC.
- (a) G. B. Wijeratne, E. M. Zolnhofer, S. Fortier, L. N. Grant, P. J. Carroll, C.-H. Chen, K. Meyer, J. Krzystek, A. Ozarowski, T. A. Jackson, D. J. Mindiola and J. Telser, Inorg. Chem., 2015, 54, 10380–10397 CrossRef CAS PubMed; (b) M. Kessler, S. Hansen, D. Hollmann, M. Klahn, T. Beweries, A. Spannenberg, A. Brückner and U. Rosenthal, Eur. J. Inorg. Chem., 2011, 627–631 CrossRef CAS; (c) C. Adler, N. Frerichs, M. Schmidtmann and R. Beckhaus, Organometallics, 2016, 35, 3728–3733 CrossRef CAS; (d) A. F. R. Kilpatrick, J. C. Green and F. G. N. Cloke, Organometallics, 2015, 34, 4816–4829 CrossRef CAS PubMed.
- (a) K. Kaleta, M. Kessler, T. Beweries, P. Arndt, A. Spannenberg and U. Rosenthal, Eur. J. Inorg. Chem., 2011, 3388–3393 Search PubMed; (b) A. F. Dunlop-Brière, M. C. Baird and P. H. M. Budzelaar, Organometallics, 2015, 34, 5245–5253 CrossRef; (c) F. Hermant, E. Urbańska, S. S. de Mazancourt, T. Maubert, E. Nicolas and Y. Six, Organometallics, 2014, 33, 5643–5653 CrossRef CAS; (d) Y. Takii, P. M. Gurubasavaraj, S. Katao and K. Nomura, Organometallics, 2012, 31, 8237–8248 CrossRef CAS.
- (a) X. Wang, Y. Wang, S. Li, Y. Zhang and P. Ma, J. Phys. Chem. A, 2016, 120, 5457–5463 CrossRef CAS PubMed; (b) P. J. Tiong, A. Nova, E. Clot and P. Mountford, Chem. Commun., 2011, 47, 3147–3149 RSC; (c) P. J. Tiong, A. Nova, A. D. Schwarz, J. D. Selby, E. Clot and P. Mountford, Dalton Trans., 2012, 41, 2277–2288 RSC; (d) K. Altenburger, F. Reiβ, K. Schubert, W. Baumann, A. Spannenberg, P. Arndt and U. Rosenthal, Eur. J. Inorg. Chem., 2015, 1709–1715 CrossRef CAS.
- (a) A. M. Chapman and D. F. Wass, Dalton Trans., 2012, 41, 9067–9072 RSC; (b) P. González-Navarrete, M. Calatayud, J. Andrés, F. Ruipérez and D. Roca-Sanjuán, J. Phys. Chem. A, 2013, 117, 5354–5364 CrossRef PubMed; (c) A. V. Chuchuryukin, R. Huang, M. Lutz, J. C. Chadwick, A. L. Spek and G. van Koten, Organometallics, 2011, 30, 2819–2830 CrossRef CAS; (d) T. Miyazaki, Y. Tanabe, M. Yuki, Y. Miyake and Y. Nishibayashi, Organometallics, 2011, 30, 3195–3199 Search PubMed.
- (a) S. K. Guchhait, V. Chaudhary and C. Madaan, Org. Biomol. Chem., 2012, 10, 9271–9277 RSC; (b) W. Sha, J.-T. Yu, Y. Jiang, H. Yang and J. Cheng, Chem. Commun., 2014, 50, 9179–9181 RSC; (c) Y. Li, A. Chao and F. F. Fleming, Chem. Commun., 2016, 52, 2111–2113 RSC; (d) G. Lesma, I. Bassanini, R. Bortolozzi, C. Colletto, R. Bai, E. Hamel, F. Meneghetti, G. Rainoldi, M. Stucchi, A. Sacchetti, A. Silvani and G. Viola, Org. Biomol. Chem., 2015, 13, 11633–11644 RSC; (e) M. Tobisu and N. Chatani, Chem. Lett., 2011, 40, 330–340 CrossRef CAS.
- (a) T. Buyck, D. Pasche, Q. Wang and J. Zhu, Chem.–Eur. J., 2016, 22, 2278–2281 CrossRef CAS PubMed; (b) B. Zhang and A. Studer, Org. Lett., 2014, 16, 1216–1219 CrossRef CAS PubMed; (c) B. Zhang and A. Studer, Org. Lett., 2014, 16, 3990–3993 CrossRef CAS PubMed; (d) Q. Dai, J.-T. Yu, X. Feng, Y. Jiang, H. Yang and J. Cheng, Adv. Synth. Catal., 2014, 356, 3341–3346 CrossRef CAS.
- (a) A. Dewanji, C. Mück-Lichtenfeld, K. Bergander, C. G. Daniliuc and A. Studer, Chem.–Eur. J., 2015, 21, 12295–12298 CrossRef CAS PubMed; (b) A. Hinz, A. Schulz and A. Villinger, J. Am. Chem. Soc., 2015, 137, 9953–9962 CrossRef CAS PubMed; (c) N. Shao, G.-X. Pang, C.-X. Yan, G.-F. Shi and Y. Cheng, J. Org. Chem., 2011, 76, 7458–7465 CrossRef CAS PubMed; (d) S. U. Dighe, A. K. K. S., S. Srivastava, P. Shukla, S. Singh, M. Dikshit and S. Batra, J. Org. Chem., 2015, 80, 99–108 CrossRef CAS PubMed.
- (a) Y. Li and F. F. Fleming, Angew. Chem., Int. Ed., 2016, 55, 14770–14773 CrossRef CAS PubMed; (b) D. Riedel, T. Wurm, K. Graf, M. Rudolph, F. Rominger and A. S. K. Hashmi, Adv. Synth. Catal., 2015, 357, 1515–1523 CrossRef CAS; (c) M. Seidl, M. Schiffer, M. Bodensteiner, A. Y. Timoshkin and M. Scheer, Chem.–Eur. J., 2013, 19, 13787–13791 CrossRef PubMed; (d) S. Tong, Q. Wang, M.-X. Wang and J. Zhu, Angew. Chem., Int. Ed., 2015, 54, 1293–1297 CrossRef CAS PubMed.
- (a) S. Tong, Q. Wang, M.-X. Wang and J. Zhu, Chem.–Eur. J., 2016, 22, 8332–8338 CrossRef CAS PubMed; (b) R. M. Wilson, J. L. Stockdill, X. Wu, X. Li, P. A. Vadola, P. K. Park, P. Wang and S. J. Danishefsky, Angew. Chem., Int. Ed., 2012, 51, 2834–2848 CrossRef CAS PubMed; (c) B. Zhang, C. Mück-Lichtenfeld, C. G. Daniliuc and A. Studer, Angew. Chem., Int. Ed., 2013, 52, 10792–10795 CrossRef CAS PubMed; (d) A. S. K. Hashmi, C. Lothschütz, C. Böhling and F. Rominger, Organometallics, 2011, 30, 2411–2417 CrossRef CAS.
- (a) H. Zhang, D. Shi, S. Ren, H. Jin and Y. Liu, Eur. J. Org. Chem., 2016, 4224–4229 CrossRef CAS; (b) R. S. Chay, K. V. Luzyanin, V. Y. Kukushkin, M. F. C. G. da Silva and A. J. L. Pombeiro, Organometallics, 2012, 31, 2379–2387 CrossRef CAS; (c) H. V. Le and B. Ganem, Org. Lett., 2011, 13, 2584–2585 CrossRef CAS PubMed; (d) M. Maj, C. Ahn, D. Kossowska, K. Park, K. Kwak, H. Han and M. Cho, Phys. Chem. Chem. Phys., 2015, 17, 11770–11778 RSC.
- (a) M. Adib, S. Feizi, M. S. Shirazi, L.-G. Zhu and H. R. Bijanzadeh, Helv. Chim. Acta, 2014, 97, 524–531 CrossRef CAS; (b) H. Stöckmann, A. A. Neves, S. Stairs, K. M. Brindle and F. J. Leeper, Org. Biomol. Chem., 2011, 9, 7303–7305 RSC; (c) G. Bianchini, G. L. Sorella, N. Canever, A. Scarso and G. Strukul, Chem. Commun., 2013, 49, 5322–5324 RSC.
- (a) E. Vitaku, D. T. Smith and J. T. Njardarson, J. Med. Chem., 2014, 57, 10257–10274 CrossRef CAS PubMed; (b) S. D. Roughley and A. M. Jordan, J. Med. Chem., 2011, 54, 3451–3479 CrossRef CAS PubMed; (c) J. S. Carey, D. Laffan, C. Thomson and M. T. Williams, Org. Biomol. Chem., 2006, 4, 2337–2347 RSC.
- (a) D. M. Stout and A. I. Meyers, Chem. Rev., 1982, 82, 223–243 CrossRef CAS; (b) R. Lavilla, J. Chem. Soc., Perkin Trans. 1, 2002, 141–1156 Search PubMed; (c) J. A. Bull, J. J. Mousseau, G. Pelletier and A. B. Charette, Chem. Rev., 2012, 112, 2642–2713 CrossRef CAS PubMed.
- (a) A. Molnár, Chem. Rev., 2011, 111, 2251–2320 CrossRef PubMed; (b) T. J. Colacot and J. Matthey, Platinum Met. Rev., 2011, 55, 84–90 CrossRef; (c) C. Beemelmanns and H.-U. Reissig, Chem. Soc. Rev., 2011, 40, 2199–2210 RSC; (d) C. S. Yeung and V. M. Dong, Chem. Rev., 2011, 111, 1215–1292 CrossRef CAS PubMed; (e) T. Ahrens, J. Kohlmann, M. Ahrens and T. Braun, Chem. Rev., 2015, 115, 931–972 CrossRef CAS PubMed.
- (a) A. A. O. Sarhan and C. Bolm, Chem. Soc. Rev., 2009, 38, 2730–2744 RSC; (b) F. Monnier and M. Taillefer, Angew. Chem., Int. Ed., 2009, 48, 6954–6971 CrossRef CAS PubMed; (c) L. Yin and J. Liebscher, Chem. Rev., 2007, 107, 133–173 CrossRef CAS PubMed; (d) J.-P. Corbet and G. Mignani, Chem. Rev., 2006, 106, 2651–2710 CrossRef CAS PubMed.
- (a) D. A. Colby, R. G. Bergman and J. A. Ellman, Chem. Rev., 2010, 110, 624–655 CrossRef CAS PubMed; (b) L. Souillart and N. Cramer, Chem. Rev., 2015, 115, 9410–9464 CrossRef CAS PubMed; (c) M. Shibasaki and M. Kanai, Chem. Rev., 2008, 108, 2852–2873 CrossRef PubMed; (d) E. M. Beccalli, G. Broggini, M. Martinelli and S. Sottocornola, Chem. Rev., 2007, 107, 5318–5365 CrossRef CAS PubMed.
- (a) N. M. G. Franssen, A. J. C. Walters, J. N. H. Reek and B. de Bruin, Catal. Sci. Technol., 2011, 1, 153–165 RSC; (b) S. G. Modha, V. P. Mehta and E. V. Van der Eycken, Chem. Soc. Rev., 2013, 42, 5042–5055 RSC; (c) R. Kumar and E. V. Van der Eycken, Chem. Soc. Rev., 2013, 42, 1121–1146 RSC; (d) W. Shi, C. Liu and A. Lei, Chem. Soc. Rev., 2011, 40, 2761–2776 RSC.
- (a) K. Huang, C.-L. Sun and Z.-J. Shi, Chem. Soc. Rev., 2011, 40, 2435–2452 RSC; (b) A. P. Thankachan, S. Asha, K. S. Sindhu and G. Anilkumar, RSC Adv., 2015, 5, 62179–62193 RSC; (c) J. Legros and B. Figadère, Nat. Prod. Rep., 2015, 32, 1541–1555 RSC; (d) U. Schneider and S. Kobayashi, Acc. Chem. Res., 2012, 45, 1331–1344 CrossRef CAS PubMed.
- (a) A. Zeiler, M. Rudolph, F. Rominger and A. S. K. Hashmi, Chem.–Eur. J., 2015, 21, 11065–11071 CrossRef CAS PubMed; (b) G. Pendecy and S. Batra, RSC Adv., 2015, 5, 28875–28878 RSC; (c) H. Gu, Z. Qiu, Z. Zhang, J. Li and B. Yan, Dalton Trans., 2015, 44, 9839–9846 RSC; (d) H. Jiang, H. Gao, B. Liu and W. Wu, Chem. Commun., 2004, 50, 15348–15351 RSC.
- (a) L. Xiang and Z. Xie, Organometallics, 2016, 35, 233–241 CrossRef CAS; (b) L. Xiang and Z. Xie, Organometallics, 2016, 35, 1430–1439 CrossRef CAS; (c) K. Takamatsu, K. Hirano and M. Miura, Org. Lett., 2015, 17, 4066–4069 CrossRef CAS PubMed; (d) T. N. Valadez, J. R. Norton, M. C. Neary and P. J. Quinlivan, Organometallics, 2016, 35, 3163–3169 CrossRef CAS.
- (a) F. Foschi, T. Roth, H. Wadepohl and L. H. Gade, Org. Lett., 2016, 18, 5182–5185 CrossRef CAS PubMed; (b) H. Braunschweig, M. A. Celik, R. D. Dewhurst, K. Ferkinghoff, A. Hermann, J. O. C. Jimenez-Halla, T. Kramer, K. Radacki, R. Shang, E. Siedler, F. Weiβenberger and C. Werner, Chem.–Eur. J., 2016, 22, 11736–11744 CrossRef CAS PubMed; (c) C.-H. Lei, D.-X. Wang, L. Zhao, J. Zhu and M.-X. Wang, J. Am. Chem. Soc., 2013, 135, 4708–4711 CrossRef CAS PubMed; (d) W. Lu, H. Lu, Y. Li, R. Ganguly and R. Kinjo, J. Am. Chem. Soc., 2016, 138, 6650–6661 CrossRef CAS PubMed.
- (a) H.-Y. Tu, Y.-R. Liu, J.-J. Chu, B.-L. Hu and X.-G. Zhang, J. Org. Chem., 2014, 79, 9907–9912 CrossRef CAS PubMed; (b) M. Ma, A. Stasch and C. Jones, Chem.–Eur. J., 2012, 18, 10669–10676 CrossRef CAS PubMed; (c) Y. Odabachian, S. Tong, Q. Wang, M.-X. Wang and J. Zhu, Angew. Chem., Int. Ed., 2013, 52, 10878–10828 CrossRef CAS PubMed; (d) A. G. Tskhovrebov, K. V. Luzyanin, F. M. Dolgushin, M. F. C. G. da Silva, A. J. L. Pombeiro and V. Y. Kukushkin, Organometallics, 2011, 30, 3362–3370 CrossRef CAS; (e) M. Okazaki, K. Suto, N. Kudo, M. Takano and F. Ozawa, Organometallics, 2012, 31, 4110–4113 CrossRef CAS.
- G. Greidanus-Strom, C. A. G. Carter and J. M. Stryker, Organometallics, 2002, 21, 1011–1013 CrossRef CAS.
- T. N. Valadez, J. R. Norton and M. C. Neary, J. Am. Chem. Soc., 2015, 137, 10152–10155 CrossRef CAS PubMed.
- (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed; (b) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 83, 284–298 CrossRef.
- A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS.
- A. Höllwarth, M. Böhme, S. Dapprich, A. W. Ehlers, A. Gobbi, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 82, 237–240 CrossRef.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1972, 72, 650–654 CrossRef.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2011, 22, 976–984 CrossRef.
- (a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- (a) R. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef PubMed; (b) V. Singh, Y. Nakao, S. Sakaki and M. M. Deshmukh, J. Org. Chem., 2017, 82, 289–301 CrossRef CAS PubMed.
- L. R. Groom, A. D. Schwarz, A. Nova, E. Clot and P. Mountford, Organometallics, 2013, 32, 7520–7539 CrossRef CAS.
- M. Etienne and A. S. Weller, Chem. Soc. Rev., 2014, 43, 242–259 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Choice of calculated method, Schemes S1 and S2, Fig. S1–S12, Tables S1–S4, and calculated Cartesian coordinates and electronic energies (E) for the species involved in the work. See DOI: 10.1039/c7ra05680j |
| ‡ These authors contributed equally to this paper. |
| This journal is © The Royal Society of Chemistry 2017 |