View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/C7RA05764D (Paper) RSC Adv., 2017, 7, 38179-38186

A family of lanthanide compounds based on nitronyl nitroxide radicals: synthesis, structure, magnetic and fluorescence properties†

Xue-Hui Lva, Shuai-Liang Yanga, Yuan-Xia Lia, Chen-Xi Zhang*ab and Qing-Lun Wang*bc
aCollege of Chemical Engineering and Materials Science, Tianjin University of Science and Technology, Tianjin 300457, P. R. China. E-mail: zcx@tust.edu.cn
bKey Laboratory of Advanced Energy Materials Chemistry (Ministry of Education), Nankai University, Tianjin 300071, P. R. China. E-mail: wangql@nankai.edu.cn
cCollege of Chemistry, Nankai University, Tianjin 300071, P. R. China

Received 22nd May 2017 , Accepted 27th July 2017

First published on 9th August 2017

Abstract

A series of lanthanide nitronyl nitroxide radical compounds, [Ln(hfac)3(NITPh-p-N(CH3)2)2]·xC7H16 (Ln = La (1), Eu (2), Gd (3), Tb (4), Dy (5), Er (6), hfac = hexafluoroacetylacetonate; NITPh-p-N(CH3)2 = 4′-dimethylamino-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide, x = 2/3 for complexes 1, 2, 3 and 6, and 0 for 4 and 5), have been synthesized and structurally characterized. X-Ray crystallographic analyses show that the structures of the six compounds are similar and all consist of isolated molecules, in which central Ln(III) ions are coordinated to six oxygen atoms from three hexafluoroacetylacetonate ligands and two oxygen atoms from nitronyl nitroxide radicals. Variable-temperature magnetic susceptibility studies reveal ferromagnetic interactions between the Gd(III) ion and nitronyl nitroxide radical in complex 3. Ac magnetic susceptibility measurements of complexes 4 and 5 exhibit frequency-dependent out-of-phase signals, indicating single-molecule magnet (SMM) behavior.

Introduction

The study of molecular nanomagnets showing slow relaxation of the magnetization is one of the key topics in the field of molecular magnetism.1 Molecular nanomagnets mainly include single-molecule magnets (SMMs)2 and single-chain magnets (SCMs).3 SMMs and SCMs not only permit the observation of fascinating quantum phenomena but also are investigated as potential candidates for future high-density data storage materials. SMMs and SCMs exhibit slow relaxation of magnetization due to a large ground-state spin quantum number (S), a significant uniaxial magneto-anisotropy (D < 0), and a good magnetic isolation of the molecule.

Lanthanide (Ln) ions have become attractive candidates for constructing new SMMs and SCMs because most of them have significant magnetic anisotropy arising from the large unquenched orbital angular momentum. As a result, many lanthanide complexes with SMM behavior have become attractive synthetic targets for chemists.4

The stability of the radicals like nitronyl nitroxide at a relatively high temperature has made them potential systems in molecular magnetism.5 Recently, nitronyl nitroxides and lanthanide ions were successfully synthesized to obtain the SMMs and SCMs,6 especially heavy lanthanide ions such as terbium(III) and dysprosium(III).7 Since the terbium(III) and dysprosium(III) ions have large anisotropies,8 synthesis and characterization of terbium(III) and dysprosium(III) with the nitronyl nitroxide have already set the fashion in the field of molecular magnetism.9–11 For example, complex [Tb3(hfac)9(NIT-2thien)3]n showed the coexistence of spin canting, metamagnetism, spin dynamic relaxation and magnetic ordering.9 [Dy(hfac)3(PyNO)]2 shows a remarkable SMM behavior with complex hysteresis at 1.4 K.10 One-dimensional chain complex [Tb(hfac)3(NITPhSCH3)]n is the first example of radical–metal SMM units in the construction of an SCM system.11

It is very interesting to develop new nitronyl nitroxide complexes and better understand the nature of 2p–4f magnetic interaction. In this paper, by using a new nitronyl nitroxide radical NITPh-p-N(CH3)2 and lanthanide ions, a series of novel 2p–4f complexes were synthesized. Herein we report a detailed study of the magnetic properties of a novel family of 2p–4f complexes: [Ln(hfac)3(NITPh-p-N(CH3)2)2]·xC7H16, (Ln = La (1), Eu (2), Gd (3), Tb (4), Dy (5) and Er (6), x = 2/3 for complexes 1, 2, 3 and 6 while 0 for 4 and 5). Complexes 4 and 5 present slow relaxation of the magnetization at low temperature, suggesting single-molecule magnet behavior.

Experimental section

Materials and physical measurements

All reagents and solvents were purchased from commercial sources and used without purification. Ln(hfac)3·2H2O (La, Eu, Gd, Tb, Dy, Er)12 and NITPh-p-N(CH3)2 (ref. 13) were synthesized according to the reported methods.

Infrared spectra were recorded on a Perkin-Elmer Spectrum One spectrometer using KBr pellets in the region 4000–400 cm−1. Elemental analyses for C, H, and N were measured by a Perkin-Elmer 240 elemental analyzer. The X-ray powder diffraction patterns (PXRD) have been recorded on a Shimadzu LabX XRD-6100 diffractometer, operated at 40.0 kV and 30.0 mA, using a Cu target tube and graphite monochromator. The intensity data were recorded by continuous scan in 2θ/θ mode from 5° to 50° with a step size of 0.02° and a scan speed of 5° min−1. The thermogravimetry-differential thermal analysis (TG-DTA) was studied by SDT-Q600 at a heating rate of 20 C min−1 in nitrogen atmosphere, and nitrogen gas of high purity (>99.999%) with a flow rate of 100 mL min−1 was used as carrier gas. The sample was heated from ambient temperature to 600 °C. Luminescence properties were recorded on an F-4500 FL spectrophotometer with a xenon arc lamp as the light source. The magnetic measurements were carried out with a MPMS XL-7 SQUID magnetometer. The samples are embedded in grease to avoid preferential orientation of the micro-crystallites. Diamagnetic corrections were made with Pascal's constants for all of the constituent atoms.14

Synthesis procedures

Syntheses of [La(hfac)3(NITPh-p-N(CH3)2)2]·2/3C7H16 (1). 41 mg (0.05 mmol) of La(hfac)3·2H2O was dissolved in 15 mL of boiling heptanes for azeotropically removing hydration water of molecules. Then the solution was cooled to 70 °C, a solution of NITPh-p-N(CH3)2 (30 mg, 0.1 mmol) in 3 mL CH2Cl2 was added. The resulting blue solution was stirred for 15 min and cooled down to room temperature. The filtrate was allowed standing for 5 days, and dark green crystals suitable for X-ray diffraction were obtained. Anal. calc. for C45H70F18LaN6O10 (yield: 42%): C 40.44%, H 5.24%, N 6.29%. Found: C 40.23%, H 5.18%, N 6.19%. IR (KBr) ν/cm−1: 1650 (vs), 1606 (w) 1552 (w), 1378 (w), 1359 (w), 1256 (vs), 1200 (vs), 1098 (w), 734 (w), 665 (w).
Syntheses of [Eu(hfac)3(NITPh-p-N(CH3)2)2]·2/3C7H16 (2). Compound 2 was obtained in a similar manner for 1 except that Eu(hfac)3·2H2O was used instead of La(hfac)3·2H2O. Anal. calc. for C45H70F18EuN6O10 (yield: 45%): C 40.05%, H 5.19%, N 6.23%. Found: C 39.94%, H 5.04%, N 6.14%. IR (KBr) ν/cm−1: 1653 (vs), 1611 (w) 1553 (w), 1373 (w), 1347 (w), 1253 (vs), 1202 (vs), 1095 (w), 738 (w), 622 (w).
Syntheses of [Gd(hfac)3(NITPh-p-N(CH3)2)2]3·2/3C7H16 (3). Compound 3 was obtained in a similar manner for complex 1 except that Gd(hfac)3·2H2O was used instead of La(hfac)3·2H2O. Anal. calc. for C45H70F18GdN6O10 (yield: 43%): C 39.89%, H 5.17%, N 6.20%. Found: C 39.96%, H 5.20%, N 6.25%. IR (KBr) ν/cm−1: 1609 (vs), 1556 (w), 1375 (w), 1347 (w), 1255 (vs), 1198 (vs), 1095 (w), 791 (w), 664 (w).
Syntheses of [Tb(hfac)3(NITPh-p-N(CH3)2)2] (4). Compound 4 was obtained in a similar manner for complex 1 except that Tb(hfac)3·2H2O was used instead of La(hfac)3·2H2O. Anal. calc. for C45H70F18TbN6O10 (yield: 40%): C 39.84%, H 5.16%, N 6.20%. Found: C 39.68%, H 5.02%, N 6.04%. IR (KBr) ν/cm−1: 1609 (vs), 1609 (w) 1553 (w), 1375 (w), 1356 (w), 1254 (vs), 1198 (vs), 1097 (w), 736 (w), 624 (w).
Syntheses of [Dy(hfac)3(NITPh-p-N(CH3)2)2] (5). Compound 5 was obtained in a similar manner for complex 1 except that Dy(hfac)3·2H2O was used instead of La(hfac)3·2H2O. Anal. calc. for C45H70F18DyN6O10 (yield: 38%): C 39.74%, H 5.15%, N 6.18%. Found: C 39.66%, H 5.07%, N 6.03%. IR (KBr) ν/cm−1: 1655 (vs), 1528 (w), 1387 (w), 1352 (w), 1255 (vs), 1199 (vs), 1095 (w), 795 (w), 661 (w).
Syntheses of [Er(hfac)3(NITPh-p-N(CH3)2)2]3·2/3C7H16 (6). Compound 6 was obtained in a similar manner for complex 1 except that Er(hfac)3·2H2O was used instead of La(hfac)3·2H2O. Anal. calc. for C45H70F18ErN6O10 (yield: 36%): C 39.60%, H 5.13%, N 6.16%. Found: C 39.43%, H 5.01%, N 6.14%. IR (KBr) ν/cm−1: 1610 (vs), 1558 (w) 1531 (w), 1379 (w), 1346 (w), 1256 (vs), 1204 (vs), 1103 (w), 739 (w), 623 (w).

Crystal structure determination

Crystals of complexes 1–6 were mounted on glass fibers. Determination of the unit cell and data collection were performed with Mo-Kα radiation (λ = 0.71073 Å) on a Bruker SMART 1000 diffractometer and equipped with a CCD camera. The ω–φ scan technique was employed. The structures were solved primarily by direct method and second by Fourier difference techniques and refined by the full-matrix least-squares method. The computations were performed with the SHELXL-97 program.15 Non-hydrogen atoms were refined anisotropically. The hydrogen atoms were set in calculated positions and refined as riding atoms with a common fixed isotropic thermal parameter. A summary of the crystallographic data and structure refinement is given in Table 1. Selected bond distances and angles for 1–6 are listed in Table S1 (see ESI†). CCDC 1063970 (1), 1063969 (2), 1063967 (3), 1063968 (4), 957789 (5), 1063966 (6), contain the supplementary crystallographic data for this paper.†
Table 1 Crystal data and structure refinements for complexes 1–6
Compound 1 2 3 4 5 6
Formula C149H173La3F54N18O30 C149H173Eu3F54N18O30 C149H173Gd3F54N18O30 C135H141Tb3F54N18O30 C45H47DyF18N6O10 C149H173Er3F54N18O30
Fw 4138.78 4177.93 4193.80 3998.42 1336.39 4223.83
Crystal system Monoclinic Monoclinic Monoclinic Monoclinic Monoclinic Monoclinic
Space group C2/c C2/c C2/c C2/c P21/n C2/c
a (Å) 50.575(6) 50.142(5) 49.926(3) 49.914(19) 12.6610(12) 49.977(11)
b (Å) 12.6932(12) 12.6433(12) 12.6037(5) 12.461(4) 17.3720(15) 12.631(3)
c (Å) 28.871(3) 28.692(2) 28.6405(16) 28.558(10) 24.491(2) 28.671(6)
α (°) 90 90 90 90 90 90
β (°) 100.922(3) 101.271(3) 101.279(3) 101.821(8) 93.967(6) 101.550(10)
γ (°) 90 90 90 90 90 90
V (Å3) 18[thin space (1/6-em)]298(3) 17[thin space (1/6-em)]389(3) 17[thin space (1/6-em)]674.0(16) 17[thin space (1/6-em)]386(11) 5373.8(8) 17[thin space (1/6-em)]733(7)
Z 4 4 4 4 4 4
Dcalcd (Mg m−3) 1.511 1.566 1.576 1.528 1.652 1.582
μ (mm−1) 0.816 1.169 1.241 1.333 8.547 1.535
F(0 0 0) 8360 8432 8444 7992 2668 8492
Crystal size (mm3) 0.26 × 0.24 × 0.22 0.24 × 0.22 × 0.22 0.26 × 0.24 × 0.22 0.22 × 0.20 × 0.18 0.20 × 0.18 × 0.14 0.20 × 0.18 × 0.12
θ range for data collection (°) 1.84–25.02 1.45–25.02 1.45–25.02 1.46–25.02 3.12–72.72 1.45–25.02
Reflections collected/unique 68[thin space (1/6-em)]912/15[thin space (1/6-em)]954 68[thin space (1/6-em)]008/15[thin space (1/6-em)]737 70[thin space (1/6-em)]381/15[thin space (1/6-em)]574 59[thin space (1/6-em)]484/15[thin space (1/6-em)]238 42[thin space (1/6-em)]338/10[thin space (1/6-em)]500 68[thin space (1/6-em)]448/15[thin space (1/6-em)]647
R(int) 0.0786 0.0381 0.0423 0.0540 0.0807 0.0360
Data/restraints/parameters 15[thin space (1/6-em)]954/295/1244 15[thin space (1/6-em)]737/295/1244 15[thin space (1/6-em)]574/295/1244 15[thin space (1/6-em)]238/228/1183 10[thin space (1/6-em)]500/57/762 15[thin space (1/6-em)]647/474/1370
GOF on F2 1.143 1.118 1.059 1.045 1.080 1.072
R1 [I > 2δ(I)] 0.0468 0.0388 0.0320 0.0433 0.0587 0.0504
wR2 [I > 2δ(I)] 0.1155 0.0887 0.0784 0.1110 0.1498 0.1169
R1 (all data) 0.0508 0.0407 0.0346 0.0511 0.0685 0.0524
wR2 (all data) 0.1180 0.0898 0.0800 0.1164 0.1682 0.1182

Results and discussion

Crystal structure

Complexes 1, 2, 3, 4 and 6 crystallize in the monoclinic space group C2/c, while 5 crystallizes in the monoclinic space group P21/n. There are solvent molecules in complexes 1, 2, 3 and 6, while no solvent molecule in complexes 4 and 5. Crystal data and details of structural determination refinement are summarized in Table 1, and selected bond distances and angles for complexes 1–6 are listed in Table S1 in the ESI.†

The structural analyses show that complexes 1–6 are very similar; hence, only the crystal structure of complex 3 is described here. Complex 3 consists of the [Gd(hfac)3(NITPh-p-N(CH3)2)2]3 unit and solvent molecule of C7H16. The structure of [Gd(hfac)3(NITPh-p-N(CH3)2)2]3 unit in complex 3 is shown in Fig. 1. In complex 3, the Gd(III) ion is eight-coordinated in slightly distorted dodecahedron geometry. Two oxygen atoms of the N–O groups from nitronyl nitroxide radicals and six oxygen atoms from three different hfac anions are coordinated to the metal ions. The bond lengths of Gd(1)–O(radical) are Gd(1)–O(1) 2.3328(20) Å and Gd(1)–O(3) 2.3412(18) Å, while the bond lengths of Gd(1)–O(hfac) are in the range of 2.3481(22)–2.4155(20) Å. These bond lengths are comparable to the reported lanthanide–nitronyl nitroxide complexes.16 The angles between the N–O groups from two radical ligands and Gd(III) ion are: N(1)–O(1)–Gd(1) 137.429(16)°, N(4)–O(3)–Gd(1) 138.962(16)° and O(1)–Gd(1)–O(3) 139.416(68)°. The nitronyl nitroxide moiety O1–N1–C1–N2–O2 makes a dihedral angle of 2.020(24)° with the plane of benzene ring.


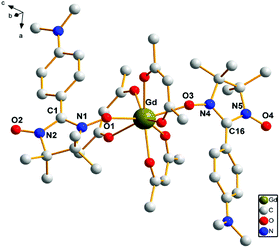image file: c7ra05764d-f1.tif
Fig. 1 The crystal structure of complex 3. Fluorine and hydrogen atoms are not shown for the sake of clarity.

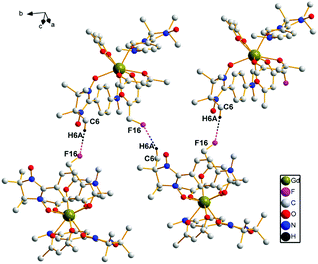
In complex 3, the intermolecular hydrogen bonds occur between one carbon atom from one radical group and one fluorine atom from another hfac ion group (3.364 Å, C(6)–H6A⋯F(16)). This kind of alternate hydrogen bonds form 1D chain structure in complex 3, which is demonstrated in Fig. 2.


image file: c7ra05764d-f2.tif
Fig. 2 A sketch of the intermolecular hydrogen bonds of complex 3.

The structure of the complexes 1, 2, 4, 5 and 6 are similar to complex 3, except for the substitution of Gd(III) with La(III), Eu(III), Tb(III), Dy(III) and Er(III) ions, which makes the bond distances and angles vary a little (Table S1†). In complex 1, the nitronyl nitroxide moiety O1–N1–C1–N2–O2 makes a dihedral angle of 1.556(27)° with the plane of benzene ring, while in complex 2 is 1.861(35)°, complex 4 is 2.493(37)°, complex 5 is 4.061(43)° and complex 6 is 3.212(57)°. The structure of complexes 1, 2, 4, 5 and 6 is shown in Fig. S1–S5 (ESI†).

The shape measure

There are many kinds of coordination geometries in eight-coordinated complexes. Three high-symmetry polyhedra are used as a method of analysis of the shape. They are: the trigonal dodecahedron (D2d-DD), the bicapped trigonal prism (C2v-TP), and the square antiprism (D4d-AP) respectively.17 There exists an intrinsic relationship between the dihedral angles (one for each pair of adjacent triangular planes) and the notion of shape, i.e., the symmetry. Therefore, the geometry of complexes was analyzed by comparing all observed dihedral angles in a given structure and the corresponding ideal values.

Based on the crystal data, we carried out the calculations of the shape factor S to estimate the degree of distortion of the coordination structure in first coordination sphere. The S value is the minimal variance of dihedral angles along all edges given by eqn (1):

 
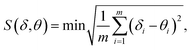image file: c7ra05764d-t1.tif(1)
in which m is the number of possible edges (m = 18 in this study), δi and θi are the dihedral angle between planes along the ith edge, in particular, the value of δi is measured in a given structure and the value of θi is observed in a ideal structure respectively. The observed dihedral angle between planes along the ith edge (θi), the dihedral angle for the ideal structure (δi) and the estimated S values of complexes 1–6 are listed in Tables S2–S7 (ESI†).

The following S values of shape measures calculations are showed in Table 2. By comparing the value of S, the coordination environments of complexes 1–6 are all distorted dodecahedron.

Table 2 S values of shape-measure calculations for complexes 1–6
Ln(III) S(D2d) S(C2v) S(D4d)
La (1) 6.08 12.06 9.73
Eu (2) 5.15 12.65 10.24
Gd (3) 4.95 12.62 10.43
Tb (4) 9.58 11.77 10.06
Dy (5) 5.51 20.98 18.52
Er (6) 4.83 20.53 10.58

Powder X-ray diffraction and TG analyses

To confirm whether the crystal structures are truly representative of the bulk materials, the X-ray powder diffraction patterns (PXRD) of complexes 1–6 have been recorded which are shown in Fig. S6–S8 (ESI†). These patterns indicate that the PXRD patterns are in good agreement with the results simulated from the single crystal date, indicating the purity of the bulk-synthesized materials.

In order to investigate the thermal stability of complexes 1–6, the thermogravimetry-differential thermal analysis (TG-DTA) was studied, and the TG-DTA curve is depicted in Fig. S9–S11 (ESI†). The TG-DTA curves of 1–6 were similar. Herein, complex 1 as a representative example is selected to describe the thermal stability in details. For complex 1, the first stage takes place from 25.00 to 150 °C (the peak of DTA at 150.83 °C) with the weight loss of 11%, corresponding to losing solvent molecules. The second stage takes place from 150 to 500 °C (the peak of DTA at 302.35 °C) with the weight loss of 70%, corresponding to the skeleton of compound begins collapsed, implying the decomposition of hfac and (NITPh-p-N(CH3)2)2.

Luminescence properties

The luminescent measurements of complexes 2 and 4 were investigated at room temperature in ethanol solution. The results reveal that these compounds exhibit the characteristic emission peaks. For complex 2 (Fig. 3, top), the excitation wavelength for emission spectra is 325 nm. The emission spectra are composed of four main bands at 591 nm (5D0 → 7F1), 614 nm (5D0 → 7F2), 650 nm (5D0 → 7F3), and 700 nm (5D0 → 7F4). The electric dipole transitions emission peak at 614 nm (5D0 → 7F2) is clearly stronger than the magnetic dipole transitions peak at 591 nm (5D0 → 7F1). The fluorescence spectra show the characteristic emission peaks of europium ions.18 For complex 4 (Fig. 3, bottom), the excitation wavelength for emission spectra is 290 nm. The emission peak at 490 nm could be attributed to the 5D4 → 7F6 transition, and the other three peaks at 544, 582, and 619 nm could be assigned to the 5D4 → 7F5, 5D4 → 7F4, and 5D4 → 7F3 transitions, respectively. Among them, the 5D4 → 7F5 transition is the strongest. The fluorescence spectra show the characteristic emission peaks of terbium ions.19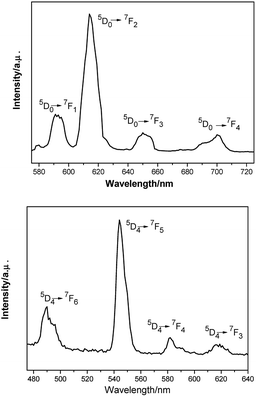
image file: c7ra05764d-f3.tif
Fig. 3 Room-temperature luminescence spectra of complex 2 (λex = 325 nm, top) and complex 4 (λex = 290 nm, bottom) in ethanol solution.

Magnetic properties

Static magnetic properties of 1–6. The temperature dependence of the magnetic susceptibilities of complexes 1–6 were measured for polycrystalline sample in the temperature range 2–300 K under an external magnetic field of 1 kOe. The magnetic behaviors for complexes 1–6 are shown in Fig. 4 and 5.
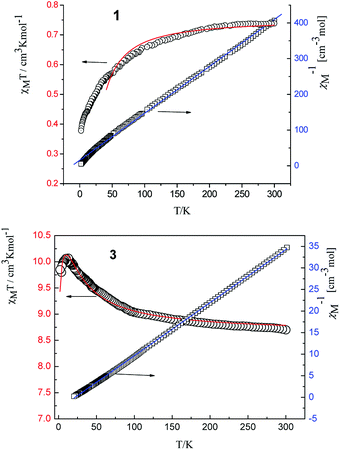image file: c7ra05764d-f4.tif
Fig. 4 Temperature dependence of χMT (○) and plot of χM−1 vs. T of complexes 1 and 3. The solid lines represent the theoretical values based on the corresponding equations.

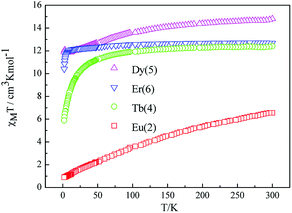
image file: c7ra05764d-f5.tif
Fig. 5 Temperature dependence of χMT for complexes 2, 4, 5, 6 at 1000 Oe.

The room temperature values of χMT are 0.73, 8.64, 12.41, 14.80 and 12.69 cm3 mol−1 K for 1, 3, 4, 5, 6 respectively, in good agreement with the expected values of 0.75, 8.63, 12.23, 14.92 and 12.23 cm3 mol−1 K for one free LnIII ion (LaIII,7F0; GdIII, g = 2, 8S7/2; TbIII, g = 3/2, 7F6; DyIII, g = 4/3, 6H15/2; ErIII, g = 6/5, 4I15/2) plus two isolated radicals (g = 2, S = 1/2).19 For 2, the χMT value at room temperature is 3.09 cm3 mol−1 K is much higher than the theoretical value of 0.75 cm3 mol−1 K for EuIII ion (7F0) in the ground state and two organic radicals (S = 1/2, 0.375 cm3 mol−1 K), due to the population of the excited states of EuIII ion at room temperature. Upon cooling, the χMT versus T plots of 1–6 display different behaviors respectively. For complexes 1, 2, 4, 5 and 6, as the temperature is reduced, the χMT value continuously decreases to reach a minimum of 0.38 cm3 mol−1 K for 1, 0.419 cm3 mol−1 K for 2, 5.89 cm3 mol−1 K for 4, 10.41 cm3 mol−1 K for 5 and 11.89 cm3 mol−1 K for 6 at T = 2 K. This probably governed by the depopulation of the Stark sublevels and/or significant antiferromagnetic interaction.

For complex 1, since the La(III) ion is diamagnetic, the magnetic analysis was thus carried out by using the isotropic spin Hamiltonian Ĥ = −2J(Ŝ1Ŝ2) (eqn (2)). Also, intermolecular exchange interaction (zJ′) in the molecular field approximation was involved (eqn (3)).

 
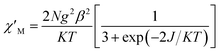image file: c7ra05764d-t2.tif(2)
 
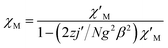image file: c7ra05764d-t3.tif(3)
in which J is intramolecular exchange integral between radicals, and zj′ is the intermolecular interaction. The points below 45 K cannot be reproduced well with this model. The best fitting above 45 K gives g = 2.01, J = −8.2 cm−1 and zj′ = 1.1 cm−1. The negative value of J indicates the antiferromagnetic interaction between nitronyl nitroxide radicals. Moreover, the little positive of zj′ shows the very weak ferromagnetic interaction between two adjacent molecules. The plot of χM−1 vs. T obeys the Curie–Weiss law between 300 and 2 K, and yields C = 0.756 cm3 mol−1 K with θ = −12.8 K. The negative value of θ further confirms the existence of antiferromagnetic coupling between spin carriers.

For complex 3, with the temperature decreases, the χMT value gradually increases to a maximum of 10.03 cm3 mol−1 K at 7.97 K, indicating the existence of ferromagnetic coupling between Gd(III) ion and nitronyl nitroxide. Below 7.97 K, χMT decreases quickly to 9.84 cm3 mol−1 K at 1.99 K. Based on the isotropic Hamiltonian Ĥ = −J1(ŜGd × Ŝrad1 + ŜGd × Ŝrad2) − J2Ŝrad1 × Ŝrad2, eqn (4) is introduced to analyze the magnetic coupling strength, where J1 and J2 represent the magnetic coupling for the Gd–radical and radical–radical, respectively.

 
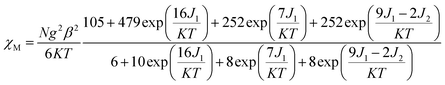image file: c7ra05764d-t4.tif(4)

The best fitting results give J1 = 2.0 cm−1, J2 = −7.8 cm−1 and g = 2.00, which is in the range for other similar Gd–radical compounds.16 The positive value of J1 shows the ferromagnetic coupling between the Gd(III) ion and nitronyl nitroxide radical, while the negative J2 indicates the next nearest-neighbor (NNN) antiferromagnetic coupling between the intramolecular radicals. The plot of χM−1 vs. T obeys the Curie–Weiss law 1/χM = (T − θ)/C between 300 and 2 K, and yields C = 8.8 cm3 mol−1 K with θ = 3.2 K. The positive value of θ further confirms the existence of ferromagnetic coupling between spin carriers. The magnetization data of the field dependent magnetization at 2.0 K (Fig. S12†) climbs up quickly until 10 kOe, and then rises up gradually to 70 kOe with an effective moment of 8.38 μB, which is in smaller than the expected value of S = 9/2 under ferromagnetic interaction per GdRad2 unit (9.00 μB), indicating significant spin frustration behaviour because of the competing exchange interactions between J1 and J2.

Dynamic magnetic properties of 4 and 5. To study the slow relaxation of the magnetization of compounds 4 and 5, ac magnetic susceptibility studies were performed in a zero applied dc field, which were oscillating at frequencies in the range 111–2311 Hz. For complexes 4 and 5, no peaks of frequency-dependent in-phase signals (χ′) were observed (Fig. 6 for 5 and Fig. S13 for 4 in the ESI†), moreover, the out-of-phase susceptibilities (χ′′) clearly display frequency-dependent signals, which indicate the presence of slow magnetic relaxation in complexes 4 and 5.20 No peaks of frequency-dependent out-phase signals (χ′′) were observed, which revealed that the quantum tunneling mechanical (QTM) process in 4 and 5 are pronounced. In order to reduce the QTM effect, the variable-temperature ac susceptibilities were determined again under a dc field of 2000 Oe (Fig. 7 for 5 and Fig. S14 for 4 in the ESI†). For 5, good peak shapes in both in-phase (χ′) and out-of-phase (χ′′) curve were evidently observed; these phenomena indicate that the QTM effect is basically suppressed in 5 under an external 2000 Oe dc field. However, there are still no maxima peaks in both in-phase and out-of-phase curve for complex 4, which illustrate larger QTM effect in 4.
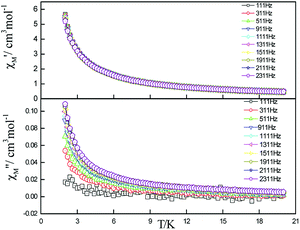image file: c7ra05764d-f6.tif
Fig. 6 Frequency dependence of in-phase (top) and out-of-phase (down) components of the ac magnetic susceptibility for 5 under zero applied dc field.

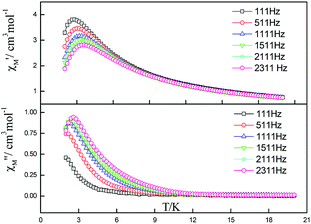image file: c7ra05764d-f7.tif
Fig. 7 Frequency dependence of in-phase (top) and out-of-phase components of the ac magnetic susceptibility for 5 under 2000 Oe applied dc field.

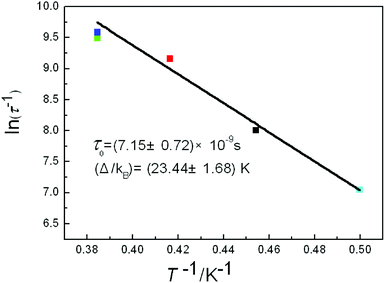
For complex 5, the Cole–Cole diagrams (Fig. 8), which were measured at temperatures of 2.0, 2.2 and 2.4 K, exhibit a quasi-semicircular shape that can be fitted to the generalized Debye model with α values of 0.34, 0.39 and 0.37, from 2 K to 2.4 K. The parameter φ (φ = (ΔTp/Tp)/Δ(log[thin space (1/6-em)]f)) was calculated and a value of 0.36 was obtained, which excludes the possibility of a spin-glass (0.01 < φ < 0.08).21 Plots of ln[thin space (1/6-em)]τ−1 versus T−1 display linear dependence indicating spin reversal by the thermally activated Orbach mechanism process (Fig. 9). The Arrhenius fit (τ = τ0[thin space (1/6-em)]exp(Δeff/kBT)) gives the effective energy barrier (Δeff/kB) of (23.44 ± 1.68) K and the pre-exponential τ0 of (7.15 ± 0.72) × 10−9 s (R = 0.925) by ac versus T data under a dc field of 2000 Oe, which fall in the range well for SMMs.22,23


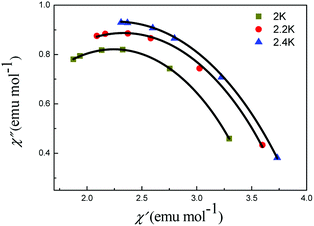image file: c7ra05764d-f8.tif
Fig. 8 Cole–Cole plots of 5 under 2000 Oe. The black lines are results of fitting using the Debye model.

image file: c7ra05764d-f9.tif
Fig. 9 Plot of ln[thin space (1/6-em)]τ−1 vs. T−1 of 5 under 2000 Oe dc field. The black line is the fitting result using the Arrhenius law.

Conclusions

In summary, six lanthanide coordination complexes have been synthesized and structurally characterized. Dc magnetic studies show that ferromagnetic metal–radical interactions take place in complex 3. Ac magnetic studies for compounds 4 and 5 show clear frequency dependence of the out-of-phase susceptibility. With the application of external field (2000 Oe), good peak shapes of the out-of-phase and in-phase signals were obtained in 5, which give an energy barrier of (23.44 ± 1.68) K. It should be noted that multiple relaxation events can occur for single lanthanide sites. Thus, a more precise result must wait for low temperature measurements (T < 1.0 K) by using a micro-SQUID or more AC curves under different magnetic fields.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21371104, 20771081, 21101096, and 21471084) and MOE Innovation Team (IRT13022) of China.

Notes and references

  1. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
  2. (a) R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrichson, J. Am. Chem. Soc., 1993, 115, 1804–1806 CrossRef CAS; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Nature, 1993, 365, 141–143 CrossRef CAS; (c) S. M. J. Aubin, M. W. Wemple, D. M. Adams, H.-L. Tsai, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1996, 118, 7746–7754 CrossRef CAS; (d) S. L. Castro, Z. Sun, C. M. Grant, J. C. Bollinger, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1998, 120, 2365–2375 CrossRef CAS; (e) H. Oshio, N. Hoshino and T. Ito, J. Am. Chem. Soc., 2000, 122, 12602–12603 CrossRef CAS.
  3. (a) A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760–1763 CrossRef CAS; (b) R. Clérac., H. Miyasaka, M. Yamashita and C. Coulon, J. Am. Chem. Soc., 2002, 124, 12837–12844 CrossRef; (c) R. Lescouëzec, J. Vaissermann, C. Ruiz-Pérez, F. Lloret, R. Carrasco, M. Julve, M. Verdaguer, Y. Dromzee, D. Gatteschi and W. Wernsdorfer, Angew. Chem., Int. Ed., 2003, 42, 1483–1486 CrossRef PubMed; (d) T.-F. Liu, D. Fu, S. Gao, Y.-Z. Zhang, H.-L. Sun, G. Su and Y.-J. Liu, J. Am. Chem. Soc., 2003, 125, 13976–13977 CrossRef CAS PubMed.
  4. (a) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed; (b) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS; (c) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
  5. (a) L. Bogani, C. Sangregorio, R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2005, 44, 5817–5821 CrossRef CAS PubMed; (b) H.-X. Tian, R.-N. Liu, X.-L. Wang, P.-P. Yang, Z.-X. Li, L.-C. Li and D.-Z. Liao, Eur. J. Inorg. Chem., 2009, 4498–4502 CrossRef CAS; (c) F. Ortu, J. Liu, M. Burton, J. M. Fowler, A. Formanuik, M.-E. Boulon, N. F. Chilton and D. P. Mills, Inorg. Chem., 2017, 56, 2496–2505 CrossRef CAS PubMed.
  6. (a) G. Poneti, K. Bernot, L. Bogani, A. Caneschi, R. Sessoli, W. Wernsdorfer and D. Gatteschi, Chem. Commun., 2007, 1807–1809 RSC; (b) F. Pointillart, K. Bernot, G. Poneti and R. Sessoli, Inorg. Chem., 2012, 51, 12218–12229 CrossRef CAS PubMed; (c) R.-N. Liu, C.-X. Xiong, S.-P. Zhao, J. Wu, Q. Li and D. Fang, Inorg. Chem. Commun., 2012, 22, 104–107 CrossRef CAS.
  7. R.-N. Liu, L.-C. Li, X.-L. Wang, P.-P. Yang, C. Wang, D.-Z. Liao and J.-P. Sutter, Chem. Commun., 2010, 46, 2566–2568 RSC.
  8. S. Das, A. Dey, S. Biswas, E. Colacio and V. Chandrasekhar, Inorg. Chem., 2014, 53, 3417–3426 CrossRef CAS PubMed.
  9. R.-N. Liu, Y. Ma, P.-P. Yang, X.-Y. Song, G.-F. Xu, J.-K. Tang, L.-C. Li, D.-Z. Liao and S.-P. Yan, Dalton Trans., 2010, 39, 3321–3325 RSC.
  10. X.-H. Yi, K. Bernot, F. Pointillart, G. Poneti, G. Calvez, C. Daiguebonne, O. Guillou and R. Sessoli, Chem.–Eur. J., 2012, 18, 11379–11387 CrossRef CAS PubMed.
  11. X.-L. Wang, X. Bao, P.-P. Xu and L. Li, Eur. J. Inorg. Chem., 2011, 3586–3591 CrossRef CAS.
  12. K. Bernot, L. Bogani, A. Caneschi, D. Gatteschi and R. Sessoli, J. Am. Chem. Soc., 2006, 128, 7947–7956 CrossRef CAS PubMed.
  13. (a) P. Hu, M. Zhu, X.-L. Mei, H.-X. Tian, Y. Ma, L.-C. Li and D.-Z. Liao, Dalton Trans., 2012, 41, 14651–14656 RSC; (b) E. F. Ullman, J. H. Osiecki, D. G. B. Boocock and R. Darcy, J. Am. Chem. Soc., 1972, 94, 7049–7059 CrossRef CAS.
  14. (a) Theory and Applications of Molecular Paramagnetism, ed. E. A. Boudreaux and L. N. Mulay, Wiley-Interscience, New York, 1976 Search PubMed; (b) G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
  15. (a) G. M. Sheldrick, SHELXS 97, University of Gottingen, Göttingen, Germany, 1997 Search PubMed; (b) G. M. Sheldrick, SHELXL 97, University of Gottingen, Göttingen, Germany, 1997 Search PubMed.
  16. (a) M.-Y. Song, Y.-F. Hou, L.-M. Wen, S.-P. Wang, S.-T. Yang, J.-J. Zhang, L.-N. Geng and S.-K. Shi, J. Mol. Struct., 2016, 1107, 174–181 CrossRef CAS; (b) P. Hu, H.-F. Guo, Y. Li and F.-P. Xiao, Inorg. Chem. Commun., 2015, 59, 91–94 CrossRef CAS; (c) M.-Y. Song, L.-M. Wen, S.-P. Wang, S.-T. Yang, J.-J. Zhang, L.-N. Geng and S.-K. Shi, Inorg. Chim. Acta, 2015, 430, 1–7 CrossRef CAS; (d) X.-L. Wang, Inorg. Chim. Acta, 2012, 387, 20–24 CrossRef CAS.
  17. (a) J. L. Hoard and J. V. Silverton, Inorg. Chem., 1963, 2, 235–242 CrossRef CAS; (b) S. J. Lippard and B. J. Russ, Inorg. Chem., 1968, 7, 1686–1688 CrossRef CAS; (c) V. V. Fomenko, L. I. Kopaneva, M. A. Porai-Koshits and T. N. Polynova, J. Struct. Chem., 1974, 15, 244–249 CrossRef; (d) D. L. Kepert, Prog. Inorg. Chem., 1978, 24, 179–183 CAS.
  18. (a) S. Swavey and R. Swavey, Coord. Chem. Rev., 2009, 253, 2627–2638 CrossRef CAS; (b) Z. Ahmed and K. Iftikhar, Inorg. Chim. Acta, 2012, 392, 165–176 CrossRef CAS; (c) P. Coppo, M. Duati, V. N. Kozhevnikov, J. W. Hofstraat and L. De Cola, Angew. Chem., 2005, 117, 1840–1844 CrossRef; (d) Y. Lu and B. Yan, J. Mater. Chem. C, 2014, 2, 7411–7416 RSC.
  19. (a) Y.-L. Wang, Y.-Y. Gao, Y. Ma, Q.-L. Wang, L.-C. Li and D.-Z. Liao, J. Solid State Chem., 2013, 202, 276–281 CrossRef CAS; (b) C. Lescop, G. Bussière, R. Beaulac, H. Bélisle, E. Belorizky, P. Rey, C. Reber and D. Luneau, J. Phys. Chem. Solids, 2004, 65, 773–779 CrossRef CAS.
  20. D. Visinescu, A. M. Madalan, M. Andruh, C. Duhayon, J.-P. Sutter, L. Ungur, W. V. Heuvel and L. F. Chibotaru, Chem.–Eur. J., 2009, 15, 11808–11814 CrossRef CAS PubMed.
  21. J. A. Mydosh, Spin glasses: an experimental introduction, Taylor & Francis, London, 1993 Search PubMed.
  22. (a) L. Bogani, C. Sangregorio, R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2005, 117, 5967–5971 CrossRef; (b) K. Bernot, L. Bogani, R. Sessoli and D. Gatteschi, Inorg. Chim. Acta, 2007, 360, 3807–3812 CrossRef CAS.
  23. (a) R.-N. Liu, C.-M. Zhang, X.-L. Mei, P. Hu, H.-X. Tian, L.-C. Li, D.-Z. Liao and J.-P. Sutter, New J. Chem., 2012, 36, 2088–2093 RSC; (b) H.-X. Tian, X.-F. Wang, X.-L. Mei, R.-N. Liu, M. Zhu, C.-M. Zhang, Y. Ma, L.-C. Li and D.-Z. Liao, Eur. J. Inorg. Chem., 2013, 2013, 1320–1325 CrossRef CAS; (c) P. Hu, X.-F. Wang, Y. Ma, Q.-L. Wang, L.-C. Li and D.-Z. Liao, Dalton Trans., 2014, 43, 2234–2243 RSC.

Footnote

† Electronic supplementary information (ESI) available: Appendix A. CCDC 1063970 (1), 1063969 (2), 1063967 (3), 1063968 (4), 957789 (5), 1063966 (6) contain the supplementary crystallographic data for this paper. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra05764d
This journal is © The Royal Society of Chemistry 2017
Click here to see how this site uses Cookies. View our privacy policy here.