Prediction of mechanical properties of 2D solids with related bonding configuration

Abstract

Our knowledge of the mechanical behavior of 2D solids lags far behind the information available on their electronic properties, despite their relevance for any technological application. A chemistry-based reference model is introduced that allows the unknown mechanical properties to be estimated from a limited data base for groups of atomic and molecular monolayers with similar bonding configuration. This nanometrological approach is demonstrated for the well-studied graphene-like monolayers boronitrene and phosphorene, and the group IV-A monolayers graphene, silicene, germanene, and stanene with hexagonal structure. Comparable results were obtained for the less studied group VI-B molecular layers WS₂, MoS₂, WSe₂, MoSe₂, WTe₂, and MoTe₂. With the ratios of a known property of the group members to that of the reference compound, unknown fracture properties were extracted using a prototype for calibration of this property. The reference model yields very good agreement with existing data for the graphene-like monolayers. For the transition metal dichalcogenides (TMDs) results are still needed for a detailed comparison. The model can be applied to any group of atomic- and molecular layers with a related bonding configuration and stoichiometry. In view of the fast-growing family of 2D solids, the chemical reference model will provide a versatile tool to estimate unknown fracture properties from a minimal data base.

---

1. Introduction

The mechanical properties of selected two-dimensional (2D) solids have been extensively studied and are considered to be unique and outstanding. However, the properties relevant for stability and durability under the mechanical forces occurring during application are not as well known for most members of the rapidly increasing 2D family as other properties, such as their electronic properties.¹ The mechanical properties are crucial for manufacturing, their integration into devices, and their performance during operation.² Especially experimental studies on freely suspended monolayers are lagging far behind the fast growth of the number of 2D solids with promising properties.³ In fact, measurements of the Young's modulus and fracture strength, e.g., by nanoindentation, are limited to a few systems.

While for the best-studied monolayer, graphene, the value of the linear Young's modulus is known quite well, the nonlinear fracture strengths given in the literature for uniaxial tension in the zigzag and armchair directions and for biaxial tension exhibit scatter over a window of more than 30%. This uncertainty further increases when the line or edge energy of graphene is considered.⁴ The situation becomes worse if we include other 2D group IV-A materials, going from graphene to silicene, germanene, and stanene. Most of them possess promising properties of practical interest.^5–7 For other groups of 2D solids with related chemical and physical properties and similar bonding configuration, such as the group VI-B transition metal dichalcogenides (TMDs or TMDCs), even less is known, especially for the group members with high mass, despite increasing attention.^8,9

The main source of information on mechanical behavior comes from density functional theory (DFT) calculations and to some extent from molecular dynamics (MD) simulations. Since MD simulations often deviate systematically from the more accurate DFT calculations, the latter are presently the most reliable and most extended source for mechanical properties. For this reason predominantly first-principles DFT data is used in this study to extend our knowledge of fracture mechanics with the ‘reference model’ introduced below.

The main purpose of this work is to introduce a generally applicable chemical reference model that allows the simultaneous treatment of all members of a group of 2D crystals with related chemistry and bonding configuration. The extraction of information by this model is demonstrated for the most extensively studied groups of 2D solids, namely the graphite-like monolayers of h-BN and phosphorene, the group IV-A elements, and the three-layer molecular sheets of group VI-B TMDs. These groups are currently attracting special interest owing to their spectrum of electronic properties ranging from conductors to semiconductors and insulators.

2. Methods

As mentioned above, in this work the intrinsic mechanical properties of 2D materials with the same type of covalent 2D bonding configuration are investigated. This allows a systematic estimate of unknown fracture properties of a group of 2D solids with a minimal data base. To achieve this goal, for example, the strongest 2D solid of the group (often the best studied member of the group) is selected as a reference or standard. By relating a known property of the group members, such as the Young's modulus, to that of the reference material, ratios can be determined that give access to other related but unknown properties of the group, such as failure properties. To verify this procedure the property to be extracted for the group members must be known for just one compound, which is used as a representative or prototype of the group for this partially unknown property. Consequently, the accuracy of this particular property of the prototype plays an important role in the estimation of this property for the other group members, since the prototype is used for calibration. Property ratios of the already known property, needed for evaluation, were studied here for both linear and nonlinear mechanical properties of single-atomic monolayers and of tri-atomic molecular layers.

The theoretical basis for the general applicability of the concept is a similar chemical bonding configuration, such as a hexagonal honeycomb layer, where localized covalent bond stretching and bond rupture processes occur in a comparable chemical environment. This environment controls bond extension and dissociation and therefore to a large extent the mechanical behavior. In the case of the Young's modulus or stiffness it is the extension of bonds in the linear regime and in the case of fracture it is bond breaking, which takes place in the nonlinear region of the interaction potential. For this reason ratios of the Young's moduli and of the fracture strengths were compared to extract information on the influence of nonlinearity in the mechanical behavior.

The correlation within a group of related 2D compounds is based on the rather unique combination of interrelated chemical and physical properties, which is hardly observed in conventional materials. Furthermore, in binary systems, such as TMDs, the composition plays an important role. Relationships between elementary and composed compounds preferentially exist within the different groups of the periodic table, which is mainly responsible for the generation of characteristic sets of related compounds. The specific 2D behavior is due to the strong covalent in-plane bonding with the same stoichiometry in these atomic and molecular layers. The crucial influence of stoichiometry on the mechanical behavior of these nanostructures can hardly be overestimated. Another important point, already mentioned above, is the reduced dimensionality, leading to chemically closed 2D structures with saturated covalent bonds.

In the following study mainly mean mechanical properties originating from DFT computations are considered, often neglecting anisotropy effects (zigzag, armchair), the type of applied tension (uniaxial, biaxial), and the influence of temperature. At present, the deviations between independent studies are often much larger than the variation of mechanical properties with the direction of the applied tension or the nature of strain. The purpose is to find a consistent set of quantities describing fracture mechanics reliably, avoiding the large uncertainties still found in the literature, or to supply the first estimates. Reliable intrinsic values are urgently needed to judge the detrimental effects of defects on the ideal mechanical behavior. Furthermore, such a set of mechanical properties may also be sufficient for rough estimates relevant, for example, for the simulation of complex biological systems or practical engineering purposes.

3. Results

3.1 Single-atomic graphene-like monolayers

3.1.1 Ratios of Young's moduli and fracture strengths. The mean values of the Young's moduli of the single-atomic monolayers of graphene,⁴ boronitrene,¹⁰ phosphorene,^11–14 silicene,^6,7,15,16 germanene,^6,7 and stanene^6,7,17 are collected in Table 1. From these values the ratios of the stiffness of the individual group members to that of the reference, graphene, is calculated. In addition, to these ratios, Table 1 shows the fracture strengths estimated with these stiffness ratios, taking the strength of graphene as the prototype for calibration. Furthermore, literature values of the fracture strengths of graphene,⁴ boronitrene,¹⁰ phosphorene,¹¹ silicene,⁷ germanene,⁷ stanene,⁷ are shown for a comparison with the reference model. It is important to note that the strength values originating from the literature and from the ratios of the Young's moduli allow a comparison of strengths derived from a linear elastic deformation property with those from DFT calculations, taking nonlinearity into account. As can be seen, the differences are relatively small and within the accuracy of the data at one's disposal. This surprisingly good agreement of the DFT calculations with the linear metrological approach can be explained, at least partially, by the brittle nature of these monolayers. Another reason may be the widespread use of linear models in both experimental data evaluation and theoretical treatments.

Table 1 The Young's moduli from different sources and their ratios to graphene as the reference yield the correlated fracture strengths, using the strength of graphene as prototype, in comparison with the strength values taken from the literature

	E^2D (N m^−1) (stiffness)	Ratios (from stiffness)	σ^2D (N m^−1) (from stiffness)	σ^2D (N m^−1) (literature)
Graphene	340 (ref. 4)	1.0	37 prototype	37 (ref. 4)
Boronitrene	270 (ref. 10)	0.79	29 correlation	28 (ref. 10)
Phosphorene	92 (ref. 11)	0.27	10 correlation	10 (ref. 11)
Silicene	61 (ref. 7)	0.18	6.7 correlation	6.6 (ref. 7)
Germanene	43 (ref. 7)	0.13	4.7 correlation	4.4 (ref. 7)
Stanene	25 (ref. 7)	0.074	2.7 correlation	2.4 (ref. 7)

---

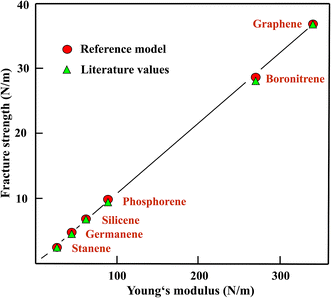
Fig. 1 shows the fracture strengths obtained with the reference model from the ratios of the Young's moduli and the strengths taken from the literature, plotted versus the corresponding Young's moduli. This figure supports the finding of a useful, easy access to the strength values of the whole chemically related group of monolayers with a plane or buckled hexagonal structure by the reference model, taking graphene as the reference of the Young's moduli of the group and also as a prototype for the strength of these graphene-like compounds.

Fig. 1 Comparison of strength values derived with the reference model from Young's moduli with literature values, plotted as a function of the Young's modulus for the graphene-like monolayers.

3.1.2 Determination of line (edge) energies. The line or edge energy is one of the most critical failure properties because reconstruction occurs at the highly reactive edges with dangling bonds initially formed upon cleavage. Furthermore, experimental measurements are widely lacking for this property. It is the 1D analogue of the conventional surface energy that does not depend on the thickness of the monolayer. Its exact value varies with the chemical status of the cleaved edge, which may change its nature substantially with the direction of cleavage and the composition of the layer owing to specific reconstruction processes.

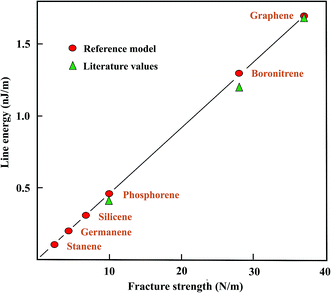
In the following, values of the largely unknown line (edge) energies of plane and buckled graphene-like monolayers are determined from strength ratios obtained from the literature values. Graphene is used as the prototype, with a mean line energy of 1.7 nJ m⁻¹,^18–20 to estimate the line energies of the graphene-like monolayers. It should be mentioned that also larger line energies of graphene of 2.0 and 2.5 nJ m⁻¹ have been reported for the armchair and zigzag directions, respectively,²¹ which would require a higher line energy for calibration. The correlation of the ratios of the fracture strengths with line energies are presented in Table 2. In addition, Table 2 collects the sparsely available literature data, originating mainly from DFT studies.

Table 2 Ratios of the fracture strengths and the resulting line energies, taking the line energy of graphene as the prototype for calibration, are displayed with the line energies available from the literature

	Strength ratios (from literature)	γ ^1D (nJ m^−1) (from strength)	γ^1D (nJ m^−1) DFT calc.
Graphene	1.0	1.7 prototype	1.7 (ref. 18–20)
Boronitrene	0.76	1.3 correlation	1.2 (ref. 22 and 23)
Phosphorene	0.27	0.46 correlation	≤0.39 (ref. 24–26)
Silicene	0.18	0.31 correlation	—
Germanene	0.12	0.20 correlation	—
Stanene	0.065	0.11 correlation	—

---

The graphical presentation in Fig. 2 illustrates the correlation between the line energies, estimated with the fracture strength ratios and theoretical calculations. The strength ratios lead to upper limits since edge stabilization by reconstruction is not taken into account. Good agreement between the correlated and theoretical line energies of the armchair direction is found for boronitride,^22,23 and for phosphorene edges.^24–26 The line energies resulting from the strength correlation may decrease within the group of related compounds by more than a factor of ten, as can be seen in Fig. 2. Unfortunately, no results could be found for the three remaining group IV-A elements.

Fig. 2 Comparison of the line energies derived with the reference model from the strength values with literature values, plotted as a function of fracture strength for the graphene-like monolayers.

3.1.3 Determination of the fracture toughness. A detailed discussion of the fracture toughness of graphene has been provided recently.^4,10 Its mean value of K_IC = 1.1 × 10⁻³ N m^−1/2 is used here for calibration of the strength ratios. Table 3 displays the toughnesses of the other group members obtained with the ratios of the fracture strengths. Independent values from literature are available for h-BN. These results include 0.82 × 10⁻³ N m^−1/2 and 1.05 × 10⁻³ N m^−1/2,²⁷ as well as 0.77 × 10⁻³ N m^−1/2 and 0.69 × 10⁻³ N m^−1/2 for the armchair and zigzag directions,²⁸ respectively, but also the higher values 1.78 × 10⁻³ N m^−1/2 and 1.71 × 10⁻³ N m^−1/2 for the armchair and zigzag directions, respectively.²⁹ The experimentally observed toughness of K_IC = 1.8 × 10⁻³ N m^−1/2 is considered to be higher than that of smooth single edges generated by ideal brittle fracture along the zigzag and armchair directions. This interpretation is based on the assumption of the authors of crack meandering caused by disordered layer stacking and crack branching in the multilayer systems investigated in this work.²⁷ For silicene MD simulations provided the much lower values of 0.14 × 10⁻³ N m^−1/2 and 0.18 × 10⁻³ N m^−1/2 for the zigzag and armchair directions, respectively.²⁸

Table 3 For the graphene-like monolayers the fracture toughness was determined with the presented strength ratios, using the toughness of graphene as the prototype for calibration. The literature values available for boronitrene and silicene are shown

	Strength ratios (from literature)	KIC (N m^−1/2) (from strength)	KIC (N m^−1/2) (literature)
Graphene	1.0	1.1 × 10^−3 prototype	1.1 × 10^−3 (ref. 4 and 10)
Boronitrene	0.76	0.84 × 10^−3 correlation	0.94 × 10^−3 (ref. 27), 0.73 × 10^−3 (ref. 28)
Phosphorene	0.27	0.30 × 10^−3 correlation	—
Silicene	0.18	0.20 × 10^−3 correlation	0.16 × 10^−3 (ref. 28)
Germanene	0.12	0.13 × 10^−3 correlation	—
Stanene	0.065	0.07 × 10^−3 correlation	—

---

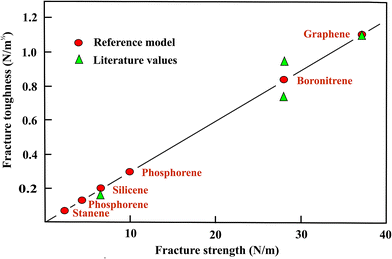
In Fig. 3 the toughness values based on the strength ratios with graphene as the reference are displayed as a function of the fracture strengths. Similar to the situation observed for the line energies, the strength ratios provide a good description of fracture toughness. Since it is still not clear whether the armchair or zigzag direction has the lowest toughness in boronitrene, mean values are shown in Fig. 3. The only result presently available for silicene indicates a large decrease of the fracture toughness within the considered group of monolayers that is consistent with the comparable variation of the fracture strength ratios (see Fig. 3).

Fig. 3 Comparison of the fracture toughnesses derived with the reference model from the strength values with available literature values, plotted as a function of fracture strength for the graphene-like monolayers.

3.2 Results for transition metal dichalcogenides

3.2.1 Ratios of Young's moduli and fracture strengths. The 2D group VI-B TMDs are currently attracting increasing attention primarily owing to their semiconducting properties.^30–33 The TMD sheets have a central plane of transition metals (M: Mo, W) sandwiched between two chalcogenide (X: S, Se, Te) planes. The M–X bonds have a significant ionic character with negatively charged chalcogenide atoms around positively charged metal atoms. Charge transfer decreases linearly from the sulfides to the tellurides according to the decreasing electronegativity of the chalcogenides. Experimental values are rare and the Young's modulus measured for suspended multilayers of WSe₂ is smaller than the theoretical values.³⁴ The Young's moduli provided by independent DFT calculations for all TMDs³¹ agree within ∼10% with those of a comprehensive DFT study of the intrinsic stiffness and fracture strength performed for both the molybdenum and tungsten dichalcogenides.³⁵ This latter comprehensive study on the intrinsic stiffness and critical breaking strength of TMDs together with the single-layer thicknesses^36,37 allowed a systematic application of the reference model to the fracture mechanics of the 2D molecular layers of TMDs.

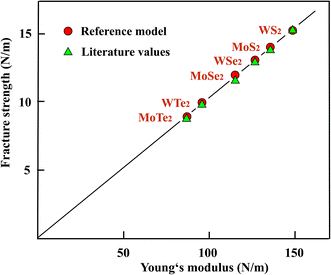
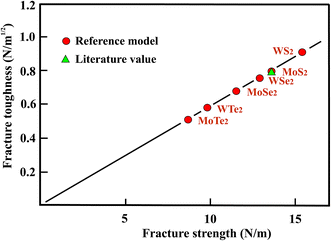
In Table 4 the average values of the zigzag and armchair directions of the Young's moduli and fracture strengths are displayed, together with the ratio of the stiffness of each compound normalized to WS₂, which has the highest stiffness in this group. For the best-studied tungsten chalcogenide, WS₂, the Young's modulus measured by nanoindentation^38,39 is somewhat larger than the stiffness obtained by DFT calculations.³¹ While DFT calculations indicate a relatively small anisotropy for the Young's moduli, a substantial anisotropy is predicted for the fracture strengths.³⁵ It is important to note that the fracture strength determined experimentally for MoS₂ is substantially larger than the one calculated for the weakest zigzag direction, however, it is in reasonable agreement with the strengths in the armchair direction.⁴⁰ The Young's moduli and mean strengths of the TMDs presented in Table 4 follow surprisingly well the factor 10 rule. Note that this is no longer true for the strengths in the zigzag or armchair directions.

Table 4 The literature values of the Young's moduli and their ratios with WS₂ as the reference yield the correlated fracture strengths, using the strength of WS₂ as the prototype for calibration. These results are compared with the strength values taken from the literature

	E^2D (N m^−1) DFT^35	Ratios (stiffness)	σ^2D (N m^−1) (from stiffness)	σ^2D (N m^−1) DFT^35
WS2	149	1.0	15.4 prototype	15.4
MoS2	136	0.91	14.0 correlation	13.6
WSe2	127	0.85	13.1 correlation	12.9
MoSe2	115	0.77	11.9 correlation	11.5
WTe2	96	0.64	9.9 correlation	9.8
MoTe2	87	0.58	8.9 correlation	8.7

---

In Fig. 4 the fracture strengths resulting from the reference model applied to the stiffness and strength values from the literature are plotted versus the Young's moduli of the TMDs. As can be seen in Fig. 4, the reference model allows a reasonable estimate of the mean fracture strengths of the chemically more complex three-layer sheets of TMDs, just as in the case of atomic monolayers. It is important to note that also the Young's moduli can be used to estimate useful strength values. The stiffness belongs to the most easily accessible and most accurate mechanical properties and therefore provides an easy access.

Fig. 4 Comparison of strength values derived with the reference model from Young's moduli with available literature values, plotted as a function of the Young's modulus for the TMDs.

3.2.2 Determination of the line (edge) energies. Results on the line or edge energies of TMDs are very limited. Line energies are of current interest in connection with nanoribbons, where the effect of size on the physical properties is studied. Besides a first principles study of the electronic properties of the whole group of TMDs,⁴¹ their reactivity, for example, with environmental gases, such as oxygen, is a matter of concern.⁴² Owing to their reactivity, TMDs may find applications in catalysis, where the dissociation energy of edge bonds plays a dominant role. For example, the edge sites of MoSe₂ and WSe₂ possess a catalytic activity for the electrochemical hydrogen evolution reaction (HER) that is comparable to or possibly higher than that of the mainly studied MoS₂.⁴³ Note that the W–S dissociation energy per bond of 2.89 eV per bond is approximately 10% higher than the Mo–S value of 2.59 eV per bond.⁴³

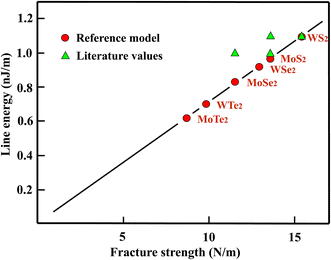
For WS₂ a line energy of 1.1 nJ m⁻¹ was found by DFT calculations that is taken as the prototype.⁴⁴ As expected from the bond energy, the line energy of MoS₂ is with 1.0 nJ m⁻¹ about 10% smaller.⁴⁴ Comparable values, obtained by first principles calculations, have been reported for the zigzag direction of MoS₂ (1.1 nJ m⁻¹) and MoSe₂ (1.0 nJ m⁻¹).⁴⁵ Based on these latter results the line energy of WS₂ should be around 1.2 nJ m⁻¹. Such a higher line energy is supported by a much larger value of 1.4 nJ m⁻¹ reported for MoS₂.⁴⁶ The line energies estimated by the reference model with the ratios of the fracture strengths and 1.1 nJ m⁻¹ as the prototype value, as well as the results of DFT calculations are displayed in Table 5.

Table 5 The ratios of the fracture strengths together with the line energy of WS₂, used as the prototype, yield the correlated line energies for the remaining compounds. Literature values of MoS₂ and MoSe₂ are included for comparison

	Strength ratios (from literature)	γ^1D (nJ m^−1) (from strength)	γ^1D (nJ m^−1) DFT, MO
WS2	1.0	1.1 prototype	1.1 (ref. 44)
MoS2	0.88	0.97 correlation	1.0 (ref. 44), 1.1 (ref. 45)
WSe2	0.84	0.92 correlation	—
MoSe2	0.75	0.83 correlation	1.0 (ref. 45)
WTe2	0.64	0.70 correlation	—
MoTe2	0.56	0.62 correlation	—

---

In addition, the complete set of calculated and correlated line energy data is plotted in Fig. 5 versus the critical fracture strengths. For the well-studied sulfides the results agree well within the relatively large errors involved in this quantity. Unfortunately, results are still completely missing for the tellurides.

Fig. 5 Comparison of the line energies derived with the reference model from the strength values with available literature values, plotted as a function of fracture strength for the TMDs.

3.2.3 Determination of the fracture toughness. As in the case of the line energies, the fracture toughness was estimated from the ratios of the fracture strengths presented in Table 6. Since no toughness values could be found for WS₂ but only for MoS₂, the latter compound is taken as the prototype compound for calibration. For pure mode I loading in the zigzag direction a value of 0.80 × 10⁻³ N m^−1/2 has been reported for MoS₂, which is near the lower limit of the range of toughness values of 0.74–1.1 × 10⁻³ N m^−1/2, simulated for different directions and loading modes.⁴⁷ With the appropriate strength ratio of WS₂/MoS₂ we find 0.91 × 10⁻³ N m^−1/2 for the stronger WS₂ toughness. For the other dichalcogenides experimental and/or theoretical results on the fracture toughness are needed for an estimate of the accuracy of the reference-based metrological approach.

Table 6 For the TMDs sheets the fracture toughness was determined with the strength ratios using the toughness of MoS₂ for calibration of the ratios. The unknown toughness of WS₂ was estimated with the corresponding strength ratio. The only literature value of MoS₂ is shown

	Strength ratios (from literature)	KIC (N m^−1/2) (from strength)	KIC (N m^−1/2) (literature)
WS2	1.0	0.91 × 10^−3 corr.	—
MoS2	0.88	0.80 × 10^−3 prot.	0.80 × 10^−3 (ref. 47)
WSe2	0.84	0.76 × 10^−3 corr.	—
MoSe2	0.75	0.68 × 10^−3 corr.	—
WTe2	0.64	0.58 × 10^−3 corr.	—
MoTe2	0.56	0.51 × 10^−3 corr.	—

---

In Fig. 6 the predictions of the reference model for the critical stress intensity factor of the TMDs are shown, based on the only toughness value obtained by MD simulations for MoS₂. Therefore, a comparison with literature data was not possible and additional results on the heavier TMDs are urgently needed to come to a final conclusion on the predictive power of the reference model in this case.

Fig. 6 The fracture toughnesses derived with the reference model from the strength values with the MoS₂ toughness value, plotted as a function of fracture strength for the TMDs.

4. Discussion

The groups of 2D solids investigated above suggest a comparable accuracy for ratios originating from the Young's moduli and the fracture strengths (see Fig. 1 and 4). This surprising result indicates that the more versatile stiffness data, usually available first for any new material, may allow to extract reasonable information on the mechanical failure behavior. It is worth noting that the linear Young's modulus, describing linear bond extension and not nonlinear bond dissociation, is usually the most accurate mechanical property. This is an important conclusion concerning the quite limited data base needed for an application of the reference model to estimate unknown data.

Furthermore, the best-studied group member and not necessarily the strongest compound can be selected as a representative for a particular property to be determined for the remaining group members. Of course, without any experimental or theoretical information a compound cannot be included in the correlation. However, for many chemically related groups in the fast-growing family of 2D solids theoretical values of the Young's moduli usually become available very soon after their discovery. Therefore, the application of the reference model allows early insight into the varying mechanical behavior resulting from the characteristic changes in the related chemical bonding configurations.

For the presently best studied group of the graphene-like monolayers, a comparison of estimated fracture properties with theoretical results for at least some compounds was possible. The modeled and calculated properties agree quite well, using the Young's moduli and fracture strengths to determine the reference ratios. Since much less information on fracture mechanics is available for the TMDs it is currently not possible to draw a final conclusion on the accuracy of the values predicted for the line energy and fracture toughness. In fact, a toughness value could be found only for one representative of the group, which was employed as the prototype and therefore an independent comparison of estimated toughnesses was not possible.

The TMDs form a rich family of 2D crystals, which contains, besides the most commonly studied group of VI-B compounds considered here, also the group V–B compounds NbS₂, NbSe₂, and TaS₂. Very limited or no mechanical information exists for the new classes of 2D materials uncovered only recently such as the group IV-A monochalcogenides with the formula MX (M = Ge, Sn and X = S, Se), the hexagonally structured group III–VI binary monolayers MX (M = B, Al, Ga, In and X = O, S, Se, Te)⁴⁸ and the group IV-B transition metal trichalcogenides (TMTs) with the common formula MX₃ (M = Ti, Zr, Hf and X = S, Se, Te).⁴⁹ The main representative of the latter group is TiS₃ with first information on its favorable mechanical stability and electronic properties.⁴⁹

In an exhaustive data collection, 103 2D compounds were categorized, distinguishing between atomic materials such as graphene, rare earth materials, semimetals, TMDs and halides, and synthetic organic materials.⁵⁰ To date, experimental data exists only for a very small fraction of these compounds. For TMDs and oxides, the electronic structure has been studied for 51 compounds by first-principles calculations.⁵¹ Computations of the binding energy of prospective layered structures identified 1053 easily and 791 potentially exfoliable compounds, containing many structural prototypes.⁵² This prospect broadens the basis of 2D materials for groups with chemical relationships substantially and demands for an enormous effort in the characterization of the mechanical behavior of at least those potential 2D materials with promising chemical and physical properties.

5. Conclusions

It is demonstrated that the Young's moduli and fracture strengths of graphene-like monolayers can be used to estimate intrinsic fracture properties such as the strength, line energy, and fracture toughness by employing the reference model. These ideal properties are of great value to judge the detrimental effects of defects. The reference model provides a versatile method to determine unknown mechanical properties of the compounds of a chemically related group if for one group member used as prototype for calibration, the mechanical property required is already known. The whole family of potentially 1844 2D solids consists of many such groups,⁵² which can be treated by the reference model with a minimum data base of experimental and/or theoretical information. Consequently, the introduced nanometrological approach will be a versatile and easily applied tool to complement our knowledge of fracture mechanics.

Acknowledgements

Financial support of the work by the Steinbeis Technology Transfer Center Heidelberg (STZ 269) is gratefully acknowledged.

References

1. S. Z. Butler, S. M. Hollen, L. Gao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Torrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926.
2. D. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, K. M. Liechti, N. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Jakobson, T. Zhang, Y.-W. Zhang, Y. Zhou and Y. Zhu, Extreme Mechanics Letters, 2017, 13, 42–77.
3. A. Castellanos-Gomez, V. Singh, H. S. J. van der Zant and G. A. Steele, Ann. Phys., 2014, 527, 27–44.
4. P. Hess, J. Appl. Phys., 2016, 120, 124303.
5. B. Peng, H. Zhang, H. Shao, Y. Xu, G. Ni, R. Zhang and H. Zhu, Phys. Rev. B, 2016, 94, 245420.
6. R. John and B. Merlin, Cryst. Struct. Theory Appl., 2016, 5, 43–55.
7. B. Mortazavi, O. Rahaman, M. Makaremi, A. Dianat, G. Cuniberti and T. Rabczuk, Phys. E, 2017, 87, 228–232.
8. X. Huang, Z. Zeng and H. Zhang, Chem. Soc. Rev., 2013, 42, 1934–1946.
9. M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275.
10. P. Hess, Nanotechnology, 2017, 28, 064002.
11. Q. Wei and X. Peng, Appl. Phys. Lett., 2014, 104, 251915.
12. Z.-D. Sha, Q.-X. Pei, Z. Ding, J.-W. Jiang and Y.-W. Zhang, J. Phys. D: Appl. Phys., 2015, 48, 395303.
13. V. Sorkin, Y. Cai, Z. Ong, G. Zhang and Y. W. Zhang, Crit. Rev. Solid State Mater. Sci., 2017, 42, 1–82.
14. N. Lui, J. Hong, R. Pidaparti and X. Wang, Nanoscale, 2016, 8, 5728–5736.
15. H. Zhao, Phys. Lett. A, 2012, 376, 3546–3550.
16. J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang, C. C. Liu, H. Zhong, N. Han, J. Lu, Y. Yao and K. Wu, Prog. Mater. Sci., 2016, 83, 24–151.
17. L. Tao, C. Yang, L. Wu, L. Han, J. Song, S. Wang and P. Lu, Mod. Phys. Lett. B, 2016, 30, 1650156.
18. A. I. Rusanov, Nanoscale, 2014, 6, 8130–8133.
19. K. Kim, V. I. Artyukhov, W. Regan, Y. Liu, M. F. Crommie, B. I. Yakobson and A. Zettl, Nano Lett., 2012, 12, 293–297.
20. T. Zhang, X. Li, S. Kadkhodaei and H. Gao, Nano Lett., 2012, 12, 4605–4610.
21. K. V. Bets and B. I. Jakobson, Nano Res., 2009, 2, 161–166.
22. Y. Liu, S. Bhowmick and B. I. Yakobson, Nano Lett., 2011, 11, 3113–3116.
23. B. Huang, H. Lee, B.-L. Gu, F. Liu and W. Duan, Nano Res., 2012, 5, 62–72.
24. J. Gao, X. Liu, G. Zhang and Y.-W. Zhang, Nanoscale, 2016, 8, 17940–17946.
25. V. Vierimaa, A. V. Krasheninnikov and H.-P. Komsa, Nanoscale, 2016, 8, 7949–7957.
26. V. Sorkin and Y. W. Zhang, Nanotechnology, 2015, 26, 235707.
27. X. Wei, S. Xiao, F. Li, D.-M. Tang, Q. Chen, Y. Bando and D. Golberg, Nano Lett., 2015, 15, 689–694.
28. T. Rakib, S. Mojumder, S. Das, S. Saha and M. Motalab, 2017, arXiv:1701.01193 [cond-mat.mtrl-sci].
29. A. Tabarraei and X. Wang, Mater. Sci. Eng., A, 2015, 641, 225–230.
30. V. Sorkin, H. Pan, H. Shi, S. Y. Quek and Y. W. Zhang, Crit. Rev. Solid State Mater. Sci., 2014, 39, 319–367.
31. J. Kang, S. Tongay, J. Zhou, J. Li and J. Wu, Appl. Phys. Lett., 2013, 102, 012111.
32. H.-P. Komsa, J. Kotakoski and S. Kurasch, Phys. Rev. Lett., 2012, 109, 035503.
33. Z. Lin, B. R. Carvalho, E. Kahn, R. Lv, R. Rao, H. Terrones, M. A. Pimenta and M. Terrones, 2D Mater., 2016, 3, 022002.
34. R. Zhang, V. Koutsos and R. Cheung, Appl. Phys. Lett., 2016, 108, 042104.
35. J. Li, N. V. Medhekar and V. B. Shenoy, J. Phys. Chem. C, 2013, 117, 15842–15848.
36. D. M. Guzman and A. Strachan, J. Appl. Phys., 2014, 115, 243701–243708.
37. M. K. Jana, A. Singh, D. J. Late, C. R. Rajamathi, K. Biswas, C. Felser, U. V. Waghmare and C. N. R. Rao, J. Phys.: Condens. Matter, 2015, 27, 285401.
38. K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Nano Lett., 2014, 14, 5097–5103.
39. K. Liu and J. Wu, J. Mater. Res., 2016, 31, 832–844.
40. S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709.
41. Y. Ding, Y. Wang, J. Ni, L. Shi, S. Shi and W. Tang, Phys. B, 2011, 406, 2254–2260.
42. H. Lui, N. Han and J. Zhao, RSC Adv., 2015, 5, 17572–17582.
43. H. Toulhoat, P. Raybaud, S. Kasztelan, G. Kresse and J. Hafner, Catal. Today, 1999, 50, 629–636.
44. S.-L. Xiao, W.-Z. Yu and S.-P. Gao, Surf. Sci., 2016, 653, 107–112.
45. Y. Yang, X. Li, M. Wen, E. Hacopian, W. Chen, Y. Gong, J. Zhang, B. Li, W. Zhou, P. M. Ajayan, Q. Chen, T. Zhu and J. Lou, Adv. Mater., 2016, 29, 1604201.
46. Z. Qi, P. Cao and H. S. Park, J. Appl. Phys., 2013, 114, 163508.
47. X. Wang, A. Tabarraei and D. E. Spearot, Nanotechnology, 2015, 26, 175703.
48. S. Demirci, N. Avazil, E. Durgun and S. Cahangirov, Phys. Rev. B, 2017, 95, 115409.
49. J. Dai, M. Li and X. C. Zeng, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 211–220.
50. P. Miro, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537–6554.
51. F. A. Rasmussen and K. S. Thygesen, J. Phys. Chem. C, 2015, 119, 13169–13183.
52. N. Mounet, M. Gibertini, P. Schwaller, A. Merkys, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, 2016, arXiv:1611.05234vl [cond-mat.mtrl-sci].

---