DOI:
10.1039/C7RA06125K
(Paper)
RSC Adv., 2017,
7, 47190-47195
Vibrational characteristics of DNA nanostructures obtained through a mass-weighted chemical elastic network model†
Received
1st June 2017
, Accepted 1st October 2017
First published on 6th October 2017
Abstract
Using the programmable and self-assembly characteristics of DNA, various DNA nanostructures have been designed and synthesized for specific applications, such as nanomachinery and chemical/biological sensors. Although their physical features and feasibility in engineering applications can be conjectured using experimental techniques such as atomic force microscopy and Raman spectroscopy, their vibration characteristics at low frequency states, which are the most dominant factors that determine their structural functions, are difficult to observe experimentally because it is almost impossible to capture the real-time atomic motion of DNA nanostructures. Here, we propose a novel method to elucidate the vibration characteristics of DNA nanostructures in atomic detail using a normal mode analysis based on a mass-weighted chemical elastic network model (MWCENM). Because the MWCENM is a precise method for modeling molecular structures that considers both chemical bond information and inertia effects, it can calculate both vibration frequencies and the corresponding mode shapes in atomic detail. In terms of vibration frequencies, our simulation results show good agreement, within an error deviation of 4.0%, with experimental data measured by Raman spectroscopy. Therefore, the proposed theoretical approach is a feasible method for understanding DNA nanostructure's vibration characteristics, including both frequencies and mode shapes, in atomic detail, adding to the molecular fingerprint provided by the conventional Raman spectrum.
Introduction
For the past 30 years, DNA molecules have been considered one of the most promising building blocks for various dimensional nanostructures due to the programmability of their base sequences.1–7 Recently, DNA nanostructures have been used in many different applications in the fields of science, engineering, and nanobiotechnology.8–10 To build useful DNA nanostructures for specific applications, researchers need to statically and dynamically verify their engineering feasibility in terms of structural stability and vibrational characteristics. In a previous study, we used vibrational mode analysis to explain the basic self-assembly mechanism for the formation of circular DNA tubes made of planar double-crossover (DX) DNA tiles.11
Although certain physical characteristics are difficult to observe experimentally due to the measuring limitations of the apparatus or sample preparation, simulations can easily provide significant insights about physical properties. For instance, atomic vibration at low frequency (under 300 cm−1), which is of significant importance for understanding biological functionality and optimizing synthesis, is hard to measure experimentally. However, by using simulation, mode shapes from collective motion to local vibration can be analyzed at atomic level as shown in Fig. 1. In this study, we (i) suggest a way to sample atoms in DNA molecules for applying a mass-weighted chemical elastic network model (MWCENM), (ii) propose an intrinsic frequency analysis method based on the MWCENM, (iii) measure Raman spectrum of rectangular-shape DNA DX tiles, and (iv) validate the reliability of the proposed frequency analysis method by comparing its results with experimental data.
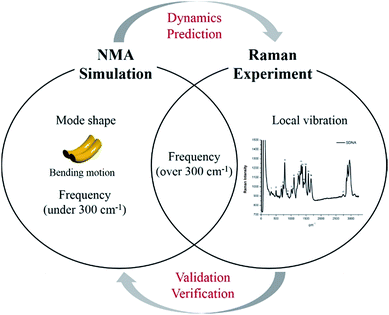 |
| | Fig. 1 Highlight of the proposed frequency analysis method. Raman spectrum experiment has been widely utilized as a tool for identification of nanostructure by means of its vibrational fingerprint within a limited frequency range (i.e., over 300 cm−1). However, this experimental technique cannot capture structural features and dynamics, which are the most important factors to be understood at atomic details because their functions are mainly determined by their low-frequency vibrations (i.e., collective motions). On the other hand, the proposed MWCENM based NMA simulation enables us to calculate all the vibration frequencies and their corresponding mode shapes from collective motions to local vibrations. By direct comparison of vibration frequencies between Raman and NMA, one can assure that low-frequency dynamics of DNA nanostructures can be predicted by simulation at atomic details. | |
Materials and methods
Mass-weighted chemical elastic network model (MWCENM)
In the traditional elastic network model (ENM), representative atoms are modeled as unit point masses and their interaction is represented by a uniform spring network having a cutoff distance (e.g., 12 Å in a typical Cα coarse-grained protein model).12–16 In contrast to ENM, MWCENM is a more precise modeling method because it considers both the inertia effect and chemical bond information of the target system. The inertia effect is given by lumped masses to representative atoms of the target system, and chemical bonds are considered by assigning different spring constants, as shown in Table 1.17,18 Therefore, both the frequencies and mode shapes of the target system can be obtained using the MWCENM. This method was already validated for both protein and DNA dynamics simulation elsewhere.17,20
Table 1 Various spring constants given by the type of chemical bond. In the MWCENM, van der Waals, hydrogen, ion, disulfide, and covalent bonds are assigned different spring constants. The spring constant ratio of van der Waals, hydrogen, and covalent bonds is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100
| Chemical bond |
Spring constant [N m−1] |
| van der Waals bond |
7 |
| Hydrogen bond |
70 |
| Ion bond |
70 |
| Disulfide bond |
70 |
| Covalent bond |
700 |
Normal mode analysis (NMA)
We performed MWCENM-based NMA to calculate the frequencies of two different DX DNA tiles. Suppose there is a system of N particles. Each particle is a representative atom chosen through sampling and a lumped mass that includes the weight of surrounding atoms. We construct a spring network between particles using the chemical bond types (Table 1) and then construct the equation of motion for the system as follows. The position of the ith atom at time t, xi(t), can be represented by the initial position xi(0) and a small displacement δ(t) so that xi(t) = xi(0) + δ(t) where xi(t) is a 3 × 1 vector. Then, the kinetic energy of the system can be defined as| |
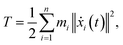 | (1) |
where mi is the weight of a specific lumped mass. The kinetic energy can be rewritten in matrix form as| |
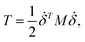 | (2) |
where M is a global mass matrix consisting of the lumped masses and δ is a 3N × 1 matrix. In addition, the potential energy can be written as| |
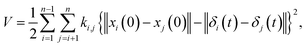 | (3) |
where ki,j is the spring constant between the ith and jth atoms. By using a Taylor series approximation, we can rewrite eqn (3) as| |
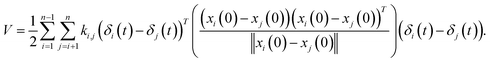 | (4) |
Then, we can derive the equation of motion using Lagrange's equation.| |
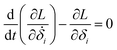 | (5) |
Here, L = T − V. Therefore, the equation of motion for the system is| |
M![[greek delta with two dots above]](https://www.rsc.org/images/entities/i_char_e19b.gif) + Kδ = 0. + Kδ = 0.
| (6) |
By solving eqn (6), we can obtain both the vibrational frequencies and corresponding vibration mode from the eigenvalues and eigenvector, respectively.19
DNA sampling model
In this study, we conducted DNA sampling as shown in Fig. 2. In the sugar–phosphate backbone part, P, C1, and C4 atoms were selected. In each base part, we chose 3 or 4 atoms related to the backbone and hydrogen bonds between base pairs.
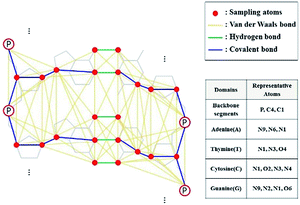 |
| | Fig. 2 DNA sampling model and its representative atoms. Three or four atoms were chosen to represent the atoms at each domain, and they are colored red. van der Waals, hydrogen, and covalent bonds are set by cutoff distance (8 Å), coordinates of DNA structure, and DNA linkages (such as glycosidic and ester links), respectively. | |
Frequency calculation
If there is an eigenvalue λ from the solution to eqn (6), the frequency calculation is written as follows:| |
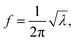 | (7) |
where the unit of f is Hz. The unit for the Raman spectroscopy data is cm−1, so we converted the unit of frequency to cm−1 according to| |
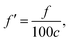 | (8) |
where c is the speed of the light.
Raman spectrum measurement
We performed the Raman measurements of DNA molecules at room temperature with a confocal Raman microscope (WITEC, alpha 300 R) at 532 nm. The spectral reading was obtained using a 600 gr per mm diffraction grating with the height for each blade at 500 nm. Due to the different atomic arrangements in the molecules, vibrational spectra obtained from Raman spectroscopy provide intrinsic characteristics of the molecules. To prevent the buffer effect during measurement of the Raman spectrum, we used pristine duplex DNA molecules extracted from salmon.
Results and discussion
The design scheme for DX DNA tiles and representative atomic force microscope (AFM) images of DX DNA lattices composed of DX tiles are shown in Fig. 3. A DX tile with the dimension of 12.6 × 4.0 nm2 is made of two duplexes connected by two crossover junctions. Two types of DX tiles—DX0 (no hairpin) and DX1 (with a single full turn-length duplex hairpin protruding upward with respect to the surface of the DX tile)—are used to test the frequency analysis method based on MWCENM (more detailed information about sample preparation and AFM imaging is in experimental section and Fig. S1 of the ESI†).20 In addition, we introduce DX0C (DX1C) to verify the structural stability of DX0 (DX1) lattices, which are composed of DX0 and DX0C (DX1 and DX1C) tiles. The vibrational characteristics of DX0 lattice (consisted of four DX0 tiles) are also obtained from the frequency analysis method and compared with Raman experimental data.
 |
| | Fig. 3 Schematics of double crossover (DX) DNA building blocks and representative AFM images of DX lattices. (a, b) A DX0 (green) is a planar DX building block without a hairpin, and a DX0C (red) connects DX0s. (c) A representative AFM image of a DX lattice comprised of DX0 and DX0C tiles. (d, e) A DX1 (blue) is a hairpin-embedded DX building block, and a DX1C connects DX1s. (f) An AFM image of a DX lattice composed of DX1 and DX1C tiles. The scan size of the AFM images is 150 × 150 nm2. | |
Raman experimental data
Table 2 shows the experimentally obtained Raman spectra and vibrational mode assignments of DNA molecules in the range between 400 cm−1 and 1200 cm−1 (Raman spectra and band assignments in the full range are shown in Fig. S3 and Table S1 of ESI†). The significant Raman spectra of DNA nucleotides are categorized into two regions: 400–750 cm−1 for nucleobases and 750–1200 cm−1 for sugar phosphate backbone groups.21,22 Due to a certain limitation when taking Raman spectra through the synthetic DX tiles—exceeding the Raman signal of the 1× TAE/Mg2+ buffer (40 mM Tris base, 20 mM acetic acid, 1 mM EDTA (pH 8.0), and 12.5 mM magnesium acetate) rather than the signal of the DNA molecules—we alternatively obtained them from the natural DNA duplexes extracted from salmon, which are also valid because the frequency range compared with the simulation is higher than 300 cm−1. In that relatively high frequency range, the DNA molecule generally shows the local vibrational characteristics of backbones and specific bases.
Table 2 Raman spectrum data for pristine DNA molecules obtained from salmon. Seven representative Raman spectral peaks in the range between 400 cm−1 and 1200 cm−1 are displayed to validate the calculated frequencies (Raman spectra in the full range are shown in Table S1 of ESI)
| No. |
Raman shift (cm−1) |
DNA vibrational modes |
| 1 |
497 |
Phosphoionic scissor |
| 2 |
678 |
Ring breathing vibrations of G and T |
| 3 |
732 |
Ring breathing vibrations of A |
| 4 |
786 |
Vibrations of C, T, and symmetric stretching of PO2− |
| 5 |
890 |
Deoxyribose ring vibrations |
| 6 |
1012 |
C–O stretching vibrations of deoxyribose |
| 7 |
1095 |
Phosphodiester stretching vibrations |
Frequency analysis data
The MWCENM based frequency analysis simulation was performed to calculate the frequencies of individual DX tiles (i.e., DX0 and DX1). Here the fixed boundary condition was applied in order to reflect the experimental set up such as DNA duplex fixed on a substrate (refer to simulation section of ESI†). By solving eqn (6), we obtained the eigenvalues at each vibrational mode of DX0 and DX1, and then we calculated the frequencies at each mode by solving eqn (7) and (8) in sequence. We found that the main modes of DX0 are bending and twisting, like general rod motions, whereas DX1 bends and twists with a hairpin bending motion (vibrational mode shapes of DX0 and DX1 are both available in Fig. S2 of ESI†). As frequency increases, in both tile structures, the overall vibrational characteristics evolve from global collective motions such as bending and twisting to local molecular vibrations as demonstrated in Fig. 4.
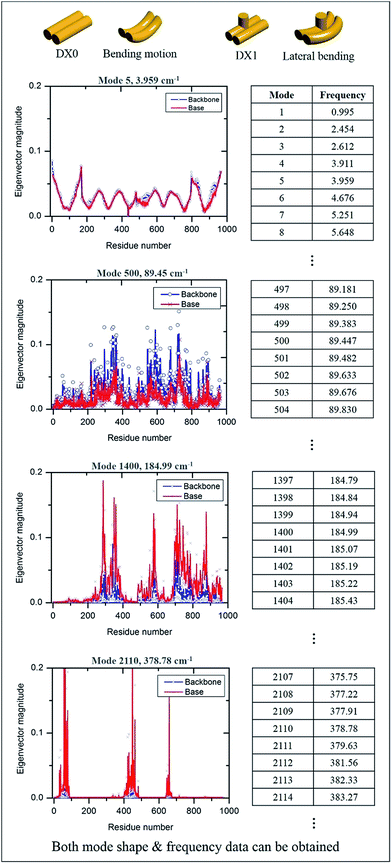 |
| | Fig. 4 Vibrational properties of DX0 and DX1 and their frequencies. By solving the equation of motion and using frequency calculations, we obtained both vibrational mode shapes and their corresponding frequencies. The number of modes depends on the number of sample atoms, and the vibrational characteristics from low to high frequency show dynamic motion, from collective motion to local vibration. Four vibrational characteristic graphs are obtained from the equation of motion of DX0 (the characteristics of DX1 are not shown here because they are similar to those of DX0). | |
For instance, in case of DX0 at fixed condition, its frequencies are divided into four parts such as the collective part (9.5–21.6 cm−1), phosphate backbone part (22.1–150.9 cm−1), base part (151.0–265.0 cm−1), and specific region part (265.2–1166.9 cm−1). Likewise, the other simulation cases are also summarized in Table S2 of ESI.† The collective part exhibits collective motions of both phosphate backbone and base to the same direction. However, the phosphate backbone part (the base part) has high mobility only at phosphate backbone (base). Furthermore, the specific region part shows high mobility in some local bases. We systematically counted the number of occurrence of high mobility in each base when its magnitude of eigenvector is higher than 0.1. This number counting yields automatic classification of the frequency ranges, in each of which only the same base types dominantly show high mobility. Through this procedure, specific frequency ranges were confirmed to each corresponding Raman peak. For instance, as shown in Fig. 5, the frequency range of DX0 at fixed condition that shows high mobility in adenine is 727–734 cm−1. This simulation result matches well with the third Raman peak (732 cm−1) which is known as a ring breathing motion of adenine.
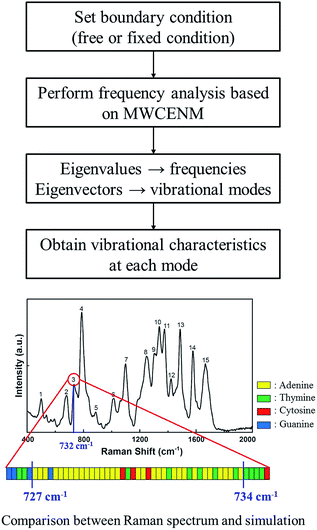 |
| | Fig. 5 Identification procedure of base type in the specific region part. In case of DX0 at fixed boundary condition, a total of 2823 different normal modes including both frequencies and vibrational mode shapes were obtained and classified into 4 parts as shown in Fig. 4. In the specific region part, there were particularly local vibrations in which only a few atoms show high mobility in specific bases. Systematically, if their eigenvector magnitudes are larger than 0.1, we considered them to have high mobility and they were sorted by their base types. Finally, such base type and corresponding frequency information were compared with Raman experimental data. For example, corresponding to the third Raman peak (732 cm−1) which is known as a ring breathing motion of adenine, the MWCENM simulation successfully identified high mobility in adenine (727–734 cm−1). Although a few other bases also appeared in this frequency range, adenine is the most dominant and followed by thymine as its complementary base. | |
Moreover, in order to investigate the boundary condition effect, we additionally performed simulation at free boundary condition for both DX0 and DX1. It is noted that the first six zero eigenvalues, in the standard mathematical framework of NMA, are to be excluded because they correspond to rigid body motions (i.e., three translational motions and three rotational motions) of the given system at free boundary condition.
In our comparison between the simulation frequencies of DX0 (DX1) and the experimental Raman data, shown in Fig. 6a, b (c, d), the percentages of error deviations (defined as 100 × |Raman data − simulation data|/Raman data) are relatively smaller at fixed condition, 1.9% (1.6%), compared to free condition, 4.0% (2.0%). Although small error deviations are observable, the overall trends between simulation and experiment are similar for both free and fixed conditions. Therefore, we not only validated the proposed frequency analysis method based on MWCENM, but also demonstrated the reliability of comparison between predicted frequency data and Raman experimental data. After successful validation of modelling and simulation using a single tile structure, furthermore, we investigated the vibrational characteristics of DX0 lattice structure at fixed condition. As shown in Fig. 6e, it has similar vibrational features of DX0 (DX1) single tile but the error with Raman data dramatically reduces down to 0.7%. Although here we only conducted the validation of the proposed frequency analysis method at the high frequency range due to experimental limits, it implies that the MWCENM simulation can predict vibrational features (i.e., both frequency and mode shape) of DNA tile structures very precisely and effectively in terms of accuracy and computational cost, respectively.
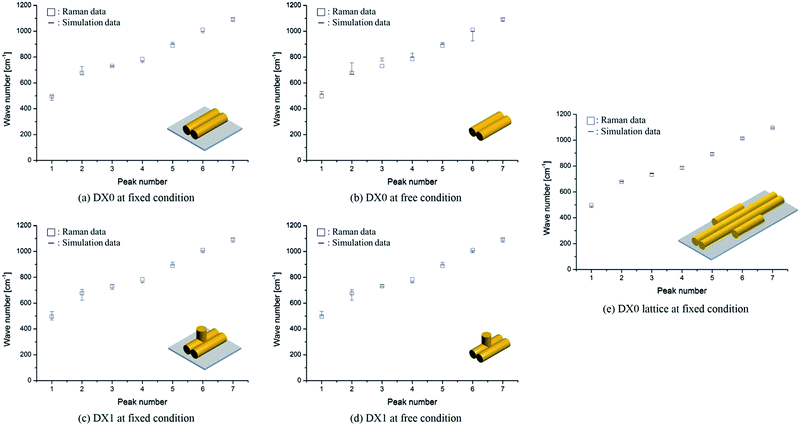 |
| | Fig. 6 Vibrational frequency comparison between Raman spectra and the MWCENM simulation. (a, b) Vibrational frequencies (squares for experimentally obtained Raman data and bars for theoretically computed frequency ranges) of DX0 at fixed (bound on the substrate) and free conditions. The computed frequency ranges of DX0 in the fixed (free) condition are 463–501, 660–726, 727–734, 755–766, 897–914, 986–1000, and 1074–1100 cm−1 (514–532, 668–755, 769–792, 800–830, 896–911, 924–1000, and 1074–1100 cm−1) as the peak number increases from 1 to 7, respectively. Although the free and fixed conditions show similar trends, the error (difference between experimental values and the median of the computed frequency range) in the fixed condition is relatively smaller than the error in the free condition because of better consideration of the experimental setup. The average error decreased from 4.0% (free condition) to 1.9% (fixed). (c, d) Vibrational frequencies of DX1 at fixed and free conditions. The computed frequency ranges of DX1 in the fixed (free) condition are 467–535, 621–705, 706–745, 756–763, 892–915, 988–1006, and 1070–1100 cm−1 (500–535, 621–705, 725–745, 756–763, 892–915, 988–1006, and 1070–1100 cm−1). The average error decreases from 2.0% (free condition) to 1.6% (fixed). (e) Vibrational frequencies of DX0 lattice at fixed condition. The computed frequency ranges are 479–493, 678–682, 741–744, 773–795, 883–903, 1007–1021, and 1090–1098 cm−1. This simulation result shows the highest accuracy with an error of 0.7%. | |
Conclusions
In this study, we compared frequencies calculated using the MWCENM method with Raman experimental data. In order to confirm the reliability of calculated frequencies and boundary effect, we considered both free and fixed boundary conditions in case of DX0 and DX1 single tiles. Moreover, the vibrational characteristics of DX0 lattice at fixed condition were also investigated and compared with Raman spectrum of DNA duplex. Due to experimental limits, we just compared our simulation result with Raman experimental data at the high frequency range. That is, only local vibrational characteristics of backbone and base of DNA molecules can be obtained through experiment, whereas simulation can capture the wide range of atomic motions from the low frequency (collective motion) to the high frequency (local vibration). For all cases, the proposed frequency analysis method successfully captured vibrational features of DNA tile structures, at most, with an error of 4.0%. Consequently, it is expected that this study will play an important role in prediction of structural stability and functional dynamics of biomolecules at atomic level which are still hardly obtained through any state-of-the-art experimental method.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2015R1D1A1A01057280, M. K. K.), (2014R1A2A1A11053213, S. H. P.).
Notes and references
- N. C. Seeman, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS PubMed
 .
. - E. Winfree, F. Liu, L. A. Wnzler and N. C. Seeman, Nature, 1998, 394, 539–544 CrossRef CAS PubMed
 .
. - S. Hamada and S. Murata, Angew. Chem., Int. Ed., 2009, 48, 6820–6823 CrossRef CAS PubMed
 .
. - P. Yin, R. F. Hariadi, S. Sahu, H. M. Choi, S. H. Park, T. H. Labean and J. H. Reif, Science, 2008, 321, 824–826 CrossRef CAS PubMed
 .
. - D. Liu, M. Wang, Z. Deng, R. Walulu and C. Mao, J. Am. Chem. Soc., 2004, 126, 2324–2325 CrossRef CAS PubMed
 .
. - P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed
 .
. - B. Wei, M. Dai and P. Yin, Nature, 2012, 485, 623–626 CrossRef CAS PubMed
 .
. - N. C. Seeman, Annu. Rev. Biophys. Biomol. Struct., 1998, 27, 225–248 CrossRef CAS PubMed
 .
. - A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed
 .
. - M. Zahid, B. Kim, R. Hussain, R. Amin and S. H. Park, Nanoscale Res. Lett., 2013, 8, 119 CrossRef PubMed
 .
. - P. F. Qian, S. Seo, J. Kim, S. Kim, B. S. Lim, W. K. Liu, B. J. Kim, T. H. LaBean, S. H. Park and M. K. Kim, Nanotechnology, 2012, 23, 105704 CrossRef PubMed
 .
. - A. D. Schuyler and G. S. Chirikjian, J. Mol. Graphics Modell., 2004, 22, 183–193 CrossRef CAS PubMed
 .
. - V. Tozzini, Curr. Opin. Cell Biol., 2005, 15, 144–150 CAS
 .
. - P. Doruker, A. R. Atilgan and I. Bahar, Proteins, 2000, 40, 512–524 CrossRef CAS
 .
. - A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505–515 CrossRef CAS PubMed
 .
. - K. Hinsen, Proteins, 1998, 33, 417–429 CrossRef CAS
 .
. - M. H. Kim, S. Seo, J. I. Jeong, B. J. Kim, W. K. Liu, B. S. Lim, J. B. Choi and M. K. Kim, Protein Sci., 2013, 22, 605–613 CrossRef CAS PubMed
 .
. - M. Hu, S. Raj, B. Kim, W. K. Liu, S. Baik, T. Kim, B. S. Lim and M. K. Kim, J. Mech. Sci. Technol., 2010, 24, 1771–1780 CrossRef
 .
. - M. K. Kim, G. S. Chirikjian and R. L. Jernigan, J. Mol. Graphics Modell., 2002, 21, 151–160 CrossRef CAS PubMed
 .
. - B. Kim, S. Jo, J. Son, J. Kim, M. H. Kim, S. U. Hwang, S. R. Dugasani, B. D. Kim, W. K. Liu, M. K. Kim and S. H. Park, Nanotechnology, 2014, 25, 105601 CrossRef PubMed
 .
. - A. Kulkarni, B. Kim, S. R. Dugasani, P. Joshirao, J. A. Kim, C. Vyas, V. Manchanda, T. Kim and S. H. Park, Sci. Rep., 2013, 3, 2062 CrossRef PubMed
 .
. - B. Gnapareddy, S. R. Dugasani, T. Ha, B. Paulson, T. Hwang, T. Kim, J. H. Kim, K. Oh and S. H. Park, Sci. Rep., 2015, 5, 12722 CrossRef CAS PubMed
 .
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06125k |
| ‡ These authors contributed equally. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Junyoung Son‡b,
Byung Ho Leea,
Sreekantha Reddy Dugasani
a,
Junyoung Son‡b,
Byung Ho Leea,
Sreekantha Reddy Dugasani b,
Sung Ha Park*b and
Moon Ki Kim
b,
Sung Ha Park*b and
Moon Ki Kim *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100
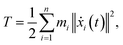
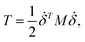
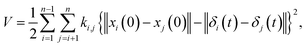
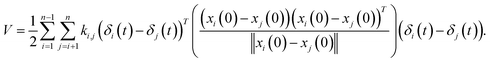
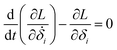
![[greek delta with two dots above]](https://www.rsc.org/images/entities/i_char_e19b.gif) + Kδ = 0.
+ Kδ = 0.
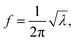
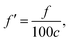

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





