Open Access Article
Open Access ArticleStepwise study on Janus-like particles fabricated by polymeric mixtures within soft droplets: a Monte Carlo simulation
Yuping Sheng *a,
Li Xiaa,
Guanzhou Yanga,
Yiqing Xia
*a,
Li Xiaa,
Guanzhou Yanga,
Yiqing Xia ac,
Yong Huanga,
Chuanjiang Pana and
Yutian Zhu
ac,
Yong Huanga,
Chuanjiang Pana and
Yutian Zhu *b
*b
aAnalytical and Testing Center, Sichuan University of Science and Engineering, Zigong 643000, People's Republic of China. E-mail: ypsheng_suse@163.com
bState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, People's Republic of China. E-mail: ytzhu@ciac.ac.cn
cCollege of Materials Science and Engineering, Sichuan University of Science and Engineering, Zigong 643000, People's Republic of China
First published on 7th August 2017
Abstract
Using Monte Carlo simulations, a stepwise study (from simple to complex) is followed to investigate Janus particles self-assembled from polymer mixtures within soft droplets. When the polymer mixtures are changed from a homopolymer/homopolymer (A/D) mixture to a diblock copolymer/homopolymer (AB/D) mixture and then to a triblock copolymer/homopolymer (ABC/D) mixture, the self-assembled structures transform from classic Janus particles to hierarchical Janus structures with novel hemi-domains. The effects of the incompatibility between two components, polymer–solvent interactions and the ratio of two components of the mixture on the Janus structure are systematically examined. It is found that the Janus structure is highly related to the incompatibility between two components of the mixture, while the sizes of the two hemispheres in a Janus particle can be well tuned by adjusting the ratio of the components in the mixture. Moreover, the corresponding incompatibility between two components of the mixture for the transformation point is increased when the mixture is changed from the A/D to the AB/D and then to the ABC/D mixture. More interestingly, it is found that the variation of the aggregation degree of the changed component with time gradually lags behind that of the homopolymer component (D) during the formation of Janus particles when the component in the mixture changes from A to AB and then to ABC. The simulation result could provide theoretical guidance for the preparation of designable Janus particles.
1. Introduction
Anisotropic polymeric Janus particles with two distinct compositions on the opposite sides have gained considerable attention owing to their unique surface properties and promising applications in many fields, such as catalysts,1–3 electronics,4–6 solid surfactants,7,8 biomedicines,9,10 nanoprobes11 and so forth. Up to now, numerous methods have been developed to synthesize polymeric Janus colloidal particles,12–14 including microfluidic techniques, self-organized precipitation, and emulsion polymerization. For instance, well defined Janus spheres,15 discs16 and cylinders17,18 have been generated via the steps of solution casting, cross-linking and redissolving of the triblock copolymers. A microfluidic technique was often used for the fast and continuous production of Janus particles with a controlled size and structure.19 In addition, the self-assembly of block copolymer mixtures with electrostatic interaction20 or hydrogen bonding21,22 was also an effective method to fabricate Janus micelles. Basically, the above methods need complex processing procedure or additional interactions between the self-assembly units, which limited the application of Janus materials in various areas.Recently, it was proved that the confined self-assembly of block copolymers or a polymer mixture within emulsion droplets is a facile and practicable approach to generate asymmetric Janus structures.23–30 As the solvent evaporated from the emulsion droplet, micro-phase separation of the block copolymers occurs, resulting in the formation of the asymmetric Janus structures. For example, Deng et al. fabricated Janus nanoparticles with a tunable aspect size ratio from the solvent evaporation induced assembly of poly(4-vinylpyridine) (P4VP)-based block copolymers within emulsion droplets.31 In addition, confining the polymer mixture inside the emulsion droplet is a useful strategy to create Janus nanoparticles due to the microphase-separation of different polymers or different blocks that occurs within the droplets. Kietzke et al. studied the biphasic morphologies from the miniemulsion with the mixtures of two immiscible polymers.32 Janus particles with a tunable volume ratio and well-defined structure were prepared in their study. By means of the phase separation of a binary blend in an emulsion droplet, i.e. the diblock copolymer polystyrene-b-poly(4-vinylpyridine) (PS-b-P4VP) and the homopolymer poly(methyl methacrylate) (PMMA), Deng et al. designed a series of unique Janus colloidal particles with hierarchical structures.33 It was found that the internal structures of the Janus particles depended on the copolymer composition, solvent selectivity, particle size, and polymer/aqueous solution interfacial property. Although remarkable performances and progress have been achieved for the fabrication of Janus nanoparticles via the confined self-assembly of block copolymers or polymer mixtures in emulsion droplets, there is still a lack of a clear understanding of this method. For example, some fundamental information, such as the evolution of the chain conformation, control factors and the formation mechanism of the Janus particles, is still not very clear.
On the other hand, it has been proved that computer simulation is a powerful tool to study the self-assembly of block copolymers in solutions.34–41 In our previous study, we applied a lattice Monte Carlo method to investigate the co-assembly of AB/BC diblock copolymer mixture in a selected solvent, which predicted a variety of novel Janus micelles with a controllable micellar shape and Janus architecture.40 Recently, a simulated annealing method was developed to mimic the self-assembly of block copolymers in an emulsion droplet.31,37,42 Li and co-workers proposed that the annealing method made the solvent environment gradually change from a good solvent to a poor solvent, resulting in the aggregation of block copolymers, which agrees well with the soft-confinement of the block copolymers within the emulation droplets.37 Combing with the experiments, they also applied this method to examine the self-assembly of P4VP-based block copolymers within emulsion droplets.31 In our previous study, we have successfully applied this annealing simulation method to study the self-assembly of ABA triblock copolymers under soft confinement induced by poor solvent.38 Thereafter, we extended this method to mimic the self-assembly of AB diblock copolymers28 and ABC triblock copolymers39 under the soft confinement. The simulation results imply that both the shape and internal structure of self-assembled nanoparticles can be tuned by the block copolymer properties, interfacial selectivity, and the confinement size.
In this study, the simulated annealing method is also used to investigate the confined self-assembly of polymer mixtures within soft droplet. The solvent environment for polymer mixture is changed from good to poor gradually to mimic the evaporation of organic solvent in emulsion droplet. Three types of polymer mixtures, i.e. homopolymer (A)/homopolymer (D), diblock copolymer (AB)/homopolymer (D) and linear triblock copolymer (ABC)/homopolymer (D), are used to fabricate Janus particles in sequence. Various control parameters, such as the incompatibility between two components, polymer–solvent interactions and the ratio of the components in the mixture, are examined to reveal their influences on Janus structures. Moreover, the average contact numbers, mean square end-to-end distance and the formation pathways of some representative Janus particles are presented to explicate the formation mechanisms of the Janus structure.
2. Simulation model and method
Lattice Monte Carlo (MC) method is used in this simulation. This method has been widely employed to examine the self-assembly of block copolymers.42–47 In this study, the coarse grained chains are placed in a cubic lattice of volume V = L × L × L (L = 40) with periodic boundary conditions imposed in all three directions. Each monomer occupies one lattice site, and then the remaining vacancy of the lattice represents the solvent. Excluded volume interactions are implemented to guarantee that only one monomer occupies one lattice site. Bond crossing is not allowed. The single-site bond fluctuation model48–50 is applied in this simulation, so the bond length of the polymer chain is limited as 1 and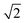 . The initial state is from the randomly dispersed polymer molecules. The self-assembly evolves via the exchange between the monomer and the solvent, i.e. a chain monomer is randomly chosen to exchange with the solvent on its 18 nearest neighbors when this exchange neither violates the bond length nor allows bond crossing. The partial-reptation algorithm51 is also used in this simulation: when the exchange induces a single break in the chain, the newly generated break will continue to exchange with the following monomers along the chain until the chain reconnects. Whether the tentative exchange is acceptable or rejective is further determined by the Metropolis rule.52 The exchange is accepted when the energy change ΔE is negative or it is accepted with a probability of p = exp[−ΔE/kBT], where
. The initial state is from the randomly dispersed polymer molecules. The self-assembly evolves via the exchange between the monomer and the solvent, i.e. a chain monomer is randomly chosen to exchange with the solvent on its 18 nearest neighbors when this exchange neither violates the bond length nor allows bond crossing. The partial-reptation algorithm51 is also used in this simulation: when the exchange induces a single break in the chain, the newly generated break will continue to exchange with the following monomers along the chain until the chain reconnects. Whether the tentative exchange is acceptable or rejective is further determined by the Metropolis rule.52 The exchange is accepted when the energy change ΔE is negative or it is accepted with a probability of p = exp[−ΔE/kBT], where 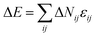 is the energy change aroused by the tentative move; ΔNij is the number difference for the nearest neighbor pairs of components i and j induced by the exchange; i and j represent A, B, C, D and S (solvent), respectively; εij is the reduced interaction of components i and j; kB is the Boltzmann constant and it is fixed as 1 in this simulation; T is the reduced temperature. The annealing method is used in this simulation. This method is used to simulate the evaporation of the organic solvent in an emulsion droplet, which induces the polymer to gradually remain in a poor solvent environment and self-assemble into various structures. The inverse temperature 1/T changes from 0 to 0.07 to achieve the annealing process. The annealing rate is set as 0.0002 per step, and 1/T is fixed as 0.07 after 350 steps and then another 650 steps are taken to ensure the final equilibrium state.
is the energy change aroused by the tentative move; ΔNij is the number difference for the nearest neighbor pairs of components i and j induced by the exchange; i and j represent A, B, C, D and S (solvent), respectively; εij is the reduced interaction of components i and j; kB is the Boltzmann constant and it is fixed as 1 in this simulation; T is the reduced temperature. The annealing method is used in this simulation. This method is used to simulate the evaporation of the organic solvent in an emulsion droplet, which induces the polymer to gradually remain in a poor solvent environment and self-assemble into various structures. The inverse temperature 1/T changes from 0 to 0.07 to achieve the annealing process. The annealing rate is set as 0.0002 per step, and 1/T is fixed as 0.07 after 350 steps and then another 650 steps are taken to ensure the final equilibrium state.
In this simulation, the self-assembly of the mixtures of homopolymer/homopolymer (A/D), diblock copolymer/homopolymer (AB/D) and triblock copolymer/homopolymer (ABC/D) within soft droplets are examined respectively. The concentration of the mixture is fixed as 10% and all the chain lengths are set as le = 18. The parameters between the same monomers are set as εAA = εBB = εCC = εDD = εSS = 0. The interaction parameters, i.e. εAS, εBS, εCS and εDS, represent the interactions between different blocks and the solvent. εDS, εAS, εBS and εCS are set as positive values to ensure the solvent is poor for all the blocks.
3. Results and discussion
In this study, we applied Monte Carlo simulation to investigate the formation of Janus particles from the self-assembly of polymer mixtures within soft droplets. The self-assemblies of A/D, AB/D and ABC/D polymer mixtures are examined in sequence. For the three kinds of mixtures, the influences of the incompatibility between two components, the polymer–solvent interaction and the ratio of the components in the mixture on the self-assembly of the polymer mixtures are all systematically examined. Then, the average contact numbers, mean square end-to-end distance and formation pathways of some representative Janus particles are presented to illustrate their chain conformation and formation mechanisms.3.1 Janus particles from the mixtures of homopolymer/homopolymer
Fig. 1 presents a series of self-assembled morphologies from an A18/D18 mixture as a function of the incompatibility between the A and D homopolymers (εAD). The polymer–solvent interactions, i.e. εAS and εDS, are fixed as 3, and the ratio of A and D is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. When εAD = 0, i.e. A and D blocks are compatible with each other, a spherical mixed particle is formed with A and D blocks mixing homogeneously. As εAD is increased to 0.15, microphase-separation between A and D occurs, resulting in the formation of a Janus structure. When εAD is further increased from 1 to 5, Janus particles with two hemispheres are obtained and the shape of the Janus particle changes from spherical to calabash-like. Clearly, the join of the A and D hemispheres becomes increasingly small with the increasing εAD. As εAD is increased to 6, the macro-phase separation between A and D occurs, causing the formation of two distinct A and D spheres. Fig. 1 implies that the incompatibility between A and D plays an important role in the formation of the Janus structure.
1. When εAD = 0, i.e. A and D blocks are compatible with each other, a spherical mixed particle is formed with A and D blocks mixing homogeneously. As εAD is increased to 0.15, microphase-separation between A and D occurs, resulting in the formation of a Janus structure. When εAD is further increased from 1 to 5, Janus particles with two hemispheres are obtained and the shape of the Janus particle changes from spherical to calabash-like. Clearly, the join of the A and D hemispheres becomes increasingly small with the increasing εAD. As εAD is increased to 6, the macro-phase separation between A and D occurs, causing the formation of two distinct A and D spheres. Fig. 1 implies that the incompatibility between A and D plays an important role in the formation of the Janus structure.
Beside the incompatibility between A and D, the interfacial selectivity of the flexible confinement space, i.e. εAS and εDS, also greatly affects the resulting structures. In Fig. 2a, various self-assembled morphologies from the A18/D18 mixtures that changed with εAS are presented. Here, the incompatibility between A and D is fixed as εAD = 2 and the D homopolymer–solvent interaction is set as εDS = 3. The ratio of A and D is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. When the solvent has equal selectivity for A and D, i.e. εAS = εDS = 3, a classic Janus particle is obtained. As εAS is increased from 4 to 5.3, the A domain is gradually covered by the D domain. Thus, mushroom-like Janus particles are observed when εAS = 5 and εAS = 5.3. In experiments, Masayoshi et al. synthesized the mushroom-like Janus particles, which were severed as double stimuli-responsive particulate surfactants.53 However, when εAS is further increased to 6, an onion-like particle is found instead of the Janus particle. Due to the increased hydrophobicity for A18 homopolymers, the A domain is totally covered by the D domain to avoid contact with solvent.
1. When the solvent has equal selectivity for A and D, i.e. εAS = εDS = 3, a classic Janus particle is obtained. As εAS is increased from 4 to 5.3, the A domain is gradually covered by the D domain. Thus, mushroom-like Janus particles are observed when εAS = 5 and εAS = 5.3. In experiments, Masayoshi et al. synthesized the mushroom-like Janus particles, which were severed as double stimuli-responsive particulate surfactants.53 However, when εAS is further increased to 6, an onion-like particle is found instead of the Janus particle. Due to the increased hydrophobicity for A18 homopolymers, the A domain is totally covered by the D domain to avoid contact with solvent.
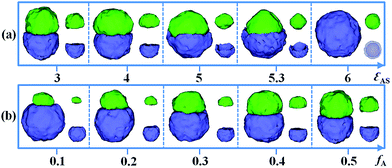 | ||
| Fig. 2 Self-assembled morphologies of A18/D18 mixtures as a function of εAS (a) and fA (b). The parameter εAD is fixed as 2. For clarity, the A and D domains are shown on the right of each corresponding snapshot. The domains of the D blocks are transparent to show the inner structure at εAS = 6. The color codes of the images are the same as in Fig. 1. | ||
The volume fraction of each individual composition also plays an important role on the Janus structure. The influence of fA (the volume fraction of A homopolymers in the mixture) on the formation of Janus particles is examined. Other parameters are fixed as εAS = εDS = 3 and εAD = 2. In Fig. 2b, we show a series of self-assembled morphologies with fA increased from 0.1 to 0.5. When fA = 0.1, A homopolymers form a small domain on one side, while D homopolymers aggregate as a big domain on another side, which makes a snowman-shape Janus particle. As fA is increased from 0.1 to 0.4, the size of the A hemisphere is gradually increased. When fA = 0.5, the A and D homopolymers form two equivalent hemispheres, as shown in Fig. 2b. This implies that one can easily tune the size of the two domains of the Janus particles by changing the ratio of the components in the mixtures. In experiments, Deng et al.31 successfully tuned Janus structures via adjusting the block ratio of P4VP and PS in the confined self-assembly of PS-b-P4VP diblock copolymers within emulsion droplets. Moreover, Kietzke et al.32 fabricated the biphasic blend particles with different sizes of polystyrene (PS) and poly(propylene carbonate) (PPC) domains from PS/PPC mixtures by altering the composition ratios. These experimental observations agree well with the morphological transition in our simulations.
3.2 Janus particles from the mixtures of diblock copolymer/homopolymer
In this section, the self-assembly of AB/D mixtures is examined to explore more interesting Janus particles. The effect of incompatibility between the diblock copolymer (AB) and the homopolymer (D) in a mixture (i.e. εAD and εBD) on the formation of Janus particles is investigated. The incompatibilities between AB and D are set as the same value, i.e. εAD = εBD = εDPH. Moreover, the incompatibility between the A and B blocks (εAB) is set as 2, the parameters of the polymer–solvent interactions, i.e. εAS, εBS and εDS, are fixed as 3, and the ratio of the AB diblock copolymer and the D homopolymer is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fig. 3 shows the self-assembled morphologies of the symmetric diblock copolymer/homopolymer mixtures (A9B9/D18 mixtures) and the asymmetric diblock copolymer/homopolymer mixtures (A7B11/D18) as a function of εDPH. When the AB diblock copolymer and the D homopolymer are compatible with each other, i.e. εDPH = 0, spherical particles with homogeneously distributed A, B and D domains are formed by the A9B9/D18 mixture (Fig. 3a1). As εDPH is increased to 0.5, microphase-separation between the AB diblock copolymers and the D homopolymers occurs, leading to the D-sphere covered by a segmented AB-shell (Fig. 3b1 and c1). As εDPH is increased from 1 to 3, further microphase-separation between AB and D occurs, and A and B monomers form segmented hemi-spheres in the Janus particle, as shown in Fig. 3d1–f1. When εDPH is further increased from 4 to 5, it is observed that the segmented AB hemisphere gradually moves away from the D hemisphere, as shown in Fig. 3g1–h1. Finally, macroscopic phase separation between AB diblock copolymers and D homopolymers is observed when the εDPH is increased to 6 (Fig. 3i1). The morphologies of A7B11/D18 mixtures as a function of the incompatibility between AB and D are also shown in Fig. 3. Similar to A9B9/D18 mixtures, a mixed spherical particle is formed by A7B11/D18 mixtures when two components (AB and D) are compatible with each other (εDPH = 0, Fig. 3a2). As εDPH is increased from 1 to 5, various Janus particles with AB hemispheres and D hemispheres are observed (Fig. 3d2–h2). When εDPH is further increased to 6, A7B11 diblock copolymers and D18 homopolymers formed AB patchy-like spheres and D spheres, respectively (Fig. 3i2). Fig. 3 indicates that we can create a series of novel Janus particles with AB hemispheres and D hemispheres via the self-assembly of AB/D mixtures within emulsion droplets. Moreover, the internal structures of the AB hemispheres can be well controlled by the incompatibility between AB and D.
1. Fig. 3 shows the self-assembled morphologies of the symmetric diblock copolymer/homopolymer mixtures (A9B9/D18 mixtures) and the asymmetric diblock copolymer/homopolymer mixtures (A7B11/D18) as a function of εDPH. When the AB diblock copolymer and the D homopolymer are compatible with each other, i.e. εDPH = 0, spherical particles with homogeneously distributed A, B and D domains are formed by the A9B9/D18 mixture (Fig. 3a1). As εDPH is increased to 0.5, microphase-separation between the AB diblock copolymers and the D homopolymers occurs, leading to the D-sphere covered by a segmented AB-shell (Fig. 3b1 and c1). As εDPH is increased from 1 to 3, further microphase-separation between AB and D occurs, and A and B monomers form segmented hemi-spheres in the Janus particle, as shown in Fig. 3d1–f1. When εDPH is further increased from 4 to 5, it is observed that the segmented AB hemisphere gradually moves away from the D hemisphere, as shown in Fig. 3g1–h1. Finally, macroscopic phase separation between AB diblock copolymers and D homopolymers is observed when the εDPH is increased to 6 (Fig. 3i1). The morphologies of A7B11/D18 mixtures as a function of the incompatibility between AB and D are also shown in Fig. 3. Similar to A9B9/D18 mixtures, a mixed spherical particle is formed by A7B11/D18 mixtures when two components (AB and D) are compatible with each other (εDPH = 0, Fig. 3a2). As εDPH is increased from 1 to 5, various Janus particles with AB hemispheres and D hemispheres are observed (Fig. 3d2–h2). When εDPH is further increased to 6, A7B11 diblock copolymers and D18 homopolymers formed AB patchy-like spheres and D spheres, respectively (Fig. 3i2). Fig. 3 indicates that we can create a series of novel Janus particles with AB hemispheres and D hemispheres via the self-assembly of AB/D mixtures within emulsion droplets. Moreover, the internal structures of the AB hemispheres can be well controlled by the incompatibility between AB and D.
The effect of polymer–solvent interactions on the formation of Janus particles is also studied in this section. Four types of polymer mixtures, i.e., A9B9/D18, A7B11/D18, A6B12/D18 and A5B13/D18, are considered in the examination. The incompatibilities between A, B and D (εAB, εAD and εBD) are set as the same value, i.e. εPP = 2, and the ratio of the AB diblock copolymers and the D homopolymers is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fig. 4a shows various Janus particles at different values of εPS. The polymer–solvent interactions are set as equal, i.e. εAS = εBS = εDS = εPS. For the mixtures of symmetric A9B9 diblock copolymers and D18 homopolymers, they self-assemble into Janus particles with segmented AB hemispheres and D hemispheres when εPS = 3 or εPS = 4. As εPS is increased to 5 or 6, A and B blocks aggregate into the double-helix structure as the AB hemispheres. For the mixture of A7B11/D18, a different morphological transition sequence for the AB hemisphere with an increase of εPS is observed, i.e., the structure transitions from the aggregate of piled disks and rings (εPS = 3) to a twisted-stripe structure (εPS = 4), a double-helix structure (εPS = 5), and a patchy-like structure (εPS = 6). For the self-assembly of A6B12/D18 and A5B13/D18 mixtures, the structures of the AB hemisphere are independent of εPS, and always form the patchy-like structures as εPS is increased from 3 to 6. Furthermore, we also studied the effects of diblock copolymer–solvent interaction (εDPS) and homopolymer–solvent interaction (εHS) on the Janus structure from A9B9/D18 and A5B13/D18 mixtures. When the parameter εDPS (or εHS) is changed from 3 to 6, the value of εHS (or εDPS) is fixed as 3. In Fig. 4b, as εDPS increased from 3 to 5.3, the AB domain is gradually covered by the D domain, inducing the mushroom-like Janus particles. When εDPS is increased to 6, the AB domain is totally covered by the D domain to keep away from solvent. The structure of the AB domain is kept as a segment aggregate for A9B9/D18 mixtures, while the AB-domain is always a patchy-like structure for A5B13/D18 mixtures. Moreover, as εHS increases from 3 to 6, the D domain changes from a hemisphere to a sphere and gradually covers the AB domain. When εDPS = 5.3 and 6, the A9B9 and A5B13 diblock copolymer self-assemble into a stripe-like shell and a patchy-like shell outside the D sphere.
1. Fig. 4a shows various Janus particles at different values of εPS. The polymer–solvent interactions are set as equal, i.e. εAS = εBS = εDS = εPS. For the mixtures of symmetric A9B9 diblock copolymers and D18 homopolymers, they self-assemble into Janus particles with segmented AB hemispheres and D hemispheres when εPS = 3 or εPS = 4. As εPS is increased to 5 or 6, A and B blocks aggregate into the double-helix structure as the AB hemispheres. For the mixture of A7B11/D18, a different morphological transition sequence for the AB hemisphere with an increase of εPS is observed, i.e., the structure transitions from the aggregate of piled disks and rings (εPS = 3) to a twisted-stripe structure (εPS = 4), a double-helix structure (εPS = 5), and a patchy-like structure (εPS = 6). For the self-assembly of A6B12/D18 and A5B13/D18 mixtures, the structures of the AB hemisphere are independent of εPS, and always form the patchy-like structures as εPS is increased from 3 to 6. Furthermore, we also studied the effects of diblock copolymer–solvent interaction (εDPS) and homopolymer–solvent interaction (εHS) on the Janus structure from A9B9/D18 and A5B13/D18 mixtures. When the parameter εDPS (or εHS) is changed from 3 to 6, the value of εHS (or εDPS) is fixed as 3. In Fig. 4b, as εDPS increased from 3 to 5.3, the AB domain is gradually covered by the D domain, inducing the mushroom-like Janus particles. When εDPS is increased to 6, the AB domain is totally covered by the D domain to keep away from solvent. The structure of the AB domain is kept as a segment aggregate for A9B9/D18 mixtures, while the AB-domain is always a patchy-like structure for A5B13/D18 mixtures. Moreover, as εHS increases from 3 to 6, the D domain changes from a hemisphere to a sphere and gradually covers the AB domain. When εDPS = 5.3 and 6, the A9B9 and A5B13 diblock copolymer self-assemble into a stripe-like shell and a patchy-like shell outside the D sphere.
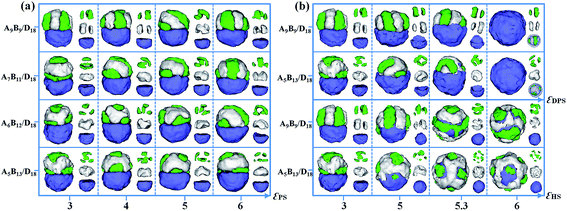 | ||
| Fig. 4 (a) Self-assembled morphologies of the A9B9/D18, A7B11/D18, A6B12/D18 and A5B13/D18 mixtures as a function of εPS. (b) Self-assembled morphologies of A9B9/D18 and A5B13/D18 mixtures as a function of εDPS and εHS. The parameters εPP are fixed as 2. For clarity, A, B and D domains are shown on the right of each corresponding snapshot. The color codes of the images are the same as in Fig. 3. | ||
In order to study the effect of the ratio of two components in a mixture on the formation of Janus particles, the self-assembly of four kinds of mixtures, i.e. A9B9/D18, A7B11/D18, A6B12/D18 and A5B13/D18, are examined in this section. The volume fraction of the AB diblock copolymers (fAB) in the mixture is changed from 0.1 to 0.9 in Fig. 5. Other parameters are fixed, i.e. εPS = 3 and εPP = 2. For the mixtures of A9B9/D18, the Janus spherical particles form with two different domains on two sides. As fAB is increased, the morphologies formed by the AB diblock copolymers are always kept as a segmented structure, while the size of the AB domain and the number of disks gradually increase with fAB. For A7B11/D18 mixtures, the size of the AB domain in a Janus spherical particle also gradually increases with the increase of fAB, but the morphologies change from segmented structures to aggregates of piled disks and rings. When fAB is increased in A6B12/D18 mixtures, the variation of the AB domain is similar to the morphological change in the mixtures of A7B11/D18. The segmented structure, patchy-like structure and aggregate of piled disks and rings are also observed. For A5B13/D18 mixtures, the AB diblock copolymers form hamburger-like structures at fAB = 0.1, and then the A blocks tend to form lumps or strips on the B domain when fAB is increased from 0.2 to 0.9. The result illustrates that the structure of the AB domain in a Janus particle is independent of fAB for the symmetric copolymer/homopolymer mixtures, while the AB-structure varied with the increase of fAB for the asymmetric copolymer/homopolymer mixtures. Moreover, the size of the two domains and the internal structures of the AB domains can be well tuned by changing the ratio of the two components in the mixture.
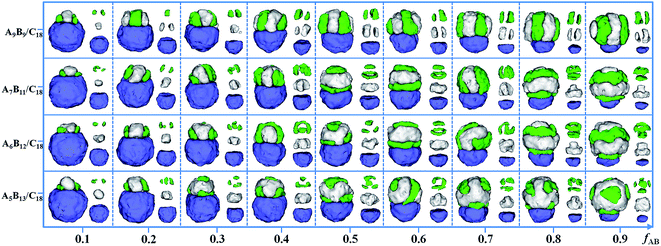 | ||
| Fig. 5 Self-assembled morphologies of A9B9/D18, A7B11/D18, A6B12/D18 and A5B13/D18 mixtures as a function of fAB. The parameters εPS are fixed as 3, and εPP are fixed as 2. For clarity, A, B and D domains are shown on the right of each corresponding snapshot. The color codes of the images are the same as in Fig. 3. | ||
3.3 Janus particles from the mixtures of triblock copolymer/homopolymer
In this section, one component in the mixture is changed to a linear triblock copolymer (ABC) while another component is fixed as a homopolymer (D). Due to the complex chain architecture, the linear triblock copolymer is expected to exhibit a unique self-assembly behavior in the mixture. In Fig. 6, we examine the effect of incompatibility between the triblock copolymer (ABC) and the homopolymer (D) in a mixture (i.e. εAD, εBD and εCD) on the formation of Janus particles. The parameter εTPH is used to represent εAD, εBD and εCD because they are set as equal values. Moreover, the parameters εAS, εBS, εCS and εDS are fixed as 3, and the ratio of the ABC triblock copolymer and the D homopolymer is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
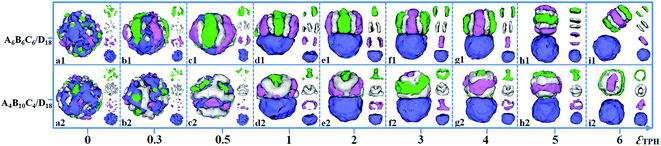
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The incompatibilities between A, B and C blocks, i.e. εAB, εAC and εBC, are fixed as 2. The self-assembled morphologies of A6B6C6/D18 mixtures (triblock copolymer with equal block length) and A4B10C4/D18 mixtures (triblock copolymer with relatively long middle block) as a function of εTPH are shown in Fig. 6. When ABC triblock copolymer is compatible with the D homopolymer, i.e. εTPH = 0, a spherical particle with homogeneously distributed A, B, C and D domains is formed by the A6B6C6/D18 blend (Fig. 6a1). As εTPH is increased to 0.5, microphase-separation between the ABC triblock copolymers and the D homopolymers occurs, inducing the D sphere to be covered by ABC stripes (Fig. 6b1 and c1). As εTPH is increased from 1 to 3, further microphase-separation between ABC and D results in Janus particles with segmented ABC hemispheres and D hemispheres, as shown in Fig. 6d1–f1. When εTPH is increased from 4 to 5, the segmented ABC hemisphere gradually parts from the D hemisphere (Fig. 6g1–h1). Then, macroscopic phase separation between the ABC triblock copolymers and the D homopolymers appears when εTPH is further increased to 6 (Fig. 6i1). The morphologies of the A4B10C4/D18 mixtures that change with the incompatibility between ABC and D are also shown in Fig. 6. Similarly, A4B10C4/D18 mixtures self-assemble into mixed spherical particles when the two components are compatible with each other (εTPH = 0, Fig. 6a2). As εTPH is increased from 0.3 to 0.5, microphase-separation between A, B, C and D occurs, as shown in Fig. 6b2–c2. When εTPH is increased from 1 to 5, Janus particles with ABC hemispheres and D hemispheres are observed, and the ABC domain gradually moves away from the D domain, inducing a calabash-like Janus particle (Fig. 6d2–h2). The structure of the ABC domain is mainly kept as a rod-like structure (A or C) surrounded by a hollow B-lump and strips (A or C). As εTPH is further increased to 6, a macroscopic phase separation between the ABC triblock copolymers and the D homopolymers appears (Fig. 6i2). Fig. 6 indicates that the Janus structure closely depends on εTPH, and different shapes of the Janus particles could be fabricated via adjusting the incompatibilities between ABC and D.
1. The incompatibilities between A, B and C blocks, i.e. εAB, εAC and εBC, are fixed as 2. The self-assembled morphologies of A6B6C6/D18 mixtures (triblock copolymer with equal block length) and A4B10C4/D18 mixtures (triblock copolymer with relatively long middle block) as a function of εTPH are shown in Fig. 6. When ABC triblock copolymer is compatible with the D homopolymer, i.e. εTPH = 0, a spherical particle with homogeneously distributed A, B, C and D domains is formed by the A6B6C6/D18 blend (Fig. 6a1). As εTPH is increased to 0.5, microphase-separation between the ABC triblock copolymers and the D homopolymers occurs, inducing the D sphere to be covered by ABC stripes (Fig. 6b1 and c1). As εTPH is increased from 1 to 3, further microphase-separation between ABC and D results in Janus particles with segmented ABC hemispheres and D hemispheres, as shown in Fig. 6d1–f1. When εTPH is increased from 4 to 5, the segmented ABC hemisphere gradually parts from the D hemisphere (Fig. 6g1–h1). Then, macroscopic phase separation between the ABC triblock copolymers and the D homopolymers appears when εTPH is further increased to 6 (Fig. 6i1). The morphologies of the A4B10C4/D18 mixtures that change with the incompatibility between ABC and D are also shown in Fig. 6. Similarly, A4B10C4/D18 mixtures self-assemble into mixed spherical particles when the two components are compatible with each other (εTPH = 0, Fig. 6a2). As εTPH is increased from 0.3 to 0.5, microphase-separation between A, B, C and D occurs, as shown in Fig. 6b2–c2. When εTPH is increased from 1 to 5, Janus particles with ABC hemispheres and D hemispheres are observed, and the ABC domain gradually moves away from the D domain, inducing a calabash-like Janus particle (Fig. 6d2–h2). The structure of the ABC domain is mainly kept as a rod-like structure (A or C) surrounded by a hollow B-lump and strips (A or C). As εTPH is further increased to 6, a macroscopic phase separation between the ABC triblock copolymers and the D homopolymers appears (Fig. 6i2). Fig. 6 indicates that the Janus structure closely depends on εTPH, and different shapes of the Janus particles could be fabricated via adjusting the incompatibilities between ABC and D.
The effect of polymer–solvent interactions on the formation of Janus particles is examined in this section. Four types of polymer mixtures, i.e., A6B6C6/D18, A7B4C7/D18, A4B10C4/D18 and A12B3C3/D18, are considered in the self-assembly. The polymer–solvent interactions are set as equal, i.e. εAS = εBS = εCS = εDS = εPS, and the ratio of the ABC diblock copolymers and the D homopolymers is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fig. 7a shows various Janus particles at different values of εPS. The mixtures of A6B6C6 triblock copolymers and D18 homopolymers self-assemble into Janus particles with a segmented ABC hemisphere and a D hemisphere when εPS increases from 3 to 8. As εPS increases to 10, the ABC triblock copolymers aggregate into a hemisphere with a patchy-like structure. Similar to the A6B6C6/D18 mixture, Janus particles with a segmented ABC hemisphere and a D hemisphere are also observed from the mixture of A7B4C7/D18. But the disks formed by the B block are relatively thin in the segmented structure due to the short length of the B block. For the mixture of A4B10C4/D18, the A4B10C4 triblock copolymers self-assemble into core–shell hemisphere when εPS = 3. As εPS is increased from 6 to 10, the hemisphere formed by A4B10C4 is changed into A and C particles dispersed on the B domain. For the self-assembly of A12B3C3/D18 mixtures, the structures of the ABC hemisphere are independent of εPS, the B and C blocks always form Janus lamellae located on the surface of the A domain as εPS is increased from 3 to 10. Furthermore, the effects of the triblock copolymer–solvent interaction (εTPS) and homopolymer–solvent interaction (εHS) on the Janus structures from the A6B6C6/D18 and A12B3C3/D18 mixtures are also examined. When the parameter εTPS (or εHS) is changed from 3 to 6, the value of εHS (or εTPS) is fixed as 3. In Fig. 7b, as εTPS increases from 3 to 5, the ABC domain is kept as a segmented structure (A6B6C6) or as BC lumps on an A aggregate (A12B3C3), and gradually covered by the D domain. When εTPS is increased to 6, the ABC domain is totally covered by the D domain induced by the strong hydrophobicity of the triblock copolymer. Moreover, when εHS is increased from 3 to 6, the D domain transforms from a hemisphere into a sphere and totally covers the ABC domain after εHS = 5. The structure of the A6B6C6 domain changes from a segmented structure (εHS = 3 and 4.5) to a stripe-like shell (εHS = 5) and a helix shell (εHS = 6). For the A12B3C3 triblock copolymers, they self-assemble into BC lumps on the A aggregate at εHS = 3 and εHS = 4.5, and then aggregate as a patchy-like shell covering the D sphere at εHS = 5 and εHS = 6.
1. Fig. 7a shows various Janus particles at different values of εPS. The mixtures of A6B6C6 triblock copolymers and D18 homopolymers self-assemble into Janus particles with a segmented ABC hemisphere and a D hemisphere when εPS increases from 3 to 8. As εPS increases to 10, the ABC triblock copolymers aggregate into a hemisphere with a patchy-like structure. Similar to the A6B6C6/D18 mixture, Janus particles with a segmented ABC hemisphere and a D hemisphere are also observed from the mixture of A7B4C7/D18. But the disks formed by the B block are relatively thin in the segmented structure due to the short length of the B block. For the mixture of A4B10C4/D18, the A4B10C4 triblock copolymers self-assemble into core–shell hemisphere when εPS = 3. As εPS is increased from 6 to 10, the hemisphere formed by A4B10C4 is changed into A and C particles dispersed on the B domain. For the self-assembly of A12B3C3/D18 mixtures, the structures of the ABC hemisphere are independent of εPS, the B and C blocks always form Janus lamellae located on the surface of the A domain as εPS is increased from 3 to 10. Furthermore, the effects of the triblock copolymer–solvent interaction (εTPS) and homopolymer–solvent interaction (εHS) on the Janus structures from the A6B6C6/D18 and A12B3C3/D18 mixtures are also examined. When the parameter εTPS (or εHS) is changed from 3 to 6, the value of εHS (or εTPS) is fixed as 3. In Fig. 7b, as εTPS increases from 3 to 5, the ABC domain is kept as a segmented structure (A6B6C6) or as BC lumps on an A aggregate (A12B3C3), and gradually covered by the D domain. When εTPS is increased to 6, the ABC domain is totally covered by the D domain induced by the strong hydrophobicity of the triblock copolymer. Moreover, when εHS is increased from 3 to 6, the D domain transforms from a hemisphere into a sphere and totally covers the ABC domain after εHS = 5. The structure of the A6B6C6 domain changes from a segmented structure (εHS = 3 and 4.5) to a stripe-like shell (εHS = 5) and a helix shell (εHS = 6). For the A12B3C3 triblock copolymers, they self-assemble into BC lumps on the A aggregate at εHS = 3 and εHS = 4.5, and then aggregate as a patchy-like shell covering the D sphere at εHS = 5 and εHS = 6.
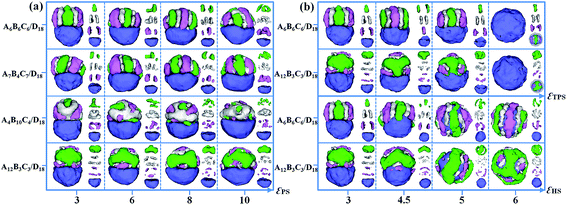 | ||
| Fig. 7 (a) Self-assembled morphologies of A6B6C6/D18, A7B4C7/D18, A4B10C4/D18 and A12B3C3/D18 mixtures as a function of εPS. (b) Self-assembled morphologies of A6B6C6/D18 and A12B3C3/D18 mixtures as a function of εTPS and εHS. The parameters εPP are fixed as 2. For clarity, the A, B, C and D domains are shown on the right of each corresponding snapshot. The color codes of the images are the same as in Fig. 6. | ||
The influence of fABC (the volume fraction of the ABC triblock copolymers in the mixture) on the formation of the Janus particles is examined through the self-assembly of four kinds of mixtures, i.e. A6B6C6/D18, A7B4C7/D18, A4B10C4/D18 and A12B3C3/D18. Other parameters are fixed, i.e. εPS = 3 and εPP = 2. The Janus structure changes with fABC are shown in Fig. 8. For the mixtures of A6B6C6/D18, the domains formed by the ABC triblock copolymers in the Janus spherical particles always remain segmented structures as fABC increased from 0.1 to 0.9. Segmented structures are also observed in A7B4C7/D18, while the B disks are thinner than the A and C disks. For A4B10C4/D18 mixtures, the A4B10C4 domain changes from a segmented structure (fABC = 0.1–0.3) to an aggregate of rod-like structures (A or C) surrounded by a hollow B-lump and strips (A or C) with the increase of fABC. When fABC is increased in A12B3C3/D18 mixtures, the structure for A12B3C3 triblock copolymers is kept as BC lumps on an A aggregate. Fig. 8 shows that the size of the ABC domain in Janus particles gradually increases with fABC for the four kinds of mixtures when fABC is increased from 0.1 to 0.9. The result proves that the size of the two domains in Janus particles can be tuned well by changing the volume fraction of compositions in triblock copolymers/homopolymer mixture.
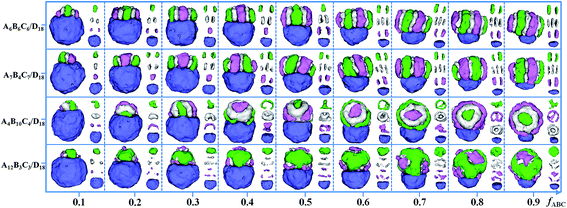 | ||
| Fig. 8 Self-assembled morphologies of A6B6C6/D18, A7B4C7/D18, A4B10C4/D18 and A12B3C3/D18 mixtures as a function of fABC. The parameters εPS are fixed as 3, and εPP are fixed as 2. For clarity, A, B, C and D domains are shown on the right of each corresponding snapshot. The color codes of the images are the same as in Fig. 6. | ||
In previous simulations, classic Janus particles, such as Janus-like spheres, cylinders and vesicles, were self-assembled by amphiphile AB/BC mixtures in the selected solvent.21,22,40 These studies proved that the repulsive interaction between the hydrophilic A and C blocks played a crucial role in the formation of Janus architecture, while the micellar shape was mainly controlled by the solvent quality of the solvophobic blocks. Moreover, Janus particles could be prepared by binary surfactant mixtures absorbed onto the surface of colloid. The combination of elements, colloid size, immiscibility and length of surfactant would determine the formation of various patterns.54–56 In addition, the confined self-assembly of a polymer mixture was proved to be a facile method to prepare Janus spheres with two well-defined hemispheres.31,42,57,58 The confinement size, the ratio of two components, the volume fraction of blocks and the interactions between different blocks greatly affect the self-assembled morphologies under confinement. In our simulation, it was also indicated that the Janus structure appeared with the appropriate repulsive interaction between two components of the mixture, and too weak or too strong a repulsive interaction induced mixed or separated particles. Through adjusting the solvent quality of one component in the mixture, mushroom-like Janus particles were prepared. The Janus particles with tuned sizes of two domains were achieved by changing the ratio of two components in the mixture. These effects on Janus structures are applicable in the self-assembly of the three kinds of polymer mixtures (A/D, AB/D and ABC/D mixtures).
3.4 Statistics and comparison
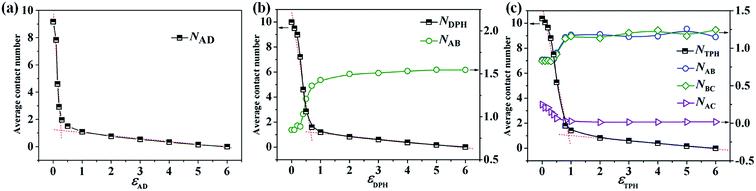
Clearly, the phase separation between two components dominates the formation of Janus structures, so we calculate the average contact numbers between two components in the mixtures, which can monitor well the microphase-separation degree of the homopolymer (D) and another component (A, AB or ABC). Fig. 9a presents the variation of NAD (average contact numbers between A and D) of the resulting particles from A18/D18 mixtures changed with εAD. It is observed that NAD declines rapidly as εAD is increased from 0 to 0.3, and the morphology changes from a mixed particle to a Janus particle with two hemispheres, as shown in Fig. 1. Thereafter, NAD decreases slowly when εAD is further increased (0.3 < εAD < 6), corresponding to the morphologies transformed from the spherical Janus particle to the calabash-like Janus particle in Fig. 1. It is worth noting that NAD reaches 0 when εAD = 6, indicating a macro-phase separation occurs between A and D. With the application of a linear fit for the data at εAD < 0.3 and εAD > 0.3, it is predicted that the transformation point from a mixed particle to a Janus particle is εAD = 0.3. The variation of NDPH (average contact numbers between A9B9 diblock copolymer and D18 homopolymer) and NAB (average contact numbers between A and B) of the resulting particles with εDPH are shown in Fig. 9b. The incompatibility between A and B is fixed, i.e. εAB = 2. Similar to A18/D18 mixtures, NDPH for A9B9/D18 mixtures changed as εDPH declines rapidly (εDPH < 0.7) and then decreases slowly (εDPH > 0.7), corresponding to the following morphological transition: mixed particles → spherical Janus particle → calabash-like Janus particle → two separated particles (Fig. 3). When we make the linear fit for the curve of NDPH, it is observed that the transformation point from the mixed particle to the Janus particle is εDPH = 0.7. Moreover, the variation of NAB with εDPH of the resulting particles self-assembled from the A9B9/C18 mixture is also shown in Fig. 9b. The curve of NAB increases rapidly as εDPH is increased from 0 to 0.7. This is attributed to the micro-phase separation between AB diblock copolymers and C homopolymers, causing an increase of the contacts between the A and B blocks. And then there is almost no change after the Janus particle forms (εDPH > 0.7), which is induced by the unchanged segmented structure of the AB domain. In Fig. 9c, the variation of NTPH (average contact numbers between the ABC triblock copolymer and the D homopolymer) changes with εTPH are shown. Similarly, NTPH declines rapidly at first and then decreases slowly. According to the morphologies shown in Fig. 6a1–i1, the structures changed from mixed particles to Janus particles and then to two separated particles. By means of making a linear fit for the curve of NTPH, the transformation point from a mixed particle to a Janus particle for A6B6C6/D18 mixtures is εTPH = 1. Furthermore, the average contact numbers between different polymer monomers for the A6B6C6 triblock copolymers, i.e. NAB, NBC and NAC, are also shown in Fig. 9c. It is observed that NAB and NBC increase as εTPH is increased from 0 to 1. This is because the microphase-separation between ABC triblock copolymers and D homopolymers results in an increase of the contacts between the A and B blocks or between the B and C blocks (Fig. 6a1–d1). The curve for NAC decreases as εTPH is increased from 0 to 1, which is induced by the microphase-separation between A, B and C. NAC is decreased to zero because of the formation of an ABC-segmented hemisphere with the A and C disks totally divided by the B disk. When εTPH is increased from 1 to 6, NAB, NBC and NAC are almost unchanged due to the unchanged segmented structure for the ABC domain after εTPH = 1. After comparing the curves of NAD, NDPH and NTPH in Fig. 9, it is found that the transformation point from the mixed particle to the Janus particle exists in all the mixtures, and the corresponding incompatibility between two components (εAD, εDPH or εTPH) for the transformation point increases from 0.3 to 0.7 and then to 1 when the mixture is changed from A/D to AB/D and then to ABC/D mixtures.Through changing the volume fraction of one component in the mixture, the size of the two domains in self-assembled Janus particles can be tuned well, as shown in Fig. 2b, 5 and 8. In this section, the values of the mean square end-to-end distance for the chains of two components in different mixtures (〈RX2〉, X represents different polymer chains) are calculated to illustrate the variation of chain conformation. Fig. 10a shows the variation of 〈RA2〉 and 〈RD2〉 of the Janus particles self-assembled by the A18/D18 mixture changes with fA, corresponding to the morphologies in Fig. 2b. It is observed that 〈RA2〉 is increased with the increase of fA, while 〈RD2〉 is decreased with the increase of fA. This indicates that the chains of the A homopolymer stretch with the growing volume fraction in the resulting structure, while the chains of the D homopolymer become more folded when the size of the D domain becomes smaller. It is worth noting the curves of 〈RA2〉 and 〈RD2〉 converge at fA = 0.5, which illustrates that their stretch degrees are similar when the volume fractions for A and D are the same. Fig. 10b shows the variation of 〈RAB2〉 and 〈RD2〉 of the resulting particles self-assembled by A9B9/D18 (Fig. 5) with the increase of fAB. Similar to Fig. 10a, 〈RAB2〉 increases and 〈RD2〉 decreases with the increase of fAB, indicating that AB diblock copolymers stretch and D homopolymers fold with growing fAB. Moreover, 〈RAB2〉 is always greater than 〈RD2〉 because the incompatibility between A and B makes the chain of the AB diblock copolymer more extended than the D homopolymer. Fig. 10c shows how the variation of 〈RABC2〉 and 〈RD2〉 of the Janus particles self-assembled by the A6B6C6/D18 mixture changed with fABC (Fig. 8). 〈RABC2〉 increases in general with the increase of fAB, indicating that the ABC triblock copolymer becomes extended as fABC increases from 0.1 to 0.9. 〈RD2〉 decreases with the increase of fABC. Similar to Fig. 10b, the value of 〈RABC2〉 is always greater than 〈RD2〉 in Fig. 10c because the incompatibility between A, B and C makes the chains more extended.
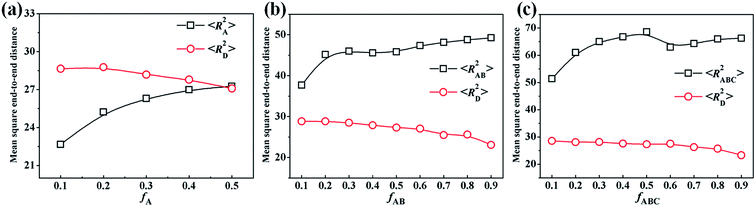 | ||
| Fig. 10 Mean square end-to-end distance of the chains of the Janus particles self-assembled from an A18/D18 (a), A9B9/D18 (b) or A6B6C6/D18 (c) mixture as a function of fA, fAB or fABC. | ||
The formation pathways of typical Janus particles are investigated to reveal the formation mechanism on the Janus structures. In Fig. 11, NHS represents the average contact numbers of the homopolymer (D) component with solvent, and NAS, NDPS and NTPS represent another component (A, AB or ABC) with solvent, which can indicate the aggregation degree of the polymer chains. NAH, NDPH and NTPH represent the average contact number between homopolymer (D) and another component (A, AB and ABC) respectively, and NAB, NAC and NBC represent the average contact number between A, B and C-type monomers, indicating the microphase-separation degree between different monomers. For the classic Janus particle with two hemispheres self-assembled by the A18/D18 mixture (Fig. 1, εAS = εDS = 3 and εAD = 2), the variations of the contact numbers (NAS, NHS and NAH) with time (t) and the corresponding snapshots at different times are shown in Fig. 11a. The inserted snapshots show that the A18 and D18 homopolymers self-assemble into two loose aggregates separately at first (Fig. 11a2, t = 77), and then these two aggregates keep growing but with two distinct phases (Fig. 11a3, t = 85). As the time is further increased, the aggregates shrink and connect together (Fig. 11a4 and a5, t = 150 and t = 300), resulting in the formation of the final stable Janus particle (Fig. 11a6). Moreover, NAS and NHS in Fig. 11a show remarkable decreases with time until t = 300, which implies that homopolymers gradually aggregate into particles. Thereafter, NAS and NHS remain almost unchanged with a further increase of time, indicating the aggregation of the A and D homopolymers has finished. It is worth noting that the curves of NAS–t and NHS–t completely overlap because of the similar aggregation degree induced by the same polymer–solvent interactions of the A and D homopolymers. The NAH–t curve is increased at first due to the rapid aggregation at the beginning (Fig. 11a1, t = 70), and then it starts to decline because of the microphase-separation between A and D (Fig. 11a3, t = 85). Thereafter, NAH shows a slight increase with time as the A and D aggregates shrink gradually (Fig. 11a5, t = 300) and then it keeps almost unchanged as time is further increased.
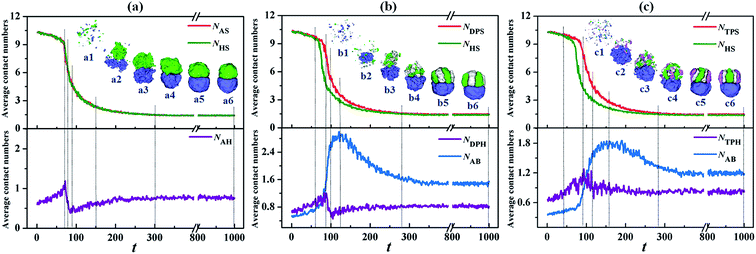 | ||
| Fig. 11 Variations of the contact numbers with time (t) during the formations of Janus particles self-assembled by the A18/D18 (a), A9B9/D18 (b), and A6B6C6/D18 (c) mixtures. The inserted snapshots show the formation pathway of the Janus particles. The dotted lines correspond to time (t) for the inserted snapshots. The color codes of the inserted images are the same as in Fig. 6. | ||
Fig. 11b shows the formation pathway of Janus particle with a segmented AB hemisphere and D hemisphere from the self-assembly of the A9B9/D18 mixture (Fig. 3, εDPH = 2). The variations of the contact numbers, i.e. NDPS, NHS, NDPH and NAB, with t and some typical snapshots at different times are presented to visualize the formation pathways. The inserted snapshots show that D18 homopolymers aggregate into a loose aggregate at first, while AB diblock copolymers are still uniformly dispersed (Fig. 11b2, t = 85). Maybe this is because the incompatibility between the A and B blocks impedes the aggregation of the AB diblock copolymers. As t increased to 120, the AB diblock copolymers gradually self-assemble into an aggregate, as shown in Fig. 11b3 and b4. With a further increase of t, microphase-separation between A and B occurs, resulting in the formation of a segmented structure in the AB hemisphere (Fig. 11b5, t = 280). Thereafter, the morphology of the Janus particle remains almost unchanged till t = 1000 (Fig. 11b6). The variations of how the contact numbers changed with t are also shown in Fig. 11b. It is found that the curves of NDPS–t and NHS–t obviously decrease until t = 280 and then remain almost unchanged with an increase in time, which implies that the polymers self-assemble into the aggregate at first and then the aggregate shrinks to form the final particle. However, because of the prior aggregation of the D homopolymers in the mixture (Fig. 11b2–b4), the decrease of NDPS lags behind that of NHS from t = 60 to t = 280. The curve of NDPH–t increases firstly due to the rapid aggregation at the beginning (Fig. 11b2, t = 85), and then it declines because of the aggregation of the AB diblock copolymers and the microphase-separation between the AB and D domains (Fig. 11b3, t = 100). Then the curve remains almost unchanged with a further increase of t. The NAB–t curve increases remarkably and then declines, corresponding to the aggregation of the mixture (Fig. 11b4, t = 120) and the flowing microphase-separation between A and B (Fig. 11b5, t = 280). Then NAB remains almost unchanged with the increase of t.
Then, the formation pathway of the Janus particle with the segmented ABC hemisphere and D hemisphere from the self-assembly of the A6B6C6/D18 mixture (Fig. 6, εTPH = 2) is shown in Fig. 11c. The variations of the contact numbers, NTPS, NHS, NTPH and NAB, with t and some typical snapshots at different times are presented. The inserted snapshots show that the D18 homopolymers aggregate into a loose aggregate at first, while for the ABC triblock copolymers some small particles are still dispersed (Fig. 11c2, t = 90). Similar to the aggregate in Fig. 11b2, it is inferred that the incompatibility between the A, B and C blocks impedes the aggregation of the ABC triblock copolymers. When t is increased to 120, the ABC triblock copolymers gradually self-assemble into an aggregate (Fig. 11c3 and c4). As t is further increased, microphase-separation between A, B and C occurs, resulting in the formation of a segmented ABC hemisphere (Fig. 11c5, t = 280). Then the morphology of the Janus particle remains almost unchanged until t = 1000 (Fig. 11c6). Fig. 11c also shows the variations of the contact numbers with t. It is observed that NTPS and NHS show obvious decreases until t = 280 and then remain almost unchanged with a further increase of t. This indicates that the polymer mixture self-assembles into the aggregate and then the aggregate shrinks to form the final Janus particle. However, the prior aggregation of the D18 homopolymers in the mixture (Fig. 11c2–c4) makes the decrease of NTPS lag behind that of the NHS from t = 40 to t = 280. The curve of NTPH shows an obvious fluctuation till t = 160, but it increases firstly and then declines in general. The increase of NTPH is induced by the rapid aggregation at the beginning (Fig. 11c2, t = 90), and the decrease is because of the aggregation of the ABC triblock copolymers and the microphase-separation between the ABC and D domains (Fig. 11c3, t = 120). Then the curve remains almost unchanged with a further increase of t. The variation of NAB is shown in Fig. 11c; NBC and NAC are not shown because the tendencies of their variation are similar to those of NAB. The NAB–t curve increases obviously and then decreases, corresponding to the aggregation of the polymer mixture (Fig. 11c4, t = 160) and the flowing microphase-separation between A and B (Fig. 11c5, t = 280). Then NAB remains almost unchanged with an increase of t. Through comparing Fig. 11a–c, it is found that all the curves of NHS show almost the same variation with t, while the contact number between another component and the solvent (NAS, NDPS or NTPS) lags behind NHS with the growing gap between two curves when the components change from A to AB and then to ABC.
4. Conclusions
Janus particles self-assembled from different polymer mixtures within soft droplets are investigated using the MC method. The mixtures of homopolymer/homopolymer (A/D) diblock copolymer/homopolymer (AB/D) and triblock copolymer/homopolymer (ABC/D) are considered in sequence. The controlled parameters, such as the incompatibility between two components, polymer–solvent interactions and the ratio of the components in the mixture, are systematically examined to illustrate their effects on the formation of Janus particles. The Janus structures are closely related to the incompatibility between two components in the mixture. It is also observed that several mushroom-like Janus particles could be prepared by changing the polymer–solvent interactions, and various Janus particles with tuned sizes of two domains are obtained by adjusting the ratio of two components in a mixture. Both the average contact numbers and mean square end-to-end distance are calculated to explain the chain conformations of the polymers. Furthermore, the formation pathways of some representative Janus particles are shown to illustrate their formation mechanisms. The simulation result is expected to provide theoretical guidance to prepare novel Janus particles.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grants No. 21644013 and 11647029), by the Key Project of Education Department of Sichuan Province (Grant No. 17ZA0283), and by the Scientific Research Project of Sichuan University of Science and Engineering (Grant No. 2015RC32). The simulations were also supported by the High Performance Computing Center, Sichuan University of Science and Engineering.References
- D. J. Cole-Hamilton, Science, 2010, 327, 41–42 CrossRef CAS PubMed.
- Z. W. Seh, S. Liu, M. Low, S. Y. Zhang, Z. Liu, A. Mlayah and M. Y. Han, Adv. Mater., 2012, 24, 2310–2314 CrossRef CAS PubMed.
- Y. Wang, R. M. Hernandez, D. J. Bartlett, J. M. Bingham, T. R. Kline, A. Sen and T. E. Mallouk, Langmuir, 2006, 22, 10451–10456 CrossRef CAS PubMed.
- T. Nisisako, T. Torii, T. Takahashi and Y. Takizawa, Adv. Mater., 2006, 18, 1152–1156 CrossRef CAS.
- Z. Yu, C. F. Wang, L. Ling, L. Chen and S. Chen, Angew. Chem., Int. Ed. Engl., 2012, 51, 2375–2378 CrossRef CAS PubMed.
- P.-C. Chen, X. Liu, J. L. Hedrick, Z. Xie, S. Wang, Q.-Y. Lin, M. C. Hersam, V. P. Dravid and C. A. Mirkin, Science, 2016, 352, 1565–1569 CrossRef CAS PubMed.
- N. Glaser, D. J. Adams, A. Böker and G. Krausch, Langmuir, 2006, 22, 5227–5229 CrossRef CAS PubMed.
- J.-W. Kim, D. Lee, H. C. Shum and D. A. Weitz, Adv. Mater., 2008, 20, 3239–3243 CrossRef CAS.
- A. M. Percebom, J. J. Giner-Casares, N. Claes, S. Bals, W. Loh and L. M. Liz-Marzán, Chem. Commun., 2016, 52, 4278–4281 RSC.
- H. Xing, Z. D. Wang, Z. D. Xu, N. Y. Wong, Y. Xiang, G. L. G. Liu and Y. Lu, ACS Nano, 2012, 6, 802–809 CrossRef CAS PubMed.
- L. Y. Wu, B. M. Ross, S. Hong and L. P. Lee, Small, 2010, 6, 503–507 CrossRef CAS PubMed.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed.
- F. Wurm and A. F. M. Kilbinger, Angew. Chem., Int. Ed., 2009, 48, 8412–8421 CrossRef CAS PubMed.
- A. Walther and A. H. E. Müller, Soft Matter, 2008, 4, 663–668 RSC.
- R. Erhardt, A. Böker, H. Zettl, H. Kaya, W. Pyckhout-Hintzen, G. Krausch, V. Abetz and A. H. E. Müller, Macromolecules, 2001, 34, 1069–1075 CrossRef CAS.
- A. Walther, X. André, M. Drechsler, V. Abetz and A. H. E. Müller, J. Am. Chem. Soc., 2007, 129, 6187–6198 CrossRef CAS PubMed.
- Y. Liu, V. Abetz and A. H. E. Müller, Macromolecules, 2003, 36, 7894–7898 CrossRef CAS.
- A. Walther, M. Drechsler, S. Rosenfeldt, L. Harnau, M. Ballauff, V. Abetz and A. H. E. Müller, J. Am. Chem. Soc., 2009, 131, 4720–4728 CrossRef CAS PubMed.
- T. Nisisako, Curr. Opin. Colloid Interface Sci., 2016, 25, 1–12 CrossRef CAS.
- I. K. Voets, A. de Keizer, P. de Waard, P. M. Frederik, P. H. H. Bomans, H. Schmalz, A. Walther, S. M. King, F. A. M. Leermakers and M. A. Cohen Stuart, Angew. Chem., Int. Ed., 2006, 45, 6673–6676 CrossRef CAS PubMed.
- Y. Han and W. Jiang, J. Phys. Chem. B, 2011, 115, 2167–2172 CrossRef CAS PubMed.
- Y. Han, J. Cui and W. Jiang, J. Phys. Chem. B, 2012, 116, 9208–9214 CrossRef CAS PubMed.
- R. Deng, F. Liang, J. Zhu and Z. Yang, Mater. Chem. Front., 2017, 1, 431–443 RSC.
- R. Deng, H. Li, F. Liang, J. Zhu, B. Li, X. Xie and Z. Yang, Macromolecules, 2015, 48, 5855–5860 CrossRef CAS.
- K. H. Ku, Y. Kim, G.-R. Yi, Y. S. Jung and B. J. Kim, ACS Nano, 2015, 9, 11333–11341 CrossRef CAS PubMed.
- J. Xu, Y. Yang, K. Wang, J. Li, H. Zhou, X. Xie and J. Zhu, Langmuir, 2015, 31, 10975–10982 CrossRef CAS PubMed.
- J. Xu, Y. Yang, K. Wang, Y. Wu and J. Zhu, Mater. Chem. Front., 2017, 1, 507–511 RSC.
- N. Yan, Y. Zhu and W. Jiang, J. Phys. Chem. B, 2016, 120, 12023–12029 CrossRef CAS PubMed.
- N. Yan, H. Liu, Y. Zhu, W. Jiang and Z. Dong, Macromolecules, 2015, 48, 5980–5987 CrossRef CAS.
- R. Deng, F. Liang, X. Qu, Q. Wang, J. Zhu and Z. Yang, Macromolecules, 2015, 48, 750–755 CrossRef CAS.
- R. Deng, H. Li, J. Zhu, B. Li, F. Liang, F. Jia, X. Qu and Z. Yang, Macromolecules, 2016, 49, 1362–1368 CrossRef CAS.
- T. Kietzke, D. Neher, M. Kumke, O. Ghazy, U. Ziener and K. Landfester, Small, 2007, 3, 1041–1048 CrossRef CAS PubMed.
- R. H. Deng, S. Q. Liu, F. X. Liang, K. Wang, J. T. Zhu and Z. Z. Yang, Macromolecules, 2014, 47, 3701–3707 CrossRef CAS.
- J. G. E. M. Fraaije and G. J. A. Sevink, Macromolecules, 2003, 36, 7891–7893 CrossRef CAS.
- J. Ma, J. Cui, Y. Han, W. Jiang and Y. Sun, RSC Adv., 2015, 5, 86473–86484 RSC.
- J. Fan, J. Cui, Y. Han and W. Jiang, RSC Adv., 2014, 4, 50351–50360 RSC.
- P. Chi, Z. Wang, B. Li and A.-C. Shi, Langmuir, 2011, 27, 11683–11689 CrossRef CAS PubMed.
- Y. Sheng, J. An and Y. Zhu, Chem. Phys., 2015, 452, 46–52 CrossRef CAS.
- N. Yan, Y. Zhu and W. Jiang, Soft Matter, 2016, 12, 965–972 RSC.
- Y. Sheng, X. Yang, N. Yan and Y. Zhu, Soft Matter, 2013, 9, 6254–6262 RSC.
- Y. Han, H. Yu, H. Du and W. Jiang, J. Am. Chem. Soc., 2010, 132, 1144–1150 CrossRef CAS PubMed.
- J. Zhang, W. Kong and H. Duan, Langmuir, 2017, 33, 3123–3133 CrossRef CAS PubMed.
- Y. Sheng, N. Yan, J. An and Y. Zhu, Chem. Phys., 2014, 441, 47–52 CrossRef CAS.
- Y. Sheng, Y. Zhu, W. Jiang and Z. Dong, Mater. Chem. Front., 2017, 1, 487–494 RSC.
- Y. Zhu, H. Yu, Y. Wang, J. Cui, W. Kong and W. Jiang, Soft Matter, 2012, 8, 4695–4707 RSC.
- Y. Zhu, X. Yang, W. Kong, Y. Sheng and N. Yan, Soft Matter, 2012, 8, 11156–11162 RSC.
- Y. Zhu and W. Jiang, Macromolecules, 2007, 40, 2872–2881 CrossRef CAS.
- I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823 CrossRef CAS.
- R. G. Larson, J. Chem. Phys., 1988, 89, 1642–1650 CrossRef CAS.
- R. G. Larson, J. Chem. Phys., 1992, 96, 7904–7918 CrossRef CAS.
- S. Ji and J. Ding, Langmuir, 2005, 22, 553–559 CrossRef PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- T. Tanaka, M. Okayama, H. Minami and M. Okubo, Langmuir, 2010, 26, 11732–11736 CrossRef CAS PubMed.
- I. C. Pons-Siepermann and S. C. Glotzer, Soft Matter, 2012, 8, 6226–6231 RSC.
- I. C. Pons-Siepermann and S. C. Glotzer, ACS Nano, 2012, 6, 3919–3924 CrossRef CAS PubMed.
- E. Edlund, O. Lindgren and M. N. Jacobi, Soft Matter, 2014, 10, 2955–2960 RSC.
- R. Yang, B. Li and A.-C. Shi, Langmuir, 2012, 28, 1569–1578 CrossRef CAS PubMed.
- N. Li, A. Z. Panagiotopoulos and A. Nikoubashman, Langmuir, 2017, 33, 6021–6028 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |