Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calculations of the absolute binding free energies for Ralstonia solanacearum lectins bound with methyl-α-L-fucoside at molecular mechanical and quantum mechanical/molecular mechanical levels†
Wei Liua,
Xiangyu Jia‡
*a,
Meiting Wanga,
Pengfei Lia,
Xiaohui Wanga,
Wenxin Hub,
Jun Zhengb and
Ye Mei *acd
*acd
aState Key Laboratory of Precision Spectroscopy, School of Physics and Materials Science, East China Normal University, Shanghai 200062, China. E-mail: xj6@nyu.edu; ymei@phy.ecnu.edu.cn
bThe Computer Center, School of Computer Science and Software Engineering, East China Normal University, Shanghai 200062, China
cNYU-ECNU Center for Computational Chemistry at NYU Shanghai, Shanghai 200062, China
dCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
First published on 7th August 2017
Abstract
A method that can reliably predict protein–ligand binding free energies is essential for rational drug design. Much effort has been devoted to this field, but it remains challenging especially for flexible ligands. In this work, both a molecular mechanical (MM) method and a hybrid quantum mechanical/molecular mechanical (QM/MM) method have been applied in the study of the binding affinities of methyl-α-L-fucoside to Ralstonia solanacearum lectins. The free energy at the MM level was calculated using the double-decoupling method (DDM) and the free energy change at each step was calculated via a series of intermediate states using the Bennett acceptance ratio (BAR). The binding free energy agrees well with the experimental measurement, no matter whether the general AMBER force field or GLYCAM06j was applied to the ligand. Nonetheless, slow convergence for some intermediate states has been observed, which requires substantially longer simulations than were used in many other studies. The QM/MM free energy was calculated by thermodynamic perturbation (TP) from the MM states. This strategy has been shown to yield minimal variance for the calculated free energy without direct sampling at the QM/MM level in a previous study. However, after this MM-to-QM/MM correction, the agreement with the experimental value decreased. This study serves as an implication of the demand for substantially longer simulations for the alchemical process than those that were used in many other studies and for further improvement of QM/MM methods, especially the description of interactions between the QM and MM regions.
Introduction
Carbohydrates, like other biomolecules such as proteins and nucleic acids, are essential components of life. Emerging evidence suggests a pivotal role for carbohydrate–protein interactions in participating in and regulating a broad range of biologically relevant processes such as cell–cell adhesion, cell differentiation and in-cell signaling.1 Aside from this, such interactions are associated with a vast array of diseases such as viral2 and bacterial infections,3,4 lysosomal storage disorders,5 inflammatory processes,6 immune system response,7 and neurodegenerative disorders.8 Carbohydrates are sorted by size into four chemical groups, viz. monosaccharide, disaccharide, oligosaccharide, and polysaccharide. The open-chain and the closed-ring forms often coexist in a monosaccharide and the latter is more common. In cells, it is found that the majority of carbohydrates are attached to proteins or lipids.9 A variety of proteins are involved in carbohydrate interactions and recognitions, including enzymes, antibodies, sugar transporters and lectins.10 The elucidation of the mechanisms that modulate protein recognition in the carbohydrate-combining sites is clearly of immense importance.11 Lectins hold the promise to bind mono- and oligosaccharides reversibly with high specificity.10 Each lectin protein conventionally possesses two or more carbohydrate-binding sites.10 Currently, carbohydrate-based drug design presents enormous opportunities for therapeutic development and has become one of the novel frontiers in pharmacology and medicinal chemistry.12,13 For instance, the inhibition of the binding of adhesin proteins to host glycans provides possibilities for anti-adhesion therapies.14 Developing and improving theoretical methods to predict the binding affinity between carbohydrates and carbohydrate-binding proteins is currently a central issue of many studies.15,16 Numerous investigations17–22 have been focusing on the binding free energy calculations of lectin–carbohydrate complexes, with approaches at different levels of complexity and sophistication.Alchemical free energy calculation methods are widely employed in the calculations of both relative and absolute free energies. For the calculation of absolute binding free energies, the most widely used method nowadays is the double decoupling method (DDM).23–25 The free energies of binding are achieved by switching off the interaction of the ligand with its surroundings progressively. Based on a non-physical thermodynamic cycle, the binding free energy is computed as the sum of multiple intermediate steps during the cycle. However, it is impractical to leverage this method directly as the decoupled ligand can drift away from the binding site and move around in the simulated system. Thus, the endpoint and the intermediate standard states of the ligand cannot be defined correctly, which is detrimental to convergence.23–27 To solve this problem, intermediate alchemical states with restraint potentials on the translational and rotational degrees of freedom relative to the protein are introduced. Then, the free energy contribution associated with these restraints can be subtracted analytically.23,24 It is evident that both geometrically unbinding methods using the potential of mean force (PMF) and alchemically unbinding methods can be used for the calculations of free energies associated with ligand–protein binding.23 Generally, geometrically unbinding methods are employed with a superiority for charged ligands.28 Whereas, alchemically unbinding methods are more suitable for ligands deeply buried in the interior of a receptor.23 Recent reviews on alchemical free energy calculation methods can be found in ref. 26 and 29–33.
Over the past decade, a variety of carbohydrate force fields such as AMBER,34 CHARMM,35,36 GLYCAM,37,38 GROMOS,39,40 OPLS,41,42 TRIPOS,43 and MM4 (ref. 44–46) were developed with different functional forms and components, and have been applied to a wealth of studies related to glycans as well as carbohydrate–protein binding complexes.47–49 Most of the carbohydrate force fields (CHARMM, GLYCAM, GROMOS, OPLS, etc.) are developed to be compatible with simulations in the wider context of biomolecular (proteins, lipids, and nucleic acids) force fields in order to avoid the differences in force field parameterization protocols and/or functional forms between them. Therefore, these carbohydrate force fields adopt similar functional forms as biomolecular force fields including energy components of bonds, angles, torsion, Lennard-Jones interactions, electrostatic interactions and improper torsion.50 However, the development of carbohydrate force field parameters is hampered by several difficulties. (1) The structural study of carbohydrates is complicated by virtue of their exceptionally high number of chiral centers.50 (2) Subtle electronic effects occur during conformation changes such as the anomeric, the exo-anomeric, and the gauche effects.51,52 These electronic features make the prediction and modeling of the structural and electrostatic landscapes quite challenging.50 (3) The monosaccharide units can be connected in a variety of ways. Therefore, oligosaccharides and polysaccharides have the vast majority of achievable linear and branched conformations. Additionally, the glycosidic linkages and the ring conformations are highly flexible, resulting in an enormous conformational space and a huge number of possible low-energy conformations.50 (4) It would be fairly difficult to mimic the situation by classic force fields where the open-chain form and the closed-ring form coexist in the monosaccharide.53 Overall, carbohydrate force fields appear to be reaching a limit in terms of what is possible within its conventional functional form.50,53,54 This implies that carbohydrate force fields are in need of improvement in order to predict the ring conformation preferences, describe the electrostatic characteristics, and treat the flexible glycosidic linkages. However, force field refinement is a time-consuming process, and it normally takes years to validate the new parameters.
The hybrid quantum mechanical/molecular mechanical (QM/MM) method has become a sought-after tool, which has been extensively applied in the studies of enzyme catalysis, drug design, and protein engineering.55 QM/MM calculations circumvent the need for parameterization and explicitly consider polarization, charge transfer, and many-body effects.56,57 QM/MM approaches have been applied to the calculations of protein–ligand interaction frequently by combination with associated free energy estimators.58–60 However, in order to calculate ensemble averaged properties such as free energy, uncorrelated samples are necessary. For biological systems in the condensed phase, the energy correlation time is usually on a scale of picoseconds. In order to obtain a reliable ensemble average, the simulation time should not be shorter than one nanosecond, which requires 106 propagations with a normal time step on the femtosecond scale. For most cases, direct QM/MM simulations are not feasible for free energy calculations because of the enormous computational expense. Therefore, reference-potential methods were developed,61 in which energy and probability corrections are applied to a restricted number of structures from a low level simulation, and the free energy difference between the low level and the high level Hamiltonians is obtained by reweighting the snapshots from low level simulations with the energy difference between these two Hamiltonians.56 This process can be achieved using various methods, namely, non-Boltzmann thermodynamics perturbation (NBTP),62,63 non-Boltzmann Bennett acceptance ratio (NBB),61,64 MBAR65 and BAR + TP.65,66 It has been proved both analytically and numerically that the BAR + TP method provides more precise results than NBB with only half of the expense of QM/MM calculations.66 BAR + TP is a special case of MBAR.65
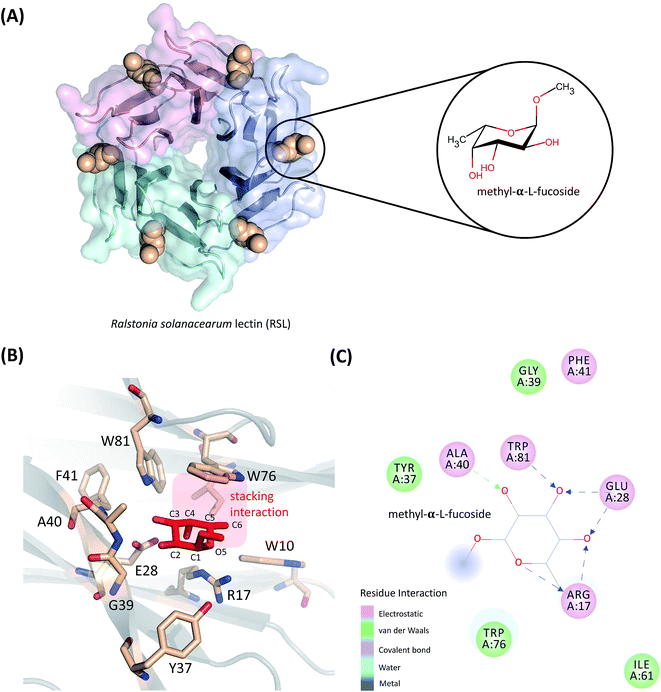
In this work, the absolute binding free energy of Ralstonia solanacearum lectins (RSL) in complex with methyl-α-L-fucoside was calculated using the double-decoupling method. The structure is shown in Fig. 1. Both the general AMBER force field and GLYCAM were applied to methyl-α-L-fucoside and the results were compared. At each step in the double-decoupling process at MM level, the free energy change was calculated using BAR. Finally, the binding free energy at the QM/MM level was estimated from the MM level via thermodynamic perturbation, without running formidably expensive QM/MM dynamics.
Method
Free energy calculation
For protein–ligand binding, the equilibrium constant can be expressed as23
 | (1) |
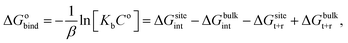 | (2) |
The free energy difference between adjacent states, of which the potential energies are denoted as U0 and U1 respectively, can be estimated by BAR as
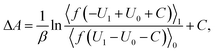 | (3) |
 | (4) |
The absolute binding free energy obtained on a MM potential can be corrected to a QM/MM Hamiltonian by the TP method. The correction term can be estimated by the following equation
 | (5) |
| ΔGQM/MMbinding = ΔGMMbinding − ΔGbulkMM→QM/MM + ΔGsiteMM→QM/MM. | (6) |
Molecular dynamics simulations
In order to remove close-contact in the system, an energy relaxation with 3000 steps was carried out using a steepest descent algorithm. Then, the entire system was heated up from 0 to 300 K in 100 ps, followed by an equilibration simulation for 400 ps. The production run was carried out in an NPT ensemble with isotropic periodic boundary conditions at 300 K. The temperature was regulated using the Langevin dynamics with a collision frequency of 1 ps−1. The integration time step was set to 1.0 fs and SHAKE69 algorithm was applied. The particle mesh Ewald70,71 method was used to calculate the long-range electrostatic interactions, and the cutoff on non-bonded interactions in real space was set to 12 Å. The trajectories were saved every 10 ps. Varying simulation lengths, which are collected in Table 1, were utilized for each step of the transformation in the thermodynamic cycle determined by the convergence rate.
| Force field | ΔGbulkint | ΔGsiteint − ΔGsitet+r | ΔGbulkMM→QM/MM | ΔGsiteMM→QM/MM |
|---|---|---|---|---|
| GAFF | 50 | >50 | 200 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
300 (6000) |
| GLYCAM | 50 | >50 | 200 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
300 (6000) |
 | (7) |
 | (8) |
The free energy changes in the processes (b to c, e to g) were estimated using the BAR method. The free energy in terms of the change of state c to d was estimated by the same formula used in ref. 23 analytically.
| Vbias = ΔEMMele − (ΔEQM/MMele + ΔEQM/MMwfd), | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames were used in bulk water and 6000 frames were used in the binding pocket.
000 frames were used in bulk water and 6000 frames were used in the binding pocket.Results and discussion
Force constants of the applied restraints
In this work, the strengths of the six restraints in GLYCAM and GAFF simulations were carefully chosen in order to make the distributions of the restrained distance and angles/dihedrals at state e consistent with the distributions of the degrees of freedom at state g (see Fig. 2 for the definition of states). This is critical to guarantee sufficient overlaps between these two states. The force constants utilized are listed in Table S3.† Because of the difference in the parameters of GAFF and GLYCAM, different force constants were used for the restraint potential. Fig. S1† shows the RMSD fluctuations of the heavy atoms of the protein (solid black line) as well as the ligand (solid red line) during the simulations, implying that the simulated system under both GAFF and GLYCAM force fields was fairly stable and methyl-α-L-fucoside possessed some flexibility in the pocket. The distributions of the six coordinates associated with the translational and rotational degrees of freedom (DOF) (namely, r, θ, ϕ, α, β and γ) in the simulations are shown in Fig. S2.† Their means and root mean square fluctuations (RMSFs) are collected in Table S4.† Employing GAFF for the ligand, in the decoupled but restrained state e, the means of the six DOF can well reproduce those in the unrestrained but coupled state g. The RMSFs show small deviations, which are acceptable. The largest deviation is seen for α (1.32°). Similar results can be observed in the simulations using GLYCAM, with the largest deviation seen for ϕ (1.30°). Sufficient overlap in these distributions is critical for the free energy calculation between state e and state g.Long autocorrelation time for the weak binding intermediates
The decay of auto-correlation functions over time for several intermediate states in the binding site is quite slow under both GAFF and GLYCAM force fields. The plots of time correlation functions from the simulations employing GAFF and GLYCAM force fields are presented in Fig. S3 and S4† respectively. Correlation may reduce the effective number of the samples, because when two samples are not independent of each other, the second sample can only be taken as a fractional one. Therefore, the number of uncorrelated samples is smaller than the actual number of samples, which may increase the variance of the calculated means. The number of uncorrelated samples is defined as N/g, where g is defined in eqn (20) in ref. 76. The number of uncorrelated samples for windows 9 (λ = 0.4), 10 (λ = 0.45), 11 (λ = 0.5), and 12 (λ = 0.55) was 9, 8, 8, and 91 when the ligand was parameterized by GAFF. While employing the GLYCAM force field, the number of uncorrelated samples for windows 9 (λ = 0.4), 10 (λ = 0.45), and 15 (λ = 0.7) was 6, 13, and 8. Such small numbers of uncorrelated samples can be ascribed to the multiple binding modes of the ligand in the pocket when the interaction between the ligand and the receptor is weak. Evidence can be partly found in the displacement of the restrained distance (r) as shown in Fig. S5.† When λ = 0.4, 0.45, 0.5, and 0.55, the restrained distance has remarkable fluctuations implying that when its interaction with the protein is weak, the ligand explores the phase space and searches for more favorable binding patterns within the pocket in order to lower the free energy. However, the seeking process requires a considerably long time to assess various binding positions and orientations, leading to a long correlation time (even reaching a time scale of ns), especially when the ligand is trapped in several favorable regions in the pocket. The GLYCAM force field has similar behavior as shown in Fig. S6.† It can also be observed that these long-time-correlation trajectories appear constantly for λ around 0.4 and 0.7, which is caused by the implementation of soft-core potentials and has been reported elsewhere.27 The restrained angles and dihedrals presented similar trends for these intermediates (data not shown). The MD simulation time of these windows was lengthened to over 70 ns. Before calculating the free energies of ΔGsiteint − ΔGsitet+r, we discarded the first 30 ns for λ = 0.4 and 35 ns for λ = 0.5 in the trajectories employing GAFF, and discarded the first 20 ns for λ = 0.4 and 25 ns for λ = 0.45 in the trajectories utilizing the GLYCAM force field, which were considered as the time for the ligand to search for more favorable binding modes.Alchemical binding free energies
Because long time simulations were conducted and the ensemble means were calculated over large samples, the standard errors of ΔGbulkint and ΔGsiteint − ΔGsitet+r are very small with the largest one being 0.07 kcal mol−1. With these negligible uncertainties, all the free energy components are unambiguously determined. ΔGbulkint is the energy penalty in turning off the interaction between the solute and the solvent in aqueous solution, which is the solvation free energy of the solute molecule. Employing GAFF, the solvation free energy of methyl-α-L-fucoside is −15.92 kcal mol−1. While employing GLYCAM, the solvation free energy of this ligand molecule is slightly larger (more negative), which is −16.52 kcal mol−1. The difference is only 0.6 kcal mol−1 and is within 5 percent of the total solvation free energy. For homogeneous environments such as water and vacuum, ΔGbulkt+r can be calculated analytically.23 Because restraints with different strengths were utilized, there is a small difference (0.4 kcal mol−1) in ΔGbulkt+r under the two force fields, which are 11.84 kcal mol−1 for GAFF and 11.41 kcal mol−1 for GLYCAM. These two force fields yielded very close results for ΔGsiteint − ΔGsitet+r, which are −37.32 kcal mol−1 and −37.27 kcal mol−1 for GAFF and GLYCAM respectively. The difference is only 0.05 kcal mol−1. With these free energy components and the thermodynamic cycle in Fig. 2, the binding free energy at the molecular mechanical level can be calculated, and is −9.56 kcal mol−1 and −9.34 kcal mol−1. These calculated binding affinities are slightly stronger than the experimentally measured binding affinity (−8.4 ± 0.3 kcal mol−1 (ref. 77)). This difference may have originated from the many approximations adopted during the calculations, one of which is the representation of methyl-α-L-fucoside.The free energies (see Table S5†) calculated from short simulations may deviate from those from the long simulations. When only 5 ns trajectories were used in the calculations of ΔGbulkint, the results differ by nearly 2 kcal mol−1 for GAFF from that based on the 50 ns trajectories. But for the GLYCAM force field, these 5 ns trajectories already provided converged results for ΔGbulkint. The different behaviors of the GAFF and GLYCAM force fields may come from the different ruggedness of their corresponding potential energy surfaces (PES) when the ligand is in the binding pocket. This can be attributed to the difference between the GAFF and GLYCAM force fields, especially the difference in atomic charges. The partial charges of the GLYCAM06 force field are calculated by restrained fitting to the electrostatic potential (ESP) from QM calculations but are scaled to reproduce crystal unit-cell geometries. Unique charge sets are also provided for α-anomers. Besides, in order to reproduce molecular ESPs properly, GLYCAM06 adopts ensemble-averaged partial charge sets which are specific for each anomer. Moreover, restraints are employed to ensure that the charges on aliphatic hydrogen atoms are zero.15 The van der Waals parameters in GLYCAM06 are taken from AMBER PARM94. The parameters for torsion terms are obtained by fitting to QM rotational energy curves.53 As shown in Fig. S7,† the atomic charges from the GAFF and GLYCAM force fields have evident differences. The methyl hydrogen atoms have no partial charge in the GLYCAM force field, which may smooth the PES. These differences have a great influence on sampling, which further leads to the differences in the calculated free energies. GLYCAM serves as a specialized force field for carbohydrates, showing its superiority while conducting the simulations involving carbohydrates. GAFF is a general force field for most organic molecules but is not specialized for carbohydrates. For the solvation free energy, however, it is relatively easier to reach convergence. Thus, long-time simulations and short-time simulations have only negligible discrepancies. For instance, under the GLYCAM force field, the solvation free energy was −16.66 kcal mol−1 in a 10 ns simulation. A more lengthy simulation (50 ns) provided a slightly smaller solubility (−16.52 kcal mol−1). Such a small difference suggests that the calculation of the solvation free energy of methyl-α-L-fucoside has reached convergence. Similarly, GAFF achieves convergence quickly with the evidence that the solvation free energy has only a slight change (0.06 kcal mol−1) while increasing the MD simulation time from 10 to 50 ns.
In our QM/MM calculations, methyl-α-L-fucoside is described using quantum mechanics at the BLYP/6-31G(d) level, in which the discrete point charges are replaced by continuous electron densities and its Coulomb interaction with the environment is calculated at the QM level. However, in order to avoid expensive QM/MM molecular dynamics simulations, the QM/MM free energies were calculated using thermodynamic perturbations from the MM Hamiltonian to the QM/MM Hamiltonian. The results are listed in Table 2. The corrected free energies from GAFF to QM/MM are smaller than those from GLYCAM to QM/MM, which may be because atomic charges in GAFF are fitted from electrostatic potentials at the QM level and are more compatible with QM methods. For the solvation free energy in bulk water, the correction from GAFF to QM/MM (ΔGbulkMM→QM/MM) is only 0.44 kcal mol−1, while that from GLYCAM to QM/MM is −1.21 kcal mol−1. After the MM to QM/MM correction, the solvation free energies at the QM/MM level are −15.48 kcal mol−1 and −17.73 kcal mol−1. Although both of these solvation free energies are at the same QM/MM level, this difference is not unexpected. The van der Waals interactions between the QM and MM regions in the QM/MM Hamiltonian were borrowed from the force fields in this work. Besides, the biasing potential was not rigorously calculated. Instead, the biasing potential was calculated as the difference in the interaction energies by assuming that the potential energy surfaces of the isolated QM region were the same under the QM and MM Hamiltonians. Therefore, the exact Hamiltonians corresponding to these two QM/MM solvation free energies were not the same. In the binding pocket, the correction free energy from GAFF to QM/MM is −1.04 kcal mol−1, and that from GLYCAM to QM/MM is −4.10 kcal mol−1. The difference is over 3 kcal mol−1. The final binding free energies at the QM/MM level are −11.04 kcal mol−1 and −12.23 kcal mol−1, which deviated further from the experimental measurement.
| Ligand FF | ΔGbulkint | ΔGbulkt+r | ΔGsiteint − ΔGsitet+r | ΔGMMbinding | ΔGbulkMM→QM/MM | ΔGbulkQM/MM | ΔGsiteMM→QM/MM | ΔGQM/MMbinding |
|---|---|---|---|---|---|---|---|---|
| GAFF | −15.92 ± 0.05 | 11.84 | −37.32 ± 0.03 | −9.56 ± 0.06 | 0.44 ± 0.06 | −15.48 ± 0.09 | −1.04 ± 0.13 | −11.04 ± 0.15 |
| GLYCAM | −16.52 ± 0.07 | 11.41 | −37.27 ± 0.03 | −9.34 ± 0.08 | −1.21 ± 0.06 | −17.73 ± 0.12 | −4.10 ± 0.07 | −12.23 ± 0.12 |
It might be surprising that this QM/MM method yielded worse results than the MM method, although the former one is far more demanding than the latter one. It can be explained that the MM method used in this study has been well parameterized but the QM/MM method is yet to be calibrated. Albeit there is rigorous treatment of the intramolecular interaction for the QM region at the density functional theory level, the intermolecular interaction between the QM and MM regions has not been well parameterized. In this QM/MM study, like in most of the QM/MM studies, the interaction between the QM and MM regions included only electrostatic and vdW interactions. The QM region was embedded in the point charges of the MM atoms and the electrostatic interaction between the MM and QM atoms was calculated as the interaction between the point charges and the diffusive electron density. Since no Pauli repulsion is considered, there are no forces that can prevent electron density from spilling out into the MM region.78,79 It is well know that this undamped Coulomb interaction overestimates the interaction because a point charge is not a good approximation for the atoms in the vicinity of the QM region.80–86 This Coulomb interaction can be corrected by introducing a damping factor or by smearing the charge distribution on the MM atoms. Moreover, the vdW interaction between the QM and MM regions is not calibrated consistently with the Coulomb interaction. Instead, the vdW interactions were calculated at the MM level, which does not depend on the electron density of the QM region. Although this vdW scheme is inexpensive, it can introduce considerable errors into the results.87–91
Conclusion
In this work, the binding affinity of methyl-α-L-fucoside to RSL was studied at both molecular mechanical and quantum mechanical/molecular mechanical levels and further with TP correction at the QM/MM level. The free energy at the MM level was calculated using the double-decoupling method and the free energy change at each step was calculated via a series of intermediate states using Bennett’s acceptance ratio (BAR). The QM/MM free energy was calculated by thermodynamic perturbation from the MM Hamiltonians. The main observations of this study are:• Molecular mechanical methods with fine calibration can well describe the binding affinity of methyl-α-L-fucoside to RSL with errors around 1.0 kcal mol−1. However, the convergence of the free energies is very slow. Normally very long simulations are required for the real states as well as some intermediate states in the alchemical path. Careful checking of the correlation of the potential energy along the trajectory is critical.
• Simulations using GLYCAM converge much faster than those using the general AMBER force field, due to the ensemble-averaged atomic charges and the null charges for the aliphatic hydrogen atoms in GLYCAM.
• Although the hybrid quantum mechanical/molecular mechanical methods provide more accurate presentation of the charge distribution and the response of the molecule to external fields, the accuracy of these methods is limited by the approximations in the description of the interaction between the quantum mechanical (core) region and the molecular mechanical region (environment). These limitations include the over-polarization by the point charges nearby and the van der Waals interaction being incompatible with the wavefunctions of the quantum mechanical region, which have been observed in some other studies.80,81,86–91
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 21173082), Shanghai Sailing Program (Grant No. 17YF1413200) and the Large Instruments Open Foundation of East China Normal University. CPU time was supported by the Supercomputer Center of East China Normal University. WL and YM thank Dr Yu Kang for many helpful discussions.References
- R. S. Haltiwanger and J. B. Lowe, Role of Glycosylation In Development, Annu. Rev. Biochem., 2004, 73, 491–537 CrossRef CAS PubMed.
- M. M. Alen, S. J. Kaptein, T. D. Burghgraeve, J. Balzarini, J. Neyts and D. Schols, Antiviral Activity of Carbohydrate-binding Agents and the Role of DC-SIGN in Dengue Virus Infection, Virology, 2009, 387, 67–75 CrossRef CAS PubMed.
- P. H. Seeberger, Chemical Glycobiology: Why Now?, Nat. Chem. Biol., 2009, 5, 368–372 CrossRef CAS PubMed.
- Y. Kang, U. Gohlke, O. Engstrom, C. Hamark, T. Scheidt, S. Kunstmann, U. Heinemann, M. Santer and S. Barbirz, Bacteriophage Tailspikes and Bacterial O-antigens as a Model System to Study Weak-Affinity Protein-Polysaccharide Interactions, J. Am. Chem. Soc., 2016, 138, 9109–9118 CrossRef CAS PubMed.
- J.-C. Michalskia and A. Klein, Glycoprotein lysosomal storage disorders: α- and β-mannosidosis, fucosidosis and α-N-acetylgalactosaminidase deficiency, Biochim. Biophys. Acta, Mol. Basis Dis., 1999, 1455, 69–84 CrossRef.
- B. J. Campbell, L.-G. Yu and J. M. Rhodes, Altered Glycosylation in Inflammatory Bowel Disease: A Possible Role in Cancer Development, Glycoconjugate J., 2001, 18, 851–858 CrossRef CAS PubMed.
- B. A. Cobb and D. L. Kasper, Coming of Age: Carbohydrates and Immunity, Eur. J. Immunol., 2005, 35, 352–356 CrossRef CAS PubMed.
- H. E. Murrey and L. C. Hsieh-Wilson, The Chemical Neurobiology of Carbohydrates, Chem. Rev., 2008, 108, 1708–1731 CrossRef CAS PubMed.
- R. A. Dwek, Glycobiology: Toward Understanding the Function of Sugars, Chem. Rev., 1996, 96, 683–720 CrossRef CAS PubMed.
- H. Lis and N. Sharon, Lectins: Carbohydrate-Specific Proteins That Mediate Cellular Recognition, Chem. Rev., 1998, 98, 637–674 CrossRef CAS PubMed.
- S. Tsuzuki, T. Uchimaru and M. Mikami, Magnitude and Nature of Carbohydrate-Aromatic Interactions: Ab Initio Calculations of Fucose-Benzene Complex, J. Phys. Chem. B, 2009, 113, 5617–5621 CrossRef CAS PubMed.
- C. H. Wong, Carbohydrate-Based Drug Discovery, Wiley-VCH Verlag GmbH & Co. KGaA, 2003 Search PubMed.
- M. M. Fuster and J. D. Esko, The Sweet and Sour of Cancer: Glycan as Novel Therapeutic Targets, Nat. Rev. Cancer, 2005, 5, 526–542 CrossRef CAS PubMed.
- N. Sharon, Carbohydrates as Future Anti-Adhesion Drugs for Infectious Disease, Biochim. Biophys. Acta, 2006, 1760, 527–537 CrossRef CAS PubMed.
- E. Fadda and R. J. Woods, Molecular Simulations of Carbohydrates and Protein-Carbohydrate Interactions: Motivation, Issues and Prospects, Drug Discovery Today, 2010, 15, 596–609 CrossRef CAS PubMed.
- O. C. Grant and R. J. Woods, Recent Advances in Employing Molecular Modelling to Determine the Specificity of Glycan-Binding Proteins, Curr. Opin. Struct. Biol., 2014, 28, 47–55 CrossRef CAS PubMed.
- M. Wimmerová, S. Kozmon, I. Nečasová, S. K. Mishra, J. Komárek and J. Koča, Stacking Interactions between Carbohydrate and Protein Quantified by Combination of Theoretical and Experimental Methods, PLoS One, 2012, 7, e46032 Search PubMed.
- R. Sommer, T. E. Exner and A. Titz, A Biophysical Study with Carbohydrate Derivatives Explains the Molecular Basis of Monosaccharide Selectivity of the Pseudomonas aeruginosa Lectin LecB, PLoS One, 2014, 9, e112822 Search PubMed.
- N. K. Mishra, Z. Kříž, M. Wimmerová and J. Koča, Recognition of Selected Monosaccharides by Pseudomonas Aeruginosa Lectin II Analyzed by Molecular Dynamics and Free Energy Calculations, PLoS One, 2014, 9, e112822 Search PubMed.
- S. K. Mishra, G. Calabró, H. H. Loeffler, J. Michel and J. Koča, Evaluation of Selected Classical Force Fields for Alchemical Binding Free Energy Calculations of Protein-Carbohydrate Complexes, J. Chem. Theory Comput., 2015, 11, 3333–3345 CrossRef CAS PubMed.
- C. Clarke, R. J. Woods, J. Gluska, A. Cooper, M. A. Nutley and G.-J. Boons, Involvement of Water in Carbohydrate-Protein Binding, J. Am. Chem. Soc., 2001, 123, 12238–12247 CrossRef CAS PubMed.
- R. Kadirvelraj, B. L. Foley, J. D. Dyekjær and R. J. Woods, Involvement of Water in Carbohydrate-Protein Binding: Concanavalin A Revisited, J. Am. Chem. Soc., 2008, 130, 16933–16942 CrossRef CAS PubMed.
- Y. Deng and B. Roux, Calculation of Standard Binding Free Energies: Aromatic Molecules in the T4 Lysozyme L99A Mutant, J. Chem. Theory Comput., 2006, 2, 1255–1273 CrossRef CAS PubMed.
- S. Boresch, F. Tettinger and M. Leitgeb, Absolute Binding Free Energies: A Quantitative Approach for Their Calculation, J. Phys. Chem. B, 2003, 107, 9535–9551 CrossRef CAS.
- J. Hermans and L. Wang, Inclusion of Loss of Translational and Rotational Freedom in Theoretical Estimates of Free Energies of Binding. Application to a Complex of Benzene and Mutant T4 Lysozyme, J. Am. Chem. Soc., 1997, 119, 2707–2714 CrossRef CAS.
- N. Hansen and W. F. van Gunsteren, Practical Aspects of Free-Energy Calculations: A Review, J. Chem. Theory Comput., 2014, 10, 2632–2647 CrossRef CAS PubMed.
- D. L. Mobley, J. D. Chodera and K. A. Dill, On the Use of Orientational Restraints and Symmetry Corrections in Chemical Free Energy Calculations, J. Chem. Phys., 2006, 125, 084902 CrossRef PubMed.
- H.-J. Woo and B. Roux, Calculation of Absolute Protein-Ligand Binding Free Energy from Computer Simulations, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6825–6830 CrossRef CAS PubMed.
- J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Alchemical Free Energy Methods for Drug Discovery: Progress and Challenges, Curr. Opin. Struct. Biol., 2011, 21, 150–160 CrossRef CAS PubMed.
- C. D. Christ, A. E. Mark and W. F. van Gunsteren, Basic Ingredients of Free Energy Calculations: A Review, J. Comput. Chem., 2010, 31, 1569–1582 CAS.
- X. Du, Y. Li, Y.-L. Xia, S.-M. Ai, J. Liang, P. Sang, X.-L. Ji and S.-Q. Liu, Insights into Protein-Ligand Interactions: Mechanisms, Models, and Methods, Int. J. Mol. Sci., 2016, 17, 144 CrossRef PubMed.
- D. L. Mobley and P. V. Klimovich, Perspective: Alchemical Free Energy Calculations for Drug Discovery, J. Chem. Phys., 2012, 137, 230901 CrossRef PubMed.
- M. R. Shirts, D. L. Mobley and J. D. Chodera, in Annual Reports in Computational Chemistry, ed. D. C. Spellmeyer and R. Wheeler, Elsevier, 2007, vol. 3, pp. 41–59 Search PubMed.
- H. Senderowitz, C. Parish and W. C. Still, Carbohydrates: United Atom AMBER* Parameterization of Pyranoses and Simulations Yielding Anomeric Free Energies, J. Am. Chem. Soc., 1996, 118, 2078–2086 CrossRef CAS.
- E. P. Raman, O. Guvench and A. D. MacKerell Jr, CHARMM Additive All-Atom Force Field for Glycosidic Linkages in Carbohydrates Involving Furanoses, J. Phys. Chem. B, 2010, 14, 12981–12994 CrossRef PubMed.
- O. Guvench, S. S. Mallajosyula, E. P. Raman, E. Hatcher, K. Vanommeslaeghe, T. J. Foster, F. W. Jamison and A. D. Mackerell, CHARMM Additive All-Atom Force Field for Carbohydrate Derivatives and Its Utility in Polysaccharide and Carbohydrate-Protein Modeling, J. Chem. Theory Comput., 2011, 7, 3162–3180 CrossRef CAS PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. Gonzàlez-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, GLYCAM06: A Generalizable Biomolecular Force Field. Carbohydrates, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- M. Basma, S. Sundara, T. Vernali and R. J. Woods, Solvated Ensemble Averaging in the Calculation of Partial Atomic Charges, J. Comput. Chem., 2001, 22, 1125–1137 CrossRef CAS PubMed.
- K.-H. Ott and B. Meyer, Parametrization of GROMOS Force Field for Oligosaccharides and Assessment of Efficiency of Molecular Dynamics Simulations, J. Comput. Chem., 1996, 17, 1068–1084 CrossRef CAS.
- S. A. H. Spieser, J. A. Van Kuik, L. M. J. Kroonbatenburg and J. Kroon, ImprovedCarbohydrate Force Field for Gromos: Ring and Hydroxymethyl Group Conformations and Exo-Anomeric Effect, Carbohydr. Res., 1999, 322, 264–273 CrossRef CAS.
- W. Damm, A. Frontera, J. T. Rives and W. L. Jorgensen, OPLS All-atom Force Field for Carbohydrates, J. Comput. Chem., 1997, 18, 1955–1970 CrossRef CAS.
- D. Kony and W. F. Van Gunsteren, An Improved OPLS-AA Force Field for Carbohydrates, J. Comput. Chem., 2002, 23, 1416–1429 CrossRef CAS PubMed.
- A. Imberty, E. Bettler, M. Karababa, K. Mazeau, P. Petrova and S. Perez, in Perspectives in Structural Biology, ed. M. Vijayan, N. Yathindra and A. S. Kolaskar, Indian Academy of Sciences and Universities Press, Hyderabad, 1999, pp. 392–408 Search PubMed.
- N. L. Allinger, K.-H. Chen, J.-H. Lii and K. A. Durkin, Alcohols, Ethers, Carbohydrates, and Related Compounds. I. The MM4 Force Field for Simple Compounds, J. Comput. Chem., 2003, 24, 1447–1472 CrossRef CAS PubMed.
- J. H. Lii, K. H. Chen, K. A. Durkin and N. L. Allinger, Alcohols, Ethers, Carbohydrates, and Related Compounds. II. The Anomeric Effect, J. Comput. Chem., 2003, 24, 1473–1489 CrossRef CAS PubMed.
- J. H. Lii, K. H. Chen and N. L. Allinger, Alcohols, Ethers, Carbohydrates, and Related Compounds. IV. Carbohydrates, J. Comput. Chem., 2003, 24, 1504–1513 CrossRef CAS PubMed.
- Y. Kang, S. Barbirz, R. Lipowsky and M. Santer, Conformational Diversity of O-Antigen Polysaccharides of the Gram-negative Bacterium Shigella Flexneri Serotype Y, J. Phys. Chem. B, 2014, 118, 2523–2534 CrossRef CAS PubMed.
- S. Andre, T. Velasco-Torrijos, R. Leyden, S. Gouin, M. Tosin, P. V. Murphy and H. J. Gabius, Phenylenediamine-Based Bivalent Glycocyclophanes: Synthesis and Analysis of the Influence of Scaffold Rigidity and Ligand Spacing on Lectin Binding in Cell Systems with Different Glycomic Profiles, Org. Biomol. Chem., 2009, 7, 4715–4725 CAS.
- A. Singh, M. B. Tessier, K. Pederson, X. Wang, A. P. Venot, G. Boons, J. H. Prestegard and R. J. Woods, Extension and Validation of the GLYCAM Force Field Parameters for Modeling Glycosaminoglycans, Can. J. Chem., 2016, 94, 1–9 CrossRef PubMed.
- B. L. Foley, M. B. Tessier and R. J. Woods, Carbohydrate Force Fields, WIREs Computational Molecular Science, 2012, 2, 652–697 CrossRef CAS PubMed.
- F. V. Toukach and V. P. Ananikov, Recent Advances in Computational Predictions of NMR Parameters for the Structure Elucidation of Carbohydrates: Methods and Limitations, Chem. Soc. Rev., 2013, 42, 8376–8415 RSC.
- A. J. Kirby and N. H. Williams, in The Anomeric Effect and Associated Stereoelectronic Effect, ed. G. R. J. Thatcher, ACS Symposium Series, 1993, vol. 539, pp. 6–25 Search PubMed.
- X. Xiong, Z. Chen, B. P. Cossins, Q. Shao, K. Ding, W. Zhu and J. Shi, Force Fields and Scoring Functions for Carbohydrate Simulation, Drug Discovery Today, 2015, 401, 73–81 CAS.
- J. F. Matthews, G. T. Beckham, M. Bergenstråhle-Wohlert, J. W. Brady, M. E. Himmel and M. F. Crowley, Comparison of Cellulose Iβ Simulations with Three Carbohydrate Force Fields, J. Chem. Theory Comput., 2012, 8, 735–748 CrossRef CAS PubMed.
- X. Lu, D. Fang, S. Ito, Y. Okamoto, V. Ovchinnikov and Q. Cui, QM/MM Free Energy Simulations: Recent Progress and Challenges, Mol. Simul., 2016, 42, 1056–1078 CrossRef CAS PubMed.
- U. Ryde and P. Söderhjelm, Ligand-Binding Affinity Estimates Supported by Quantum Mechanical Methods, Chem. Rev., 2016, 116, 5520–5566 CrossRef CAS PubMed.
- A. J. Sodt, Y. Mei, G. König, P. Tao, R. P. Steele, B. R. Brooks and Y. Shao, Multiple Environment Single System Quantum Mechanical/Molecular Mechanical(MESS-QM/MM) Calculations. 1. Estimation of Polarization Energies, J. Phys. Chem. A, 2015, 119, 1511–1523 CrossRef CAS PubMed.
- M. R. Reddy and M. D. Erion, Relative Binding Affinities of Fructose-1,6-Bisphosphatase Inhibitors Calculated Using a Quantum Mechanics-Based Free Energy Perturbation Method, J. Am. Chem. Soc., 2007, 129, 9296–9297 CrossRef CAS PubMed.
- R. S. Rathore, R. N. Reddy, A. K. Kondapi, P. Reddanna and M. R. Reddy, Use of Quantum Mechanics/molecular Mechanics-based FEP Method for Calculating Relative Binding Affinities of FBPase Inhibitors for Type-2 Diabetes, Theor. Chem. Acc., 2012, 131, 1096 CrossRef.
- K. Swiderek, S. Marti and V. Moliner, Theoretical Studies of HIV-1 Reverse Transcriptase Inhibition, Phys. Chem. Chem. Phys., 2012, 14, 12614–12624 RSC.
- G. König, P. S. Hudson, S. Boresch and H. L. Woodcock, Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennet Reweighting Schemes, J. Chem. Theory Comput., 2014, 10, 1406–1419 CrossRef PubMed.
- T. P. Straatsma and J. A. McCammon, Treatment of Rotational Isomeric States. III. The Use of Biasing Potentials, J. Chem. Phys., 1994, 101, 5032–5039 CrossRef CAS.
- M. Leigeb, C. Schroder and S. Boresch, Alchemical Free Energy Calculations and Multiple Conformational Substates, J. Chem. Phys., 2005, 122, 084109 CrossRef PubMed.
- G. König, I. F. C. Pickard, Y. Mei and B. R. Brooks, Predicting Hydration Energies with a Hybrid QM/MM Approach: An Evaluation of Implicit and Explicit Solvation Models in SAMPL4, J. Comput.-Aided Mol. Des., 2014, 28, 245–257 CrossRef PubMed.
- E. Dybeck, G. König, B. R. Brooks and M. R. Shirts, Comparison of Methods To Reweight from Classical Molecular Simulations to QM/MM Potentials, J. Chem. Theory Comput., 2016, 12, 1466–1480 CrossRef CAS PubMed.
- X. Jia, M. Wang, Y. Shao, G. König, B. R. Brooks, J. Z. H. Zhang and Y. Mei, Calculations of Solvation Free Energy through Energy Reweighting from Molecular Mechanics to Quantum Mechanics, J. Chem. Theory Comput., 2016, 12, 499–511 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandresekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. A. Case, J. T. Berryman, R. M. Betz, D. S. Cerutti, T. E. I. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke and A. W. Goetz, et al., AMBER 15, University of California, San Francisco, 2015 Search PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes, J. Chem. Phys., 1977, 23, 327–341 CAS.
- T. Darden, D. York and L. Pedersen, Particle Mesh Ewald: An Nlog(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera and M. L. Berkowitz, A Smooth Particle Mesh Ewald Method, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- A. D. Becke, Density-functional Exchange-energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- G. König, Y. Mei, I. F. C. Pickard, A. C. Simmonett, B. T. Miller, J. M. Herbert, H. L. Woodcock, B. R. Brooks and Y. Shao, Computation of Hydration Free Energies Using the Multiple Environment Single System Quantum Mechanical/Molecular Mechanical Method, J. Chem. Theory Comput., 2016, 12, 332–344 CrossRef PubMed.
- J. D. Chodera, W. C. Swope, J. W. Pitera, C. Seok and K. A. Dill, Use of the Weighted Histogram Analysis Method for the Analysis of Simulated and Parallel Tempering Simulations, J. Chem. Theory Comput., 2007, 3, 26–41 CrossRef CAS PubMed.
- S. K. Mishra, J. Adam, M. Wimmerová and J. Koča, In Silico Mutagenesis and Docking Study of Ralstonia solanacearum RSL Lectin: Performance of Docking Software To Predict Saccharide Binding, J. Chem. Inf. Model., 2012, 52, 1250–1261 CrossRef CAS PubMed.
- L. J. Nåbo, J. M. H. Olsen, N. H. List, L. M. Solanko, D. Wüstner and J. Kongsted, Embedding Beyond Electrostatics–The Role of Wave Function Confinement, J. Chem. Phys., 2016, 145, 104102 CrossRef PubMed.
- G. Groenhof, in Biomolecular Simulations: Methods and Protocols, ed. L. Monticelli and E. Salonen, Humana Press, 2013, pp. 43–66 Search PubMed.
- D. D. Das, K. P. Eurenius, E. M. Billings, P. Sherwood, D. C. Chatfield, M. Hodošček and B. R. Brooks, Optimization of Quantum Mechanical Molecular Mechanical Partitioning Schemes: Gaussian Delocalization of Molecular Mechanical Charges and the Double Link Atom Method, J. Chem. Phys., 2002, 117, 10534–10547 CrossRef CAS.
- G. A. Cisneros, S. N.-I. Tholander, O. Parisel, T. A. Darden, D. Elking, L. Perera and J.-P. Piquemal, Simple Formulas for Improved Point-charge Electrostatics in Classical Force Fields and Hybrid Quantum Mechanical/Molecular Mechanical Embedding, Int. J. Quantum Chem., 2008, 108, 1905–1912 CrossRef CAS PubMed.
- B. Wang and D. G. Truhlar, Geometry Optimization Using Tuned and Balanced Redistributed Charge Schemes for Combined Quantum Mechanical and Molecular Mechanical Calculations, Phys. Chem. Chem. Phys., 2011, 13, 10556–10564 RSC.
- B. Wang and D. G. Truhlar, Partial Atomic Charges and Screened Charge Models of the Electrostatic Potential, J. Chem. Theory Comput., 2012, 8, 1989–1998 CrossRef CAS PubMed.
- G. Hou, X. Zhu, M. Elstner and Q. Cui, A Modified QM/MM Hamiltonian with the Self-Consistent-Charge Density-Functional-Tight-Binding Theory for Highly Charged QM Regions, J. Chem. Theory Comput., 2012, 8, 4293–4304 CrossRef CAS PubMed.
- B. Wang and D. G. Truhlar, Tuned and Balanced Redistributed Charge Scheme for Combined Quantum Mechanical and Molecular Mechanical (QM/MM) Methods and Fragment Methods: Tuning Based on the CM5 Charge Model, J. Chem. Theory Comput., 2013, 9, 1036–1042 CrossRef CAS PubMed.
- B. Wang and D. G. Truhlar, Screened Electrostatic Interactions in Molecular Mechanics, J. Chem. Theory Comput., 2014, 10, 4480–4487 CrossRef CAS PubMed.
- M. Freindorf and J. Gao, Optimization of the Lennard-Jones Parameters for a Combined ab initio Quantum Mechanical and Molecular Mechanical Potential Using the 3-21G Basis Set, J. Comput. Chem., 1996, 17, 386–395 CrossRef CAS.
- D. Riccardi, G. Li and Q. Cui, Importance of van der Waals Interactions in QM/MM Simulations, J. Phys. Chem. B, 2004, 108, 6467–6478 CrossRef CAS PubMed.
- M. Freindorf, Y. Shao, T. R. Furlani and J. Kong, Lennard-Jones parameters for the combined QM/MM method using the B3LYP/6-31G*/AMBER potential, J. Comput. Chem., 2005, 26, 1270–1278 CrossRef CAS PubMed.
- T. J. Giese and D. M. York, Charge-dependent Model for Many-body Polarization, Exchange, and Dispersion Interactions in Hybrid Quantum Mechanical/Molecular Mechanical Calculations, J. Chem. Phys., 2007, 127, 194101 CrossRef PubMed.
- E. R. Kuechler, T. J. Giese and D. M. York, Charge-dependent Many-body Exchange and Dispersion Interactions in Combined QM/MM Simulations, J. Chem. Phys., 2015, 143, 234111 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06215j |
| ‡ Current address: NYU-ECNU Center for Computational Chemistry at NYU Shanghai, Shanghai 200062, China. |
| This journal is © The Royal Society of Chemistry 2017 |