View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/C7RA06290G (Paper) RSC Adv., 2017, 7, 47063-47072

A dynamic prediction of stability for nitromethane in external electric field†

Fu-de Ren*a, Duan-lin Caoa, Wen-jing Shib and Min Youa
aCollege of Chemical Engineering and Environment, North University of China, Taiyuan 030051, China. E-mail: fdren888@126.com; Fax: +86 351 3922117; Tel: +86 351 3922117
bThe Third Hospital of Shanxi Medical University, Taiyuan 030053, China

Received 5th June 2017 , Accepted 29th September 2017

First published on 5th October 2017

Abstract

Adding an external electric field into an energetic material system can increase the energy but the stability may be reduced. In this paper, the effects of external electric fields on the initiation reaction dynamics of CH3NO2 (intermolecular and 1,3-intramolecular hydrogen transferences) were investigated using the MP2/6-311++G(2d,p) and CCSD/6-311++G(2d,p) methods. The results show that, when the external electric field is in the −y-direction of the CH3NO2 dimer (perpendicular to the O⋯N⋯N plane), the barriers of intermolecular hydrogen transference are lower than the C–NO2 bond dissociation energies, leading to a preference for the hydrogen transference path over the C–NO2 bond dissociation, and the sensitivities are higher than in the absence of an external electric field. However, in the other fields (except for the C–NO2 bond axis direction with a field strength larger than +0.0060 a.u.), the C–NO2 bond scission is favored and the sensitivities are almost equal to those in the absence of an external electric field. Although due to many obstacles, at present the proposition of adjusting the explosive sensitivity with external electric field does not make any sense in practice, the external-electric-field effect on explosive sensitivity must arouse intense interest in future.

1. Introduction

Although adding an external electric field into an energetic material system can increase the energy content of conduction gases in the vicinity of the detonation front and consequently accelerate detonation velocity and enhance detonation pressure,1–3 the stability of an energetic material may be reduced, leading to an increased explosive sensitivity.

There are mainly two reasons for reducing the stability of explosives. One is that the external electric field may elongate the bond length and reduce the bond dissociation energy (BDE) of the “trigger linkage”,4,5 the breaking of which is a key factor in the initiation of detonation.6–9 Thus, the trigger linkage is more prone to breakage in an external electric field than in the absence of an external electric field, leading to a higher explosive sensitivity. The other is that the external electric field may lower the activation energy of chemical reactions.10 For an explosive molecule, if the external electric field lowers the activation energy of the first step of the reaction (i.e., the detonation initiation), decomposition will be easier, and thus explosive sensitivity will become higher. The lower the activation energy, the more susceptibly the detonation initiation occurs, accompanied by a higher explosive sensitivity.7–9 Indeed, in our recent dynamic prediction of nitromethane → methyl nitrite isomerization in an external electric field, the barrier heights were decreased and the explosive sensitivities were increased with the increase of the electric field in the −x-direction.11 Therefore, in order to predict the stability of an explosive molecule in an external electric field, it is necessary to examine the changes in the strength of the trigger linkage and the activation energy of detonation initiation.

Nitromethane (CH3–NO2) is a prototypical explosive. Its decomposition mechanism has been extensively investigated in the absence of external electric field.12–20 Due to the lowest C–NO2 BDE, the C–NO2 bond scission was regarded as the first step.12 However, the viewpoint that the 1,3-intramolecular hydrogen transference and oxygen transfer from the nitro to methyl group were prior to the C–NO2 bond scission was supported based on the first principle.13–16,18 Then, what about in the presence of external electric field? Furthermore, will the sensitivity be increased in the external electric field? Recently, we investigated the changes of the C–NO2 BDEs and the barriers of CH3NO2 → CH3ONO isomerization in the presence of external electric field using the MP2 and CCSD methods.11 To our knowledge, few theoretical investigations on the stability and sensitivity of explosive molecule in external electric field were presented.

The hydrogen transference is a typical reaction mechanism. In this work, a dynamic investigation into the effect of external electric field on the intramolecular and intermolecular hydrogen transferences in detonation initiation of nitromethane was presented. The changes of the stability and explosive sensitivity were predicted according to the change of activation energy in external electric field. This investigation must be useful to add efficiently electric field to the energetic material system to avoid the catastrophic explosion in external electric field.

2. Computational details

All calculations were performed with Gaussian 03 programs.21 All the reactants and transition states (TS) were fully optimized using the MP2/6-311++G(2d,p) method in external electric fields (as well as no field). Energy minima of them were confirmed by the absence of imaginary frequency and only one imaginary frequency, respectively. The rate constants for each reaction path were calculated in the different field strengths and orientations at the MP2/6-311++G(2d,p) level, and AIM (atoms in molecules)22,23 results were obtained at the same level of theory. The activation energies were evaluated at the CCSD/6-311++G(2d,p)//MP2/6-311++G(2d,p) level.

In the coordinate systems used for the dynamic analysis of the reaction paths of 1,3-intramolecular hydrogen transference, the carbon is at the origin and the nitrogen is on the +z-axis; the x-axis is in the C–NO2 plane and the y-axis is perpendicular to it. For the intermolecular hydrogen transference, the N2⋯N2′ orientation is on the z-axis, with z increasing from N2 to N2′ for all the CH3NO2 dimers. The x-axis is in the O4⋯N2⋯N2′ plane, and the y-axis is perpendicular to it (see Fig. 1). In three orthogonal directions (x, y, and z), the field strengths of ±0.002, ±0.004, ±0.006, ±0.008 and ±0.010 a.u. were considered.


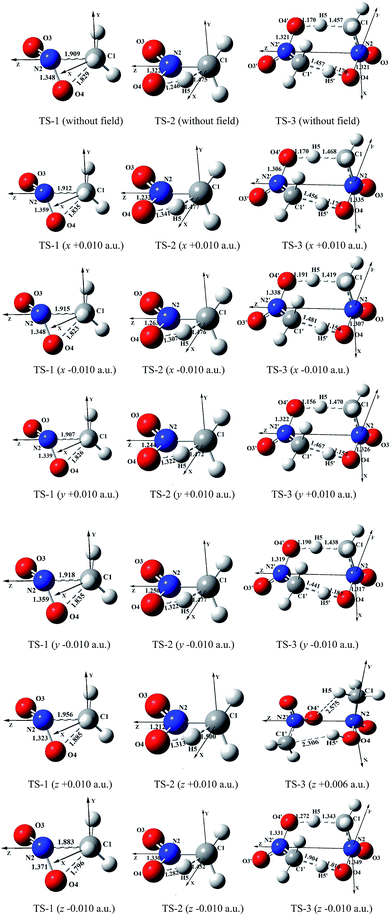image file: c7ra06290g-f1.tif
Fig. 1 Selected structures of the transition states in the different external electric field strengths and orientations (including those in the absence of field) at the MP2/6-311++G(2d,p) level (geometric parameters are in Å) (the figures of TS-1 are from literature11).

According to literature,10 in the absence and presence of various field strengths, conventional transition state theory (CTST)24,25 with wigner tunneling correction26–28 was used to provide estimates of the rate constants.

3. Results and discussion

In the absence of external electric field, three kinds of feasible mechanisms of the first step of the CH3NO2 decomposition are shown in Fig. 1: unimolecular isomerization to trans-eclipsed methyl nitrite CH3ONO via TS1,11 1,3-intramolecular hydrogen transference to C1 symmetrical aci-nitromethane CH2N(O)OH via TS2 and intermolecular hydrogen transfer via TS3. The barriers of TS2 and TS3 are 285.11 and 274.82 kJ mol−1 at the CCSD/6-311++G(2d,p)//MP2/6-311++G(2d,p) level, respectively. The C–NO2 BDE (275.21 kJ mol−1) is lower than the barrier of CH3NO2 → CH3ONO11 or CH3NO2 → CH2N(O)OH, but slightly higher than that of the intermolecular hydrogen transfer.

Note that the hydrogen transference is the initiation reaction in the decomposition process of nitromethane.19 So the following sections only give a comparison of the effect of external electric field on the barrier heights of intramolecular and intermolecular hydrogen transference reaction paths with the C–NO2 BDEs (see ESI data, Table S1†) in the different field strengths and orientations. For comparison, the results of “nitromethane → methyl nitrite CH3ONO via TS1 (ref. 11)” is also cited (see Fig. 1 and 2).


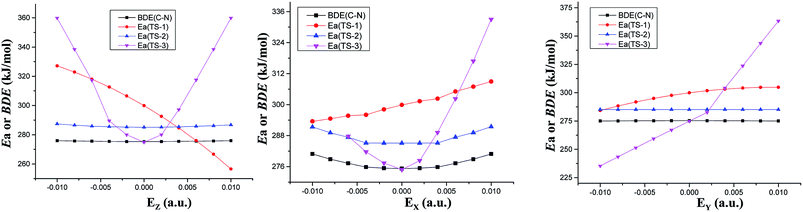image file: c7ra06290g-f2.tif
Fig. 2 Barriers (Ea) of three decomposition paths or C–NO2 BDEs versus field strengths in the different field orientations (EX, EY and EZ) at the CCSD/6-311++G(2d,p)//MP2/6-311++G(2d,p) level.

3.1 1,3-Intramolecular hydrogen transference

The fields parallel to the x-axis affect the barrier heights more than those parallel to the y- or z-axis. From Table S2 (see ESI data†) and Fig. 2, in the presence of the field in the y- or z-direction, barrier heights remain essentially unchanged even in the stronger electric fields. Furthermore, in the x-, y- and z-oriented fields, the barriers are all higher than the C–NO2 BDEs, showing that the external electric field causes preference of the C–NO2 bond dissociation over the 1,3-intramolecular hydrogen transference.

For TS2, the C1⋯H5 distances do not show unambiguous trends with the changes of field strengths in the x-direction (see ESI data, Table S3†). As the field is increased in the +x-direction, the N2–O4 bond lengths increase, while the O4⋯H5 distances decrease, as is in accordance with the AIM results. The opposite trends are found in the −x-direction. In the +z-direction, as the field is increased, the C1⋯H5 distances decrease, while the O4⋯H5 distances and N2–O4 bond lengths increase. Fields in the negative z-direction correspondingly show the opposite trends. From Fig. 3 and 4, in the x-direction, the linear correlations between the changes of bond lengths or corresponding electron densities and field strengths are found with the R2 equal to the range of 0.9954–0.9966 or 0.9968–0.9977. In the z-direction, several good (R2 = 0.9991–0.9997 or 0.9993–0.9999) linear correlations between them are also observed. However, in the y-direction, the linear correlation is not obvious.


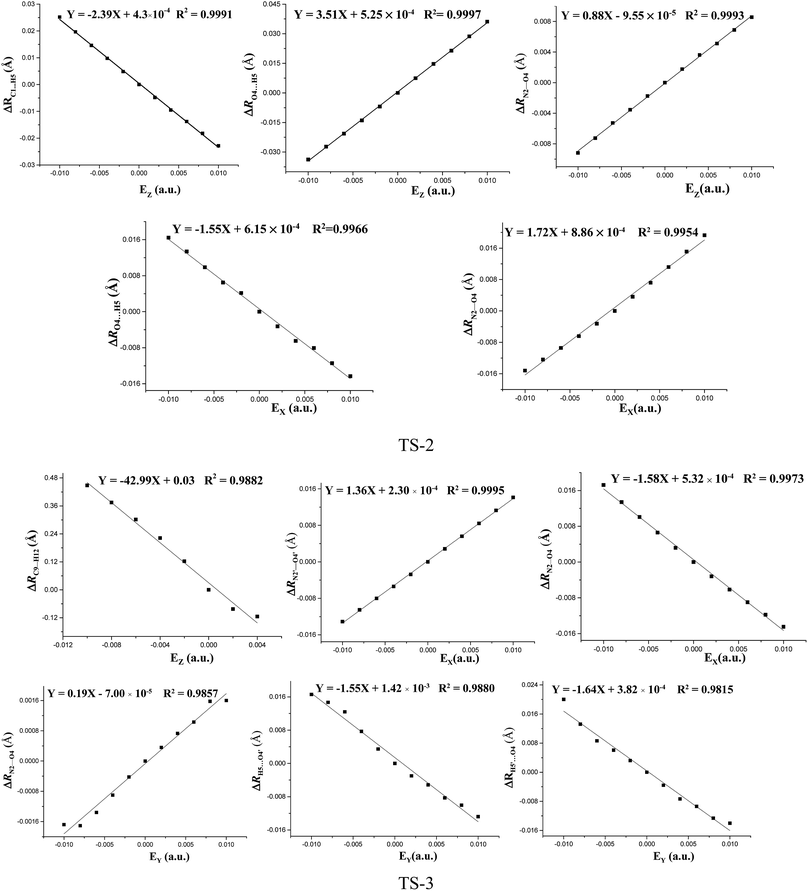image file: c7ra06290g-f3.tif
Fig. 3 Changes of the bond lengths or interatomic distances versus field strengths in the different field orientations (EX, EY and EZ) for transition states at the MP2/6-311++G(2d,p) level.

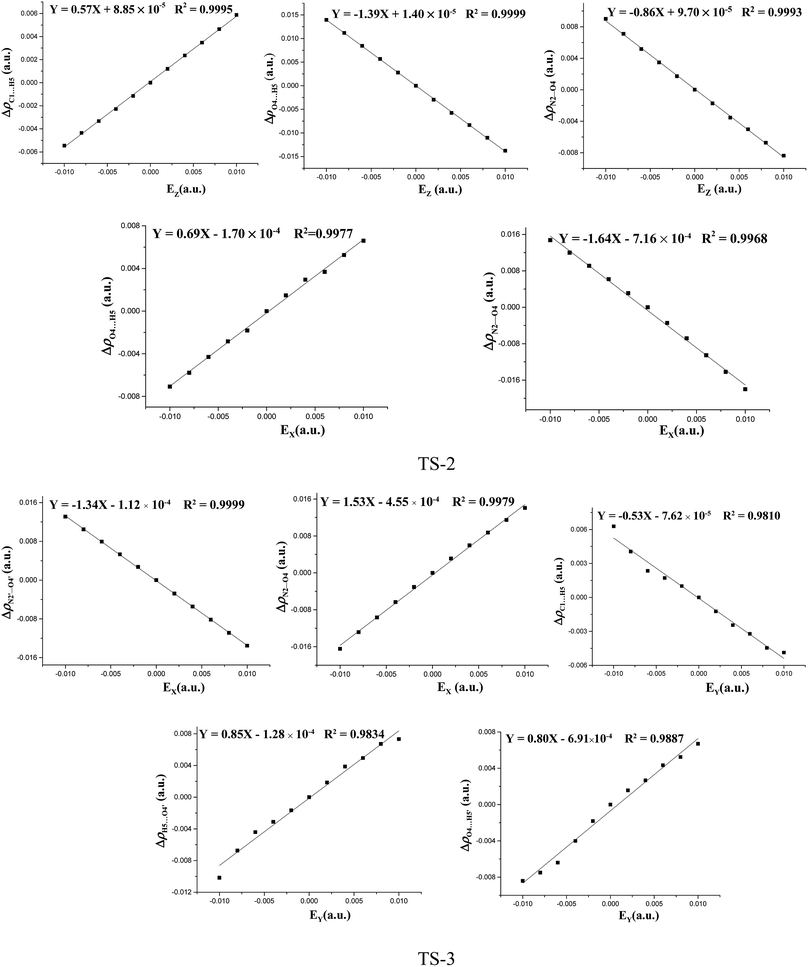image file: c7ra06290g-f4.tif
Fig. 4 The changes of the electron densities versus field strengths in the different field orientations (EX, EY and EZ) for transition states at the MP2/6-311++G(2d,p) level.

From Table 1, fields oriented parallel to the x- or y-axes have a minor effect on the imaginary vibrations, while fields along the z-direction, i.e. the direction of proton transfer, have a significant effect on them. The imaginary frequencies are decreased in the −z-direction while are increased in the +z-direction. Thus, the field-induced flattening of the potential energy surface is suggested in the −z-direction.

Table 1 Transition states imaginary frequencies (Imν), Gibbs energies (ΔG, kJ mol−1), reaction rate constants (k, s−1) and corrected reaction rate constants (k298.15 K,C and k688 K,C, s−1), and Wigner tunneling corrections (κ) in the absence and presence of fields of varying strengths and directions for the 1,3-intramolecular hydrogen transference path at the MP2/6-311++G(2d,p) level
Field (a.u.) Imν ΔG298.15 K k298.15 K κ298.15 K k298.15 K,C ΔG688 K k688 k κ688 K k688 K,C
No field 2226.6 264.53 2.81 × 10−34 5.849 1.64 × 10−33 282.75 4.95 × 10−9 1.903 9.42 × 10−9
Z − 0.0100 2090.1 261.12 1.11 × 10−33 5.273 5.86 × 10−33 272.67 2.88 × 10−8 1.796 5.17 × 10−8
Z − 0.0080 2126.7 261.22 1.07 × 10−33 5.424 5.79 × 10−33 273.82 2.36 × 10−8 1.824 4.30 × 10−8
Z − 0.0060 2156.3 261.58 9.23 × 10−34 5.548 5.12 × 10−33 275.30 1.82 × 10−8 1.847 3.36 × 10−8
Z − 0.0040 2181.8 262.28 6.95 × 10−34 5.656 3.93 × 10−33 277.34 1.27 × 10−8 1.867 2.38 × 10−8
Z − 0.0020 2206.0 263.29 4.64 × 10−34 5.760 2.67 × 10−33 279.86 8.20 × 10−9 1.886 1.55 × 10−8
Z + 0.0020 2245.1 255.78 9.58 × 10−33 5.930 5.68 × 10−32 290.88 1.20 × 10−9 1.918 2.29 × 10−9
Z + 0.0040 2260.1 256.08 8.49 × 10−33 5.996 5.09 × 10−32 253.16 8.72 × 10−7 1.930 1.68 × 10−6
Z + 0.0060 2272.9 256.48 7.22 × 10−33 6.053 4.37 × 10−32 253.65 8.01 × 10−7 1.941 1.55 × 10−6
Z + 0.0080 2284.1 256.98 5.91 × 10−33 6.103 3.61 × 10−32 254.20 7.27 × 10−7 1.950 1.42 × 10−6
Z + 0.0100 2293.8 257.56 4.68 × 10−33 6.146 2.87 × 10−32 254.85 6.49 × 10−7 1.958 1.27 × 10−6
X − 0.0100 2243.8 263.73 3.87 × 10−34 5.924 2.29 × 10−33 282.50 5.17 × 10−9 1.917 9.92 × 10−9
X − 0.0080 2241.8 265.04 2.29 × 10−34 5.915 1.35 × 10−33 283.02 4.72 × 10−9 1.915 9.04 × 10−9
X − 0.0060 2238.2 264.49 2.85 × 10−34 5.900 1.68 × 10−33 283.29 4.50 × 10−9 1.912 8.61 × 10−9
X − 0.0040 2235.0 265.02 2.31 × 10−34 5.886 1.36 × 10−33 283.70 4.20 × 10−9 1.910 8.01 × 10−9
X − 0.0020 2231.4 264.69 2.63 × 10−34 5.870 1.54 × 10−33 283.07 4.68 × 10−9 1.907 8.93 × 10−9
X + 0.0020 2221.2 264.59 2.74 × 10−34 5.825 1.60 × 10−33 282.90 4.82 × 10−9 1.899 9.16 × 10−9
X + 0.0040 2215.8 264.12 3.31 × 10−34 5.802 1.92 × 10−33 281.84 5.80 × 10−9 1.894 1.10 × 10−8
X + 0.0060 2210.8 264.71 2.61 × 10−34 5.780 1.51 × 10−33 283.33 4.48 × 10−9 1.890 8.46 × 10−9
X + 0.0080 2204.4 263.79 3.78 × 10−34 5.753 2.17 × 10−33 283.10 4.66 × 10−9 1.885 8.78 × 10−9
X + 0.0100 2196.5 263.72 3.89 × 10−34 5.719 2.22 × 10−33 282.97 4.76 × 10−9 1.879 8.95 × 10−9
Y − 0.0100 2246.3 260.84 1.24 × 10−33 5.935 7.38 × 10−33 274.10 2.24 × 10−8 1.919 4.30 × 10−8
Y − 0.0080 2284.1 261.56 9.31 × 10−34 6.103 5.68 × 10−33 275.80 1.67 × 10−8 1.950 3.25 × 10−8
Y − 0.0060 2237.3 266.80 1.13 × 10−34 5.896 6.63 × 10−34 287.85 2.03 × 10−9 1.912 3.88 × 10−9
Y − 0.0040 2233.6 266.55 1.24 × 10−34 5.879 7.30 × 10−34 287.32 2.23 × 10−9 1.909 4.25 × 10−9
Y − 0.0020 2230.1 265.98 1.56 × 10−34 5.864 9.17 × 10−34 286.11 2.75 × 10−9 1.906 5.25 × 10−9
Y + 0.0020 2222.8 264.06 3.39 × 10−34 5.832 1.98 × 10−33 281.67 5.97 × 10−9 1.900 1.13 × 10−8
Y + 0.0040 2220.0 262.75 5.75 × 10−34 5.820 3.35 × 10−33 278.70 1.00 × 10−8 1.898 1.91 × 10−8
Y + 0.0060 2217.1 261.91 8.08 × 10−34 5.808 4.70 × 10−33 276.79 1.40 × 10−8 1.895 2.66 × 10−8
Y + 0.0080 2213.3 261.38 9.98 × 10−34 5.791 5.78 × 10−33 275.59 1.73 × 10−8 1.892 3.27 × 10−8
Y + 0.0100 2210.6 260.73 1.30 × 10−33 5.780 7.51 × 10−33 274.09 2.25 × 10−8 1.890 4.25 × 10−8

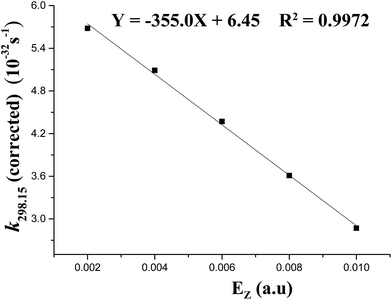
The Wigner corrections are in the range of about 5.2–6.2 at 298.15 K, suggesting the notable tunneling-corrected effects on rate constants. However, at 688 K, they are no more than 2.0, indicating the weakened tunneling-corrected effects (see Table 1). A good (R2 = 0.9972) linear correlation is obtained between the tunneling-corrected rate constants and the z-field strengths (see Fig. 5). They fit the following equation:

k298.15(corrected) = −335.0Ez + 6.45


image file: c7ra06290g-f5.tif
Fig. 5 Rate constant (k/s−1) at 298.15 K obtained from CTST after Wigner's tunneling correction versus field strengths in z-orientations for 1,3-intramolecular hydrogen transference at the MP2/6-311++G(2d,p) level.

3.2 Intermolecular hydrogen transference

In previous experimental and theoretical investigations, three bimolecular mechanisms with head-to-tail transition state geometry (C–N bond collinear) of two nitromethane molecules were discussed.29–31 The first reaction pathway resulted in the simultaneous production of nitrosomethane, formaldehyde and HONO with the unrealistically high activation energy (497.7 kJ mol−1).31 The second reaction pathway involved an association reaction joining two nitromethane molecules in a rearranged dimer formed by the intermolecular H-bonding interaction between the hydrogen and oxygen atoms, which led to a CH3–N(OH)–CH(OH)–NO2 product. However, this mechanism did not provide a direct pathway to the production of broadband absorbing species.32 The third models involved a bimolecular exchange of an oxygen atom to form nitrosomethane and nitromethanol.29 For this model, we have obtained a very high activation energy, in excess of 300.0 kJ mol−1 at the MP2/6-311++G(2d,p) level. Due to the very high activation energies of above three paths, Zeman et al. stated that the bimolecular reactions in the initiation of nitromethane were not probable.33 Therefore, above three bimolecular mechanisms were not considered in this work.

However, in this work, a new bimolecular side by side C1 symmetry CH3NO2 dimer transition state, TS3, formed by two intermolecular H-bonds between the hydrogen and oxygen atoms is found (see Fig. 1). IRC calculation confirms the transformation from a side-by-side nitromethane dimer to a side-by-side aci-nitromethane dimer. In the absence of external electric field, the barrier is far lower than those in the previous bimolecular mechanisms,31–33 indicating that this mechanism may be the most favored bimolecular reaction pathway. Furthermore, as mentioned above, the barrier of TS3 is lower slightly than the C–NO2 BDE, showing that this pathway might occur in the most competition with the C–NO2 bond rupture at the initial stage of CH3NO2 decomposition.

The previous calculations of CH3NO2 dimer using the MINDO/3-HB technique indicated that a cyclic dimer, in which four weak intermolecular H-bonds were formed, was energetically most favorable.34 However, at the MP2/6-311++G(2d,p) level, this structure is not obtained but a stable CH3NO2 dimer with only two intermolecular H-bonds is found with C1 point group symmetry by unequal H⋯O distances (see ESI data, Fig. S1†). IRC calculation confirms the transformation from it to a side-by-side geometry aci-nitromethane dimer via TS3. For this reactant, the intermolecular O4′⋯H5 (or O4⋯H5′) hydrogen-bond distance is significantly altered by the field in the z-direction (see ESI data, Fig. S1†). In particular, when the field strength is larger than −0.0060 a.u. in the −z-direction or +0.0040 a.u. in the +z-direction, the O4′⋯H5 or O4⋯H5′ distance is increased to 3.193 or 7.584 Å, i.e., the intermolecular O4′⋯H5 (or O4⋯H5′) hydrogen-bond is broken, and the side-by-side geometry is changed into the head-to-tail structure. In the +y-direction, an obvious trend that the dipoles antiparallel side-by-side geometry turns into the dipoles aligned side-by-side structure is found.

The effects of fields on the geometries of TS3 are far weaker than those on the structures of reactants (see ESI data, Table S4†). All the TS3 structures are the dipoles antiparallel side-by-side geometries in the absence and presence of external fields. Furthermore, the fields parallel to the z- and y-axes affect the structures of TS3 more than those parallel to the x-axis. As the field is increased in the z-direction, one of the O⋯H distances increases while the other one decreases. Similar changes of the C⋯H distances are also found. In other words, with the increased fields in the z-direction, the double-proton transfer reaction turns into the single-proton transfer reaction. Indeed, from Fig. 1, when the field strength is up to 0.0100 a.u. in the −z direction, one O⋯H distance is increased to 1.272 Å, and there exists only one imaginary frequency corresponding to this proton transfer. However, the other O⋯H distance is decreased to 1.010 Å, very close to the covalent bond length of O–H bond, and no imaginary frequency mode corresponding to this hydrogen vibration is found. As the field is increased in the +y direction, the C⋯H distances increases significantly and the O⋯H distances remarkably decreases. Fields in the −y direction correspondingly show the opposite trends. From Table S4 (see ESI data†), except for the C1⋯H5, C1′⋯H5′, O4′⋯H5 and O4⋯H5′ distances involving with the proton transfer, the other bond lengths are slightly altered by the fields. Fig. 3 shows several linear correlations between the changes of the bond lengths or the corresponding electron densities and field strengths with the linear correlation coefficients R2 equal to the range of 0.9815–0.9995 or 0.9810–0.9999 along the x- and y-oriented fields.

The energies of the reactants decrease while those of TS3 increase with increasing field strengths in the ±x-, +y- and ±z-directions (see ESI data, Table S2†). Thus, the barriers increase. Furthermore, all the barriers are higher than the C–NO2 BDEs, indicating that the fields in the ±x-, +y- and ±z-directions cause preference of the C–NO2 bond dissociation over the intermolecular hydrogen transference.

However, in the −y-direction, the barriers of the intermolecular hydrogen transference reactions are lower than the C–NO2 BDEs (see Fig. 2), suggesting that the applied field in the −y-direction causes preference of the intermolecular hydrogen transference reaction over the C–NO2 bond dissociation. Although the energies of reactant and TS3 decrease with increasing field strength in the −y-direction, the energies of TS3 decrease more significantly than those of reactant (see ESI data, Table S2†), and hence the barrier heights are decreased. At the maximal field strength, the barrier height is lowered to 14.38% of its field-free value.

Fields oriented parallel to the x- or y-axis have a minor effect on the imaginary frequency. However, fields along the z-axis have a significant effect on the imaginary vibration. The imaginary vibrations decrease: from its field-free value 1955.4 to 1396.7 cm−1 at maximal field strength (see Table 2). The magnitude of the imaginary frequency decreases by 28.6% under the influence of the maximal field intensity in the z-direction when compared to the zero-field case. Thus, a field-induced flattening of the potential energy surface is suggested. From Table 2, at 298.15 K, the Wigner corrections in the x- and z-directions is notable (about 4.3–5.3).

Table 2 Transition states imaginary frequencies (Imν), Gibbs energies (ΔG, kJ mol−1), reaction rate constants (k, s−1) and corrected reaction rate constants (k298.15 K,C and k688 K,C, s−1), and Wigner tunneling corrections (κ) in the absence and presence of fields of varying strengths and directions for the intermolecular hydrogen transference path at the MP2/6-311++G(2d,p) level
Field (a.u.) Imν ΔG298.15 K k298.15 K κ298.15 K k298.15 K,C ΔG688 K k688 K κ688 K k688 K,C
a IRC involving the transformation from a side-by-side geometry nitromethanol dimer to a side-by-side geometry aci-nitromethane dimer is not found.
No field 1955.4 266.93 1.06 × 10−34 4.740 5.04 × 10−34 329.82 1.32 × 10−12 1.696 2.25 × 10−12
Z − 0.0100 1396.7 280.96 3.71 × 10−37 2.908 1.08 × 10−36 344.29 1.06 × 10−13 1.355 1.43 × 10−13
Z − 0.0080 1469.2 280.28 4.88 × 10−37 3.111 1.52 × 10−36 346.29 7.45 × 10−14 1.393 1.04 × 10−13
Z − 0.0060 1547.2 273.10 8.84 × 10−36 3.341 2.95 × 10−35 325.25 2.94 × 10−12 1.436 4.22 × 10−12
Z − 0.0040 1618.9 263.18 4.84 × 10−34 3.563 1.72 × 10−33 341.40 1.75 × 10−13 1.477 2.58 × 10−13
Z − 0.0020 1807.1 265.44 1.95 × 10−34 4.194 8.17 × 10−34 330.98 1.08 × 10−12 1.595 1.72 × 10−12
Z + 0.0020 1825.0 269.22 4.24 × 10−35 4.258 1.80 × 10−34 330.95 1.09 × 10−12 1.607 1.74 × 10−12
Z + 0.0040 1658.3 274.87 4.33 × 10−36 3.690 1.60 × 10−35 344.71 9.81 × 10−14 1.501 1.47 × 10−13
Z + 0.0060 273.3 291.26 5.82 × 10−39 1.073 6.24 × 10−39 362.20 4.61 × 10−15 1.014 4.68 × 10−15
Z + 0.0080 1468.4 280.31 4.83 × 10−37 3.109 1.50 × 10−36 346.22 7.53 × 10−14 1.393 1.05 × 10−13
Z + 0.0100 1396.7 —a — 2.908 — — — 1.355 —
X − 0.0100 2019.5 —a — 4.989 — — — 1.743 —
X − 0.0080 2008.7 —a — 4.946 — — — 1.735 —
X − 0.0060 1994.4 259.27 2.34 × 10−33 4.890 1.14 × 10−32 307.95 6.05 × 10−11 1.724 1.04 × 10−10
X − 0.0040 1981.7 269.29 4.11 × 10−35 4.841 1.99 × 10−34 336.92 3.83 × 10−13 1.715 6.57 × 10−13
X − 0.0020 1968.9 268.96 4.69 × 10−35 4.792 2.25 × 10−34 335.43 4.96 × 10−13 1.706 8.47 × 10−13
X + 0.0020 1944.2 270.44 2.58 × 10−35 4.697 1.21 × 10−34 338.31 3.00 × 10−13 1.688 5.07 × 10−13
X + 0.0040 1933.5 271.43 1.74 × 10−35 4.657 8.08 × 10−35 347.96 5.55 × 10−14 1.681 9.34 × 10−14
X + 0.0060 1924.6 269.82 3.32 × 10−35 4.623 1.53 × 10−34 343.46 1.22 × 10−13 1.675 2.04 × 10−13
X + 0.0080 1919.3 269.64 3.57 × 10−35 4.603 1.64 × 10−34 342.13 1.54 × 10−13 1.671 2.57 × 10−13
X + 0.0100 1914.8 258.25 3.53 × 10−33 4.586 1.62 × 10−32 306.27 8.12 × 10−11 1.668 1.35 × 10−10
Y − 0.0100 2087.4 220.66 1.36 × 10−26 5.262 7.16 × 10−26 343.69 1.17 × 10−13 1.794 2.10 × 10−13
Y − 0.0080 2058.5 231.38 1.80 × 10−28 5.144 9.26 × 10−28 339.78 2.32 × 10−13 1.772 4.12 × 10−13
Y − 0.0060 2034.3 241.25 3.36 × 10−30 5.048 1.70 × 10−29 336.15 4.38 × 10−13 1.754 7.67 × 10−13
Y − 0.0040 2008.5 250.35 8.54 × 10−32 4.945 4.22 × 10−31 332.97 7.63 × 10−13 1.735 1.32 × 10−12
Y − 0.0020 1981.9 258.51 3.18 × 10−33 4.842 1.54 × 10−32 329.87 1.31 × 10−12 1.715 2.25 × 10−12
Y + 0.0020 1919.7 273.10 8.86 × 10−36 4.604 4.08 × 10−35 326.76 2.26 × 10−12 1.671 3.78 × 10−12
Y + 0.0040 1906.2 278.97 8.29 × 10−37 4.554 3.78 × 10−36 —a — 1.662 —
Y + 0.0060 1884.6 281.96 2.48 × 10−37 4.474 1.11 × 10−36 333.15 7.40 × 10−13 1.647 1.22 × 10−12
Y + 0.0080 1858.6 284.89 7.62 × 10−38 4.379 3.34 × 10−37 329.98 1.29 × 10−12 1.629 2.10 × 10−12
Y + 0.0100 1850.7 286.41 4.12 × 10−38 4.350 1.79 × 10−37 327.21 2.09 × 10−12 1.624 3.39 × 10−12

To sum up, in conjunction with our previous study on “CH3NO2 → CH3ONO” via TS1,11 the barriers of three reaction paths are all higher than the C–NO2 BDEs in the x-oriented fields. Thus, the x-oriented fields do not induce the change of the reaction pathways relative to those in the absence of field,19 and the C–NO2 bond scission is always kinetically favored. Therefore, in the x-oriented fields, the explosive sensitivity of CH3NO2 can be evaluated by the strength of the C–NO2 bond. The C–NO2 BDEs remain nearly unchanged in the external electric fields (275.38–280.90 kJ mol−1 in x-direction), indicating that the explosive sensitivity remains nearly unchanged in the x-oriented external electric fields. Furthermore, the sensitivities are almost equal to those in the absence of field since the C–NO2 BDEs in the x-oriented fields are very close to that in the absence of external field.

However, when the field is in the −y-direction of dimer, due to the lower barriers than the C–NO2 BDEs, intermolecular hydrogen transference reaction occur preferentially over the C–NO2 bond scission. In the −y-direction, the explosive sensitivity can be evaluated by the strength of the C–H bond and the C–H bond becomes the trigger linkage. Our recent investigation shows that when the field strength is larger than +0.0060 a.u. in the +z-direction, the CH3NO2 → CH3ONO reaction occur preferentially.11 Thus, when the field strength is larger than +0.0060 a.u. in the +z-direction of CH3NO2 or the field is in the −y-direction of dimer, the detonation initiation occurs more easily and thus the explosive sensitivities are increased in comparison with those in the absence of external electric field. In the other fields along the y- and z-orientations, the C–NO2 BDEs are all lower than the barriers of above three reaction paths, and the C–NO2 bond scission is kinetically favored (see Fig. 2). Thus, the sensitivities are almost equal to those in the absence of external electric field since the C–NO2 BDEs in the external electric fields of y- and z-directions (274.97–275.90 kJ mol−1) are almost equal to those in no field.

Since, in theory, the change of the directions and strengths of external electric fields can alter the reaction pathways and thus change the explosive stability and sensitivity, can the stability and sensitivity of explosive be adjusted with external electric field in practice? At present, thus proposition does not make any sense for four reasons at least: (1) one can not specify (let alone control) the orientation of a macroscopic sample of explosive that are randomly oriented in gas, solid or liquid solution form with respect to an externally-applied field. (2) One can not find out the electromagnetic (EM) field applied to the system in this paper. These are several orders of magnitude below any fields that can have any effect on barriers or energies of reactions – to have an effect an applied field must have at least a strength of 107 or 108 volts per m way stronger than an macroscopic field that can be achieved on a macroscopic sample whether intentionally or from stray EM fields. Therefore, the experiments that the external electric fields are imposed to energetic materials can be not designed. (3) The system studied in this paper is a single CH3CO2 molecule or a H-bonded complex formed by two CH3CO2 molecules in gas phase. In reality, the CH3CO2 molecule may also exist in an oily liquid state or a solid state under different conditions. Furthermore, for each of three states, there would be an increased probability of alignment along the electric field in competition with kinetic translational and rotational motion in the presence of an electric field. Moreover, this would have a temperature dependence: in general, the higher the temperature, the larger this probability would be. However, as mentioned above, the electric field in different directions has different effects on the stability and sensitivity of the explosive molecules. In other words, only the molecule is exposed to a particular direction of the field relative to its own orientation, would there be an increased chance of ignition. At a particular temperature, these results follow the probabilistic distribution of statistical mechanical sense. Here, a molecular dynamics calculation was performed with Materials Studio 7.0 program.35 The molecular number of CH3NO2 was set to 12, and the placement of 12 molecules consist of two patterns: random and all the molecules regularly pointing to the same direction. In the x-axis direction, the external electric field strength of 0.006 a.u. was considered. For the second pattern, the C⋯NO2 orientation was on the x-axis (see Fig. 6). The temperature was set as 298, 350, 500, 900, 1800 K, respectively. Then, these models were considered as NVT ensembles to make MD simulations by CASTEP module. The finally equilibrium structures for two patterns were obtained at all the temperatures. Furthermore, the single point energy of the random pattern was higher than that of the pattern that all the molecules pointed to the same direction at each of the temperatures, indicating that the latter was more stable than the former. These results indirectly confirm that the molecules have an increased tendency to align along the field and the increased chance of ignition follows the probabilistic distribution of statistical mechanical sense in the external electric field at a particular temperature. (4) The decomposition process of nitromethane itself is very complex. For example, a recent ReaxFF molecular dynamics simulation has indicated that the fragments from the decomposition of nitromethane, like H2O, NO, NO2, HONO, play a role of catalysis. Furthermore, the decomposition of nitromethane can lead to many different structures of carbon clusters, and the configuration of cluster is dependent on external conditions.36


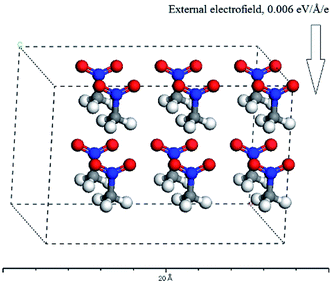image file: c7ra06290g-f6.tif
Fig. 6 The equilibrium structure in the external electric field for the pattern that all the molecules regularly point to the same direction.

To date there are still many obstacles to add external electric field into energetic material system in experiment. However, the external electric field effect itself of changing the reaction pathways and stability (sensitivity) of explosive is remarkable enough to arouse the intense interest of researchers and keep them full of confidence to achieve experimental goals in energetic material field, since the orientation of molecules could be determined by Langmuir–Blodgett techniques,37,38 and the investigations on electron transports of molecular-scale systems have been launched in experiment.39 Furthermore, the observation of large reversible switching behavior in the electronic device that uses molecules as the active component has been reported.40–42

4. Conclusions

The effects of external electric field on the detonation initiation reaction dynamics of CH3NO2 were investigated by the MP2 and CCSD methods. The results show that a new bimolecular intermolecular hydrogen transference mechanism, from a side-by-side nitromethane dimer formed by two intermolecular H-bonding interactions to a side-by-side aci-nitromethane dimer, is the most favored bimolecular reaction pathway. Furthermore, this pathway occurs in the most competition with the C–NO2 bond rupture at the initial stage of CH3NO2 decomposition in the absence of external electric field. Some linear correlations between the changes of bond lengths or electron densities and field strengths in different field orientations are obtained.

In particular, when the field is in the −y-direction of CH3NO2 dimer (the orientation perpendicular to the O⋯N⋯N plane), the barriers of intermolecular hydrogen transference are lower than the C–NO2 BDEs. Therefore, when the field in the −y-direction causes preference of the intermolecular hydrogen transference reaction. In the −y-direction, the C–H bond may be trigger linkage. Furthermore, in this case, the explosive sensitivities are increased in comparison with those in the absence of field. However, in the other fields, the barriers of hydrogen transference reaction paths are all higher than the C–NO2 BDEs. Thus, the fields do not induce the change of the reaction pathways relative to those in the absence of external electric field and the C–NO2 bond scission is kinetically favored in initiating detonation. In these cases, the explosive sensitivities can be evaluated by the strength of the C–NO2 bond and they are almost equal to those in the absence of external electric field. The change of the directions and strengths of external electric fields can change the reaction pathways and stabilities (sensitivities) of explosives. This theoretical investigation must be useful to safely add external electric field into energetic material systems to increase the energy, detonation velocity and detonation pressure in future.

Conflicts of interest

The authors declare no conflicts of interest for this work.

References

  1. D. Tasker, The properties of condensed explosives for electromagnetic energy coupling, NSWC T.R., 1985, pp. 85–360 Search PubMed.
  2. D. Demske, The experimental aspects of coupling electrical energy into a dense detonation wave: Part 1, NSWC T.R., 1982, pp. 79–143 Search PubMed.
  3. T. Piehler, C. Hummer, R. Benjamin, E. Summers, K. McNesby and V. Boyle, Preliminary study of coupling electrical energy to detonation reaction zone of primasheet-1000 explosive, 27th International Symposium on Ballistics, Freiburg, Germany, 2013, pp. 22–26 Search PubMed.
  4. P. Politzer, J. S. Murray, M. C. Concha and P. Lane, Cent. Eur. J. Energ. Mater., 2007, 4, 3–21 CAS.
  5. P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2009, 109, 534–539 CrossRef CAS.
  6. J. S. Li, J. Hazard. Mater., 2010, 180, 768–772 CrossRef CAS PubMed.
  7. C. Z. Cao and S. Gao, J. Phys. Chem. B, 2007, 111, 12399–12402 CrossRef CAS PubMed.
  8. J. Zhao, X. L. Cheng, B. He and X. D. Yang, Struct. Chem., 2006, 17, 501–507 CrossRef CAS.
  9. B. S. Tan, X. P. Long, R. F. Peng, H. B. Li, B. Jin, S. J. Chu and H. S. Dong, J. Hazard. Mater., 2010, 183, 908–912 CrossRef CAS PubMed.
  10. A. A. Arabi and C. F. Matta, Phys. Chem. Chem. Phys., 2011, 13, 13738–13748 RSC.
  11. F.-d. Ren, D.-l. Cao and W.-j. Shi, J. Mol. Model., 2016, 22, 96 CrossRef PubMed.
  12. J. B. Pedley, R. D. Naylor and S. P. Kirby, Thermochemical data of organic compounds, Chapman, New York, 2nd edn, 1986 Search PubMed.
  13. D. Margetis, E. Kaxiras, M. Elstner, T. Frauenheim and M. R. Manaa, J. Chem. Phys., 2002, 117, 788–799 CrossRef CAS.
  14. M. Citroni, R. Bini, M. Pagliai, G. Cardini and V. Schettino, J. Phys. Chem. B, 2010, 114, 9420–9428 CrossRef CAS PubMed.
  15. S. P. Han, A. C. T. van Duin, W. A. Goddard and A. Strachan, J. Phys. Chem. B, 2011, 115, 6534–6540 CrossRef CAS PubMed.
  16. F. Guo, X. Cheng and H. Zhang, J. Phys. Chem. A, 2012, 116, 3514–3520 CrossRef CAS PubMed.
  17. T. L. Cottrell, T. E. Graham and T. J. Reid, Trans. Faraday Soc., 1951, 47, 1089–1092 RSC.
  18. J. Chang, P. Lian, D. Q. Wei, X. R. Chen, Q. M. Zhang and Z. Z. Gong, Phys. Rev. Lett., 2010, 105, 188302–188305 CrossRef PubMed.
  19. W. F. Hu, T. J. He, D. M. Chen and F. C. Liu, J. Phys. Chem. A, 2002, 106, 7294–7303 CrossRef CAS.
  20. F.-d. Ren, D.-l. Cao, W.-j. Shi, M. You and M. Li, J. Mol. Model., 2015, 21, 145–153 CrossRef PubMed.
  21. M. J. Frisch, et al., Gaussian 03, Revision B.03, Gaussian, Inc., Pittsburgh PA, 2003 Search PubMed.
  22. R. F. W. Bader, Atoms in molecules, a quantum theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
  23. F. W. B. König, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317–328 CrossRef.
  24. C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, John Wiley & Sons, Ltd., New York, 2002 Search PubMed.
  25. J. I. Steinfeld, J. S. Fransisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, New Jersey, 2nd edn, 1999 Search PubMed.
  26. E. P. Wigner, Z. Phys. Chem., Abt. B, 1932, 19, 203–216 Search PubMed.
  27. H. Eyring and E. M. Eyring, Modern Chemical Kinetics, Reinhold Publishing Corporation, New York, 1963 Search PubMed.
  28. S. Glasstone, K. J. Laidler and H. Eyring, The Theory of Rate Processes, McGraw-Hill Book Company, Inc., New York, 1st edn, 1941 Search PubMed.
  29. R. D. Bardo, Ninth symposium (international) on detonation, Office of Naval Research, Arlington, 1989, p. 235 Search PubMed.
  30. R. D. Bardo, Eighth symposium (international) on detonation, Naval Surface Weapons Center, White Oak, 1985, p. 855 Search PubMed.
  31. M. D. Cook, J. Fellows and P. J. Haskins, Decomposition, Combustion, and Detonation Chemistry of Energetic Materials, Materials Research Society, Symposium Proceedings, Materials Research Society, Pittsburgh, 1996, vol. 48, pp. 267–275 Search PubMed.
  32. J. M. Winey and Y. M. Gupta, J. Phys. Chem. B, 1997, 101, 9333–9340 CrossRef CAS.
  33. S. Zeman, T. Atalar, Z. Friedl and X.-H. Ju, Cent. Eur. J. Energ. Mater., 2009, 6, 119–133 CAS.
  34. E. B. Burgina, V. P. Baltakhinov, E. V. Boldyreva, E. S. Stoyanov, N. Y. Zhanpeisov and G. M. Zhidomirov, J. Mol. Struct., 1993, 296, 53–59 CrossRef CAS.
  35. Accelrys Software Inc., Materials Studio 7.0., San Diego, 2013 Search PubMed.
  36. L. Zhang and L. Chen, Acta Phys. Sin., 2013, 62, 138201–138210 Search PubMed.
  37. K. Arnold, D. Hoekstra and S. Ohki, Biochim. Biophys. Acta, 1992, 1124, 88–94 CrossRef CAS.
  38. H. Brockman, Curr. Opin. Struct. Biol., 1999, 9, 438–443 CrossRef CAS PubMed.
  39. L. Benitez, D. Cristancho, J. M. Seminario, J. M. Martinez de la Hoz and P. B. Balbuena, Electrochim. Acta, 2014, 140, 250–257 CrossRef CAS.
  40. J. Chen, M. A. Reed, A. M. Rawlett and J. M. Tour, Science, 1999, 286, 1550–1552 CrossRef CAS PubMed.
  41. M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
  42. J. Chen, W. Wang, M. A. Reed, A. M. Rawlett, D. W. Price and J. M. Tour, Appl. Phys. Lett., 2000, 77, 1224–1226 CrossRef CAS.

Footnote

† Electronic supplementary information (ESI) available: The optimized geometrical parameters and AIM results of reactants, TS-2, TS-3, and the C–NO2 BDEs and barriers of three paths in different field strengths and orientations at the different levels of theory. See DOI: 10.1039/c7ra06290g
This journal is © The Royal Society of Chemistry 2017
Click here to see how this site uses Cookies. View our privacy policy here.