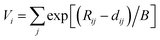DOI:
10.1039/C7RA06382B
(Paper)
RSC Adv., 2017,
7, 40152-40157
Characterization of blue-excited yellow phosphor (Y,Ca)6+x/3Si11(N,O)21:Ce by the bond valence sum model
Received
7th June 2017
, Accepted 4th August 2017
First published on 16th August 2017
Abstract
The new bright yellow phosphor (Y,Ca)6+x/3Si11(N,O)21:Ce (CYSON) providing broad emission excited by blue LED is the product of extensive substitution (about 70% of Y) of Y3+ → Ca2+ and N3− → O2− in the Y6Si11ON20:Ce parent host, which exhibits a weak emission excited by near UV-excitation only. Such a considerable difference is caused by particular distribution of substituting ions through the crystal lattice sites. For the first time for the title host, these intricate effects have been thoroughly studied in the present paper. We analyzed distribution of cations and their anion surrounding for each of the three Y sites. In addition, the local charge balance was also considered in detail by calculating the Brown's bond valence sum (BVS). The results suggest that the number of oxygen ligands is likely to be 0 at the Y1 and Y2 sites, 2–3 at the Ca1 and Ca2 sites, 0–1 at the Y3 site, and 3–4 at the Ca3 site (the subscript enumerates the inequivalent sites in the CYSON lattice). These data indicate that the Ca ions are likely to be coordinated by a greater number of the oxygen ions than the Y ions, which leads to the conclusion that the Y–N bond should be extensively substituted by the Ca–O bond. Therefore, agglomeration of an increased number of the oxygen ions far away from the Ca2+ ions is suppressed. It is suggested that as the bond lengths of the cation–anion pairs in CYSON are much larger than the sum, 2.28 Å, of the ionic radii of the Y3+ and O2− ions (which yields a smaller BVS and a small local charge balance), the substituted Ca2+–O2− pair contributes to the stabilization of electric charge distribution. This is the first detailed study of the structural properties of this new phosphor that allowed to identify most probable coordination around each and every cation site in this complicated structure with many inequivalent crystallographic positions.
1 Introduction
For about a couple of decades, white phosphor-converted light-emitting diodes (LEDs) have been important devices because they provide an efficient conversion of electric energy to visible light. In addition, they are environmentally friendly, since no toxic Hg is used in their production compared to conventional incandescent and fluorescent lamps.1 One of the main goals on the phosphor markets is the improved luminous efficacy of novel phosphors for various applications. The phosphors excited by the light of 450 nm-peak of efficient blue LED require a much longer wavelength of excitation than the conventional 254 nm wavelength of the excitation light. The nitridosilicates activated by Eu2+ or Ce3+ (ref. 2–10) ions are likely to have a strong crystal field splitting (CFS) and a low position of the Eu2+ or Ce3+ 5d states centroid due to coordination by the N3− ions forming highly covalent chemical bonds. This leads to the enhanced nephelauxetic effect, which in turn decreases the energy difference between the ground 4f and the lowest 5d states of the lanthanide ions. In this case, the longest wavelength of excitation, equivalent to the energy difference between the 4f state and the lowest 5d state, increases.
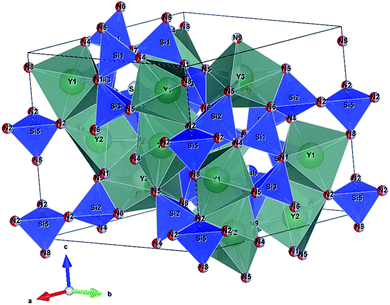
Seto et al. found the new blue-excited yellow phosphor, (Y,Ca)6+x/3Si11(N,O)21:Ce,11 (here and thereafter called CYSON) which has two prominent distinguished features. Firstly, extensive substitution (about 70% of Y) of Y3+ → Ca2+ and N3− → O2− in Y6Si11ON20:Ce results in (i) much better crystallinity and (ii) brighter emission under a usual condition of synthesizing nitridosilicate phosphor. The prepared Y6Si11ON20:Ce itself is not a blue-excited phosphor but a near UV-excited phosphor, with much lower crystallinity and weaker emission. The crystal structure of CYSON is shown in Fig. 1. There are three Y3+ sites that can be partially substituted by the Ca2+ or Ce3+ ions and nine sites for the O2−, N3− anions, as shown in Fig. 2.
 |
| | Fig. 1 Crystal structure of (Y,Ca)6+x/3Si11(N,O)21:Ce. Y1, Y2, and Y3 indicates three sites of Y or Ca substituted for Y. N1–N9 indicates nine sites of nitrogen or oxygen. | |
 |
| | Fig. 2 Coordination of Y1 site (a), Y2 site (b), and Y3 site (c), respectively. Occupancy of Y, Ca, or Ce at each Yn site is expressed by blue, green, or yellow colours, respectively. | |
In the present paper we set our goal to investigate whether such extensive and simultaneous substitution provides stable structure from the point of view of the electric charge balance at each cation site. For this purpose, we calculated the Brown's bond valence sum (BVS)12 for each and every cation site, with and without taking into account effect of the crystal lattice relaxation upon the substitution. The analysis of the obtained results revealed certain peculiar features of coordination of various cations and allowed to understand how such extended cation substitution is realized in the CYSON crystal lattice.
2 Procedure of calculation
The Brown's equation has a wider area of application than the original Pauling's equation on the bond valence sum so far. According to Brown, the bond valence of cation i coordinating anion j can be calculated from the following eqn (1).12–14| |
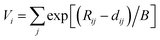 | (1) |
where Rij is the bond valence parameter of a cation i coordinating by an anion j, dij is the bond length between the cation i and anion j, and B is a constant value (the most reliable value for this parameter is 0.37 Å). The bond valence sum can be obtained for each atomic distance, cation species, and species of anion ligands.
We used the values of all dij, Rij, and B from the reference to the CYSON structure,11 and Brown's list of the bond balance parameter.13,14 The Rij value depends on the cation and anion species coordinating a particular cation.
CYSON's space group is P31c (no. 159) and its typical composition is Y6+(x/3)-yCaySi11N20+x−yO1−x+y:Ce (x = 1.2, y = 4.5, Ce molar ratio = 0.06). Each cation's occupancy in CYSON is shown in Table 1,11 whereas the atomic distances (all in Å) in CYSON are shown in Table 2.11 It is seen that the Y3+, Ca2+, or Ce3+ ions can occupy all three cationic sites. Taken together with anion substitution, this makes an analysis of the structural properties of this phosphor to be a non-trivial problem.
Table 1 Occupancies of Y, Ca, and Ce at each site determined by Rietveld refinement11
| |
Ln1 site |
Ln2 site |
Ln3 site |
| Y |
0.2171 |
0.3318 |
0.1978 |
| Ca |
0.7764 |
0.6645 |
0.3036 |
| Ce |
0.0066 |
0.0038 |
0.0243 |
Table 2 Atomic distances determined by Rietveld refinement11
| Ln1 site: |
Ln1–(O/N)1 |
2.553(3) |
Si1 site: Si1–(O/N)1 |
1.693(5) |
| Ln1–(O/N)2 |
2.356(4) |
Si1–(O/N)4 |
1.695(3) |
| Ln1–(O/N)3 |
2.420(3) |
Si1–(O/N)6 |
1.798(5) |
| Ln1–(O/N)4 |
2.453(4) |
Si1–(O/N)7 |
1.781(2) |
| Ln1–(O/N)5 |
2.519(1) |
Si2 site: Si2–(O/N)2 |
1.665(3) |
| Ln1–(O/N)8 |
2.500(3) |
Si2–(O/N)4 |
1.757(5) |
| Ln2 site: |
Ln2–(O/N)1 |
2.577(3) |
Si2–(O/N)5 |
1.678(5) |
| Ln2–(O/N)2 |
2.535(3) |
Si2–(O/N)6 |
1.816(4) |
| Ln2–(O/N)3 |
2.477(4) |
Si3 site: Si3–(O/N)1 |
1.754(5) |
| Ln2–(O/N)4 |
2.471(2) |
Si3–(O/N)3 |
1.722(3) |
| Ln2–(O/N)5 |
2.520(4) |
Si3–(O/N)5 |
1.823(3) |
| Ln2–(O/N)9 |
2.288(2) |
Si3–(O/N)6 |
1.690(5) |
| Ln3 site: |
Ln3–(O/N)5 |
2.592(1) |
Si4a site: Si4a–(O/N)3 × 3 |
1.684(6) |
| Ln3–(O/N)5 |
2.592(1) |
Si4b–(O/N)9 |
1.916(2) |
| Ln3–(O/N)5 |
2.592(1) |
Si4b site: Si4b–(O/N)3 × 3 |
1.665(3) |
| Ln3–(O/N)6 |
2.531(4) |
Si4b–(O/N)7 |
2.218(11) |
| Ln3–(O/N)6 |
2.531(4) |
Si5 site: Si5–(O/N)2 × 3 |
1.797(3) |
| Ln3–(O/N)6 |
2.531(4) |
Si5–(O/N)8 |
1.648(8) |
| Ln3–(O/N)9 |
2.252(7) |
|
|
The bond valence parameters Rij used in the present calculation are 2.17 (Rij for the Y–N pair), 2.14 (Ca–N), 2.019 (Y–O), and 1.967 (Ca–O).13,14 Strictly speaking, due to the partial occupancies of the crystal lattice sites in CYSON it is not known how many N3− or O2− anions coordinate each of the Y3+, Ca2+, or Ce3+ ions, respectively. To eliminate any ambiguity in this important issue and understand better the reasons for the improved crystallinity and enhanced luminescence of the substituted phosphor, we considered all possible cases of the N3− or O2− configurations coordinating every Y3+ or Ca2+ cation at each Lnq site. As Ln1, Ln2, and Ln3 sites receive 6, 6, and 7 anion ligands, respectively (Fig. 2), there are 26, 26, and 27 possible configurations of nitrogen and/or oxygen ligands coordinating the Ln1, Ln2, and Ln3 sites, respectively.
As an example, Table 3 shows just a few anion arrangements out of all 64 cases of the nitrogen or oxygen coordination around the Y3+ or Ca2+ cations at the Ln1 site. Table 4 shows the typical results of the BVS calculations for the case no. 9 from Table 3 (one of all 64 cases), including the difference between the BVS and cation's valence, which is called the value of charge imbalance here. All other cases can be calculated in a similar way and are not shown here for the sake of brevity. We present all the calculated results in the next section in the form of diagrams.
Table 3 Parts of all 64 cases that nitrogen or oxygen coordinates each Y or Ca of Ln1 site
| Cation–(anion)site no. |
Species of anion ligand (the above: case number) |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
… |
61 |
62 |
63 |
64 |
| Y–(O/N)1 |
N |
O |
N |
N |
N |
N |
N |
O |
O |
… |
O |
O |
N |
O |
| Y–(O/N)2 |
N |
N |
O |
N |
N |
N |
N |
O |
N |
… |
O |
N |
O |
O |
| Y–(O/N)3 |
N |
N |
N |
O |
N |
N |
N |
N |
O |
… |
N |
O |
O |
O |
| Y–(O/N)4 |
N |
N |
N |
N |
O |
N |
N |
N |
N |
… |
O |
O |
O |
O |
| Y–(O/N)5 |
N |
N |
N |
N |
N |
O |
N |
N |
N |
… |
O |
O |
O |
O |
| Y–(O/N)8 |
N |
N |
N |
N |
N |
N |
O |
N |
N |
… |
O |
O |
O |
O |
| Ca–(O/N)1 |
N |
O |
N |
N |
N |
N |
N |
O |
O |
… |
O |
O |
N |
O |
| Ca–(O/N)2 |
N |
N |
O |
N |
N |
N |
N |
O |
N |
… |
O |
N |
O |
O |
| Ca–(O/N)3 |
N |
N |
N |
O |
N |
N |
N |
N |
O |
… |
N |
O |
O |
O |
| Ca–(O/N)4 |
N |
N |
N |
N |
O |
N |
N |
N |
N |
… |
O |
O |
O |
O |
| Ca–(O/N)5 |
N |
N |
N |
N |
N |
O |
N |
N |
N |
… |
O |
O |
O |
O |
| Ca–(O/N)8 |
N |
N |
N |
N |
N |
N |
O |
N |
N |
… |
O |
O |
O |
O |
| Number of oxygen in 6 ligands |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
… |
5 |
5 |
5 |
6 |
Table 4 Example of the BVS and the difference between BVS and cation's valence (charge imbalance) calculated in case no. 9 (one of all 64 cases of N/O coordination)
| |
R |
dij (Å) |
BV |
|
R |
dij (Å) |
BV |
| Y1–O1 |
2.019 |
2.553 |
0.236 |
Ca1–O1 |
1.967 |
2.553 |
0.223 |
| Y1–N2 |
2.17 |
2.356 |
0.604 |
Ca1–N2 |
2.14 |
2.356 |
0.514 |
| Y1–O3 |
2.019 |
2.42 |
0.338 |
Ca1–O3 |
1.967 |
2.42 |
0.319 |
| Y1–N4 |
2.17 |
2.453 |
0.465 |
Ca1–N4 |
2.14 |
2.453 |
0.396 |
| Y1–N5 |
2.17 |
2.519 |
0.389 |
Ca1–N5 |
2.14 |
2.519 |
0.331 |
| Y1–N8 |
2.17 |
2.5 |
0.410 |
Ca1–N8 |
2.14 |
2.5 |
0.349 |
| BVS |
|
|
2.442 |
|
|
|
2.131 |
| Charge imbalance |
|
|
0.558 (=3 − 2.442) |
|
|
|
0.131 (=2.131 − 2) |
3 Results and discussion
Fig. 3(a)–(c) show all the values of the calculated charge imbalance at the Ln1, Ln2, and Ln3 sites, respectively. The smallest value of charge imbalance is obtained in the case of all nitrogen ligands, if the Y3+ ions occupy the Ln1, Ln2, and Ln3 sites, whereas when the Ca2+ ions occupy the same sites, the smallest value is obtained in the case of 3 oxygen and 3 nitrogen ligands for the Ln1 and Ln2 sites, and in the case of 4 oxygen and 3 nitrogen ligands for the Ln3 site. To understand the conditions that minimize the charge imbalance all the sets of the O2− and N3− ligands providing the smallest three values of charge imbalance are shown in Table 5. The minimal values of charge imbalance are relatively high, 0.2688, 0.3016, and 0.1120 for the Y1, Y2, and Y3 sites, while the same values are much smaller, 0.0037, 0.0049, and 0.0014 for the Ca1, Ca2, and Ca3 sites.
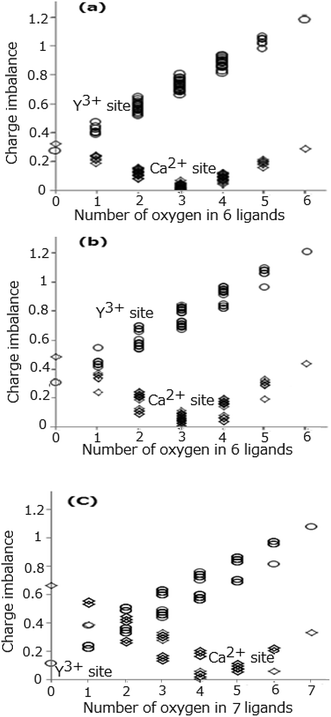 |
| | Fig. 3 Difference (charge imbalance) between BVS and cation's valence at Ln1 site (a), Ln2 site (b), and Ln3 site (c), respectively. | |
Table 5 The sets of O2− and N3− ligands providing the smallest values of charge imbalance
| Sets of Y3+/Ca2+–O2−/N3− |
Values of charge imbalance |
| Y1–[N1, N2, N3, N4, N5, N8] |
0.2688 |
| Y1–[O1, N2, N3, N4, N5, N8] |
0.3877 |
| Y1–[N1, N2, N3, N4, O5, N8] |
0.3992 |
| Ca1–[O1, O2, N3, O4, N5, N8] |
0.0037 |
| Ca1–[N1, O2, N3, O4, O5, N8] |
0.0040 |
| Ca1–[O1, O2, O3, N4, N5, N8] |
0.0060 |
| Y2–[N1, N2, N3, N4, N5, N9] |
0.3016 |
| Y2–[O1, N2, N3, N4, N5, N9] |
0.4131 |
| Y2–[N1, O2, N3, N4, N5, N9] |
0.4265 |
| Ca2–[O1, O2, N3, N4, N5, O9] |
0.0049 |
| Ca2–[O1, N2, N3, N4, O5, O9] |
0.0101 |
| Ca2–[N1, O2, N3, N4, O5, O9] |
0.0239 |
| Y3–[N5, N5, N5, N6, N6, N6, N9] |
0.1120 |
| Y3–[N5, N5, O5, N6, N6, N6, N9] |
0.2191 |
| Y3–[N5, O5, N5, N6, N6, N6, N9] |
0.2191 |
| Ca3–[N5, N5, N5, O6, O6, O6, O9] |
0.0014 |
| Ca3–[N5, N5, O5, N6, O6, O6, O9] |
0.0182 |
| Ca3–[N5, O5, N5, N6, O6, O6, O9] |
0.0182 |
We may take another consideration that the atomic distance determined by the Rietveld analysis in Table 2 (ref. 11) may be an average of the corresponding distances for the Y3+-anion, Ca2+-anion, and Ce3+-anion. Then the actual distances for these three cation–anion sets may be slightly deviating from the average distance. For simply clarifying the behaviour of the substitution, Y3+ → Ca2+ and N3− → O2−, the Ce3+-anion pair is neglected due to a tiny contribution of the Ce ions (because of low concentration) to the average distance. To account for a difference between the interionic distances, we use the following approach. For the quantitative estimation of the 5d-level energies of the Ce3+-activated phosphors Dorenbos15 assumed that the phosphor's anions relax radially inward or outward by half the difference ΔR between the ionic radius of the cation A and the ionic radius of the cation B for which the cation A substitutes. As the next step, we take the Dorenbos assumption, where the difference in distance between the Y3+-anion and Ca2+-anion pairs in the CYSON crystal should be 0.5ΔR = 0.5 × 0.10 Å because the corresponding Shannon radii are 0.90 Å (Y3+, coordination number (CN):6), 1.00 Å (Ca2+, CN:6), 0.96 Å (Y3+, CN:7), and 1.06 Å (Ca2+, CN:7). We take the distance in the Y3+-anion pair as (−0.025 Å + the distance of Lnx-anion in Table 2) and the distance in the Ca2+-anion pair as (0.025 Å + the distance of Lnx-anion in Table 2), where the 0.05 Å value (half of the difference in distance between Y3+-anion and Ca2+-anion) can be obtained from a relation [0.025 Å − (−0.025 Å)]. The BVS and the value of charge imbalance are calculated from these values of reasonably re-estimated in such way cation–anion distances. Fig. 4(a)–(c) show all the values of charge imbalance at the Ln1, Ln2, and Ln3 sites originated from the modified bond distance, respectively. The sets of the O2− and N3− ligands providing the smallest three values of charge imbalance are shown in Table 6. The smallest value of charge imbalance significantly decreases from 0.2688 to 0.0779 (Y1 site), from 0.3016 to 0.1131 (Y2 site), and from 0.1120 to 0.0247 (Y3 site) when the two Y3+-anion and Ca2+-anion distances at the same site are modified taking into account differences of the ionic radii in the corresponding pairs. The coordination number of oxygen yielding the smallest value of charge imbalance is slightly changed from 3 to 2 (Ca1 and Ca2 sites), from 4 to 3 (Ca3 site), from 0 to 1 (Y3 site).
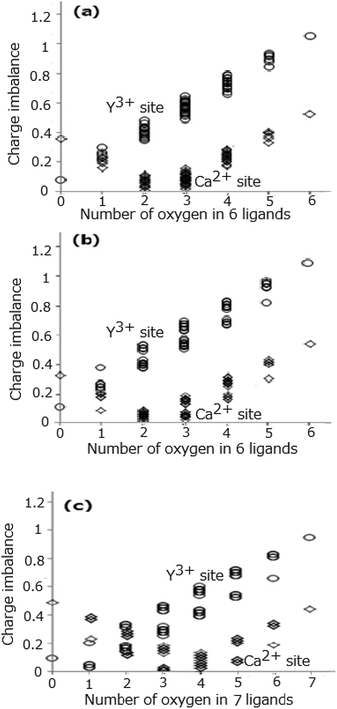 |
| | Fig. 4 Difference (charge imbalance) between the BVS and cation's valence at the Ln1 site (a), Ln2 site (b), and Ln3 site (c), respectively. | |
Table 6 The sets of O2− and N3− ligands providing the smallest three values of charge imbalance
| Sets of Y3+/Ca2+–O2−/N3− |
Values of charge imbalance |
| Y1–[N1, N2, N3, N4, N5, N8] |
0.0779 |
| Y1–[O1, N2, N3, N4, N5, N8] |
0.2051 |
| Y1–[N1, N2, N3, N4, O5, N8] |
0.2174 |
| Ca1–[N1, O2, O3, N4, N5, N8] |
0.0042 |
| Ca1–[N1, O2, N3, O4, N5, N8] |
0.0098 |
| Ca1–[O1, N2, N3, N4, O5, O8] |
0.0174 |
| Y2–[N1, N2, N3, N4, N5, N9] |
0.1131 |
| Y2–[O1, N2, N3, N4, N5, N9] |
0.2322 |
| Y2–[N1, O2, N3, N4, N5, N9] |
0.2466 |
| Ca2–[O1, N2, N3, N4, N5, O9] |
0.0153 |
| Ca2–[O1, O2, N3, N4, O5, N9] |
0.0262 |
| Ca2–[N1, O2, N3, N4, N5, O9] |
0.0281 |
| Y3–[N5, N5, O5, N6, N6, N6, N9] |
0.0247 |
| Y3–[N5, O5, N5, N6, N6, N6, N9] |
0.0247 |
| Y3–[O5, N5, N5, N6, N6, N6, N9] |
0.0247 |
| Ca3–[N5, N5, O5, N6, N6, O6, O9] |
0.0076 |
| Ca3–[N5, O5, O5, N6, N6, O6, O9] |
0.0076 |
| Ca3–[O5, N5, O5, N6, N6, O6, O9] |
0.0076 |
On total consideration including both cases of the same distance (Table 2) and the different distances, the number of the oxygen ligands seems to be 0–1 at the Y sites and 2–4 at the Ca sites, which suggests that the Ca ions are likely to be coordinated by more oxygen ions than the Y ions. The result coincides with the rough but essential Pauling's second rule16 where O2− should be substituted for the N3− site near the Ca2+ ions rather than near Y3+ ions because it can minimize the local volume where the sum of electric charge, −1, caused by the Y3+ → Ca2+ substitution, is localized. The ratio O/(O + N) is likely to be 0% at Y3+, 33–50% at Ca2+ at the Ln1 and Ln2 sites, 0–14% at Y3+, 43–57% at Ca2+ at the Ln3 site. Then, on the consideration of occupancies of (Y + tiny amount of Ce) and Ca in Table 1, the average ratio O/(O + N) is likely to be 26–39% at Ln1 site, 22–33% at Ln2 site, and 25–39% at Ln3 site, respectively. Total ratio of O/(O + N) in CYSON is (1–1.2 + 4.5)/21 = 21%, which is roughly at the same level with the above ratios in all three Ln sites.
Table 2 and Fig. 1 shows that there are six four-fold coordinated sites for the Si4+ ions (Si1, Si2, Si3, Si4a, Si4b, Si5). We also calculated the BVS and the values of charge imbalance for these Si sites, which are shown in Table 7. The minimum value of charge imbalance is obtained for the Si–(O, N, N, N) composition in almost every Si site in CYSON. It means that the ratio O/(O + N) at Si sites, ∼25%, providing the minimum instability value, is almost at the same level as total ratio O/(O + N) of CYSON, 21%, again. From the above consistent results, it is considered that one of the reason for successful extensive substitution of Y–N → Ca–O is an existence of the structure with the bond lengths much greater than the sum, 2.28 Å, of radii of Y3+ (CN:6) and O2− ions yielding a smaller BVS, which leads to an increased oxygen coordination and the stabilization of charge distribution near the Ca2+ ions.
Table 7 A set of anion ligands providing the minimum value of charge imbalance at each Si4+ site
| A set of Si4+ and O/N ligands |
Value of charge imbalance |
| Si1–[O7, N1, N4, N6] |
0.0331 |
| Si2–[O2, N1, N4, N5] |
0.0914 |
| Si3–[O5, N1, N3, N6] |
0.0036 |
| Si4a–[O3, N3, N3, N9] |
0.0418 |
| Si4b–[O3, N3, N3, N7] |
0.1536 |
| Si5–[O2, N2, N2, N8] |
0.1287 |
It is notable that the new type of calculation by use of Brown's BVS in this work shed light on the phenomenon, the substitution of O2− for the N3− site coordinating Ca2+ ions rather than Y3+ ions, because the phenomenon is consistent with the principle of ceramics that cations and anions are arranged so that local region forming electric charge as a sum might be minimized.
4 Conclusions
The unique extensive substitution (about 70% of Y) of Y3+ → Ca2+ and N3− → O2− in the blue-excited yellow phosphor (Y,Ca)6+x/3Si11(N,O)21:Ce was investigated by calculating the Brown's bond valence sums at each three Y/Ca/Ce cation sites, including all inequivalent positions. Due to the partial occupancy of the cation and anion sites in the “parent” CYSON structure, the coordination of anions at each cationic site was not known up to now. The obtained results for the first time allow to determine the number of anions of different kinds at each site. In particular, the number of the oxygen ligands is likely to be 0 at Y1 and Y2 sites and 2–3 at Ca1 and Ca2 sites, 0–1 at Y3 site, and 3–4 at Ca3 site. It indicates that the oxygen ions prefer to form coordination around the Ca ions rather than around the Y ions, which leads to a further conclusion that the Y–N bond should be extensively substituted by the Ca–O bond instead of agglomeration of the oxygen ions far apart from the Ca2+ ions. On the basis of the performed analysis, it became possible to find a chemically-based strong explanation for the successful extensive substitution of the Y–N pairs by the Ca–O pairs. It can be realized on account of formation of a stable structure having the bond lengths much greater than the simple sum (equal to 2.28 Å) of the ionic radii of the six-fold coordinated Y3+ and O2− ions. Such substitution yields smaller BVS values and is accompanied by increased oxygen coordination and the stabilization of charge distribution near the Ca2+ ions. The performed analysis can be efficiently applied to other crystals with partial cation/anion occupancy or solid solutions; it helps to understand the local coordination around various sites in crystal lattice. The method acquires a special importance for the doped phosphor materials, since in this case the nearest coordination of an impurity ion determines the crystal field strength, point symmetry and, as such, the overall pattern of the crystal field splitting of impurity ions energy levels, and, finally, spectroscopic properties of such doped material.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are thankful to Samsung R&D Research Institute for the published details of CYSON. M.G. Brik thanks the supports from the Recruitment Program of High-end Foreign Experts (Grant No. GDW20145200225), the Programme for the Foreign Experts offered by Chongqing University of Posts and Telecommunications, Ministry of Education and Research of Estonia, Project PUT430, and European Regional Development Fund (TK141).
Notes and references
- S. Nakamura and G. Fasol, The blue laser diode: GaN Based Light Emitters and Lasers, Springer, Berlin, 1997 Search PubMed.
- K. Uheda, N. Hirosaki, H. Yamamoto, H. Yamane, Y. Yamamoto, W. Inami and K. Tsuda, The 206th Annual Meeting of the Electrochemical Society (Abstract No. 2073), Honolulu, Oct 3 2004 Search PubMed.
- N. Kijima, T. Seto and N. Hirosaki, ECS Trans., 2009, 25, 247–252 CrossRef.
- H. A. Hoppe, H. Lutz, P. Morys, W. Schnick and A. Seilmeier, J. Phys. Chem. Solids, 2000, 61, 2001–2006 CrossRef CAS.
- C. Hecht, F. Stadler, P. J. Schmidt, J. S. Gunne, V. Baumann and W. Schnick, Chem. Mater., 2009, 21, 1595–1601 CrossRef CAS.
- Y. Q. Li, A. C. A. Delising, G. de With and H. T. Hintzen, Chem. Mater., 2005, 17, 3242–3248 CrossRef CAS.
- R.-J. Xie, M. Mitomo, K. Uheda, F.-F. Xu and Y. Akimune, J. Am. Ceram. Soc., 2002, 85, 1229–1234 CrossRef CAS.
- N. Hirosaki, R.-J. Xie, K. Kimoto, T. Sekiguchi, Y. Yamamoto, T. Suehiro and M. Mitomo, Appl. Phys. Lett., 2005, 86, 211905 CrossRef.
- Y. Liu, X. Zhang, Z. Hao, X. Wang and J. Zhang, J. Mater. Chem., 2011, 21, 6354–6358 RSC.
- Y. Liu, J. Zhang, C. Zhang, J. Xu, G. Liu, J. Jiang and H. Jiang, Adv. Opt. Mater., 2015, 3, 1096–1101 CrossRef CAS.
- T. Seto and T. Izawa, ECS J. Solid State Sci. Technol., 2015, 4, R83–R88 CrossRef CAS.
- I. D. Brown, Structure and Bonding in Crystals, Academic Press, New York, 1981, vol. 2, pp. 1–30 Search PubMed.
- I. D. Brown and D. Altermatt, Acta Crystallogr., 1985, 41, 244–247 CrossRef.
- N. E. Brese and M. O'Keeffe, Acta Crystallogr., 1991, 47, 192–197 Search PubMed.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15640–15649 CrossRef CAS.
- P. E. D. Morgan, J. Mater. Sci., 1986, 21, 4305–4309 CrossRef CAS.
Footnote |
| † T. Seto is currently at Advanced Technologies Research Institute, Denka Corporation, while he has done this work at the above address with M. G. Brik. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Mikhail G. Brikbcd
a and
Mikhail G. Brikbcd