Impeding phonon transport through superlattices of organic–inorganic halide perovskites

Abstract

Superlattice structures present a strategy to impede lattice thermal transport through organic–inorganic halide perovskites and improve their potential for thermoelectric applications. We investigate the phonon characteristics of such novel configurations and compare against predictions of the simple perovskite lattices using first principle calculations. Our results show the existence of structural instabilities due to distortions in the octahedral cage surrounding the methylammonium ion. In the superlattices, a strong phonon incoherence reduces the group velocities while interfacial resistance enhances scattering and limits the phonons impeding heat conduction. Although heat transfer is anisotropic in these perovskites, the interfaces in the superlattice obstruct phonon transport along all directions.

---

Introduction

Organic–inorganic halide perovskites have received significant attention over the past half a decade because of their excellent photovoltaic conversion efficiencies.^1–7 One of the building blocks of these hybrid chemistries is the central cation. Amongst the perovskites, methylammonium lead iodide (MAPbI₃), where MA representing the CH₃NH₃⁺ cation is a molecular ion, has demonstrated a very high potential for solar cells as well thermoelectric applications.^8–14 Reducing the thermal conductivity (κ), especially that due to lattice vibrations (phonons), with minimal or no deterioration to electrical properties is considered the key to improving the thermoelectric figure of merit. Introducing interfaces through superlattice structural forms for increased interfacial thermal resistance is a strategy to decrease κ.^15–18 The decrease in κ is achieved with the destruction of the lattice periodicity, as described previously in numerous studies on different types of superlattices such as those of Si/Ge^17,19–21 and Bi₂Te₃/Sb₂Te₃.^22–24 These efforts have shown considerable decrease in κ relative to the parent materials with simple lattices. In superlattices, thermal transport is predominantly governed by the scattering of long and short wavelength phonons, and hence the thermal conductivity can be controlled by both the period and the total thickness of the structures.^25,26 Therefore, thermal transport can be potentially modified by manipulating these two characteristic geometric properties of superlattice structures.

Here, we employ the same concept of introducing interfaces by creating superlattice structures of organic–inorganic halide perovskites. Materials with perovskite type lattices assume complex structural landscapes because the atoms arrange accordingly for the ABX₃ representation, where the cation A is at the center of BX₆ octahedra located at the corners of the cubic lattice. Hybrid organic–inorganic perovskites have a very high Seebeck coefficient and low thermal conductivity,^27–29 the latter being attributed to a number of factors. Some studies have suggested the cause to be the rotational motion of the organic cation,²⁹ due to the inorganic atoms³⁰ as well as by the coupling between the organic and inorganic parts of the molecule.²⁹ Here, we show that the thermal transport is further reduced in heterogeneous structures (superlattices) of hybrid organic–inorganic halide perovskites. We have already proved that electrical conductivity and Seebeck coefficient persists with values in superlattice structures similar to those determined for simple lattice configurations.³¹ Hence, the objective of this paper is to understand the phonon transport mechanisms in the superlattices and suggest opportunities to engineer these materials for energy applications. The limited literature only provides κ predictions of MAPbI₃ and suggests of the transitional states due to instabilities arising from certain soft modes.^{27–30,32–38} We investigate the phonon dynamics through dispersion curves, density of states (DOS) and group velocities, and predict the specific heats for a set of superlattice structures of MAPbI₃ and methylammonium tin iodide (MASnI₃) relative to the simple perovskite forms. The presence of interfaces decreases the phonon group velocities, creating localized regions of phonons that contribute to increased scattering and reduced κ.

Computational methods

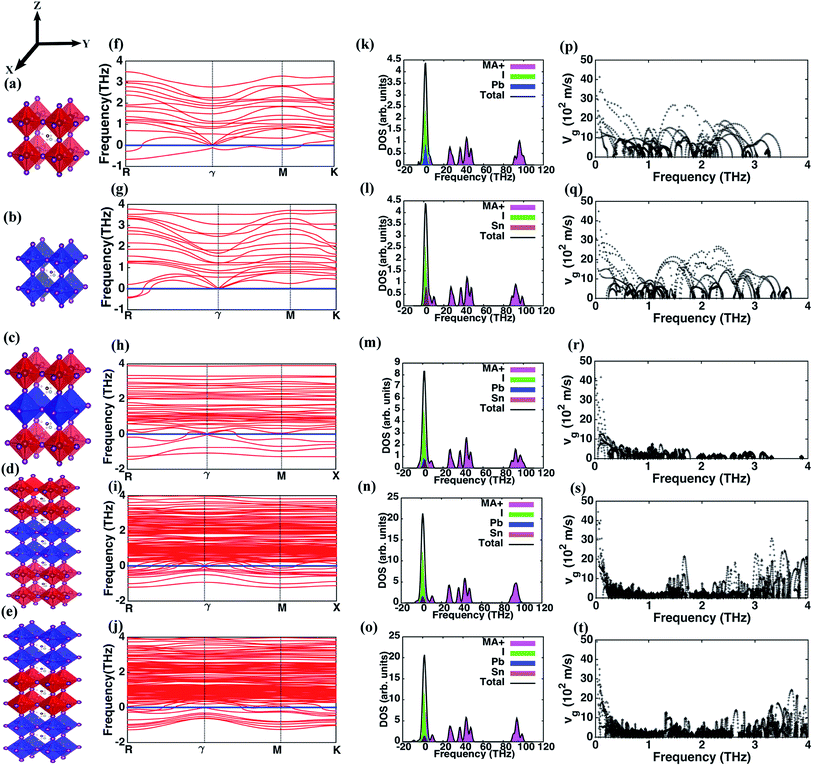
We employ density functional theory (DFT) calculations for optimizing the geometry of the perovskite and superlattice structures followed by computations of phonon properties. Self-consistent pseudo-potential plane wave approximation, as implemented in the Vienna Ab initio Simulation Package (VASP),^39,40 is used. The exchange correlation functional is approximated using Perdew–Burke–Ernzerhof (PBE) Generalized Gradient Approximation (GGA).⁴¹ The five structures (I through V) investigated here are illustrated in Fig. 1(a–e). We choose pseudo-cubic phases for these structures while the MA molecules are arranged in 〈1 1 1〉 direction. We choose an 800 eV cut-off for the energy minimization with a plane wave basis set and consider a 4 × 4 × 4, 4 × 4 × 4, 5 × 5 × 2, 5 × 5 × 3 and 5 × 5 × 3 Monkhorst–Pack k-point mesh for the different structures, respectively. An optimization criterion for the computed force on each atom of less than 0.01 eV Å⁻¹ is used in all the calculations. The details about the structure and the k mesh convergence tests are provided in Table 1. The experimental demonstration of the superlattices has been provided in our earlier work where scanning electron microscopy images and characterization of the energy dispersion validate the successful creation of these superlattice structures.³¹

Fig. 1 Molecular representation, phonon spectrum, density of states and group velocity of the different organic–inorganic perovskite structures. The molecular structures are (a) methylammonium lead iodide (MAPbI₃, structure I), (b) methylammonium tin iodide (MASnI₃, structure II), (c) structure III with a layer of MASnI₃ sandwiched between two layers of MAPbI₃, (d) structure IV with two layers of MASnI₃ sandwiched between four MAPbI₃ layers, and (e) structure V with two layers of MAPbI₃ sandwiched between four MASnI₃ layers. The phonon spectra for the different structures are correspondingly presented in figures (f)–(j). The dispersion curves predict negative frequencies representing a transitional state for structures I and II only at the boundary points while a stable configuration is located at the gamma point. However, for the superlattice structures III, IV and V, phonon modes with negative frequencies (soft modes) are observed throughout the (k) spectrum. Soft modes increase from structure I through V reflecting an increase in the instabilities of the lattice configurations. Figures (k)–(o) shows the partial and total density of states (DOS) of the perovskite structures. The contributions of the MA⁺ ion, Pb, and I have been illustrated in the DOS. Similar contributions from Pb and Sn atoms are noted for the superlattice structures implying that vibration at the corresponding lattice sites facilities phonons of similar frequencies. The velocity distribution over the frequency domain is presented in figures (p)–(t) for structures I, II, III, IV and V respectively. Phonons with non-zero group velocities are predominant in the low frequency sub-domain of the simple perovskite structures, while those in the superlattice are recorded in the medium and high frequency regions. At each frequency level, phonon number density is obtained as the ratio of the number of phonons at that frequency to the number of atoms in the primitive cell of the corresponding structure. The phonon number density for the frequency range from 0–1 THz with velocities greater than 500 m s⁻¹ are 23, 27, 8, 5 and 7 phonons per unit cell for structures I–V respectively, suggesting a lower thermal conductivity of the superlattice perovskites due to reduced number of modes available for heat conduction.

Table 1 Structural parameters are presented for the structure I, II, III, IV and V. The details include the equilibrium lattice constants, and the number of atoms per unit cell. The table also lists the convergence test performed in terms of energy variation with k-point meshes for the five structures. The data is presented for two values of k-meshes, one based on which results are analyzed and a second denser mesh

Structure	Lattice constants			No. of atoms/unit cell
	a (Å)	b (Å)	c (Å)
I	6.432	6.515	6.445	12
II	6.302	6.428	6.303	12
III	6.401	6.514	12.809	24
IV	6.372	6.492	31.811	60
V	6.378	6.507	31.780	60

---

Convergence tests for k-mesh
Structure	k-Point mesh (reported)	k-Point mesh (denser)	Energy (eV) (reported k)	Energy (eV) (denser k)	% difference
I	4 × 4 × 4	6 × 6 × 6	−50.85	−50.96	0.20
II	4 × 4 × 4	6 × 6 × 6	−50.90	−50.93	0.05
III	5 × 5 × 2	10 × 10 × 2	−101.42	−101.85	0.40
IV	5 × 5 × 3	10 × 10 × 4	−254.40	−254.60	0.07
V	5 × 5 × 3	10 × 10 × 4	−254.40	−254.60	0.07

---

Phonon dispersion is obtained from Phonopy⁴² within the harmonic approximation and with the force constants derived from DFT. The calculations are performed by the supercell approach within the framework of density functional perturbation theory⁴³ and frozen cell method.⁴⁴ The supercell chosen for our study is 2 × 2 × 2 for structures I, II, III and 1 × 1 × 1 for structures IV and V. In both cases, the second order derivative of total energy required to calculate the force constants is computed relative to atomic displacements. Using these force constants, phonon frequencies are obtained that subsequently provide us with the phonon dispersion and the DOS. Specific heat⁴² (C) is evaluated from 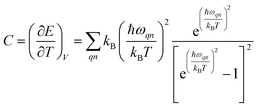, where k_B is the Boltzmann constant, n the band index, q the reciprocal lattice vector, ω the phonon frequency, T the temperature and E the total energy. Likewise, group velocity⁴² 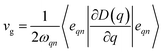, where D is the dynamical matrix, and e the eigenvector at the band index n and reciprocal point q.

Results and discussion

The phonon dispersion curves for the different perovskites, presented in Fig. 1(f–j), show that all the structures have negative frequencies (soft modes) indicative of their respective transitional states. Comparable results for MAPbI₃ have been reported elsewhere that show negative frequencies at the boundary k points and similar phonon dispersion curves.^33,35 Perovskite structures assume different crystalline phases at different temperatures and minimal distortion in the structure induces a transitional state causing instability. MAPbI₃ and MASnI₃ exist in three structural phases at different temperatures – below 162 K MAPbI₃ assumes the orthorhombic phase, transforms to the tetragonal phase at higher temperatures and transitions from tetragonal to cubic at 327 K.⁴⁵ Similarly, MASnI₃ undergoes three temperature dependent phase transitions – it is in a monoclinic form at low temperatures, changes to rhombohedral at 331 K and subsequently to cubic phase beyond 463 K.^46,47 These instabilities are more pronounced in superlattice structures with greater number of negative frequencies noted in structures IV and V. The per-atom negative frequencies for structures I, II, III, IV and V at k-point R are 1/6, 1/6, 1/6, 1/5, and 1/4 respectively. Likewise, at ϒ point the per-atom negative frequencies observed are 0, 0, 1/12, 1/6 and 1/5. As different perovskite structures are introduced in the primitive cell, these instabilities increase because the various layers independently show dissimilar lattice dynamics behavior under the same thermodynamic conditions. The relative stability of these structures is analyzed based on the binding energies E_b, derived using the free energies of structures I and II, as

E_b = E_str − (nE_I + mE_II)

where E_I is the free energy of MAPbI₃, E_II is the free energy of MASnI₃, n and m are the number of layers of MAPbI₃ and MASnI₃ respectively. E_b for structures III, IV and V are 0.287 eV, 0.118 eV and 0.067 eV respectively. The positive values are reflective of the instability in the structure because of the lattice mismatch, which also lead to the soft modes in these structures. Although the presence of these soft modes implies that these structures are in the transitional phase, the absolute values of these negative frequencies are small. The low frequencies imply that the difference in energies between the two stable structures while negligible, impede the structure from reaching a particular stable configuration. The effect of the soft modes on the overall superlattice is enhanced because a distortion in one layer creates instability in the entire perovskite structure. In structures I and II (Fig. 1(f and g)), the phonon modes with negative frequency are observed at the boundaries (R and M points) and zero frequency occurs at the ϒ point. This result suggests the two pure structures are susceptible to small perturbations and the soft modes at R(111) and M(100) are characteristic of the rotational tendency of MA⁺ ion and the distortion of the octahedra.³³ The dispersion behavior for structures III, IV and V suggest instabilities at both the ϒ point and the boundaries.

Next, we investigate the phonon DOS for the different structures and present in Fig. 1(k–o) the contributions of different atoms in the lattice. The DOS for all the structures reveal the presence of three distinct sub-domains of high, intermediate and low frequencies. The high and intermediate frequencies are due to the phonons arising from the MA⁺ ion with a minor contribution of the Pb atom in structures IV and V, while the predominant low frequency contributions are from Pb–I and Sn–I pairs. As shown in Fig. 1(m–o), for structures III, IV and V the effect of Sn and Pb atoms are identical. We predict that characteristic vibrational frequencies due to the metal atoms are similar and thus might permit energy transfer across the interfaces of dissimilar perovskites in the superlattice using two-phonon scattering processes. Hence, interfacial thermal resistance within the superlattice structure is weakly influenced by the characteristic phonon modes of the metal atoms in these hybrid perovskites. Fig. 1(k–o) also reveal the underlying causes driving the structural instability in these structures. Since the negative frequency phonons are predominantly due to MA⁺ ion and I, structural disorder arises in the MA⁺ ion and Pb/Sn–I sub-lattices. Atoms in these sub-lattices occupy more than one non-equivalent lattice site.⁴⁸ While MAPbI₃ and MASnI₃ exhibit disorder in their structures with MA⁺ ion occupying non-equivalent positions in adjacent cages,⁴⁸ the octahedral cage (here Pb/Sn–I sub-lattices) are known to show disorder even in other perovskites such as CaTiO₃, SrTiO₃ and BaTiO₃.⁴⁹ Additionally, the extra degree of freedom in the angular orientation of MA⁺ ion that occurs in organic–inorganic halide perovskites creates further hindrance to an optimal configuration for an overall stable structure with suitable positioning of the MA⁺ ion and Pb/Sn–I sub-lattices.

The lattice contribution to κ is directly proportional to the average group velocity of phonons. Fig. 1(p–t) present the variation of the group velocity with frequency for the five structures. The group velocities in this figure are reported for every q and n, where n is the band index, q is the reciprocal lattice vector. The phonons in the low frequency range of 0–4 THz that have non-zero group velocities predominantly contribute to heat conduction. The number density (ratio of the number of phonons at each frequency level to the number of atoms in the primitive cell of the structure) of such phonons with finite group velocities is highest in structures I and II relative to the superlattices. The phonon number density in the frequency range from 0–1 THz for group velocities greater than 500 m s⁻¹ is 23, 27, 8, 5 and 7 phonons per unit cell for I, II, III, IV and V respectively. These phonons with low scattering rates and relatively longer mean free paths conduct thermal energy across extended distances in the perovskite lattice. There is a strong decrease in the number of these phonons in the superlattice structures. The presence of different layers in the superlattice imposes dissimilar behavior of the phonons across the adjacent layers, effectively reducing the number density. Thus, the total energy transport by phonons is reduced including the fraction of lattice vibrations with long mean free path, and this impedes heat conduction. So, the reduction in phonon number density is still observed even after considering that different metal toms (Pb and Sn) show similar frequencies as per the density of states (Fig. 1(k–o)). Therefore, we corroborate that phonon contribution to κ in superlattices is significantly diminished relative to that in the simple perovskite lattices represented by structures I and II. Similar predictions derived in the frequencies between 1 and 2 THz are 26, 24, 8, 3 and 4 phonons per unit cell and between 2 and 3 THz are 24, 25, 0, 2 and 3 phonons per unit cell for the five structures, I through V, respectively.

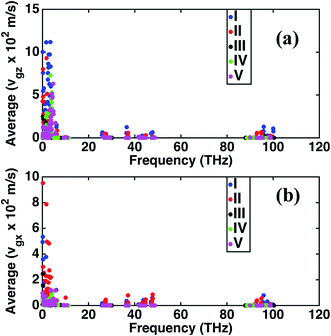
The frequency dependence of the mean in-plane (v_gx) and cross-plane (v_gz) group velocities are presented in Fig. 2. The average group velocities represent the mean over all the band indices calculated by dividing the sum of group velocities at each frequency with the number of bands. The superlattice structures have low group velocities over the entire frequency domain. Lattice κ is related to the group velocity as (κ = Cv_g²τ), where τ is the average relaxation time and v_g is the phonon group velocity averaged over all polarizations and directions. κ being directly proportional to the square of the group velocity, superlattice structures have poor heat conduction through them. Together with the interfacial thermal resistance, superlattices break the phonon coherence and reduce κ in a direction normal to the interacting surfaces between dissimilar perovskites. Fig. 2 shows that structure I has the highest v_gz, while v_gx is maximum for structure II. Structure III has the minimum v_gz suggesting a strong phonon incoherence relative to the other structures. Previous experiments⁵⁰ and theoretical modeling⁵¹ show that in superlattices heat conduction is diminished in both the in-plane and cross-plane directions. Our calculations reveal that group velocities along the in-plane direction are significantly lower than that perpendicular to the interfaces, especially in the low frequency range for the superlattice structures IV and V. The reduction in in-plane group velocities as observed in superlattices is due to the change in phonon spectrum with the introduction of interfaces. Fig. 1 shows the spectrum of structures 1 to 5 and the value of frequency at various k points. Especially the spectrum between ϒ → M → X is responsible for in-plane properties. The spectrum becomes flat in the superlattice structures at boundary k-points and results in the low group velocities. Among the structures considered in this study, structure IV is predicted to have the lowest group velocity and is hence predicted to have the lowest thermal conductance. On one hand, we predict that superlattices have reduced κ relative to structures I and II, on the other hand the distribution of the group velocities reveal a strong anisotropic feature of thermal transport for all the perovskites considered. Although interfaces are present normal to the longitudinal z-direction, group velocities and hence heat conduction along the transverse directions are also reduced in the superlattices relative to the simple perovskite structures.

Fig. 2 Variation of average phonon group velocities with frequency for the different structures. The figures show that for both (a) cross-plane (z-direction) and (b) in-plane (x-direction) group velocities, superlattices have lower predictions relative to structures I and II due to phonon incoherence and interfacial thermal resistance. Since these velocities are directly proportional to thermal conductivities, the dissimilar predictions along the two directions as shown in the figures are reflective of the anisotropic heat conduction in the longitudinal and transverse directions of all the perovskite structures.

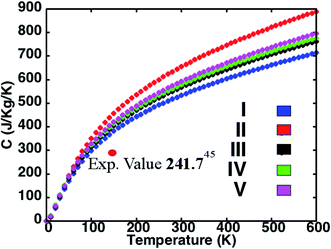
The variation of specific heat C with temperature for the five structures in presented in Fig. 3. While C of structure II is highest and that of structure I is lowest among the perovskites investigated, the predictions for the superlattices lie in between. In accord with the simple Debye model, we observe that at low temperatures C is proportional to T³. Also, as the density of a material is inversely proportional to the C and the density order of the investigated perovskite structures being I > IV > V > II, we find the order for the specific heat to be I < IV < V < II. Structures with an average lighter mass require relatively lesser amount of energy than those with heavier atoms for excitation at the lattice sites and facilitate heat conduction by phonons across the material. This amount of energy reflects in the C predictions for the different perovskites investigated here. While our predictions differ from some corresponding measurements in the literature,⁵² the results do compare well with recent experimental reports.⁵³ For instance, the computed C of 301.62 J kg⁻¹ K⁻¹ compares well with the measured result of 241.94 J kg⁻¹ K⁻¹ at 150 K.

Fig. 3 Variation of specific heat of the different perovskite structures with temperature. The figure illustrates that the specific heat, C, (i) varies as T³ at low temperatures and (ii) is inversely proportional to the density of the corresponding perovskite structure. These predictions are in agreement with the simple Debye model for specific heat. Specific heat of the different superlattices, especially at higher temperatures, are lower than the average of the specific heat of the simple perovskite lattices. The specific heat variations are shown up to 600 K, which is approximately the melting point for halide perovskites.

Conclusions

In summary, we investigate the lattice dynamics of superlattice structures of organic–inorganic halide perovskites and compare their phonon dispersion, density of states, group velocities and specific heat against the corresponding predictions for the simple lattice forms using first principle calculations. The phonon vibrational spectra of the superlattices reveals the presence of negative frequencies or soft modes indicating transitional states in the structural configurations. Through the partial density of states, we find that the I and MA⁺ ion predominantly contribute to these soft modes. Our results suggest that these perovskite lattices are sensitive to the distortions in the octahedral cage surrounding the MA⁺ ion and rotations of the MA⁺ ion, and the future need for methods beyond the harmonic approximation for an accurate treatment of phonons. We predict that a strong phonon incoherence causes significant reductions in the group velocities of the superlattice configurations, both parallel to and perpendicular to the interfaces, relative to the simple forms. Similar results noted for the number density of phonons implies that an enhanced scattering and interfacial resistance to energy transport by lattice vibrations impedes heat conduction and diminishes thermal conductivity. While the frequency dependence of mean group velocities ascertains the anisotropic heat transfer characteristics of these structures, the interfaces between dissimilar perovskites obstruct phonon transport in both the in-plane and cross-plane directions. The specific heat of the structures agrees with the Debye model at low temperatures as well as inverse dependence on the material density. Overall, our investigation highlights that superlattice perovskite structures reduce lattice thermal transport that could contribute towards employing organic–inorganic halide perovskites as potential thermoelectrics.

Acknowledgements

We thank Prof. Vikram Dalal of the Microelectronics Research Center for his encouragement and the Catron Center for Solar Energy Research for the graduate fellowship. The research was partly supported by the National Science Foundation (NSF) grant no. CMMI-1404938 and the High Performance Computing HPC@ISU equipment at Iowa State University, some of which has been purchased through NSF funding under MRI grant no. CNS 1229081 and CRI grant no. 1205413.

References

1. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
2. H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Sci. Rep., 2012, 2, 591.
3. M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398.
4. H. A. Abbas, R. Kottokkaran, B. Ganapathy, M. Samiee, L. Zhang, A. Kitahara, M. Noack and V. L. Dalal, APL Mater., 2015, 3, 016105.
5. L. Etgar, P. Gao, Z. Xue, Q. Peng, A. K. Chandiran, B. Liu, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2012, 134, 17396–17399.
6. J. H. Heo, S. H. Im, J. H. Noh, T. N. Mandal, C.-S. Lim, J. A. Chang, Y. H. Lee, H. Kim, A. Sarkar, K. NazeeruddinMd, M. Gratzel and S. Il Seok, Nat. Photonics, 2013, 7, 486–491.
7. J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–320.
8. Q. Chen, N. De Marco, Y. Yang, T. Bin Song, C. C. Chen, H. Zhao, Z. Hong, H. Zhou and Y. Yang, Nano Today, 2015, 10, 355–396.
9. J. Bisquert, J. Phys. Chem. Lett., 2013, 4, 2597–2598.
10. N. G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429.
11. NREL, Best Research-Cell Efficiencies, Retrieved from, https://www.nrel.gov/pv/assets/images/efficiency-chart.png.
12. Y. He and G. Galli, Chem. Mater., 2014, 26, 5394–5400.
13. C. Lee, J. Hong, A. Stroppa, M.-H. Whangbo and J. H. Shim, RSC Adv., 2015, 5, 78701–78707.
14. X. Mettan, R. Pisoni, P. Matus, A. Pisoni, J. Jacimovic, B. Náfrádi, M. Spina, D. Pavuna, L. Forró and E. Horváth, J. Phys. Chem. C, 2015, 3, 2488–2492.
15. J. Garg and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–5.
16. L. Hu, G. Shao, T. Jiang, D. Li, X. Lv, H. Wang, X. Liu, H. Song, J. Tang and H. Liu, ACS Appl. Mater. Interfaces, 2015, 7, 25113–25120.
17. S.-M. Lee, D. G. Cahill and R. Venkatasubramanian, Appl. Phys. Lett., 1997, 70, 2957.
18. G. Balasubramanian and I. K. Puri, Appl. Phys. Lett., 2011, 99, 013116.
19. I. Savic, D. Donadio, F. Gygi and G. Galli, Appl. Phys. Lett., 2013, 102, 073113.
20. T. A. R. Adetic and R. O. G. Ronsky, Superlattices Microstruct., 2000, 28, 199–206.
21. P. Ferrando-villalba, A. F. Lopeandía, F. X. Alvarez, B. Paul, C. De and J. Rodriguez-viejo, Nano Res., 2015, 8, 2833–2841.
22. M. Winkler, X. Liu, U. Schürmann, J. D. König, L. Kienle, W. Bensch and H. Böttner, Mater. Res. Soc. Symp. Proc., 2013, 1490, 205–222.
23. F. He, W. Wu and Y. Wang, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 1–5.
24. M. N. Touzelbaev and P. Zhou, J. Appl. Phys., 2001, 90, 763.
25. Y. Chen, D. Li, J. R. Lukes, Z. Ni and M. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 174302, 1–6.
26. J. Jiang, J. Wang and B. Wang, Appl. Phys. Lett., 2011, 43109, 97–100.
27. S. Y. Yue, X. Zhang, G. Qin, J. Yang and M. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 1–10.
28. X. Qian, X. Gu and R. Yang, Appl. Phys. Lett., 2016, 108, 063902.
29. T. Hata, G. Giorgi and K. Yamashita, Nano Lett., 2016, 16, 2749–2753.
30. C. Caddeo, C. Melis, M. I. Saba, A. Filippetti, L. Colombo and A. Mattoni, Phys. Chem. Chem. Phys., 2016, 18, 24318–24324.
31. R. Singh, R. Kottokkaran, V. L. Dalal and G. Balasubramanian, Nanoscale, 2017, 9, 8600–8607.
32. A. Pisoni, J. Jaćimović, O. S. Barišić, M. Spina, R. Gaál, L. Forró and E. Horváth, J. Phys. Chem. Lett., 2014, 5, 2488–2492.
33. F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goni, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–8.
34. Y.-Y. Zhang, S. Chen, P. Xu, H. Xiang, X.-G. Gong, A. Walsh and S. Wei, Nat. Commun., 2015, 11.
35. M. Wang and S. Lin, Adv. Funct. Mater., 2016, 26, 5297–5306.
36. A. Mattoni, A. Filippetti, M. I. Saba, C. Caddeo and P. Delugas, J. Phys. Chem. Lett., 2016, 7, 529–535.
37. D. Vanderbilt and W. Zhong, Ferroelectrics, 1998, 206, 181–204.
38. E. Cockayne and B. P. Burton, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 3743, 3735–3743.
39. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
40. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
43. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
44. R. P. Stoffel, C. Wessel, M. W. Lumey and R. Dronskowski, Angew. Chem., Int. Ed., 2010, 49, 5242–5266.
45. M. T. Weller, O. J. Weber, P. F. Henry, M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183.
46. I. Borriello, G. Cantele and D. Ninno, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–9.
47. A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373.
48. T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Gratzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628.
49. M. Johnsson and P. Lemmens, Crystallography and Chemistry of Perovskites, John Wiley & Sons, Ltd., New York, 2007, p. 11.
50. T. Yao, Appl. Phys. Lett., 1987, 51, 1798–1800.
51. G. Chen, J. Heat Transfer, 1997, 119, 220.
52. N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395.
53. D. H. Fabini, T. Hogan, H. A. Evans, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, J. Phys. Chem. Lett., 2016, 7, 376–381.

---