Gap maximum of graphene nanoflakes: a first-principles study combined with the Monte Carlo tree search method

Abstract

The energy gap of graphene nanoflakes is important for their potential application in nano-devices; however, it is still a challenge to perform a systemic search of systems with large gaps due to the presence of numerous candidates. Herein, we showed an ideal feasible approach that involved structural recognition, simplified effective evaluation, and successive optimization strategy. Considering the local bonding environment of carbon atoms, we first proposed a tight-binding model with the parameters fitted from the first-principles calculations of possible GNFs; this model provided an ideal avenue to screen the candidates with high accuracy and efficiency. Via combining the Monte Carlo tree search method and the congruence check, we determined the correlation between structures and the gap distributions according to the carbon numbers, and the results were confirmed via the first-principles calculations. The structural stabilities of the candidates with different numbers of hydrogen atoms might be modulated by the chemical potential of hydrogen, whereas the candidates with larger gaps might be more stable for the isomers with the same number of C and H atoms. Note that the gap variation is dominated by the structural features despite the quantum confinement effect since the gap maximum fluctuates rather than gradually decreasing with the increase in size. Our finding shows the gap variety of GNFs due to the configuration diversity, which may help explore the potential application of GNFs in nano-devices and fluorescence labeling in biomedicine.

---

1. Introduction

Graphene, a two-dimensional honeycomb crystal structure consisting of carbon atoms, is a zero band gap semiconductor.^1,2 With the confinement of the edge, the gaps of graphene nano-ribbons (GNRs) appear where the effects are different for armchair and zigzag edges.^3–7 The edge will also rearrange the sub-bands⁸ and introduce the anti-ferromagnetic edge states to break the symmetry^9–11 that effectively modulate the band gap of armchair and zigzag GNRs. Some numerical simulation methods such as classic Monte Carlo (MC) simulation, mean field theory, and series expansion have been widely used in carbon nanomaterials^12–15 and some alloys^16–19 to investigate their magnetic properties. For graphene nanoflakes (GNFs), it has been reported that the photoluminescence (PL) peak energy reduces with the increase in size from 5 to 17 nm due to the quantum confinement effect (QCE), whereas the PL peak energy anomalously increases for the larger GNFs due to the change in the edges.²⁰

Theoretically, the structural stabilities and electronic properties of GNFs have been intensively investigated. With hydrogen passivation, the carbon cluster tends to be a graphene-like structure with zigzag edges.²¹ The energy gaps E_g of GNFs with zigzag edges are smaller than those with armchair structures in general.²² On the basis of the Lieb's theorem, the energy gaps will disappear when the number of carbon atoms N_C is odd due to the imbalance of sublattices.^23–27 Herein, we focused on the GNFs with even N_C. To date, it is challenging to systematically investigate the GNFs due to two main obstacles: (i) for a given N_C, it is difficult to screen the possible structures in a fast way, and there are numerous candidates as the N_C increases and (ii) for a given structure, we have to determine the corresponding electronic properties, especially E_g, where the first-principles calculations are often computationally expensive.

To make the screening efficient, we can either reduce the time of evaluating the candidates or speed up the seeking procedure. Structure recognition and comparison^28,29 are necessary to avoid the repetitious calculations, and we have developed an effective indexing scheme for the lattice clusters that enables fast structure comparison and congruence check. In our recent study,³⁰ the Hückel molecular orbital (HMO) method was used for the fast estimation of the gaps of GNFs with N_C < 25; however, there is disagreement for some structures with large gaps. In addition, the successive optimization strategy³¹ should be adopted to search larger GNFs based on the properties of the smaller GNFs since the enumeration is impossible due to the numerous possible candidates. Thus, a systemic search of candidates should include structural recognition, simplified and effective evaluation, and successive optimization strategy.

Herein, we have proposed an effective tight-binding (TB) model for the electronic properties of the hydrogen-terminated GNFs focusing on the effect of carbon atoms' local bonding. The parameters were fitted with the enumerated structures of GNFs with N_C ≤ 34 based on the first-principles calculations. For larger GNFs, we combined the Monte Carlo tree search method with the congruence check to search the structures with large E_g under the TB model that were further confirmed by the first-principles calculations with higher accuracy. Finally, we obtained the maximum E_g as a function of size, and the typical structures with large gaps have been summarized for discussion.

2. Methods

2.1. Tight-binding model for the gaps of GNFs

The first-principles calculations were based on the density functional theory (DFT), as was implemented in the Vienna ab initio simulation package (VASP).^32,33 We employed the projector augmented wave (PAW) method and the Perdew–Burke–Ernzerhof (PBE) functional of generalized gradient approximation (GGA)^34,35 for the calculations of E_g. The plane wave cut-off energy was 520 eV, with the Brillouin zone sampled by a 1 × 1 × 1 Gamma-centered mesh. All the structures were fully relaxed by the conjugate gradient minimization, and the convergence of the energy on each atom was less than 10⁻³ eV.

Taking into account the p_z orbit of carbon atoms, the Hamiltonian can be written as follows:

where ε_i is the site energy and can be set to 0, t_ij is the hopping integral, subscript <i,j> represents the nearest neighbor carbon atoms, and c^†_i, c_j are the creation and the annihilation operators of the π electron at sites i and j, respectively. For GNRs and some few GNF structures, the hopping integral in the TB method^8,10,11,27 is fixed because the proportion of edge atoms is low and the structures are isotropic in a long range. Owing to the diversities of GNF structures, the edge atoms will have a stronger influence on electronic properties since the distributions of bond length are position-dependent (Fig. 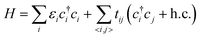S1†).

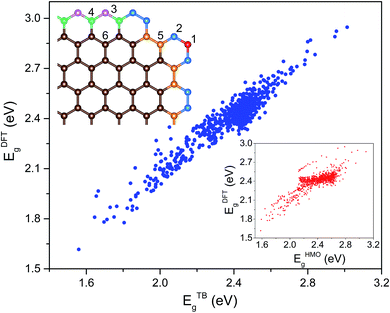
To characterize the environment effect, we divided the carbon atoms into six types according to the number of nearest neighbor carbon atoms, as shown in Fig. 1; this procedure resulted in thirteen types of hopping integral. We adopted the following procedure to fit these parameters. We performed DFT calculations on the 541 GNF structures with N_C ≤ 34, which contained all the parameters, where all these 13 values were initialized in the range of ±0.5 eV around a general hopping integral of −3 eV.²⁷ With the limitation in a range of ±2 eV, the parameters were optimized to make average deviations between TB and DFT results below the given precision.

Fig. 1 The scatter diagram about E_g which was predicted by the TB method with different parameters and the DFT method for a few hundred GNF structures. The inset on the lower right is the corresponding scatter diagram about the classic HMO method and the DFT method and that on the upper left shows a corner of a general GNF. The red, blue, violet, green, orange, and brown balls represent 1(2 | 2,2), 2(2 | 2,3), 3(2 | 3,3), 4(3 | 2,2,3), 5(3 | 2,3,3), and 6(3 | 3,3,3) types of carbon atoms, respectively. The number on the left of the line in a bracket represents the number of the nearest neighbor atoms and that on the right reflects the corresponding information of every nearest neighbor atom.

Considering that there exist all 541 proper GNF structures when N_C ≤ 34, the number is only 451 when N_C = 36. Note that the GNF structures are the fragments of the planar hexagonal lattice with hydrogen atoms on the edge to maintain the sp² hybridizations of graphene, where the center points of hexagons correspond to the fragments of the triangular lattice. As shown in Fig. S2 and S3,† an effective indexing scheme was adopted for the congruence check, where the structures with obvious deformation (Fig. S4†) were excluded. To balance the accuracy and efficiency, we enumerated 541 GNF structures with N_C ≤ 34 and obtained the Hamilton matrices containing all transfer energies, where the E_g calculated by the DFT method was used to fit these thirteen parameters. These parameters are

t′₁₁ = −2.54, t′₁₂ = −2.67, t′₂₂ = −3.02, t′₂₄ = −2.97, t′₂₅ = −2.69, t′₃₄ = −2.84, t′₃₅ = −2.40, t′₄₄ = −3.19, t′₄₅ = −2.24, t′₄₆ = −2.26, t′₅₅ = −2.66, t′₅₆ = −2.65, t′₆₆ = −3.11

that are expressed in eV and t′_ij = t′_ji due to Hermitian of the Hamiltonian. For comparison, the corresponding results of the classic HMO method are shown in the inset of Fig. 1, where the average and maximum deviations are 0.11 eV and 0.45 eV, respectively. According to our TB model, the average and maximum deviations are reduced to 0.04 eV and 0.30 eV, respectively, and the results of our TB model with thirteen types of hopping integral have a better linear relation with the DFT results than those of the classic HMO method. Thus, our TB method provides a proper prediction of the gaps of GNFs.

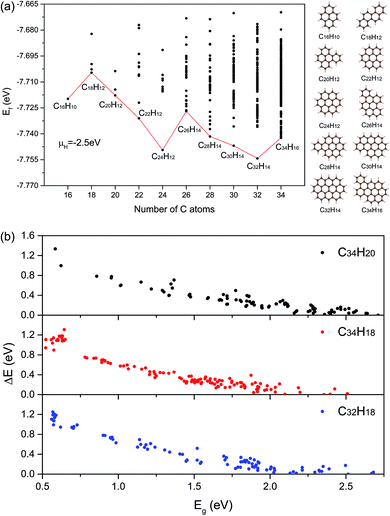
To describe the structural stabilities of GNFs, we defined the formation energy (E_f) as follows:³⁶

where E_tot is the total energy of a structure, m and n represent the number of C and H atoms, respectively, μ_C0/μ_H0 is the isolated energy of C/H atom, and μ_H is the chemical potential of the H atoms. The structure with lower E_f will be more stable, which may be modulated by the number of H atoms in the system (an example is shown in Fig. S5a†). According to the DFT calculation result of H₂ molecule, we found that the chemical potential in H₂ molecules (half of its cohesive energy) was −2.26 eV, which might be a common reference. However, Fig. S5a† shows that μ_H = −2.1 eV is a critical value, and the same E_f variation would be expected for different μ_H below −2.1 eV. Fig. 2a shows the E_f variation at μ_H = −2.5 eV as a function of N_C and the corresponding structures with the lowest E_f, where the most stable structures tend to be those with less H atoms. For the structures with given N_C, the most stable structures might not be those with the largest E_g (Fig. S5b†). However, for the structures with the same number of C and H atoms, the total energy differences of the isomers linearly depend on the gaps (Fig. 2b), indicating that the isomers with larger gaps will be more stable. For the structure with a large E_g, the corresponding HOMO level should be lower and consequently decrease the total energy. Hereinafter, we focused on the gap distributions of GNFs.

Fig. 2 (a) The curve about the lowest E_f of structures for N_C from 16 to 34. The corresponding structures and molecular formulas have also been shown. Black points represent all structures we have calculated. (b) The relations between stabilities and electronic properties of three kinds of molecular formula structures. The vertical axis represents the difference in total energy compared with the minimum energy of each formula structure.

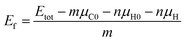2.2. Monte Carlo tree search method

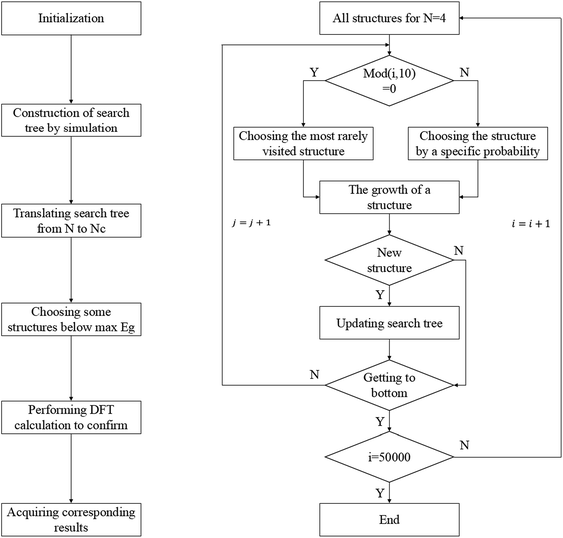
According to the enumeration with the congruence check, we obtained the gap distribution of the GNF structures with N_C ≤ 34, as shown in Fig. S6.† Note that the gap maximum of GNFs with the given N_C would not gradually decrease. In our TB model, the gap of GNFs can be easily estimated. However, the enumeration is impossible due to numerous candidates. Therefore, we introduced the Monte Carlo tree search with the previous TB method to screen possible structures with large E_g and confirmed the results using the DFT calculations with higher accuracy. Note that our Monte Carlo tree search method has a great difference from the classic MC simulation. Our method tends to find the GNF structures with large E_g rather than a simulation from initial states to equilibrium states. Therefore, the detailed balance is not pledged in our method.

Fig. 3 shows the flow chart for searching the max E_g of GNFs with the Monte Carlo tree search method. The main idea of our strategy to screen the triangular candidates is select → expand → select. For example, we selected a structure with N centers of hexagons from the candidates according to a specific probability and randomly added a center to expand the structure to that with N + 1 centers of hexagons. The congruence check was performed to confirm that this new candidate has not been visited previously. These operations are repeated until N = 20, such that a simulation step gets finished. The probability of choosing a structure is determined by its E_g, which has been found by our TB model, where the selection probability (P_c) of searching for larger E_g structures can be written as follows:

P_c = e^−βE_g (3)

where β is a positive constant. It should be noted that the constant β herein is different from that in the classic MC simulation. This parameter in classic MC simulation is inversely proportional to temperature since a wide range of temperature effects will be simulated. However, β in the Monte Carlo tree search method is not related to the realistic temperature, which is derived from the P_c value that herein only provides a strategy to acquire large E_g structures and does not pledge detailed balance to reach the equilibrium state. In the simulation, this constant could be adjusted to balance the depth and breadth of the search to improve the efficiency. Moreover, only the most rarely visited structure should be chosen when we arrive at every layer of the Monte Carlo tree; this procedure would prevent simulation from falling into local extremum. As the simulation is repeated, more and more candidates are visited, where the GNFs with larger E_g are found. For each given N_C, we rank the structures according to their E_g and the proper energy windows are chosen due to different distributions of E_g, where 18–66 candidates are selected for the further first-principles calculations.

Fig. 3 Flow chart of the tree search method. The flow chart on the left-hand side is the whole process of finding maximum E_g structures for the given N_C and that on the right-hand side is the second step of the whole process, where i represents the ith simulation step and j is the jth process of growth.

3. Results and discussion

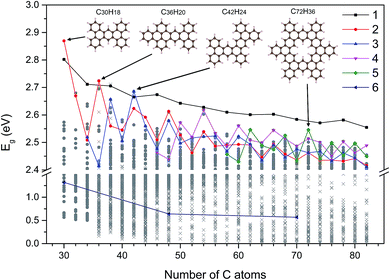
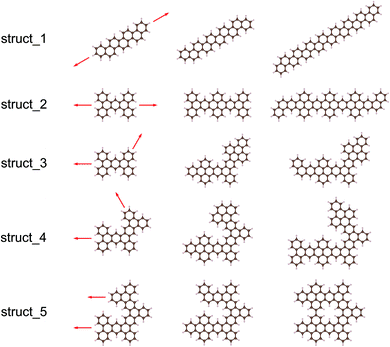
Using the Monte Carlo tree search method, we obtained the gap distribution of the possible largest E_g candidates and determined the structures with the largest E_g for various given N_C. As shown in Fig. 4, we have screened the gap distribution for the structures with N_C from 36 to 82 via our TB model; this data points indicate the breadth of the Monte Carlo tree search. The structures with large E_g are confirmed by the first-principles calculations, where those with the largest E_g are listed (Fig. S7†). There is a linear dependence between the results obtained from the first-principles calculations and those obtained from our TB model, where the structures with large gaps are screened, reflecting the reliability and efficiency of our method.

Fig. 4 The largest E_g value of these five types of GNF structures for different given N_C values. The representation of shapes and colors has been shown. Gray circles and crosses represent DFT results and TB results, respectively. Struct_6 is the diamond structure with zigzag edges, which indicates that the QCE would decrease with the increasing size in contrast to that of other structures. The ring structure pointing to the green diamond is the structure with the largest E_g value for N_C = 72 and we classified it to struct_5. Other three structures correspond to three local extremums, respectively.

Herein, we extracted five typical kinds of structures with the largest E_g, as shown in Fig. 5. Struct_1 has the shape of a straight line and all consist of armchair edge atoms, with similar electronic properties to the narrowest armchair GNRs.³ As shown in Fig. 4, the gaps of struct_1 in most cases are the largest, which would decrease slowly and close to 2.5 eV. Struct_2 is also a kind of candidates with a line shape, where the edge is of saw-tooth. For struct_3–5, the corners gradually appear to form a hexagon ring, where the red arrows indicate the expansion of the GNFs. The E_g curves of struct_2–5 show more fluctuations, which are commonly below that of struct_1. The gap variation of struct_6 is for the GNFs with the shape of rhombus with zigzag edges, where the gaps gradually decrease with the size. On comparing struct_6 with struct_1–5, it was found that the former had pure zigzag edges and the latter had high proportions of armchair edges. The type of edges for a GNF structure would have great effect on the E_g. We could expect that a narrow structure with a high proportion of armchair edges would be that with a large E_g, which is less influenced by the increase in size. These results are in agreement with the experimental²⁰ observation, where the PL peak energy is anomalously increased with the increasing size due to the change in edge types. Note that struct_2 and struct_3 have larger E_g than struct_1 at N_C = 30, N_C = 36, N_C = 42, where the three corresponding structures are of axial symmetry. Interestingly, the E_g of C₇₂H₃₆ is the local maximum of struct_5, with the symmetry of D_6h. Thus, the GNFs' gap is dominated by the structural details since the largest E_g might fluctuate rather than gradually decreasing with the increasing size.

Fig. 5 Five types of GNF structures that can characterize all structures with the largest E_g values for N_C > 34. The structures in this figure with red arrows represent the original structures and the corresponding direction of growth. The rest of the structures in this figure are some examples of these five types of GNF structures.

4. Conclusions

In summary, we have theoretically performed a systemic investigation of GNFs. The structures with N_C ≤ 34 were enumerated with the structural recognition for the first-principles calculations, which were used to fit the parameters in our TB model considering the local bonding of carbon atoms. The average deviation of gap estimation with our TB model is as small as 0.04 eV, which provides a proper prediction of the GNFs' gaps. For the structures with N_C > 34, the gap distribution was determined by the Monte Carlo tree search method, as confirmed by the first-principles calculations, where the typical structures with large gaps were found. Despite the QCE, the gap maximum fluctuates rather than gradually decreasing with the increasing size. The properties of GNFs should be further modulated via the control of structural details; this phenomenon might extend the potential application of GNFs. In addition, the Monte Carlo tree search combined with structural recognition provides an inversed property design approach for GNFs as well as other nanomaterials.

Acknowledgements

This work was supported by NSFC (Grant No. 11474100 and 11574088) and Guangdong Natural Science Funds for Distinguished Young Scholars (Grant No. 2014A030306024).

References

1. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
2. D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261.
3. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
4. S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041408.
5. L. Pisani, J. A. Chan, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064418.
6. L. Brey and H. A. Fertig, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235411.
7. O. Hod, J. E. Peralta and G. E. Scuseria, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 233401.
8. H. Zheng, Z. F. Wang, T. Luo, Q. W. Shi and J. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165414.
9. H. Lee, Y.-W. Son, N. Park, S. Han and J. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174431.
10. K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954.
11. M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920.
12. R. Masrour and A. Jabar, J. Magn. Magn. Mater., 2017, 426, 225.
13. R. Masrour and A. Jabar, Superlattices Microstruct., 2016, 98, 78.
14. R. Masrour, A. Jabar, A. Benyoussef and M. Hamedoun, J. Magn. Magn. Mater., 2015, 395, 7.
15. R. Masrour, L. Bahmad, M. Hamedoun, A. Benyoussef and E. K. Hlil, Solid State Commun., 2013, 162, 53.
16. R. Masrour, A. Jabar, E. K. Hlil, M. Hamedoun, A. Benyoussef, A. Hourmatallah, A. Rezzouk, K. Bouslykhane and N. Benzakour, J. Magn. Magn. Mater., 2017, 428, 12.
17. R. Masrour, E. K. Hlil, M. Hamedoun, A. Benyoussef, O. Mounkachi and H. El Moussaoui, J. Magn. Magn. Mater., 2014, 361, 197.
18. R. Masrour, E. K. Hlil, M. Hamedoun, A. Benyoussef, O. Mounkachi and H. El Moussaoui, Phys. A, 2014, 414, 249.
19. R. Masrour, L. Bahmad, M. Hamedoun, A. Benyoussef and E. K. Hlil, Phys. Lett. A, 2014, 378, 276.
20. S. Kim, et al., ACS Nano, 2012, 6, 8203.
21. D. P. Kosimov, A. A. Dzhurakhalov and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195414.
22. A. Kuc, T. Heine and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085430.
23. E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201.
24. J. Fernández-Rossier and J. J. Palacios, Phys. Rev. Lett., 2007, 99, 177204.
25. O. V. Yazyev, Phys. Rev. Lett., 2008, 101, 037203.
26. W. L. Wang, O. V. Yazyev, S. Meng and E. Kaxiras, Phys. Rev. Lett., 2009, 102, 157201.
27. M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245415.
28. L. Liao, Y. Zhao, Z. Cao and X. Yang, Sci. Rep., 2017, 7, 392.
29. X. Li, X. Yang and Y. Zhao, J. Chem. Phys., 2017, 146, 154108.
30. L. Qu, Z. Liu and X. Yang, Mol. Simul., 2017, 43, 558.
31. D. Silver, et al., Nature, 2016, 529, 484.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891.
36. X. Yang, Y. Zhao, H. Xu and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205314.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06891c

---