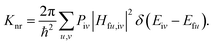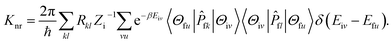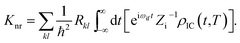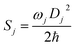Theoretical perspective of the excited state intramolecular proton transfer for a compound with aggregation induced emission in the solid phase

Abstract

In this study, we have investigated the excited state intramolecular proton transfer (ESIPT) for the diphenylethylene-modified 2-(2-hydroxyphenyl)benzothiazole derivative (HBT-d-Ph) with aggregation induced emission (AIE) in the solid phase through a combined quantum mechanics and molecular mechanics (QM/MM) approach and thermal vibration correlation formalism for non-radiative decay rate. In comparison with the molecule in the solid phase, we find that the ESIPT for HBT-d-Ph is prone to occur in toluene due to the intramolecular hydrogen bonding (H-bond). In addition, the rotation of benzene units involved in the low frequency vibration modes (<500 cm⁻¹) is effectively impeded due to the intermolecular interaction in the solid state, thus the energy consumption pathway through the rotation of benzene units could be blocked. Further, a dual fluorescence with blue and green emission in the solid phase could be obtained. Our study could provide some useful information for designing highly efficient emitting materials with ESIPT and AIE features.

---

1. Introduction

Recently, the excited state intramolecular proton transfer (ESIPT) compounds have been extensively investigated due to their wide application in serving as model systems in chemical processes and in organic light emitting diodes (OLEDs).^1–3 Since the phenomenon was first observed by Weller in 1955, a number of theoretical and experimental studies have been reported.^4–7 Moreover, the ESIPT is an ultrafast process which occurs in the femtosecond to picosecond time scale (10⁻¹⁵–10⁻¹² s). For ESIPT compounds, the proton transfers from a proton donor to an acceptor group via an intramolecular H-bond (or H-bonding) bridge. Under photoexcitation, the ESIPT process is an intrinsic peculiar four level photophysical cycle: absorption, proton transfer, emission and proton back-transfer. Thus, ESIPT compounds usually possess a large Stokes shift, which could diminish self-absorption, and they are expected to be potentially intrinsic luminescent materials.⁸ As reported in literature, numerous investigations of ESIPT in luminescent organic compounds were carried out in solution because their emission in the solid state is usually weak, and uneven.⁹ This is generally attributed to the so-called aggregation caused quenching (ACQ) effect. Impeding the self-quenching or non-radiative processes in aggregates is a challenging task. Pioneering investigations were carried out by Tang et al.; the group synthesized a series of aromatic compounds that exhibited unique enhanced emission rather than fluorescence quenching in aggregates.¹⁰ These aggregation induced emission (AIE) compounds are sensitive to the surrounding environment due to their unique molecular structures. Thus, it is important to reveal the environmental effect on the ESIPT process as well as the AIE mechanism in the solid phase, which is quite helpful for developing new efficient OLEDs with ESIPT and AIE features.

In this article, we adopt the newly synthesized diphenylethylene-modified 2-(2-hydroxyphenyl)benzothiazole derivative (HBT-d-Ph) as a model (shown in Fig. 1a) to explore the effect of the surrounding environment on ESIPT and AIE based on first-principles calculations.¹¹ The results also provide a few insights on the relationship between luminescence properties and the molecular configurations and contribute to the design of new organic light emitting materials.

Fig. 1 Chemical structure of HBT-d-Ph for the normal state (a) and the ESIPT state (b). ONIOM model: the centered molecule is treated as the high layer and the surrounding molecules are fixed as the low layer (c).

2. Theoretical method and computational details

In this paper, the optimization and the electronic structures of the molecule in the ground state are performed using density functional theory (DFT) method. The excited states are studied using the time-dependent density functional theory (TD-DFT) method. In all the above calculations, the PBE0 functional and 6-31G(d) basis set are applied. The first-principles calculation would provide some insights on the relationship between the structures and the proton transfer reaction. In order to clarify the effect of the surrounding environment on the molecular photophysical properties, the polarizable continuum model (PCM) was used to simulate the solvent effect and the combined quantum mechanics and molecular mechanics (QM/MM) approach was adopted to consider the packing surrounding in the crystal. In the QM/MM calculation, the initial crystal structure for HBT-d-Ph is obtained from the experimentally detected crystal structure. The QM/MM calculation was realized using the ONIOM method, which has been applied in our previous study.¹² The model consists of two “layers” (shown in Fig. 1c). The central molecule is treated as a high layer and is calculated by the quantum mechanical method. The surrounding molecules are treated as a low layer and are computed by the molecular mechanics method on applying the universal force field (UFF). Besides, the electronic embedding scheme is adopted in the ONIOM calculation. Using these methods, the potential energy surfaces (PES) of S₀ and S₁ states in toluene and in the solid phase are obtained. All computations mentioned above were performed using the Gaussian 09, Revision D.01 software package.¹³

Based on the information obtained in the above calculations, the excited states dynamics could be investigated. The radiative decay rate is computed using the Einstein spontaneous emission equation:

where f is the oscillator strength and ΔE_fi is the vertical emission energy with the unit of wavenumber (cm⁻¹). The non-radiative decay rate is deduced based on the Fermi's golden rule (FGR) and first-order perturbation theory, and could be written as follows:
P_iv denotes the initial state Boltzmann distribution function. u and v denote the vibrational quantum numbers. H denotes the interaction between two different Born–Oppenheimer states, and it contains two components:

ĤΨ_iv = Ĥ^BOΦ_i(r,Q)Θ_iv(Q) + Ĥ^SOΦ_i(r,Q)Θ_iv(Q).

Where Ĥ^BO denotes the non-adiabatic coupling and Ĥ^SO denotes the spin–orbit coupling. The non-radiative decay rate constant from S₁ to S₀ could be written as:
Here, R_kl = 〈Φ_f|P̂_fk|Φ_i〉〈Φ_i|P̂_fl|Φ_f〉 is the nonadiabatic electronic coupling. Z_i is the partition function and 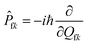represents the normal momentum operator of the kth normal mode in the final electronic state. Finally, based on the Fourier transform of the delta function, the equation could be written as
Here ρ_IC(t,T) is the thermal vibration correlation function (TVCF). Both the methodology and application of this formalism could be found in Peng and Shuai's reports.^14–16

In addition, the reorganization energy (λ) is an efficient tool to measure the energy consumption. Based on the harmonic oscillator approximation, the reorganization energy could be expressed as a summation of the contributions from the normal modes (NM) relaxation:

λ = ∑λ_j = ∑ħw_jS_j

here, D_j represents the displacement for the mode j between the equilibrium geometries of S₀ and S₁. S_j is the Huang–Rhys (HR) factor for the jth mode, which could be realized using the DUSHIN program.¹⁷ Based on the calculations mentioned above, the non-radiative decay rate between S₁ and S₀ in toluene is calculated using the TVCF method embedded in the MOMAP (Molecular Materials Property Prediction Package promoted by the institute of Chemistry Chinese Academy of Sciences and Department of Chemistry in Tsinghua University), which shows superiority in predicting and describing the optical properties of polyatomic molecules.^18–21

3. Results and discussions

3.1 Molecular geometric structures and orbital properties

As we all know, the photophysical properties of compounds are related to their molecular structures. To gain a better understanding of the molecular geometric structure of HBT-d-Ph, the key structural parameters for normal and ESIPT states in both toluene and solid phases are summarized in Table 1. Through analysis, we find that angles θ₁, θ₂ and θ₃ change by about 5°, 9° and 0°, respectively, for the normal state varied from S₀ to S₁ in toluene, while the differences in these angles become 2°, 3° and 3°, respectively, in the solid phase. For the ESIPT state, the dihedral angles of θ₁, θ₂ and θ₃ change by about 4°, 11° and 4°, respectively, in toluene, and these variations become 2°, 1° and 3°, respectively, in the solid phase. Thus, a restricted intramolecular rotation (RIR) of dihedral angles could be found when the molecule transfers from toluene to the solid phase. Among these variations, the dihedral angle of θ₂ is the most pronounced one, which means that the energy consumption path through the rotation of the benzene unit (marked as II) could be effectively hindered by the rigid environment. Besides, the units of III and IV exhibit a good planarity, which is largely due to the six-membered-ring induced by the O–H⋯N intramolecular H-bond. Moreover, the same trend could be found for the variation of bond lengths. B₂ changes by about 0.034 Å and 0.024 Å from S₀ to S₁ in toluene for normal and ESIPT states, respectively, and these variations all become 0.002 Å in the solid phase. According to the energy gap law, the larger is the structural distortion, the faster is the non-radiative decay rate. Consequently, we predict that HBT-d-Ph possesses enhanced emission efficiency in the solid phase due to the restricted intramolecular motion by rigid environments.

Table 1 Dihedral angles of θ₁ (I–III), θ₂ (II–III), θ₃ (IV–III) and bond lengths of B₁, B₂ and B₃, which are marked in Fig. 1 for normal and ESIPT states in both toluene and solid phases

	Toluene				Solid
	Normal		ESIPT		Normal		ESIPT
	S0	S1	S0	S1	S0	S1	S0	S1
θ1	118	123	120	124	163	161	162	164
θ2	60	51	61	50	88	85	88	89
θ3	178	178	179	175	174	177	176	173
B1	1.482	1.463	1.481	1.467	1.486	1.459	1.484	1.466
B2	1.487	1.453	1.487	1.463	1.490	1.488	1.491	1.489
B3	1.453	1.430	1.415	1.431	1.453	1.434	1.408	1.441

---

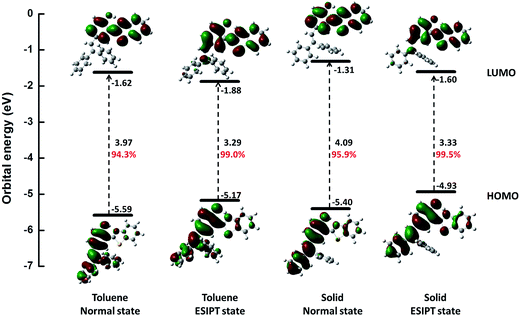
Further, we studied the electron distribution and energy levels in the frontier molecular orbitals (FMOs). The contour plots of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) as well as the corresponding energy levels are shown in Fig. 2. For all states, the electrons in HOMOs are mainly distributed in the two benzene units (I and III), while they are localized on benzothiazole (IV) and benzene (III) in LUMOs. Thus, the overlap of HOMOs and LUMOs occurs in part III. In addition, we could observe that S₁ is a locally hybridized charge transfer state with a π → π* transition nature. In comparison with the energy levels in the normal state, a higher HOMO and a lower LUMO could be observed for the ESIPT state. Moreover, the rigid environment could raise the energy levels of both HOMOs (0.19 eV in normal and 0.24 eV in ESIPT) and LUMOs (0.31 eV in normal and 0.28 in ESIPT). All these changes are closely related to the photophysical properties such as the ESIPT and AIE behaviors, and a more detailed analysis is performed in the following section.

Fig. 2 Calculated energy levels, energy gaps (in eV) and orbital composition distributions of the HOMO and LUMO for normal and ESIPT states in toluene and solid phases, respectively, at S₀ optimized geometries. The percentage of the contribution from HOMO–LUMO transition for S₁ is also listed (red number).

3.2 Excited state intramolecular proton transfer

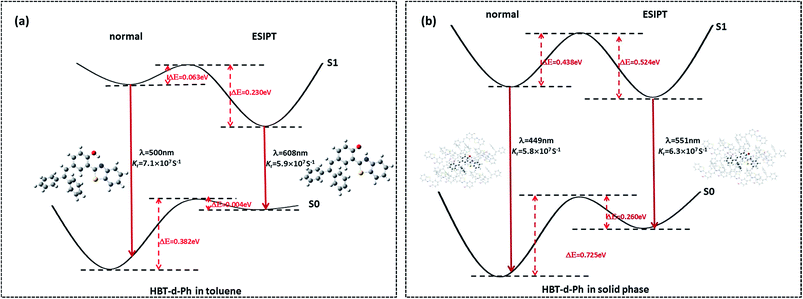
Herein, we studied the dynamics of ESIPT. As the interactions of the hydrogen bond are defined as the important driving force in the ESIPT process, the pre-requisite for ESIPT is the presence of an intramolecular hydrogen bond. First, the intramolecular H-bond between proton donor and proton acceptor in HBT-d-Ph is visualized (Fig. 3). This could be represented with the reduced density gradient (RDG) function which could be realized using the Multiwfn package.²² The RDG function is expressed as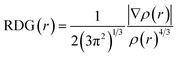 , where ρ(r) is the total electron density. Based on this function, a clear intramolecular H-bond (O–H⋯N) could be observed and an inner six-membered-ring between the benzothiazole (IV) and benzene (III) unit is formed. Besides, the van der Waals effect and strong steric hindrance could also be observed. For more details, one could refer to the study reported by Yang et al.²³ In general, when the molecule is photo-excited by photons with high energy, the higher electronic excited state (S^Normal_n) is populated. Then, two paths are provided: S^Normal_n → S^Normal₁ → S^ESIPT₁ → S^ESIPT₀ → S^Normal₀ and S^Normal_n → S^ESIPT_m → S^ESIPT₁ → S^ESIPT₀ → S^Normal₀ through internal conversion (IC) and vibrational relaxation (VR) processes. Thus, we calculated the potential energy surfaces of S₀ and S₁ for normal and ESIPT states in both toluene and solid phases (shown in Fig. 4) to illustrate the ESIPT process. Besides, the transition states in S₀-PES and S₁-PES are all calculated to obtain the energy barrier. For the molecule in toluene, the barrier from normal to ESIPT state in S₁-PES is 0.063 eV (1.45 kcal mol⁻¹), and the reverse barrier (from ESIPT to normal state) is 0.230 eV (5.30 kcal mol⁻¹). Thus, two ways of decay for the photo-excited molecule in S₁ are shown: S^Normal₁ → S^Normal₀ and S^Normal₁ → S^ESIPT₁ → S^ESIPT₀. In addition, a small barrier in S₀-PES from ESIPT to the normal state is calculated to be 0.004 eV (0.09 kcal mol⁻¹), hence the process S^ESIPT₀ → S^Normal₀ occurs easily, which means that S₁ will decay to S^Normal₀ towards the end in any pathway. Nevertheless, for the molecule in the solid phase, the forward barrier and reverse barrier is 0.438 eV (10.1 kcal mol⁻¹) and 0.524 eV (12.08 kcal mol⁻¹), respectively, in S₁-PES. The process of S^Normal₁ → S^ESIPT₁ is difficult to occur. As a result, when the molecule is electro-excited in its normal state, the formation of the ESIPT state in the solid phase is majorly due to the S^Normal_n → S^ESIPT_m → S^ESIPT₁ process. In addition, the molecule HBT-d-Ph could possess dual electroluminescence in the solid phase. One is generated by the normal state and the other is induced by the ESIPT state. More evidence would be presented in the following section. Based on the calculations in both the solvent and the solid state, we observe that different energy barriers and relaxation processes are caused due to different environments, which also result in different emission properties of the molecules.

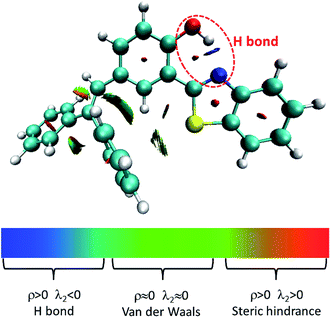Fig. 3 Visualization of intramolecular H-bond. ρ and λ₂ represents the electron density and eigenvalue of the electron-density Hessian (second derivative) matrix, respectively.

Fig. 4 (a, b) Potential energy surface of S₀ and S₁ for normal and ESIPT states in both toluene and solid phases. The index of λ and K_r represent the emission wavelength (with the unit of nm) and radiative decay rate (with the unit of s⁻¹), respectively.

3.3 Aggregation induced emission

As discussed in the above section, the surrounding environment plays an important role in the photophysical process. To analyze the influence of the environment on the photophysical process, the Huang–Rhys factor (HR) is used. HR characterizes the modification of vibrational quanta when the molecule goes from one electronic state to another, and it is an important factor which determines the non-radiative decay rate. Corresponding results are shown in Fig. 5. For normal (Fig. 5a) and ESIPT (Fig. 5b) states in toluene, modes with large HR factors (>1.0) all appear at the low frequency region (<500 cm⁻¹). A few selected HR factors and the corresponding normal modes are presented as insets. By analysis, we observe that the modes with large HR factors such as 25.82 cm⁻¹ and 58.38 cm⁻¹ in the normal state as well as 43.69 cm⁻¹ and 241.31 cm⁻¹ in the ESIPT state majorly correspond to the rotations of the benzene unit (I and II). These findings are consistent with the results shown in the Molecular geometric structures and orbital properties section. Moreover, the calculated non-radiative rate in toluene is 2.88 × 10¹¹ s⁻¹ and 4.86 × 10¹¹ s⁻¹ for the normal and ESIPT states, respectively. They are all higher than their radiative decay rates (7.1 × 10⁷ s⁻¹ and 5.9 × 10⁷ s⁻¹ for the normal and ESIPT states). Therefore, no luminescence could be observed in toluene.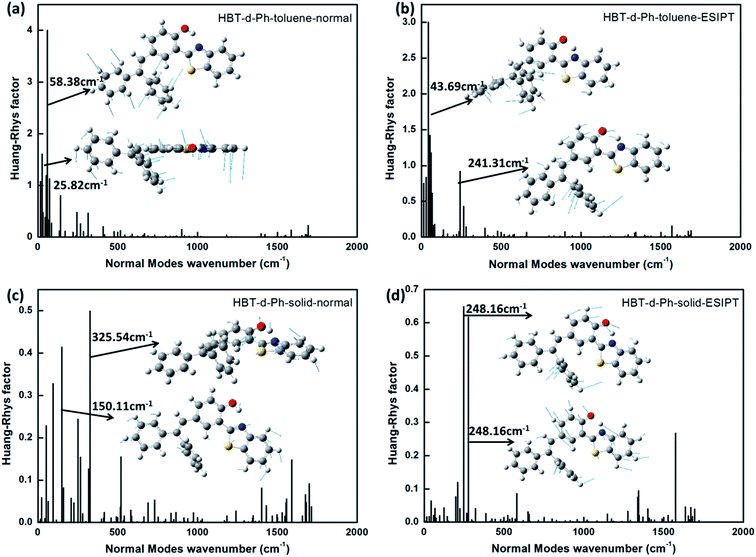

Fig. 5 (a–d) The calculated HR factors of HBT-d-Ph in toluene and solid phases for normal and ESIPT states. The corresponding vibration modes are shown as insets.

For normal (Fig. 5c) and ESIPT (Fig. 5d) states in the solid phase, all HR factors are of lower values. The largest value is not more than 0.7 (at 248.16 cm⁻¹). In addition, the rotations of the benzene unit (I and II) are largely restricted due to the rigid environment. These results show that the rotation modes of benzene in the low frequency region are hindered in the solid phase because of the intermolecular interaction. Since the radiative decay rate maintains the same order for the system in the solvent and in the solid phase (shown in Fig. 4), the non-radiative decay process is the key factor to determine the emission properties. On analyzing the HR factors and reorganization energy, we observe that excited energies in toluene are mostly consumed by the C–C stretching, C–H stretching and the rotation of benzene units. As for the molecule in the solid phase, the rotations of benzene are effectively restricted by the enhanced intermolecular interaction. Thus, the non-radiative energy consumption route is hindered in the solid phase, and the aggregation induced emission feature could be observed.

3.4 Non-radiative decay routes

To further understand the relationship between photophysical properties and the molecular structures, we also plotted the reorganization energies (λ) versus the corresponding normal modes (shown in Fig. 6) of normal and ESIPT states in toluene and solid phases. The reorganization energy is correlated with HR factors as follows: λ_i = S_i × ħω_i. Unlike the HR factors, the reorganization energies are distributed in both low and high frequency regions. For a more detailed investigation, we project the reorganization energies onto the internal coordinates of the molecules. The reorganization energies contributed from bond lengths, bond angles and dihedral angles are summarized in Fig. 7. Detailed data are summarized in Table 2. It is noted that the main contribution of reorganization energy comes from bond lengths: 60.4% and 68.2% for normal and ESIPT states, respectively, in toluene; 81.6% and 89.2% for normal and ESIPT states, respectively, in the solid phase. Meanwhile, the contributions from dihedral angles are 32.2% (132.2 meV) and 28.2% (84.2 meV) for normal and ESIPT states, respectively, in toluene, while they are sharply decreased in the solid phase: 4.4% (12.0 meV) for the normal state and 6.0% (13.9 meV) for the ESIPT state. All these results indicate that the rotations of the benzene unit in the low frequency vibrational modes are largely suppressed in the rigid environment due to the intramolecular interactions, which effectively blocks the non-radiative decay pathway. These findings further confirm that the modes of rotational motion are crucial to determine the photophysical properties.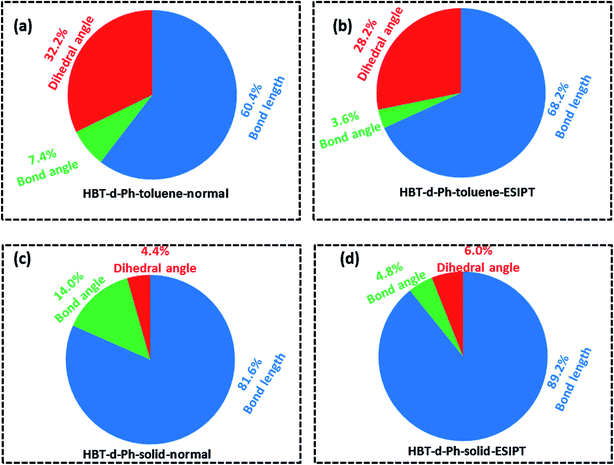

Fig. 6 (a–d) Reorganization energies in both toluene and solid phases for normal and ESIPT states.

Fig. 7 (a–d) Contributions to the reorganization energy from bond length (blue), bond angle (green) and dihedral angle (red) in toluene and solid phases for normal and ESIPT states.

Table 2 Reorganization energies (with the unit of meV) obtained by NM method for normal and ESIPT states in both toluene and solid phases

	Toluene		Solid
	Normal	ESIPT	Normal	ESIPT
Bond length	248.2	203.9	224.7	206.8
Bond angle	30.3	10.8	38.4	11.0
Dihedral angle	132.2	84.2	12.0	13.9

---

4. Conclusions

In summary, we theoretically investigated the exited state intramolecular proton transfer for HBT-d-Ph with AIE in the solid phase by employing the QM/MM method coupled with thermal vibration correlation formalism for the non-radiative decay rate. It is observed that the ESIPT process occurs more easily in a dilute environment than in the solid phase. Restricted intramolecular rotation of the benzene unit could block the non-radiative decay pathways in the solid phase; thus, a dual fluorescence with blue and green emission could be obtained. Our theoretical study could provide a few insights on the dynamics of electroluminescence in the solid phase with ESIPT and AIE features.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This study is supported by the National Natural Science Foundation of China (Grant No. 11374195 and 21403133). Thanks to the supporting of Taishan Scholar Project of Shandong Province and the Scientific Research Foundation of Shandong Normal University. Thanks to the supporting of the Promotive Research Fund for Excellent Young and Middle-aged Scientists of Shandong Province (Grant No. BS2014CL001) and the General Financial Grant from the China Postdoctoral Science Foundation (Grant No. 2014M560571). Great thanks to Professor Yi Luo and Zhigang Shuai for their helpful suggestions and discussions in the detailed calculations. Thanks to Professor Yingli Niu and Qian Peng for the usage of MOMAP.

References

1. O. A. Sytina, D. J. Heyes, C. N. Hunter, M. T. Alexandre, I. H. van Stokkum, R. van Grondelle and M. L. Groot, Nature, 2008, 456, 1001–1004.
2. Y. Xie, T.-T. Wang, X.-H. Liu, K. Zou and W.-Q. Deng, Nat. Commun., 2013, 4, 1960–1966.
3. K.-I. Sakai, T. Ishikawa and T. Akutagawa, J. Mater. Chem. C, 2013, 1, 7866–7871.
4. A. Weller, Z. Phys. Chem., 1956, 60, 1144–1147.
5. Y. Yang, J. Zhao and Y. Li, Sci. Rep., 2016, 6, 32152–32160.
6. S. Samanta, U. Manna and G. Das, New J. Chem., 2017, 41, 1064–1072.
7. Y. Zhang, M. Sun and Y. Li, Sci. Rep., 2016, 6, 25568–25574.
8. T. Mutai, T. Ohkawa, H. Shono and K. Araki, J. Mater. Chem. C, 2016, 4, 3599–3606.
9. V. S. Padalkar and S. Seki, Chem. Soc. Rev., 2016, 45, 169–202.
10. Y. Hong, J. W. Lam and B. Z. Tang, Chem. Soc. Rev., 2011, 40, 5361–5388.
11. Q. Wang, L. Xu, Y. Niu, Y. Wang, M.-S. Yuan and Y. Zhang, Dyes Pigm., 2017, 142, 365–370.
12. J. Fan, L. Cai, L. Lin and C.-K. Wang, J. Phys. Chem. A, 2016, 120, 9422–9430.
13. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, J. R. C. M. A. Robb, G. Scalmani, V. Barone, G. A. P. B. Mennucci, H. Nakatsuji, M. Caricato, H. P. H. X. Li, A. F. Izmaylov, J. Bloino, G. Zheng, M. H. J. L. Sonnenberg, M. Ehara, K. Toyota, J. H. R. Fukuda, M. Ishida, T. Nakajima, Y. Honda, H. N. O. Kitao, T. Vreven, J. A. Montgomery, F. O. J. E. Peralta, M. Bearpark, J. J. Heyd, K. N. K. E. Brothers, V. N. Staroverov, R. K. Obayashi, K. R. J. Normand, A. Rendell, J. C. Burant, J. T. S. S. Iyengar, M. Cossi, N. Rega, J. M. Millam, J. E. K. M. Klene, J. B. Cross, V. Bakken, C. Adamo, R. G. J. Jaramillo, R. E. Stratmann, O. Yazyev, R. C. A. J. Austin, C. Pomelli, J. W. Ochterski, K. M. R. L. Martin, V. G. Zakrzewski, G. A. Voth, J. J. D. P. Salvador, S. Dapprich, A. D. Daniels, J. B. F. O. Farkas, J. V. Ortiz, J. Cioslowski and G. D. J. Fox, Revision D 01, Gaussian, Inc, Wallingford CT.
14. Z. Shuai and Q. Peng, Phys. Rep., 2014, 537, 123–156.
15. Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Chem. Phys., 2007, 126, 114302.
16. Y. Niu, Q. Peng and Z. Shuai, Sci. China, Ser. B: Chem., 2008, 51, 1153–1158.
17. J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109.
18. T. Zhang, Y. Jiang, Y. Niu, D. Wang, Q. Peng and Z. Shuai, J. Phys. Chem. A, 2014, 118, 9094–9104.
19. Q. Peng, Q. Shi, Y. Niu, Y. Yi, S. Sun, W. Li and Z. Shuai, J. Mater. Chem. C, 2016, 4, 6829–6838.
20. H. Ma, W. Shi, J. Ren, W. Li, Q. Peng and Z. Shuai, J. Phys. Chem. Lett., 2016, 7, 2893–2898.
21. Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, J. Phys. Chem. C, 2017, 121, 13448–13456.
22. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
23. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.

---

Footnote

† These two authors contributed equally to this study.

---