Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New phases of 3d-transition metal–cerium binary compounds: an extensive structural search†
Xiaorui Suna,
Yawei Leia,
Rulong Zhou *a,
Bingyan Qua,
Dongdong Lia,
Bo Zhanga and
Xiao Cheng Zeng*bc
*a,
Bingyan Qua,
Dongdong Lia,
Bo Zhanga and
Xiao Cheng Zeng*bc
aLaboratory of Amorphous Matter and Science, School of Materials Science and Engineering, Hefei University of Technology, Hefei, Anhui 230009, China. E-mail: rlzhou@hfut.edu.cn
bDepartment of Chemistry, University of Nebraska-Lincoln, Lincoln, Nebraska 68588, USA. E-mail: xzeng1@unl.edu
cCollaborative Innovation Center of Chemistry for Energy Materials, University of Science and Technology of China, Hefei, Anhui 230026, China
First published on 21st August 2017
Abstract
We perform a comprehensive study to explore the low-energy crystalline phases of 3d transitional metal–cerium (TM–Ce) binary compounds using an unbiased structural search method coupled with first-principles optimization. For Ce–Sc, Ce–Ti, Ce–V, Ce–Cr and Ce–Mn binary systems, no stable crystalline phases are found from the structural search, offering an explanation for why none of these binary compounds have been observed in experiments. For Ce–Fe, Ce–Co, Ce–Ni, Ce–Cu and Ce–Zn binary systems, in addition to the previously known experimental structures, we also find several new low-energy crystalline phases. The computed electronic structures show that Ce atoms are in different states in the predicted binary compounds. In the Ce–Fe, Ce–Co and Ce–Ni compounds, the Ce 4f electrons are partially itinerant so that Ce atoms tend to adopt intermediate valence states between Ce+4 and Ce+3 due to the hybridization among Ce-4f, Ce-5d states and 3d states of TM. In the Ce–Cu and Ce–Zn binary compounds, the Ce-4f states are more localized with the charge state of Ce being close to 3+. In particular, the ferromagnetic metal (FM)-rich phases of the Ce–Fe, Ce–Co and Ce–Ni compounds tend to exhibit FM ordering in their ground states, owing to the strong exchange interaction among metal elements, whereas the non-magnetic states are usually preferred for FM-deficient phases. Magnetic orderings are also found in some other TM-rich phases of Ce–Cu and Ce–Zn compounds, where the magnetic moments are located on the Ce atoms due to the Kondo effect. Mechanic properties of these compounds are also computed based on density functional theory methods. This systematic study offers significantly new data for Ce-based alloys and will be useful to understand the intriguing behavior of the Ce-4f electron, thereby calling for future experimental confirmation of the newly predicted phases of Ce–TM compounds.
1. Introduction
Cerium and cerium-based intermetallic compounds have attracted considerable attention over the past decades due to their rich polymorphs and intriguing physical properties. Ce element itself possesses at least five crystalline phases, denoted as α, α′, β, γ, δ phases, being stable at different conditions.1,2 One of the most fascinating properties of pure Ce is the γ ⇔ α isostructural solid–solid phase transition at ∼7 kbar.1,3,4 Not only in Ce crystal, similar phase transitions were also observed in Ce liquid,5 Ce-based compounds6 and Ce-based metallic glasses.7,8 In Ce-based intermetallic compounds, Ce element can exhibit different electronic states, i.e. diamagnetic Ce4+ ([Xe]4f0), paramagnetic Ce3+ ([Xe]4f1), mixed valence or intermediate valence, thereby resulting in diverse properties such as superconductivity,9,10 heavy-fermion property,11,12 complex magnetic properties,13–15 excellent catalytic properties16–18 and high glass-forming ability,19,20 etc. The ability to adopt a different state for the Ce 4f electron in Ce-based intermetallic compounds leads to an interplay between the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction and the Kondo effect, as described by the coupling constant Jcf that reflects the correlation between the electrons of the open f subshell of Ce and the conduction electrons in the intermetallic compounds.21 Jcf is dependent on temperature, and can be modified by pressure and chemical bonding as well. So different Ce-based intermetallic compounds may exhibit very different properties at different compositions, with different crystal structures and different distances between Ce atoms etc.It is also known that the multi-valence-states of Ce can lead to richer phases of Ce-based intermetallic compounds. For example, for the Ce–Al binary compounds, crystalline phases of Ce1Al1,22 Ce1Al2,23 Ce1Al3,24 Ce1Al4 (ref. 25) and Ce3Al1 (ref. 26) were synthesized experimentally, and they exhibit very different physical properties.27–31 Among all the Ce-based binary compounds, the Ce and transition metal (Ce–TM) are of particular significance due to the interplay between the 4f electrons of Ce and 3d electrons of transition metals, which can lead to rich physical properties. For examples, Ce1Cu6 is known to be a heavy-fermion system,11 while Ce1Cu2 exhibits magnetic ordering and Kondo effects.32 And with the same crystalline structure, Ce1Co2 and Ce1Ni2 exhibit paramagnetic or non-magnetic property.33,34 Although considerable efforts have been made for the synthesis of Ce–TM binary compounds in the past decades, only several crystalline phases were successfully synthesized. To date, stable crystal structures of Ce–Sc, Ce–Ti, Ce–V, Ce–Cr and Ce–Mn binary compounds have not been reported in the literature, although some special crystalline structures have been found for the Ce–TM binary compounds, such as Ce1X2 and Ce1X5 (X = Fe, Co, Ni, Cu, Zn), CeX (X = Ni, Cu, Zn), Ce1Cu6 and Ce1Ni3 (obtained from Inorganic Crystal Structure Database), etc. Much more stable crystalline phases of Ce–TM binary compounds are expected to exist even though they have not been synthesized from experiments. Theoretical predictions of new structures of Ce–TM binary compounds would be helpful to guide future experimental synthesis.
With the state-of-the art global structure search methods, such as genetic algorithm, simulated annealing, topological modeling, and molecular packing, it is possible to identify new crystalline phases of Ce–TM binary compounds. In this study, we perform a systematic search for the stable and low-energy metastable crystalline structures of Ce–TM binary compounds CemTMn (where TM = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn) using an evolutionary algorithm combined with first-principles optimization. Besides experimentally observed phases, we found several new low-energy crystalline phases of Ce–TM (TM = Fe, Co, Ni, Cu, Zn). Detailed structures, electronic and mechanical properties of the new phases are described below.
2. Computational method
An unbiased search of stable structures of CemXn is performed using the USPEX package.35,36 The selected method is based on an evolutionary algorithm which has been proven to be reliable in identifying new phases of a number of systems.37–40 The varying composition search method is applied to seek the most optimal composition of each system. Various compositions with the m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n ratios ranging from 1
n ratios ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 to 7
7 to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with the constraint of m + n ≤ 8 are explored. Medium-sized unit cells containing 8–16 atoms are considered. Three hundreds of structures are generated in the first generation which ensures diversity of the structures at each composition. Sixty structures with different compositions are generated in the ensuing generations by using different evolutionary operations to the low-energy structures, including heredity (60% structures), soft mutation (20%), transmutation (10%) and random production (10%). All the structures are optimized using VASP package41 to achieve medium accuracy. Based on the computed energy of each structure, a rough convex-hull curve of formation energy is plotted, from which possible energetically stable structures and phases are selected out for further structural optimization at higher accuracy.
1 with the constraint of m + n ≤ 8 are explored. Medium-sized unit cells containing 8–16 atoms are considered. Three hundreds of structures are generated in the first generation which ensures diversity of the structures at each composition. Sixty structures with different compositions are generated in the ensuing generations by using different evolutionary operations to the low-energy structures, including heredity (60% structures), soft mutation (20%), transmutation (10%) and random production (10%). All the structures are optimized using VASP package41 to achieve medium accuracy. Based on the computed energy of each structure, a rough convex-hull curve of formation energy is plotted, from which possible energetically stable structures and phases are selected out for further structural optimization at higher accuracy.
The structures which are located on or slightly above the convex-hull are picked out for re-optimization using VASP package. The Perdew–Burke–Enzerhof (PBE)42 exchange-correlation functional within the generalized gradient approximation (GGA) is used. We will point that although usually a Hubbard U correction should be considered for d- and f-elements, our calculations show that standard GGA calculations can give consistent results with experiments for the Ce–TM binary compounds concerned. Furthermore, GGA without U calculations were also performed in many previous theoretical works about Ce-based intermetallic compounds and also showed great success.34,43,44 During the structural optimization, an all-electron plane-wave basis set with the energy cutoff of 300 eV and the k-point spacing smaller than 2π × 0.03 Å−1 in the Brillouin zone is used. It is done until the residual force acting on each atom is less than 0.01 eV Å−1. Then more accurate calculations with larger energy cutoff of 600 eV and denser k-point (less than 2π × 0.02 Å−1) are performed to get more accurate formation energies. Thus, relative stabilities of different structures with the same composition and those with different compositions are found based on the computed convex-hull of formation energy. Furthermore, to assure that no stable phases are missed in the structural search, we also examined structures and phases not seen from the structural search but are stable for other systems. By comparing their formation energies against those structures obtained from the structural search, we can determine the phase stability of each system with more confidence.
To check dynamic stability of all the predicted structures, phonon spectrum, using the finite-displacement approach, is calculated as implemented in the Phonopy code45 (combined with VASP). Moreover, the elastic constants of all the structures are calculated using the stress–strain relations. Mechanical stabilities of these structures can be examined according to the Born stability criteria.46–48 From the calculated stiffness constants Cij and the compliance Sij, the Voigt and Reuss bulk and shear moduli are calculated according to the following formula:49
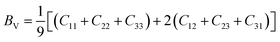 | (1) |
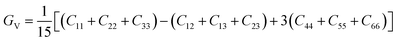 | (2) |
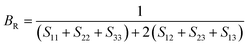 | (3) |
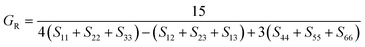 | (4) |
3. Results and discussion
3.1 Phase stabilities
We have performed an extensive search for structures of the Ce–TM binary compounds of all 3d transition metals. To determine whether the binary compound of Ce1−xTMx can be formed and is stable against decomposition into its pure constituents, we calculated the formation enthalpies of all the structures obtained from the search according to the following formula:| ΔH(Ce1−xTMx) = H(Ce1−xTMx) − (1−x)H(Ce) − xH(TM) | (5) |
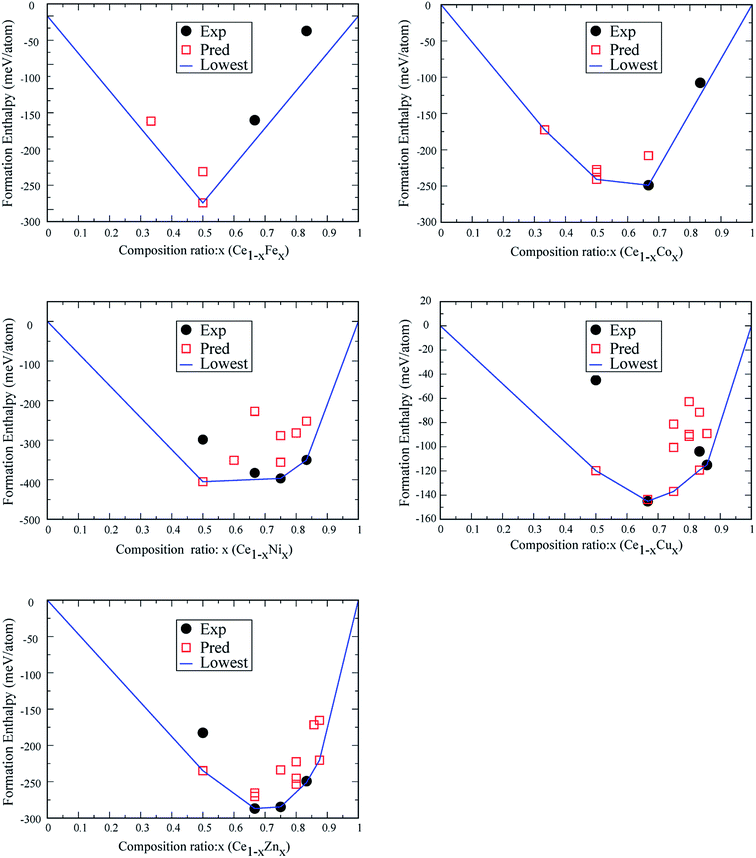
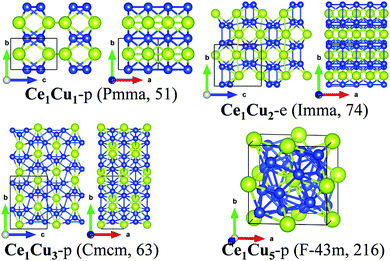
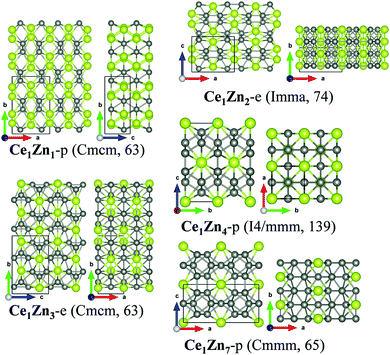
For Ce–Sc, Ce–Ti, Ce–V, Ce–Cr and Ce–Mn, no stable phases were found from the structural search since the formation enthalpies of all the searched structures are positive. So, for TM = Sc, Ti, V, Cr, and Mn, Ce–TM binary compounds are unlikely to form. For Ce–Fe, Ce–Co, Ce–Ni, Ce–Cu and Ce–Zn, interestingly, besides experimentally synthesized phases, some new structures are also found (see Fig. 1), which are also possible to be synthesized because of their low formation enthalpies.
Firstly, for the Ce–Fe binary compounds, a new phase of Ce1Fe1-p is found, which is located at the vertex of the convex-hull curve, suggesting its high stability. We also found a phase of Ce2Fe1-p whose formation energy lies slightly above the convex-hull curve, similar to Ce1Fe2-e and Ce1Fe5-e. Since both Ce1Fe2-e and Ce1Fe5-e are experimentally synthesized, the structure of Ce2Fe1-p may also have possibility of being synthesized under certain conditions.
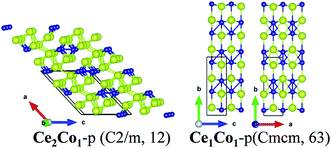
Secondly, for the Ce–Co binary compounds, besides previously synthesized phases of Ce1Co2-e and Ce1Co5-e, two new phases, Ce2Co1-p and Ce1Co1-p, are predicted. Ce2Co1-p, Ce1Co1-p and Ce1Co2-e are located at the vertex of the convex-hull of formation energy, while Ce1Co5-e lies slightly above. So, Ce2Co1-p and Ce1Co1-p are also likely to be synthesized.
Thirdly, for the Ce–Ni binary compounds, stable structures Ce1Ni1-e, Ce1Ni2-e, Ce1Ni3-e and Ce1Ni5-e have been synthesized experimentally. The experimental structure of Ce1Ni3-e cannot be found from our structural search as it contains 24 atoms in the primitive cell while we constrained the max number of atoms ≤ 16 in the unit cell. The lowest-energy structure of the Ce1Ni3-p is 40 meV higher in the formation energy than the experimental structure. Hence the experimental structure of Ce1Ni3-e is stable. A new phase of Ce1Ni1-p is obtained from the search, which is more than 100 meV lower in the calculated formation energy than the experimental structure. So, Ce1Ni1-p is also likely to be synthesized. The experimental phases of Ce1Ni3-e and Ce1Ni5-e are all located at the vertex of the convex-hull, indicating that these phases are stable. The experiment phase of Ce1Ni2-e lies just above the convex-hull curve.
Fourthly, for the Ce–Cu system, three newly predicted structures (Ce1Cu1-p, Ce1Cu3-p and Ce1Cu5-p) along with two synthesized structures (Ce1Cu2-e and Ce1Cu6-e) give rise to the convex-hull suggesting these predicted structures are also likely to be synthesized.
Lastly, for the Ce–Zn system, stable crystalline compounds with at least five compositions may exist according to the computed convex-hull. The experimental structures of Ce1Zn2-e, Ce1Zn3-e and Ce1Zn5-e are located at the vertex of the convex-hull. The new structure of Ce1Zn1-p and Ce1Zn7-p are also likely to be synthesized since they are also located at the convex-hull curve. Moreover, a structure of Ce1Zn4-p from the search may also be synthesized because its formation energy is very close to the convex-hull curve.
We will point that although extensive efforts have been paid we cannot speculate to find all the possible stable phases of Ce–TM compounds. For some complex phases which include more than sixteen atoms in the primitive cell, and those with too large compositions (x is too big or too small), we cannot find them from our structural search. Nevertheless, so many low-energy phases have been discovered which indicates that our structural search method is efficient. Based on these new phases, as well as those already known phases, we can get deeper understanding on the behavior of the Ce 4f electrons.
3.2 Structural features
The space groups and lattice constants of all the predicted phases are summarized in Table 1. For comparison, the measured lattice constants of the experimental phases are also listed. Clearly, the calculated lattice constants are in good agreement with the measured values for the experimental phases.| Phases | Space group (no.) | Lattice constant a, b, c (Å) | B (GPa) | G (GPa) | B/G | |
|---|---|---|---|---|---|---|
| α, β, γ (deg) | ||||||
| a Lattice constants derived from Inorganic Crystal Structure Database. | ||||||
| Ce2Fe1-p | Cal. | P21/m (11) | 4.78, 4.72, 5.90 | 51 | 23 | 2.22 |
| 90, 92, 90 | ||||||
| Ce1Fe1-p | Cal. | Cmcm (63) | 4.63, 4.63, 4.48 | 73 | 25 | 2.92 |
| 90, 90, 55 | ||||||
| Ce1Fe2-e | Cal. | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227) m (227) |
5.10, 5.10, 5.10 | 95 | 19 | 5.00 |
| 60, 60, 60 | ||||||
| Exp.a | 5.16, 5.16, 5.16 | 21 | ||||
| 60, 60, 60 | ||||||
| Ce1Fe5-e | Cal. | P6/mmm (191) | 4.01, 4.99, 4.99 | 104 | 58 | 1.79 |
| 120, 90, 90 | ||||||
| Exp.a | 4.00, 4.86, 4.86 | |||||
| 120, 90, 90 | ||||||
| Ce2Co1-p | Cal. | C2/m (12) | 5.91, 5.91, 9.01 | 56 | 29 | 1.93 |
| 131, 131, 35 | ||||||
| Ce1Co1-p | Cal. | Cmcm (63) | 5.88, 5.88, 3.75 | 71 | 19 | 3.74 |
| 90, 90, 36 | ||||||
| Ce1Co2-e | Cal. | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227) m (227) |
4.99, 4.99, 4.99 | 141 | 32 | 4.41 |
| 90, 90, 90 | ||||||
| Exp.a | 5.06, 5.06, 5.06 | |||||
| 90, 90, 90 | ||||||
| Ce1Co5-e | Cal. | P6/mmm (191) | 4.02, 4.88, 4.88 | 155 | 49 | 3.16 |
| 120, 90, 90 | ||||||
| Exp.a | 4.02, 4.93, 4.93 | 148 | 42 | 3.5 | ||
| 120, 90, 90 | ||||||
| Ce1Ni1-p | Cal. | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (191) m (191) |
4.58, 4.58, 4.58 | 126 | 66 | 1.91 |
| 60, 60, 60 | ||||||
| Ce1Ni2-e | Cal. | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227) m (227) |
5.10, 5.10, 5.10 | 125 | 47 | 2.66 |
| 60, 60, 60 | ||||||
| Exp.a | 5.10, 5.10, 5.10 | |||||
| 60, 60, 60 | ||||||
| Ce1Ni3-e | Cal. | P63/mmc (194) | 4.94, 4.94, 16.55 | 94 | 52 | 1.81 |
| 90, 90, 120 | ||||||
| Exp.a | 4.96, 4.96, 16.53 | |||||
| 90, 90, 120 | ||||||
| Ce1Ni5-e | Cal. | P6/mmm (191) | 4.89, 4.89, 4.00 | 142 | 69 | 2.06 |
| 90, 90, 120 | ||||||
| Exp.a | 4.89, 4.89, 4.00 | 143 | 63 | 2.27 | ||
| 90, 90, 120 | ||||||
| Ce1Cu1-p | Cal. | Pmma (51) | 4.45, 3.51, 5.17 | 56 | 36 | 1.56 |
| 90, 90, 90 | ||||||
| Ce1Cu2-e | Cal. | Imma (74) | 5.50, 5.50, 5.50 | 71 | 27 | 2.63 |
| 133, 105, 93 | ||||||
| Exp.a | Imma (74) | 5.60, 5.60, 5.60 | ||||
| 133, 102, 96 | ||||||
| Ce1Cu3-p | Cal. | Cmcm (63) | 5.23, 5.23, 6.71 | 63 | 36 | 1.75 |
| 90, 90, 47 | ||||||
| Ce1Cu5-p | Cal. | F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (216) 3m (216) |
5.03, 5.03, 5.03 | 70 | 45 | 1.56 |
| 60, 60, 60 | ||||||
| Ce1Cu6-e | Cal. | Pnma (62) | 8.09, 5.05, 10.14 | 95 | 29 | 3.28 |
| 90, 90, 90 | ||||||
| Exp.a | Pnma (62) | 8.11, 5.10, 10.16 | ||||
| 90, 90, 90 | ||||||
| Ce1Zn1-p | Cal. | Cmcm (63) | 6.35, 6.35, 4.68 | 43 | 30 | 1.43 |
| 90, 90, 67 | ||||||
| Ce1Zn2-e | Cal. | Imma (74) | 5.72, 5.72, 5.72 | 60 | 26 | 2.31 |
| 133, 105, 93 | ||||||
| Exp.a | Imma (74) | 5.80, 5.80, 5.80 | ||||
| 133, 99, 99 | ||||||
| Ce1Zn3-e | Cal. | Cmcm (63) | 5.64, 5.64, 6.50 | 63 | 42 | 1.50 |
| 90, 90, 48 | ||||||
| Exp.a | Cmcm (63) | 5.71, 5.71, 6.64 | ||||
| 90, 90, 48 | ||||||
| Ce1Zn4-p | Cal. | I4/mmm (139) | 6.01, 6.01, 6.01 | 69 | 29 | 2.38 |
| 138, 138, 60 | ||||||
| Ce1Zn5-e | Cal. | P6/mmm (191) | 5.37, 5.37, 4.26 | 78 | 43 | 1.81 |
| 90, 90, 120 | ||||||
| Exp.a | 5.39, 5.39, 4.27 | |||||
| 90, 90, 120 | ||||||
| Ce1Zn7-p | Cal. | Cmmm (65) | 6.07, 6.07, 5.75 | 68 | 41 | 1.66 |
| 60, 60, 139 | ||||||
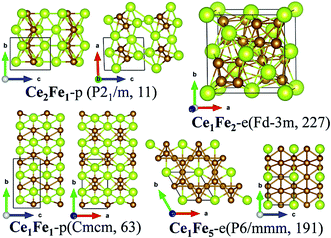
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 227). Ce1Fe5-e is a hexagonal crystal whose space group is P6/mmm (no. 191). As shown in Fig. 2, in both structures, the Ce and Fe atoms are highly coordinated, forming very compact structures. Here, the coordination number is counted at the bond-length cutoff of 3.5 Å for Ce–Ce bond, 3.2 Å for Ce–Fe bonds and 3.0 Å for Fe–Fe respectively. The same criteria are used when counting the coordination number for the other Ce–TM compounds. In Ce1Fe2-e, each Ce atom is in coordination with four Ce atoms and twelve Fe atoms, while each Fe atom is in coordination with six Ce atoms and six Fe atoms, forming a distorted icosahedron. In Ce1Fe5-e, Ce is in coordination with eighteen Fe atoms, higher than that in Ce1Fe2-e. Fe is in coordination with three Ce atoms and nine Fe atoms, the same as that in Ce1Fe2-e. In both phases, Fe atoms form tetrahedrons. The Fe tetrahedrons connect with each other via sharing the vertex, forming the structural frames. The Ce atoms are inserted into the interstitials of the structural frames.
m (no. 227). Ce1Fe5-e is a hexagonal crystal whose space group is P6/mmm (no. 191). As shown in Fig. 2, in both structures, the Ce and Fe atoms are highly coordinated, forming very compact structures. Here, the coordination number is counted at the bond-length cutoff of 3.5 Å for Ce–Ce bond, 3.2 Å for Ce–Fe bonds and 3.0 Å for Fe–Fe respectively. The same criteria are used when counting the coordination number for the other Ce–TM compounds. In Ce1Fe2-e, each Ce atom is in coordination with four Ce atoms and twelve Fe atoms, while each Fe atom is in coordination with six Ce atoms and six Fe atoms, forming a distorted icosahedron. In Ce1Fe5-e, Ce is in coordination with eighteen Fe atoms, higher than that in Ce1Fe2-e. Fe is in coordination with three Ce atoms and nine Fe atoms, the same as that in Ce1Fe2-e. In both phases, Fe atoms form tetrahedrons. The Fe tetrahedrons connect with each other via sharing the vertex, forming the structural frames. The Ce atoms are inserted into the interstitials of the structural frames.
Structures of the predicted phases Ce1Fe1-p and Ce2Fe1-p are much different from Ce1Fe2-e and Ce1Fe5-e. Both structures possess lower symmetries. Ce2Fe1-p is a monoclinic crystal with the space group of P21/m (no. 11) while Ce1Fe1-p belongs to orthorhombic crystalline system with Cmcm (no. 63) space group. In Ce2Fe1-p, there are two nonequivalent Ce atoms in the unit cell. Both are in ten-fold coordination with seven Ce atoms and three Fe atoms. The coordination number of Fe is nine, which includes seven Ce atoms and two Fe atoms. Structurally, Ce2Fe1-p can be viewed as Ce bulk with embedded Fe chains. In Ce1Fe1-p, each Ce atom is in coordination with seven Fe atoms and four Ce atoms, and each Fe atom is in coordination with seven Ce atoms and two Fe atoms. The coordination number of Ce is a little higher than that in Ce2Fe1-p while the coordination number of Fe in both structures is the same. Fe atoms also form Fe chains similar as those in Ce2Fe1-p. So, Ce2Fe1-p and Ce1Fe1-p also exhibit some similarity in structures, similar as Ce1Fe2-e and Ce1Fe5-e. It seems that the richness of Fe dominants general structural features of Ce–Fe binary compounds.
![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) , causing decreased Ce–Ce bonds and Ce–Co bonds. So, in Ce1Co1-p, the coordination number of Ce and Co is seven and nine, respectively, less than those in Ce1Fe1-p as well.
, causing decreased Ce–Ce bonds and Ce–Co bonds. So, in Ce1Co1-p, the coordination number of Ce and Co is seven and nine, respectively, less than those in Ce1Fe1-p as well.
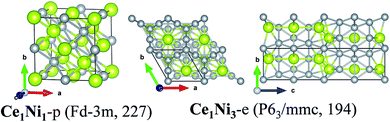
The structure of the predicted phases Ce1Ni1-p is much different from the experimental one and possesses much lower energy. Ce1Ni1-p has a cubic lattice with the space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 227). Each Ce or Ni atom is located at the center of a cubic whose vertices are occupied by four Ce or four Ni atoms, respectively. The four Ce atoms at the cubic vertices form regular tetrahedron, and so do the four Ni atoms. Thus, both Ce and Ni are in eight-fold coordination.
m (no. 227). Each Ce or Ni atom is located at the center of a cubic whose vertices are occupied by four Ce or four Ni atoms, respectively. The four Ce atoms at the cubic vertices form regular tetrahedron, and so do the four Ni atoms. Thus, both Ce and Ni are in eight-fold coordination.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 227). Ce1Cu2-e can be viewed as constructed by inserting Ce atoms between buckled Cu honeycomb slabs. Ce atoms are located directly above the center of all the hexagonal rings. The coordination number of Ce and Cu in Ce1Ni2-e is 14 and 10, respectively, both being a little less than that in Ce1Fe2-e, Ce1Co2-e and Ce1Ni2-e.
m (no. 227). Ce1Cu2-e can be viewed as constructed by inserting Ce atoms between buckled Cu honeycomb slabs. Ce atoms are located directly above the center of all the hexagonal rings. The coordination number of Ce and Cu in Ce1Ni2-e is 14 and 10, respectively, both being a little less than that in Ce1Fe2-e, Ce1Co2-e and Ce1Ni2-e.
For the predicted phases, Ce1Cu1-p possesses an orthorhombic crystalline lattice with space group of Pmma (no. 51). Both Ce and Cu atoms form zig-zag atomic chains, respectively. Each Ce atomic chain connects with four Cu atomic chains, and vice versa. Each Ce atom is in coordination with six Cu atoms and two Ce atoms, and each Cu atom is in coordination with six Ce atoms and two Cu atoms. So the coordination number of them is eight. Ce1Cu5-p is a cubic crystal with the space group of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (no. 216). In the conventional cell, there are one Ce atom located at the center of the cube and one Ce atom located at the center of each side of the cube, respectively. The Cu atoms form a face-capped pyramid structure with the Ce atom at the center. The four vertexes of the pyramid point to the four non-nearest-neighbor corners of the cube to keep the Td rotation symmetry of the structure. The central Ce atom is bonded with all the Cu atoms of the face-capped pyramid except the four corner ones. Thus its coordination number is 16. The 16 Cu atoms coordinated with the Ce atom form a polyhedron with 28 faces. There are 4 hexagons and 12 pentagons in this 28-faces polyhedron. Each Cu atom is in 12-fold coordination, giving a distorted icosahedron with the surrounded atoms. The local structure of Ce1Cu5-p is a little similar to those of Ce1Fe2-e, Ce1Co2-e and Ce1Ni2-e, where the 28-faces polyhedron and icosahedron are also formed with the center of Ce and the transition atom respectively.
3m (no. 216). In the conventional cell, there are one Ce atom located at the center of the cube and one Ce atom located at the center of each side of the cube, respectively. The Cu atoms form a face-capped pyramid structure with the Ce atom at the center. The four vertexes of the pyramid point to the four non-nearest-neighbor corners of the cube to keep the Td rotation symmetry of the structure. The central Ce atom is bonded with all the Cu atoms of the face-capped pyramid except the four corner ones. Thus its coordination number is 16. The 16 Cu atoms coordinated with the Ce atom form a polyhedron with 28 faces. There are 4 hexagons and 12 pentagons in this 28-faces polyhedron. Each Cu atom is in 12-fold coordination, giving a distorted icosahedron with the surrounded atoms. The local structure of Ce1Cu5-p is a little similar to those of Ce1Fe2-e, Ce1Co2-e and Ce1Ni2-e, where the 28-faces polyhedron and icosahedron are also formed with the center of Ce and the transition atom respectively.
For the predicted phases, the structure of Ce1Zn1-p is the same as that of Ce1Fe1-p and is similar to that of Ce1Co1-p. Ce1Zn4-p is metastable according to the computed formation energy. It is a tetragonal crystal with the space group of I4/mmm (no. 139). Each Ce atom is encapsulated by a cage constructed by 18 Zn atoms. The four sides of the Zn cage are all hexagonal rings, while the two roofs are both constructed by four rhombic rings. The coordination number of Ce is 16 and that of Zn is 8. Ce1Zn7-p possesses an orthorhombic crystalline structure and the space group of Cmmm (no. 65). Its structure is much more complicated because there are more atoms included in one conventional unit cell. All the Ce atoms are equivalent in crystallography, while there are three nonequivalent Zn atoms. Each Ce atom is in coordination with 12 Zn atoms. Zn1, Zn2, and Zn3 have a coordination number of 9, 8 and 10, respectively.
3.3 Electronic properties
The diverse physical properties such as heavy-fermion, Kondo-lattice, and intermediate-valence effects of Ce-based binary compounds are highly correlated with the behavior of the 4f electrons in Ce. For the Ce–TM binary compounds, the 3d electrons of the TM elements may also affect their properties. To compute their electronic structures, various initial arrangements of magnetic moments, such as the ferromagnetic, antiferromagnetic, were considered for each structure and the spin-polarized (SP) calculations were performed for each magnetic configuration. We also carried out a non-spin-polarized (NSP) for each structure to compute the energy of a spin-degenerate nonmagnetic phase. The optimized stable magnetic configurations, the magnetic moment on each atom, and the relative energy per atom of the ferro- or antiferro-magnetic configurations compared to that of the spin-degenerate nonmagnetic state of each structure, are all listed in Table 2. To gain deeper insight into the electronic and magnetic structures, the projected density of state (PDOS) of each phase is calculated, as shown in Fig. S2–S6 (see the ESI†).| Phase | Ground magnetic state | First excited magnetic state | Second excited magnetic state |
|---|---|---|---|
| Ce2Fe1-p | Nonmagnetic | ||
| Ce1Fe1-p | Nonmagnetic | ||
| Ce1Fe2-e | ↓↓·↑↑↑↑ | ↓↓·↑↓↑↓ | Nonmagnetic |
| Ce: −0.83 | Ce: −0.33 | ||
| Fe: 1.76 | Fe: 1.45 (−0.22) | ||
| ΔE | −94 | −27 | |
| Ce1Fe5-e | ↓·↑↑↑↑↑ | ↓·↓↑↑↑↑ | ↑·↓↓↓↑↑ |
| Ce: −0.61 | Ce: −0.38 | Ce: 0.17 | |
| Fe: 2.12 | Fe: −0.88 (1.97) | Fe: −1.78(1.40) | |
| ΔE | −203 | −110 | −97 |
| Ce2Co1-p | Nonmagnetic | ||
| Ce1Co1-p | Nonmagnetic | ||
| Ce1Co2-e | Nonmagnetic | ||
| Ce1Co5-e | ↓·↑↑↑↑↑ | O·↑↓OOO | Nonmagnetic |
| Ce: −0.74 | Ce: 0.0 | ||
| Co: 1.40 | Co1: 0.55(−0.55); Co2: 0.0 | ||
| ΔE | −69 | −1 | |
| Ce1Ni1-p | Nonmagnetic | ||
| Ce1Ni2-e | Nonmagnetic | ||
| Ce1Ni3-e | Nonmagnetic | ||
| Ce1Ni5-e | ↓·↑↑↑↑↑ | Nonmagnetic | |
| Ce: −0.23 | |||
| Ni1: 0.18; Ni2: 0.26 | |||
| ΔE | −3 | ||
| Ce1Cu1-p | Nonmagnetic | ||
| Ce1Cu2-e | ↑↓ | Nonmagnetic | |
| Ce: 0.08 (−0.08) | |||
| ΔE | −2 | ||
| Ce1Cu3-p | ↓↓ | Nonmagnetic | |
| Ce: −0.23 | |||
| ΔE | −0.07 | ||
| Ce1Cu5-p | ↓ | Nonmagnetic | |
| Ce: −0.21 | |||
| ΔE | −0.1 | ||
| Ce1Cu6-e | ↓↓↓↓ | ↓↑↑↑ | ↓↓↑↑ |
| Ce: −0.33 | Ce: −0.13(0.27) | Ce: 0.23 (−0.23) | |
| ΔE | −0.18 | −0.02 | −0.00 |
| Ce1Zn1-p | Nonmagnetic | ||
| Ce1Zn2-e | ↑↑ | ↑↓ | Nonmagnetic |
| Ce: 0.65 | Ce: 0.42(−0.42) | ||
| −6.8 | −0.5 | ||
| Ce1Zn3-e | ↑↓ | Nonmagnetic | |
| Ce: 0.34 (−0.34) | |||
| ΔE | −1 | ||
| Ce1Zn4-p | ↑ | Nonmagnetic | |
| Ce: 0.64 | |||
| ΔE | −3 | ||
| Ce1Zn5-e | ↑ | Nonmagnetic | |
| Ce: 0.73 | |||
| ΔE | −3 | ||
| Ce1Zn7-p | ↑ | Nonmagnetic | |
| Ce: 0.63 | |||
| ΔE | −2 |
From the computed PDOS, we can see that there is obvious hybridization between the 3d states of the TM elements and the 4f and 5d states of Ce atoms for the Ce–Fe, Ce–Co and Ce–Ni binary compounds, while that for the Ce–Cu and Ce–Zn binary compounds is much weaker. Due to the strong hybridization, the distribution of the Ce 4f states is apparently broadened for Ce–Fe, Ce–Co and Ce–Ni compounds. For some phases, the Ce 4f states distribute in very large energy windows (3 to 4 eV) below the Fermi level, which means that some 4f electrons of Ce become itinerant, i.e. the Ce atoms may adopt intermediate valence states in these phases. For the Ce–Cu, Ce–Zn systems, the close-shell features of the 3d orbitals of Cu and Zn render them far away from the 4f orbitals of Ce. Hence, there is little hybridization between them. As shown in Fig. S5 and S6,† the density of the 4f states of Ce in the Ce–Cu and Ce–Zn compounds is quite localized, and is crossed by EF in their lower part, indicating that the lower 4f bands are filling by electrons. In almost all the phases of Ce–Cu and Ce–Zn systems, the Ce atoms adopt trivalent states.
Moreover, as shown in Fig. S2–S6,† spin splitting occurs for some phases e.g. Ce1Fe2-e, Ce1Fe5-e, Ce1Co5-e, Ce1Ni5-e, etc., suggesting that particular magnetic orderings are energetically favored in these phases. We will discuss these ordered magnetic states in details in the following subsections.
From the computed projected magnetic moments, we can see that in the ground magnetic state of Ce1Fe2-e, the magnetic moment (1.76 μB) of Fe atoms is almost entirely originated from the 3d states, whereas that of Ce atoms is originated from both 4f (−0.58 μB) states and 5d (−0.23 μB) states. From the PDOS shown in Fig. S2,† we can see that almost all of the spin-up Fe 3d states are distributed below the Fermi level, meaning that they are almost full-filled, while the spin-down Fe 3d states distribute a little higher and some of them are located above the Fermi level. Thus, the net magnetic moments on Fe atoms are aligned upward. Moreover, because the overlapping of the spin-down Fe 3d states with the Ce 4f and 5d states, there is strong hybridization between them, which results in more Ce 4f and 5d electrons occupying the spin-down states. So the net magnetic moments on Ce atoms are aligned opposite to those on Fe atoms.
For the Ce1Fe5-e, spin-polarized computations with ten initial magnetic configurations (i.e. ↑·↑↑↑↑↑, ↑·↓↑↑↑↑, ↓·↓↑↑↑↑, ↑·↑↓↑↑↑, ↑·↓↓↑↑↑, ↓·↓↓↑↑↑, ↑·↑↓↓↑↑, ↑·↓↓↓↑↑, ↓·↓↓↓↑↑, ↓·↑↓↑↑↓), and non-spin-polarized calculation are performed. Three differently ordered magnetic configurations are found to be stable after relaxation. The most stable magnetic configuration is still ferromagnetic (↓·↑↑↑↑↑), as that of Ce1Fe2-e. The magnetic moments on Ce atoms are −0.61 μB and those on Fe atoms are 2.12 μB. The magnetic moments on Ce are also contributed by both Ce 4f and 5d electrons. As shown in Fig. S2,† similar to Ce1Fe2-e, the reason for the magnetic moments on Ce atoms is the strong hybridization between the Fe 3d and Ce 4f and 5d states due to the large splitting of the 3d spin-up and spin-down states. The energy difference between the ferromagnetic state and the nonmagnetic state is −203 meV per atom. Hence, the ferromagnetic state is quite stable. Besides the ferromagnetic state, two magnetic states, i.e. ↓·↓↑↑↑↑ and O·↓↓↓↑↑ are metastable with the energy differences of −110 meV per atom and −97 meV per atom with respect to the nonmagnetic state, respectively. Because of the large energy difference, the two magnetic states are also stable.
For the two predicted Ce–Fe phases, Ce2Fe1-p and Ce1Fe1-p, although various initial magnetic configurations are considered, all of them converge into the nonmagnetic state. It is known that with the large positive value of the exchange interaction J between Fe atoms, bulk Fe and Fe-rich alloys tend to exhibit ferromagnetic properties. As discussed above, for the Fe-rich Ce–Fe phases (Ce1Fe2-e and Ce1Fe5-e), each Fe atom is in coordination with many Fe atoms (six and nine for Ce1Fe2-e and Ce1Fe5-e, respectively). The strong exchange interaction renders the moments on the Fe atoms aligned in the same direction. Therefore, Ce1Fe2-e and Ce1Fe5-e exhibit ferromagnetic properties in the ground state. In the phases of Ce2Fe1-p and Ce1Fe1-p, each Fe atom is only in coordination with two Fe atoms. The exchange interaction between Fe atoms is much weaker compared to those in the Fe-rich phases of Ce–Fe compounds. Such a weak exchange interaction between Fe atoms cannot force the electron spins of all the Fe atoms aligned in the same direction. As a result, there is no spin splitting of 3d states of Fe for Ce2Fe1-p and Ce1Fe1-p phases. As seen in Fig. S2,† although no splitting between the spin-up and the spin-down states, the hybridization between the Fe 3d states and the Ce 4f and 5d states is also obvious. The Ce atoms in the Ce2Fe1-p and Ce1Fe1-p also adopt intermediate valence states, i.e. some 4f electrons of Ce are itinerant.
The ground states of Ce2Co1-p, Ce1Co1-p and Ce1Co2-e are all nonmagnetic (same for spin-polarized calculation and non-spin-polarized calculation). Note that the structure of Ce1Co2-e is the same as that of Ce1Fe2-e. The nonmagnetic ground state of Ce1Co2-e is surely due to the weak exchange interaction of Co. From Fig. S3† we can see that the PDOS of Ce2Co1-p, Ce1Co1-p and Ce1Co2-e are similar to that of the corresponding Ce–Fe phases except the non-spin-splitting. The distance between the main distribution of the 3d states of the TM and that of the 4f states of Ce is a little larger for Ce2Co1-p and Ce1Co1-p phases than the corresponding Ce–Fe phases. Thus, the hybridization between the Co 3d states and the Ce 4f states is weaker in both Ce–Co phases than the Ce–Fe phases. For the Ce–Co phases, the hybridization between the Co 3d states and the Ce 4f states is still strong although there is no spin-splitting in the 3d states. So in the Ce–Co phases, the Ce 4f electrons are also partial itinerant.
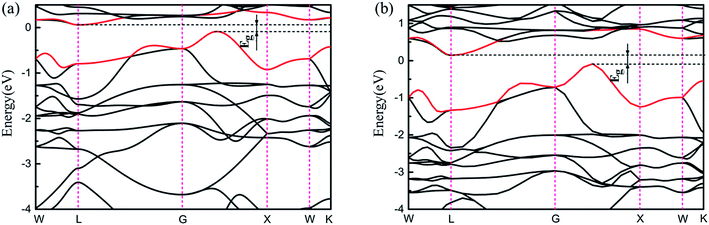
Very interestingly, as shown in Fig. S4,† there is an energy gap in which the Fermi level is located for the phase of Ce1Ni1-p, meaning that it is a semiconductor rather than a conductor. Its band structure is shown in Fig. 7. The computed band gap is 0.15 eV at PBE level. To verify the existence of the band gap, we also used the Heyd–Scuseria–Ernzerhof (HSE06) exchange-correlation functional.51 The computed HSE06 band gap is very close to the PBE value. From the PDOS, we see that the top of the valence band and the bottom of the conduction band are both mainly contributed by Ce-4f states. The appearance of the band gap at EF suggests that all the Ce-4f electrons become conducting electrons, i.e. they are delocalized. Thus, in the phase Ce1Ni1-p, the Ce atoms are in tetravalent state which is different from all the other phases of Ce–TM compounds.
The magnetic properties of Ce–Zn compounds are similar to those of Ce–Cu compounds. Ce1Zn2-e, Ce1Zn3-e, Ce1Zn4-p, Ce1Zn5-e and Ce1Zn7-p possess magnetic properties in their ground states. Ce1Zn3-e is in the antiferromagnetic state while Ce1Zn2-e, Ce1Zn4-p, Ce1Zn5-e and Ce1Zn7-p are all in ferromagnetic states. As in Ce–Cu system, the energy differences between ground magnetic state and nonmagnetic state for Ce1Zn2-e, Ce1Zn3-e, Ce1Zn4-p, Ce1Zn5-e and Ce1Zn7-p are also small. The reason for the magnetic properties of the Zn-rich phases is also the Kondo effect. For Ce1Zn1-p, its ground magnetic state is nonmagnetic state.
3.4 Mechanical properties
Considering the potential application of the Ce–TM compounds, we also computed their mechanical properties. The computed bulk modulus B and shear modulus G are listed in Table 1. Detailed elastic constants are listed in Table S1 (see the ESI†). Based on the bulk modulus and shear modulus, Pugh52 introduced a parameter B/G to distinguish whether the material is ductile or brittle. When the value of B/G is greater than 1.75, this material is ductile, otherwise it is brittle. The values of B/G for each phase are also listed in Table 1.As listed in Tables 1 and S1,† the calculated elastic constants and moduli of some experimental phases are in excellent agreement with the measured values.53–56 Because Ce is a much softer material compared to the 3d transition metals, the bulk moduli of Ce–TM compounds will increase as the concentration of the TM elements increases, as listed in Table 1. Among these different Ce–TM compounds, Ce–Co and Ce–Ni compounds usually possess larger bulk moduli than the same composition Ce–Fe, Ce–Cu and Ce–Zn compounds. The bulk modulus reflects the ability of a substance resisting the compression, and it is in relation with the bond strength in this material. Because the metallic bonding arises from the electrostatic attractive force between the conduction electrons and the positively charged metal ions, the strength of the metallic bond in a metallic substance is dependent on the valence electrons of the metal elements. For the Ce–Fe, Ce–Co, and Ce–Ni compounds, the 3d electrons of the TM elements and some of the 4f and 5d electrons of the Ce elements are conduction electrons. At the same composition, Ce–Fe compound contains relatively less amount of conduction electrons than that of Ce–Co and Ce–Ni. The metallic bonds in Ce–Fe compounds are relatively weaker than those in Ce–Co and Ce–Ni compounds. Hence, the bulk moduli of Ce–Fe compounds are smaller than those of the Ce–Co and Ce–Ni compounds. For Ce–Cu and Ce–Zn compounds, because the valence electrons of Cu and Zn are 4s electrons, the 4f electrons of Ce are localized, the conduction electrons in the Ce–Cu and Ce–Zn compounds are much less than those in the Ce–Fe, Ce–Co and Ce–Ni compounds. As such, the bond strength in the Ce–Cu and Ce–Zn compounds is weaker than that in Ce–Fe, Ce–Co and Ce–Ni compounds, which can result in relatively smaller bulk moduli.
The shear modulus reflects ability of the material resisting the shear stress, which is correlated with not only the bond strength but also the crystalline structure. For the same crystalline structure, as shown in Table 1, the Ce–Co and Ce–Ni compounds also possess the larger shear moduli. The values of the parameter B/G for Ce–Fe, Ce–Co and Ce–Ni are relatively larger than the critical value of 1.75, which means they are more ductile, while for most phases of Ce–Cu and Ce–Zn compounds the values are smaller than 1.75 so that they are more brittle. The different ductility of some phases of the Ce–Cu and Ce–Zn compounds with those of the Ce–Fe, Ce–Co and Ce–Ni compounds may be due to the different states of the 4f electrons of Ce.
4. Conclusion
We have systematically studied phase stabilities, structures and the electronic properties, as well as mechanical properties of the binary compounds of cerium and 3d-transitional metal systems at ambient pressure and 0 K, using the USPEX code coupled with first-principles calculations. For Ce–Sc, Ce–Ti, Ce–V, Ce–Cr and Ce–Mn systems, no stable crystalline phases are found. For Ce–Fe, Ce–Co, Ce–Ni, Ce–Cu and Ce–Zn binary compounds, besides the experimentally observed phases, a number of new low-energy phases are predicted. The calculated phonon spectrum and elastic constants indicate that all the newly predicted phases are dynamically and mechanically stable. The detailed structures, electronic structures, magnetic properties, and mechanic properties of these structures are computed. The computed electronic structures indicate that there is obvious hybridization between the Ce-4f and Ce-5d states and the TM-3d states in the phases of Ce–Fe, Ce–Co and Ce–Ni compounds. So the Ce atoms in these phases are usually in intermediate valence states between Ce+3 and Ce+4. The Ce-4f states in the phases of Ce–Cu and Ce–Zn compounds are much more localized, indicating that the Ce atoms in these phases are in trivalent states. The TM-rich phases of Ce–Fe, Ce–Co, Ce–Ni are usually in ferromagnetic ordering in their ground states, due to the strong exchange interaction between the TM elements. The Cu-rich and Zn-rich phases of Ce–Cu and Ce–Zn compounds also exhibit magnetic properties where magnetic moments are only located on Ce atoms, due to the Kondo effects. The relative larger bulk moduli indicate that Ce–Co and Ce–Ni compounds have relatively higher ability to resist compression. The computed Pugh parameter B/G suggests that most of Ce–Cu and Ce–Zn compounds may be more brittle because of the more localized states of Ce-4f electrons in the Ce–Cu and Ce–Zn compounds while those of Ce–Fe, Ce–Co and Ce–Ni may be more ductile. Our results offer important new data which will be useful for better understanding of intriguing behavior of Ce 4f electrons in Ce–TM compounds. The predicted new phases of the Ce–TM binary compounds will also motivate future experimental confirmation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 51322103, 5160010435, 11404085, 11104056), NSAF (Grant No. U1630118), MOST 973 Program (Grant No. 2015CB856800) and the Fundamental Research Funds for the Central Universities in China. The numerical calculations in this paper are supported by the supercomputing system in the Supercomputing Center of University of Science and Technology of China. XCZ is supported by a Qianren-B fund (1000 Talents Plan B for summer research) from USTC and a State Key R&D Fund of China (2016YFA0200604) to USTC.References
- B. Johansson, Philos. Mag., 1973, 30, 469–482 CrossRef.
- E. King, J. A. Lee, I. R. Harris and T. F. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 1, 1380 CrossRef.
- J. W. Allen and R. M. Martin, Phys. Rev. Lett., 1982, 49, 1106 CrossRef CAS.
- E. G. Ponyatovskii, Dokl. Akad. Nauk SSSR, 1958, 120, 1021 CAS.
- A. Cadien, Q. Y. Hu, Y. Meng, Y. Q. Cheng, M. W. Chen, J. F. Shu, H. K. Mao and H. W. Sheng, Phys. Rev. Lett., 2013, 110, 125503 CrossRef CAS PubMed.
- J. M. Léger, Phys. B, 1993, 190, 84–91 CrossRef.
- H. W. Sheng, H. Z. Liu, Y. Q. Cheng, J. Wen, P. L. Lee, W. K. Luo, S. D. Shastri and E. Ma, Nat. Mater., 2007, 6, 192–197 CrossRef CAS PubMed.
- Q. S. Zeng, Y. Ding, W. L. Mao, W. Yang, S. V. Sinogeikin, J. Shu, H. K. Mao and J. Z. Jiang, Phys. Rev. Lett., 2010, 104, 105702 CrossRef PubMed.
- G. Seyfarth, A. S. Rüetschi, K. Sengupta, A. Georges, D. Jaccard, S. Watanabe and K. Miyake, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205105 CrossRef.
- H. L. Luo, M. B. Maple, I. R. Harris and T. F. Smith, Phys. Lett. A, 1968, 27, 519–520 CrossRef CAS.
- Y. Ōnuki and T. Komatsubara, J. Magn. Magn. Mater., 1987, 63, 281–288 CrossRef.
- M. B. Tang, H. Y. Bai, W. H. Wang, D. Bogdanov, K. Winzer, K. Samwer and T. Egami, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 172201 CrossRef.
- S. V. Streltsov, E. Gull, A. O. Shorikov, M. Troyer, V. I. Anisimov and P. Werner, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195109 CrossRef.
- F. M. G. N. D. Mathur, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer and G. G. Lonzarich, Nature, 1998, 394, 39–43 CrossRef.
- A. P. Murani, S. J. Levett and J. W. Taylor, Phys. Rev. Lett., 2005, 95 CrossRef CAS PubMed.
- T. Yamaguchi, N. Ikeda, H. Hattori and K. Tanabe, J. Catal., 1981, 67, 324–330 CrossRef CAS.
- M. Ozawa, J. Alloys Compd., 1998, 275, 886–890 CrossRef.
- C. A. Luengo, A. L. Cabrera, H. B. MacKay and M. B. Maple, J. Catal., 1977, 47, 1–10 CrossRef CAS.
- B. Zhang, D. Q. Zhao, M. X. Pan, R. J. Wang and W. H. Wang, Acta Mater., 2006, 54, 3025–3032 CrossRef CAS.
- B. Zhang, D. Q. Zhao, M. X. Pan, W. H. Wang and A. L. Greer, Phys. Rev. Lett., 2005, 94, 205502 CrossRef CAS PubMed.
- S. F. Matar, Prog. Solid State Chem., 2013, 41, 55–85 CrossRef CAS.
- C. Becle and R. Lemaire, Acta Crystallogr., 1967, 23, 840–845 CrossRef CAS.
- J. G. Park, Philos. Mag. B, 1993, 68, 653–662 CAS.
- P. Krypyakevich and I. I. Zalutskii, Dopov. Akad. Nauk Ukr. RSR, 1965, 31, 54–56 Search PubMed.
- L. Colombo, G. L. Olcese and G. B. Bonino, Atti Accad. Naz. Lincei, Cl. Sci. Fis., Mat. Nat., Rend., 1963, 35, 53–57 CAS.
- A. C. Lawson, J. M. Lawrence, J. D. Thompson and A. Williams, Phys. B, 1990, 163, 587–590 CrossRef CAS.
- H. Asmat, B. Barbara and D. Gignoux, J. Solid State Chem., 1977, 22, 179–184 CrossRef CAS.
- I. Vedel, A. M. Redon, J. M. Mignot and J. M. Leger, J. Phys. F: Met. Phys., 1987, 17, 849–856 CrossRef CAS.
- R. A. F. G. E. Brodale, E. P. Norman and J. Floquet, Phys. Rev. Lett., 1986, 56, 390 CrossRef PubMed.
- B. D. R. M. Loewenhaupt and F. Steglich, Phys. Rev. Lett., 1979, 42, 1709 CrossRef.
- K. H. J. Buschow and H. V. Daal, AIP Conf. Proc., 1972, 5, 1464–1477 Search PubMed.
- E. Gratz, E. Bauer, B. Barbara, S. Zemirli, F. Steglich, C. D. Bredl and W. Lieke, J. Phys. F: Met. Phys., 1985, 15, 1975–1986 CrossRef CAS.
- T. M. Seixas and J. M. da Silva, Phys. B, 1999, 269, 362–367 CrossRef CAS.
- L. Nordström, M. S. S. Brooks and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3458–3464 CrossRef.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, Y. Ma, Y. Xu, I. Errea, A. Bergara and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7646–7651 CrossRef CAS PubMed.
- C. H. Hu, A. R. Oganov, Q. Zhu, G. R. Qian, G. Frapper, A. O. Lyakhov and H. Y. Zhou, Phys. Rev. Lett., 2013, 110, 165504 CrossRef PubMed.
- Q. Li, Y. Ma, A. R. Oganov, H. Wang, H. Wang, Y. Xu, H. K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506 CrossRef PubMed.
- Y. L. Li, S. N. Wang, A. R. Oganov, H. Gou, J. S. Smith and T. A. Strobel, Nat. Commun., 2015, 6, 6974 CrossRef CAS PubMed.
- J. F. l. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- O. Eriksson, L. Nordström, M. S. S. Brooks and B. Johansson, Phys. Rev. Lett., 1988, 60, 2523 CrossRef CAS PubMed.
- L. Nordström, O. Eriksson, M. S. S. Brooks and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 9111 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon press, 1954 Search PubMed.
- D. Liu, X. Dai, X. Wen, G. Qin and X. Meng, Comput. Mater. Sci., 2015, 106, 180–187 CrossRef CAS.
- Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- R. Golesorkhtabar, P. Pavone, J. Spitaler, P. Puschnig and C. Draxl, Comput. Phys. Commun., 2013, 184, 1861–1873 CrossRef CAS.
- S. J. Kennedy, P. J. Brown and B. R. Coles, J. Phys.: Condens. Matter, 1993, 5, 5169–5178 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- K. Nassau, L. V. Cherry and W. E. Wallace, J. Phys. Chem. Solids, 1960, 16, 123–130 CrossRef CAS.
- Y. Khan, J. Less-Common Met., 1974, 34, 191–200 CrossRef CAS.
- B. Butler, D. Givord, F. Givord and S. B. Palmer, J. Phys. C: Solid State Phys., 1980, 13, L743–L746 CrossRef CAS.
- L. G. Hector and J. F. Herbst, J. Alloys Compd., 2004, 379, 41–53 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07103e |
| This journal is © The Royal Society of Chemistry 2017 |