Effects of CO₂ and temperature on the structure and chemistry of C–(A–)S–H investigated by Raman spectroscopy

Abstract

Calcium (alumino)silicate hydrate (C–(A–)S–H) is the critical binding phase in modern Portland cement-based concrete, yet the relationship between its structure and stoichiometry is not completely understood. In this study, Raman spectroscopy is used to analyze the effects of varying Ca/Si molar ratio (0.6–1.6), Al/Si molar ratio (0.0–0.1), and synthesis temperature (7–80 °C) on the chemical composition and atomic configuration of C–(A–)S–H. The experimental results indicate that increasing Ca/Si molar ratio produces less cross-linked C–(A–)S–H structures, while the addition of Al into the system increases the long-range order of its chain-like structure. Furthermore, increasing the synthesis temperature leads to the formation of more polymerized structures, especially in the Al-containing samples. The Raman spectra also suggest the formation of vaterite in C–S–H samples synthesized at low temperatures. Finally, this study reveals that uptake of atmospheric CO₂ in C–S–H and C–A–S–H favors the formation of long-range ordered chain-like structures.

---

1 Introduction

Concrete is the most widely used construction material.^1,2 About 30 billion metric ton of concrete was produced globally in 2011 (ref. 3), and its usage has continued to increase. Most concrete is manufactured using Portland cement (PC) clinker, which is mainly produced by reacting limestone (lime bearing), clay (silica, alumina, and iron), and other Si/Al/Fe-rich supplementary ingredients such as iron ore, sand, and shale, at temperatures up to 1450 °C. The main reaction product of PC hydration is calcium silicate hydrate (C–S–H) gel, which precipitates as nanometer sized particles that contain a polymerized chain-like and layered structure. C–S–H is the primary binding phase in the hydrated PC matrix.⁴ The structure and composition of C–S–H gel greatly influence the strength, durability, and other physical and chemical properties of hydrated PC, and thus also PC-based concrete. The incorporation of Al into the C–S–H structure (C–A–S–H) is achieved in modern PC-based concrete by partially replacing PC with Al-bearing supplementary cementitious materials (SCMs), such as fly ash and ground granulated blast furnace slag.⁵ The valorization of industrial by-product SCMs in cement manufacturing is an effective practice towards sustainable development. Therefore, understanding the chemistry and structure of C–(A–)S–H is important to obtain concrete of desired quality and to reduce the carbon footprint of the cement industry, which is responsible for 5–8% of annual global anthropogenic CO₂ emissions.^6,7

The uptake of CO₂ by C–(A–)S–H is generally regarded as a detrimental process because it reduces the pH of pore solution and destabilizes the passive film on steel bars in reinforced concretes, which can result in corrosion of the steel bars and cause deleterious cracking.^8,9 The carbonation process also degrades the C–S–H gel structure¹⁰ and produces CaCO₃, silica gel and water. However, the carbonation process is naturally a possible method to sequester CO₂.^4,5,10 Although there are numerous studies conducted on C–S–H gels regarding the CO₂ uptake,^11–13 there is limited information on the structural changes of the C–A–S–H gels exposed to CO₂. The effect of carbonation on the structure of C–A–S–H samples has been studied using ¹³C, ²⁷Al and ²⁹Si MAS-NMR spectroscopy⁸ and XRD¹⁴ techniques.

Understanding the structural properties of C–(A–)S–H provides insight into the physical and mechanic behavior of the cement based materials.^15,16 The synthesis temperature is an important parameter affecting key properties such as, density, chemical composition, microstructure and compressive strength of cement based materials.^12,17 Moreover, due to the exothermical hydration reactions, concrete structures may experience significant temperature rise when used in large volume, e.g. in dam and foundation construction, which accounts for the change of multi-scale cementitious structure due to the varying reaction rates at different curing temperatures. In addition, the present work is relevant to cements used in warm climates.¹² Although numerous studies have investigated the effect of temperature on C–S–H, there is much less information about C–A–S–H.

Raman spectroscopy is a powerful method to probe functional groups through their molecular vibrations. This technique provides detailed insight without significant damage to the sample and is sensitive to small changes in the chemical and structural composition of local atomic environments. It can provide chemical information on both crystalline and amorphous materials. In addition, cement hydration products can be analyzed effectively and relatively quickly with no extra sample preparation steps needed.¹⁶ The sensitivity of this technique enables the analysis of poorly crystalline/amorphous carbonate phases that precipitate on the surface of C–(A–)S–H samples exposed to CO₂.

It is established that C–(A–)S–H structures are poorly crystalline and structurally defected forms of tobermorite.^19–21 The schematic representation of the defected tobermorite-like structure of C–(A–)S–H is given in Fig. 1. The main structural unit is a calcium silicate layer, which is composed of double Ca sheets sandwiched between silicon–oxygen chains on either side. These silicate chains consist of repeating units of three silicate tetrahedra, i.e., a “dreierketten”-type structure. In Fig. 1, the Qⁿ(mAl) notation describes the local coordination of silicate tetrahedra, where n is the number of connected neighboring silicate and/or aluminate tetrahedra, and m of them are aluminate tetrahedra. Subscribed b and p are used to distinguish bridging site and pair site silicate tetrahedra, respectively.^22,23 Until now, numerous studies focusing on C–A–S–H structure showed that the incorporation of aluminum occurs mainly as tetrahedrally coordinated Al(IV) in bridging tetrahedron (Q_b²).^23–26 Tobermorite is generally investigated in three different crystal structures as a function of the hydration degree.²⁰ They are known as tobermorite-9 Å, tobermorite-11 Å and tobermorite-14 Å since the basal spacings of these materials are 9.3, 11.3, and 14.0 Å, respectively.²⁷

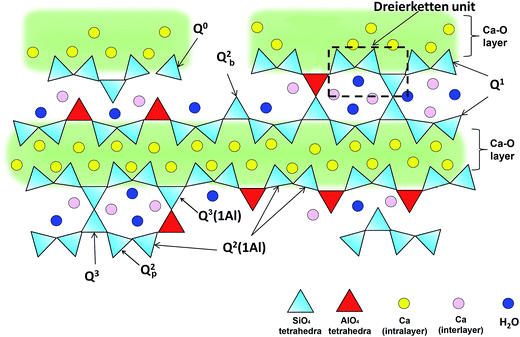Fig. 1 Schematic illustration of cross-linked and non-cross-linked C–(A–)S–H structures. Ca ions in the intralayer are charged-balanced by oxygens of the Si(Al)O₄ tetrahedra chain that are adjacent to the intralayer Ca; the oxygens that point to the interlayer are charge-balanced by interlayer Ca, protons, and partially by hydrogen bonds formed with water molecules. Adapted from ref. 5.

In this paper, we report Raman spectroscopic results obtained on C–(A–)S–H samples synthesized at different temperatures and Al/Si molar ratios. In addition, the effects of atmospheric CO₂ uptake on the chemistries and structures of C–(A–)S–H gels prepared with different Ca/Si molar ratios are investigated and discussed.

2 Experimental

2.1 Materials and method

C–S–H and C–A–S–H samples were synthesized according to the procedure described previously.^4,5 It consisted of mixing Milli-Q water (Merck Millipore), commercial SiO₂ (Aerosil 200, Evonik), CaO and CaO·Al₂O₃ in an N₂-filled glovebox at a water/solid ratio of 45. The CaO component was freshly prepared by decomposing CaCO₃ (Merck Millipore) at 1000 °C for 12 h. The CaO·Al₂O₃ component was obtained by mixing Al₂O₃ (Sigma Aldrich) and CaCO₃ (Merck Millipore) and heating for 1 h at 800 °C, 4 h at 1000 °C and 8 h at 1400 °C in a Carbolite HTF 1700 furnace (heating rate to 800 °C and between each subsequent temperature is 300 °C h⁻¹). The purity of CaO·Al₂O₃ was determined as 99.1 wt% by X-ray diffraction (XRD) with Rietveld analysis.⁵ As-prepared samples were cooled at 600 °C h⁻¹ under ambient atmosphere and were ground with a Retsch PM100 ball mill to a Blaine surface area of 3790 cm² g⁻¹. The following bulk molar ratios were investigated in this study: Ca/Si = 0.6, 0.8, 1.0, 1.2, 1.4 and 1.6; Al/Si = 0.00, 0.05, and 0.1. In order to evaluate the effect of temperature on samples, the equilibration process was performed at 7, 20, and 50 °C in polyethylene vessels, and at 80 °C in Teflon vessels. The 20 °C samples were shaken continuously at 100 rpm and the other samples were shaken twice per week. Once equilibrium was approached (1 year at 7 °C, 182 days at 20 °C, and 56 days at 50 and 80 °C), the samples were vacuum filtered with 0.45 μm nylon filters in a N₂-filled glovebox. The filtered solids were washed with a 50% v/v water–ethanol solution, followed by a > 94 vol% ethanol solution, and then freeze-dried for 7 days. The dried solids were stored in N₂-filled desiccators with humidity and CO₂ traps made from saturated CaCl₂ solutions (∼30% relative humidity, RH) and solid NaOH pellets, until analysis.

For the carbonation investigation, dry powders of the synthesized C–S–H and C–A–S–H samples (Al/Si molar ratios of 0.05 and 0.1), at Ca/Si molar ratios of 0.6 and 1.6, were exposed to atmospheric CO₂ for 10 days by storage of the samples in open polypropylene containers at 24 ± 2 °C and 51% humidity.

2.2 Technical equipment

Raman spectroscopic measurements were conducted at room temperature using a Horiba LabRAM confocal Raman spectrometer with an excitation laser line of 632.8 nm. Data interpretation and manipulation were performed using the Labspec software package. Deconvolution processes were carried out using Origin software (Origin 6.0, OriginLab Corp., Northampton, MA, USA) and the Lorentzian multi-peaks fit module. The fitting process was repeated until the squared correlation coefficients became larger than 0.995. A max–min normalization was applied to all data for ease of visualization.

3 Results and discussions

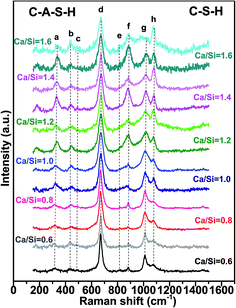
3.1 Effect of Ca/Si molar ratio on C–S–H and C–A–S–H structures synthesized at 20 °C

The Raman spectra for all the samples show intense peaks in the frequency range 175–1500 cm⁻¹. Fig. 2 shows the Raman spectra of the C–S–H and C–A–S–H (Al/Si = 0.05) samples equilibrated at 20 °C, as a function of Ca/Si molar ratio, with the peak assignments given in Table 1.

Fig. 2 Raman spectra of C–S–H (Ca/Si labels on the right) and C–A–S–H (Al/Si = 0.05, Ca/Si labels on the left) samples with Ca/Si molar ratios from 0.6 to 1.6. All samples were synthesized at 20 °C. Single letters are used to represent vibration/bending modes for simplicity: (a) Ca–O, (b) ν₂(SiO₄), (c) ν₄(SiO₄), (d) Q²-SB, (e) Q⁰-SS, (f) Q¹-SS, (g) Q²-SS, (h) CaCO₃.

Table 1 Peak assignments of Raman spectra

Peak	Frequency (cm^−1)	Assignment	Abbreviation	References
a These peaks theoretically exist in the studied system but are not clearly observed.b These peaks are obtained from deconvoluted spectra in this study.
A	≤345	Lattice vibrations of Ca–O polyhedra	Ca–O	12, 28 and 34
B	435–450	Onon–Si–Onon bending vibrations, ν2(SiO4) internal deformations	ν2(SiO4)	12 and 28
C	490	Symmetric bending vibrations of SiO4, ν4(SiO4)	ν4(SiO4)	12 and 28
^b	550–620	Si–O–Si and Si–O–Al stretching modes in Q^3 tetrahedra	Si–O–Si(Al)	12 and 28
D	671	Si–O–Si symmetric bending Q^2	Q^2-SB	12, 28, 29 and 41
^a	756	Asymmetric stretching of [AlO4]^5−/in plane mode of (O–Al–O)	ν3[AlO4]^5−	48 and 49
E	∼820	Symmetric stretching of Q^0	Q^0-SS	This study
F	∼883	ν1(SiO4) symmetric stretching of Q^1	Q^1-SS	12, 31 and 41
^b	∼955	Asymmetric stretching of Q^1	Q^1-ASS	12
^b	∼980	Al–OH bending vibration, Si–OH in plane deformation, asymmetric stretching of Si–O(Ca) in Q^1	Al–OH, Si–OH	12, 31 and 41
^b	∼1015	ν3(SiO4) asymmetric stretching of Q^2 Si–O–(Ca) or Si–O–(H)	Q^2-ASS	12
g	∼1010	ν3(SiO4) symmetric stretching of Q^2	Q^2-SS	12 and 28
^b	∼1040	Symmetric stretching of Q^3	Q^3-SS	28
h	1075–1085	Symmetric stretching of C–O group in CaCO3 precipitates such as calcite and vaterite	C–O-SS	28, 31, 34 and 43
^b	∼1130	ν6(SiO4) and/or ν7(SiO4) displacements of O atoms in Si–O–Si group	ν6(SiO4)	32 and 37
^b	∼1160	ν9(SiO4) and/or ν10(SiO4) deformation modes of Q^4	Q^4-ASS	32 and 37
^b	1040–1200	Hydroxylated species, such as Si–OH	Hydroxylated species	32

---

The frequency range of 150–400 cm⁻¹ contains the vibrational modes of possible calcium sites.²⁷ As seen in Fig. 2, the prominent peak in this range is located at about 330 cm⁻¹ (peak a) which is attributed to the vibration of Ca–O bonds. This peak sharpens with increasing Ca/Si ratio which suggests increasing ordering of the calcium environment in both Al-free and Al-containing samples, consistent with the previous study by Garbev et al.¹² However, when comparing the C–S–H and C–A–S–H systems, it is noted that in the presence of Al, the Ca–O peaks have substantially smaller areas, especially in case of high Ca/Si molar ratio. This behavior can be explained by: (i) the presence of Al in the silicate chains causes a decrease of the effective Ca/(Si + Al) ratio leading to a higher degree of polymerization of C–A–S–H structure, and (ii) for high Ca/Si molar ratios of C–A–S–H, calcium ions can provide the charge balance for different types of aluminum units located in the interlayer spacing of C–A–S–H (e.g., Al(OH)₄⁻). In the latter case, hydrated (calcium) aluminate precipitates contain Al(V) and Al(VI) states and form octahedral framework coordination.^28–30 The presence of these units in C–A–S–H samples will be further discussed when analyzing the 750–1200 cm⁻¹ spectral region.

The peaks observed in the regions of 350–500 cm⁻¹ (peak b) and 400–600 cm⁻¹ (peak c) are generally attributed to ν₂-type internal deformations and ν₄-type asymmetric bending (ASB) vibrations of SiO₄ tetrahedra, respectively.^12,32 The prominent ν₂(SiO₄) peak is observed at about 440 cm⁻¹ (peak b) for all samples, indicating non-bridging oxygen atoms attached to Si atoms. Garbev et al.¹² reported that the Si–O_non–X structure is affected by the nearest neighbor atoms and that the full width at half maximum (FWHM) values of the peaks associated with these structures change depending on the Ca/Si molar ratio. According to their observations, the nearest neighbor atom mainly consists of hydrogen in low Ca/Si molar ratio of C–S–H, and Ca in high Ca/Si molar ratio C–S–H. Thus, at low Ca content, the higher electronegativity of hydrogen causes broader, less resolved peaks. This logic is consistent with our spectra and the C–S–H literature.³³

The most intense peak in every C–(A–)S–H sample is located at about 670 cm⁻¹ (peak d), which is assigned to Q² Si–O–Si symmetric bending (SB) vibrations here. The decreasing FWHM of these Q²-SB peaks indicates a higher degree of silicate chain polymerization,^12,28,34 which occurs at lower Ca/Si molar ratios.

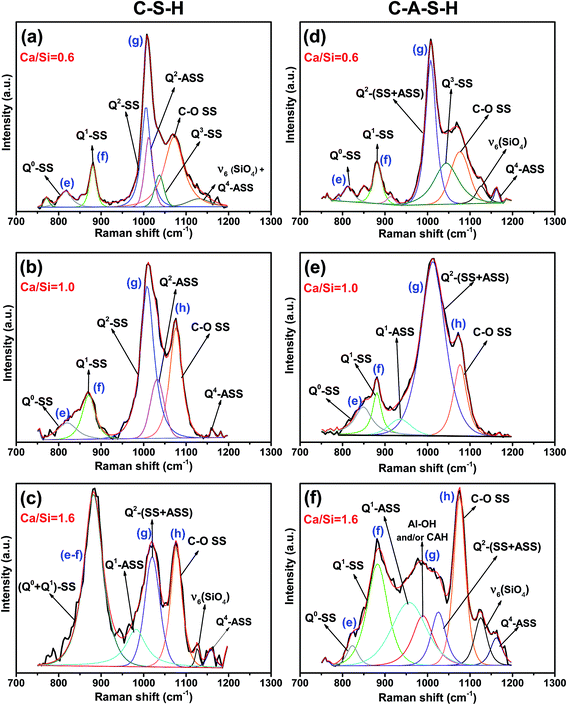
The 750–1200 cm⁻¹ region of the C–S–H and C–A–S–H spectra are deconvoluted to facilitate the analysis of these data. Deconvolution results for the samples with a Ca/Si molar ratios of 0.6, 1.0 and 1.6 are illustrated in Fig. 3(a–f) for C–(A–)S–H samples (see the ESI,† for the deconvoluted spectra for the other samples). The 750–900 cm⁻¹ region is deconvoluted mainly into two peaks. The peak around 825 cm⁻¹ (peak e) is assigned to the Q⁰ symmetric stretching (SS) vibrations of [SiO₄]⁴⁻ monomers.^10,32 Since the peak is barely above the background and we do not expect any Q⁰ in the samples, this peak is maybe due to monomers dissolved in the solution, and not incorporated into the chains during the drying process. In the low Ca/Si samples, the Q⁰-SS peak (peak e) is observed as a separate peak with a very low intensity near 820 cm⁻¹. This peak becomes more intense with increasing Ca/Si molar ratio, and overlaps with the Q¹-SS peak of SiO₄ dimers at Ca/Si molar ratios ≥1.0 (peak f). Observed peak broadening is mainly attributed to the formation of different Ca-derived structural units because stretching vibrations in this frequency region originate from Si–O and Si–O–Ca units.¹² The peak broadening is also observed in the Al/Si = 0.05 C–A–S–H samples as shown in Fig. 2, 3 and S2 (ESI†). However, the Q⁰-SS (peak e) and Q¹-SS (peak f) peaks in the C–S–H and C–A–S–H systems differ in intensity. These peaks are not significantly modified by Al at low Ca/Si ≤ 0.8, while the Ca/Si ≥ 1 samples show peak broadening in the 900–1000 cm⁻¹ region for the C–A–S–H samples. This behavior is attributed to the formation of Al-containing species in the separate phases. On the other hand, the areas of Q¹-SS peaks (peak f) are higher in the C–S–H samples relative to their C–A–S–H counterparts, indicating more long-range ordered aluminosilicate chains in the presence of aluminum. This behavior is more pronounced at higher Ca content.

Fig. 3 Representative Raman spectra and deconvolution peaks of C–(A–)S–H with Ca/Si molar ratio of (a and d) 0.6, (b and e) 1.0, (c and f) 1.6 in the frequency region of 750–1200 cm⁻¹ (equilibration temperature of 20 °C, Al/Si = 0.05 for the C–A–S–H samples). The black and red curves are measured and fitted results, respectively. Deconvoluted individual peaks are labeled accordingly.

As presented in Fig. 3 (and S1, S2 in the ESI†), the 900–1200 cm⁻¹ region in the spectra for the C–S–H samples are deconvoluted into three main peaks (Q²-SS, Q²-ASS, and C–O SS). The intensity of the Q²-SS peaks (peak g) is mainly due to vibrations of bonds connecting non-bridging oxygen (O_non) to Si-bridging oxygen (Si–O_br) atoms. With increasing Ca content, the FWHM values of the Q² peaks increase due to the higher degree of disorder in silicate chains. On the other hand, Q² type Si tetrahedra are charge-balanced more by Ca instead of hydrogen, which causes a positive frequency shift of SS vibrations of C–(A–)S–H samples. Thus, the presence of different types of Q² sites (such as Q²-paired, Q²-bridging, and Q²(1Al) tetrahedra) in C–(A–)S–H broadens the Raman signal.¹²

An additional peak located at about 985 cm⁻¹ is detected in the C–A–S–H samples relative to the C–S–H samples with Ca/Si > 1.2. This peak is assigned to the deformation modes of Si–OH and Al–OH linkages.^35,36

As discussed earlier, when comparing the C–A–S–H and C–S–H samples, a significant decrease is observed in the intensity of calcium peaks with increasing Ca/Si molar ratio for C–A–S–H (Fig. 2 and S2(e and f)†). Thus, we propose that the peak at about 985 cm⁻¹ most probably arises from interactions between calcium species and Al–OH derived phases. This result is consistent with the previous report based on the TGA and XRD analysis of C–(A–)S–H reported by Myers et al.⁵

The 1040–1080 cm⁻¹ region in the Raman spectra can be attributed to Q³-SS and C–O SS peaks.^12,29 Here, the peaks appearing at about 1053 cm⁻¹ for the Ca/Si ≤ 0.8 are attributed to the Q³-SS peaks. These peaks disappear at higher Ca/Si molar ratios due to reduced C–(A–)S–H chain polymerization. The deconvolutions also show that the Q²-ASS peaks and Q³-SS peaks overlap more with increasing Ca content.

As can be seen from Fig. 3, symmetric C–O stretching peaks located at 1077 cm⁻¹ (peak h) increase in intensity as a function of the Ca/Si molar ratio for both C–S–H and C–A–S–H systems (ESI, S1 and S2,† respectively), indicating more extensive carbonation of the higher Ca/Si samples. In the case of C–A–S–H, the C–O SS peaks show a sharper increase in intensity as a function of Ca/Si as compared to C–S–H. This behavior may be linked with the formation of secondary phases such as hemi- and mono-carboaluminate (Ca₄Al₂(OH)₁₂)[OH(CO₃)4·H₂O] in the C–A–S–H ≥ 1.2 samples. Renaudin et al.²⁹ studied Al/Si ≤ 0.1 C–(A–)S–H and observed that their C–A–S–H samples had fewer carbonated phases than their C–S–H samples, contrasting our results. This inconsistency can be attributed to the formation of different aluminum phases in the samples. Another difference between these two studies is that our samples have more crystalline structure of C–(A–)S–H, as can be understood from the sharpness of the Q²-SB and Q²-SS peaks.

The frequency range of 1100–1200 cm⁻¹ mainly contains peaks for Q⁴-SS (∼1160 cm⁻¹) and ν₆-type bond deformation modes of Si–O–Si linkages (∼1130 cm⁻¹).³⁷ These peaks become more pronounced with increasing Ca content in C–A–S–H relative to C–S–H samples. The C–A–S–H samples with Ca/Si ≥ 1.2 exhibit significant peak broadening and higher peak intensity in this frequency region. These effects are attributed to the formation of different Al containing Q⁴ silicate units such as Q⁴(1Al), Q⁴(2Al) and Q⁴(3Al).

Taken together, it is concluded that increasing Ca/Si ratio negatively affects the chain length and causes structural disorder in the C–(A–)S–H. This is consistent with previous results obtained by ²⁹Si NMR, XRD and XPS.^5,13

Incorporation of aluminum into the silicate chain depends on the Ca content of C–S–H. At low Ca/Si ratios, aluminum is observed mainly as tetrahedrally coordinated Al(IV) in the C–S–H chain, while at high Ca/Si ratios, it is taken up as Al(V) and Al(VI) states in the C–S–H structure, possibly in the interlayer. These results are in agreement with the observations of L’Hôpital et al.³⁰ Note, however, that their ²⁷Al NMR results showed precipitation of stratlingite, which is not observed in the present study, most likely because of the lower Al/Si ratios used in the experiments.

3.2 Effect of atmospheric CO₂ on the C–S–H and C–A–S–H phases

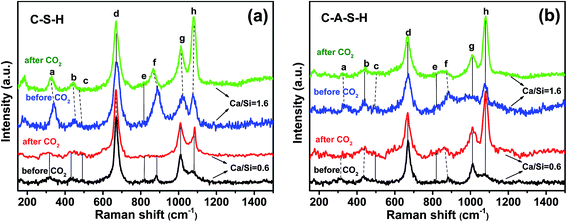
Significant changes occur in the samples after 10 days of exposure to ambient air (20 °C, ∼54% humidity), as illustrated by the spectra of C–S–H and C–A–S–H samples shown in Fig. 4a and b, respectively. Deconvolutions of the 750–1300 cm⁻¹ region are shown in Fig. S3 and S4 of ESI.† A decrease in the peak at ∼330 cm⁻¹, assigned to Ca–O bonds (peak a), is accompanied by the marked increase of peak h, assigned to C–O SS vibrations, which is indicative of Ca–O in C–(A–)S–H reacting with CO₂ to form CaCO₃.

Fig. 4 Raman spectra for (a) C–S–H and (b) C–A–S–H samples with Ca/Si molar ratios of 0.6 and 1.6 before and after exposure to ambient CO₂ for 10 days. Vertical solid lines show the same peak position while dotted lines show the peak shifts. (Al/Si = 0.05; 20 °C equilibration temperature, (a) Ca–O, (b) ν₂(SiO₄), (c) ν₄(SiO₄), (d) Q²-SB, (e) Q⁰-SS, (f) Q¹-SS, (g) Q²-SS, (h) CaCO₃).

The intensity of the Q¹-SS peak (peak f) decreases greatly after CO₂ exposure, indicating polymerization of Q¹ silicate dimers. The increase in the intensity of Q²-SS peaks (peak g) also confirms the polymerization of silicate units by the effect of CO₂ exposure. In our study, at Ca/Si = 0.6, ν₂(SiO₄) internal deformations (peak b) are observed to increase after CO₂ exposure. However, after CO₂ exposure the lack of Q⁰-SS peaks (peak e) can be due to the formation of polymerized units such as Q¹ and Q² silicate structures. These results are in line with those of previous studies performed on C–S–H using ²⁹Si MAS NMR and XPS techniques.^8,13 They suggest that carbonation processes cause decomposition of the chain structure at low Ca/Si ratios (≤0.8). This carbonation process continues until all calcium located at interlayer and Ca²⁺ ions in defect silicate chain are removed from the structure. Thus, the decalcification process results in the formation of infinite C–S–H chains. They suggest that further carbonation leads to the formation of amorphous silica gel and CaCO₃. However, it has been reported that the samples with low Ca/Si ratios are the most resistant samples for decomposition of the structure. The same conclusion is also reported by Black et al.³⁴ who studied the effect of carbonation on C–S–H fresh samples using Raman spectroscopy technique.

In the spectrum obtained at high Ca/Si molar ratio for C–S–H (Ca/Si = 1.6 in Fig. 4a and S3(c and d)†), the Ca–O polyhedra (peak a) are almost completely lost to the formation of amorphous CaCO₃ (ref. 34) after 10 days of carbonation. No significant change in the ν₂(SiO₄) internal deformation peaks (peak b) is observed, but the increasing trend in intensity and decreasing FWHM values of Q²-SS peak (peak g) indicate the formation of longer silicate chains in the C–S–H structure. Previous studies investigated the effect of CO₂ uptake on C–S–H structures for high Ca/Si ratio and showed that the decalcification process proceeds until C–S–H structure with Ca/Si ≤ 0.8 is reached.^13,34 According to Black et al.³⁴ samples with much lower Ca/Si ratios, such as 0.4 and 0.5, showed a tendency to decompose into CaCO₃ and amorphous silica gel to a greater extent than the samples with Ca/Si of 0.6–0.8.

In the spectra for the Ca/Si = 0.6 C–A–S–H samples (Fig. 4b), Q⁰-SS (peak e) and Q¹-SS (peak f) peaks show increasing trends as the samples become more carbonated, indicating structural decomposition of C–A–S–H. This behavior is completely opposite to that of C–S–H sample with Ca/Si molar ratio of 0.6. Most probably, the peak broadening observed in this region arises from Al-containing Q⁴ units. The formation of a prominent broad shoulder has been observed at 550–620 cm⁻¹ after CO₂ exposure. This frequency range has been assigned to the Si–O–Si and Si–O–Al stretching modes in Q³ tetrahedra units.^10,38,39 As can be seen from Fig. S4,† after CO₂ exposure, the FWHM value of Q²-SS peak increases, indicating the calcification of the C–A–S–H system. In addition, the peak broadening observed in the 1100 and 1200 cm⁻¹ region confirms the formation of hydroxylated species such as Si–OH.

In the case of Ca/Si = 1.6 for C–A–S–H samples, remarkable changes are observed after CO₂ exposure, especially between frequencies of 800 and 1000 cm⁻¹. As explained earlier, there is a broad peak, which consists of SS and ASS peaks of Q⁰ (peak e), Q¹ (peak f) and Q² (peak g) peaks. After introducing atmospheric CO₂, this broad peak disappears. From this point of view, it can be assumed that the Al-bearing samples with Ca/Si ≥ 1.4 show a mixture of C–A–S–H and (calcium) aluminate hydrate species in the 800–1200 cm⁻¹ region, which decompose upon carbonation.¹⁸ As observed from the high frequency region at about 3618 cm⁻¹, only this sample has portlandite when compared to all other C–(A–)S–H samples used in this study (Fig. S5, ESI†). This portlandite peak disappears and the intensity of peak a (Ca–O environment) decreases upon exposure atmospheric CO₂, precipitating CaCO₃.

3.3 Effect of synthesis temperature on the C–S–H and C–A–S–H phases

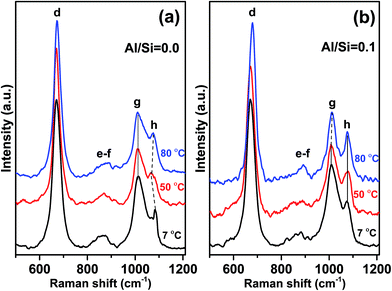
Fig. 5a and b show the effect of synthesis temperature on C–(A–)S–H phases in the 500–1200 cm⁻¹ range where the most significant changes occurred.

Fig. 5 Effect of synthesis temperature on (a) C–S–H and (b) C–A–S–H (with Al/Si = 0.1) samples for Ca/Si = 1.0. Vertical solid lines show the same peak position while dotted lines show the peak shifts. (a) Ca–O, (b) ν₂(SiO₄), (c) ν₄(SiO₄), (d) Q²-SB, (e) Q⁰-SS, (f) Q¹-SS, (g) Q²-SS, (h) CaCO₃.

The most prominent peaks in the Raman spectra for each C–(A–)S–H sample, synthesized at 7, 50, and 80 °C, are observed at 670–680 cm⁻¹. These peaks are again assigned to Q²-SB (peak d) structures in C–(A–)S–H. As shown in Fig. 5b and Table 2, an increasing trend in frequency is observed with increasing synthesis temperature for both C–S–H and C–A–S–H (Al/Si = 0.1). However, when compared these two samples, it is observed that C–A–S–H samples exhibit a larger overall shift.

Table 2 Peak locations and FWHM values of the Q²-SB peaks (peak d). For all samples Ca/Si = 1.0

Sample	Frequency (cm^−1)			FWHM (cm^−1)
	T (°C)			T (°C)
	7	50	80	7	50	80
Al/Si = 0.0	670	671	673	35	28	29
Al/Si = 0.1	670	672	680	31	29	26

---

In particular, the frequency of Q²-SB (peak d) vibrations is reported to increase with decreasing Si–O–Si bond angles.^12,40 This behavior is closely related to the high degree of coupling between the Si–O stretching vibrations.¹² Thus, it is suggested that the bond angles responsible for the FWHM values of Q²-SB peak become smaller with increasing Al content since the number of Al–O–Si bonds increases. It is reported that Q²-SB peaks shift to higher frequencies with increasing degree of structural ordering in 11 Å tobermorite, 14 Å tobermorite, C–S–H^10,12 and also cross-linking, which occurs in the 80 °C sample at Al/Si = 0.1 supporting our findings.

FWHM values of the Q²-SB peaks are also listed in Table 2. It is well known that the sharpness of Q² peaks indicates the occurrence of long-range silicate chains.^8,12 In the present study, the FWHM of this peak generally decreases with the increase in synthesis temperature and Al content. These trends are linked to the higher crystallinity, polymerization, and cross-linking of the aluminosilicate tetrahedra in C–(A–)S–H products relative to their C–S–H counterparts. These results are consistent with the NMR studies of Richardson et al.⁴¹ and Andersen et al.⁴²

For C–A–S–H samples synthesized at 50 and 80 °C, 935–970 cm⁻¹ region has more distinctive shoulder than those of Al-free samples. The frequency and the shape of this shoulder are similar with 11 Å tobermorite shown in the study of Kirkpatrick et al.¹⁰ Thus, we propose that increasing temperature leads to the higher structural order in Al containing C–S–H samples.

The Q²-SS (peak g) and [CO₃²⁻]-SS (peak h) peaks dominate the spectra of the C–(A–)S–H samples at 900–1200 cm⁻¹ (Fig. 5). A decreasing trend is observed in FWHM values of Q²-SS (peak g) and [CO₃²⁻]-SS (peak h) peaks with increasing synthesis temperature. This trend is attributed to crosslinking and presence of longer C–A–S–H chains for Q²-SS peaks. In case of [CO₃²⁻]-SS peaks, the decreasing trend of FWHM values suggests the formation of more crystalline CaCO₃ units.

In the C–S–H sample produced at 7 °C, a sharp and prominent peak is observed at about 1084 cm⁻¹ (peak h), indicating ν₁-SS of CO₃²⁻ formation, which is assigned to vaterite. It is important to note that this peak is positively shifted by 9–10 cm⁻¹ compared to the corresponding peaks in the spectra for high synthesis temperatures. There is an additional small peak located at 1068 cm⁻¹ only for this sample, which strongly implies the existence of vaterite, as it has unique Raman spectroscopic characteristics where the ν₁-SS of CO₃²⁻ peak split into doublets of 15 cm⁻¹ separation, compared with the peak shape of other anhydrous calcium carbonate polymorphs (e.g., calcite and aragonite).^43–45

For both C–S–H and C–A–S–H samples synthesized at 50 °C and 80 °C, ν₁-SS vibrations of CO₃²⁻ located at about 1075 cm⁻¹ (peak h) indicate calcium carbonate polymorphs,^10,31 mainly calcite or aragonite. Aragonite precipitation was reported in C–S–H synthesized from bulk Ca/Si < 0.83 (ref. 32) however, since our samples have Ca/Si = 1.0 we assign these peaks to calcite, which is more stable than aragonite structure at elevated temperature.^46,47

It is worth nothing that additional shoulders appear at ∼980 and ∼1040 cm⁻¹ in the C–A–S–H sample formed at 80 °C. These peaks are assigned to Q³-SB vibrations of cross-linked silicate tetrahedra (Fig. 1). No shoulder or peak is observed in the same region for Al-free samples, indicating that vibrations due to Q³(1Al) and/or Q³ units do not occur at these frequencies. Taken together, these findings show that the presence of Al in the C–S–H structure and high synthesis temperatures are the main factors for obtaining long-range order, a high degree of polymerization, and cross-linking. This result is consistent with the ²⁹Si MAS NMR studies⁵ of these materials, showing that the C–A–S–H samples (Al/Si ≥ 1) synthesized at 80 °C are cross-linked while those synthesized at lower temperatures are not.

4 Conclusion

In summary, this study presents a systematic Raman spectroscopic analysis of C–S–H and C–A–S–H samples as a function of Ca/Si molar ratio, Al/Si ratio, and synthesis temperature. The effect of ambient CO₂ uptake on the structure has been also investigated for both C–S–H and C–A–S–H samples. The results reveal that the Ca content of the C–(A–)S–H structure is the major factor affecting the degree of polymerization of the silicate chain structure. The incorporation of aluminum in the C–S–H structures causes the formation of different types of aluminum species depending on the Ca content of the sample. The low Ca/Si C–A–S–H samples contain Al(IV) in bridging tetrahedral sites and the Ca-rich C–A–S–H samples additionally contain Al(V) and Al(VI) species in a separate phase, which is tentatively assigned to a (calcium) aluminate hydrate. The experiments conducted as a function of synthesis temperature demonstrated that C–S–H produced at 7 °C consists of the vaterite polymorph in ambient temperature with limited atmospheric CO₂ exposure. On the other hand, both the presence of aluminum in the C–S–H phase and the high synthesis temperature contribute significantly to a relatively long-range ordered chain structure. It is also confirmed that increasing synthesis temperature and aluminum content in C–(A–)S–H promote the formation of an 11 Å tobermorite-like structure. Finally, the formation of CaCO₃ polymorph demonstrates that the samples are sensitive to CO₂ uptake from ambient air and that the presence of aluminum in the system leads to formation of carboaluminate phases.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This study was supported by National Science Foundation of the United States under SusChEM program, Grant #1410557, and the Scientific and Technological Research Council of Turkey (TUBITAK) 2219-International Postdoctoral Research Fellowship Program (App. No: 1059B191401401). Sinem Ortaboy acknowledges the “Istanbul University Engineering Faculty Chemistry Department” for additional financial support. The postdoctoral research of Rupert J. Myers at the University of California, Berkeley, was funded by Siam Cement Public Company (SCG) Ltd.

References

1. P. Shafigh, M. A. Nomeli, U. J. Alengaram, H. B. Mahmud and M. Z. Jumaat, J. Cleaner Prod., 2016, 135, 148–157.
2. S. Samad and A. Shah, Role of binary cement including Supplementary Cementitious Material (SCM), in production of environmentally sustainable concrete: A critical review, Int. J. Sustainable Built Environ., 2017 DOI:10.1016/j.ijsbe.2017.07.003 , in press.
3. J. J. Vahit Atakan, D. Ravikumar, L. McCandlish and N. DeCristofaro, Technologies that reduce water use in cement and concrete help global industry address mounting concerns of water scarcity, Solidia Technologies, 2016, vol. 8.
4. B. Lothenbach, L. Pelletier-Chaignat and F. Winnefeld, Cem. Concr. Res., 2012, 42, 1621–1634.
5. R. J. Myers, E. L'Hôpital, J. L. Provis and B. Lothenbach, Cem. Concr. Res., 2015, 68, 83–93.
6. E. Worrell, L. Price, N. Martin, C. Hendriks and L. O. Meida, Annu. Rev. Energy, 2001, 26, 303–329.
7. K. Celik, C. Meral, A. P. Gursel, P. K. Mehta, A. Horvath and P. J. Monteiro, Cem. Concr. Compos., 2015, 56, 59–72.
8. T. F. Sevelsted and J. Skibsted, Cem. Concr. Res., 2015, 71, 56–65.
9. R. Ylmén and U. Jäglid, Int. J. Concr. Struct. Mater., 2013, 7, 119–125.
10. R. J. Kirkpatrick, J. L. Yarger, P. F. McMillan, P. Yu and X. Cong, Adv. Cem. Based Mater., 1997, 5, 93–99.
11. A. Morandeau, M. Thiéry and P. Dangla, Cem. Concr. Res., 2014, 56, 153–170.
12. K. Garbev, P. Stemmermann, L. Black, C. Breen, J. Yarwood and B. Gasharova, J. Am. Ceram. Soc., 2007, 90, 900–907.
13. L. Black, K. Garbev and I. Gee, Cem. Concr. Res., 2008, 38, 745–750.
14. W. Hunnicutt, L. Struble and P. Mondal, Effect of synthesis procedure on carbonation of calcium-silicate-hydrate, J. Am. Ceram. Soc., 2017, 100(8), 3736–3745.
15. G. Geng, R. J. Myers, M. J. A. Qomi and P. J. M. Monteiro, Densification of the interlayer spacing governs the nanomechanical properties of calcium-silicate-hydrate, Sci. Rep., 2017, 7(1), 10986.
16. G. Geng, R. J. Myers, J. Li, R. Maboudian, C. Carraro and D. A. Shapiro, et al., Aluminum-induced dreierketten chain cross-links increase the mechanical properties of nanocrystalline calcium aluminosilicate hydrate, Sci. Rep., 2017, 7, 44032.
17. E. I. Kamitsos, J. A. Kapoutsis, H. Jain and C. H. Hsieh, Vibrational study of the role of trivalent ions in sodium trisilicate glass, J. Non-Cryst. Solids, 1994, 171(1), 31–45.
18. J. Bensted, Cem. Concr. Res., 1977, 7, 161–164.
19. I. G. Richardson, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 903–923.
20. E. Bonaccorsi, S. Merlino and A. R. Kampf, J. Am. Ceram. Soc., 2005, 88, 505–512.
21. R. J. Myers, S. A. Bernal, R. San Nicolas and J. L. Provis, Langmuir, 2013, 29, 5294–5306.
22. G. Engelhardt, in eMagRes, John Wiley & Sons, Ltd, 2007,  DOI:10.1002/9780470034590.emrstm0506.
23. R. J. Myers, S. A. Bernal, J. D. Gehman, J. S. J. van Deventer and J. L. Provis, J. Am. Ceram. Soc., 2015, 98, 996–1004.
24. R. J. Myers, Ph. D. thesis, The University of Sheffield, 2015.
25. H. Manzano, J. S. Dolado and A. Ayuela, J. Phys. Chem. B, 2009, 113, 2832–2839.
26. D. Hou, Z. Li and T. Zhao, RSC Adv., 2015, 5, 448–461.
27. S. Merlino, E. Bonaccorsi and T. Armbruster, Am. Mineral., 1999, 84, 1613–1621.
28. R. J. Kirkpatrick, J. L. Yarger, P. F. McMillan, Y. Ping and X. Cong, Adv. Cem. Based Mater., 1997, 5, 93–99.
29. G. Renaudin, J. Russias, F. Leroux, F. Frizon and C. Cau-dit-Coumes, J. Solid State Chem., 2009, 182, 3312–3319.
30. E. L’Hôpital, B. Lothenbach, D. A. Kulik and K. Scrivener, Cem. Concr. Res., 2016, 85, 111–121.
31. G. Renaudin, J. Russias, F. Leroux, C. Cau-dit-Coumes and F. Frizon, J. Solid State Chem., 2009, 182, 3320–3329.
32. P. Mcmillan, Am. Mineral., 1984, 69, 645–659.
33. E. Gartner, I. Maruyama and J. Chen, Cem. Concr. Res., 2017, 97, 95–106.
34. L. Black, C. Breen, J. Yarwood, K. Garbev, P. Stemmermann and B. Gasharova, J. Am. Ceram. Soc., 2007, 90, 908–917.
35. H. D. Ruan, R. L. Frost and J. T. Kloprogge, J. Raman Spectrosc., 2001, 32, 745.
36. J. T. Kloprogge, R. L. Frost and L. Hickey, J. Raman Spectrosc., 2004, 35, 967–974.
37. K. Kihara, T. Hirose and K. Shinoda, J. Mineral. Petrol. Sci., 2005, 100, 91–103.
38. S. V. Stefanovsky, K. M. Fox and J. C. Marra, Mater. Res. Soc. Symp. Proc., 2013, 1518, 53–58.
39. P. K. Dutta, D. C. Shieh and M. Puri, J. Phys. Chem., 1987, 91, 2332–2336.
40. A. N. Lazarev, Vibrational spectra and structure of silicates, Consultants Bureau, New York, 1972.
41. I. G. Richardson, J. Skibsted, L. Black and R. J. Kirkpatrick, Adv. Cem. Res., 2010, 22, 233–248.
42. M. D. Andersen, H. J. Jakobsen and J. Skibsted, Cem. Concr. Res., 2004, 34, 857–868.
43. S. Martinez-Ramirez, S. Sanchez-Cortes, J. V. Garcia-Ramos, C. Domingo, C. Fortes and M. T. Blanco-Varela, Cem. Concr. Res., 2003, 33, 2063–2068.
44. N. Sánchez-Pastor, M. Oehlerich, J. M. Astilleros, M. Kaliwoda, C. C. Mayr, L. Fernández-Díaz and W. W. Schmahl, Geochim. Cosmochim. Acta, 2016, 175, 271–281.
45. C. Carteret, A. Dandeu, S. Moussaoui, H. Muhr, B. Humbert and E. Plasari, Cryst. Growth Des., 2009, 9, 807–812.
46. J. Charles, A. Weiss, K. T. Cancel, R. D. Moser, P. G. Allison, E. Rae Gore, M. Q. Chandler and P. G. Malone, J. Nanotechnol., 2014, 1, 1–6.
47. S. Gopi, V. K. Subramanian and K. Palanisamy, Mater. Res. Bull., 2013, 48, 1906–1912.
48. D. Torréns-Martín, L. Fernández-Carrasco, S. Martínez-Ramírez, J. Ibáñez, L. Artús and T. Matschei, Raman Spectroscopy of Anhydrous and Hydrated Calcium Aluminates and Sulfoaluminates, J. Am. Ceram. Soc., 2013, 96(11), 3589–3595.
49. P. McMillan and B. Piriou, Raman Spectroscopy Of Calcium Aluminate Glasses and Crystals, J. Non-Cryst. Solids, 1983, 55, 221–242.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07266j

---