Open Access Article
Open Access ArticleInsulator-to-metal transition of lithium–sulfur battery
Yong Pan *a,
Weiming Guan
*a,
Weiming Guan b and
Pengyu Maoa
b and
Pengyu Maoa
aSchool of Material Science and Engineering, Southwest Petroleum University, Chengdu 610500, China. E-mail: panyong10@mails.jlu.edu; Fax: +86-871-68438950; Tel: +86-871-68328970
bState Key Laboratory of Advanced Technologies for Comprehensive Utilization of Platinum Metals, Kunming 650106, China
First published on 14th September 2017
Abstract
Li2S is a promising battery material due to the high theoretical capacity and high energy density. However, the improvement of insulation of Li2S is a challenge for its application. Naturally, the insulator-to-metal transition strongly depends on the electronic overlap between the conduction band and the valence band at the Fermi level (EF). To solve this key problem, this work investigates the insulator-to-metal transition of Li2S under high pressure. We identify a stable structure based on the phonon dispersion and thermodynamic model. It is found that Li2S with CaF2-type, Br2O-type and Cs2S-type structures are dynamically stable in the ground state. Importantly, the band gap of Li2S decreases gradually with increasing pressure. We predict that pressure leads to the insulator-to-metal transition of Li2S owing to the Li atomic pairing and the existence of Li–Li metallic bonds.
1. Introduction
With increasing global energy consumption and environmental pollution from fossil fuels, energy storage technology becomes an imminent concern both at present and in the future. Lithium–sulfurs (Li–S) are now applied in solid-state secondary batteries.1–6 In particular, the theoretical capacity and theoretical specific energy of lithium–sulfurs are up to 1675 mA h g−1 and 2600 W h kg−1, respectively.7,8 However, the insulating nature of lithium–sulfur markedly reduces the electrochemical reaction dynamics and weakens the overall energy efficiency due to the low Li-ion diffusivity rate.9–11 Importantly, the insulation of lithium–sulfurs reduces the polarization and aggravates cell impedance, which reduces the electrical transportation and energy rate of a cell. As a result, these factors further degrade the performance of a battery, cycle life, safety etc. Therefore, the improvement of the electrical properties of lithium–sulfur batteries is a key challenge for their practical application.Earlier work has shown that the obtained indirect band gap of Li2S with CaF2-type structure is about 3.297 eV.12 One viewpoint is that the insulating nature of Li2S is attributed to the Li–S bonding and insulation of pure S.13,14 Essentially, the insulating nature of Li2S derives from the formation of a wide band gap. That is to say, it is difficult to induce an electronic transition between the bottom of the conduction band and the top of the valence band. The insulator-to-metal transition of a solid strongly depends on the localized hybridization at the Fermi level (EF).15 To solve this key problem, it is necessary to improve the electronic overlap at the Fermi level. Based on the above design principle, we propose that pressure may lead to insulator-to-metal transition of Li2S.
The electrochemical reaction of crystalline α-S8 at a cathode is described by: S8 + 16Li+ + 16e− ↔ 8Li2S.16 Although the structure, electronic structure and elastic properties of Li2S have been studied,12,17 it is extremely unstable in air because of strong moisture absorption.18,19 Therefore, structural stability plays a crucial role in overall performance such as electrical properties, rate performance, rapid capacity fade, cycle life, safety etc. For the Li2S compound, there are three different structures: CaF2-type structure,20 Br2O-type structure21 and Na2S-type structure.21 However, the structural stability of Li2S at high pressure is unknown.
To explore the insulator-to-metal transition, in this work, we apply first-principles calculations within the density functional theory (DFT) method to investigate the correlation between pressure and properties of Li2S (0–350 GPa). Considering the structural features and phase stability under high pressure, we design five possible crystal structures based on main group elements. The structural stability of these structures is examined by the thermodynamic mode and phonon dispersion. Our works predict that high pressure can result in insulator-to-metal transition of Li2S.
2. Model and method
To confirm the stable structure under high pressure, we designed five possible crystal structures, namely CaF2-type (space group: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, no. 225),20 Br2O-type (space group: Pn21a, no. 33),21 Na2S-type (space group: P63/mmc, no. 194),22 K2S-type (space group: Pmma, no. 51)12,23 and Cs2S-type (space group: Pnma, no. 62),21 because of their similar structural features. The structural models of Li2S are shown in Fig. 1. Generally speaking, the structural stability of a solid is measured by thermodynamic and dynamic models. In particular, the dynamic stability of a solid is related to the vibrational frequency, which is defined as the phonon frequency.
m, no. 225),20 Br2O-type (space group: Pn21a, no. 33),21 Na2S-type (space group: P63/mmc, no. 194),22 K2S-type (space group: Pmma, no. 51)12,23 and Cs2S-type (space group: Pnma, no. 62),21 because of their similar structural features. The structural models of Li2S are shown in Fig. 1. Generally speaking, the structural stability of a solid is measured by thermodynamic and dynamic models. In particular, the dynamic stability of a solid is related to the vibrational frequency, which is defined as the phonon frequency.
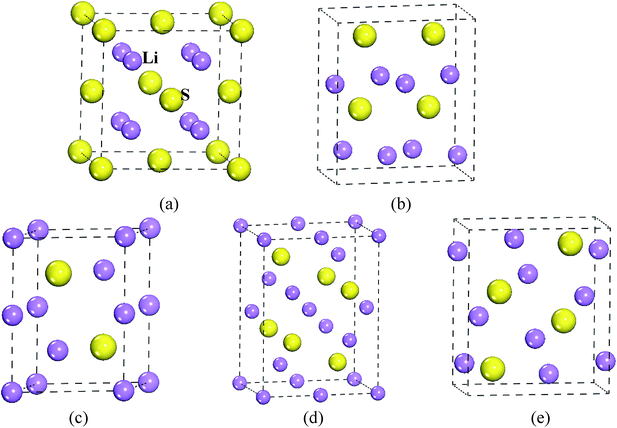 | ||
| Fig. 1 Structural model of Li2S. (a) CaF2-type structure, (b) Br2O-type structure, (c) Na2S-type structure, (d) K2S-type structure and (e) Cs2S-type structure. | ||
It is well known that the first-principles calculation within DFT is a strong tool to predict a new crystal structure at the electronic or atomic level.24 In this paper, therefore, all calculations of the five Li2S structures at zero pressure and high pressure were carried out by using first-principles calculations, as implemented in the CASTEP code.25 After convergence test, we selected the generalized gradient approximation (GGA) within PBE26 functional and the local density approximation (LDA) within CA-PZ functional27 to treat the electronic interaction and for comparison. The interaction between the ionic cores and valence electrons was treated using the ultrasoft pseudopotential. The valence electronic configurations of Li and S are 1s22s1 and 3s23p4, respectively. To ensure the total energy in the ground state to be converged, a plane-wave basis set for electron wave functions with cutoff energy of 400 eV was used. The Brillouin zone was sampled with 14 × 14 × 14, 9 × 14 × 9, 14 × 14 × 14, 9 × 10 × 9 and 9 × 14 × 9 for CaF2-type structure, Br2O-type structure, Na2S-type structure, K2S-type structure and Cs2S-type structure, respectively. The electronic energy tolerance of the SCF was treated as 1 × 10−6 eV per atom. Total energy of a system was obtained by the density-mixing scheme in conjunction with the conjugate gradient technique. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was applied to treat the relaxed system. All structures were optimized based on the periodic boundary condition. Note that all atomic positions, lattice parameters and internal coordinates in a system were fully relaxed. To estimate the dynamical stability, the phonon properties were calculated by using the PHONOPY code.28,29
3. Results and discussion
It is obvious that the assessment of structural stability of Li2S should be studied first. Essentially, the structural stability of a solid relies not only on the chemical potential between atoms but also on the vibrational frequency. Therefore, we consider the structural stability of Li2S from two aspects: thermodynamic and dynamic stabilities. The thermodynamic stability of Li2S is calculated by the formation enthalpy (ΔH), which is given by:| ΔH = E(Li2S) − 2E(Li) − E(S) | (1) |
Table 1 presents the calculated lattice parameters, volume, formation enthalpy and bulk modulus of Li2S with the five structures. It can be seen that the calculated formation enthalpy of these structures is smaller than zero, indicating that these structures are thermodynamically stable in the ground state. Importantly, the calculated formation enthalpy of Li2S with CaF2-type structure is about −4.0161 eV per atom, which is smaller than that of the other structures. That is to say, Li2S with CaF2-type structure is more thermodynamically stable than the other structures. This result is in good agreement with other theoretical results.16
| Structure | Method | a | b | c | V | ΔH | B |
|---|---|---|---|---|---|---|---|
| CaF2-type | Cal | 5.725 | 187.6 | −4.0161 | 38 | ||
| Exp20 | 5.720 | ||||||
| Na2S-type | Cal | 4.043 | 6.071 | 86.0 | −3.8846 | 36 | |
| K2S-type | Cal | 6.076 | 4.041 | 7.011 | 172.2 | −3.8847 | 37 |
| Cs2S-type | Cal | 6.326 | 3.818 | 7.281 | 185.9 | −3.9578 | 39 |
| Br2O-type | Cal | 11.463 | 4.046 | 4.049 | 187.8 | −4.0148 | 37 |
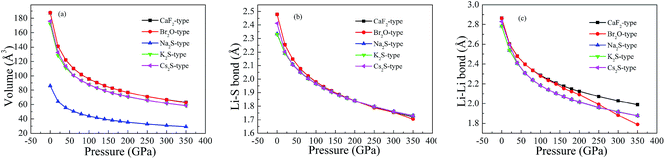
To reveal the thermodynamic stability, the structural formation and chemical bonding of Li2S are discussed here. As presented in Table 1, the calculated lattice parameter of Li2S with CaF2-type structure is a = 5.725 Å, which is in good agreement with the experimental data.20 It is clear that the structural stability of the CaF2-type structure is attributed to the symmetrical Li and S atoms. As shown in Fig. 1, Li and S atoms occupy the Wyckoff 8c (0.250, 0.2500, 0.500) and 4a (0, 0, 0) sites, respectively, which form the symmetrical Li–S bond and Li–Li metallic bond. The calculated bond lengths of Li–S bond and Li–Li metallic bond are 2.479 Å and 2.863 Å, respectively, which are in good agreement with other theoretical results.30,31 The symmetrical atomic configuration can effectively improve the structural stability of Li2S.
However, the structural features of the other four structures are different from those of the CaF2-type structure. From Fig. 1, we can see that Br2O-type, K2S-type and Cs2S-type belong to the orthorhombic structure, and Na2S-type is a hexagonal structure. Therefore, the atomic configuration of these structures is different from that of the CaF2-type structure. As presented in Table 1, the calculated value of the b-axis of Na2S-type, K2S-type, Cs2S-type and Br2O-type is smaller than the corresponding axis for CaF2-type. It is worth noticing that the calculated a-axis (except for Na2S-type) and c-axis (except for Br2O-type) of those predicted structures are larger than the corresponding axes for CaF2-type structure. The calculated volume of Br2O-type structure is slightly larger than that of CaF2-type structure. On the contrary, the calculated volume of Na2S-type, K2S-type and Cs2S-type is smaller than that of CaF2-type structure. These results indicate that the symmetrical atomic arrangement of these predicted structures is weaker than that of CaF2-type structure. As a result, the localized hybridization between atoms of the former is weaker than that of CaF2-type structure. This is why the thermodynamic stability of the CaF2-type structure is better than that of the other predicted structures.
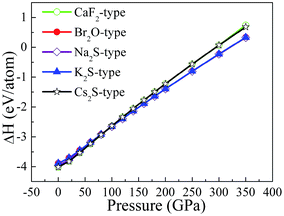
To study the influence of pressure on the structural stability of Li2S, Fig. 2 displays the calculated formation enthalpy of Li2S as a function of pressure. In particular, we examine the phase transition of Li2S (0–350 GPa). For Li2S, high pressure markedly improves the coulomb repulsion between Li atom and S atom, which results in a large chemical potential. As a result, the formation enthalpies of Li2S with the five structures increase monotonically with increasing pressure. From Fig. 2, it is observed that the calculated formation enthalpy of Li2S increases with increasing pressure. We suggest that this trend is attributed to the variation of electronic structure under pressure. To reveal the nature of formation enthalpy under pressure, Fig. 3 shows the calculated unit-cell volume and chemical bonding of Li2S with the five structures. Here, we consider the bond length of Li–S bond and Li–Li metallic bond under high pressure. It is clear that the calculated unit-cell volume and bond lengths of Li2S decrease gradually with increasing pressure. In other words, high pressure can increase the coulomb repulsion between Li atom and S atom. This is why the formation enthalpy of Li2S monotonically increases under pressure.
Importantly, we further find that pressure leads to a phase transition from CaF2-type structure to Na2S-type structure at ∼100 GPa (see Fig. 2) because the calculated formation enthalpy of CaF2-type structure is slightly smaller than that of Na2S-type structure when the pressure is below 100 GPa. On the contrary, the calculated formation enthalpy of CaF2-type structure is bigger than that of Na2S-type structure when the pressure is above 100 GPa. This discrepancy is demonstrated by the lattice parameters and chemical bonding. For CaF2-type structure, the lattice parameter decreases with increasing pressure. In particular, pressure results in charge transfer from Li–S to Li–Li atoms. Although the trend of lattice parameters of Na2S-type structure is similar to that of CaF2-type structure, the coulomb repulsion of Li–Li atoms of Na2S-type structure is less than that of the corresponding atoms for CaF2-type structure. This discrepancy can give rise to a phase transition under high pressure.
Importantly, the dynamical stability of a solid is related to the phonon frequency,32,33 which is calculated by the phonon dispersion. Generally speaking, imaginary phonon frequency indicates dynamical instability. On the contrary, no imaginary phonon frequency implies dynamical stability in the ground state. To examine the influence of pressure on dynamical stability of Li2S with the five structures, Fig. 4 and 5 present the calculated phonon dispersion curves of Li2S at 0 and 100 GPa, respectively. It can be seen that no imaginary frequencies are observed for CaF2-type structure at 0 and 100 GPa, implying that Li2S with CaF2-type structure is dynamically stable in the ground state. It is obvious that Li2S still retains the CaF2-type structure under high pressure.
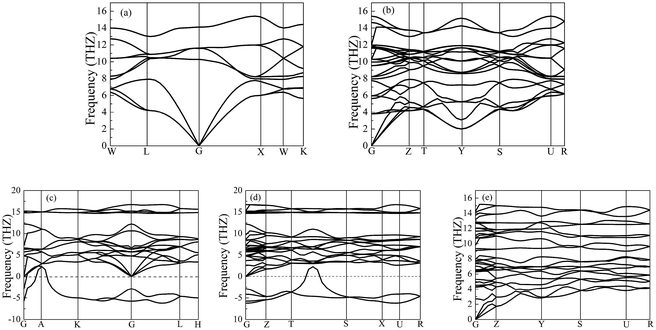 | ||
| Fig. 4 Calculated phonon dispersion curves of Li2S at 0 GPa. (a) CaF2-type structure, (b) Br2O-type structure, (c) Na2S-type structure, (d) K2S-type structure and (e) Cs2S-type structure. | ||
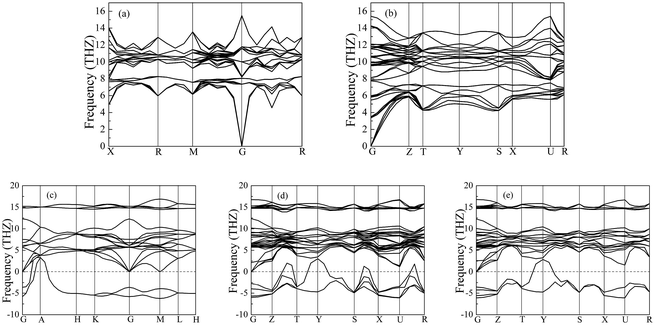 | ||
| Fig. 5 Calculated phonon dispersion curves of Li2S at 100 GPa. (a) CaF2-type structure, (b) Br2O-type structure, (c) Na2S-type structure, (d) K2S-type structure and (e) Cs2S-type structure. | ||
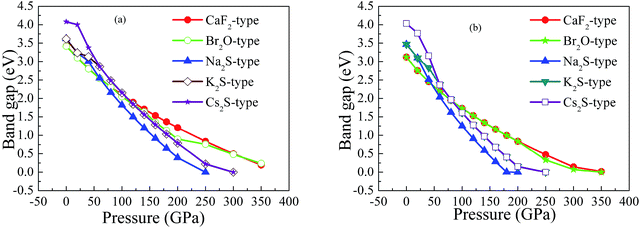
On the other hand, our predicted Cs2S-type structure is dynamically stable at zero pressure because no imaginary phonon frequency is found at 0 GPa. On the contrary, Cs2S-type structure is dynamically unstable at 100 GPa because we observe imaginary phonon frequency in this structure when pressure is up to 100 GPa. The dynamical stability of Br2O-type structure is similar to that of CaF2-type structure. It is worth noticing that Li2S with Na2S-type and K2S-type structures are dynamically unstable. To investigate the influence of pressure on the electronic properties, Fig. 6 displays the band gap of Li2S as a function of pressure. In particular, to further examine the electronic properties under high pressure, we consider and compare the GGA functional and LDA functional. It can be seen that the calculated band gap of Li2S with CaF2-type structure is about 3.422 eV by GGA and 3.120 eV by LDA, which are in excellent agreement with other theoretical results (3.297 eV).12 In addition, the band gap of Cs2S-type structure (4.081 eV by GGA and 4.035 eV by LDA) is larger than that of the other structures. These results demonstrate the insulating nature of Li2S. With increasing pressure, the band gap of the five structures decreases. Importantly, we find that the value of the band gap is close to zero when pressure is up to 350 GPa. That is to say, high pressure can result in electronic overlap between the bottom of the conduction band and the top of the valence band, which induces an electronic transition between conduction band and valence band. In particular, pressure can improve the charge overlap of atoms with further increasing pressure. As mentioned above, we can conclude that pressure gives rise to insulator-to-metal transition of Li2S.
To understand the nature of the insulator-to-metal transition, Fig. 7 and 8 show the calculated band structure and partial density of states of Li2S at 0 and 350 GPa, respectively. Considering the structural stability, we select the Ca2F-type structure, Br2O-type structure and Cs2S-type structure. The calculated results of band structure at both 0 GPa and 350 GPa are shown for comparison. At 0 GPa, it is clear that the profile of the valence band is mainly contributed by S-3p state and part of Li-2s state. The localized hybridization between S-3p state and Li-2s state forms the Li–S bond. However, the profile of the conduction band mainly derives from Li-2s state. The delocalization of electron acceptor, especially for the position of Li-2s state, determines the degree of charge interaction between the conduction band and valence band.
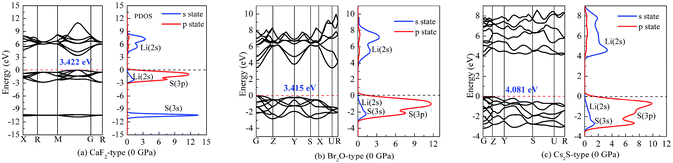 | ||
| Fig. 7 Band structure and partial density of states (PDOS) at 0 GPa: (a) Li2S with CaF2-type structure, (b) Li2S with Br2O-type structure, (c) Li2S with Cs2S-type structure. | ||
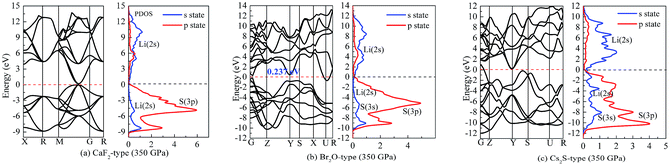 | ||
| Fig. 8 Band structure and partial density of states (PDOS) at 350 GPa: (a) Li2S with CaF2-type structure, (b) Li2S with Br2O-type structure, (c) Li2S with Cs2S-type structure. | ||
We assume that pressure can give rise to electronic transport of Li atoms from conduction band to Fermi level. This enhances the localized hybridization between Li-2s state and S-3p state. From Fig. 7, the band width of Li2S becomes narrow with increasing pressure. We further find an electronic overlap at the Fermi level when pressure is up to 350 GPa. As a result, pressure results in insulator-to-metal transition of Li2S. We suggest that the main reason is the pairing of Li atoms, especially for 2s-2s localized hybridization of Li atoms. The calculated bond length of Li–Li metallic bond is 1.990 Å. In fact, the electronic overlap is also demonstrated by lattice parameters and chemical bonding. With increasing pressure, the lattice parameters and chemical bonding of the five structures decrease. For example, the calculated lattice parameter of Li2S with CaF2-type structure at 0 GPa is a = 5.725 Å. However, this lattice parameter decreases to 3.978 Å at 350 GPa.
4. Conclusions
In conclusion, we have investigated the influence of pressure on the structure and insulator-to-metal transition of Li2S by using first-principles calculations. Five possible crystal structures are examined according to the phonon dispersion and thermodynamic model. Li2S with CaF2-type structure is more thermodynamically stable than with the other structures. The calculated phonon dispersions show that Li2S with CaF2-type, Br2O-type and Cs2S-type structures are dynamically stable in the ground state. However, Li2S with Na2S-type and K2S-type structures are dynamically unstable. The calculated results show that the structural stability of Li2S derives from the localized hybridization between Li atom and S atom. However, the Li–Li antibonding is the origin of the insulating state for Li2S. These structures exhibit an insulating nature in the ground state. With increasing pressure, the band width of the five structures decreases and the lattice parameters of these structures decrease. They lead to Li-2s orbital migrating from conduction band to valence band, and to increasing electronic overlap. Our results predict that pressure can result in insulator-to-metal transition of Li2S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (grant no. 51267007). We acknowledge discussions with Lady Yun Zheng.References
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed.
- L. C. H. Gerber, P. D. Frischmann, F. Y. Fan, S. E. Doris, X. Qu, A. M. Scheuermann, K. Persson, Y. M. Chiang and B. A. Helms, Nano Lett., 2016, 16, 549–554 CrossRef CAS PubMed.
- K. Wang, K. Jiang, B. Chung, T. Ouchi, P. J. Burke, D. A. Boysen, D. J. Bradwell, H. Kim, U. Muecke and D. R. Sadoway, Nature, 2014, 514, 348–350 CrossRef CAS PubMed.
- M. T. Mcdowell, Z. Lu, K. J. Koski, J. H. Yu, G. Zheng and Y. Cui, Nano Lett., 2015, 15, 1264–1271 CrossRef CAS PubMed.
- Y. Cheng, A. Nie, Q. Zhang, L. Y. Gan, R. S. Yassar and U. Schwingenschlgol, ACS Nano, 2014, 8, 11447–11453 CrossRef CAS PubMed.
- Y. Pan and W. Guan, Int. J. Hydrogen Energy, 2016, 41, 11033–11041 CrossRef CAS.
- G. Ma, Z. Wen, J. Jin, M. Wu, X. Wu and J. Zhang, J. Power Sources, 2016, 267, 542–546 CrossRef.
- H. Nagata and Y. Chikusa, J. Power Sources, 2016, 329, 268–272 CrossRef CAS.
- C. Barchasz, J. C. Lepretre, F. Alloin and S. Patoux, J. Power Sources, 2012, 199, 322–330 CrossRef CAS.
- J. Liu, H. Nara, T. Yokoshima, T. Momma and T. Osaka, J. Power Sources, 2015, 273, 1136–1141 CrossRef CAS.
- X. Meng, D. J. Comstock, T. T. Fister and J. W. Elam, ACS Nano, 2014, 10, 10963–10972 CrossRef PubMed.
- R. D. Eithiraj, G. Jaiganesh, G. Kalpana and M. Rajagopalan, Phys. Status Solidi B, 2007, 244, 1337–1346 CrossRef CAS.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Sci. Rep., 2013, 3, 2261 CrossRef PubMed.
- S. Urbonaite and P. Novak, J. Power Sources, 2014, 249, 497–502 CrossRef CAS.
- M. T. Winkler, D. Recht, M. J. Sher, A. J. Said, E. Mazur and M. J. Aziz, Phys. Rev. Lett., 2011, 106, 178701 CrossRef PubMed.
- H. Park, H. S. Koh and D. J. Siegel, J. Phys. Chem. C, 2015, 119, 4675–4683 CAS.
- H. Khachai, R. Khenata, A. Bouhemadou, A. H. Reshak, A. Haddoou, M. Rabah and B. Soudini, Solid State Commun., 2008, 147, 178–182 CrossRef CAS.
- H. Noh, J. Song, J. K. Park and H. T. Kim, J. Power Sources, 2015, 293, 329–335 CrossRef CAS.
- C. Wang, X. Wang, Y. Yang, A. Kushima, J. Chen, Y. Huang and J. Li, Nano Lett., 2015, 15, 1796–1802 CrossRef CAS PubMed.
- P. T. Cunningham, S. A. Johnson and E. J. Cairns, J. Electrochem. Soc., 1979, 119, 1448–1450 CrossRef.
- A. Grzechnik, A. Vegas, K. Syassen, I. Loa, M. Hanfland and M. Jansen, J. Solid State Chem., 2000, 154, 603–611 CrossRef CAS.
- A. Vegas, A. Grzechnik, K. Syassen, I. Loa, M. Hanfland and M. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 151–156 CrossRef CAS.
- A. Vegas, A. Grzechnik, M. Hanfland, C. Muhle and M. Jansen, Solid State Sci., 2002, 4, 1077–1081 CrossRef CAS.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdew, Nat. Chem., 2016, 8, 831–836 CrossRef CAS PubMed.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- K. Kaasbjerg, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115317 CrossRef.
- Y. Pan and W. Guan, J. Power Sources, 2016, 325, 246–251 CrossRef CAS.
- Z. Liu, S. Bertolini, P. B. Balbuena and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2016, 8, 4700–4708 CAS.
- Y. S. Su and A. Manthiram, Nat. Commun., 2012, 3, 1166 CrossRef PubMed.
- Y. Zhang, V. Ozolins, D. Morelli and C. Wolverton, Chem. Mater., 2014, 26, 3427–3435 CrossRef CAS.
- Y. Liu, D. Duan, X. Huang, F. Tian, D. Li, X. Sha, C. Wang, H. Zhang and T. Cui, J. Phys. Chem. C, 2015, 119, 15905–15911 CAS.
| This journal is © The Royal Society of Chemistry 2017 |