Open Access Article
Open Access ArticleSubstrate-induced changes in dynamics and molecular motions of cuticle-degrading serine protease PL646: a molecular dynamics study
Li-Quan Yang†
abc,
Peng Sang† abc,
Ruo-Peng Zhang*d and
Shu-Qun Liu*c
abc,
Ruo-Peng Zhang*d and
Shu-Qun Liu*c
aCollege of Agriculture and Biological Science, Dali University, Dali, P. R. China
bCollaborative Innovation Center for Biodiversity and Conservation in the Three Parallel Rivers Region of China, Dali University, Dali, P. R. China
cState Key Laboratory for Conservation and Utilization of Bio-Resources in Yunnan, Yunnan University, Kunming, P. R. China. E-mail: shuqunliu@ynu.edu.cn; Tel: +86-871-650-35257
dDepartment of Reproductive Medicine, The First Affiliated Hospital of Dali University, Dali, P. R. China
First published on 30th August 2017
Abstract
Cuticle-degrading serine proteases secreted by nematophagous fungi can degrade the nematode cuticle during the infection processes. PL646, an alkaline cuticle-degrading serine protease derived from the nematophagous fungus Paecilomyces lilacinus, has been shown to have a high nematicidal activity. Although the crystal structure of PL646 provides a solid basis for investigating its structure–function relationship, the detailed aspects of the dynamics involving the substrate binding, orientation, catalysis, product release, and how these processes are regulated, remain unstudied. Molecular dynamics (MD) simulations and metadynamics simulations of PL646 with and without the peptide substrate AAPV were performed to investigate the changes in structure, molecular motions, and free energy landscape (FEL) of PL646 upon substrate binding. The results indicate that during simulations, the substrate-bound PL646 adopts a more stable and compact conformation than the substrate-free form. However, a few regions located opposite the substrate binding pockets or connected to the catalytic residue show increased flexibility upon substrate binding. Combined essential dynamics (ED) analysis reveals that, upon substrate binding, the noticeable displacements occur not only in the substrate binding pockets/sites, but also in the surface-exposed loops. The dynamic pockets caused by the large concerted motions are proposed to be linked to the substrate recognition, binding, orientation, catalysis, and product release of PL646. The constructed FELs reveal that the substrate-free PL646 has a more rugged and wider free energy surface, and a higher minimum free energy level than the proteinase in complex with its substrate, indicating that the substrate binding reduces the conformational flexibility while increasing the stability of PL646. The results presented in this work will facilitate a better understanding of the structure–dynamics–function relationship of the cuticle-degrading serine protease PL646.
1. Introduction
Proteases are enzymes that can cleave peptide bonds in other proteins through catalytic reaction. Serine proteases (EC 3.4.21), which are conserved in almost all organisms, participate in an enormous number of biological processes such as digestion, immune response, blood coagulation, reproduction, and infection of host by microbial pathogen.1,2 Serine proteases exist as two main families: the trypsin-like (EC 3.4.21.4) and the subtilisin-like (EC 3.4.21.14) families. Although these two families have totally different structures, they commonly make use of a mechanism of action through an identical stereochemistry of the catalytic triad and oxyanion hole.3,4 In this mechanism, the Ser functions as the primary nucleophile, the His plays a dual role as the proton acceptor and donor at different stages in the reaction, and the Asp brings the His into the correct orientation to facilitate nucleophilic attack by the Ser.5 The oxyanion hole stabilizes the developing negative charge on the oxygen atom of the substrate during the formation of the tetrahedral intermediate.5,6Serine proteases derived from nematophagous fungi are known as one of the most important virulence determinants during infection due to their ability to degrade the nematode cuticle, a hard physical barrier that protects nematodes from physical damage or pathogen invasion.7,8 Like the majority of host–pathogen interactions, the first step of the infection by nematophagous fungi is to break open the cuticle of the nematode followed by pathogen entry. Since proteins are the main structural components of the nematode cuticle, nematophagous fungi need to produce highly efficient proteases to degrade them. Serine proteases, which have been shown to play a crucial role in digesting proteins, have become the subject of intense study.9–11
During the past decades, many cuticle-degrading proteases have been purified and characterized from different nematophagous or entomopathogenic fungi such as Arthrobotrys oligospora,12,13 Pochonia chlamydospora (syn. Verticillium chlamydosporium),14 Beauveria bassiana,15 and Metarhizium anisopliae.16 The highly nematicidal/insecticidal activities of these enzymes have been attributed to their highly catalytic activities towards the cuticle proteins. Of interest is that all these cuticle degrading proteases have been identified to belong to the subtilisin-like serine protease family according to their amino acid sequences.17
PL646, a cuticle-degrading subtilisin-like serine protease secreted by the nematophagous fungus Paecilomyces lilacinus, is an alkaline protease showing a high cuticle-degrading and nematicidal activity.8,18,19 In addition to characterizing the physiochemical properties, optimum reaction conditions, and substrate specificity of PL646, our laboratory has also determined the crystallographic structure of PL646 in complex with a substrate inhibitor, methoxysuccinyl-Ala-Ala-Pro-Val-chloromethyl ketone (MSU-AAPV-CMK).18 Similar to other subtilisin-like serine proteases, the crystal structure of PL646 (Fig. 1) shows a well-defined global fold composed of 15 β strands, six α helices and two 3/10 helices. These secondary structure elements can be divided into an internal core consisting of a nine-stranded parallel β sheet and two buried α helices, and an outer periphery, which encapsulates the internal core and is composed of four α helices and two antiparallel two-stranded β sheets. The catalytic triad of PL646 is composed of Asp41, His72 and Ser227; the oxyanion hole is formed by the Nδ atom of Asn164 and the amido N atom of Ser-227. The peptide substrate inhibitor MSU-AAPV ketone, is located in a cleft formed between the two peptide segments consisting of residues 103–107 and 135–139. There are five cysteines in the crystal structure of PL646; four of those form two disulfide bonds: Cys36–Cys126 and Cys181–Cys253, while Cys76 is free. A calcium ion is coordinated with high affinity by carbonyl oxygen atoms of Glu177, Val180, and Leu201, Oγ1 of Thr182, and Oδ2 of Asp203.
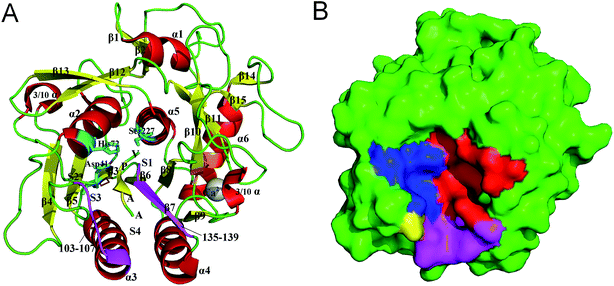 | ||
| Fig. 1 Structure and molecular surface of PL646. (A) Ribbon representation of the crystal structure of PL646 bound to its substrate inhibitor (PDB code 3F7O). The α helices, β strands and loops/links are colored red, yellow and green, respectively. The catalytic triad residues Asp41–His72–Ser227 are shown as a stick model and colored cyan. The two substrate binding segments, which are composed of residues 103–107 and 135–139 are colored purple. The two disulfide bonds (Cys36–Cys126 and Cys181–Cys253) are colored orange. The substrate binding sites S1–S4, the peptide substrate AAPV, and the calcium cation are all labeled. (B) Molecular surface of PL646. The S1, S2, S3 and S4 pocket are highlighted by red, blue, yellow and purple color, respectively. | ||
Although the crystal structure of PL646 provides a solid basis for investigating its structure–function relationship, the detailed aspects of the dynamic processes such as the substrate binding, orientation, catalysis, product release, and how these processes are regulated, remain unstudied. Proteins are dynamic entities and their biological functions are essentially rooted in their physical motions.20 Therefore, a complete understanding of a protein's function requires analyses of its dynamic behavior in addition to its static structure.
Molecular dynamics (MD) simulations is a powerful tool to investigate structural and dynamical information of macromolecular structure in atomic details.21,22 In this study, we have performed MD simulations of PL646, with and without the peptide substrate AAPV, to investigate the changes in dynamics and molecular motions of this protease induced upon substrate binding. Apart from comparison of the global structural properties of these two forms of PL646 during simulations, ED analyses were used to investigate the dynamic variations of the substrate-binding pockets/subsites, for which relevant functional implications were also discussed. By performing metadynamics simulations, we constructed the FELs of the substrate-free and substrate-bound PL646. The comparison between these two FELs sheds light on the mechanisms underlying the conformational changes of substrate-binding regions and explains the effect of substrate binding on dynamics and stability of PL646. The results presented in this paper will greatly facilitate the understandings of the structure–dynamics–function relationship of the cuticle-degrading proteases.
2. Materials and methods
2.1 Preparation of the starting structures
The crystal structure of PL646-MSU-AAPV-CMK, which was solved at a resolution of 2.1 Å, was obtained from the PDB database (PDB ID 3F7O).23 The hetero atoms, crystal waters, and the N-terminal methoxysuccinyl group and C-terminal chloromethyl ketone group in the inhibitor substrate were removed manually, and only the protein atoms, calcium cation and peptide substrate AAPV were retained. The finally obtained structural model is referred to as the substrate-bound PL646 hereafter. The model of the substrate-free PL646 was obtained by directly removing the peptide substrate from the substrate-bound PL646. These two models were used as initial coordinates for MD simulations.2.2 Molecular dynamics setup
All MD simulations were performed with the GROMACS software package24 with the GROMOS96 43a1 force field. The two starting structural models were individually solvated using the single point charge (SPC) water model25 in a cubic periodic box with a 1.0 nm solute-wall minimum distance. After the first steepest descent energy minimization, 5 chloride ions were added respectively to the substrate-free and substrate-bound systems to neutralize the overall system charge, leading to a total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 264 and 10
264 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 atoms for these two systems, respectively. Two conjugate gradient energy minimizations were subsequently performed until no significant energy change could be detected, which were followed by a 400 ps position-restrained MD simulations to better “soak” the protein into the water solvent. To ensure conformational sampling efficiency, eight independent 50 ns production MD simulations were performed for both the substrate-free and substrate-bound PL646 simulation systems. The initial atomic velocities of each simulation were taken from a Maxwell distribution. The obtained MD trajectories for the same system but characterized by different initial velocities are referred to as replicas 1–8.
271 atoms for these two systems, respectively. Two conjugate gradient energy minimizations were subsequently performed until no significant energy change could be detected, which were followed by a 400 ps position-restrained MD simulations to better “soak” the protein into the water solvent. To ensure conformational sampling efficiency, eight independent 50 ns production MD simulations were performed for both the substrate-free and substrate-bound PL646 simulation systems. The initial atomic velocities of each simulation were taken from a Maxwell distribution. The obtained MD trajectories for the same system but characterized by different initial velocities are referred to as replicas 1–8.
The production MD simulations were performed on a Linux cluster with 32 CPUs. The other simulation protocols used were: the time step was 2 fs; center-of-mass motion was removed every time step; non-bonded pair was updated every 10 time steps; long-range electrostatic interactions were treated using the Partial Mesh Ewald (PME) algorithm26 with interpolation order of 4, Fourier spacing of 0.135 nm, and coulomb radius of 1 nm; van der Waals (vdW) interactions were treated with a direct cutoff radius of 1.4 nm; protein and non-protein (solvent and counterions) were independently coupled to a 300 K heat bath with a coupling constant τ_t of 0.1 ps; pressure was maintained by weakly coupling the system to an external pressure bath at one atm with a coupling constant τ_p of 0.5 ps;27 LINCS algorithm28 with order 4 was used to constrain the bond lengths to their equilibrium positions; structural coordinates were saved every 10 ps.
2.3 Trajectory stability and sampling convergence
The stability and the equilibration were checked by monitoring the time-dependent backbone root mean square deviation (RMSD) with respect to the starting structures. For each system of the MD simulations, the equilibrated parts of each replica were concatenated together to obtain a single joined trajectory, representative of different sampling directions around the starting structure.To evaluate the convergence of conformational sampling, the cosine contents of the first few eigenvectors obtained from essential dynamics (see below for details of ED) analyses were computed, including replicas 1–8 and the single joined trajectories of each simulation system. The cosine similarity of the first few eigenvectors is a good indicator to assess whether the conformational sampling is converged or not. If the cosine content value is high (i.e., close to 1), the corresponding molecular motions in the protein dynamics resemble random diffusion, and thus the sampling is insufficient on the timescale of the simulation. In contrast, the value close to 0 means a converged sampling.
2.4 Geometrical property analyses
The conventional structural and/or geometrical properties of the proteins during MD simulations, including the number of hydrogen bonds (NHB), number of native contacts (NNC), number of residues in the secondary structural elements (SSE) (or secondary structure content, SSC), radius of gyration (Rg), solvent accessible surface area (SASA), root mean square fluctuations (RMSF), and root mean square deviations (RMSD), were calculated using the programs g_hbond, g_mindist, do_dssp,29 g_gyrate, g_sas, g_rmsf and g_rms within the GROMACS package, respectively.2.5 Essential dynamics (ED) analyses
The ED method,30 also known as the principal component analysis (PCA) in mathematics, is a powerful tool for filtering large concerted motions from an ensemble of structures determined by experimental methods or derived from computer simulation, and has been widely used for studying protein motions in relation to its function.31–35 ED analysis is based on the diagonalization of a covariance matrix built from atomic fluctuations, yielding a set of eigenvectors and eigenvalues. The eigenvectors, which indicate directions in the conformational space, describe the large concerted fluctuations of the atoms along those directions. The eigenvalues are the mean square fluctuations (MSF) of the system along the corresponding eigenvectors. The central hypothesis of ED is that only a few eigenvectors with large corresponding eigenvalues are important for describing the overall motions of a protein. ED analyses were performed on the equilibrium portions of MD trajectories using the g_covar and g_anaeig programs within GROMACS. Only the Cα atoms were included in ED analyses.Combined ED analysis is a useful method for comparing the ED properties of two simulations on similar systems.36 In this method, two or more MD trajectories fitted on the same reference structure are concatenated, and the ED analysis is performed on the combined trajectory. Analysis and comparison of the properties of different parts of the eigenvector projection provide a powerful way to assess similarities and differences in essential motions between different simulations. For example, the differences in the average values between different parts of the same eigenvector projection provide information about the difference in equilibrium fluctuations or average structures of the simulations; and the differences in the mean square displacement (MSD) between different parts of the eigenvector projection can be used to study difference in conformational shift or dynamics of the systems studied. In this study, the combined ED analysis was performed on a merged trajectory obtained through concatenating the joined MD trajectories for the substrate-free and substrate-bound forms of PL646. After the diagonalization of the covariance matrix, the merged trajectory was projected onto the first 30 combined eigenvectors, and the average values and MSDs for the two equal halves of the same combined eigenvector projection were calculated and compared.
2.6 Metadynamics and FEL
The metadynamics37,38 is a powerful tool for both accelerating rare event sampling and reconstructing FEL by introducing a history-dependent bias potential acting on a restricted number of collective variables (CVs). The well-tempered metadynamics39 is an improved version that solves the convergence problem of the standard metadynamics by decreasing the bias potential growth rate. Therefore, in this work the well-tempered metadynamics simulations were performed to reconstruct the FELs of the two systems.The CV1 and CV2 used in metadynamics simulations were the projection of MD trajectory onto the eigenvectors 1 and 2, respectively. The starting structure for metadynamics simulations was the final snapshot from the standard MD simulation. The initial Gaussian height was set to 0.4 kJ mol−1 and was added every 2 ps; the Gaussian width was set to 0.35 nm; the bias factor was set to 10. Other simulation parameters and conditions are the same as those in the standard MD simulations. The well-tempered metadynamics simulations were run for 100 ns, followed by FEL constructions using the weighted histogram analysis method.
3. Results
3.1 Structural stability and equilibration evaluation of the conformation
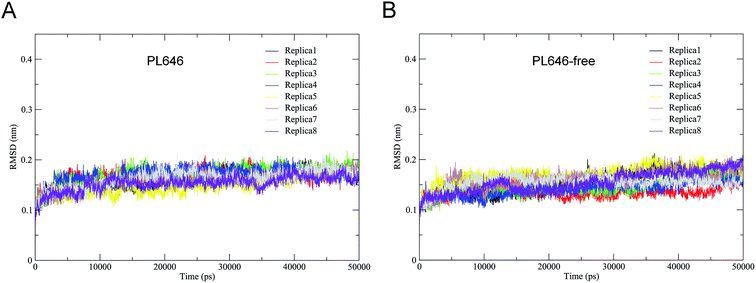
The stability and the equilibration of MD simulations were checked for each replica of the two simulation systems by monitoring the backbone RMSD with respect to the starting structures as a function of time. Fig. 2 shows that for each replica of both simulation systems the backbone RMSDs increase steadily from the start of simulations until ∼10 ns. Afterward, these curves exhibit relatively stable fluctuations. Therefore, the equilibrated portions (10–50 ns) of each replica were concatenated, thus yielding two 320 ns single joined trajectories. The single joined trajectories were used for further analyses.Table 1 shows the cosine contents for the first two eigenvectors derived from ED analyses of individual replicas and of single joined trajectories. For each replicas of the substrate-bound and substrate-free PL646 simulation systems, their eigenvector cosine contents are significantly higher than the corresponding values of the single joined trajectories. The results show that our strategy of performing multiple replica MD simulation has achieved a relatively higher degree of sampling convergence.
| Traj. | PL646 | PL646-free | ||
|---|---|---|---|---|
| Eig. 1 | Eig. 2 | Eig. 1 | Eig. 2 | |
| 1 | 0.9018 | 0.734 | 0.8802 | 0.8494 |
| 2 | 0.8322 | 0.689 | 0.7406 | 0.7273 |
| 3 | 0.8573 | 0.7437 | 0.826 | 0.6325 |
| 4 | 0.7569 | 0.1363 | 0.5604 | 0.5364 |
| 5 | 0.7954 | 0.7889 | 0.9249 | 0.859 |
| 6 | 0.8677 | 0.5534 | 0.9205 | 0.6845 |
| 7 | 0.4201 | 0.1406 | 0.718 | 0.578 |
| 8 | 0.9534 | 0.8598 | 0.9141 | 0.4015 |
| Joined | 0.1221 | 0.053 | 0.3395 | 0.219 |
3.2 Structural properties
To assess the change in structure of PL646 induced by the substrate binding, the average values and standard deviations for some structural properties, including the NHB, SASA, NNC, Rg, RMSD, and SSE, were calculated over the two joined MD trajectories (Table 2).| PL646 | NHBa | SASAb (Å2) | NNCc | Rgd (Å) |
|---|---|---|---|---|
| a Number of hydrogen bonds. A hydrogen bond is considered to exist when the donor–hydrogen–acceptor angle is larger than 120° and the donor–acceptor distance is less than 3.5 Å.b Total solvent accessible surface area.c Number of native contacts. A native contact is considered to exist if the distance between two atoms is less than 6 Å.d Radius of gyration.e Number of residues in the corresponding secondary structure elements.f RMSD relative to respective starting structures. The RMSD values were calculated through superposition on the secondary structure element backbones as defined by DSSP in the starting structure.g RMSD values of all atoms.h RMSD values of all backbone atoms.i RMSD of secondary structure backbone atoms. | ||||
| Bound | 226 (8) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 (166) 323 (166) |
137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227 (863) 227 (863) |
16.6 (0.4) |
| Free | 217 (8) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 (191) 512 (191) |
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 (919) 775 (919) |
16.6 (0.5) |
Overall, there are only minor differences in the average values of these properties between the two forms of the protease, implying no large conformational changes occur before and after substrate binding. Nevertheless, the subtle differences observed for certain geometrical properties can still reflect the effect of substrate binding on the structure of PL646. For example, the substrate-bound PL646 has higher average values of NHB and NNC than the substrate-free PL646, indicating that binding of the peptide substrate increases the number of interatomic interactions/contacts in the structure of the protease. On the contrary, the substrate-bound form of the protease has a lower SASA than the substrate-free form, indicating that substrate binding shrinks the surface of the protease, although the overall shape/size of PL646 remains unchanged upon substrate binding as reflected by the identical Rg values. In addition, the binding of the peptide substrate has a negligible effect on SSE because only a very slight increase can be observed for β-sheet and turn while α-helix remaining unchanged. Of particular note is that the substrate-bound PL646 has lower average RMSD values of “all atom”, “all bb”, and “SS bb” RMSD than the substrate-free form, indicating that substrate binding not only stabilizes the structural backbone (especially the secondary structure backbone), but also the overall protein structure that includes the amino acid residue side chain atoms. It is also worth noting that for both forms of PL646, the average RMSD values are in the order “All atom” > “All bb” > “SS bb”, implying that the conformational deviations/fluctuations likely originate from the side chains, especially the side chains of the loop regions. Finally, the relatively higher standard deviations of these structural properties for the substrate-free protease than for the substrate-bound form also indicate that the presence of the substrate reduces the structural fluctuations and as thus rigidifies to certain extent the overall protein structure.
3.3 Structural flexibility
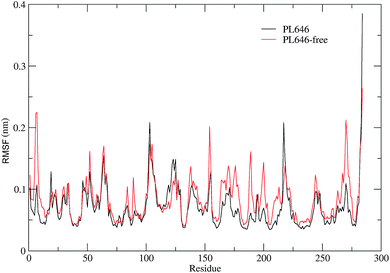
In order to assess and compare the structural flexibility of PL646 before and after substrate binding, Cα RMSF of the two forms of PL646 as a function of residue number were computed and adopted as the flexibility index (Fig. 3).As shown in Fig. 3, the two forms of PL646 have similar flexibility profiles: the regular secondary structure regions that constitute the protein structural core are characterized by low RMSF values while the N-termini, C-termini, and the loop regions exposed to the protein surface show large RMSF values. However, close inspection reveals that, among the regions characterized by different RMSF values, the most exhibit higher RMSF values in the substrate-free than in the substrate-bound PL646. This observation implies that the free form of the protease has a higher global flexibility than the bound form. The calculated average RMSF values of the substrate-free and -bound PL646 are 0.082 nm and 0.070 nm, respectively, supporting the above observation and in agreement with structural property analysis.
The regions characterized by significantly lower flexibility in the substrate-bound than in the substrate-free PL646, which were defined as those with Cα RMSF difference lower than 0.02 nm include residues 5–10, 49, 52, 82–85, 87–92, 136–138, 153–155, 161–167, 169–182, 185–192, 196–215, 241–245, and 262–275. Out of these regions, the N-, C-termini and some surface-exposed loops (i.e., residues 82–85, 87–92, and the loops located in region comprising residues 160 to 215) exhibit the most significantly higher flexibility in the substrate-free PL646. The residue segment 82–92 is a surface loop that connects α2 and β5. The N-terminus of α2 participates in the formation of the S2 pocket and the C-terminus of β5 precedes the segment 102–106 that participates in the formation of substrate binding pockets/sites S2, S3 and S4. The region 160–215 surrounds the S2 and S1 pockets but only few residues in this region directly participate in the formation of the S1 pocket. These observations suggest that the presence of the peptide substrate is able to reduce most significantly the flexibility of the loop regions opposite or in the surrounding of the substrate-binding pockets. Interestingly, the extent of the reduced flexibility of the residues that form the binding pockets (i.e., residues 134–138 participate in the formation of the S1 and S4 pockets and residues 64–69 constitute part of the S2 pocket), although also significant, is less than that of the regions in the surrounding of but not directly involved in the formation of the binding pockets. Only a few regions, i.e., residues 16–19, 113–128, and 216–218, show a significant increase (with RMSF values greater than 0.1) in flexibility upon the substrate binding. Of these regions, residues 16–19 are spatially close to the N- and C-termini and distant from the functional sites of the protease; residues 113–128, which span the C-terminal half of α3 and a well-exposed surface loop that links α3 and β6, are located opposite the substrate pockets S1, S2 and S4; the region composed of residues 216–218 is a short loop located between β12 and β13, at whose C-terminus the catalytic residue Ser227 is located. It seems likely that the improved flexibility of the latter two regions play a role in regulating the dynamics of the substrate-binding pockets and of the nucleophilic residue Ser227.
Taken together, the binding of the substrate to PL646 reduces the overall flexibility of the protease, and the significant decrease in flexibility is observed to be mainly localized in the regions surrounding or involved in the formation of the substrate-binding pockets, although a few regions located opposite the pockets or connected to the catalytic residue show increased flexibility upon binding.
3.4 Essential dynamic analysis
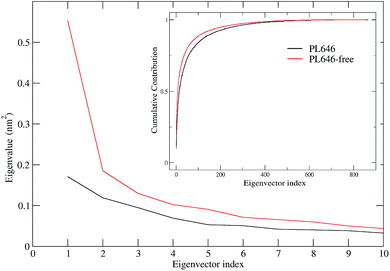
ED technique was used to investigate the large concerted motions in the two forms of PL646 and the effect of substrate binding on these motions. Covariance matrices were built from Cα atomic fluctuations in the joined MD trajectories, followed by the diagonalization of them. The obtained total MSF values are 1.87 and 2.37 nm2 for the substrate-bound and -free protease, respectively, indicating that the substrate-free PL646 experienced larger amplitude of fluctuations than the substrate-bound form during simulations. This is in agreement with the results of comparative analyses of the structural properties and the global structural flexibility described above, pointing to a common conclusion that the substrate binding reduces the conformational fluctuations/deviations and increases the overall structural rigidity of the protease.Fig. 4 shows the eigenvalues and the cumulative contribution of eigenvectors to the total MSF as a function of eigenvector index. As shown in the main plot of Fig. 4, although the eigenvalue curve of the substrate-free protease is steeper and hence causes a more sharp decrease of eigenvalues with increasing eigenvector index as compared to that of the substrate-bound form, the former has larger corresponding eigenvalues than the latter, implying that the substrate-free PL646 experiences larger amplitude of collective motions along each of the first 10 eigenvectors. As a result, when compared to the substrate-bound protease, the substrate-free protease requires fewer eigenvectors to achieve the same level of the cumulative contribution to the total MSF (inset plot, Fig. 4). For the substrate-bound PL646, the first 4 and 10 eigenvectors contribute 39.4% and 52.7% to the total MSF, respectively, while for the substrate-free PL646, the first 4 and 10 eigenvectors contribute 41.8% and 56.7% to the total MSF, respectively. These results indicate that, although the original conformational space spans the dimensions of 3N (here N = 284), most of the protein internal motions are confined within a subspace of very small dimensions. Therefore, the first 10 eigenvectors, especially the first 4 eigenvectors, can be considered to span an essential subspace within which the large-scale concerted motions take place.
3.5 Changes in molecular motions induced by substrate binding
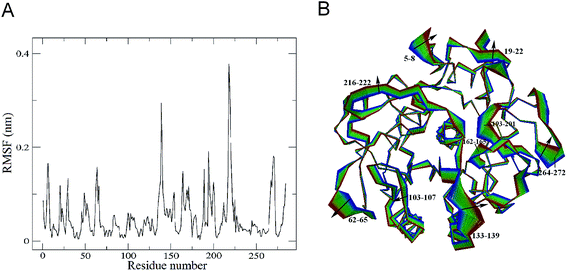
The changes in protein molecular motions upon substrate binding were investigated by performing the combined ED analysis on the merged trajectory of the two forms of the protease. The Cα root mean square fluctuations (RMSF) and the two extreme structures calculated along the first combined eigenvector of the merged trajectory are shown in Fig. 5A and B, respectively. It is important to keep in mind that the linear interpolations between the two extremes are not the conformational transition pathway between PL646 and PL646-free but emphasize merely the structural differences between them.As shown in Fig. 5A, the significant shifts (RMSF > 0.15 nm) are observed in regions of the N-termini and residues 5–8, 61–68, 133–139, 162–175, 188–190, 193–201, 215–223 and 264–272. Out of these, residues 61–68, 188–190, 193–201, 216–222 and 264–272 are surface exposed loops, residues 133–139 and 162–175 are substrate binding pocket S1 regions, residues 5–8 are close to the N-terminus. This result revealing that, upon substrate binding, the structural regions exhibiting large conformational displacements are located either in some surface-exposed loops and the N-termini, whereas the majority of the secondary structure components exhibits small shifts. This indicates that the substrate binding has a relatively minor influence on dynamics of the internal rigid core but a large effect on the external loops of PL646.
The largest displacement is seen in segment 216–222, which lies adjacent to the nucleophilic residue Ser227. Another large displacement is observed in residues 133–139, which are located in the substrate-binding region and participate in the formation of the substrate-binding subsites S1 and S4. Close inspection of the motions along eigenvector 1 (Fig. 5B) also reveals that the structural changes originate mainly from these two regions (residues 133–139 and 216–222), as well as many other surface exposed loops (such as loops 61–68, 188–190, 193–201 and 264–272) upon substrate binding.
It is interesting to note that the catalytic triad residues Asp41, His72 and Ser227 exhibit almost unchanged RMSFs in substrate-free PL646 compared to substrate-bound PL646. Therefore, the displacement and motions of residues 216–222, which lie adjacent to the nucleophilic residue Ser227, may be important as the binding and orientation of the substrate binding to S1 requires conformational adjustment of this segment.
Additionally, residues 133–139 and 162–175 participate in the formation of the substrate-binding pocket S1. As shown in Fig. 5B, the concerted shifts of these two segments towards each other lead to the closing of S1 pocket. At the same time, the outward movements of segments 103–107 and 133–139 cause the open of the substrate-binding groove. Meanwhile, most of the peripheric well-exposed loops (e.g., 5–8, 19–22, 62–65, 216–222, 266–272 and 193–200) move away from the core of the protease, thus loosening the structure of PL646 to a certain extent.
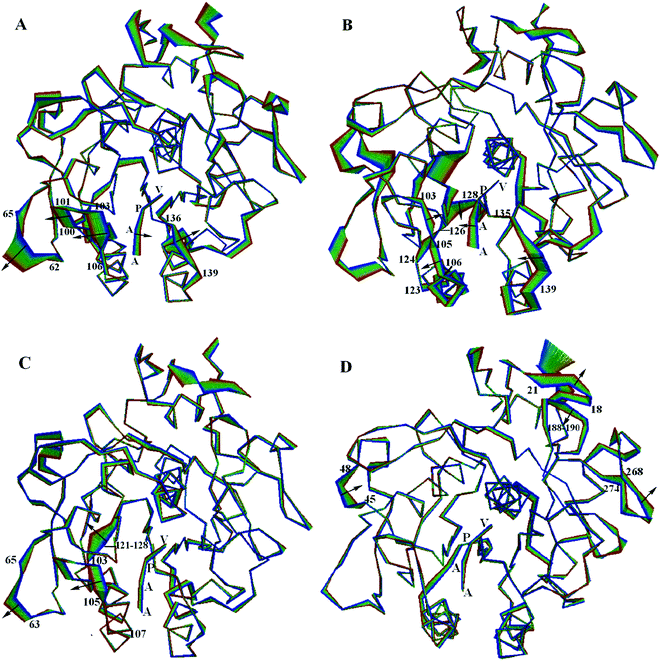
3.6 The large concerted motions of PL646
The large concerted motions of PL646 described by the first four eigenvectors (Fig. 6) could be proposed to be related to its functions.40,41In the most significant motion mode along eigenvector 1 (Fig. 6A), residues 100–106 and 136–139 move away from each other, which enlarges the substrate binding sites. At the same time, the substrate peptide AAPV moves toward the internal core of the protease. Meanwhile, the outwards concerted motions of the surface loop 62–65 also provides more spatial space for the movement of residues 100–106.
In the large concerted motion described by eigenvector 2 (Fig. 6B), the substrate binding segment 135–139 move towards the other substrate binding segment 103–107; and the segment 103–107 undergoes a twisting motion, with its upper and lower parts move towards and away from the segment 103–107, respectively. At the same time, the substrate peptide AAPV moves towards the upper part of segment 103–107. It is worth noting that the movement of segment 121–128, especially the large movement of residues 124–128. As mentioned previously, segment 121–128 connects α3 and β6; α3 follows the substrate binding segment 103–107 and β6 precedes the other substrate binding segment 135–139. Due to the small displacements of α3 and β6, we consider that the large displacement of the residue segment 121–128 could influence and modulate conformational variations of the substrate binding segments via a hinge mechanism. These motions lead to a twisting of the substrate binding groove as well as cause a closing of the S4 pocket.
In the third ranked motion mode along eigenvector 3 (Fig. 6C), the leftwards movement of the substrate binding segment 103–105, in conjunction with the same direction of movement of segment 63–65, enlarges the substrate pocket S4. Meanwhile, segment 121–128 exhibits a relatively larger displacement. We postulate that the displacement of segment 103–105 is also influenced and modulated by the large displacement of segment 121–128 via a hinge mechanism, as discussed above.
In the forth ranked motion mode along eigenvector 4 (Fig. 6D), no large displacements are observed for the substrate pockets or among the substrate binding sites. Large displacements are only observed in a few surface exposed loops (e.g., 18–21, 45–48, 188–190 and 268–274) and the C-termini regions. Those regions may have little influence on the function of PL646.
Taken together, the first few modes of the large concerted motions of PL646 can result in different consequences of conformational changes of the substrate-binding pockets, and therefore could be related to the processes of binding, orientation, catalysis and release of the substrate.
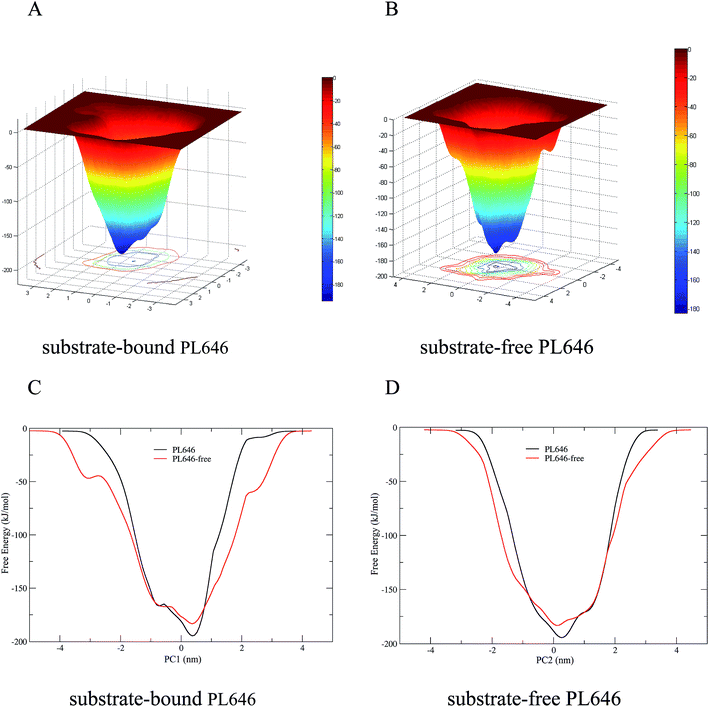
3.7 Free energy calculations
The FELs of the substrate-bound and substrate-free PL646 were constructed by performing metadynamics simulations using projections of the first (PC1) and second (PC2) eigenvectors as the CV1 and CV2, respectively. Fig. 7A and B show the constructed 2D FELs for the substrate-bound and substrate-free PL646, and Fig. 7C and D show the calculated 1D free energy profile as a function of PC1 (Fig. 7C) and of PC2 (Fig. 7D), respectively, both of which present a funnel-like shape. Furthermore, the FEL of PL646-free exhibits a more rugged and complex surface, which indicate that the FEL of PL646-free sampled a larger free energy surface than the FEL of PL646 during simulations.For the FELs of two forms of PL646, there is only one large free energy well in the global free energy minimum region, indicating only one stable conformational state residing within this well. A comparison between the full views of the FELs for PL646 and PL646-free reveals that the FEL of the substrate-free PL646 spans larger ranges of PC1 and PC2 and exhibits a more rugged free energy surface than that of the substrate-bound PL646. For instance, the FEL of substrate-free PL646 spans ranges of ∼9.30 and ∼8.65 nm along the PC1 and PC2, respectively, while the corresponding ranges for substrate-bound PL646 are ∼7.70 and ∼6.55 nm, respectively. It is worth noting that the substrate-bound PL646 has a lower minimum free energy value than the substrate-free PL646, which the difference of the value is ∼−11.21 kJ mol−1. In other words, upon substrate binding, PL646 residing within the global free energy minimum well has a lower free energy than the state of substrate-free PL646. Briefly, for the substrate-free PL646, both of its PC1 and PC2 profiles are wider and rougher than the corresponding profiles of the substrate-bound PL646.
It should be pointed out that the FELs and free energy profiles constructed from our metadynamics simulations are incomplete and represent a major portion of the native landscape, due to the limited conformational sampling and large dimensionality reduction. Therefore, the transition between the substrate binding states cannot be observed. However, such free energy calculations are still useful in characterizing the differences in thermodynamics and kinetics between substrate-free and -bound PL646.
4. Discussion
In our study, we performed relatively long and multi-replica simulation on the substrate-bound and substrate-free PL646 to investigate the molecular motions in relation to catalytic function and the influence of substrate binding on the dynamics of this protease.During MD simulations, both substrate-bound and substrate-free PL646 displayed very similar geometrical properties. However, the subtle differences in certain geometrical properties can still reflect the fact that upon substrate binding PL646 assumes a more overall compact and stable conformational state as well as a decreased overall structural flexibility than substrate-free PL646. Our observation that overall conformational flexibility of the protease decreases upon substrate binding is agreement with many studies of other enzymes.42–46 Furthermore, the binding of the substrate peptide AAPV primarily decreases the flexibility of many surface exposed loops and the N- and C-termini, whereas the structural rigidity of the structural core and the SSEs such as α helices and β sheets appears not to be affected.
Interestingly, the geometrical properties reveal that some regions exhibited a more flexible structural personality upon substrate binding. Those regions are mainly located opposite the pockets (residues 113–128) or connected to the catalytic residue (residues 216–218). We consider that the high mobility and the dynamics motions of those regions may modulate the dynamics/structural changes of the substrate-binding site through a hinge bending mechanism. The rigid structural segments connecting the high flexibility loops and the substrate binding site can serve as hinge points or intermediaries to transmit or mediate the signal of conformational changes. It is reasonable, therefore, to conclude that the conformational changes occurring opposite or far away from the substrate binding site can regulate the process of substrate binding.
Furthermore, our geometrical properties and ED analyses also indicate that there is no significant structural shift in the catalytic triad residues upon substrate binding, revealing that the architecture of the triad is well maintained whether the peptide substrate is present or not. During our ED analyses and combined ED analyses, the large concerted motions of substrate-bound and -free PL646, and the differences between the two forms, are captured by the first few eigenvectors. Among those motions, the structural movements and motions surrounding the substrate binding pockets/sites can cause dynamic variations of the binding pockets and therefore are often proposed to be related to the functional properties of the proteins.41,46–50
Based on these considerations, the large concerted motions of PL646 described by the first few eigenvectors have been discussed to link to its putative biological functions. The first ranked motion described by eigenvector 1 enlarges the substrate binding sites, thereby providing more space for the substrate residues to suit the requirements for accommodation and subsequent orientation of the substrate residues. In the second ranked motion described by eigenvector 2, the twist motion of the binding groove with the leftwards motion of the substrate peptide AAPV may relate to the orientation and catalysis of the substrate residues. The third ranked motion described by eigenvector 3 enlarges the S4 pocket, thus may lead to loose contact between the pockets and the substrate and is likely related to substrate release.
The FELs of the substrate-bound and substrate-free PL646 which constructed based on the metadynamics simulations, reveal that substrate-free PL646 has a larger, more rugged and complex free energy surface than substrate-bound PL646, demonstrating that substrate-free PL646 has more structural flexibility and more complex dynamic behaviors than substrate-bound PL646. According to the FEL theory, the nature to increase the conformational entropy of the protein (especially that of the solvent-exposed loops) and the competitive interaction between residue–residue and residue–solvent, will inevitably cause fluctuations in the free energy of the protein–solvent system, which will manifest as a rugged free energy surface.51–53 For proteins of similar size, the free energy surface of the flexible protein can be expected to be more rugged and complex than that of the rigid protein. This is in agreement with the result mentioned before that substrate-free PL646 has an overall higher flexibility than substrate-bound PL646; this is also explains why the FEL of substrate-free PL646 is more rugged and complex than substrate-bound PL646.
5. Conclusion
We have investigated the molecular motions and the effect of substrate binding on the dynamics/molecular motions of cuticle-degrading serine protease PL646 using MD simulation and metadynamics simulation methods. Upon substrate binding, PL646 adopts a more stable and compact conformation, which can be attributed to increased inter-atomic interactions and decreased loop flexibility. Combined ED analysis reveals that, upon substrate binding, the regions surrounding/opposite the substrate-binding pockets/sites exhibit large conformational displacements. Furthermore, based on ED analyses of the PL646 simulation, the dynamic pockets caused by the large concerted motions are proposed to be linked to the substrate recognition, binding, orientation, catalysis and product release. The significant displacements in regions opposite the binding groove/pockets are considered to play a role in modulating the dynamics of enzyme substrate interaction. In the end, the constructed FELs reveal that substrate-free PL646 has a more rugged and larger free energy surface than substrate-bound PL646, indicating that substrate-bound PL646 is a more stable and compact structural features than substrate-free PL646. The results of this work provide detailed information about the substrate induced changes in dynamics and molecular motions of cuticle-degrading serine protease PL646 and the dynamic features of its enzymatic mechanism.Conflicts of interest
The authors declare no conflicts of interest for this work.Acknowledgements
This study was funded by grants (31660015, 31160181 and 31370715) from the National Natural Sciences Foundation of China, the National Basic Research Program of China (2013CB127500), and the Program for Excellent Young Talents, Yunnan University, China (XT412003).References
- L. Hedstrom, Chem. Rev., 2002, 102, 4501–4523 CrossRef CAS PubMed.
- J. Neitzel, Nat. Edu., 2010, 3, 21–25 Search PubMed.
- R. J. Siezen, W. M. de Vos, J. A. Leunissen and B. W. Dijkstra, Protein Eng., Des. Sel., 1991, 4, 719–737 CrossRef CAS.
- R. J. Siezen and J. A. Leunissen, Protein Sci., 1997, 6, 501–523 CrossRef CAS PubMed.
- G. Dodson and A. Wlodawer, Trends Biochem. Sci., 1998, 23, 347–352 CrossRef CAS PubMed.
- J. Kraut, Annu. Rev. Biochem., 1977, 46, 331–358 CrossRef CAS PubMed.
- J. M. Clarkson and A. K. Charnley, Trends Microbiol., 1996, 4, 197–203 CrossRef CAS PubMed.
- J. Yang, X. Huang, B. Tian, M. Wang, Q. Niu and K. Zhang, Biotechnol. Lett., 2005, 27, 1123–1128 CrossRef CAS PubMed.
- X. W. Huang, N. H. Zhao and K. Q. Zhang, Res. Microbiol., 2004, 155, 811–816 CrossRef CAS PubMed.
- Y. Tang, F. Yu, G. Zhang, Z. Yang, F. Huang and G. Ding, Molecules, 2017, 22, 1123 CrossRef PubMed.
- K. A. Lahey, N. J. Ronaghan, J. Shang, S. P. Dion, A. Désilets, R. Leduc and W. K. MacNaughton, PLoS One, 2017, 12, e0180259 Search PubMed.
- A. Tunlid, S. Rosen, B. Ek and L. Rask, Microbiology, 1994, 140, 1687–1695 CrossRef PubMed.
- M. L. Zhao, M. H. Mo and K. Q. Zhang, Mycologia, 2004, 96, 16–22 CrossRef CAS.
- R. Segers, T. Butt, B. Kerry and J. Peberdy, Microbiology, 1994, 140, 2715–2723 CrossRef CAS PubMed.
- L. Joshi, R. J. St Leger and M. J. Bidochka, FEMS Microbiol. Lett., 1995, 125, 211–217 CrossRef CAS PubMed.
- R. J. St Leger, A. K. Charnley and R. M. Cooper, Arch. Biochem. Biophys., 1987, 253, 221–232 CrossRef CAS PubMed.
- N. D. Rawlings, A. J. Barrett and A. Bateman, Nucleic Acids Res., 2010, 38, D227–D233 CrossRef CAS PubMed.
- L. Liang, Z. Meng, F. Ye, J. Yang, S. Liu, Y. Sun, Y. Guo, Q. Mi, X. Huang and C. Zou, FASEB J., 2010, 24, 1391–1400 CrossRef CAS PubMed.
- J. K. Yang, B. Y. Tian, L. M. Liang and K. Q. Zhang, Appl. Microbiol. Biotechnol., 2007, 75, 21–31 CrossRef CAS PubMed.
- K. A. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS PubMed.
- T. Hansson, C. Oostenbrink and W. van Gunsteren, Curr. Opin. Struct. Biol., 2002, 12, 190–196 CrossRef CAS PubMed.
- L. Liang, Z. Meng, F. Ye, J. Yang, S. Liu, Y. Sun, Y. Guo, Q. Mi, X. Huang and C. Zou, FASEB J., 2010, 24, 1391–1400 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- H. Berendsen, J. Postma, W. Van Gunsteren and J. Hermans, Intermol. Forces, 1981, 11, 331–342 Search PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- H. J. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS PubMed.
- A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Proteins: Struct., Funct., Genet., 1993, 17, 412–425 CrossRef CAS PubMed.
- J. Chen, J. Wang and W. Zhu, Phys. Chem. Chem. Phys., 2017, 19, 3067–3075 RSC.
- J. Chen, RSC Adv., 2016, 6, 58573–58585 RSC.
- P. Sang, L. Q. Yang, X. L. Ji, Y. X. Fu and S. Q. Liu, PLoS One, 2014, 9, e104714 Search PubMed.
- P. Sang, Q. Yang, X. Du, N. Yang, L. Q. Yang, X. L. Ji, Y. X. Fu, Z. H. Meng and S. Q. Liu, Int. J. Mol. Sci., 2016, 17, 254 CrossRef PubMed.
- P. Sang, X. Du, L. Q. Yang, Z. H. Meng and S. Q. Liu, RSC Adv., 2017, 7, 28580–28590 RSC.
- D. M. F. van Aalten, A. Amadei, A. B. M. Linssen, V. G. H. Eijsink, G. Vriend and H. J. C. Berendsen, Proteins: Struct., Funct., Genet., 1995, 22, 45–54 CrossRef CAS PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- V. Spiwok, P. Lipovová and B. Králová, J. Phys. Chem. B, 2007, 111, 3073–3076 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- Y. Tao, Z. H. Rao and S. Q. Liu, J. Biomol. Struct. Dyn., 2010, 28, 143–157 CAS.
- L. Q. Yang, P. Sang, Y. Tao, Y. X. Fu, K. Q. Zhang, Y. H. Xie and S. Q. Liu, J. Biomol. Struct. Dyn., 2014, 32, 372–393 CAS.
- G. H. Peters, T. M. Frimurer, J. N. Andersen and O. H. Olsen, Biophys. J., 1999, 77, 505–515 CrossRef CAS PubMed.
- C. P. Barrett and M. E. Noble, J. Biol. Chem., 2005, 280, 13993–14005 CrossRef CAS PubMed.
- G. H. Peters and R. P. Bywater, Protein Eng., Des. Sel., 1999, 12, 747–754 CrossRef CAS.
- G. H. Peters, T. M. Frimurer, J. N. Andersen and O. H. Olsen, Biophys. J., 2000, 78, 2191–2200 CrossRef CAS PubMed.
- Y. Tao, Z. H. Rao and S. Q. Liu, J. Biomol. Struct. Dyn., 2010, 28, 143–157 CAS.
- S. Q. Liu, S. X. Liu and Y. X. Fu, J. Mol. Model., 2007, 13, 411–424 CrossRef CAS PubMed.
- S. Q. Liu, S. X. Liu and Y. X. Fu, J. Mol. Model., 2008, 14, 857–870 CrossRef CAS PubMed.
- S. Q. Liu, Z. H. Meng, Y. X. Fu and K. Q. Zhang, J. Mol. Model., 2010, 16, 17–28 CrossRef CAS PubMed.
- S. Q. Liu, Z. H. Meng, Y. X. Fu and K. Q. Zhang, J. Mol. Model., 2011, 17, 289–300 CrossRef CAS PubMed.
- H. M. Li, Y. H. Xie, C. Q. Liu and S. Q. Liu, Sci. China: Life Sci., 2014, 57, 287–302 CrossRef CAS PubMed.
- S. Q. Liu, X. L. Ji, Y. Tao, D. Y. Tan, K. Q. Zhang and Y. X. Fu, Protein Eng., Des. Sel., 2012, 207–252 CAS.
- L. Q. Yang, X. L. Ji and S. Q. Liu, J. Biomol. Struct. Dyn., 2013, 31, 982–992 CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |