Open Access Article
Open Access ArticleNon-additive impacts of covalent cross-linking on the viscoelastic nanomechanics of ionic polyelectrolyte complexes
Biao Hana,
Tianzhu Maa,
John H. Vergarab,
Giuseppe R. Palmeseb,
Jie Yinc,
Daeyeon Lee d and
Lin Han
d and
Lin Han *a
*a
aSchool of Biomedical Engineering, Science, and Health Systems, Drexel University, Philadelphia, PA 19104, USA. E-mail: lh535@drexel.edu; Fax: +1 215 895 4983; Tel: +1 215 571 3821
bDepartment of Chemical and Biological Engineering, Drexel University, Philadelphia, PA 19104, USA
cDepartment of Mechanical Engineering, Temple University, Philadelphia, PA 19122, USA
dDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA 19104, USA
First published on 23rd November 2017
Abstract
This study elucidates the influences of adding covalent cross-linking on the nanomechanical viscoelasticity of ionically cross-linked polyelectrolyte networks. Using layer-by-layer (LbL) assembled PAH/PAA networks, we report how adding covalent amide cross-links changes the degree of swelling, indentation modulus, and force relaxation behaviors with varying solution conditions such as pH and ionic strength, which modulate the ionic cross-link density and fixed charge density. The addition of covalent cross-linking increases both the modulus and degree of elasticity through providing permanent anchorage to the ionically linked networks. Such addition also strongly increases the relaxation times at net neutral, less swollen states. These results together underscore the synergistic interplay between the covalent and ionic cross-links in the viscoelastic nanomechanics of polyelectrolyte networks, potentially enabling the use of these stimulus-responsive materials in mechano-sensitive biomedical and engineering applications.
1. Introduction
Owing to their responsiveness to stimuli, ease of manufacturing and nano-to-microscale dimensions, layer-by-layer (LbL) assembled polyelectrolyte films have shown potential in a wide range of biomedical applications, such as cell substrates,1–5 biomaterial coatings,6,7 optical coatings,8 anti-fouling coatings,9,10 drug delivery carriers,11 and tissue engineering.12,13 Upon assembly, polyelectrolyte chains form networks held by physical cross-links, such as ionic bonding,14 hydrogen bonding15 and hydrophobic interactions.16 The highly dynamic, environment-sensitive nature of these physical cross-links endows the films with highly tunable optical, mechanical and electrical properties.17 However, physical cross-links can easily break under mechanical stress or upon environmental changes; the as-prepared, physically linked films thus do not provide structural stability in comparison to covalently linked films. Therefore, introducing additional covalent cross-links has become a common practice to increase the film stability.18 As a result of the additional cross-linking, the LbL films become microscale polyelectrolyte networks, held by a mixture of permanent, covalent cross-links and dynamic, stimulus-responsive physical cross-links.This hybrid cross-linking nature indicates that the mechanical behaviors of such films are likely different from those held by single cross-link type, either covalent or physical. Indeed, at the macroscale, hydrogels with two cross-link types have shown unique, advantageous properties, such as increased toughness,19,20 improved resistance in enzymatic degradation,21 and tunable surface chemistry.22 Therefore, hybrid cross-linking serves as an important variation of the LbL technique to meet the requirements for various applications. To date, for these films, at the microscale, it is well-known that adding covalent cross-links significantly increases the elastic modulus.23–26 However, given the deformation of polymer chains is time-dependent, a salient feature of polymer mechanics is viscoelasticity. It is unclear how this mixture of cross-link types can yield viscoelastic behaviors distinct from those held solely by physical or covalent cross-links. Since many applications rely on the mechanical properties of these films,27–29 understanding viscoelasticity at the microscale will lay the ground for the design of various mechano-sensitive biomedical and engineering applications using LbL films.
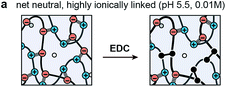
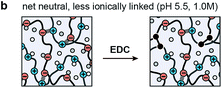
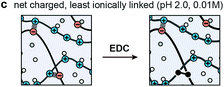
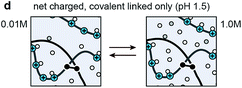
The objective of this study was to determine the impact of covalent cross-linking on the viscoelastic mechanical properties of ionic LbL polyelectrolyte networks. Following our previous study, the ionically cross-linked, LbL-assembled poly(allylamine hydrochloride)/poly(acrylic acid) (PAH/PAA, Fig. 1a) films were used as the model material.30 In aqueous solutions, the as-assembled ionic PAH/PAA network is connected by ionic pairs31 between the charged amine-groups of PAH (solution pKa ≈ 10.5) and the charged carboxyl groups of PAA (pKa ≈ 2.3 when in the form of PAH7.5/PAA3.5 LbL films).32 Since PAH and PAA are both weak polyelectrolytes, their degrees of ionization are highly dependent on solution pH and ionic strength (IS). In this work, we studied the impact of additional covalent amide bonds via 1-[3-(dimethylamino)propyl]-3-ethylcarbodiimide methiodide (EDC-I) cross-linking (Fig. 1b and c) on the viscoelasticity of PAH/PAA ionic networks under the modulation of solution pH and IS. When the solution pH changes from 5.5 to <2.0, the degree of ionization of PAA changes from >90% to 0%, while PAH remains nearly fully charged. This leads to a conformational change of the PAH/PAA film, from a net-neutral, highly ionically cross-linked network (pH 5.5), to a net charged, loosely cross-linked network (pH 2.0–2.5).33 Meanwhile, we also varied the solution IS between 0.01 M and 1.0 M to introduce variations in electrostatic interactions. In net neutral states, varying IS can influence the cross-link density without affecting the charged nature of polymers through the “doping” effect.34 In net charged states, tuning IS can also affect the magnitude of Poisson–Boltzmann double layer interactions via the Debye screening.35 After the EDC treatment, each carboxyl group on PAA and each primary amine group on PAH are connected by a covalent amide bond via the carbodiimide reaction (Fig. 1c).36 As a result, the covalent amide cross-links are not affected by changes in pH or IS. Applying our recently developed, closed-loop nanoindentation and force relaxation tests,30 we quantified the viscoelastic properties of the PAH/PAA LbL films. These results were interpreted in the context of the PAA ionization state measured by the attenuated total reflectance-Fourier transform infrared spectroscopy (ATR-FTIR, Fig. 2a), as well as the rubber elasticity42 and its modified form of the Smith theory,37 to connect the mechanical behaviors with molecular cross-linking states. The outcomes together illustrated the distinctive viscoelastic nanomechanics of polyelectrolyte networks with two types of cross-links.
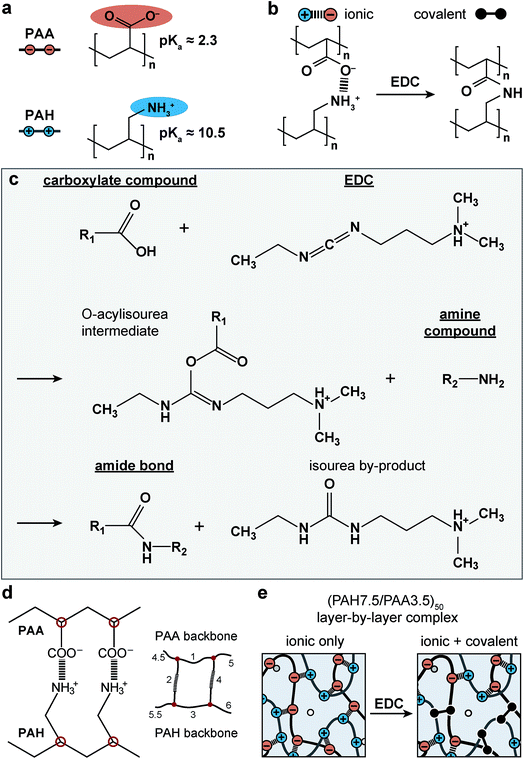 | ||
| Fig. 1 Schematics of the model material system, the layer-by-layer (LbL) assembled, ionically cross-linked poly(allylamine hydrochloride)/poly(acrylic acid) (PAH/PAA)50 networks. (a) Molecular structure of PAH and PAA and associated pKa's. (b) Impacts of EDC-treatment on the molecular structure of cross-links. (c) Chemical reactions of the formation of covalent amide bond between the carboxyl and amine groups via the carbodiimide EDC.36 (d) Schematic of the network formation via ionic cross-linking, where each pair of ionic bonding forms a network of four junctions (red circles, left panel) and six chains (numbered, right panel) according to Smith.37 (e) Schematic of the associated changes in the cross-link types of the PAH/PAA network. | ||
2. Methods
2.1 Sample preparation
Layer-by-layer assembled PAH/PAA complexes with 50-bilayers were prepared on freshly cleaned glass slides, following established procedures.38 The assembly was carried out at their partially charged states (pH 7.5 for PAH and pH 3.5 for PAA) to form a relatively isotropic network with random polymer chain conformation.38 To induce additional covalent cross-linking, the LbL complexes were incubated in NaCl + HCl aqueous solution (0.01 M, pH = 2.5) for 15 minutes, followed by 96 mg mL−1 1-[3-(dimethylamino)propyl]-3-ethylcarbodiimide methiodide (EDC-I, corresponding to the same molar concentration of 50 mg mL−1 EDC) in 2-(N-morpholino)ethanesulfonic acid (MES) buffer for 1 hour to induce covalent amide cross-links between PAH and PAA (Fig. 1b–e).39 The sample was then rinsed with 0.01 M NaCl solution for at least three times to remove residual reagents. For the control, the films underwent the same MES buffer incubation and rinsing procedures without the addition of EDC-I. This step was to ensure that the conformational changes of the networks due to incubation and rinsing were consistent between the control and EDC-treated groups.2.2 ATR-FTIR spectrometry
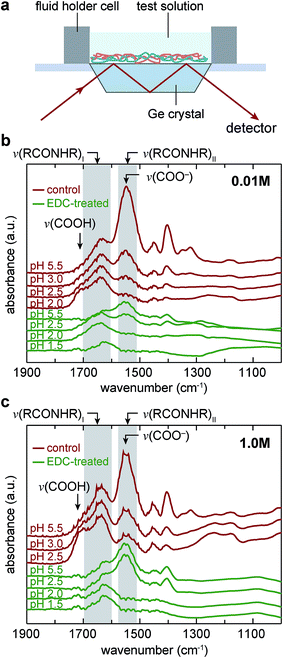
To reveal the impacts of covalent cross-linking on the pH and IS-responsive molecular states of the carboxyl groups on PAA, ATR-FTIR was applied to the PAH/PAA films prepared on a Germanium crystal puck (Specac, Orpington, United Kingdom) via the same assembly procedures. The ATR-FTIR measurement was carried out on a Nicolet Nexus 870 FT-IR Spectrometer (Thermo Fisher Scientific, Philadelphia, PA) with a Quest Single Bounce ATR accessory (Specac, Fort Washington, PA) and a custom fluid holder cell to retain the fluidic environment during the measurement (Fig. 2a), following previously reported procedures.40,412.3 AFM-nanoindentation and ramp-and-hold force relaxation
To study the elastic and viscoelastic mechanical properties, AFM-based nanomechanical tests were applied at multiple pH and IS to both EDC-treated and control samples, following our recently established and fully calibrated procedures.30 Briefly, AFM-nanoindentation was performed with polystyrene microspherical tips (R ≈ 12.5 μm) at a constant loading/unloading rate of υD = 5 μm s−1, up to a maximum indentation force ∼1 μN, followed by a ∼30 s force relaxation holding period via the indenter mode of the Molecular Force Probe 3D (Asylum Research, Santa Barbara, CA). In this closed-loop mode, the cantilever displacement was continuously adjusted to compensate for the time-dependent viscoelastic softening of the sample, resulting in constant indentation rate and constant indentation depth during relaxation. These tests were performed in pH = 1.5–5.5, IS = 0.01 M and 1.0 M NaCl + HCl aqueous solutions, which modulated the degree of ionic cross-linking and fixed charge-governed electrostatic double-layer interactions. At each IS and pH, the test was repeated on 3 samples, ≥10 locations each sample, and no significant differences were found amongst different samples. At each state, the thickness of the film, H, was measured by AFM via selective film removal followed by contact mode AFM imaging for H ≤ 10 μm, and our recently developed z-motor assisted method for H > 10 μm.30With a maximum indentation depth Dmax < 2 μm, the maximum strain was controlled at less than 20% to ensure that the deformation of PAH/PAA was in the linear regime. Linear elastic and viscoelastic models were applied to extract material mechanical properties. The effective indentation modulus, Eind, was calculated via the Hertz model with finite thickness correction,42
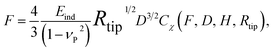 | (1) |
E(t) = E∞ + E1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + E2 exp(−t/τ1) + E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2), exp(−t/τ2),
| (2) |
Here, E∞ is the equilibrium indentation modulus, E1 and E2 are the time-dependent modulus corresponding to the short and long term relaxation mode (τ1 < τ2), respectively. The instantaneous indentation modulus, E0, was estimated as, E0 = E∞ + E1 + E2. We used the ratio of E∞/E0 as a measure of the degree of elasticity.
2.4 Estimation of effective cross-link density
To understand the contributions of covalent and ionic cross-links to the mechanical properties, we estimated the effective cross-link densities of both cross-link types via the classical rubber elasticity theory45 and its extended Smith theory.37 For covalent cross-links, the effective density was estimated by applying the linear rubber elasticity theory to the equilibrium modulus, E∞, measured at pH 1.5, IS = 1.0 M. At this state, the low pH ensures full protonation of carboxyl groups, and thus, absence of ionic cross-linking, and the high IS results in full screening of the Donnan effect. Therefore, E∞ is dominated by the rubber elasticity from covalent cross-links. The use of E∞, instead of the indentation modulus Eind, also minimized the possible overestimation from the effect of intrinsic viscoelasticity or poroelasticity. The effective polymer chain density (molar number of chains per unit volume), ν, was calculated as,| E∞ = 3ϕkBTν, | (3) |
| ν = 3cec | (4) |
For ionically cross-linked networks, the effective ionic cross-link density, cei, cannot be estimated with the same method, due to two major reasons. First, rubber elasticity is limited to loose networks where the number of monomer units between adjacent links is ≥10.46,47 This assumption is valid for covalent networks. However, for ionically cross-linked networks, especially in net-neutral conditions, where all charged groups can potentially serve as cross-linking sites, this assumption does not hold. The Smith theory37 was thus used to calculate the cross-link density ν,
3νkBT/E = (1/ϕn) − 6![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) n/(5q2 n/(5q2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ), ),
| (5) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) n is a characteristic ratio equals
n is a characteristic ratio equals ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) 0.57, and ϕn is the front factor (0.5 for
0.57, and ϕn is the front factor (0.5 for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) > 9.6). The term,
> 9.6). The term, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , is the geometric mean number of backbone bonds per chain, calculated as
, is the geometric mean number of backbone bonds per chain, calculated as
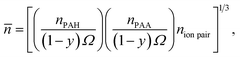 | (6) |
Second, the viscoelastic relaxation process of ionically cross-linked network is dominated by the local breaking and re-formation of ionic cross-links.30 Therefore, unlike the case of covalent networks, E∞ here does not reflect the effective ionic cross-link density at the un-deformed state. The instantaneous indentation modulus, Eind, on the other hand, was measured before the cross-link breaking or re-formation had taken place, and thus, could better reflect the ionic cross-link density at the un-deformed state. Under this scenario, the use of Eind may over-estimate cei, as it does not exclude the viscoelastic and poroelastic contributions from polymer chains conformational changes and interstitial fluid flow. However, as we demonstrated in our previous work, cross-link breaking and re-formation is the dominating viscoelasticity mechanism in ionic networks.30 These other effects are expected to be minor, and thus, Eind, rather than E∞, was used to estimate cei. Further, it should be noted that, even in the duration of indentation, ionic cross-links can break and re-form, the use of Eind is an approximation, rather than an accurate estimate of cei.
We applied eqn (4) to both the control and EDC-treated networks at pH 2.5–5.5, IS = 0.01 M and 1.0 M. For the control networks that were cross-linked solely by ionic pairing, this calculation directly yielded the intrinsic ionic pairing density, cei. For the EDC-treated networks, the application of eqn (4) yields an effective net cross-link density, cet. This effective density includes the densities of both ionic pairing and amide bonding, i.e., cet = cec + cei. Here, the effective amide bonding density, cec, was estimated using E∞ measured at pH 1.5, IS = 1.0 M and considering that the covalent cross-links remain unchanged, the cec at each condition can be estimated with the rubber elasticity theory with volume change calculated from the changes in film thickness H. Therefore, the effective ionic pairing density can be deduced as, cei = cet − cec. Here, the outcome of effective density only represents the bondings that contribute to the formation of polymer chain networks. Those not contributing to the network formation, such as the “ladder” bonding,46 do not contribute to the modulus, and thus, were not taken into account by this calculation.
3. Results
3.1 pH-dependent charging and protonation of carboxyl groups on PAA via ATR-FTIR
The ATR-FTIR results revealed a clear trend of pH-dependent charging and protonation of the carboxyl acid groups on PAA (Fig. 2b and c). The protonated carboxyl group (–COOH) absorbs infrared light at wavenumber around 1710–1700 cm−1 and the charged carboxyl group (–COO−) at 1565–1542 cm−1.33 Since other chemical bonds have minimum absorbance at this range, we focused our analysis on the wavenumber range between 1900–1300 cm−1 to illustrate the degree of ionization of the carboxyl groups on PAA. Moreover, since the absorbance peaks between –NH3+ and –CH2 groups are overlapping near 3000 cm−1 wavenumber,33 and amine groups were maintained at near fully charged state throughout this study, we did not analyze the degree of ionization for PAH.For both the control and EDC-treated networks, at both IS of 0.01 M and 1.0 M, changing the solution pH from 5.5 to 2.0 results in a substantial decrease in the peak height at the wavenumber of ν(COO−) = 1565–1542 cm−1,33 demonstrating the protonation of COO− as pH changes past its pKa. At the same time, there was an increase in the peak height at the wavenumber of ν(COOH) = 1710–1700 cm−1,33 which was less pronounced in comparison to the decrease of the peak height at ν(COO−). This is because decreasing pH results in swelling of PAH/PAA, and thus, decreases the concentration of polymer chains that is probed by ATR-FTIR. This effect attenuates the effect of increased carboxyl protonation to the peak at ν(COOH), and amplifies the effect of decreased to the peak at ν(COO−).
The trend of pH-dependence was consistent for the control and EDC-treated networks, indicating that added covalent cross-linking does not significantly alter the pH-responsiveness of the PAH/PAA ionic complex. Meanwhile, the peak at ν(COO−) for the EDC-treated network was also less pronounced than the control, which can be attributed to the larger degree of swelling, and thus, lower polymer volume concentration (Fig. 3a).
In theory, EDC-induced cross-linking results in amide bonds (–CONH–), which absorbs infrared light at wavenumber ∼1700–1600 and 1580–1510 cm−1.48 However, as shown by the results for EDC-treated network at pH 1.5, when all carboxyl groups are protonated, we did not observe significant increase at this wavenumber (Fig. 2b and c). This suggests that the overall molar ratio of amide bonds is very small compared to the number of free carboxyl acid groups, and its presence does not obscure our observation on pH-induced carboxyl protonation.
3.2 Swelling and stability of PAH/PAA
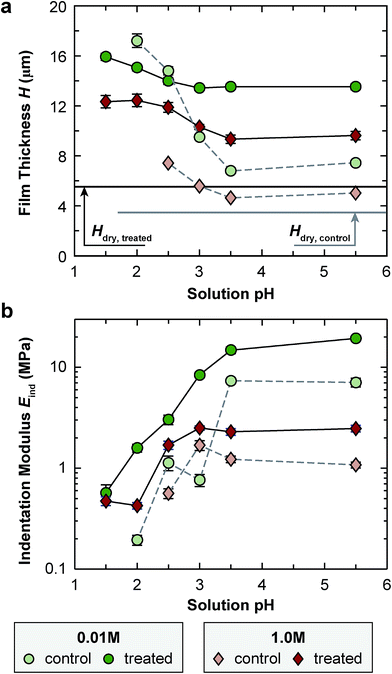
AFM-thickness measurement highlighted the differences in the swelling between EDC-treated and control networks (Fig. 3a and Table 1). At the low IS of 0.01 M (Debye length κ−1 ≈ 3 nm), for the control network, the film thickness, H, increased from 7.4 ± 0.1 μm (mean ± SEM, n ≥ 15) to 17.2 ± 0.5 μm when changing pH from 5.5 to 2.0, a 2.31 ± 0.07 × difference; for the EDC-treated one, H increased from 13.5 ± 0.2 μm to 15.0 ± 0.2 μm, a 1.12 ± 0.03 × difference. This pronounced swelling for both networks was due to the Donnan effect arising from net positive charges on PAH as PAA becomes protonated. The contrast between the control and EDC-treated ones highlighted that the presence of permanent anchoring by covalent cross-links can effectively reduce this Donnan effect-induced swelling. At the high ionic strength of 1.0 M, when Donnan effect is fully screened by the free counter ions (κ−1 ≈ 0.3 nm), reducing pH leads to less swelling for both networks.The EDC-treated network had greater H than the control at nearly all states except for the highly swollen one. While we do not fully understand the mechanism behind the increased film thickness after EDC treatment, this difference likely suggests possible conformational changes of the network due to EDC-induced covalent cross-linking, which has been shown to take place for LbL poly(L-lysine)/poly(L-glutamic acid) (PLL/PGA) nanofilms.49 However, we do not expect the lower thickness of control film, especially at the dry state, to reflect appreciable material loss during the step of 2-(N-morpholino)ethanesulfonic acid (MES) immersion. This is because the control, MES-immersed network here showed highly similar swelling and mechanical properties to our previously reported results on as-prepared PAH/PAA films, which did not undergo any solution treatment (e.g., Eind = 8.3 ± 0.8 MPa, and 7.1 ± 0.7 MPa before and after MES immersion (p > 0.05), and H = 7.1 ± 0.1 μm, and 7.4 ± 0.1 μm before and after immersion, when measured at pH 5.5, 0.01 M).30 We also do not expect appreciable reaction by-product entrapped in the EDC-treated network, since ATR-FTIR did not detect the peak associated with the alkyl form of iso-urea bonding (wavenumber ∼ 1200–1025 cm−1,50 Fig. 2b and c).
When pH was lowered to 1.5, the control network was dissolved upon complete loss of ionic cross-links, while the EDC-treated network remains stable. At this state, the network is held solely by covalent cross-links, and the greater swelling at 0.01 M than 1.0 M reflects the effects of fixed charge-induced Donnan osmotic effect.35
3.3 Elastic and viscoelastic nanomechanical properties
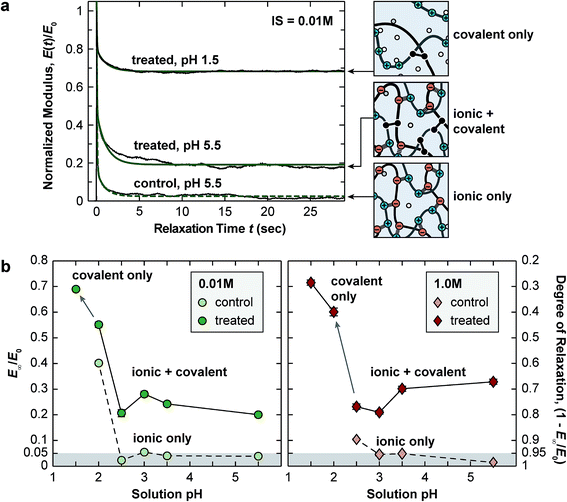
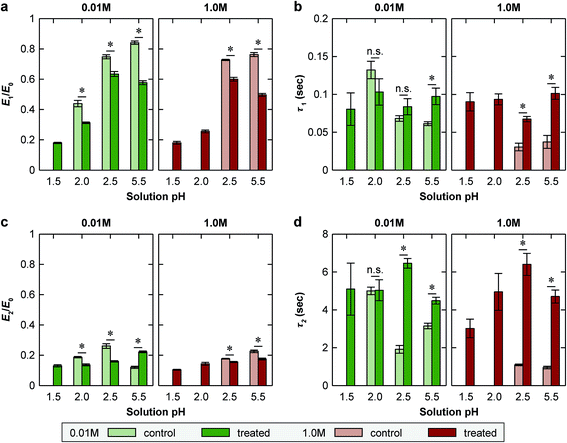
AFM-nanoindentation detected significantly higher modulus for the EDC-treated network at all tested conditions (Fig. 3b and Table 1a–c), e.g., Eind,EDC/Eind,control = 3.0 ± 0.3 at pH = 5.5, 0.01 M and 2.4 ± 0.2 at pH = 5.5, 1.0 M. However, covalent cross-linking did not substantially alter the stimulus responses of Eind to solution pH and IS. At 0.01 M IS, reducing pH from 5.5 to 2.5 resulted in a 7.3 ± 1.3 fold and 7.4 ± 0.8 fold decrease in Eind for the control and EDC-treated networks, respectively. This trend was similar at 1.0 M IS, in which, the modulus decreases by 2.1 ± 0.3 fold and 1.7 ± 0.2 fold for the control and EDC-treated networks, respectively, from pH 5.5 to 2.5. On the other hand, at pH 5.5, changing IS from 0.01 M to 1.0 M resulted in a 7.0 ± 0.9 × and 8.7 ± 0.9 × decrease in Eind for the control and EDC-treated ones, respectively. In addition, when pH was lowered to 1.5, while the control was dissolved upon complete loss of ionic cross-links, the EDC-treated network remained stable, and increasing IS from 0.01 M to 1.0 M only decreased Eind for 17 ± 2%.Closed-loop force relaxation test yielded significantly different viscoelastic behaviors (Fig. 4a). For the control, a near 100% relaxation was observed at all net neutral states (pH 2.5–5.5, 0.01–1.0 M), in which, as noted by our previous study, the relaxation is dominated by ionic cross-link breaking and re-formation.30 Adding the permanent, covalent cross-links increased the degree of elasticity (E∞/E0), and in turn, decreased the degree of relaxation (1 − E∞/E0) (Fig. 4b). For example, at pH 5.5, 0.01 M, the degree of relaxation was 96 ± 1% for the control, and was reduced to 80 ± 3% for the EDC-treated network. At the highly swollen state of pH 2.0, 0.01 M, when additional elasticity was endowed by the Donnan effect, E∞/E0 was 40 ± 2% for the control, and the treatment further increased the elasticity, E∞/E0 = 55 ± 3%.
Since adding covalent cross-links increased the degree of elasticity (E∞/E0), as expected, the contribution of the two viscoelastic modes, the short-term relaxation (E1, τ1) and long-term relaxation (E2, τ2) (see Experimental section for more details), to the overall modulus were reduced at all tested states (Fig. 5a and b and Table 1a–c). At all net neutral states (pH 2.5–5.5, 0.01 and 1.0 M), adding cross-links significantly increased both the short term, τ1, and the long term, τ2, relaxation time constants (Fig. 5c and d and Table 1a and b). At the net charged state (pH 2.0, 0.01 M), on the other hand, the cross-linked state had similar τ1 and τ2 compared to the control (Fig. 5c and d, Table 1c).
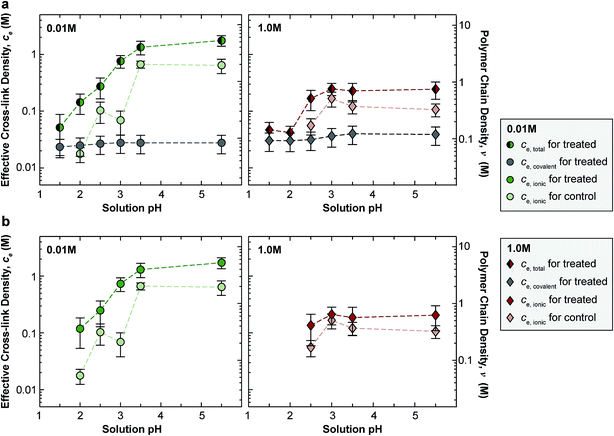
3.4 Covalent and ionic cross-link density estimation
Based on classical rubber elasticity theory,45 at pH 1.5, IS = 1.0 M, the effective covalent cross-link density, cec, was calculated to be 91 ± 33 mol m−3, or 0.09 ± 0.03 M. Values of cec at other states, which were estimated based on the swelling ratio, did not undergo substantial changes (Fig. 6). For the control network, in accordance with the pH- and IS-responsiveness of Eind, the effective ionic cross-link density, cei, also showed significant changes with pH and IS. For the EDC-treated network containing both covalent and ionic cross-links, the effective total cross-link density, cet, was higher than that of the control network at all tested states (Fig. 6a). Furthermore, after subtracting the covalent cross-link density, the effective ionic cross-link density still appears higher than that of the control network (Fig. 6b). These results highlighted a synergistic, non-additive impact between the covalent and ionic cross-links. The additional covalent cross-links can change the chain conformation of PAH and PAA, which likely affects the equilibrium state of the ionic network, leading to an increase in ionic cross-linking density.4. Discussion
4.1 Viscoelasticity at net neutral states: non-additive impacts of covalent cross-linking
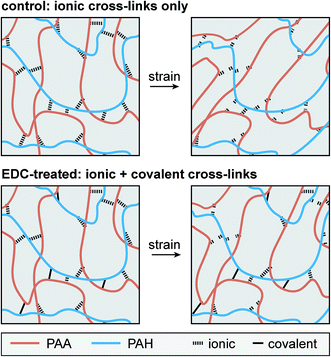
While covalent cross-linking is expected to increase Eind (Fig. 3b), the magnitude of change does not scale with the covalent cross-link density in an additive manner. For example, at pH 5.5, 0.01 M, Eind was 7.1 ± 0.7 MPa for the control, and 19.4 ± 1.1 MPa for the EDC-treated network, yielding a difference of 12.3 ± 1.8 MPa (Table 1a). By contrast, at this state, given the covalent cross-link density of 83 ± 30 mol m−3, according to eqn (3) (see Experimental section), the elastic modulus directly contributed by the covalent cross-links is 1.5 ± 0.6 MPa, much less than the measured modulus difference between the two groups. This suggests that direct contribution of covalent cross-links to Eind is not a dominant factor (≈8%). Instead, the presence of permanent covalent cross-linking can alter the dynamics of ionic cross-links, providing synergistic effects to stiffen the network. Given the breakable nature of ionic cross-links, they undergo breaking and re-formation during the indentation. Here, Eind reflects an effective indentation resistance resulted from dynamics of ionic cross-links and viscosity of polymer chain segments. Therefore, the permanent anchorage endowed by covalent cross-links can provide additional resistance to polymer segment movement, and thus, reduce the extent of ionic cross-link breaking, as illustrated in Fig. 7. This synergistic effect is likely to be the dominating mechanism leading to the increased Eind, and the higher effective ionic cross-link density, cei, for the EDC-treated network. Meanwhile, this effect is consistent across all net neutral states with both high (lower IS, 0.01 M) and low ionic cross-link densities (higher IS, 1.0 M) (Fig. 3b).One key outcome from the relaxation test is the significant increase in the degree of elasticity, E∞/E0, after covalent cross-linking (Fig. 4a and b). Similar to the case of Eind, since the covalent cross-links do not directly contribute to ≈20% of the total cross-link density (e.g., only ≈1.6% at pH 5.5, 0.01 M), this increased elasticity further highlights the synergistic, rather than additive, effect of covalent cross-linking (Fig. 7). During relaxation, the permanent anchorages can limit viscous flow of polymer segments and sustain additional molecular stresses on chain segments. This effect thus reduces ionic cross-link breaking and provides an amplified effect on the degree of elasticity. The synergistic impacts of covalent cross-linking are also illustrated by changes in viscoelastic relaxation time constants. For ionic networks, our previous study showed that the dominating, short term relaxation mode (τ1 ≈ 50 ms), is governed by the breaking and re-formation of ionic bonds.30 With added covalent cross-links, the increase in τ1 (Fig. 5c) is associated with the greater hindrance to polymer chain movement, as the permanent anchorage can decrease the mobility of polymer chain segments, and its associated ionic bond breaking or re-formation. This effect is also present for the less pronounced long-term relaxation (τ2), as the permanent anchorage can also impact the kinetics of other viscoelastic mechanisms, such as reptation, disentanglement and fluid flow.
4.2 Viscoelasticity at net charged states: differentiated impacts of covalent cross-linking
The addition of covalent cross-links also shows pronounced, yet differentiated impacts on viscoelasticity at the highly swollen, net charged state, pH 2.0, IS 0.01 M (Table 1c). At this state, fixed charge-induced Donnan effect contributes to a higher degree of elasticity than the net neutral states for the control network (E∞/E0 = 40.2 ± 2.1%). Here, adding covalent cross-links further elevates this ratio to 55.1 ± 2.8%, a similar additive impact as in net neutral states. On the other hand, contrary to the increased time constants at the net neutral states, the EDC-treated network shows no changes in τ1 and τ2 when compared to the control (Table 1c), illustrating differentiated impacts on viscoelasticity. This difference can be attributed to the different viscoelasticity mechanisms at the highly swollen state. At this state, given the loose ionic bonding and high degree of swelling, the time-dependent mechanics is dominated by polymer chain movement and fluid flow, rather than the breaking and re-formation of ionic cross-links.30,51 Therefore, since the control and EDC-treated networks are both highly swollen to a similar degree, the time constants associated with the chain segment movement and fluid flow are likely to be similar, leading to similar time constants.4.3 Viscoelasticity of polyelectrolyte networks with covalent cross-links
At the most acidic state, pH = 1.5, all ionic cross-links break due to the full protonation of the carboxyl groups. The control network is fully dissolved, and the EDC-treated one becomes a classic type polyelectrolyte network, that is, a charged network held solely by covalently cross-links.52 Here, without the ionic cross-links, the network has the highest degree of elasticity (E∞/E0 ≈ 70%, Fig. 5b and Table 1d), as viscoelasticity can only originate from polymer chain movement and fluid-polymer friction. At 1.0 M IS, the Donnan effect is minimized (Debye length κ−1 ≈ 0.3 nm), and the equilibrium modulus, E∞, is determined by the network conformational entropy. Interestingly, even for this covalent network, rubber elasticity theory alone cannot predict the modulus change from IS = 1.0 M to 0.01 M. Here, at pH = 1.5, despite the 1.31 ± 0.06 × change in H suggests ≈24% decrease in E∞, value of E∞ instead increases for ≈17%, highlighting the contribution of the Donnan osmotic pressure to the apparent modulus at the lower IS (κ−1 ≈ 3 nm). Meanwhile, at the two ionic strengths, the similarity of time constants suggests similar viscoelastic mechanisms. According to previous macroscale studies of covalent hydrogels, the dominating mechanism is likely to be the fluid flow-governed poroelasticity, especially for the short-term constant τ1.53Given the breakable nature of ionic cross-links, it is possible that the deformation mechanisms of ionic networks under creep can be distinctive from those under force relaxation. For example, constant-force creep can lead to not only viscoelastic, but also viscoplastic deformation, which has been shown for various biopolymer hydrogels at the macroscale.54 To this end, our ongoing studies are further probing the impact of covalent cross-linking on the viscoelastic and viscoplastic behaviors of ionic networks under creep. We anticipate these results will provide a more comprehensive understanding of the nanomechanics of polyelectrolyte networks held by various cross-link types.
4.4 Limitation and outlook
One limitation of this study is that the use of Hertz model does not account for mechanical nonlinearity of the polymer networks. A recent study shows that the neo-Hookean model-based finite element analysis can better capture the nonlinearity of LbL polymer network elasticity.55 To minimize this nonlinearity, we limit our maximum indentation depth in the linear deformation regime (maximum indentation depth Dmax < 0.1H),42 in which, the linear Hertz model is able to accurately account for the tip-sample contact geometry and fit the F–D curve well (R2 > 0.98). Since our focus is on viscoelasticity, instead of material nonlinearity, we only study the linear regime by limiting maximum deformation Dmax < 0.4R. However, since polymer networks can have distinctive viscoelastic behaviors in the nonlinear regime, our ongoing studies aim to adapt more complex nonlinear polymer mechanics models56–58 to further probe the viscoelasticity in the non-linear regime.Moreover, we were not able to directly quantify the portion of carboxyl–amine ionic pairs that are converted to the covalent amide bonds. Since the peak wavenumbers for amide bonds (∼1700–1600 and 1580–1510 cm−1)48 are overlapping with those for carboxyl bonds (∼1710–1700 and 1565–1542 cm−1)33 and amine bonds (∼1629–1626 and 1610–1586 cm−1),59 we cannot distinguish the two in the fashion like we delineate the protonated and charged carboxyl groups (in Fig. 2). In addition, even if the molar ratio of amides and un-converted carboxyl groups can be deduced from FTIR, this ratio does not directly represent the ratios between covalent and ionic bonds that contribute to the polyelectrolyte network modulus. This is because, first, the carboxyl groups that contribute to ionic cross-links are highly dependent on the degree of ionization33 and “doping” effect by “extrinsic” ion pairing with free ions.34 Second, ionic and covalent bonds that do not contribute to the network formation, e.g., the “ladder-forming” bonds,46 do not contribute to the mechanical properties of the network, while the “network-forming” and “ladder-forming” bonds cannot be distinguished from the FTIR results. These challenges prevented us from directly quantifying the densities of ionic and covalent cross-links at each pH and IS state at the molecular level. However, this limitation was addressed by comparison of the “effective cross-link density” deduced from the elastic modulus (Fig. 6). According to these results, it is clear that the density of covalent cross-links is very low in comparison to the ionic bonds (Fig. 6a). Despite this, we still detected substantial changes in the viscoelastic behaviors (Fig. 4 and 5), highlighting the non-additive, synergistic effects of the two cross-link types.
5. Conclusions
This study revealed the impacts of adding covalent cross-linking on the nanomechanical viscoelasticity of ionically cross-linked polyelectrolyte networks. Through modulating solution pH and IS, we probed the different effects of covalent cross-links on ionic networks at various cross-link and fixed charge densities. The addition of covalent cross-linking, despite at relatively low concentration, can substantially increase both the elastic modulus and the degree of elasticity in a synergistic, non-additive manner. At less swollen, net neutral states, adding covalent cross-linking increases relaxation time constants through providing greater hindrance to polymer chain reorganization and reducing ionic cross-link breaking/re-formation. At the highly swollen, net charged state, this modification does not substantially alter the time constants, possibly due to similar viscoelastic mechanisms with or without covalent cross-linking. These results highlighted the unique viscoelastic nanomechanics of polyelectrolyte networks with hybrid cross-link types. Since mechanical characteristics are key determinants of many stimulus-responsive biomaterial-based applications,60,61 this study provides a basic knowledge foundation for a better informed design of polymer hydrogels and LbL films at the microscale.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Faculty Start-up Grant at Drexel University (LH), the Faculty Start-up Grant at Temple University (JY), and NSF DMR-1055594 (DL). It was also supported by the Drexel Areas of Research Excellence (DARE) initiative (LH). We thank the Nano/Bio Interface Center at the University of Pennsylvania for the use of MFP-3D.References
- L. Richert, P. Lavalle, D. Vautier, B. Senger, J. F. Stoltz, P. Schaaf, J. C. Voegel and C. Picart, Biomacromolecules, 2002, 3, 1170–1178 CrossRef CAS PubMed.
- J. D. Mendelsohn, S. Y. Yang, J. Hiller, A. I. Hochbaum and M. F. Rubner, Biomacromolecules, 2003, 4, 96–106 CrossRef CAS PubMed.
- A. J. Engler, L. Richert, J. Y. Wong, C. Picart and D. E. Discher, Surf. Sci., 2004, 570, 142–154 CrossRef CAS.
- D. E. Discher, D. J. Mooney and P. W. Zandstra, Science, 2009, 324, 1673–1677 CrossRef CAS PubMed.
- K. F. Ren, T. Crouzier, C. Roy and C. Picart, Adv. Funct. Mater., 2008, 18, 1378–1389 CrossRef CAS PubMed.
- P. Schultz, D. Vautier, L. Richert, N. Jessel, Y. Haikel, P. Schaaf, J. C. Voegel, J. Ogier and C. Debry, Biomaterials, 2005, 26, 2621–2630 CrossRef CAS PubMed.
- J. Zhang and D. M. Lynn, Macromolecules, 2006, 39, 8928–8935 CrossRef CAS PubMed.
- J. Hiller, J. D. Mendelsohn and M. F. Rubner, Nat. Mater., 2002, 1, 59–63 CrossRef CAS PubMed.
- X. Zhu, D. Janczewski, S. S. Lee, S. L. Teo and G. J. Vancso, ACS Appl. Mater. Interfaces, 2013, 5, 5961–5968 CAS.
- X. Y. Cao, M. E. Pettitt, F. Wode, M. P. A. Sancet, J. H. Fu, J. A. Ji, M. E. Callow, J. A. Callow, A. Rosenhahn and M. Grunze, Adv. Funct. Mater., 2010, 20, 1984–1993 CrossRef CAS.
- K. C. Wood, J. Q. Boedicker, D. M. Lynn and P. T. Hammond, Langmuir, 2005, 21, 1603–1609 CrossRef CAS PubMed.
- C. J. Detzel, A. L. Larkin and P. Rajagopalan, Tissue Eng., Part B, 2011, 17, 101–113 CrossRef CAS PubMed.
- S. Jana, B. J. Tefft, D. B. Spoon and R. D. Simari, Acta Biomater., 2014, 10, 2877–2893 CrossRef CAS PubMed.
- G. Decher, Science, 1997, 277, 1232–1237 CrossRef CAS.
- W. B. Stockton and M. F. Rubner, Macromolecules, 1997, 30, 2717–2725 CrossRef CAS.
- N. A. Kotov, Nanostruct. Mater., 1999, 12, 789–796 CrossRef.
- T. Boudou, T. Crouzier, K. F. Ren, G. Blin and C. Picart, Adv. Mater., 2010, 22, 441–467 CrossRef CAS PubMed.
- J. J. Harris, P. M. DeRose and M. L. Bruening, J. Am. Chem. Soc., 1999, 121, 1978–1979 CrossRef CAS.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- Y. Chen and K. Shull, Macromolecules, 2017, 50, 3637–3646 CrossRef CAS.
- H. Peng, K. Rubsam, F. Jakob, U. Schwaneberg and A. Pich, Biomacromolecules, 2016, 17, 3619–3631 CrossRef CAS PubMed.
- W. H. Kuo, M. J. Wang, H. W. Chien, T. C. Wei, C. Lee and W. B. Tsai, Biomacromolecules, 2011, 12, 4348–4356 CrossRef CAS PubMed.
- M. D. Moussallem, S. G. Olenych, S. L. Scott, T. C. S. Keller III and J. B. Schlenoff, Biomacromolecules, 2009, 10, 3062–3068 CrossRef CAS PubMed.
- L. Richert, A. J. Engler, D. E. Discher and C. Picart, Biomacromolecules, 2004, 5, 1908–1916 CrossRef CAS PubMed.
- A. Schneider, G. Francius, R. Obeid, P. Schwinte, J. Hemmerle, B. Frisch, P. Schaaf, J. C. Voegel, B. Senger and C. Picart, Langmuir, 2006, 22, 1193–1200 CrossRef CAS PubMed.
- Y. Min and P. T. Hammond, Chem. Mater., 2011, 23, 5349–5357 CrossRef CAS.
- D. E. Discher, P. Janmey and Y. L. Wang, Science, 2005, 310, 1139–1143 CrossRef CAS PubMed.
- D. Mertz, J. Hemmerle, J. Mutterer, S. Ollivier, J. C. Voegel, P. Schaaf and P. Lavalle, Nano Lett., 2007, 7, 657–662 CrossRef CAS PubMed.
- L. Xiao, J. Zhu, D. J. Londono, D. J. Pochan and X. Jia, Soft Matter, 2012, 8, 10233–10237 RSC.
- B. Han, D. R. Chery, J. Yin, X. L. Lu, D. Lee and L. Han, Soft Matter, 2016, 12, 1158–1169 RSC.
- S. S. Shiratori and M. F. Rubner, Macromolecules, 2000, 33, 4213–4219 CrossRef CAS.
- S. E. Burke and C. J. Barrett, Langmuir, 2003, 19, 3297–3303 CrossRef CAS.
- J. Choi and M. F. Rubner, Macromolecules, 2005, 38, 116–124 CrossRef CAS.
- T. R. Farhat and J. B. Schlenoff, J. Am. Chem. Soc., 2003, 125, 4627–4636 CrossRef CAS PubMed.
- P. C. Hiemenz and R. Rajagopalan, in Principles of Colloid and Surface Chemistry, Marcel Dekker, New York, NY, 1997, ch. 11, pp. 499–533 Search PubMed.
- D. G. Hoare and D. E. Koshland Jr, J. Biol. Chem., 1967, 242, 2447–2453 CAS.
- T. L. Smith, J. Polym. Sci., Polym. Symp., 1974, 46, 97–114 CrossRef CAS.
- P. V. Pavoor, A. Bellare, A. Strom, D. Yang and R. E. Cohen, Macromolecules, 2004, 37, 4865–4871 CrossRef CAS.
- P. Schuetz and F. Caruso, Adv. Funct. Mater., 2003, 13, 929–937 CrossRef CAS.
- S. A. Sukhishvili and S. Granick, Macromolecules, 2002, 35, 301–310 CrossRef CAS.
- R. W. Farndale, D. J. Buttle and A. J. Barrett, Biochim. Biophys. Acta, 1986, 883, 173–177 CrossRef CAS.
- E. K. Dimitriadis, F. Horkay, J. Maresca, B. Kachar and R. S. Chadwick, Biophys. J., 2002, 82, 2798–2810 CrossRef CAS PubMed.
- M. Ahearne, Y. Yang, A. J. El Haj, K. Y. Then and K. K. Liu, J. R. Soc., Interface, 2005, 2, 455–463 CrossRef CAS PubMed.
- C. Zener, Elasticity and Anelasticity of Metals, Chicago University Press, Chicago, IL, 1948 Search PubMed.
- P. J. Flory, in Principles of Polymer Chemistry, Cornell University Press, 1953, pp. 432–494 Search PubMed.
- J. A. Jaber and J. B. Schlenoff, J. Am. Chem. Soc., 2006, 128, 2940–2947 CrossRef CAS PubMed.
- J. A. Jaber and J. B. Schlenoff, Macromolecules, 2005, 38, 1300–1306 CrossRef CAS.
- J. L. R. Arrondo, A. Muga, J. Castresana and F. M. Goñi, Prog. Biophys. Mol. Biol., 1993, 59, 23–56 CrossRef CAS PubMed.
- C. Wu, S. Aslan, A. Gand, J. S. Wolenski, E. Pauthe and P. R. Van Tassel, Adv. Funct. Mater., 2013, 23, 66–74 CrossRef CAS.
- R. M. Silverstein, F. X. Webster and D. J. Kiemle, in Spectrometric Identification of Organic Compounds, John Wiley & Sons, Hoboken, NJ, 7th edn, 2005, pp. 72–126 Search PubMed.
- J. A. Jaber and J. B. Schlenoff, Chem. Mater., 2006, 18, 5768–5773 CrossRef CAS.
- P. J. Flory, in Principles of Polymer Physical Chemistry, Cornell University Press, 1953, pp. 595–639 Search PubMed.
- Y. Lai and Y. Hu, Soft Matter, 2017, 13, 852–861 RSC.
- S. Nam, J. Lee, D. G. Brownfield and O. Chaudhuri, Biophys. J., 2016, 111, 2296–2308 CrossRef CAS PubMed.
- T. Sherstova, B. T. Stokke, B. Skallerud, G. Maurstad and V. E. Prot, Soft Matter, 2016, 12, 7338–7349 RSC.
- Y. Takano, Polym. J., 1974, 6, 61–71 CrossRef CAS.
- S. Hayashi, Polym. J., 1985, 17, 597–606 CrossRef CAS.
- E. M. Arruda and M. C. Boyce, J. Mech. Phys. Solids, 1993, 41, 389–412 CrossRef CAS.
- A. Barth, Prog. Biophys. Mol. Biol., 2000, 74, 141–173 CrossRef CAS PubMed.
- M. A. Cohen Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef CAS PubMed.
- M. Wang, Y. Gao, X. Li and M. J. Serpe, Polym. Chem., 2017, 8, 127–143 RSC.
| This journal is © The Royal Society of Chemistry 2017 |