DOI:
10.1039/C7RA08526E
(Paper)
RSC Adv., 2017,
7, 47689-47694
Photodissociation kinetics of the isobutanal radical cation: a combined experimental and theoretical study
Received
2nd August 2017
, Accepted 4th October 2017
First published on 10th October 2017
Abstract
The competitive photodissociation kinetics of the isobutanal radical cation ((CH3)2CHCHO+˙, 1) were investigated using experimental and theoretical methods. The photodissociation was followed by the 2 + 1 REMPI process in the gas phase. The reaction pathways for the main product ions with m/z 43 and 29 were determined by calculating the potential energy surface of the dissociation with the G4 method. Through a kinetic analysis using RRKM calculations, we proposed that the main photodissociation pathways were 1 → (CH3)2CH+ + CHO˙, 1 → (CH3)2CH+ + H˙ + CO, and 1 → CH3CH2COCH3+˙ → CH3CH2+ + CH3˙ + CO.
1 Introduction
Reaction dynamics of polyatomic molecules and ions lie at the heart of modern advanced chemistry to ultimately explore the state distributions of products upon the reaction pathways, which are defined as the ground and excited potential energy surfaces of relevant systems.1,2 The initial assessments for specific reaction pathways of molecules and ions are thus a prerequisite for elucidating the reaction dynamics of polyatomic molecules and ions. However, it is still a long standing and challenging issue to elucidate photodissociation mechanisms of molecule ions which are mainly considered as important intermediates in the fields of atmospheric chemistry and astrochemistry. The reason is mainly associated with the difficulties of experimental tools and their identifications.3–5
Very recently, astronomical observations of simple carbonyl-bearing molecules in the interstellar medium (ISM) have been recognized as a significant stepping stone in the field of astrochemistry owing to their crucial roles as key precursors of biologically relevant molecule evolutions in ISM.6–8 Particularly, the isobutanal radical cation ((CH3)2CHCHO+˙, 1) is a simple aliphatic aldehyde cation which could be recognized as one of important intermediate molecules in isomerization reactions.7 In fact, small aldehyde molecules such as isobutanal and acetaldehyde have been emerged as benchmark molecules for astrochemical relevant model systems in the interstellar medium. It is likely because they are involved in the astrochemical evolution of cold molecular clouds and of star forming regions.7 Isobutanal molecule has two stable isomers as gauche and trans on the ground electronic state.9 The relative population of gauche conformer is known to be about 90% at room temperature. Based on ab initio calculation, Metha and co-workers reported that the gauche conformer is slightly more stable than the trans conformer by 69 cm−1 in the ground electronic state, while the trans conformer is slightly more stable than the gauche conformer by 115 cm−1 for the (n, 3s) Rydberg state.10 On the other hand, the photodissociation study of 1 has been rarely considered. Recently, Shen and co-workers have performed photoion and photoelectron imaging by (2 + 1) resonance enhanced multiphoton ionization (REMPI) via the (n, 3s) Rydberg state transitions.10 The results suggested that extensive fragmentations by the multiphoton absorptions are inevitable so that it could not be possible to access toward the well-defined excited electronic states of parent ions in the specific conformational or vibrational ground electronic states. They have also studied the photodissociation dynamics of 1 leading to several product channels by ion imaging technique. They concluded that there is no evidence of vibrational mode or conformational isomer dependence on either the product branching or dynamics. In addition, they identified that the formation of the ions with m/z 43 and 29 are major fragmentation channels.11 It was then proposed that it is likely the result of the two step processes involving the secondary decomposition. It is greatly favourable after the absorption of additional one photon from the ground electronic states of ions generated by a (2 + 1) REMPI process of isobutanal. As a consequence, they suggested that two major fragmentation channels leading to the ions with m/z 43 and 29 follow the typical statistical unimolecular decay process. It is consistent with the result of the isotropic angular distribution implying long life time prior to dissociation.11,12
Despite these considerations, unfortunately, the photodissociation processes of 1 remain mainly inconclusive and could not be explained with limited evidence of reaction products for complex reaction dynamics. In fact, to reveal the reaction mechanisms for the unimolecular dissociation of 1, it is necessary to thoroughly explore the potential energy surface for all possible fragmentation channels.13–15 In this study, therefore, we theoretically examine the photodissociation process of 1 with the competitive reaction product channels after one-photon excitation from the cationic ground state prepared by a (2 + 1) REMPI scheme. The quantum chemical calculation alongside experimental observations will further provide insights to the photodissociation dynamics of 1 in the gas phase.
2 Experimental and computational methods
The experimental setup for the photodissociation has been previously described in detail elsewhere,16 and only a brief description is provided here. The sample soaked in quartz wool was placed into a sample holder located behind a solenoid-pulsed nozzle (General Valve Series 9, orifice size 0.8 mm) operating at 10 Hz with Ne carrier gas at 1 atm. The molecular beam generated by a 1 mm skimmer (Beam Dynamics Inc.) was ionized by a frequency-doubled (using BBO crystal) UV output (1 mJ) of a dye laser (Continuum, ND 6000, LDS 751) pumped by a Nd:YAG (Continuum, Surelite II-10) operating at 10 Hz. The accurate laser wavelength at 373.87 nm was achieved by the calibration using a wavemeter. The generated ions were accelerated and subsequently detected by a microchannel plate (Galileo Electro-Optics, FTD 2003) detector in a linear time-of-flight (TOF) mass spectrometer (R. M. Jordan Co.) the mass signal was fed into a preamplifier (EG & G Ortec, 9305), digitized and stored by a digital storage oscilloscope (Lecroy, 42MXs-B), and subsequently processed with a LabVIEW program.
The high resolution mass spectrum of isobutanal was obtained by 70 eV electron ionization (EI) with a resolution higher than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. A Loco Pegasus GC-HRT high resolution TOF mass spectrometer was used for acquisition of the spectrum.
000. A Loco Pegasus GC-HRT high resolution TOF mass spectrometer was used for acquisition of the spectrum.
To obtain the potential energy surface for the dissociation of 1, molecular orbital calculations were performed using the Gaussian 09 program.17 The geometries of the local minima and transition states were optimized at the unrestricted B3LYP level of the density functional theory (DFT) using the 6-31G(d) basis set. The transition state geometries were verified by calculating the intrinsic reaction coordinates at the same level. For higher energy accuracy, Gaussian-4 (G4)18 calculations were performed.
The Rice–Ramsperger–Kassel–Marcus (RRKM) expression was used to calculate the microcanonical rate constant, k(E), for a unimolecular reaction.19
| |
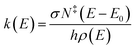 | (1) |
where
E is the internal energy of the reactant,
E0 is the critical energy of the reaction,
N‡ is the sum of the transition states,
ρ is the density of the reactant states,
σ is the reaction path degeneracy, and
h is Planck's constant.
N‡ and
ρ were evaluated by a direct count of the states using the Beyer–Swinehart algorithm.
20 The
E0 values for the individual steps were obtained from the G4 calculations and were used for RRKM calculations. Each normal mode of vibration was treated as a harmonic oscillator. The vibrational frequencies that were obtained from the B3LYP/6-31G(d) calculations were scaled down by a factor of 0.9614.
21
3 Results and discussion
Fig. 1a shows the photodissociation mass spectrum of 1 generated by the (2 + 1) REMPI at 53495.0 cm−1, which is the origin band (0–0) of the 3s ← n transition. The photofragment ions are originated from absorption of an additional photon of the REMPI-generated isobutanal cation if we exclude the possibility of multiphoton absorption at relatively low laser power. The candidates for the major fragment ions with m/z 43 and 29 are (CH3)2CH+ and CHO+, respectively, considering only direct bond cleavages of 1. Unfortunately, the resolution of the TOF mass analyzer used for our photodissociation experiment was too low to measure the ion mass accurately. We obtained a high resolution EI mass spectrum of isobutanal as shown in Fig. 1b. Surprisingly, each of the peaks at m/z 43 and 29 was clearly split into doublets, which are not resolved in Fig. 1b. Those at m/z 43 were assigned by C3H7+ and C2H3O+, and those at m/z 29 were assigned by C2H5+ and CHO+ as listed in Table 1.
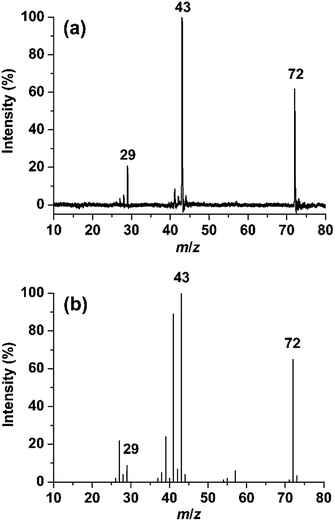 |
| | Fig. 1 (a) Photodissociation mass spectrum of the isobutanal radical cation generated by REMPI at 53495.0 cm−1. (b) 70 eV electron ionization mass spectrum of isobutanal. | |
Table 1 Accurate mass measurement data for the peaks at m/z 43 and 29 in the 70 eV EI spectrum
| m/z |
Intensity (%) |
Elemental composition |
Calculated mass |
Measured mass |
Error (mmu) |
| 43 |
100 |
C3H7 |
43.0548 |
43.0542 |
−0.6 |
| 43 |
4 |
C2H3O |
43.0184 |
43.0178 |
−0.6 |
| 29 |
10 |
C2H5 |
29.0391 |
29.0386 |
−0.5 |
| 29 |
7 |
CHO |
29.0027 |
29.0022 |
−0.5 |
The internal energy of 1 undergoing the photodissociation is 3.3 eV accepting the analysis by Shen et al.11 Comparing the two spectra, the main peaks at m/z 43 and 29 in the photodissociation spectrum appear also in the EI spectrum. The peaks at m/z 41, 39, 27, etc., probably corresponding to the fragments formed by consecutive dissociations from the ions with m/z 43 and 29, are shown in the EI mass spectrum but not in the photodissociation spectrum. This indicates a considerable portion of the isobutanal ions generated by 70 eV EI possesses energies higher than 3.3 eV. Therefore, the observation of doublets for the peaks at m/z 43 and 29 in the EI spectrum is not an evidence for that each of the photofragment ions with m/z 43 and 29 would consist of two different ions also. Instead, the observation in the EI spectrum suggests that the photofragment ions with m/z 43 can be C3H7+ and/or C2H3O+ and the photofragment ions with m/z 29 can be C2H5+ and/or CHO+, which will be determined through following theoretical investigations.
Rearrangements should precede dissociations to produce C2H3O+ and C2H5+ from 1, whereas the products (CH3)2CH+ and CHO+ are formed by direct cleavages. To investigate the pathways for the production of C2H3O+ and C2H5+, we calculated the potential energy surface for the dissociation of 1 occurring through isomerizations. Previously, Shen et al. reported theoretical endoergicity data for some dissociation channels of 1, calculated with the Gaussian-3 method.10 However, they did not try to explore the potential energy surface. We carried out G4 calculations and their resultant energies at absolute zero are presented here. 1 has two conformers, gauche (1g) and trans (1t). The energy of 1t is lower than 1g by 0.033 eV, and their isomerization barrier is located at 0.080 eV above 1t. The lowest energy pathways for the following reactions, occurring by direct bond cleavages, are shown in Fig. 2.
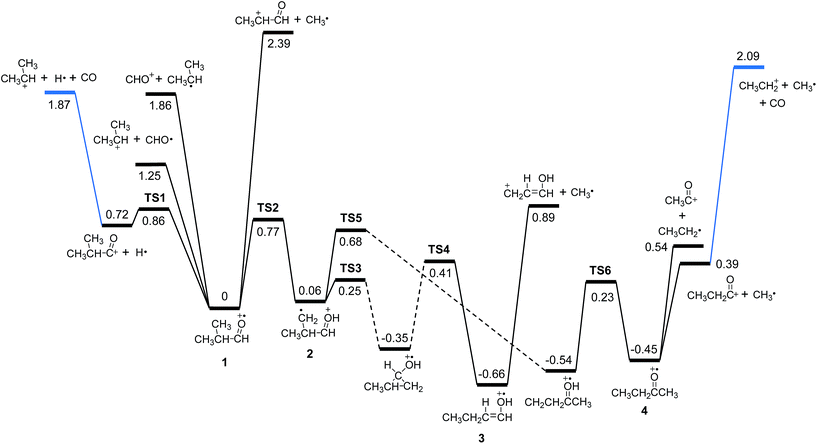 |
| | Fig. 2 Potential energy diagram for the primary and some secondary dissociation of the isobutanal radical cation, which was derived from the G4 calculations. The energies at absolute zero are presented in eV. The pathway denoted by dashed line occurs through more than one step. See Fig. 3 for full pathways. | |
All these reactions occur without reverse barriers except reaction (2). On the other hand, 1 can isomerize to a distonic ion (2) by a H migration from C to O through a five-membered transition state (TS2) (See Fig. 2 and 3). 2 can isomerize finally to either 1-buten-1-ol cation (3) or 2-butanone cation (4) prior to dissociation. The formation of 3 from 2 occurs through several steps including a skeleton rearrangement and H migrations as shown in Fig. 3. The calculation of this pathway was based on the report using DFT calculations by Hudson and McAdoo.22 3 can lose CH3˙ to form CH2CHCHOH+.
| | |
1 → 3 → CH2CHCHOH+ + CH3˙
| (6) |
Formation of
4 from
2 occurs through consecutive migrations of the methyl group and H of the OH group (
Fig. 3).
4 can lose CH
3˙ or CH
3CH
2˙ to form CH
3CH
2CO
+ or CH
3CO
+, respectively.
| | |
1 → 4 → CH3CH2CO+ + CH3˙
| (7) |
| | |
1 → 4 → CH3CO+ + CH3CH2˙
| (8) |
The product ions of reactions
(2) and
(7) can undergo further CO losses as follows:
| | |
1 → (CH3)2CH+ + H˙ + CO
| (9) |
| | |
1 → CH3CH2+ + CH3˙ + CO
| (10) |
These reactions can occur in the photodissociation of
1 having internal energy of 3.3 eV because their endoergicities are 1.87 and 2.09 eV, respectively. However, the reaction
1 → CH
3+ + CH
3CH
2˙ + CO through reaction
(8) cannot occur in the photodissociation because its endoergicity is 3.79 eV.
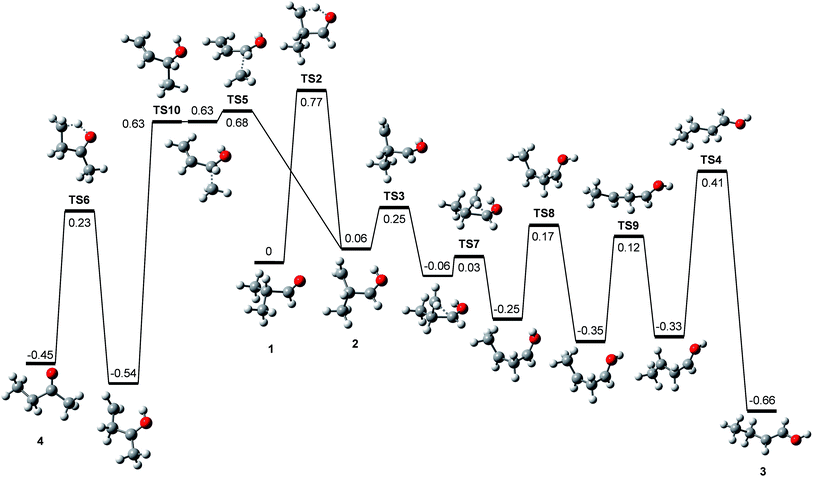 |
| | Fig. 3 Potential energy diagram for the isomerizations of the isobutanal radical cation, which was derived from the G4 calculations. The energies at absolute zero are presented in eV. | |
To investigate the kinetics of the competitive dissociations described above, k(E)s for some unimolecular reaction steps were calculated using eqn (1). For the steps occurring without reverse barriers, the vibrational frequencies of the transition states were adjusted for the activation entropy at 1000 K to become 24 J mol−1 K−1, a typical value for reactions occurring through a loose transition state.23 The energy dependences of the rate constants for reactions (2)–(5) and the isomerization 1 → 2 are shown in Fig. 4, and their values at the ion energy of 3.3 eV are 2.0 × 1011, 5.8 × 1010, 1.8 × 108, 3.2 × 105, and 1.2 × 1010 s−1, respectively. This predicts that reactions (2) and (3) and the isomerization to 2 would compete with the ratio of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, whereas reactions (4) and (5) would hardly occur in the photodissociation. However, no peak at m/z 71 corresponding to the H loss appears in the photodissociation spectrum (Fig. 1a). This strongly suggests the occurrence of the consecutive dissociation, finally producing (CH3)2CH+, H˙ and CO. The (CH3)2CHCO+ ions formed by the photodissociation have the energy of around 2.6 eV, ignoring the kinetic energy release in reaction (2). At the energy, the rate constant for the loss of CO was calculated to be 3 × 1010 s−1, suggesting that most of the (CH3)2CHCO+ ions underwent the further dissociation to (CH3)2CH+ and CO because their flight times were a few microseconds in our instrument. This indicates that the major ions with m/z 43 observed in the photodissociation are (CH3)2CH+, formed directly from 1 (reaction (3)) and by the consecutive loss of H˙ and CO (reaction (9)). According to the RRKM calculations, k for reaction (4) is smaller than that for reaction (2) at 3.3 eV by three orders of magnitude, which means that the formation of CHO+ with m/z 29 would not compete with the other dissociations. The other candidate for the ion with m/z 29 is C2H5+, which could be formed by reaction (10). Because the RRKM calculations reasonably predict that the isomerization 1 → 2 is competitive with reactions (2) and (3), the further reaction to CH3CH2CO+ + CH3˙ via 4 could be also competitive. However, the abundance of the corresponding peak with m/z 57 is very small in the photodissociation spectrum, suggesting its further dissociation to CH3CH2+ and CO. The CH3CH2CO+ ions formed by the photodissociation have the energy of around 2.9 eV, ignoring the kinetic energy release in reaction (7). At the energy, the calculated rate constant for the loss of CO is 1 × 1010 s−1, indicating that most of the CH3CH2CO+ ions underwent the further dissociation to CH3CH2+ and CO. Therefore, the main photodissociation pathways to produce the ions with m/z 43 and 29 are summarized as Scheme 1. The CH3CO+ ion formed by reaction (8) would contribute to the ions with m/z 43. Then, why could the CHO+ ion be detected in the EI experiment? Fig. 4 shows that at high energies the formation of CHO+ ion (reaction (4)) can be competitive with reactions (2) and (3) and the isomerization to 2. Because the molecular ions generated by EI have energies with a broad distribution, the detection of CHO+ in the EI experiment could be possible.
4, whereas reactions (4) and (5) would hardly occur in the photodissociation. However, no peak at m/z 71 corresponding to the H loss appears in the photodissociation spectrum (Fig. 1a). This strongly suggests the occurrence of the consecutive dissociation, finally producing (CH3)2CH+, H˙ and CO. The (CH3)2CHCO+ ions formed by the photodissociation have the energy of around 2.6 eV, ignoring the kinetic energy release in reaction (2). At the energy, the rate constant for the loss of CO was calculated to be 3 × 1010 s−1, suggesting that most of the (CH3)2CHCO+ ions underwent the further dissociation to (CH3)2CH+ and CO because their flight times were a few microseconds in our instrument. This indicates that the major ions with m/z 43 observed in the photodissociation are (CH3)2CH+, formed directly from 1 (reaction (3)) and by the consecutive loss of H˙ and CO (reaction (9)). According to the RRKM calculations, k for reaction (4) is smaller than that for reaction (2) at 3.3 eV by three orders of magnitude, which means that the formation of CHO+ with m/z 29 would not compete with the other dissociations. The other candidate for the ion with m/z 29 is C2H5+, which could be formed by reaction (10). Because the RRKM calculations reasonably predict that the isomerization 1 → 2 is competitive with reactions (2) and (3), the further reaction to CH3CH2CO+ + CH3˙ via 4 could be also competitive. However, the abundance of the corresponding peak with m/z 57 is very small in the photodissociation spectrum, suggesting its further dissociation to CH3CH2+ and CO. The CH3CH2CO+ ions formed by the photodissociation have the energy of around 2.9 eV, ignoring the kinetic energy release in reaction (7). At the energy, the calculated rate constant for the loss of CO is 1 × 1010 s−1, indicating that most of the CH3CH2CO+ ions underwent the further dissociation to CH3CH2+ and CO. Therefore, the main photodissociation pathways to produce the ions with m/z 43 and 29 are summarized as Scheme 1. The CH3CO+ ion formed by reaction (8) would contribute to the ions with m/z 43. Then, why could the CHO+ ion be detected in the EI experiment? Fig. 4 shows that at high energies the formation of CHO+ ion (reaction (4)) can be competitive with reactions (2) and (3) and the isomerization to 2. Because the molecular ions generated by EI have energies with a broad distribution, the detection of CHO+ in the EI experiment could be possible.
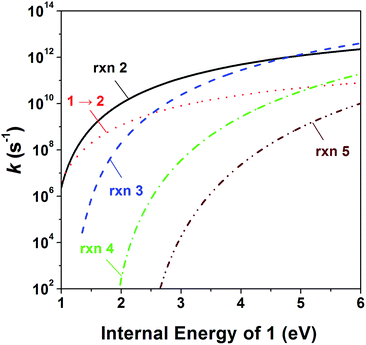 |
| | Fig. 4 Energy dependences of the RRKM rate constant for reactions (2)–(5) and 1 → 2. | |
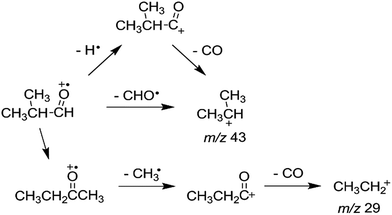 |
| | Scheme 1 Main photodissociation pathways of 1. | |
4 Conclusions
The main photodissociation pathways of 1 at 3.3 eV were carefully determined as Scheme 1 through the kinetic analysis using RRKM calculations based on the obtained potential energy surface. The production of CH3CH2+ from 1, not mentioned in any previous study, was confirmed indirectly by accurate mass measurement with the EI mass spectrometry. The successful explanation of the photodissociation with the RRKM theory indicates that the photoexcited ions dissociate statistically on the potential energy surface of the ground electronic state although photoabsorption initially leads to an excited electronic state. Further experimental studies measuring dissociation rate constants as a function of energy using other techniques such as photoelectron–photoion coincidence spectroscopy will be helpful for more accurate theoretical investigations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was financially supported by Ewha Womans University and by the National Institute of Supercomputing and Network/Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2017-C1-0001).
Notes and references
- F. F. Crim, J. Phys. Chem., 1996, 100, 12725 CrossRef CAS.
- S. L. Anderson, Acc. Chem. Res., 1997, 30, 28 CrossRef CAS.
- S. T. Park, S. K. Kim and M. S. Kim, Nature, 2002, 415, 306 CrossRef PubMed.
- M. H. Kim, L. Shen, H. L. Tao, T. J. Martinez and A. G. Suits, Science, 2007, 315, 1561–1565 CrossRef CAS PubMed.
- N. J. Kim, H. Kang, G. Jeong, Y. S. Kim, K. T. Lee and S. K. Kim, J. Phys. Chem. A, 2000, 104, 6552–6557 CrossRef CAS.
- R. I. Kaiser, S. Maity and B. M. Jones, Phys. Chem. Chem. Phys., 2014, 16, 3399–3424 RSC.
- A. I. Vasyunin and E. Herbst, Astrophys. J., 2013, 769, 34 CrossRef.
- M. A. Buntine, G. F. Metha, D. C. McGilvery and R. J. S. Morrison, J. Mol. Spectrosc., 1994, 165, 12 CrossRef CAS.
- S. Cuadrado, J. R. Goicoechea, J. Cernicharo, A. Fuente, J. Pety and B. Tercero, Astron. Astrophys., 2017, 603, A124 CrossRef PubMed.
- D. C. Metha, M. A. Buntine, G. F. McGilvery and R. J. S. Morrison, J. Mol. Spectrosc., 1994, 165, 32 CrossRef.
- L. Shen, P. C. Singh, M. Kim, B. Zhang and A. G. Suits, J. Phys. Chem. A, 2009, 113, 68 CrossRef CAS PubMed.
- L. Shen, B. Zhang and A. G. Suits, J. Phys. Chem. A, 2010, 114, 3114–3120 CrossRef CAS PubMed.
- C. E. Hudson, L. Vaela, L. L. Griffin and D. J. McAdoo, Int. J. Mass Spectrom., 2006, 249, 120–129 CrossRef.
- J. R. Cao, M. George and J. L. Holmes, J. Am. Soc. Mass Spectrom., 1992, 3, 99–107 CrossRef CAS PubMed.
- D. J. McAdoo, F. W. McLafferty and T. E. Parks, J. Am. Chem. Soc., 1972, 94, 1601 CrossRef CAS.
- A. Min, A. An, C. J. Moon, J. H. Lee, Y. G. Seong and S. K. Kim, Phys. Chem. Chem. Phys., 2017, 19, 4840–4848 RSC.
- M. J. Frisch, et al., Gaussian 09, revision A. 02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, New York, 1996 Search PubMed.
- T. Beyer and D. R. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- A. P. Scott and L. Radom, J. Phys. Chem. A, 1996, 100, 16502–16513 CrossRef CAS.
- C. E. Hudson and D. J. McAdoo, Int. J. Mass Spectrom., 2000, 199, 41–57 CrossRef CAS.
- M. K. Yim and J. C. Choe, J. Phys. Chem. A, 2011, 115, 3087–3094 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Myung Hwa Kim
b and
Myung Hwa Kim *c
*c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. A Loco Pegasus GC-HRT high resolution TOF mass spectrometer was used for acquisition of the spectrum.
000. A Loco Pegasus GC-HRT high resolution TOF mass spectrometer was used for acquisition of the spectrum.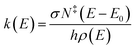



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, whereas reactions (4) and (5) would hardly occur in the photodissociation. However, no peak at m/z 71 corresponding to the H loss appears in the photodissociation spectrum (Fig. 1a). This strongly suggests the occurrence of the consecutive dissociation, finally producing (CH3)2CH+, H˙ and CO. The (CH3)2CHCO+ ions formed by the photodissociation have the energy of around 2.6 eV, ignoring the kinetic energy release in reaction (2). At the energy, the rate constant for the loss of CO was calculated to be 3 × 1010 s−1, suggesting that most of the (CH3)2CHCO+ ions underwent the further dissociation to (CH3)2CH+ and CO because their flight times were a few microseconds in our instrument. This indicates that the major ions with m/z 43 observed in the photodissociation are (CH3)2CH+, formed directly from 1 (reaction (3)) and by the consecutive loss of H˙ and CO (reaction (9)). According to the RRKM calculations, k for reaction (4) is smaller than that for reaction (2) at 3.3 eV by three orders of magnitude, which means that the formation of CHO+ with m/z 29 would not compete with the other dissociations. The other candidate for the ion with m/z 29 is C2H5+, which could be formed by reaction (10). Because the RRKM calculations reasonably predict that the isomerization 1 → 2 is competitive with reactions (2) and (3), the further reaction to CH3CH2CO+ + CH3˙ via 4 could be also competitive. However, the abundance of the corresponding peak with m/z 57 is very small in the photodissociation spectrum, suggesting its further dissociation to CH3CH2+ and CO. The CH3CH2CO+ ions formed by the photodissociation have the energy of around 2.9 eV, ignoring the kinetic energy release in reaction (7). At the energy, the calculated rate constant for the loss of CO is 1 × 1010 s−1, indicating that most of the CH3CH2CO+ ions underwent the further dissociation to CH3CH2+ and CO. Therefore, the main photodissociation pathways to produce the ions with m/z 43 and 29 are summarized as Scheme 1. The CH3CO+ ion formed by reaction (8) would contribute to the ions with m/z 43. Then, why could the CHO+ ion be detected in the EI experiment? Fig. 4 shows that at high energies the formation of CHO+ ion (reaction (4)) can be competitive with reactions (2) and (3) and the isomerization to 2. Because the molecular ions generated by EI have energies with a broad distribution, the detection of CHO+ in the EI experiment could be possible.
4, whereas reactions (4) and (5) would hardly occur in the photodissociation. However, no peak at m/z 71 corresponding to the H loss appears in the photodissociation spectrum (Fig. 1a). This strongly suggests the occurrence of the consecutive dissociation, finally producing (CH3)2CH+, H˙ and CO. The (CH3)2CHCO+ ions formed by the photodissociation have the energy of around 2.6 eV, ignoring the kinetic energy release in reaction (2). At the energy, the rate constant for the loss of CO was calculated to be 3 × 1010 s−1, suggesting that most of the (CH3)2CHCO+ ions underwent the further dissociation to (CH3)2CH+ and CO because their flight times were a few microseconds in our instrument. This indicates that the major ions with m/z 43 observed in the photodissociation are (CH3)2CH+, formed directly from 1 (reaction (3)) and by the consecutive loss of H˙ and CO (reaction (9)). According to the RRKM calculations, k for reaction (4) is smaller than that for reaction (2) at 3.3 eV by three orders of magnitude, which means that the formation of CHO+ with m/z 29 would not compete with the other dissociations. The other candidate for the ion with m/z 29 is C2H5+, which could be formed by reaction (10). Because the RRKM calculations reasonably predict that the isomerization 1 → 2 is competitive with reactions (2) and (3), the further reaction to CH3CH2CO+ + CH3˙ via 4 could be also competitive. However, the abundance of the corresponding peak with m/z 57 is very small in the photodissociation spectrum, suggesting its further dissociation to CH3CH2+ and CO. The CH3CH2CO+ ions formed by the photodissociation have the energy of around 2.9 eV, ignoring the kinetic energy release in reaction (7). At the energy, the calculated rate constant for the loss of CO is 1 × 1010 s−1, indicating that most of the CH3CH2CO+ ions underwent the further dissociation to CH3CH2+ and CO. Therefore, the main photodissociation pathways to produce the ions with m/z 43 and 29 are summarized as Scheme 1. The CH3CO+ ion formed by reaction (8) would contribute to the ions with m/z 43. Then, why could the CHO+ ion be detected in the EI experiment? Fig. 4 shows that at high energies the formation of CHO+ ion (reaction (4)) can be competitive with reactions (2) and (3) and the isomerization to 2. Because the molecular ions generated by EI have energies with a broad distribution, the detection of CHO+ in the EI experiment could be possible.

