Open Access Article
Open Access ArticleFacile synthesis and characterization of ultrathin δ-MnO2 nanoflakes
Xiang Chen ,
Shaojiu Yan*,
Nan Wang,
Sikan Peng,
Chen Wang,
Qihu Hong,
Xiaoyan Zhang and
Shenglong Dai
,
Shaojiu Yan*,
Nan Wang,
Sikan Peng,
Chen Wang,
Qihu Hong,
Xiaoyan Zhang and
Shenglong Dai
Research Center of Graphene Applications, Beijing Institute of Aeronautical Materials, Beijing 100095, China. E-mail: shaojiuyan@126.com; Fax: +86 10 6249 6834; Tel: +86 10 6249 6426
First published on 8th December 2017
Abstract
Ultrathin MnO2 with a 2D structure is extremely attractive, especially in the field of energy storage, as its high surface area enables faradaic charge storage and provides short transport paths for electrons and ions. In this paper, we report a facile synthesis of ultrathin δ-MnO2 nanoflakes with wrinkled morphology via the reduction of potassium permanganate by ethanol in an aqueous solution. The obtained δ-MnO2 nanoflakes were potassium manganese oxide hydrate (K-birnessite) with the chemical formula K0.25MnO2.06·0.51H2O and had a lamellar structure with monoclinic symmetry. The lateral dimensions of the nanoflakes were in the range of 150–200 nm, as determined by transmission electron microscopy (TEM). A further high-resolution-TEM analysis indicated that these nanoflakes were composed of nano-grains with a thickness of 4–5 nm. It is speculated that the nanoflakes assembled from crystal nuclei 4–5 nm in size, corresponding to ∼7 lamellar layers, along the layer directions. As a result, the assembled nanoflakes inherited the ultrathin nature of these crystal nuclei. Cyclic voltammetry measurements demonstrated the excellent electrochemical properties of the nanoflakes, which can potentially serve as supercapacitor electrode materials.
Introduction
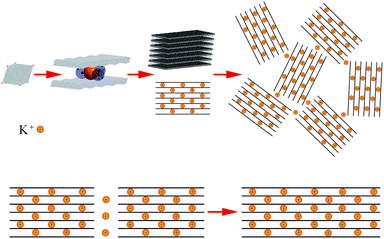
Two-dimensional (2D) materials have become one of the most exciting research fields in materials science over the years1 because they present novel properties different from their bulk counterparts when reduced to their physical limits.2 These materials have high surface areas and flexibility,3 and some of them exhibit high mechanical strength, high electrical and thermal conductivities, and high dielectric constants.4,5With its unique 2D nanostructure, layered MnO2 has been extensively investigated and widely used in the areas of ion-exchangers,6 adsorbents,7 catalysis,8 and energy storage.9 Layered MnO2 is typically a ternary phase with the general formula RxMnO2·yH2O, where water molecules and cationic species are located between the layers composed of MnO6 octahedral units10 so as to balance the charges. The interlayer spacing between the octahedral layers is around 7 Å,11 which is suitable for cation migration and thus leads to excellent ion-exchange properties and electrochemical performance.12 In energy storage applications, MnO2 uses only a nanometer-thick portion of its surface to store charge; therefore, a high-surface area MnO2 nanoflake with nanometer thickness could be ideal for enhanced charge storage. Besides, the ultrathin MnO2 nanoflakes could tolerate volume alteration during the charge–discharge cycles due to their flexibility, leading to improved stability.
Layered MnO2 can be synthesized through the reduction/decomposition of a Mn(VII) compound or the oxidization of a Mn(II) compound. After years of effort, several synthetic routes such as co-precipitation,13 hydrothermal,14 sol–gel,15 decomposition,16 and microwave-assisted methods17,18 have been developed. The morphology of layered MnO2 is affected by several synthetic parameters such as the type, concentration, and ratio of reactants, and the temperature and pH of the reaction. Liu et al.19 reported a simple synthesis of acid K-birnessite nanoparticles by adding NH2OH·HCl to KMnO4 solution under ambient condition. The particle size could be decreased by adding an excess of the NH2OH·HCl reductant. Wang et al.20 synthesized K-birnessite nanoparticles by a redox reaction between KMnO4 and (NH4)2C2O4 at 90 °C. The morphology of the obtained nanoparticles was dominated by the reactant ratio of KMnO4 to (NH4)2C2O4. The particles exhibited flower-like morphology when the reactant ratio was 0.5. When the ratio increased to 2.25, the surface of the nanoparticles became denser and the flower-like structure disappeared. Although much effort has been devoted to improving the fabrication methods to control the morphology of layered MnO2, the obtained products are most often granular or have flower-like shapes. Extra exfoliation is usually required to achieve a flaky morphology. For instance, Beatriz et al.21 reported a two-step exfoliation route to achieving flaky MnO2. Firstly, he fabricated flower-shaped MnO2 nanostructures with a typical co-precipitation method, and then exfoliated them into nanoflakes with isopropanol. The obtained flakes possessed lateral dimensions of 20–40 nm and thickness of 3.2 nm. Omomo et al.22 synthesized unilamellar two-dimensional crystallites of MnO2 with a thickness of ∼0.8 nm by intercalating layered protonic MnO2 (H0.13MnO2·0.7H2O) with tetrabutylammonium ions during an ion-exchange treatment. Besides, 2D MnO2 nanoflakes were also reported, synthesized with the aid of surfactants and templates. For example, Kang's group23,24 synthesized amorphous MnO2 nanosheets via the reduction of KMnO4 aqueous solution dispersed in isooctane with sodium bis(2-ethylhexyl) sulfosuccinate. Zhao et al.25 reported an in situ synthesis of MnO2 nanosheets from graphene oxide templates.
However, the synthesis of perfect 2D MnO2 nanoflakes especially with an ultrathin feature is still challenging; the current synthesis procedures are generally multi-step, time-consuming, or high-cost, invariably involve toxic or expensive chemicals, and are not suitable for scale production. Therefore, it is necessary to spend some effort on developing a simple synthesis method for ultrathin 2D MnO2 nanoflakes. Moreover, their characterization and growth mechanism are also worth the attention. Herein, we report the preparation of 2D δ-MnO2 nanoflakes by a simple chemical co-precipitation method. The chemical formula and structure of δ-MnO2 were determined, and its growth mechanism was proposed based on TEM observation and structural analysis. Finally, we investigated the supercapacitive performance of the as-prepared δ-MnO2 nanoflakes.
Experimental
Synthesis procedure
δ-MnO2 nanoflakes were prepared through a redox reaction between KMnO4 and C2H6O. The reagents with 99.5% purity were supplied by Sinopharm Chemical Reagent. In brief, 1 g of KMnO4 was dissolved in 500 ml of distilled water and excess of C2H6O was added dropwise under vigorous stirring. The reaction was carried out at ambient temperature for 2 h until the purple solution turned brown. The obtained precipitate was filtered under pressure, and washed with distilled water and then ethanol. Finally, the purified precipitate was desiccated at 80 °C for 12 h in an electric thermostatic drying oven, and a brown powder was obtained.Characterization
Chemical analysis was carried out using an inductively coupled plasma-atomic emission spectrometer (PerkinElmer Optima 7300 ICP-AES). The thermal decomposition was studied with a differential scanning calorimeter (DSC-214, NETZSCH) in an argon flow using an aluminum crucible. The valence state was determined by X-ray photoelectron spectroscopy (XPS) under ultra-high-vacuum condition using monochromatic Al Kα X-rays (1486.6 eV). Powder X-ray diffraction (XRD) patterns were obtained using a diffractometer (Bruker D8 advance) with Cu Kα radiation (30 kV, 30 mA, λ = 1.5406 Å). TEM and selected area electron diffraction (SAED) were performed utilizing a transmission electron microscope (FEI Tecnai G2 F30) at an accelerating voltage of 100 kV, equipped with a high-resolution accessory. A Fourier transform infrared spectroscope (FTIR Spectrum 400) was used to determine the crystal structure of the as-prepared MnO2. Raman scattering spectra were recorded with a Raman spectrometer (HORIBA LabRAM HR800, Japan) at room temperature.Electrochemical measurements
To prepare the working electrode, 70 wt% of as-prepared MnO2, 20 wt% acetylene black, and 10 wt% polytetrafluoroethylene (PTFE) were uniformly mixed using an agate mortar and pestle for 30 min. The mixture was dispersed in ethanol in an ultrasonic bath (37 kHz, 200 W) for 20 min. The dispersion was then dropped on a well-polished glassy carbon electrode and desiccated under infrared light. The electrochemical properties of the electrode were examined via cyclic voltammetry in a three-electrode electrochemical cell, which consisted of a Ag/AgCl reference electrode and a platinum-wire counter-electrode with 0.5 M K2SO4 electrolyte (the pH was adjusted to 10 with a dilute buffer solution).Results and discussion
Chemical composition and crystal structure
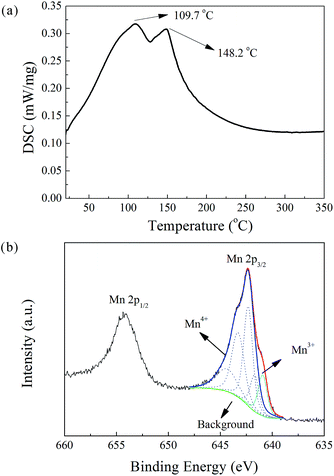
Prepared in a K-rich aqueous solution, the obtained powder is anticipated to contain K and crystal water. Thus, chemical analysis (by ICP-AES) and synchronous thermal analysis (by DSC) were carried out in sequence. The K and Mn content were determined as 8.72 wt% and 48.44 wt%, respectively. The DSC analysis detected two endothermic peaks in the temperature range from room temperature to 200 °C. A similar phenomenon was reported by Bach et al. In their DSC study of Na-birnessite, two departures of water were observed at 85 and 150 °C.26·As shown in Fig. 1a, the peaks at 109.7 °C and 148.2 °C are believed to have originated from the evaporation of adsorbed water and interlayer water, respectively. The integration of both the peaks yields a vaporization heat of 163 J g−1, which, when compared to the standard vaporization heat of water (2.257 kJ g−1), gives an estimated water content of 7.22 wt%. In addition, the water content was determined by weighing the mass loss after the DSC test, which yielded a value of 8.62 wt%. The reported values of the water content of potassium manganese oxide hydrate range from 4.3 to 14.1 wt%.27–29 This discrepancy is probably due to the presence of adsorbed water, which can vary with environmental humidity and preheating conditions. The valence state of Mn was determined by XPS (Fig. 1b). The Mn 2p3/2 peak was fitted with five multiplet components in conformity with the parameters established by Biesinger et al.30 The atomic ratio of Mn3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn4+ was evaluated by their relative peak areas, and the average oxidation state of Mn was found to be 3.87. Finally, the chemical formula of the MnO2-based powder was determined as K0.25MnO2.06·0.51H2O. The co-precipitation reaction between KMnO4 and C2H6O can be described by the following equation:
Mn4+ was evaluated by their relative peak areas, and the average oxidation state of Mn was found to be 3.87. Finally, the chemical formula of the MnO2-based powder was determined as K0.25MnO2.06·0.51H2O. The co-precipitation reaction between KMnO4 and C2H6O can be described by the following equation:| K+ + 4MnO4− + 3.13C2H6O → 4K0.25MnO2.06·0.51H2O↓ + 3.13CH3COO− + 2.59H2O + 0.13H+ | (1) |
 | ||
| Fig. 1 Thermal decomposition and compositional analysis of the as-prepared powder. (a) DSC curve. (b) XPS spectra. | ||
Phase determination of the as-prepared powder was carried out by XRD, and the result is presented in Fig. 2a. The pattern coincides well with the reference JCPDS00-042-1317 (potassium manganese oxide hydrate, K0.25MnO2·0.75H2O, star quality). The main peaks appear at 12.48°, 25.21°, 36.74°, and 65.77° corresponding to the (001), (002), (110), and (020) planes with interplanar spacing of 7.09, 3.53, 2.45, and 1.42 Å, respectively. The reference phase (a = 5.150 Å, b = 2.844 Å, c = 7.159 Å, α = γ = 90°, β = 100.64°) belongs to the face-centered (C) monoclinic crystal system. Its [010] axis has a two-fold rotational symmetry, and the vertical plane perpendicular to the [010] axis is a mirror symmetry plane. The XRD analysis hence confirmed the layered structure of the as-prepared powder, which can be denoted as K-birnessite or δ-MnO2. The layered δ-MnO2 is commonly generated from the redox reaction between KMnO4 and C2H6O, and the presence of K+ is believed to stabilize its 2D layered structure.
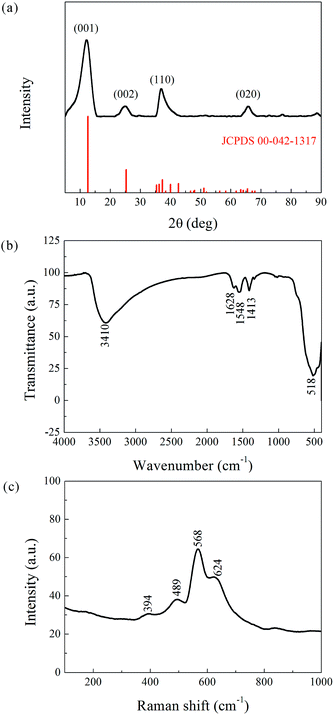 | ||
| Fig. 2 Structural characterization of the as-prepared powder. (a) XRD pattern. (b) FTIR Spectra. (c) Raman scattering. | ||
In addition, the XRD peaks were significantly broad compared to the standard patterns. This phenomenon is attributed to the small crystalline grain size, as estimated by the Debye–Scherrer equation, Dhkl = fλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, where Dhkl is the mean size of the crystalline domains (or grain size), f is a dimensionless shape factor with a value close to unity (typically 0.9), λ is the X-ray wavelength, β is the full width at half maximum (FWHM, expressed in radians), and ϑ is the Bragg angle (in degrees). The corresponding results, listed in Table 1, indicate an ultrafine grain structure for the δ-MnO2 material.
ϑ, where Dhkl is the mean size of the crystalline domains (or grain size), f is a dimensionless shape factor with a value close to unity (typically 0.9), λ is the X-ray wavelength, β is the full width at half maximum (FWHM, expressed in radians), and ϑ is the Bragg angle (in degrees). The corresponding results, listed in Table 1, indicate an ultrafine grain structure for the δ-MnO2 material.
| No. | 2ϑ (°) | d (Å) | β (rad) | (hkl) | Dhkl (Å) |
|---|---|---|---|---|---|
| 1 | 12.48 | 7.09 | 0.038 | (001) | 40.34 |
| 2 | 25.21 | 3.53 | 0.043 | (002) | 36.96 |
| 3 | 36.74 | 2.45 | 0.021 | (110) | 76.18 |
| 4 | 65.77 | 1.42 | 0.034 | (020) | 53.62 |
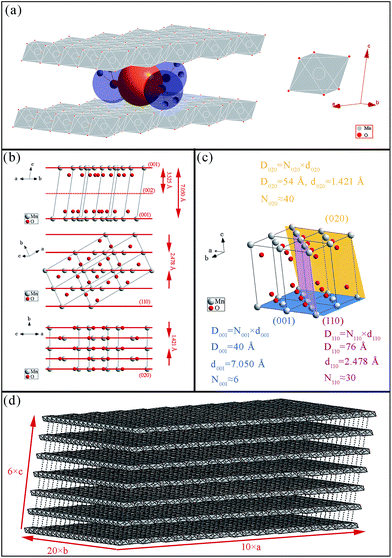
FTIR and Raman characterizations further elucidated the crystal structure of the nanoflake grains. Fig. 2b shows the IR spectra of δ-MnO2. The bands at 3410 cm−1 and 1400–1650 cm−1 correspond to the stretching31 and bending32 vibrations of H2O, respectively, and the presence of several O–H bending vibration modes in the 1400–1650 cm−1 range indicates the co-existence of adsorbed and crystal water.33 Another important observation is the band at 518 cm−1, which represents the Mn–O bond vibration.34 Fig. 2c shows the Raman spectra of δ-MnO2, where an intense band at 568 cm−1 and three weak bands at 394, 489, and 624 cm−1 are observed. The Raman band located at 624 cm−1 can be attributed to the symmetric stretching vibration ν2(Mn–O) of MnO6. The band at 568 cm−1 is generally attributed to the ν3(Mn–O) stretching vibration in the MnO6 layer, and its strong intensity is believed to be related to the high content of quadrivalent Mn atoms in the birnessite structure. The bands at 489 and 394 cm−1 are assigned to the ν5(Mn–O) and ν7(Mn–O) stretching vibrations of MnO6, respectively. These features correspond to a layered birnessite MnO2 material consisting of layers composed of MnO6 units,35 in which six oxygen atoms surround a central manganese atom in an approximate octahedral coordination, and crystal water between the layers, as shown in Fig. 3a. Based on the above characterization, crystal parameters, and data from Table 1, we determined the structure of a typical δ-MnO2 grain (Fig. 3d). Three independent lattice planes—(001), (110), and (020)—were chosen to estimate the dimensions of a typical grain (Fig. 3b). Nhkl is the number of atomic layers in a grain in its [hkl] direction, and is calculated as Dhkl/dhkl (Fig. 3c). N100, N010, and N001 were calculated as 10, 20, and 6, and a 7-layer 3D grain was accordingly drawn in Fig. 3d.
Morphology observation and analysis
A TEM image of the as-prepared δ-MnO2 is displayed in Fig. 4a, which shows a typical layered flake-shape morphology. The wrinkling, along with the highly transparent flake border, points to ultrathin nanoflakes. In the figure, one can distinguish wrinkled flakes with a lateral size of 150–200 nm. Despite their nanoscale dimensions, these individual nanoflakes are not monocrystals (Fig. 4d), but, on the contrary, exhibit dozens of crystalline grains within an HR-TEM-analyzed region, with a lateral size of about 5 nm. Lamellar stripes are observed along the border or the wrinkled region of these nanoflakes. As shown in Fig. 4b, two obvious distinctions can be made between these stripes and the ordinary crystal lattice stripes. First, the stripe spacing is much wider for the lamellar structures, i.e., 6–7 Å measured here, as opposed to the ordinary crystal lattice stripe spacing of 1–3 Å. Second, while the ordinary crystal lattice stripes are equidistantly aligned, the lamellar stripes can be flexuous in shape. From the measurements of these lamellar stripes, the average thickness of the nanoflakes was determined to be 4 nm, similar to the lateral crystalline grain size. It is noteworthy that the observation of the lamellar structure is the most direct visual identification of the product as a layered birnessite.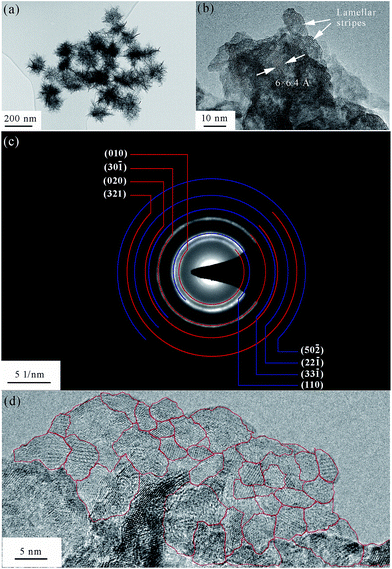 | ||
| Fig. 4 TEM analysis of the as-prepared δ-MnO2. (a) TEM and (b) HR-TEM image of lamellar stripes within the nanoflakes. (c) SAED pattern and (d) HR-TEM image of polycrystalline grains. | ||
As expected, the SAED pattern (Fig. 4c) consisted of polycrystalline rings. Since the incident electron beam was vertical to the δ-MnO2 nanoflake plane (i.e., along its [001] normal direction), only the planes vertical to the (001) plane would generate rings in the SAED image. Table 2 lists the planes that are approximately vertical to the (001) plane, their corresponding d-spacing values, and the angles they form with the (001) plane. The d-spacing values obtained from the SAED polycrystalline rings are also given in Table 2, as well as the theoretical value of the (001) plane spacing and the measured value obtained from the HR-TEM images. The theoretical d-spacing values are about 1.1 times larger than the measured ones. The narrowing of the δ-MnO2 interlayer spacing (d001) has already been reported,33 and is believed to be induced by dehydration caused by exposure to an electron beam in vacuum. In this paper, we found that not only d001, but also d010 and d110 reduced at the same rate after the dehydration of δ-MnO2. In other words, hydration expands the δ-MnO2 unit cell at the same rate in all directions.
| Plane (hkl) | Theoretical angle with (001) plane# | d (Å) | R♣ | |
|---|---|---|---|---|
| Theoretical# | Measured | |||
a 1. Data marked with # are calculated from the monoclinic crystal parameters (a = 5.150 Å, b = 2.844 Å, c = 7.159 Å, α = γ = 90°, β = 100.64°). 2. Data marked with ^ are derived from the electron diffraction rings. 3. Data marked with * were obtained from the direct measurement of the lamellar spacing. 4. R♣ = dTheoretical![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dMeasured. dMeasured. |
||||
| (010) | 90° | 2.843 | 2.61^ | 1.09 |
| (110) | 85° | 2.478 | 2.24^ | 1.11 |
(30![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
87° | 1.714 | 1.59^ | 1.08 |
(31![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
87° | 1.468 | 1.37^ | 1.07 |
| (020) | 90° | 1.421 | 1.30^ | 1.09 |
(22![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
85° | 1.240 | 1.13^ | 1.10 |
(32![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
88° | 1.094 | 1.01^ | 1.08 |
(50![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) ) |
84° | 1.024 | 0.92^ | 1.14 |
| (001) | 0° | 7.050 | 6.40* | 1.10 |
Growth mechanism
Considering that the δ-MnO2 nanoflakes assembled from layered nano-grains, as illustrated in Fig. 3d, we propose a possible growth mechanism of these flakes. In the first stage, δ-MnO2 crystal nuclei with a lamellar structure consisting of MnO6 octahedron layers, cations, and water were generated. These negatively charged crystal nuclei repulsed each other while attracting K+. The crystal nuclei therefore tended to assemble along the lamellar directions, yielding the nano-grains observed by HR-TEM in Fig. 4d, and shown by the parallel lines in Fig. 5. This self-assembly is believed to be controlled by coulombic interactions36 and driven by surface energy reduction. However, defects inevitably formed during the self-assembly and finally led to an imperfect wrinkled nanoflake morphology. It is worth mentioning that δ-MnO2 nanoflakes were assembled along the lamellar directions, and hence, their thicknesses were determined by the thicknesses of their component crystal nuclei. A sufficient condition to achieve ultrathin δ-MnO2 nanoflakes is to control the thicknesses of their original crystal nuclei.Supercapacitive performance
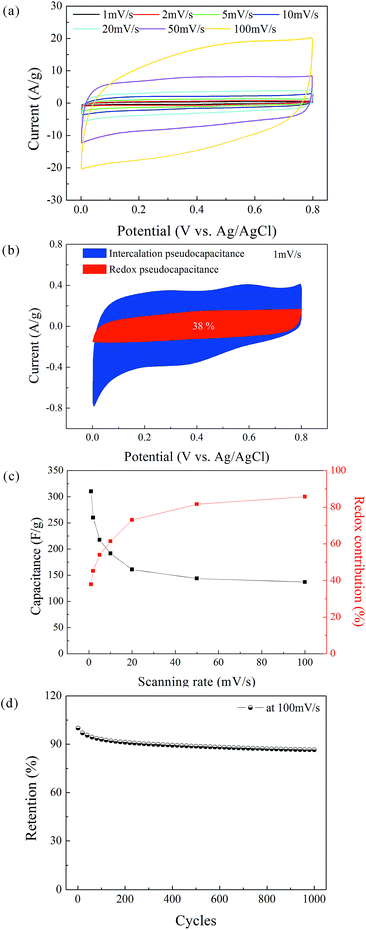
The CV measurements of the δ-MnO2 electrode were performed at a scanning rate in the range of 1–100 mV s−1 (Fig. 6a). The nearly rectangular shapes of the CV curves indicate a nearly ideal supercapacitive behavior. The area under the CV curve increases with increasing scanning rate, while the curve retains its shape. According to Simon's mechanism, δ-MnO2 stores the charges mainly by pseudo-capacitive reactions occurring at the surface and bulk of the solid MnO2 phase, as shown below:37| Mn(IV)O2 + xC+ + yH+ + (x + y)e− ↔ Mn(III)(x+y), Mn(IV)1−(x+y)OOCxHy, | (2) |
The specific capacitance of the electrode can be obtained from the area under the CV curve using the following equation:41–43
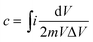 | (3) |
At a high scanning rate, cation diffusion through interlayer gaps is restricted; therefore, the redox pseudocapacitance at the surface of δ-MnO2 is the major contributor to the capacitance (86% at 100 mV s−1). By contrast, the capacitance mainly originates from the insertion and extraction of cations into and from the δ-MnO2 layers at a low scanning rate, and the redox pseudocapacitance contributes only 38% of total capacitance at 1 mV s−1. Note that the theoretical specific capacitance of δ-MnO2 (chemical formula: K0.25MnO2.06·0.51H2O) can be obtained according to Cao's method,44 which was calculated as 862 F g−1. Considering the 7-layered lamellar structure of δ-MnO2, the surface redox pseudocapacitance provides only one-seventh of the theoretical capacitance. The poor rate performances shown in Fig. 6c are mainly due to the structure of δ-MnO2. On one hand, the large lateral dimensions of δ-MnO2 nanoflakes result in a long-range diffusion path for ions through the interlayer gaps, and the intercalation pseudocapacitance becomes dependent on the scan rate in the concerned range. On the other hand, the lamellar layer number of the δ-MnO2 nanoflakes is not small enough to provide a large redox pseudocapacitance. To further evaluate the stability of the δ-MnO2 electrode, long-term cycling was carried out at 100 mV s−1; the corresponding result is shown in Fig. 6d. The δ-MnO2 electrode exhibited about 86.5% of the initial specific capacitance after 1000 cycles. The good electrochemical stability indicates that a highly reversible redox reaction occurred at the surface and in the interlayer gaps of the δ-MnO2 electrode.
Conclusions
In summary, δ-MnO2 nanoflakes were synthesized via the reduction of KMnO4 by C2H6O in an aqueous solution. The so-obtained δ-MnO2 nanoflakes exhibited a lamellar structure and wrinkled morphology. In the first stage of nanoflake formation, nuclei with a size of ∼4 nm, corresponding to ∼7 lamellar layers, crystallized as K0.25MnO2.06·0.51H2O in the face-centered (C) monoclinic crystal system. Then, the nuclei self-assembled into nanoflakes with a thickness of ∼4 nm and lateral dimensions in the range of 150–200 nm. Defects formed during the self-assembly, which led to the observed wrinkled morphology. However, the obtained nanoflakes exhibited excellent electrochemical properties. In 0.5 M K2SO4 aqueous solution, the specific capacitance of the δ-MnO2 electrode reached 310 F g−1 at a scanning rate of 1 mV s−1, and 86.5% of the initial specific capacitance remained after 1000 cycles at 100 mV s−1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Program of Graphene Special Innovative Fund of AECC Beijing Institute of Aeronautical Materials. We would like to thank Editage [http://www.editage.cn] for English language editing.Notes and references
- T. M. Higgins, D. McAteer, J. C. Coelho, S. B. Mendoza, Z. Gholamvand, G. Moriarty, N. McEvoy, N. C. Berner, G. S. Duesberg and V. Nicolosi, ACS Nano, 2014, 8, 9567–9579 CrossRef CAS.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano and V. R. Cooper, ACS Nano, 2015, 9, 11509–11539 CrossRef CAS PubMed.
- F. Bonaccorso, L. Colombo, G. Yu, M. Stoller, V. Tozzini, A. C. Ferrari, R. S. Ruoff and V. Pellegrini, Science, 2015, 347, 1246501 CrossRef PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- L. Chen, X. Xu, J. Song, X. Zhu and Z. Qi, Sep. Sci. Technol., 2015, 51, 1–9 Search PubMed.
- J. Zhao, J. Liu, N. Li, W. Wang, J. Nan, Z. Zhao and F. Cui, Chem. Eng. J., 2016, 304, 737–746 CrossRef CAS.
- G. Zhao, J. Li, X. Ren, J. Hu, W. Hu and X. Wang, RSC Adv., 2013, 3, 12909–12914 RSC.
- X. Sun, H. Wang, Z. Lei, Z. Liu and L. Wei, RSC Adv., 2014, 4, 30233–30240 RSC.
- X. Zhang, X. Sun, H. Zhang, C. Li and Y. Ma, Electrochim. Acta, 2014, 132, 315–322 CrossRef CAS.
- K. S. Abou, M. Askar and R. Schöllhorn, Solid State Ionics, 2002, 150, 116 Search PubMed.
- M. Toupin, T. Brousse and D. Bélanger, Chem. Mater., 2004, 16, 3184–3190 CrossRef CAS.
- Q. Feng, L. Liu and K. Yanagisawa, J. Mater. Sci. Lett., 2000, 19, 1567–1570 CrossRef CAS.
- L. Liu, Q. Feng, K. Yanagisawa and Y. Wang, J. Mater. Sci. Lett., 2000, 19, 2047–2050 CrossRef CAS.
- S. Ching, D. J. P. And, M. L. Jorgensen and S. L. Suib, Inorg. Chem., 1997, 36, 883–890 CrossRef CAS.
- X. Hu, L. Shi, D. Zhang, X. Zhao and L. Huang, RSC Adv., 2016, 6, 14192–14198 RSC.
- X. Zhang, W. Miao, C. Li, X. Sun, K. Wang and Y. Ma, Mater. Res. Bull., 2015, 71, 111–115 CrossRef CAS.
- L. Wang, W. Ma, Y. Li and H. Cui, J. Sol-Gel Sci. Technol., 2017, 82, 85–91 CrossRef CAS.
- L. Liu, Y. Luo, W. Tan, Y. Zhang, F. Liu and G. Qiu, J. Colloid Interface Sci., 2016, 482, 183–192 CrossRef CAS PubMed.
- J. Wang, J. Li, C. Jiang, P. Zhou, P. Zhang and J. Yu, Appl. Catal., B, 2017, 204, 147–155 CrossRef CAS.
- C. João, M.-S. Beatriz, P. Henrik, P. Anuj, K. M. Eva, L. Edmund, M. Lorcan, P. B. Alan and N. Valeria, 2D Mater., 2015, 2, 025005 CrossRef.
- Y. Omomo, T. Sasaki and M. Watanabe, J. Am. Chem. Soc., 2003, 34, 3568–3575 CrossRef PubMed.
- C. Xu, S. Shi, Y. Sun, Y. Chen and F. Kang, Chem. Commun., 2013, 49, 7331–7333 RSC.
- S. Shi, C. Xu, C. Yang, Y. Chen, J. Liu and F. Kang, Sci. Rep., 2013, 3, 2598 CrossRef PubMed.
- G. Zhao, J. Li, L. Jiang, H. Dong, X. Wang and W. Hu, Chem. Sci., 2012, 3, 433–437 RSC.
- P. L. Goff, N. Baffier and S. Bach, et al., Mater. Res. Bull., 1996, 31, 63–75 CrossRef.
- R. Chen, P. Zavalij and M. S. Whittingham, Chem. Mater., 1996, 8, 1275–1280 CrossRef CAS.
- K. L. Holland, Clays Clay Miner., 1996, 44, 744–748 CAS.
- J. E. Posr, Am. Mineral., 1990, 75, 477–489 Search PubMed.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- L. Kang, M. Zhang, Z.-H. Liu and K. Ooi, Spectrochim. Acta, Part A, 2007, 67, 864–869 CrossRef PubMed.
- F. Qi, J. Mater. Sci. Lett., 2003, 22, 999–1001 CrossRef.
- K. S. Abou, Solid State Ionics, 2002, 150, 407–415 CrossRef.
- Q. Feng, K. Yanagisawa and N. Yamasaki, J. Mater. Sci. Lett., 1997, 16, 110–112 CrossRef CAS.
- C. Julien, M. Massot, R. Baddour-Hadjean, S. Franger, S. Bach and J. P. Pereira-Ramos, Solid State Ionics, 2003, 159, 345–356 CrossRef CAS.
- D. Yan, P. X. Yan, G. H. Yue, J. Z. Liu, J. B. Chang, Q. Yang, D. M. Qu, Z. R. Geng, J. T. Chen, G. A. Zhang and R. F. Zhuo, Chem. Phys. Lett., 2007, 440, 134–138 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- X. Xiong, C. Yang, G. Wang, Y. Lin, X. Ou, J. Wang, B. Zhao, M. Liu, Z. Linand and K. Huang, Energy Environ. Sci., 2017, 10, 1757–1763 CAS.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 CAS.
- P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211 CrossRef CAS PubMed.
- A. Bello, F. Barzegar, D. Momodu, J. Dangbegnon, F. Taghizadeh and N. Manyala, Electrochim. Acta, 2015, 151, 386–392 CrossRef CAS.
- P. Yang and W. Mai, Nano Energy, 2014, 8, 274–290 CrossRef CAS.
- X. Xiong, D. Ding, D. Chen, G. Waller, Y. Bu, Z. Wang and M. Liu, Nano Energy, 2015, 11, 154–161 CrossRef CAS.
- J. Cao, X. Li, Y. Wang, F. Walsh, J. Ouyang, D. Jia and Y. Zhou, J. Power Sources, 2015, 293, 657–674 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |