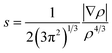Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The nature of the multicenter bonding in π-[TCNE]22− dimer: 4c/2e, 12c/2e, or 20c/2e?
Yujie Cuia and
Longjiu Cheng *ab
*ab
aDepartment of Chemistry, Anhui University, Hefei, Anhui 230601, P. R. China. E-mail: clj@ustc.edu
bAnhui Province Key Laboratory of Chemistry for Inorganic/Organic Hybrid Functionalized Materials, Hefei, Anhui 230601, P. R. China
First published on 25th October 2017
Abstract
The dianion dimer of tetracyanoethylene (TCNE), π-[TCNE]22−, represents an unusual class of organic compounds, that possess exceptionally long C–C bonding interactions (∼2.96 Å). It is twice that of conventional C–C bonds but shorter than the sum of the van der Waals radii. Experimental and computational studies best characterize the intradimer bonding as a multi-center C–C bond. A number of theoretical studies indicate that the π-[TCNE]22− dimer exhibits long, four-centers/two-electron (4c/2e) C–C bonds. However, there is still some disputation about the number of centers involved in the multicenter bonding. This work focuses on quantitative understanding of the nature of the long, multicenter bonding in the π-[TCNE]22− dimer. By the chemical bonding analysis, it is found that ∼68% of electrons in the long bond locate on the –CC– groups and the remaining locate on the –CN groups. The substituent effect is investigated by comparing the interaction energy curves of the [C2X4]22− dimer (X = H, Cl and CN). The deep local well at 3.0 Å for X = CN indicates a strong bonding interaction. However, there is no obvious local well in the curves for X = H and Cl, which indicates that the [C2Cl4]22− and [C2H4]22− dimer are unstable. Herein, the –CN plays an important role in the bonding of the π-[TCNE]22− dimer, and it is more reasonable to take the long bond as 20c/2e (12 carbon plus 8 nitrogen). Moreover, we found an abnormal charge redistribution from TCNE to TCNE−, and the charge distribution of [TCNE]22− is very similar to that of TCNE−, which benefits the formation of the dianion dimer.
Introduction
The dianion dimer of tetracyanoethylene (TCNE), π-[TCNE]22− have attracted reasonable interest both experimentally and theoretically over the past few years because of their exceptionally long C–C bonding interaction.1–5 It is well known that chemical bonding is one of the most fundamental concepts in chemistry,6 organic chemistry has been exceptionally well served by the two-electron, two-center (2e/2c) bonding description and the concept of resonance. However, the study of electron-deficient boranes expanded bonding concepts to more than two centers. The π-[TCNE]22− dimer as a representative example of possessing long (∼2.96 Å) multi-center C–C bonds have been focus of several recent studies. The 2.96 Å intradimer separation for the eclipsed π-[TCNE]22− dimer was too long for a conventional C–C bond (≤1.54 Å), and too short for a van der Waals interaction (i.e., <3.4 Å). These long, multicenter C–C bonds within a dimer of neutral or charged radicals have been proved by spectroscopic (UV/Vis/NIR, IR, ESR, NMR and FITR-Rama) studies, structural (crystallographic) evidence, and theoretical support.7–12 In addition to π-[TCNE]22− other species exhibit sub-van der Waals separations suggestive of the presence of long, multi-center C–C bonding. Examples include anionic species, e.g., 7,7,8,8-tetracyano-p-quinodimethanide ([TCNQ]−),13–15 1,2,4,5-tetracyanobenzene ([TCNB]−),16,17 1,2,4,5-tetracyanobenzene ([TCNP]−);18 cationic species, e.g., tetrathiafulvalenium ([TTF]+),19 tetramethylphenylenediaminium ([TMPD]+),20 and octamethylbiphenylenium;21 as well as neutral radicals, e.g., substituted phenalenyl.22–25 However, nature of the long C–C bonding in these π-dimer is still under discussion.There have been a number of theoretical studies about the nature of such a long, multicenter bond.3,26–30 From the pictures of molecular orbitals (MOs), Novoa and co-workers1,2 thought that π-[TCNE]22− dimer possess a 4c/2e long bond with two C⋯C components. By MO and atoms-in-molecules (AIM) analysis, Graham and co-workers3 think that there are a 6c/2e long bond in a non-eclipsed π-[TCNE]22− dimer. For some other systems, there are also arguments on the number of centers involved in the long, multicenter bonds.29,31,32 This piqued our curiosity as to the nature of the long, multicenter bond. Hence, we carried out a chemical bonding analysis for the π-[TCNE]22− dimer about the number of centers involved in the long bond. It is found that ∼68% electrons in the long bond locate on the –CC– groups and the remains locate on the –CN groups. Herein, the –CN group plays an important role in the bonding of π-[TCNE]22− dimer. It is more reasonable to take the long bond as 20c/2e (12 carbon plus 8 nitrogen) in π-[TCNE]22− dimer.
Computational methods
Geometries of TCNE, TCNE− and π-[TCNE]22− are relaxed by density functional theory (DFT) calculations using the M06L functional33 with 6-311+G* basis set,34 which was proved to be reliable for such long bond systems.28,35–37 Potential energy curves were evaluated at M06-2X38/aug-cc-PVTZ which were corrected for basis set superposition error (BSSE) throughout. All DFT calculations are carried out using the GAUSSIAN 09 package.39 To give an alternative and vivid view on the chemical bonding of the π-[TCNE]22−, we employ the adaptive natural density partitioning (AdNDP)40 method as a tool for analysis, using long-range corrected functional (LC-M06L) which has been proved to be reliable in the study of electron delocalization in conjugated bonds over long distances.41,42 Molecular orbital (MO) visualization is performed using MOLEKEL 5.4.43 Non-covalent interaction (NCI) plots are plotted using Multiwfn44,45 and VMD46 packages.Results and discussion
A. Geometries and electronic properties
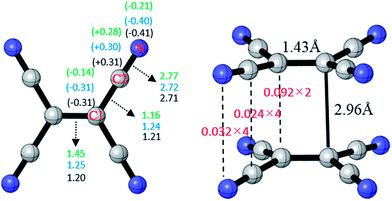
The optimized structure of TCNE22− was shown in Fig. 1 with D2h symmetry. The distance of the center C–C is 1.43 Å, the distance of TCNE− dimer is 2.96 Å in good agreement with the experimental data.47 Meanwhile, we calculate the charge distribution between atoms of TCNE, TCNE− and [TCNE]22−, respectively. As labeled in Fig. 1, we define the central carbon atom as C1, and the –CN carbon atom as C2. In TCNE, NPA charges on C1, C2 and N are −0.14|e|, +0.28|e| and −0.21|e|, respectively. With an additional electron, in TCNE−, negative charges on C1 (−0.31|e|) and N (−0.40|e|) increase. However, charge on C2 (+0.30|e|) becomes more positive in TCNE−, which is abnormal. Moreover, the charge distribution of [TCNE]22− dimer and TCNE− are almost consistent. This indicates that the electronic structure does not change much in the formation of the dianion dimer, which may benefit the formation of the [TCNE]22− dimer.Delocalization index (DI)48–51 is a quantitative measure of the number of electron pairs delocalized (or say shared) between two atomic spaces, which is also known as fuzzy bond order in fuzzy atomic space. In TCNE, the fuzzy bond order of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 is only 1.45 much less double bond order 2.0, the fuzzy bond order of C1–C2 is 1.16 slightly higher than single bond order 1.0, and the fuzzy bond order of C2
C1 is only 1.45 much less double bond order 2.0, the fuzzy bond order of C1–C2 is 1.16 slightly higher than single bond order 1.0, and the fuzzy bond order of C2![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N is 2.77 slightly less than triple bond order 3.0. This indicates certain delocalization of the π electrons, which weakens the double and triple bonds and strengthens the single bonds. With an additional electron, in TCNE−, the fuzzy bond orders of C1
N is 2.77 slightly less than triple bond order 3.0. This indicates certain delocalization of the π electrons, which weakens the double and triple bonds and strengthens the single bonds. With an additional electron, in TCNE−, the fuzzy bond orders of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 (1.45 to 1.25) and C2
C1 (1.45 to 1.25) and C2![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (2.77 to 2.72) decrease, however, the fuzzy bond order of C1–C2 increases (1.16 to 1.24). This indicates that the extra electron enters the π*-C1C1 and π*-C2N anti-bonding orbitals, which weakens the C1
N (2.77 to 2.72) decrease, however, the fuzzy bond order of C1–C2 increases (1.16 to 1.24). This indicates that the extra electron enters the π*-C1C1 and π*-C2N anti-bonding orbitals, which weakens the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 and C2
C1 and C2![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds. In π-[TCNE]22− dimer, the fuzzy bond orders of C1
N bonds. In π-[TCNE]22− dimer, the fuzzy bond orders of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1, C1–C2 and C2
C1, C1–C2 and C2![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (1.20, 1.21 and 2.71) decrease slightly compared to those in TCNE−, which may due to the delocalization of electrons between two monomers (bonding). Then, we calculated the fuzzy bond order between two monomers. The fuzzy bond orders between each pairs of C1, C2, and N in two monomers are 0.092, 0.024 and 0.032, respectively. There are two pairs of C1–C1, four pairs of C2–C2, and four pairs of N–N between two monomers, and so the total fuzzy bond order between the two monomers can be roughly calculated: 0.092 × 2 + 0.024 × 4 + 0.032 × 4 = 0.41. This indicates a fairly strong covalent interaction between two monomers in the π-[TCNE]22− dimer.
N (1.20, 1.21 and 2.71) decrease slightly compared to those in TCNE−, which may due to the delocalization of electrons between two monomers (bonding). Then, we calculated the fuzzy bond order between two monomers. The fuzzy bond orders between each pairs of C1, C2, and N in two monomers are 0.092, 0.024 and 0.032, respectively. There are two pairs of C1–C1, four pairs of C2–C2, and four pairs of N–N between two monomers, and so the total fuzzy bond order between the two monomers can be roughly calculated: 0.092 × 2 + 0.024 × 4 + 0.032 × 4 = 0.41. This indicates a fairly strong covalent interaction between two monomers in the π-[TCNE]22− dimer.
B. Chemical bonding analysis
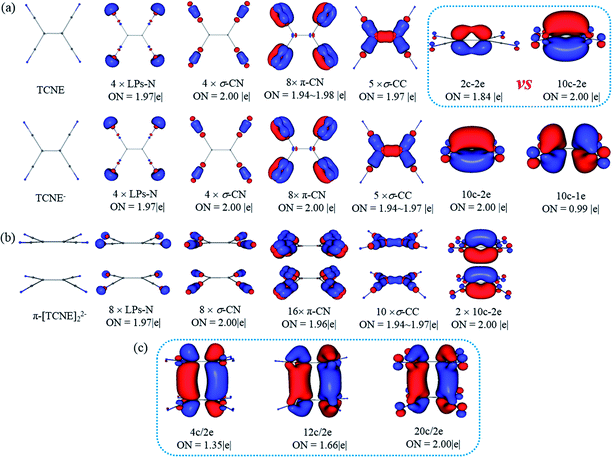
The fuzzy bond order gives indirect evidence of the covalent bond between two monomers in π-[TCNE]22− dimer. To gain more direct insight into the nature of the bonding in π-[TCNE]22−, we apply adaptive natural density partitioning (AdNDP) method to obtain patterns of chemical bonding. The method was developed by Zubarev and Boldyrev,52–54 which has been successfully applied in a number of systems.55–60 AdNDP is based on the concept of the electron pair as the main element of chemical bonding models, which recovers both Lewis bonding elements (1c/2e and 2c/2e objects) and delocalized bonding elements (nc/2e). AdNDP is consistent with the recently developed Electron Density of Delocalized Bonds (EDDB)61 method.The geometric structure and the results of AdNDP analysis of neutral TCNE, TCNE− anion and π-[TCNE]22− dimer are shown in Fig. 2. For neutral TCNE, there are one lone pairs (LPs) in each N, twelve 2c/2e CN bonds (four C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bonds, including four σ and eight π bonds) and five 2c/2e CC σ bonds with nearly idealized occupy numbers (ONs = 1.97–2.00|e|). However, ON of the π-C1C1 bond is only 1.84|e|, indicating delocalization of the π bond (in consist with the low fuzzy bond order of C1
N triple bonds, including four σ and eight π bonds) and five 2c/2e CC σ bonds with nearly idealized occupy numbers (ONs = 1.97–2.00|e|). However, ON of the π-C1C1 bond is only 1.84|e|, indicating delocalization of the π bond (in consist with the low fuzzy bond order of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1). If the π orbital is taken as delocalized 10c/2e bond, it has an idealized ON (2.00|e|), and the orbital shape is reasonable (delocalized over four π*-CN anti-bonding orbital). Thus it is more reasonable to take the π-C1C1 bond as a 10c/2e delocalized π bond (Fig. 2a).
C1). If the π orbital is taken as delocalized 10c/2e bond, it has an idealized ON (2.00|e|), and the orbital shape is reasonable (delocalized over four π*-CN anti-bonding orbital). Thus it is more reasonable to take the π-C1C1 bond as a 10c/2e delocalized π bond (Fig. 2a).
AdNDP chemical bonding framework in TCNE− is exactly same as that in TCNE. The extra electron occupies a 10c/1e delocalized bond, which is composed of π*-C1C1 and π*-C2N anti-bonding orbital from the symmetry (Fig. 2a).
As shown in Fig. 2b, for the π-[TCNE]22− dimer, the chemical bonding framework of each monomer is also same as that of neutral TCNE. The extra two electrons occupy a 20c/2e bond (ON = 2.00|e|) delocalized over two monomers, which can be seen as a bonding orbital composed by the 10c/1e bonds as shown in TCNE− from the symmetry. There are some disputes in literatures1–3 about the number of centers involved in the π-[TCNE]22− dimer, so the situations of 4c/2e (4 × C1) and 12c/2e (4 × C1 + 8 × C2) are also considered (Fig. 2c). Obvious, the 4c/2e (ON = 1.35|e|) and 12c/2e (1.66|e|) bonds can be seen as fragments of the 20c/2e bond from the orbital symmetry, and the ONs are obviously lower. Thus, it is more reasonable to take the long bond as 20c/2e (12 carbon plus 8 nitrogen) in the π-[TCNE]22− dimer.
Previous studies think that the long distance bond is formed by two π*-CC bonds,1,2 which is 4c/2e. However, it is more reasonable to take the long distance bond as a 20c/2e bond instead a 4c/2e one from AdNDP analysis. To give more clearly evidence from the composition of the bonding orbital, the AdNDP 20c/2e bonding orbital is enlarged in Fig. 3. As labeled, it is clearly seen that the orbital in each monomer is composed by one π*-CC and four π*-CN anti-bonding orbital. Moreover, contribution of each atom in the 20c/2e bond can also be roughly calculated from the ONs in AdNDP analysis. If only the four C1 atoms are involved in the long distance bond (4c/2e), ON is 1.35|e|, which indicates that the contribution of C1 atoms is 1.35|e|. When the eight C2 atoms are taken into accounts (12c/2e), the ON increases from 1.35|e| to 1.66|e|, which means that the contribution of eight C2 atoms is 0.31|e| (1.66|e| − 1.35|e|). Then ON reaches the standard 2.00|e| including the eight N atoms (20c/2e), and so the contribution of eight N atoms is 0.34|e| (2.00|e| − 1.66|e|). Thus, it can be educed that the partial electron numbers on C1, C2 and N are 1.35|e|, 0.31|e| and 0.34|e|, respectively. The ratio is 68% for π*-CC and 32% for π*-CN in the 20c/2e bond. Therefore, although the long distance bond is mainly formed by π*-CC orbital, the π*-CN anti-bonding orbitals also play an important role for the stability of the dimer, and the long distance bond should be 20c/2e.
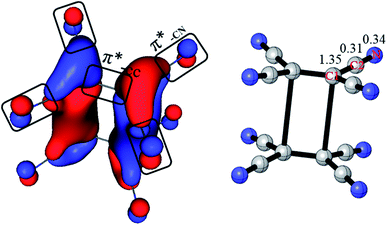 | ||
| Fig. 3 Composition of the 20c–2e bonding orbital in π-[TCNE]22− dimer (left, enlarged from Fig. 2c). Labeled are partial ONs on C1, C2 and N of the 20c–2e bond (right). | ||
C. Substituent effect
From the electronic properties and AdNDP analysis, it is shown that CN group plays an important role for the stability of the π-[TCNE]22− dimer, and the long distance bond should be 20c/2e. To further verify the responsibility of CN in stabilizing π-[TCNE]22−, the substituent effect is investigated by comparing the interaction energy curves of [C2X4]22− dimer (X = H, Cl and CN). Fig. 4 plots the interaction energy (at the M06-2X/aug-cc-pVTZ level with BSSE corrections) of the dimer (X = H, Cl and CN) as a function of the separation distance (RC1–C1). As expected, there is a deep local well at 3.0 Å for X = CN indicating strong bonding interaction. However, there is no obvious local well in the curves for X = H and Cl, which indicates that the [C2Cl4]22− and [C2H4]22− dimer are unstable. The substituent effect givers further evidence for the role of –CN group in the stability of π-[TCNE]22− dimer.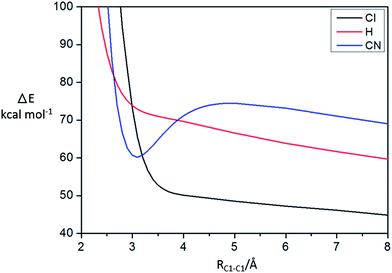 | ||
| Fig. 4 BSSE-corrected M06-2X/aug-cc-pVTZ interaction potential curve for [C2H4]22− (red line), [C2Cl4]22− (black line), and π-[TCNE]22− (blue line). RC1–C1 gives the separation distance, Å. | ||
D. NCI analysis
The long distance multicenter bond is not so strong, which has similar energy level with some secondary bonding, such as hydrogen bonding. As we know, π–π stacking can be rather strong in some cases. There are both long bonding and π–π stacking interactions in π-[TCNE]22− dimer. However, there is only π–π stacking interaction in the triplet state.32,62 Herein, we use the non-covalent interaction (NCI) index approach to detect non-covalent interactions based on electron density and its derivatives, which has been successfully applied to investigate the weak interaction in a number of systems.63–65 NCI index provides a rich representation of non-covalent interactions, such as, van der Waals interactions, hydrogen bonds, and steric repulsion. Besides the non-covalent interactions, NCI index can also provide representation for weak covalent interactions. Thus, we can use NCI analysis to compare the long distance multicenter bond and π–π stacking interactions. NCI involves the reduced density gradient (RDG) and the electron density (ρ). RDG is defined as:and the representation of s versus ρ shows characteristic peak sat low density values in the presence of non-covalent interactions. The sign of the second eigenvalue (λ2) of the electron-density Hessian matrix is used to distinguish between bonded (λ2 < 0) and non-bonded (λ2 > 0) interactions. The visualization of the gradient isosurface can be seen in real space through VMD program. The gradient isosurfaces are colored according to the corresponding values of sign (λ2)ρ, which is found to be a good indicator of interaction strength. A RGB (red-blue-green) scale is used.
Fig. 5a compares the scatter diagram of the singlet and triplet states (blue for singlet and red for triplet) of the π-[TCNE]22− dimer. The singlet and triplet states have similar spikes at 0.02 a.u. (coulomb repulsion), 0.01 a.u. (steric repulsion) and −0.01 a.u. (van der waals attraction). The spike at −0.02 a.u. in the triplet should be π–π stacking, and the spike at −0.025 a.u. in the singlet is bonding interaction. The isosurfaces (Fig. 5b) of the singlet and triplet states are also similar. NCI analysis directly shows the long distance bonding interaction, which is not so strong but is clearly stronger than π–π stacking.
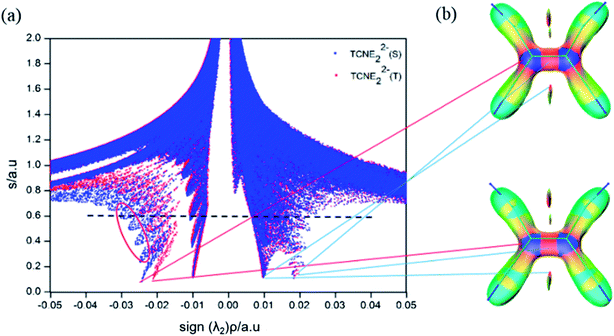 | ||
| Fig. 5 (a) Plots of the reduced density gradient versus the electron density multiplied by the sign of the second Hessian eigenvalue, S-singlet; T-triplet, and (b) NCI isosurfaces (s = 0.60). | ||
Conclusion
In summary, the geometric structure and chemical bonding of the π-[TCNE]22− dimer are investigated by using the DFT method, relying on M06L functional. The nature of the long multicenter bond in π-[TCNE]22− dimer is studied by electronic properties, substituent effects and chemical bonding analysis with AdNDP method. The fuzzy bond order between the two monomers is 0.41, which indicates a fairly strong covalent bond between two monomers in the π-[TCNE]22− dimer. As expected, AdNDP analysis locates all localized bonds in each TCNE monomer in the π-[TCNE]22− dimer. The remaining two electrons tend to form 20c/2e delocalized bond between two monomers. It is clearly seen that the orbital in each monomer is composed by one π*-CC and four π*-CN anti-bonding orbital. Furthermore, the ratio is ∼68% for π*-CC and ∼32% for π*-CN in the 20c/2e bond from the partial electron numbers on C1, C2 and N. The substituent effect givers further evidence for the role of –CN group in the stability of π-[TCNE]22− dimer. There is no obvious local well in the curves for X = H and Cl, however, there is a deep local well at 3.0 Å for X = CN. Hence, the π*-CN orbitals also play an important role for the stability of the dimer, and the long distance bond should be 20c/2e.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financed by the National Natural Science Foundation of China (21573001), and by the Foundation of Distinguished Young Scientists of Anhui Province.References
- J. J. Novoa, P. Lafuente, R. E. D. Sesto and J. S. Miller, Angew. Chem., Int. Ed., 2001, 40, 2540–2545 CrossRef CAS PubMed.
- R. E. D. Sesto, J. S. Miller, P. Lafuente and J. J. Novoa, Chem.–Eur. J., 2002, 8, 4894–4908 CrossRef.
- A. G. Graham, F. Mota, E. Shurdha, A. L. Rheingold, J. J. Novoa and J. S. Miller, Chem.–Eur. J., 2015, 21, 13240–13245 CrossRef CAS PubMed.
- J. Casado, B. Mayorga, P. B. Mayorga, F. J. Ramirez, N. Lopez, J. T. L. Navarrete, S. H. Lapidus, P. W. Stephens, H. L. Vo, J. S. Miller, F. Mota and J. J. Novoa, Angew. Chem., Int. Ed., 2013, 52, 6421–6425 CrossRef CAS PubMed.
- B. Braida, K. Hendrickx, D. Domin, J. P. Dinnocenzo and P. C. Hiberty, J. Chem. Theory Comput., 2013, 9, 2276–2285 CrossRef CAS PubMed.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- J. J. Novoa, P. Lafuente, R. E. Del Sesto and J. S. Miller, CrystEngComm, 2002, 4, 373–377 RSC.
- J. M. Lu, S. V. Rosokha and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 12161–12171 CrossRef PubMed.
- J. Jakowski and J. Simons, J. Am. Chem. Soc., 2003, 125, 16089–16096 CrossRef CAS PubMed.
- Y. Jung and M. Head-Gordon, Phys. Chem. Chem. Phys., 2004, 6, 2008–2011 RSC.
- J. S. Miller, Acc. Chem. Res., 2007, 40, 189–196 CrossRef CAS PubMed.
- I. Garcia-Yoldi, J. S. Miller and J. J. Novoa, J. Phys. Chem. A, 2007, 111, 8020–8027 CrossRef CAS PubMed.
- S. Z. Goldberg, B. Spivack, G. Stanley, E. Richard, D. M. Braitsch, J. S. Miller and M. Abkowitz, J. Am. Chem. Soc., 1977, 99, 110–117 CrossRef CAS.
- C. Willi, A. H. Reis, E. Gebert and J. S. Miller, Inorg. Chem., 1981, 20, 313–318 CrossRef CAS.
- M. T. Azcondo, L. Ballester, S. Golhen, A. Gutierrez, L. Ouahab, S. Yartsev and P. Delhaes, J. Mater. Chem., 1999, 9, 1237–1244 RSC.
- M. L. Taliaferro, M. S. Thorum and J. S. Miller, Angew. Chem., Int. Ed., 2006, 45, 5326–5331 CrossRef CAS PubMed.
- J. D. Bagnato, W. W. Shum, M. Strohmeier, D. M. Grant, A. M. Arif and J. S. Miller, Angew. Chem., Int. Ed., 2006, 45, 5322–5326 CrossRef CAS PubMed.
- E. B. Vickers, T. D. Selby and J. S. Miller, J. Am. Chem. Soc., 2004, 126, 3716–3717 CrossRef CAS PubMed.
- B. A. Scott, S. J. L. Placa, J. B. Torrance, B. D. Silverman and B. Welber, J. Am. Chem. Soc., 1977, 99, 6631–6639 CrossRef CAS.
- M. J. Hove, B. M. Hoffman and J. A. Ibers, J. Chem. Phys., 1972, 56, 3490–3502 CrossRef CAS.
- J. K. Kochi, R. Rathore and P. L. Maguères, J. Org. Chem., 2000, 65, 6826–6836 CrossRef CAS PubMed.
- R. L. Zhong, H. L. Xu, S. L. Sun, Y. Q. Qiu, L. Zhao and Z. M. Su, J. Chem. Phys., 2013, 139, 124314 CrossRef PubMed.
- Y. Morita, J. Kawai, K. Fukui, S. Nakazawa, K. Sato, D. Shiomi, T. Takui and K. Nakasuji, Org. Lett., 2003, 5, 3289–3291 CrossRef CAS PubMed.
- K. Goto, T. Kubo, K. Yamamoto, K. Nakasuji, K. Sato, D. Shiomi, T. Takui, M. Kubota, T. Kobayashi, K. Yakusi and J. Ouyang, J. Am. Chem. Soc., 1999, 121, 1619–1620 CrossRef CAS.
- Z. H. Cui, A. Gupta, H. Lischka and M. Kertesz, Phys. Chem. Chem. Phys., 2015, 17, 23963–23969 RSC.
- I. Garcia-Yoldi, J. S. Miller and J. J. Novoa, Phys. Chem. Chem. Phys., 2008, 10, 4106–4109 RSC.
- J. J. Novoa, P. W. Stephens, M. Weerasekare, W. W. Shum and J. S. Miller, J. Am. Chem. Soc., 2009, 131, 9070–9075 CrossRef CAS PubMed.
- M. Capdevila-Cortada and J. J. Novoa, Chem.–Eur. J., 2012, 18, 5335–5344 CrossRef CAS PubMed.
- D. Small, V. Zaitsev, Y. S. Jung, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Am. Chem. Soc., 2004, 126, 13850–13858 CrossRef CAS PubMed.
- Z. H. Cui, H. Lischka, T. Mueller, F. Plasser and M. Kertesz, ChemPhysChem, 2014, 15, 165–176 CrossRef CAS PubMed.
- D. Small, S. V. Rosokha, J. K. Kochi and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 11261–11267 CrossRef CAS PubMed.
- F. Mota, J. S. Miller and J. J. Novoa, J. Am. Chem. Soc., 2009, 131, 7699–7707 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- M. Capdevila-Cortada, J. Ribas-Arino and J. J. Novoa, J. Chem. Theory Comput., 2014, 10, 650–658 CrossRef CAS PubMed.
- M. Fumanal, M. Capdevila-Cortada, J. S. Miller and J. J. Novoa, J. Am. Chem. Soc., 2013, 135, 13814–13826 CrossRef CAS PubMed.
- C. Capel Ferron, M. C. Ruiz Delgado, V. Hernandez, J. T. Lopez Navarrete, B. Vercelli, G. Zotti, M. Capdevila Cortada, J. J. Novoa, W. Niu, M. He and F. Hartl, Chem. Commun., 2011, 47, 12622–12624 RSC.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, revision D. 01, Gaussian, Inc., Wallingford, CT, 2009, vol. 200 Search PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- D. W. Szczepanik, M. Solà, M. Andrzejak, B. Pawełek, J. Dominikowska, M. Kukułka, K. Dyduch, T. M. Krygowski and H. Szatylowicz, J. Comput. Chem., 2017, 38, 1640–1654 CrossRef CAS PubMed.
- D. W. Szczepanik, E. Zak and J. Mrozek, Comput. Theor. Chem., 2017, 1115, 80–87 CrossRef CAS.
- U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Centre, Manno, Switzerland, 2009 Search PubMed.
- H.-P. Loock, L. M. Beaty and B. Simard, Phys. Rev. A, 1999, 59, 873–875 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. T. Johnson, C. F. Campana, B. M. Foxman, W. Desmarais, M. J. Vela and J. S. Miller, Chem.–Eur. J., 2000, 6, 1805–1810 CrossRef CAS.
- R. F. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399 CrossRef CAS.
- R. F. Bader, S. Johnson, T.-H. Tang and P. Popelier, J. Phys. Chem., 1996, 100, 15398–15415 CrossRef CAS.
- R. F. Bader, A. Streitwieser, A. Neuhaus, K. E. Laidig and P. Speers, J. Am. Chem. Soc., 1996, 118, 4959–4965 CrossRef CAS.
- R. F. Bader, Coord. Chem. Rev., 2000, 197, 71–94 CrossRef CAS.
- D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 251–268 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- D. Y. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251–9258 CrossRef CAS PubMed.
- L. J. Cheng, Y. Yuan, X. Z. Zhang and J. L. Yang, Angew. Chem., Int. Ed., 2013, 52, 9035–9039 CrossRef CAS PubMed.
- L. R. Liu, P. Li, L. F. Yuan, L. J. Cheng and J. L. Yang, Nanoscale, 2016, 8, 12787–12792 RSC.
- L. F. Li and L. J. Cheng, J. Chem. Phys., 2013, 138, 094312 CrossRef PubMed.
- Y. Yuan and L. J. Cheng, J. Chem. Phys., 2013, 138, 024301 CrossRef PubMed.
- L. F. Li, C. Xu and L. J. Cheng, Comput. Theor. Chem., 2013, 1021, 144–148 CrossRef CAS.
- L. J. Cheng, C. D. Ren, X. Z. Zhang and J. L. Yang, Nanoscale, 2013, 5, 1475–1478 RSC.
- D. W. Szczepanik, M. Andrzejak, K. Dyduch, E. Żak, M. Makowski, G. Mazur and J. Mrozek, Phys. Chem. Chem. Phys., 2014, 16, 20514–20523 RSC.
- Z. H. Cui, H. Lischka, H. Z. Beneberu and M. Kertesz, J. Am. Chem. Soc., 2014, 136, 5539–5542 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, E. R. Johnson and J. Contreras-Garcia, Phys. Chem. Chem. Phys., 2012, 14, 12165–12172 RSC.
- Y. Liu, Z. M. Tian and L. J. Cheng, RSC Adv., 2016, 6, 4705–4712 RSC.
- Z. M. Tian and L. J. Cheng, RSC Adv., 2016, 6, 30311–30319 RSC.
| This journal is © The Royal Society of Chemistry 2017 |