Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Superhard B2CO phases derived from carbon allotropes†
Chao Liu a,
Mingwei Chenb,
Julong Hec,
Shuangshuang Yua and
Tongxiang Liang*a
a,
Mingwei Chenb,
Julong Hec,
Shuangshuang Yua and
Tongxiang Liang*a
aSchool of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China. E-mail: liang_tx@126.com
bInstitute of Engineering Research, Jiangxi University of Science and Technology, Ganzhou 341000, China
cState Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China
First published on 10th November 2017
Abstract
Two new orthorhombic B2CO structures (oP16- and oC16-B2CO) have been predicted theoretically by manual construction. The calculations of independent elastic constants and phonon dispersion spectra have confirmed the mechanical and dynamical stabilities of oP16- and oC16-B2CO at zero pressure. Their formation enthalpies are both negative and lower than several B2CXO (X = 1, 2, 3, 5) phases, suggesting they are thermodynamically stable. Based on first-principles calculations, oP16- and oC16-B2CO are both superhard materials with indirect band gaps. With excellent hardness and tunable band gaps, B2CO will attract extensive attention for industrial applications and scientific research.
1. Introduction
Since B–C–O system compounds have been synthesized with compositions B6C1.1O0.33 to B6C1.28O0.31 (ref. 1 and 2) and B(C, O)0.155 (ref. 3) experimentally, great attention has been attracted towards designing superhard materials using B–C–O compounds due to strong sp3 B–O/C covalent bonds.4–7 Li et al. studied B2CO compounds, which are considered as the simplest ternary B–C–O compounds and are isoelectronic with diamond, and then proposed two new structures, tP4 (tP4-B2CO) and tI16 (tI16-B2CO), as superhard materials.4 In Li's opinion, B2CO tends to be stable in the form of tetragonal structures with strong sp3 covalent B–C and B–O bonds. Inspired by Li's report, B–C–O system compounds have attracted considerable attention in recent years. Zhang et al. studied B2CXO compounds and predicted three superhard B2CXO (X ≥ 2) phases: I41/amd-B2C2O, I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2-B2C3O and P
m2-B2C3O and P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2-B2C5O.5 During their research, a reasonable relation between the carbon content and mechanical behavior of B2CXO was established and it was suggested that elastic moduli and hardness will benefit from the high carbon content. In 2016, Wang et al. explored the B–C–O system in a pressure range of 0–50 GPa, and proposed a new superhard phase, B4CO4, which is metastable under ambient conditions, but thermodynamically stable at high pressures above 23 GPa.6 However all superhard B–C–O phases belong to the tetragonal crystal system.4–6 Our previous work reveals that there exist some other superhard B–C–O phases with non-tetragonal crystal system, as oP8-B2CO.7 Actually, 2-dimensional B–C–O materials have also been studied and proposed as a promising 2-dimensional electronic device materials with tunable band gaps and high carrier mobility.8
m2-B2C5O.5 During their research, a reasonable relation between the carbon content and mechanical behavior of B2CXO was established and it was suggested that elastic moduli and hardness will benefit from the high carbon content. In 2016, Wang et al. explored the B–C–O system in a pressure range of 0–50 GPa, and proposed a new superhard phase, B4CO4, which is metastable under ambient conditions, but thermodynamically stable at high pressures above 23 GPa.6 However all superhard B–C–O phases belong to the tetragonal crystal system.4–6 Our previous work reveals that there exist some other superhard B–C–O phases with non-tetragonal crystal system, as oP8-B2CO.7 Actually, 2-dimensional B–C–O materials have also been studied and proposed as a promising 2-dimensional electronic device materials with tunable band gaps and high carrier mobility.8
Carbon, which is widely used in industrial applications and scientific research, has numerous allotropes with abundant properties. Considering that B can combine O/C with strong covalent bonds in solid matter as B–O compounds,9–12 and B–C compounds.13–15 Inspired by that tP4-, and tI16-B2CO are both diamond-like structures,4 oP8-B2CO is a lonsdaleite-like structure,7 even the B2CXO (X ≥ 2) phases are also diamond-like structures and can be derived from different tP4-B2CO supercells with partial B and O replacing by C.5 Hence, we are curious about that whether the fabricated B–C–O compounds with replacement of partial C atoms by B and O atoms in carbon allotropes are stable and what properties do they possess.
In this paper, we carried out the work with the simplest ternary B–C–O compounds B2CO as a typical example. Numerous new phases of B2CO have been constructed manually. Undergo rigorous structural stability analysis including mechanical and dynamical stabilities, two orthorhombic phases were discovered. The formation enthalpies were calculated to demonstrate their thermodynamic stabilities. Based on density function theory (DFT), the mechanical and electronic properties of newly discovered phases have been systematically studied.
2. Computational methods and details
Although evolutionary simulation methods like CALYPSO16–18 and USPEX19–21 have been played a significant role in successfully predicting superhard materials4–7,22,23 all potential crystal structures studied here were constructed manually. Here we conceived and constructed new structures following the steps below: (a) extensively selected carbon allotropes with strong sp3 C–C covalent bonds; (b) if the original structure contained 4n (n represents integer) atoms, skip step (b), otherwise constructed supercell to make sure the supercell contains 4n atoms; (c) broken symmetry and replaced a quarter of C atoms by O atoms, and a half of C atoms by B atoms. C and O atoms are separated by B atoms; (d) found and imposed symmetry.The underlying geometry optimizations were performed in CASTEP code24 using DFT. The exchange-correlation functional was adopted CA-PZ form of the local density approximation.25,26 The another typically functional PBE of generalized gradient approximation was performed.27 To compare two different algorithms, the calculated results were listed in the ESI.† To ensure the convergence accuracy less than 1 meV, the norm conserving pseudopotential was adopted at a plane wave cutoff kinetic energy of 960 eV and Monkhorst–Pack K points were generated by utilizing 2π × 0.04 Å−1 as K-points separation.28 During the geometry optimizations via BFGS method,29 iterations were continued until energy change per atom was less than 5 × 10−6 eV; force tensor on atoms was reduced to 0.01 eV Å−1; displacement on atom didn't exceed 5 × 10−4 Å and stress no more than 0.02 GPa. The phonon calculation was implemented in CASTEP via the linear response method30,31 and the elastic constants were calculated by employing the efficient stress–strain method with 9 distorted structures generated for each strain pattern and maximum distortion 0.003. The conventional cells were adopted within the entire research, and the symmetry points for the Brillouin zone are G (0, 0, 0); Z (0, 0, 0.5); T (−0.5, 0, 0.5); Y (−0.5, 0, 0); S (−0.5, 0.5, 0); X (0, 0.5, 0); and R (−0.5, 0.5, 0.5).
3. Results and discussion
Two newly discovered B2CO structures have been proposed and their crystal structures schematic at zero pressure are shown in Fig. 1. Both of them are orthorhombic system and have 16 atoms per conventional cell. The first, denoted as oP16-B2CO, is a primitive centered structure with space group Pbam, and another, denoted as oC16-B2CO, is a C-centered (0.5, 0.5, 0) structure with space group Cmmm. All coordination numbers of the atoms in oP16 and oC16 phases are 4, and there are only sp3 hybridization B–C/O covalent bonds in oP16-, and oC16-B2CO.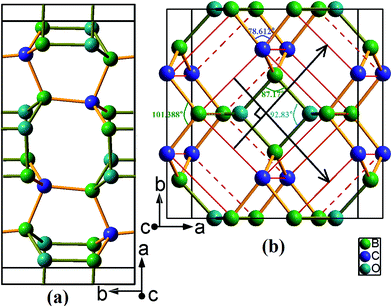 | ||
| Fig. 1 Structure graphs for (a) oP16-, and (b) oC16-B2CO. The sticks in colour dark yellow and light orange represent the bonds B–O and B–C, respectively. | ||
As depicted in Fig. 1a, oP16-B2CO has a crystal structure similar to Cco-C8 (when B and O are replaced by C, oP16-B2CO change its symmetry to Cmmm and form Cco-C8),32 and the structure is symmetric about the plane c = 0.5. Different with Cco-C8, oP16-B2CO has no bonds rigid parallel to c axis. oC16-B2CO, displayed in Fig. 1b, has more higher symmetry than oP16-B2CO. The structure is symmetric about (0.5, 0.5, 0.5), and constructed from Bct-C4.33 In the ab plane, oC16-B2CO can be viewed as the structural units (Fig. 1b, remarked by red line) connected by B–C bonds with 1.596 Å. Also, all the structural units can be viewed as the middle one slipping alone the directions marked by black lines at a given distance 4.443 Å. Once B and O atoms in the structural units are replaced by C atoms, Bct-C4 appeared. In Bct-C4, four neighbour C atoms in the plane c = 0/0.5 formed a square. However, in oC16-B2CO, the neighbour 2B and 2O atoms in the plane c = 0.5 formed a rhombus with length 1.631 Å and angles 〈87.17°, 92.83°〉; the neighbour 2B and 2C atoms in the plane c = 0 formed a rhombus with length 1.596 Å and angles 〈78.612°, 101.388°〉. More detailed information for the optimized structures at zero pressure is exhibited in Table 1.
| S.G. | a | b | c | ρ | A.W.P. | |
|---|---|---|---|---|---|---|
| oP16 | Pbam | 8.847 | 4.364 | 2.603 | 3.280 | B1 4h(0.824, 0.181, 0.5); B2 4g(0.911, 0.694, 0); C 4h(0.342, 0.680, 0.5); O 4g(0.409, 0.177, 0) |
| oC16 | Cmmm | 6.142 | 6.421 | 2.601 | 3.214 | B1 4j(0, 0.816, 0.5); B2 4g(0.165, 0.5, 0); C 4i(0, 0.692, 0); O 4h(0.317, 0.5, 0.5) |
The structural stabilities of oP16-, and oC16-B2CO are checked by calculating the independent elastic constants Cijs and the phonon dispersion spectra, as presented in Table 2 and Fig. 2, respectively. For an orthorhombic structure, Born criteria are listed in eqn (1).34
| Cii > 0; (i = 1, 4, 5, 6); C11C22 > C122; C11C22C33 + 2C12C13C23 − C11C232 − C22C132 − C33C122 > 0; | (1) |
| C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | B | G | E | μ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| oP16 | 664.6 | 760.3 | 757.0 | 236.0 | 269.0 | 244.5 | 112.7 | 98.2 | 72.7 | 305.2 | 273.9 | 632.6 | 0.155 |
| oC16 | 542.4 | 619.1 | 778.1 | 266.7 | 214.6 | 218.5 | 169.1 | 61.2 | 129.9 | 293.3 | 241.5 | 568.4 | 0.177 |
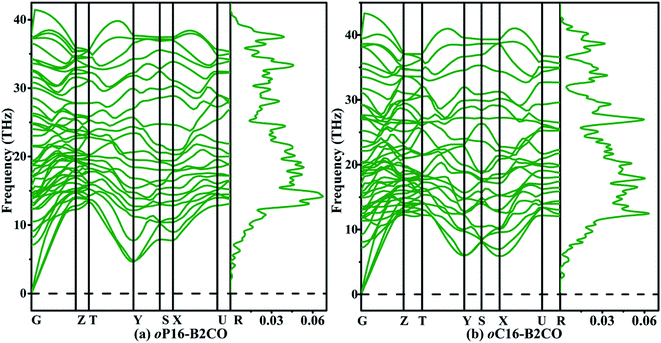 | ||
| Fig. 2 Phonon dispersion spectra (left panel) and phonon density of states (right panel) of (a) oP16-, and (b) oC16-B2CO at zero pressure. | ||
There is no doubt that from Table 2 the Cijs satisfy the criteria above, indicating oP16-, and oC16-B2CO are mechanical stable. And no negative frequency was found, which indicates the dynamical stability of these two new B2CO structures.
For further experimental synthesis, there is necessity to explore the thermodynamic stability of oP16-, and oC16-B2CO. Fig. 3 summarizes the formation enthalpies normalized on a per-atom basis of known B2CXO (X = 1, 2, 3, 5) compounds. The formation enthalpy (ΔHf), which with respect to the separate phases, is quantified by eqn (2):
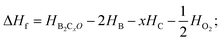 | (2) |
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2-B2C3O; and 497 meV: P
m2-B2C3O; and 497 meV: P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2-B2C5O). Hence, oP16-, and oC16-B2CO may exist as metastable phases. Both formation enthalpy of oP16-, and oC16-B2CO decrease with the pressure increase, which indicate these two new B2CO may be acquired through the synthesis path with loading pressure.
m2-B2C5O). Hence, oP16-, and oC16-B2CO may exist as metastable phases. Both formation enthalpy of oP16-, and oC16-B2CO decrease with the pressure increase, which indicate these two new B2CO may be acquired through the synthesis path with loading pressure.
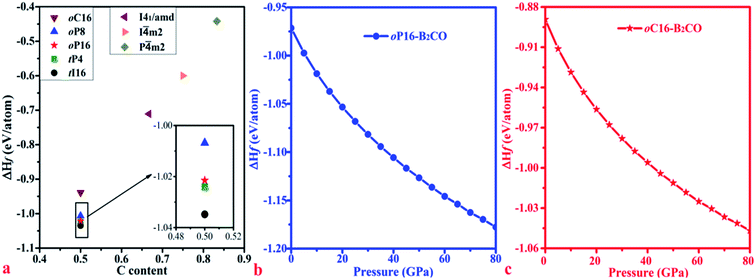 | ||
| Fig. 3 Calculated formation enthalpies of B2CXO phases with different C contents as x/(1 + x) at zero pressure (a) and formation enthalpies of (b) oP16-, and (c) oC16-B2CO as a function of pressure. | ||
The third-order Birth–Murnaghan equation of state (EOS) for the pressure (P)–volume (V) relation of oP16-, and oC16-B2CO is adopted to fit the 17 pair P–V data for these two new B2CO compounds, as presented in Fig. 4.
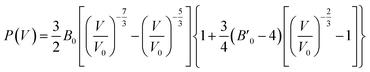 | (3) |
 | ||
| Fig. 4 Volume–pressure relationships for oP16-, and oC16-B2CO. The geometric patterns and solid lines represent the calculated data and fitting results, respectively. | ||
The equilibrium volume (V0), bulk modulus (B0) and its first order pressure derivative (B′0) are obtained from eqn (4) and displayed in insert table in Fig. 4.
When loading with hydrostatic pressure to 80 GPa, both oP16-, and oC16-B2CO sustain the volume shrinkage without mutation and share the similar shrinkage rates, 17.15% for oP16-B2CO and 17.60% for oC16-B2CO.
The mechanical property parameters including bulk modulus B, shear modulus G, Young modulus E, and Poisson ratio μ of oP16-, and oC16-B2CO are listed in Table 2. B and G can be acquired by independent elastic parameter, then E and μ can be obtained by B and G.37 Generally speaking, B represents the ability to resist volume deformation by loading pressure, G characterizes the ability to resist deformation upon shear stress.38 Both oP16-, and oC16-B2CO have very large B (∼300 GPa) and G (above 240 GPa), indicating the excellent resistance to volume deformation by pressure stress and shear stress.
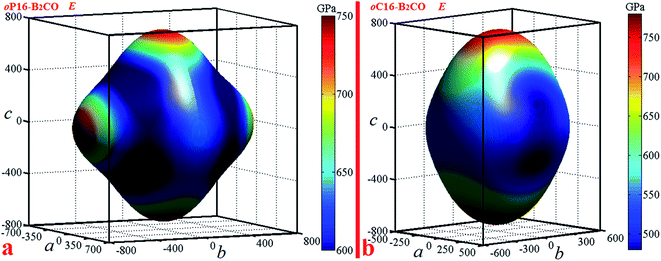
Elastic anisotropy can give a prediction of the arrangement of the atoms in each direction, the bonding properties, and some chemical characteristics in different directions of materials. An illustrative way of the elastic anisotropy is described by a three-dimensional surface map representation. The curved surface map shows the variation of elastic modulus with crystallographic direction. For orthorhombic crystal, the directional dependence of the Young's modulus is given by eqn (4)39
| E−1 = l14S11 + 2l12l22S12 + 2l12l32S13 + l24S22 + 2l22l32S23 + l34S33 + l22l32S44 + l12l32S55 + l12l22S66; | (4) |
Actually, Young's modulus of the three main axis direction satisfy the following relations: E[100]=1/S11, E[010]=1/S22, E[001]=1/S33. For oP16-B2CO, the b and c axes have the almost consistent Young's modulus (736 GPa and 738 GPa, respectively), which higher that of a axis with 100 GPa. For oC16-B2CO, Young's modulus for three main axes a, b, and c are 495 GPa, 550 GPa and 750 GPa, the gradually increasing values also illustrated the obvious anisotropy.
For an isotropic crystal, the 3D curved surface would exhibit a spherical shape. The deviation degree from the spherical surface indicates the extent of anisotropy (Fig. 5).
As material' fundamental mechanical property, hardness is extensively used and can be theoretically predicted. Here, we calculated the Vickers hardness (HV) of oP16-, and oC16-B2CO by adopting bond resistance model.40,41
| HV = 350Ne2/3e−1.191fid−2.5 | (5) |
| fi = [1 − exp(−|Pc − P|/P)]0.735 | (6) |
The calculated hardness of oP16-, and oC16-B2CO displayed in Table 3 are both beyond 40 GPa, indicating that the two newly explored B2CO are superhard materials. The B–C–O system compounds may have potential industrial applications as superhard materials.
| V | μ | dμ | nμ | Nμe | fμi | HμV | HV | |
|---|---|---|---|---|---|---|---|---|
| oP16 | 100.504 | B–C(I) | 1.541 | 8 | 0.612 | 0.323 | 58.268 | 47.817 |
| B–C(II) | 1.582 | 4 | 0.565 | 0.181 | 61.233 | |||
| B–C(III) | 1.588 | 4 | 0.559 | 0.110 | 65.585 | |||
| B–O(I) | 1.596 | 4 | 0.709 | 0.785 | 33.951 | |||
| B–O(II) | 1.621 | 4 | 0.676 | 0.831 | 29.956 | |||
| B–O(III) | 1.623 | 8 | 0.673 | 0.495 | 44.397 | |||
| oC16 | 102.560 | B–C(I) | 1.524 | 8 | 0.619 | 0.333 | 59.685 | 46.222 |
| B–C(II) | 1.596 | 8 | 0.539 | 0.181 | 58.071 | |||
| B–O(I) | 1.602 | 8 | 0.685 | 0.521 | 45.061 | |||
| B–O(II) | 1.631 | 8 | 0.649 | 0.816 | 29.226 |
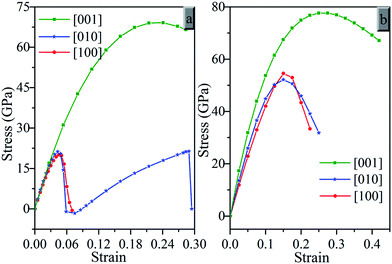
A popular approach42–45 to understand the structural deformation and strength has been extensively applied to solid material under specified strains.46 It is the material's ideal strength which is defined as the stress at which a perfect crystal changes mechanically unstable, that sets an upper limit for material strength. The atomistic mechanism for structural deformation and failure models can be thorough understanding with the studies of strain–stress relations and bond-breaking processes.
Fig. 6 presents the calculated strain–stress relations for oP16-, and oC16-B2CO under tensile strains in three principal symmetry crystallographic directions ([100], [010], and [001]). It can be seen that both oP16-, and oC16-B2CO have large stresses with strain exist in the [001] than [010] and [100] directions. Along the [001] direction, oP16-B2CO has a peak tensile stresses 69.1 GPa with a strain of 0.225, and 77.6 GPa with strain 0.275 for oC16-B2CO. The tensile strengths of oC16-B2CO along the [100] and [010] both reach a peak tensile stresses at strain 0.15 with 54.5 GPa and 52.1 GPa, respectively. oP16-B2CO has a peak tensile stress 20.1 GPa with a strain of 0.045. As for the [010] direction of oP16-B2CO, there are two observable peak 21.3 GPa, corresponding these bonds along b axis as B–O bonds breaking with a strain of 0.04 and B–C bonds breaking with a strain of 0.27 respectively. The calculated strain–stress relations reveal anisotropy of oP16-, and oC16-B2CO.
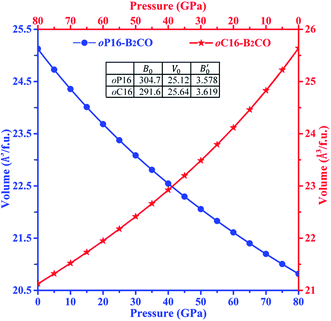
The band structures of these superhard B2CO phases along the symmetry points for the Brillouin zone at zero pressure are calculated and shown in Fig. 7. Both oP16-, and oC16-B2CO are semiconductors with indirect band gaps. For oP16-B2CO, the valence band (VB) maximum and conduction band (CB) minimum are located at G point and U point, respectively, and they are separated by a forbidden band of 3.159 eV. For oC16-B2CO, the VB maximum and CB minimum are located at G point and Z point, respectively, and separated by a forbidden band of 3.412 eV. For oP16-, and oC16-B2CO, the calculated band gaps are 3.159 eV and 3.412 eV, respectively. With the different crystal systems and their atomic stack, these superhard B2CO (tP4-, tI16-, and oP8-B2CO within) with the tuneable band gaps from 1.7 eV to 3.5 eV may have potential application in semiconductor industry in future (Fig. 7).
 | ||
| Fig. 7 Calculated electronic band structures for oP16-, and oC16-B2CO at zero pressure. The Fermi level is represented by a horizontal red line. | ||
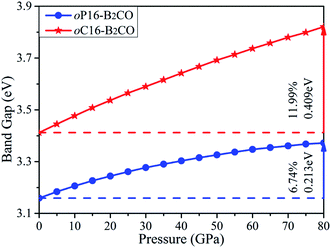
The values of band gaps as a function of pressure in ranges of 0–80 GPa are calculated and plotted in Fig. 8. The band gap of oP16-, and oC16-B2CO increases with pressure simultaneously within the whole studied pressure range. For oC16-B2CO, the gap's increase degree is 0.409 eV/11.99%, higher than that of oP16-B2CO (0.213 eV/6.74%).
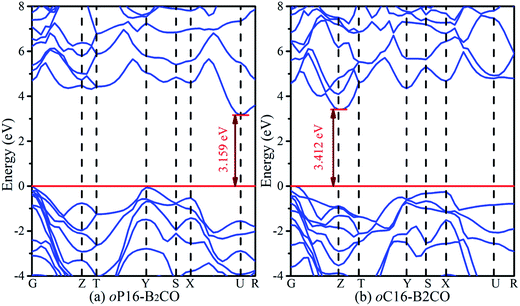
With the pressure increasing, bonding states and antibonding states appear gradually emerges, result in the energy of VB decline and the energy of CB increase, the VB expand to the lower energy region and CB to the higher energy region, the gap increases. The influence on electronic band can be analyzed based on partial specific band morphology under different pressures. Thus the bands with the minimum CB and maximum VB at 0 GPa are selected, and their morphology under different pressure are studied, as Fig. 9. We denoted the difference between maximum and minimum of the selected CB as ΔC, and of VB as ΔV.
 | ||
| Fig. 9 The maximum value band and minimum conduction band for (a) oP16-, and (b) oC16-B2CO at different pressures. The Fermi level is represented by a horizontal black line. | ||
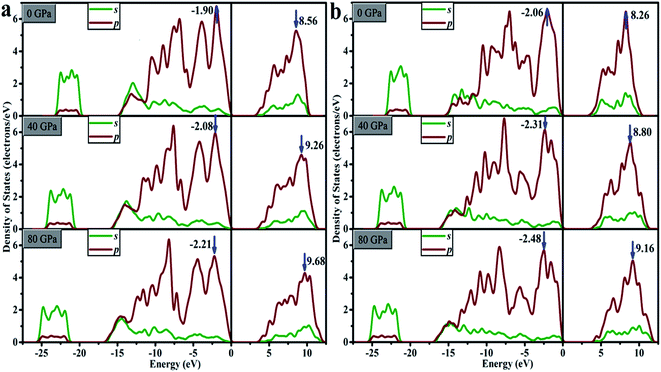
For oP16-B2CO with pressure in 0–80 GPa, the minimum energy of CB increase, lead to the gap increases uninterruptedly. The ΔV and ΔC both increase with pressure, indicates the energy range of the selected bands are broaden. It's not just an exception, thus as a whole, the energy range of VB and CB are both broader. The energy of VB is lower, while for CB is higher. The pressure's influence can also be detected based on entire density of states (DOS). As displayed in Fig. 10a, for oP16-B2CO, during the pressure increasing, the energy category of VB (CB) continuously enlarge to the low (high) energy region; the position of the highest peak of VB (CB) has been moved to lower (higher) energy region and the peak height has been reduced.
As for oC16-B2CO, the ΔC increases with pressure, indicates the energy range of the selected bands are broaden, while the ΔV undergoes a process with increase–decrease. As displayed in Fig. 10b, for oC16-B2CO, the energy category of VB (CB) continuously enlarge to the low (high) energy region; the position of the highest peak of VB (CB) has been moved to lower (higher) energy region and the peak height has been reduced.
4. Conclusions
By manual building B2CO phases from widely known allotropes of carbon, we proposed two new B2CO (oP16-, and oC16-B2CO), derived from Cco-C8 and Bct-C4, respectively. Based on the first-principles study, the elastic constants and phonon dispersion spectra declare that oP16-, and oC16-B2CO are mechanically and dynamically stable. Their formation enthalpies, respected to the separate phases, are both negative and lower than that of B2CXO (X = 1, 2, 3, 5), suggesting thermodynamically stable. oP16-B2CO even has the formation enthalpy which is closed with tP4-B2CO and lower than oP8-B2CO. Based on bond resistance model for hardness prediction, oP16-, and oC16-B2CO are both superhard with high hardness values of 47.817 GPa and 46.222 GPa, respectively. Electronic property calculation illustrates that the two newly discovered phases are all semiconductors with indirect band gaps of 3.159 eV and 3.412 eV, respectively. The band gap value as a function of pressure in ranges of 0–100 GPa indicate that pressure has an obvious influence on the band gaps of oP16-, and oC16-B2CO. The excellent mechanical and electronic properties indicate the attractive prospect for B–C–O compounds in industrial application and scientific research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation of China (Grant No. 91326203 and 51421091) and Jiangxi University of Science and Technology Scientific Research Starting Foundation (jxxjbs17053).References
- L. A. J. Garvie, H. Hubert, W. T. Petuskey, P. F. McMillan and P. R. Buseck, J. Solid State Chem., 1997, 133, 365–371 CrossRef CAS.
- H. Hubert, L. A. Garvie, B. Devouard and P. F. McMillan, MRS Proceedings, 1997, 499, 315–320 CrossRef.
- N. Bolotina, T. Dyuzheva and N. Bendeliani, Crystallogr. Rep., 2001, 46, 734–740 CrossRef.
- Y. Li, Q. Li and Y. Ma, Europhys. Lett., 2011, 95, 66006 CrossRef.
- M. Zhang, H. Yan, B. Zheng and Q. Wei, Sci. Rep., 2015, 5, 15481 CrossRef CAS PubMed.
- S. Wang, A. R. Oganov, G. Qian, Q. Zhu, H. Dong, X. Dong and M. M. D. Esfahani, Phys. Chem. Chem. Phys., 2016, 18, 1859–1863 RSC.
- C. Liu, Z. Zhao, K. Luo, M. Hu, M. Ma and J. He, Diamond Relat. Mater., 2016, 73, 87–92 CrossRef.
- S. Zhou and J. Zhao, Nanoscale, 2016, 8, 8910–8918 RSC.
- T. Endo, T. Sato and M. Shimada, J. Mater. Sci. Lett., 1987, 6, 683–685 CrossRef CAS.
- M. Kobayashi, I. Higashi, C. Brodhag and F. Thevenot, J. Mater. Sci., 1993, 28, 2129–2134 CrossRef CAS.
- H. Hubert, B. Devouard, L. A. Garvie, M. O'Keeffe, P. R. Buseck, W. T. Petuskey and P. F. McMillan, Nature, 1998, 391, 376–378 CrossRef.
- H. Dong, A. R. Oganov, Q. Wang, S. N. Wang, Z. Wang, J. Zhang, M. M. Esfahani, X. F. Zhou, F. Wu and Q. Zhu, Sci. Rep., 2016, 6, 31288 CrossRef CAS PubMed.
- V. L. Solozhenko, O. O. Kurakevych, D. Andrault, Y. Le Godec and M. Mezouar, Phys. Rev. Lett., 2009, 102, 015506 CrossRef PubMed.
- P. Zinin, L. Ming, H. Ishii, R. Jia, T. Acosta and E. Hellebrand, J. Appl. Phys., 2012, 111, 114905 CrossRef.
- M. Chen, J. W. McCauley and K. J. Hemker, Science, 2003, 299, 1563–1566 CrossRef CAS PubMed.
- Y. C. Wang, J. A. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS.
- X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101 CrossRef PubMed.
- Q. Yan, B. Wang, Y. X. Wang, J. Yang and G. Yang, J. Chem. Phys., 2014, 140, 224704 CrossRef PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- D. M. Ceperley and B. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 58, 1861–1864 CrossRef CAS PubMed.
- P. Giannozzi, S. De Gironcoli, P. Pavone and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7231–7242 CrossRef CAS.
- Z. Zhao, B. Xu, X. F. Zhou, L. M. Wang, B. Wen, J. He, Z. Liu, H. T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502 CrossRef PubMed.
- X. F. Zhou, G. R. Qian, X. A. Dong, L. X. Zhang, Y. J. Tian and H. T. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134126 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- B. Decker and J. Kasper, Acta Crystallogr., 1959, 12, 503–506 CrossRef CAS.
- Y. A. Freiman and H.-J. Jodl, Phys. Rep., 2004, 401, 1–228 CrossRef CAS.
- Z. Wu, E. Zhao, H. Xiang, X. Hao, X. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- H. B. Ozisik, K. Colakoglu, E. Deligoz and H. Ozisik, J. Mol. Model., 2012, 18, 3101–3112 CrossRef CAS PubMed.
- J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford University Press, 1985 Search PubMed.
- F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed.
- Y. J. Tian, B. Xu and Z. S. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- D. Roundy and C. R. Krenn, Phys. Rev. Lett., 1999, 82, 2713–2716 CrossRef CAS.
- D. Roundy, C. R. Krenn, M. L. Cohen and J. W. Morris, Philos. Mag. A, 2001, 81, 1725–1747 CAS.
- B. B. Karki, G. J. Ackland and J. Crain, J. Phys.: Condens. Matter, 1997, 9, 8579–8589 CrossRef CAS.
- C. R. Krenn, D. Roundy, J. W. Morris Jr and M. L. Cohen, Mater. Sci. Eng., A, 2001, 319–321, 111–114 CrossRef.
- Y. Zhang, H. Sun and C. Chen, Phys. Rev. Lett., 2005, 94, 145505 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09277f |
| This journal is © The Royal Society of Chemistry 2017 |