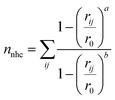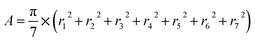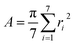Open Access Article
Open Access ArticleMetadynamics supports molecular dynamics simulation-based binding affinities of eucalyptol and beta-cyclodextrin inclusion complexes†
Bodee Nuthoa,
Nadtanet Nunthaboot*b,
Peter Wolschanncde,
Nawee Kungwan fg and
Thanyada Rungrotmongkol
fg and
Thanyada Rungrotmongkol *chi
*chi
aProgram in Biotechnology, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand
bDepartment of Chemistry, Center of Excellence for Innovation in Chemistry, Faculty of Science, Mahasarakham University, Mahasarakham 44150, Thailand. E-mail: nadtanet@gmail.com; nadtanet.n@msu.ac.th
cStructural and Computational Biology Research Group, Department of Biochemistry, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand. E-mail: t.rungrotmongkol@gmail.com; thanyada.r@chula.ac.th
dDepartment of Pharmaceutical Technology and Biopharmaceutics, University of Vienna, Vienna 1090, Austria
eInstitute of Theoretical Chemistry, University of Vienna, Vienna 1090, Austria
fDepartment of Chemistry, Faculty of Science, Chiang Mai University, Chiang Mai 50200, Thailand
gResearch Center on Chemistry for Development of Health Promoting Products from Northern Resources, Chiang Mai University, Chiang Mai, 50200, Thailand
hPh.D. Program in Bioinformatics and Computational Biology, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand
iMolecular Sensory Science Center, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand
First published on 1st November 2017
Abstract
The development of various molecular dynamics methods enables the detailed investigation of association processes, like host–guest complexes, including their dynamics and, additionally, the release of the guest compound. As an example of the application of such methods, the inclusion complexation of cyclodextrins with eucalyptol is described. Eucalyptol is the major constituent of eucalyptus oil, which exhibits anti-inflammatory properties. This compound has many applications including flavors, fragrances and medical therapies. However, its pharmaceutical applications are limited due to volatility and low water solubility. Cyclodextrins (CDs) are compounds that are capable of forming inclusion complexes with eucalyptol to enhance solubility and stability. In the present work, molecular dynamics (MD) simulations and free energy calculations were performed to determine the molecular structure, dynamical behaviour and binding affinities of the host–guest inclusion complexes of eucalyptol with native beta-cyclodextrin (βCD) and its derivatives, 2,6-dimethyl-βCD (2,6-DMβCD) and the three hydroxypropyl-βCDs (2-HPβCD, 6-HPβCD and 2,6-DHPβCD). In the inclusion complex, eucalyptol preferentially locates within the hydrophobic cavity with all βCDs studied here. The binding affinities were calculated by MM/PBSA and QM/PBSA with the M06-2X/6-31G(d,p) level of theory and are in relatively good agreement with the experimental stability constants in the order of 2,6-DMβCD > βCD > 2-HPβCD. In addition, recently developed metadynamics simulations were applied to investigate the eucalyptol's release pathways from the cavity of the CDs. The results from this study show that MD simulations, metadynamics and related free energy calculations provide an excellent support for experimental studies, and they give additional information about the structural and dynamical behaviour of inclusion complexes as well as the energetic details about host–guest interactions. Moreover, the releasing direction and possible dissociation rates of the inclusion complexes were also predicted.
1 Introduction
Essential oils have been widely used in traditional medicine, perfumery, cosmetics and as a condiment in food and beverages.1,2 They consist of a complex mixture of volatile aroma compounds that are synthesized in plants to protect them against various pathogens. The broad pharmacological profiles of essential oils and their constituents have been reported, including antibacterial,3 antifungal,4 antiviral,5 anticancer,6 antioxidant and anti-inflammatory7 activities. The main components of essential oils are monoterpenes (C10H16) obtained from the condensation of two isoprene units (C5H8). The monocyclic monoterpene ether eucalyptol (Fig. 1a), also known as 1,8-cineol, is the major constituent of eucalyptus oil, an essential oil isolated from Eucalyptus globulus.8 It is also found in small amounts in herbs such as rosemary (Rosmarinus officinalis)9 and Psidium species (Psidium pohlianum Berg and Psidium guyanensis Pers.).10 Eucalyptol has several pharmacological properties used in therapeutics. It plays an important role in the treatment of diseases involved in upper and lower airways, such as sinusitis and chronic rhinitis, chronic obstructive pulmonary disease and bronchial asthma.11,12 It has anti-inflammatory properties that operate, according to in vitro studies, by inhibiting the cytokine and prostaglandin production of stimulated monocytes.13 Eucalyptol shows a strong inhibition to tumor necrosis factor alpha (TNF-α) and interleukin 1 beta (IL-1β) in cultured human lymphocytes and monocytes.14 In addition, in vivo experiments revealed an anti-nociceptive effect of eucalyptol in Swiss mice and Wistar rat animal models.15 Further studies displayed a gastric protection of eucalyptol in rats against ethanol-induced gastric injury16 and liver failure in an in vivo murine model of endotoxemic shock.17 Recently, Mulyaningsih and co-workers18 reported the direct antibacterial activity of eucalyptol against multidrug-resistant bacterial pathogens. From this point of view, there is a growing interest in the application of eucalyptol in pharmaceutical products to improve human health functions. However, essential oils like eucalyptol are sensitive to light, oxygen, humidity and temperature. Additionally, volatility and low water solubility are considered to be important limitations of their use. Thus, many techniques are focused on preserving the product quality and enhancing the shelf-life, as well as improving the stability and solubility without altering the chemical properties of the oil. One interesting method to solve these problems is the encapsulation of such compounds in a cavity of proper host molecules.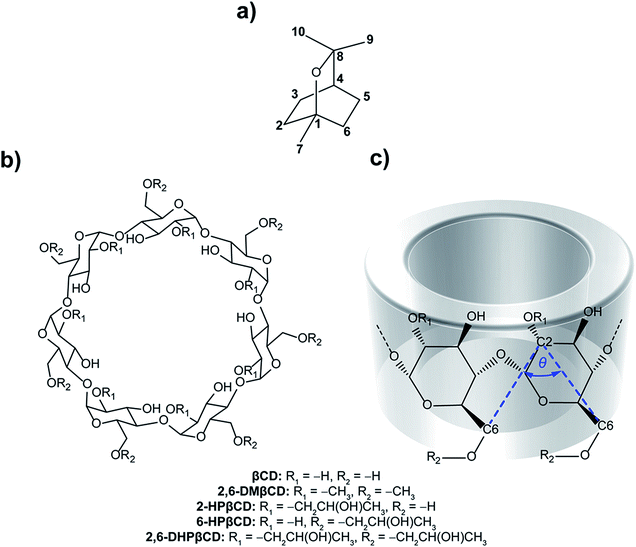 | ||
| Fig. 1 Chemical structures of (a) eucalyptol, (b) β-cyclodextrins and (c) CD fragment where atomic labels and structural angle parameter, θ[C6(n)–C2(n+1)–C6(n+1)], are also shown. | ||
Cyclodextrins (CDs) are a group of cyclic oligosaccharides consisting of α-D-glucoses with 1 → 4 glycosidic linkages.19 Natural CDs are composed of six, seven and eight glucopyranose units, referred to as αCD, βCD and γCD, respectively. The molecular shape of CDs is that of a truncated cone with the inner cavity being lipophilic and the outer surface relatively hydrophilic. Each glucopyranose subunit of the ring system contains a primary hydroxyl group at position C6 and two secondary hydroxyl groups at positions C2 and C3, and collectively these form the primary and secondary rims of the CD. The primary hydroxyl groups of each glucose subunit are located at the narrow edge, while the secondary hydroxyl groups are present on the wider rim of the truncated cone of the CD ring. The relative hydrophobic cavity of CDs can interact with guest molecules mainly by van der Waals interactions.20,21 Therefore, complexation with CD is an effective strategy to increase the aqueous solubility of guest molecules and, additionally, to protect them from oxidation, thermal degradation and evaporation.22 CD inclusion complexes have been applied as drug delivery systems,23 in agriculture,24 separation technology25 and chemical protection.26 Among different CDs, βCD (Fig. 1b) is the most widely used due to its easy synthetic access and its relatively low price.27 Although βCD has a suitable cavity size for a wide range of guest molecules, some applications are limited because of its relatively low water solubility (18.4 mg ml−1, at 25 °C).28 Other βCD derivatives like 2,6-dimethyl-βCD (2,6-DMβCD) and 2-hydroxypropyl-βCD (HPβCD) have increased water solubility (570 and >600 mg ml−1, respectively).29,30 They are considered to exhibit improved bioavailability and bioactivity of the guest molecule.31,32
Besides experimental studies, computational modeling investigations on CDs and their inclusion complexes have been performed to give a better understanding of the preferable binding mode of guest molecules, and for determining host–guest interactions as well as the dynamic behavior of inclusion complexes at the molecular level. Many studies have used molecular dynamics (MD) simulations as the main computational tool to investigate CD inclusion complexes in aqueous solution.33–36 In our previous studies,37,38 naringenin and pinostrobin complexing with βCD and its derivatives was studied by MD simulation and free energy calculations were performed. The results indicated that both guest molecules bind to 2,6-DMβCD better than native βCD.
An intrinsic limitation of MD simulation is that the simulation can be trapped in a local minimum and it is difficult to observe the transition from one minimum to another. Metadynamics is one of the advanced sampling techniques that can overcome these limitations by introducing a biased potential to allow the system under investigation to explore the free energy surface (FES) as a function of determined collective variables (CVs).39 Metadynamics has been successfully applied to study the release processes of small DNA intercalating agents,40–42 small protein inhibitors43,44 and drugs from protein–DNA complexes.45 Although, there have been many reported MD simulations of CD inclusion complexes, no metadynamics has been applied for this particular host–guest complex. Therefore, in the present study, we utilized this advanced sampling method for the first time on CD–guest inclusion complexes to investigate the disassociation routes.
Up to now, experimental information about the eucalyptol/βCDs inclusion complexation has been published together with results obtained from molecular docking.46–48 The main aim of this work was to investigate the binding formation and the releasing pathway of eucalyptol in the nano-cavity of βCD and its derivatives. Therefore, the structural and dynamical properties of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 inclusion complexes of eucalyptol with βCD and its related analogues, 2,6-DMβCD and the HPβCD, were investigated by all-atom MD simulations in aqueous solution. Various computational methods, including MM-PBSA/GBSA and M06-2X/6-31G(d,p)//QM-PBSA/GBSA, were applied to predict the binding free energies of the eucalyptol/βCDs inclusion complexes in comparison with experimental data. In addition, their releasing mechanisms or dissociation processes were further examined using metadynamics methodology. The obtained information could possibly help for the selection of the most suitable CD derivative of eucalyptol with enhanced bioavailability.
1 inclusion complexes of eucalyptol with βCD and its related analogues, 2,6-DMβCD and the HPβCD, were investigated by all-atom MD simulations in aqueous solution. Various computational methods, including MM-PBSA/GBSA and M06-2X/6-31G(d,p)//QM-PBSA/GBSA, were applied to predict the binding free energies of the eucalyptol/βCDs inclusion complexes in comparison with experimental data. In addition, their releasing mechanisms or dissociation processes were further examined using metadynamics methodology. The obtained information could possibly help for the selection of the most suitable CD derivative of eucalyptol with enhanced bioavailability.
To compare to the natural βCD, we selected 2,6-DMβCD (on an industrial scale an isomeric mixture, RAMEB, is used). In the case of HPβCDs, where the substitution can be modified by the alkalinity,49,50 we have chosen three HPβCDs, namely 2-HPβCD, 6-HPβCD and 2,6-HPβCD, as representative structures.
2 Simulation details
2.1 System preparation
The optimized structures of βCD, 2,6-DMβCD, 2-HPβCD, 6-HPβCD and 2,6-DHPβCD were taken from our previous studies.38,51 The eucalyptol geometry was optimized at the HF/6-31G(d) level of theory using the Gaussian 09 program.52 The inclusion complexes between eucalyptol and βCD and the respective βCD derivatives were constructed by AUTODOCK 4.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 with the Lamarckian Genetic Algorithm combined with a local search method. A three-dimensional box of 40 Å × 40 Å × 40 Å with grid point spacing of 0.375 Å was employed. Kollman united atom charges and Gasteiger–Marsili54 charges were assigned to the CDs and eucalyptol, respectively. The CD molecule was kept as a fixed truncated cone structure and for the guest molecules free motion was allowed. One hundred independent docking runs were applied to each complex. The docking calculation results of each eucalyptol/CDs inclusion complex were clustered into different groups based on their root mean-square deviation values of complex atomic position of less than 2 Å. From the docking results, eucalyptol displays a single possible conformation in all systems, with both methyl groups likely inserted into the relative lipophilic cavity of the CDs. The complex with the lowest binding energy was selected as a representative structure for further investigation using MD simulations to obtain detailed insight into molecular behavior of these complexes in aqueous solution.
53 with the Lamarckian Genetic Algorithm combined with a local search method. A three-dimensional box of 40 Å × 40 Å × 40 Å with grid point spacing of 0.375 Å was employed. Kollman united atom charges and Gasteiger–Marsili54 charges were assigned to the CDs and eucalyptol, respectively. The CD molecule was kept as a fixed truncated cone structure and for the guest molecules free motion was allowed. One hundred independent docking runs were applied to each complex. The docking calculation results of each eucalyptol/CDs inclusion complex were clustered into different groups based on their root mean-square deviation values of complex atomic position of less than 2 Å. From the docking results, eucalyptol displays a single possible conformation in all systems, with both methyl groups likely inserted into the relative lipophilic cavity of the CDs. The complex with the lowest binding energy was selected as a representative structure for further investigation using MD simulations to obtain detailed insight into molecular behavior of these complexes in aqueous solution.
2.2 Classical molecular dynamics simulation
The structures of βCD and its derivatives complexed with eucalyptol in aqueous solution were simulated with three different initial velocities by MD simulations utilizing the standard procedure applied to biomolecular systems55–58 using the AMBER14 software package.59 βCD and its dimethyl and hydroxypropyl derivatives were treated using the Glycam-06h carbohydrate force field.60 The standard procedures based on our previous studies for small organic molecules61–64 were used for the preparation of the partial atomic charges and parameters of eucalyptol. Briefly, the optimized structure of eucalyptol was used to calculate the electrostatic potential (ESP) charges with the HF/6-31G(d) level of theory using Gaussian 09. After that, a charge fitting calculation was applied to evaluate the restrained electrostatic potential (RESP) charges of eucalyptol using the antechamber module65 as implemented in AMBER14. The molecular parameters of eucalyptol were then taken from the parmchk program based on the general AMBER force field (GAFF).66 All hydrogen atoms of each system were minimized with 1000 steps of steepest descents (SD) followed by 3000 steps of conjugated gradients (CG) to remove bad contacts and steric hindrances. Each inclusion complex was then solvated using simple point charge (SPC) water molecules in a periodic truncated octahedron water box that had a minimum distance from the system surface of 12 Å. The total size of the truncated octahedron periodic water box was approximately 54 Å × 54 Å × 54 Å and roughly consisted of 2000 water molecules. After the solvation of the initial structure, the water molecules were first optimized alone with SD (1000 steps) and CG (3000 steps), and then the entire system was optimized using the same procedure. The long-range electrostatic interactions were treated using the particle mesh of Ewald's summation method,67 whilst a short-range cutoff of 10 Å for non-bonded interactions was applied. The SHAKE algorithm68 was utilized to constrain all covalent bonds involving hydrogen atoms. The temperature of each system was increased from 10 K up to 298 K over a period of 100 ps. The simulation was then further continued at this temperature and with a pressure of 1 atm for 70 more ns. A periodic boundary condition with isobaric-isothermal (NPT) ensemble was applied for all simulations using the PMEMD module in AMBER.69 The simulation time step was set at 2 fs and the trajectories were collected every 2 ps for analysis. All individual βCDs were simulated with the same procedure for comparison.The system was judged to be in an equilibrium state by the root mean square displacement (RMSD) and the two-dimensional root mean square displacement (2D-RMSD). The mobility of eucalyptol in the cavity of βCD and each derivative was determined by measuring the distance between the centers of mass of eucalyptol and of each respective CD molecule. The conformational changes of each CD upon the inclusion complex were determined in terms of the distributions of the distances between the hydroxyl groups on the secondary wider rim of the adjacent α-D-glucopyranoses (O3(n)–O2(n+1)) and the distance between the glycosidic oxygen atoms (O4(n)–O4(n+1)), as well as the angle, θ[C6(n)–C2(n+1)–C6(n+1)], to determine the flips of (α-1,4)-linked α-D-glucopyranose units. In addition, the averaged radius of gyration (Rg) and the averaged cavity area (A) were calculated to investigate the shape of βCDs upon complex formation. The total host–guest binding free energy (ΔGbind) was estimated by means of MM-PBSA/GBSA approaches in accordance with the other flavonoid/CD inclusion complexes.35,37 Furthermore, the ΔGbind was subsequently corrected by replacing the MM energy (ΔEMM) with energy obtained the from quantum mechanics (ΔEQM) calculated at the density functional theory (DFT) with the M06-2X/6-31G(d,p) level of theory35 using Gaussian 09. All structural analyses were computed by the cpptraj module,70 while the ΔGbind was calculated using the MMPBSA.py module71 implemented in AMBER14.
2.3 Metadynamics
The eucalyptol dissociation process from the cavity of βCD and its derivatives was studied by metadynamics39 using the PLUMED 2.0 package72 patched to the AMBER14 program. The metadynamics algorithm based on a dimensional reduction uses a set of CVsi (i = 1,…, NCVs), which are a function of the coordinates of the system x = {x1, x2,…, xN}, where N is the number of particles. Such coordinates are evolved with standard MD supplemented by a history-dependent potential, which can add penalties to the system discouraging it from visiting previously sampled conformations. In the standard implementation, the history-dependent potential is built-up by Gaussians of NCVs-th dimension, height (w) and widths (δsi; i = 1,…, NCVs), deposed at time intervals (τG) along the CVs trajectory. The choice of these w, δsi, and τG parameters is the key to achieve for obtaining an accurate reproduction of the FES in reasonable time. Within the limit of a long metadynamics run, the sum of these penalty terms tends to compensate the underlying FES in the reduced space, thus permitting a reconstruction of the FES explored up to time t.73The two CVs used here to describe eucalyptol dissociation from the CD cavity are based on a protocol applied to the dissociation of the minor groove binders of DNA.40 CV1 is the distance between the centers of mass of the eucalyptol and CDs (dCOMs). CV2 is the number of hydrophobic contacts (nnhc) between the non-polar carbons of eucalyptol and the CDs modeled as a coordination number via a continuous, differentiable switching function:
To identify the representative structures of the intermediate states during the dissociation process, the k-means clustering algorithm75 implemented in AMBER14 was applied to cluster the structures from the trajectories based on their structural similarities. The RMSD calculations were applied only to the heavy atoms of eucalyptol and βCDs.
3 Results and discussion
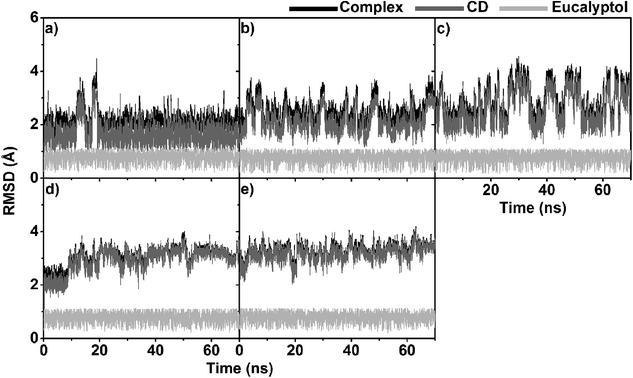
The three independent MD simulations on each system displayed relatively similar results (Fig. S1 and S2 in ESI†). For simplification, the data from only one MD simulation are presented here.3.1 System stability
To obtain information about the dynamic stability of the inclusion complexes, the 1D-RMSD of each MD system relative to its initial structure for all atoms of the complexes, CDs (βCD, 2,6-DMβCD, 2-HPβCD, 6-HPβCD and 2,6-DHPβCD), and eucalyptol versus simulation time were measured and displayed in Fig. 2. The 2D-RMSD plots of all atoms in the complexes where the RMSD values of each snapshot against all other snapshots are plotted and depicted in Fig. 3. As can be seen from Fig. 2 and 3, the averaged RMSDs of all modified βCDs were higher than those of the parent βCD due to the presence of substituents. Among all five simulated systems, a noticeably high RMSD fluctuation was observed with eucalyptol/2-HPβCD (Fig. 2c and 3c). The cyan and green areas in the 2D-RMSD plots (RMSDs of 1.5–3.0 Å in Fig. 3a, b and d) indicate that the complexes of βCD, 2,6-DMβCD and 6-HPβCD with eucalyptol are relatively more stable than the other two systems. From this finding, it can be inferred that the βCD with hydroxypropyl substitution at all O2 positions causes more widespread conformer fluctuations than when substitution occurs at all O6 positions. From a comparison of the CD structures in the complex to those of individual CDs,38 the lowered RMSDs in Fig. 2 and 3 suggest that the complexation with eucalyptol leads to more rigid CD conformations.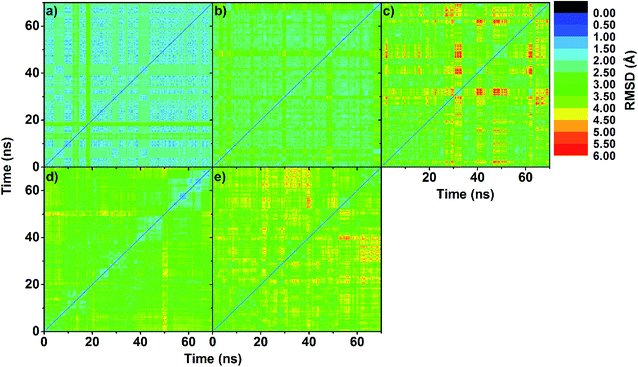 | ||
| Fig. 3 2D-RMSD plots of all atoms in inclusion complex of (a) eucalyptol/βCD, (b) eucalyptol/2,6-DMβCD, (c) eucalyptol/2-HPβCD, (d) eucalyptol/6-HPβCD and (e) eucalyptol/2,6-DHPβCD. | ||
The RMSDs of eucalyptol in complexation with all CDs were similar (0.5–1.0 Å in Fig. 2). Additionally, it is seen that the differences in the RMSD fluctuations of each complex came from the structural and dynamical properties of eucalyptol binding inside the nano-pore of the CDs (discussed in the next section). For a relative comparison of all investigated inclusion complexes, trajectories within the same range of the last 20 ns in Fig. 2 were extracted for further analysis.
3.2 Eucalyptol mobility and preferential displacement in CD cavity
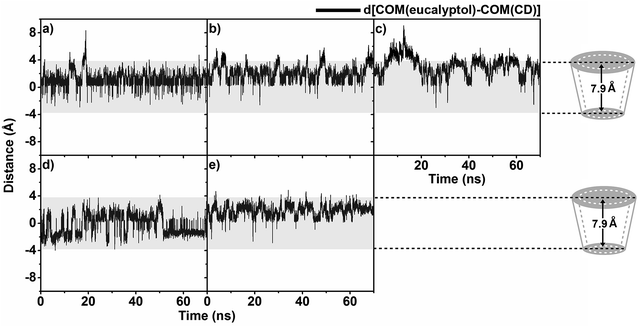
To determine the eucalyptol behavior inside the five different βCD cavities, the distance between the center of mass of the eucalyptol and the center of mass of each CD, defined as d[COM(eucalyptol)–COM(CD)], without taking into account the substituent groups of the respective modified βCD molecules is measured and plotted in Fig. 4. The horizontal dashed lines positioned at −3.95 Å and 3.95 Å on the y-axis are approximately related to the positions of the primary and secondary rims of βCD, respectively. The negative and positive distance values consecutively represent the position of the eucalyptol molecule below and above the center of mass of each CD in the direction of the primary and secondary rims, accordingly.The distance analysis evidently shows that the eucalyptol molecule preferentially occupies the hydrophobic cavities of all five different CDs. It is mainly located near the center of these host cavities but more towards the wider rim (0.5–3.2 Å), in particular in the eucalyptol/2-HPβCD complex (mostly 3.4–4.2 Å). In the 6-HPβCD system, the eucalyptol is on average located in the middle of the cavity. In the 2-HPβCD system, the eucalyptol molecule initially moved up over 4 Å at simulation time ≈15 ns and then moved down to be steadily located at 1.5–3.6 Å until the end of the simulation. This finding implies that the eucalyptol/2-HPβCD inclusion complex is less stable than the other four complexes. It is worth to note that the other two independent simulations for each complex provide similar results in which the eucalyptol is likely to stay near the wider rim of 2-HPβCD (Fig. S2 in the ESI†).
3.3 CD conformation upon complexation
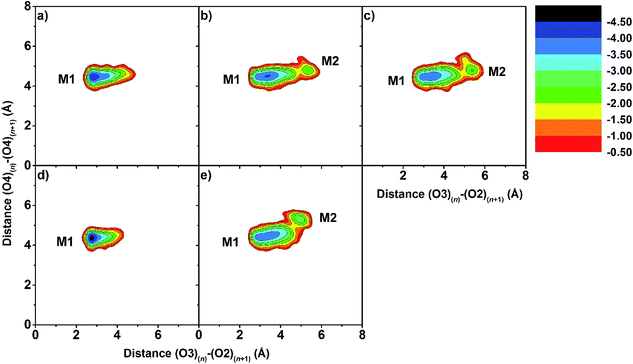
Changes in the molecular shapes of the CD molecules during the process of complexation was investigated by monitoring the distance between the secondary hydroxyl groups at C3 and the adjacent C2 positions (O3(n)–O2(n+1)) and the distance between the glycosidic oxygen atoms (O4(n)–O4(n+1)) obtained from the last 20 ns of the simulation. It is worth noting that the former distances correlate with a possible formation of flip-flop intramolecular hydrogen bonds, which are structural characteristics of CDs. Fig. S3 in the ESI† displays the distance distributions of O3(n)–O2(n+1) and O4(n)–O4(n+1) for the five simulated complexes. The O3(n)–O2(n+1) distance related to the strong intramolecular hydrogen bonds on the wider rim was observed only in the case of eucalyptol complexed with either βCD or 6-HPβCD with their most probable distance of less than 3.0 Å. Weaker interactions were found in the other cases (≈3.5 Å), due to the substitution with methyl or hydroxypropyl at the C2 positions. The O4(n)–O4(n+1) distances were found at ≈4.5 Å in all eucalyptol/βCDs similar to pinostrobin and various CD derivative inclusion complexes studied previously.38To further investigate the local minima of CD conformations upon complex formation, the 2D free energy landscape (equivalent to potential of mean force) based on conformational ensemble is calculated and plotted in Fig. 5. According to this approach,76–78 the free energy profile expressed as a function of the probability distribution of the two parameters P(x,y), O3(n)–O2(n+1) and O4(n)–O4(n+1) distances, is calculated using the following equation:
F(x,y) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P(x,y)) ln(P(x,y)) |
The O3(n)–O2(n+1) distances of the M2 minima are lengthened, which is connected with the loss of intramolecular hydrogen bond interactions on the secondary rim.79 This results in the distortion of the CD geometry that can be measured in terms of the structural angle parameter θ[C6(n)–C2(n+1)–C6(n+1)] for a pair with an angle of adjacent glucose subunits (Fig. 1c). A glucopyranose pair with an angle of >90 degrees was considered as a flip or turn conformation. From the last 20 ns, the number of snapshots with different turns for βCDs with and without eucalyptol bounds are compared in Table 1. Three different CD conformations defined as no-, 1- and 2-turns are observed. As expected, the encapsulation of eucalyptol significantly increases the amount of no-turn conformations of βCDs to over 80%, indicating an increased rigidity of the system upon complexation. This was particularly true for the βCD and 6-HPβCD inclusion complexes, which had the highest percentage of no-turn conformations (98%). This finding was associated with the dominant population of M1 for all inclusion complexes (Fig. 5). Without eucalyptol bounds, 3-turn conformations are detected only in 2,6-DMβCD (15%), whereas in the other complexes 1-turn and/or 2-turn conformations were only found.
| Number of turn | Percentage of turn conformation (%) | ||||
|---|---|---|---|---|---|
| Eucalyptol/βCD | Eucalyptol/2,6-DMβCD | Eucalyptol/2-HPβCD | Eucalyptol/6-HPβCD | Eucalyptol/2,6-DHPβCD | |
| No-turn | 98 (23) | 86 (0) | 83 (12) | 98 (18) | 86 (12) |
| 1-Turn | 2 (53) | 14 (38) | 17 (47) | 2 (78) | 14 (44) |
| 2-Turn | 0 (24) | 0 (47) | 0 (49) | 0 (3) | 1 (44) |
| 3-Turn | 0 (0) | 0 (15) | 0 (0) | 0 (0) | 0 (0) |
The shapes of the native βCD and its derivatives upon complexation were further investigated in terms of parameters Rg and A. The Rg representing the mass weighted scalar length of each atom from the center of mass of the molecule is used to measure the size and shape of a molecule. The parameter A 79,80 describing the averaged cavity area of βCD molecule (assumed as a circle area) is calculated from the distances between βCD's center and the group of atoms of each glucose unit using the following equation:
herein, ri (i = 1,…, 7) is the distance between the center of mass of the βCD molecule and all heavy atoms of each glucose subunit (7 subunits for βCDs). The results of Rg and A of all βCDs in complex form compared to their free forms are given in Table 2. Upon complexation A is enlarged in all βCDs by ≈10–20 Å2, as an indication that the host molecule adapts its cavity according to the size of the guest, the eucalyptol molecule. This is also shown by an increased Rg value (of ≈0.2–0.7 Å). It should be noted that the higher variance in Rg for the modified βCDs reflects an increase in molecular size fluctuations caused by the flexibility of the functional groups added to the parent βCD molecule at the O2 and/or O6 positions. Especially in the case of 2-HPβCD, the hydroxypropyl substitution at the O2 positions leads to a larger number of conformations compared to substitutions at the O6 positions in 6-HPβCD, which is consistent with the previously reported MD study by Yong et al.49
| Eucalyptol/βCD | Eucalyptol/2,6-DMβCD | Eucalyptol/2-HPβCD | Eucalyptol/6-HPβCD | Eucalyptol/2,6-DHPβCD | |
|---|---|---|---|---|---|
| Rg (Å) | 6.3 (6.0) | 6.7 (6.0) | 7.4 (7.1) | 6.8 (6.6) | 7.7 (7.4) |
| A (Å2) | 102.4 (93.2) | 100.4 (82.6) | 98.4 (90.6) | 96.6 (89.3) | 100.4 (90.8) |
3.4 Binding free energy analysis
To estimate the free energy of binding or ΔGbind between eucalyptol and the different types of βCDs in aqueous solution, a set of 100 snapshots was extracted from the production phase of each simulated system. The MM- and QM-PBSA/GBSA approaches were used to predict the free energy of binding for each host–guest inclusion complex. The binding free energy of the inclusion complex can be calculated by the free energy difference between the complex, the isolated βCDs, and the guest molecule. The energetic components are comprised of the gas phase energy (ΔEMM) gained by the summation between electrostatic (ΔEele) and van der Waals (ΔEvdW) energies, free energy of solvation (ΔGsolv) and entropy contribution (TΔS). Based on the MM/PBSA and MM/GBSA methods, the polar solvation free energy term can be determined from the Poisson–Boltzmann (PB) and the generalized Born (GB) models.81 However, the non-polar component of both techniques is similarly estimated from the solvent accessible surface area (SASA). For the QM-PBSA, the enthalpy term is computed by a QM approach in which a density functional method using the M06-2X functional with 6-31G(d,p) basis set is applied to describe the QM part of the inclusion complex. The entropy term for conformational changes of the two individual molecules upon complex formation was taken from a normal mode (NMODE) analysis.82 The estimated binding free energies along with their corresponding energy contributions of eucalyptol in complex with the different βCDs and the experimental binding free energy (ΔGexp) converted from their stability constant values (Kf)46 are given and compared in Table 3.| Component | Eucalyptol/βCD | Eucalyptol/2,6-DMβCD | Eucalyptol/2-HPβCD | Eucalyptol/6-HPβCD | Eucalyptol/2,6-DHPβCD |
|---|---|---|---|---|---|
a Experimental values, ΔGexp, were obtained using equation ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kf based on experimental stability constant Kf at 25 °C.b RAMEB is randomly methylated-βCD.c CRYSMEB is low methylated-βCD.d DS is degree of substitution that is number of methyl/hydroxypropyl groups per CD molecule. Kf based on experimental stability constant Kf at 25 °C.b RAMEB is randomly methylated-βCD.c CRYSMEB is low methylated-βCD.d DS is degree of substitution that is number of methyl/hydroxypropyl groups per CD molecule. |
|||||
| ΔEele | −0.35 ± 0.42 | −0.35 ± 0.51 | −0.38 ± 0.49 | −0.36 ± 0.36 | −0.44 ± 0.71 |
| ΔEvdW | −22.22 ± 1.97 | −22.95 ± 2.21 | −22.89 ± 2.45 | −30.01 ± 1.82 | −25.40 ± 1.92 |
| ΔEMM | −22.57 ± 2.21 | −23.30 ± 2.52 | −23.27 ± 2.65 | −30.37 ± 1.86 | −25.84 ± 2.21 |
| ΔEQM | −16.67 ± 2.46 | −17.32 ± 1.92 | −16.93 ± 1.97 | −22.29 ± 1.84 | −18.64 ± 3.07 |
| ΔGsolv(PBSA) | 1.78 ± 0.78 | 2.08 ± 0.74 | 2.34 ± 0.84 | 2.68 ± 0.69 | 3.14 ± 1.20 |
| ΔGsolv(GBSA) | 1.20 ± 0.47 | 0.35 ± 0.55 | 0.56 ± 0.53 | 0.67 ± 0.51 | 0.08 ± 0.77 |
| −TΔS | 12.11 ± 1.70 | 12.30 ± 1.81 | 12.60 ± 1.80 | 13.96 ± 1.52 | 12.60 ± 1.90 |
| ΔGbind(MM/PBSA) | −8.68 ± 1.45 | −8.91 ± 1.59 | −8.28 ± 1.95 | −13.73 ± 1.25 | −10.10 ± 3.15 |
| ΔGbind(MM/GBSA) | −9.26 ± 1.41 | −10.64 ± 1.58 | −10.06 ± 1.92 | −15.74 ± 1.23 | −13.16 ± 1.51 |
| ΔGbind(QM/PBSA) | −2.78 ± 1.54 | −2.94 ± 1.37 | −1.99 ± 1.40 | −5.65 ± 1.24 | −2.90 ± 1.90 |
| ΔGbind(QM/GBSA) | −3.36 ± 1.51 | −4.67 ± 1.35 | −3.77 ± 1.36 | −7.66 ± 1.22 | −5.96 ± 1.85 |
| Kf (M−1)46 | 615 | 673 (bRAMEB; DS = 12.6) | 334 (DS = 5.6) | ||
| 688 (cCRYSMEB; dDS = 4.9) | |||||
| aΔGexp | −3.80 | −3.86 | −3.44 | ||
Since the structural and dynamical behavior of eucalyptol bound inside each CD cavity is somewhat similar, the binding free energies predicted by MM- and QM-PBSA/GBSA methods for all complexes are not significantly different (within 2 kcal mol−1), except for the eucalyptol/6-HPβCD inclusion complex, which had the lowest binding free energy predicted with all energetic methods. In comparison with the experimental binding free energy of the eucalyptol/βCD complex converted from Kf,46 the introduction of the QM approach was found to improve the absolute binding free energy prediction of the host–guest inclusion complex. Encapsulation by 2,6-DMβCD did not significantly improve the stability of the inclusion complex, compared to βCD. This is somewhat experimentally supported by the complexation with randomly methylated-βCD (with degree of substitution (DS) related to the number of methyl groups per CD molecule of 12.6 with Kf of 673 M−1) and the low methylated-βCD (DS of 4.9, Kf of 688 M−1).46 Among the three HPβCD related structures, the binding free energies of the 6-HPβCD and 2,6-DHPβCD inclusion complexes were predicted to be more stable than that of 2-HPβCD. However, from the NMR and MALDI-TOF MS study,83 all HPβCDs had different average DSs with 50–60% of the hydroxypropyl substituents at the O2 position, while the expected peaks and couplings resulting from substitutions at positions O3 and/or O6 were probably too broad and too weak to be detected. Taken together with our predicted binding free energies, this could be a reason why the Kf value of the eucalyptol/2-HPβCD complex is relatively low.
Due to the high lipophilicity of eucalyptol, no hydrogen bonds between the guest and the host molecule were detected. This is in agreement with the small contribution of the electronic interaction (ΔEele ≈ −0.4 kcal mol−1) between eucalyptol and all five different βCDs. On the other hand, the main contribution for eucalyptol inclusion arises from the van der Waals interaction (ΔEvdW of at least −20 kcal mol−1). Similar to our previous studies,35,37,38,55 the van der Waals forces were found to play a key role in the formation of inclusion complexes between CDs and the non-polar guest molecules. The solvation free energies (ΔGsolv) predicted by the PBSA and GBSA approaches suggest that the different solvation effects in the modified βCDs slightly increased with PBSA or decreased with GBSA relative to βCD.
3.5 Metadynamics
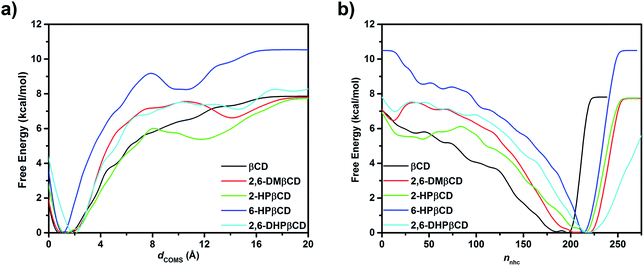
Although MD simulations and the binding free energy calculations are able to describe the structural dynamics and the main driving force in the complexes at the equilibrium state to some extent, they cannot identify the guest releasing pathway from the cavity of the host molecule during the dissociation process. Therefore, in this study, metadynamics simulations were applied to investigate the releasing mechanism of eucalyptol from the hydrophobic cavity of βCDs. Enhanced sampling of eucalyptol configurations within each type of βCD was obtained by multiple repetitions of the metadynamics runs. The free energy profiles are calculated when the number of hydrophobic contacts between the non-polar carbons of guest and host molecules (nnhc, CV2) approaches to zero, at this point the eucalyptol has completely moved out from the βCDs cavity. It should be noted that sampling is enhanced by accumulating the configurations of five independent runs. Nevertheless, the data obtained here cannot be related to the dissociation constant (Kd) of the guest because a calculation of Kd would require a full sampling of the unbound state.The calculated underlying free energy profiles along the predefined sets of CVs (dCOMs and nnhc) are given in Fig. 6. The metadynamics simulations illustrate that the binding free energy of the eucalyptol/βCDs inclusion complexes achieved from both profiles was in the order of 6-HPβCD > 2,6-DHPβCD > 2,6-DMβCD ≈ βCD ≈ 2-HPβCD. This observation is consistent with the binding free energy estimated from the MM- and QM-PBSA approaches. Only one energy minimum corresponding to the bound state of each system along the investigated CVs was detected. Along the CV1 parameter (Fig. 6a), the dCOMs at the energy minimum was found to be ≈1 Å for all inclusion complexes except for 2,6-DHPβCD (where it was ≈2 Å). The free energy minimum obtained along the CV2 coordinate yielded a lower value of nnhc in the native βCD system (≈190) than those of the modified ones (≈220) as shown in Fig. 6b.
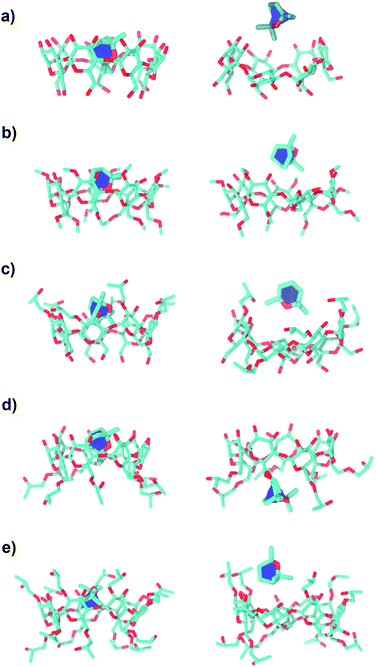
The FES landscapes corresponding to the eucalyptol dissociation from the cavity of βCD and the βCD derivatives, plotted as a function of dCOMs and nnhc, are depicted in Fig. 7. The surface plot indicates the presence of the deep minima (blue area) accounting for the bound form of eucalyptol with each studied βCD. This bound state is characterized by a large number of hydrophobic contacts (≈200–230) and a dCOMs close to zero. In the intermediate state, where the eucalyptol releases from the CD cavity, a small number of hydrophobic contacts along with an energy barrier at dCOMs ≈ 6 Å is observed for all inclusion complexes. It is worth noting that the free-energy differences between the intermediate and the bound states relate to an estimation of the activation energies for the guest dissociation processes. Our results suggest that the activation energies of the eucalyptol dissociation mechanism were in the order of 6-HPβCD > 2,6-DMβCD ≈ 2,6-DHPβCD > βCD ≈ 2-HPβCD. This finding is associated with the eucalyptol dissociation rate. In Fig. 8, the corresponding snapshots of the most populated cluster, the bound state (left), and the representative structures of the intermediate state, which refers to the eucalyptol releasing pathway (right), for each of the systems are illustrated. It is clearly seen that the dissociation mechanism of the inclusion complexes of eucalyptol with βCD, 2,6-DMβCD, 2-HPβCD and 2,6-DHPβCD occurred via the wider rim of each CD host molecule. Surprisingly, in the case of 6-HPβCD inclusion, the eucalyptol migrates from the central cavity through the narrow rim of the CD to the aqueous phase and this reaction is connected with a relatively high free energy barrier of ≈9 kcal mol−1 (Fig. 6). This situation is possibly due to the enlargement of the 6-HPβCD's narrow rim resulting from the substitution by a 2-hydroxypropyl group at the O6 position, leading to a greater possibility for releasing eucalyptol. In summary, the results of the metadynamics simulations presented here have successfully investigated the releasing direction and dissociation rate of the eucalyptol/βCDs inclusion complexes.
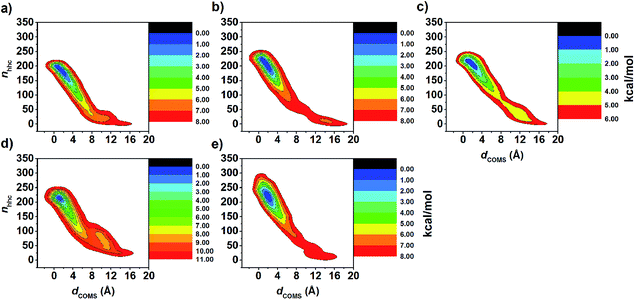 | ||
| Fig. 7 FES map of eucalyptol dissociation from cavity of (a) βCD, (b) 2,6-DMβCD, (c) 2-HPβCD, (d) 6-HPβCD and (e) 2,6-DHPβCD using CV1 and CV2 collective variables as defined in simulation details. | ||
4 Conclusions
In the present study, the stability of eucalyptol complexed with five different types of βCDs was investigated theoretically using MD simulations and four different binding free energy calculations. Based on MD simulations, the eucalyptol molecule was mostly found to stay near the center of the hydrophobic cavity of βCD and its derivatives except in the case of the eucalyptol/2-HPβCD complex in which the eucalyptol molecule preferably binds to the secondary rim of 2-HPβCD. In addition, the free energy landscape analysis reveals that all inclusion complexes are mainly found in the M1 conformation. The eucalyptol/βCDs host–guest inclusion complexes were mainly stabilized through van der Waals interactions. The binding free energy calculations based on MM/PBSA describes the experimental stabilities of the host–guest inclusion complexes somewhat better (stability ranking: 2,6-DMβCD > βCD > 2-HPβCD) than that of MM/GBSA. The energy correction with the QM theory significantly improved the absolute values of the free energy of binding. Among the four different methods applied here for the energy calculation, the QM/PBSA method seems to be the most appropriate approach to estimate the binding free energy between eucalyptol and the CDs. Furthermore, metadynamics simulations have successfully provided a model for the eucalyptol dissociation reaction. The results reveal that the eucalyptol moves out from the central cavity through the wider edge more easily in all studied CDs except in the case of 6-HPβCD where the guest molecule releases from the CD cavity via the narrower rim. The results show that classical MD simulation together with metadynamics is helpful for the investigation of host–guest systems, to understand the inclusion mechanism and the releasing rate, which is also important for the selection of proper CD derivatives to form inclusion complexes with special properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been supported by the Ratchadaphiseksomphot Endowment Fund 2013 of Chulalongkorn University (CU-56-912-AM). The authors would like to thank the Structural and Computational Biology Research Group, Special Task Force for Activating Research (STAR), Faculty of Science, Chulalongkorn University. B. N. thanks the Royal Golden Jubilee Ph.D. Program (PHD/0020/2558). N. N. would like to acknowledge the financial support from Mahasarakham University (fiscal year 2017) and the Center of Excellence for Innovation in Chemistry (PERCH-CIC). P. W. is thankful for a short-term visit grant from Chulalongkorn University. N. K. thanks Research Center on Chemistry for Development of Health Promoting Products from Northern Resources, Chiang Mai University for financial support. The Computer Chemistry Unit Cell (CCUC), and the Vienna Scientific Cluster (VSC-2) are acknowledged for facilities and computing resources. Dr Jolyon Dodgson was acknowledged for proofreading of this article.References
- H. Surburg and J. Panten, Wiley-VCH Verlag GmbH & Co. KGaA, in Common Fragrance and Flavor Materials, 2006, pp. 177–238 Search PubMed.
- S. Burt, Int. J. Food Microbiol., 2004, 94, 223–253 CrossRef CAS PubMed.
- S. G. Deans and G. Ritchie, Int. J. Food Microbiol., 1987, 5, 165–180 CrossRef.
- F. C. d. Silva, S. M. Chalfoun, V. M. d. Siqueira, D. M. d. S. Botelho, N. Lima and L. R. Batista, Rev. Bras. Farmacogn., 2012, 22, 1002–1010 CrossRef.
- A. Astani, J. Reichling and P. Schnitzler, Evid. base. Compl. Alternative Med., 2011, 2011, 8 Search PubMed.
- Y. Bhalla, V. K. Gupta and V. Jaitak, J. Sci. Food Agric., 2013, 93, 3643–3653 CrossRef CAS PubMed.
- M. G. Miguel, Molecules, 2010, 15, 9252–9287 CrossRef PubMed.
- R. Marmulla and J. Harder, Front. Microbiol., 2014, 5, 1–14 Search PubMed.
- K. A. Kovar, B. Gropper, D. Friess and H. P. T. Ammon, Planta Med., 1987, 53, 315–318 CrossRef CAS PubMed.
- M. A. Neto, J. W. de Alencar, A. N. Cunha, E. R. Silveira and T. G. Batista, J. Essent. Oil Res., 1994, 6, 299–300 CrossRef.
- H. Worth, C. Schacher and U. Dethlefsen, Respir. Res., 2009, 10, 1–7 CrossRef PubMed.
- U. R. Juergens, U. Dethlefsen, G. Steinkamp, A. Gillissen, R. Repges and H. Vetter, Respir. Med., 2003, 97, 250–256 CrossRef CAS PubMed.
- U. R. Juergens, M. Stober, L. Schmidt-Schilling, T. Kleuver and H. Vetter, Eur. J. Med.Res., 1998, 3, 407–412 CAS.
- U. R. Juergens, T. Engelen, K. Racké, M. Stöber, A. Gillissen and H. Vetter, Pulm. Pharmacol. Ther., 2004, 17, 281–287 CrossRef CAS PubMed.
- F. A. Santos and V. S. N. Rao, Phytother. Res., 2000, 14, 240–244 CrossRef CAS PubMed.
- F. A. Santos and V. S. N. Rao, Dig. Dis. Sci., 2001, 46, 331–337 CrossRef CAS PubMed.
- F. A. Santos, R. M. Silva, A. R. Tomé, V. S. N. Rao, M. M. L. Pompeu, M. J. Teixeira, L. A. R. De Freitas and V. L. De Souza, J. Pharm. Pharmacol., 2001, 53, 505–511 CrossRef CAS PubMed.
- S. Mulyaningsih, F. Sporer, J. Reichling and M. Wink, Pharmaceut. Biol., 2011, 49, 893–899 CrossRef CAS PubMed.
- J. Szejtli, Chem. Rev., 1998, 98, 1743–1754 CrossRef CAS PubMed.
- M. E. Brewster and T. Loftsson, Adv. Drug Delivery Rev., 2007, 59, 645–666 CrossRef CAS PubMed.
- T. Loftsson and M. E. Brewster, J. Pharm. Sci., 1996, 85, 1017–1025 CrossRef CAS PubMed.
- H. M. C. Marques, Flavour Fragrance J., 2010, 25, 313–326 CrossRef.
- F. W. H. M. Merkus, J. C. Verhoef, E. Marttin, S. G. Romeijn, P. H. M. van der Kuy, W. A. J. J. Hermens and N. G. M. Schipper, Adv. Drug Delivery Rev., 1999, 36, 41–57 CrossRef CAS PubMed.
- J. Szejtli, Springer, Netherlands, Cyclodextrins in Pesticides, 1988, vol. 1, pp. 335–364 Search PubMed.
- S. Li and W. C. Purdy, Chem. Rev., 1992, 92, 1457–1470 CrossRef CAS.
- L. Szente and J. Szemán, Anal. Chem., 2013, 85, 8024–8030 CrossRef CAS PubMed.
- E. M. M. Del Valle, Process Biochem., 2004, 39, 1033–1046 CrossRef CAS.
- L. Szente and J. Szejtli, Adv. Drug Delivery Rev., 1999, 36, 17–28 CrossRef CAS PubMed.
- T. Loftsson and M. Masson, Int. J. Pharm., 2001, 225, 15–30 CrossRef CAS PubMed.
- J. C. d. Miranda, T. E. A. Martins, F. Veiga and H. G. Ferraz, Braz. J. Pharm. Sci., 2011, 47, 665–681 CrossRef.
- R. Challa, A. Ahuja, J. Ali and R. K. Khar, AAPS PharmSciTech, 2005, 6, E329–E357 CrossRef PubMed.
- R. L. Carrier, L. A. Miller and I. Ahmed, J. Controlled Release, 2007, 123, 78–99 CrossRef CAS PubMed.
- Y. Ikeda, S. Motoune, T. Matsuoka, H. Arima, F. Hirayama and K. Uekama, J. Pharm. Sci., 2002, 91, 2390–2398 CrossRef CAS PubMed.
- K. Boonyarattanakalin, P. Wolschann, P. Toochinda and L. Lawtrakul, Eur. J. Pharm. Sci., 2012, 47, 752–758 CrossRef CAS PubMed.
- B. Nutho, W. Khuntawee, C. Rungnim, P. Pongsawasdi, P. Wolschann, A. Karpfen, N. Kungwan and T. Rungrotmongkol, Beilstein J. Org. Chem., 2014, 10, 2789–2799 CrossRef PubMed.
- Z. Ying, H. L. C. Albert and S. H. Ian, Lett. Drug Des. Discovery, 2008, 5, 512–520 CrossRef.
- W. Sangpheak, W. Khuntawee, P. Wolschann, P. Pongsawasdi and T. Rungrotmongkol, J. Mol. Graphics Modell., 2014, 50, 10–15 CrossRef CAS PubMed.
- J. Kicuntod, W. Khuntawee, P. Wolschann, P. Pongsawasdi, W. Chavasiri, N. Kungwan and T. Rungrotmongkol, J. Mol. Graphics Modell., 2016, 63, 91–98 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- A. V. Vargiu, P. Ruggerone, A. Magistrato and P. Carloni, Nucleic Acids Res., 2008, 36, 5910–5921 CrossRef CAS PubMed.
- M. Wilhelm, A. Mukherjee, B. Bouvier, K. Zakrzewska, J. T. Hynes and R. Lavery, J. Am. Chem. Soc., 2012, 134, 8588–8596 CrossRef CAS PubMed.
- D. Luo and Y. Mu, J. Phys. Chem. B, 2015, 119, 4955–4967 CrossRef CAS PubMed.
- A. K. Pathak and T. Bandyopadhyay, Proteins: Struct., Funct., Bioinf., 2014, 82, 1799–1818 CrossRef CAS PubMed.
- L. Milanos, N. Saleh, R. C. Kling, J. Kaindl, N. Tschammer and T. Clark, Angew. Chem., Int. Ed., 2016, 55, 15277–15281 CrossRef CAS PubMed.
- A. Coletta and A. Desideri, Nucleic Acids Res., 2013, 41, 9977–9986 CrossRef CAS PubMed.
- A. Ciobanu, D. Landy and S. Fourmentin, Food Res. Int., 2013, 53, 110–114 CrossRef CAS.
- M. Kfoury, L. Auezova, S. Fourmentin and H. Greige-Gerges, J. Inclusion Phenom. Macrocyclic Chem., 2014, 80, 51–60 CrossRef CAS.
- L. Lawtrakul, K. Inthajak and P. Toochinda, ScienceAsia, 2014, 40, 145–151 CAS.
- C. W. Yong, C. Washington and W. Smith, Pharm. Res., 2007, 25, 1092–1099 CrossRef PubMed.
- J. Pitha, C. Trinadha Rao, B. Lindberg and P. Seffers, Carbohydr. Res., 1990, 200, 429–435 CrossRef CAS PubMed.
- W. Snor, E. Liedl, P. Weiss-Greiler, A. Karpfen, H. Viernstein and P. Wolschann, Chem. Phys. Lett., 2007, 441, 159–162 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, J. Comput. Chem., 2009, 30, 2785–2791 CrossRef CAS PubMed.
- J. Gasteiger and M. Marsili, Tetrahedron, 1980, 36, 3219–3228 CrossRef CAS.
- C. Rungnim, S. Phunpee, M. Kunaseth, S. Namuangruk, K. Rungsardthong, T. Rungrotmongkol and U. Ruktanonchai, Beilstein J. Org. Chem., 2015, 11, 2306–2317 CrossRef CAS PubMed.
- N. Nunthaboot, T. Rungrotmongkol, M. Malaisree, N. Kaiyawet, P. Decha, P. Sompornpisut, Y. Poovorawan and S. Hannongbua, J. Chem. Inf. Model., 2010, 50, 1410–1417 CrossRef CAS PubMed.
- P. Decha, T. Rungrotmongkol, P. Intharathep, M. Malaisree, O. Aruksakunwong, C. Laohpongspaisan, V. Parasuk, P. Sompornpisut, S. Pianwanit, S. Kokpol and S. Hannongbua, Biophys. J., 2008, 95, 128–134 CrossRef CAS PubMed.
- T. Rungrotmongkol, A. J. Mulholland and S. Hannongbua, J. Mol. Graphics Modell., 2007, 26, 1–13 CrossRef CAS PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Goetz, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M. J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, AMBER 14, San Francisco: University of California, 2014 Search PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- A. Meeprasert, W. Khuntawee, K. Kamlungsua, N. Nunthaboot, T. Rungrotmongkol and S. Hannongbua, J. Mol. Graphics Modell., 2012, 38, 148–154 CrossRef CAS PubMed.
- P. Sornmee, T. Rungrotmongkol, O. Saengsawang, U. Arsawang, T. Remsungnen and S. Hannongbua, J. Comput. Theor. Nanosci., 2011, 8, 1385–1391 CrossRef CAS.
- A. Meeprasert, S. Hannongbua and T. Rungrotmongkol, J. Chem. Inf. Model., 2014, 54, 1208–1217 CrossRef CAS PubMed.
- N. Kaiyawet, T. Rungrotmongkol and S. Hannongbua, J. Chem. Inf. Model., 2013, 53, 1315–1323 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- B. A. Luty and W. F. van Gunsteren, J. Phys. Chem., 1996, 100, 2581–2587 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- B. R. Miller, T. D. McGee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- A. Laio, A. Rodriguez-Fortea, F. L. Gervasio, M. Ceccarelli and M. Parrinello, J. Phys. Chem. B, 2005, 109, 6714–6721 CrossRef CAS PubMed.
- S. Della-Longa and A. Arcovito, J. Comput.-Aided Mol. Des., 2015, 29, 23–35 CrossRef CAS PubMed.
- J. MacQueen, in Proceedings of the Fifth Berkeley Symposium on Math, Statistics, and Probability, 1967, vol. 1, pp. 281–297 Search PubMed.
- M. T. Woodside and S. M. Block, Annu. Rev. Biophys., 2014, 43, 19–39 CrossRef CAS PubMed.
- F. Pietrucci, Rev. Phys., 2017, 2, 32–45 CrossRef.
- A. M. Westerlund, T. J. Harpole, C. Blau and L. Delemotte, arXiv preprint arXiv:1704.00343, 2017.
- W. Khuntawee, T. Rungrotmongkol, P. Wolschann, P. Pongsawasdi, N. Kungwan, H. Okumura and S. Hannongbua, Carbohydr. Polym., 2016, 141, 99–105 CrossRef CAS PubMed.
- W. Khuntawee, M. Karttunen and J. Wong-ekkabut, Phys. Chem. Chem. Phys., 2017, 19, 24219–24229 RSC.
- G. Rastelli, A. D. Rio, G. Degliesposti and M. Sgobba, J. Comput. Chem., 2010, 31, 797–810 CAS.
- B. Xu, H. Shen, X. Zhu and G. Li, J. Comput. Chem., 2011, 32, 3188–3193 CrossRef CAS PubMed.
- C. Schonbeck, P. Westh, J. C. Madsen, K. L. Larsen, L. W. Stade and R. Holm, Langmuir, 2010, 26, 17949–17957 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09387j |
| This journal is © The Royal Society of Chemistry 2017 |