Open Access Article
Open Access ArticleA robust method to calculate the volume phase transition temperature (VPTT) for hydrogels and hybrids†
Sulalit Bandyopadhyay *a,
Anuvansh Sharma
*a,
Anuvansh Sharma a,
Muhammad Awais Ashfaq Alvia,
Rajesh Rajub and
Wilhelm Robert Glommac
a,
Muhammad Awais Ashfaq Alvia,
Rajesh Rajub and
Wilhelm Robert Glommac
aUgelstad Laboratory, Department of Chemical Engineering, Norwegian University of Science and Technology (NTNU), N-7491 Trondheim, Norway. E-mail: sulalit.bandyopadhyay@ntnu.no; ratnavo@gmail.com; Tel: +47-73550339
bDepartment of Chemistry, Norwegian University of Science and Technology (NTNU), N-7491 Trondheim, Norway
cDepartment of Biotechnology and Nanomedicine, SINTEF Materials and Chemistry, N-7465 Trondheim, Norway
First published on 17th November 2017
Abstract
Here, we report three different methods to determine the volume phase transition temperature (VPTT) of various systems including poly(N-isopropylacrylamide) (pNIPAm) based nanogels, Au nanoclusters and a combination of inorganic and polymeric systems. Although all the methods reveal close VPTT values, we suggest that method III is the least computation dependent and most reliable. In an attempt to define the overall system reversibility, a predictive reversibility parameter (RP) was defined that explains the system behavior at each state point. RP takes into consideration all the system states during both heating and cooling cycles. Reversible systems were found to have RP values less than 1, while irreversible systems were observed to have RP values of 2. We predict that real systems will show RP values between 1 and 2. Thus, by knowing both the system's VPTT and its reversibility, a particular application can be designed or upgraded.
1. Introduction
Systems undergoing phase change have a myriad of applications that range from drug delivery,1–6 membrane separation,7–10 flow control,11,12 and bio-sensing13–15 among others. In order to exploit the material properties of such systems, it is important to definitively characterize the phase transition that happens above the lower critical solution temperature (LCST) of the polymer.16 Below the LCST, the polymer is in a hydrated state, while above the LCST, it becomes hydrophobic due to disruption of hydrogen bonds by water, leading to changes in solubility as well as aggregation behaviour.17 In a similar way, the cross-linked systems obtained from this polymer swell in water at a critical temperature called the volume phase transition temperature (VPTT) and collapse above it.18 While the LCST or VPTT is defined as a single temperature from a thermodynamic standpoint, real systems undergo phase transition over a range of temperatures owing to inherent polydispersity stemming from different chain lengths, branching, crystallinity and so on.2A common method to estimate this transition temperature is to measure a spectroscopic parameter like optical density, turbidity, absorbance or size or specific heat as a function of temperature and assign the transition temperature at the average of the sigmoidal plot of the curve or at the mid-point of the range.19–23 There exists no study to our knowledge where VPTT of such phase changing systems have been exhaustively calculated using a well-defined method with experimental data from both heating and cooling cycles. Our group were among the first to incorporate data from both heating and cooling experiments to understand the behaviours of nanoparticle (NP) based systems coupled with phase changing polymers.24,25 Understanding the phase behavior during both the cycles is the first step towards understanding system reversibility.
Thermodynamic reversibility for systems undergoing phase change has been studied taking into consideration only the initial and final state points. However, the effect of temperature or any other independent parameter on the constituting polymer chains will cause the system to go through several state points along the path, which may not be equal during heating and cooling cycles or during repeated cycles. It is therefore deemed important to consider the journey of the system through these various state points while defining system responsiveness rather than bias the system at the end state points. In addition, the understanding of phase behaviours of pNIPAm based systems is of fundamental interest, since osmotic pressure or gel swelling behaviour are closely related to correct determination of VPTT. It also throws light on unresolved issues in regards to demixing transitions of such systems.
Herein, we report for the first time a comprehensive methodology to determine the VPTT of phase changing systems that include both heating and cooling cycle datasets. Three methods to estimate VPTT have been discussed highlighting their inherent strengths and weaknesses, culminating in a simple and reliable method (method III) to effectively characterize such a system. Thereafter, in order to describe system reversibility, a new parameter called reversibility parameter (RP) has been discovered. It is not only capable of accurately defining system reversibility based on all state points, but also predicting future state points of the system. Within the scope of this work, we have been able to ascribe values of RP less than 1 as reversible systems, while RP values equaling 2 as irreversible systems. We predict that intermediate systems having RP values between 1 and 2 would resemble real systems based on such materials.
2. Materials and methods
The methods devised for determining VPTTs of phase changing systems were evaluated for a wide range of samples including poly(N-isopropylacrylamide) (pNIPAm) based nanogels, Au nanoclusters and combination of inorganic and polymeric systems. The synthesis of these are highlighted in this section.Materials
N-Isopropylacrylamide (NIPAm), poly(ethylene glycol) dimethacrylate (PEGDMA) (average Mn-400, 550, 750, 1000), poly(ethylene glycol) methacrylate (PEGMA) (average Mn-360), acrylic acid (AAc), N,N′-methylenebis(acrylamide) (BIS), ammonium persulfate (APS) and sodium dodecyl sulfate (SDS), acrylic acid (AAc) (d = 1.051 g mL−1), potassium persulphate (KPS), iron pentacarbonyl (Fe(CO)5, 99.99%), octadecene (ODE, 90%), oleylamine (OAm, 70%), choloauric acid (99.999%), sodium citrate, O-[2-(3-mercaptopropionylamino)ethyl]-O′-methylpolyethylene glycol (PEG-SH) of molecular weight 5000 Da, and human serum immunoglobulin G were purchased from Sigma-Aldrich. Poly(ethylene glycol) dimethacrylate (PEGDMA) (average Mn-200) was purchased from Polysciences. N-Hexane and hydrochloric acid (HCl, 37% fuming) were purchased from Merck Millipore®. Sodium hydroxide (pellet AnalaR NORMAPUR® ACS) was purchased from VWR. Gold nanoparticles (Au NPs, 30 and 80 nm) were purchased from British BioCell/Ted Pella INc. Uranyl acetate (SPI chemicals) was used as the staining agent. All solutions were prepared using distilled de-ionized water (resistivity ∼18.2 μΩ cm) purified by Simplicity® Millipore water purification system. They were further purified using 0.2 μm syringe filters. Cellulose dialysis tubing (Sigma-Aldrich) with an MWCO of 14 kDa was used both for performing dialysis and purification of the nanogels.Synthesis of polymeric core–shell nanogels
Core–shell pNIPAm based nanogels were synthesized as outlined in our previous work.26 The synthesis proceeds via free radical polymerization in which different cores of p[NIPAm-co-PEGMA (Mn-360)] were synthesized using PEGDMA as a crosslinker with different molecular weights of 200, 400, 750 and 1000 Da. NIPAm, PEGDMA and PEGMA(Mn-360) were dissolved in 25 mL deoxygenated water with different mole percentages. The resulting colourless solution was purged with nitrogen for two hours followed by the addition of APS (0.005 g, 1 mM) to the reaction mixture to initiate the polymerization. The reaction was carried out at 82–84 °C for 60 min under nitrogen atmosphere. 10 mL of p[NIPAm-co-PEGMA] core nanogels were redispersed in 40 mL deoxygenated water containing NIPAM, BIS and AAc with 71%, 15% and 14% mole percent respectively, along with 5 mM SDS. The resulting turbid reaction mixture was heated to 74–76 °C under a gentle stream of nitrogen. To this heated mixture, solid APS (0.01 g, 1 mM) was added to initiate the polymerization and this reaction was then allowed to proceed for 60 min. The mixture was then cooled and transferred into a pre-washed dialysis tube, dialysing the core–shell solution for 12 hours. These core–shell nanogel samples have been named pNIPAm/PEGn-pNIPAm/AAc, with n varying as 200, 400, 750 and 1000, depending on the average molecular weight of the crosslinker used in their synthesis.Synthesis of polymeric–inorganic nanogels
Prior to synthesizing polymeric–inorganic nanogels, pNIPAm/AAc nanogel was synthesized as per our previously reported work.27 pNIPAm, AAc and BIS, with mole ratios 85%, 10% and 5% respectively, have been used. 1.6 mM of NIPAm and 90.8 μM of BIS were put directly into the reactor under nitrogen atmosphere. Thereafter, 10 mL of 4.2 mM SDS solution was added, and the solution left to stir under nitrogen flow for 30 min. Prior to addition of the initiator KPS (400 μL of 103.6 mM), AAc (126 μL of 1.46 M) was added into the solution. The reaction was allowed to run for 3 h. The nanogel solution was poured into a prewashed dialysis tube (MWCO 14 kDa) and dialysed overnight to remove unreacted monomers and residual reactants. The synthesized nanogel, without the incorporation of inorganic NPs, was used as a control. This particular sample is mentioned as pNIPAm/AAc nanogels in this work.To incorporate inorganic NPs into the nanogel system, Fe NPs were synthesized followed by a shell of Au atop the Fe NPs. Thereafter, these Fe@Au NPs were coated with PEG-SH followed by pNIPAm/AAc nanogel following the work already performed by our group.27 Synthesis of PEGylated Fe@Au NPs was carried out following our previous work. (Cite reference of our Fe@Au paper) In a typical Fe NP synthesis protocol, 50 mL ODE and 740 μL OAm was degassed under Ar atmosphere and vigorous stirring at 120 °C for 30 min. The temperature was raised to 180 °C, following which 1.8 mL of Fe(CO)5 was injected, and the reaction was allowed to continue for 20 min. After cooling down to room temperature, the magnetic bar coated with Fe NPs was washed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (by volume) of hexane and acetone. Fe NPs were magnetically separated and washed with acetone before drying under nitrogen.
2 ratio (by volume) of hexane and acetone. Fe NPs were magnetically separated and washed with acetone before drying under nitrogen.
For growing Au shell atop the Fe NPs, 5 mg of dried Fe NPs were dissolved in 10 mL of 10 mM sodium citrate solution by using sonication at 80 °C for half an hour. 10 mL of 1.5 mM chloroauric acid was added dropwise to the Fe seed NPs under vigorous stirring and the reaction was allowed to run for 20 min. Thereafter, the solution was cooled down to room temperature, and Fe@Au NPs were magnetically separated to remove free Au NPs. This was followed by PEG-SH coating in which 2 mg of PEG-SH was mixed with 5 mg of Fe@Au NPs in a total volume of 5 mL MQ water and left to stir for 1 h. PEG coated Fe@Au NPs were collected by centrifugation at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 rpm for 20 min.
500 rpm for 20 min.
The nanogel coating was done as follows. 3.3 mg of the pNIPAm/AAc nanogel was added to 5 mL solution of Fe@Au NPs (concentration of 1 mg mL−1) and left to stir at 500 rpm for 2 h. Thereafter, the NG-coated Fe@Au NPs were separated by using centrifugation at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 rpm for 20 min. This sample has been referred to as Fe@Au_PEG_nanogel in the present work.
500 rpm for 20 min. This sample has been referred to as Fe@Au_PEG_nanogel in the present work.
Synthesis of gold nanoclusters
A typical procedure for adsorbing IgG onto Au NPs involved mixing of 2.7 mL of the gold colloid suspension with 0.3 mL of an IgG solution (10 μM in citrate (10 mM)). All samples were measured within 24–48 h after mixing as reported in previous studies conducted by our group.28 These samples have been referred to as 30 nm Au IgG nanoclusters and 80 nm Au IgG nanoclusters respectively in the present work.Measurement of spectroscopic parameter
The size distribution and zeta potential of the nanogels were measured using a Malvern Zetasizer Nano-ZS instrument and the manufacturer's own software. The samples were allowed to equilibrate for 3 minutes before starting the measurements. Thereafter, the hydrodynamic sizes of the particles were measured at different temperatures in intervals of 5 °C. The instrument standardized heating and cooling rates were used for all the samples. All measurements were done in aqueous solutions, and results were averaged over triplicate measurements.UV-Vis measurements for Au nanoclusters have been directly taken from our previously reported studies conducted using Sgimadu UV-2401PC instrument, equipped with a TCC-240 temperature control unit.28 An equilibration time of 15 minutes was used for the samples with 5 °C temperature intervals.
Calculation of VPTT
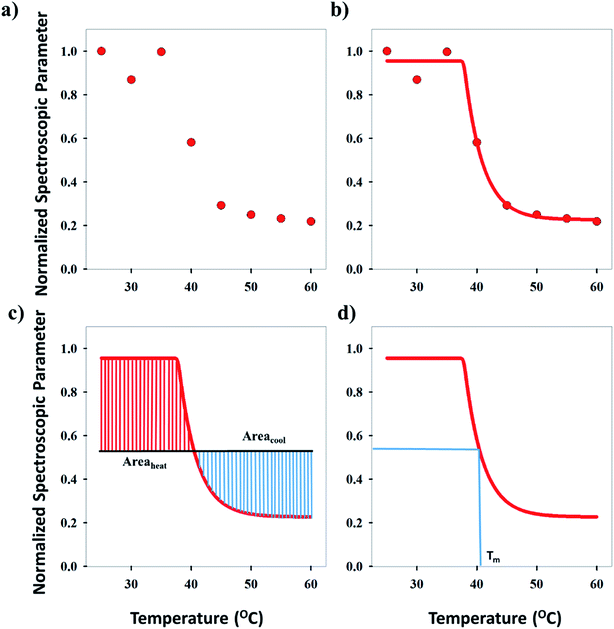
Three methods have been devised to obtain the VPTTs of phase changing systems under study which are named as methods I, II and III respectively. Fig. 1 highlights the underlying principle used in method I and II. As the temperature of the system is increased, the particles start collapsing. Particles with a lower VPTT collapse first, thus, at any particular position on the heating or cooling curves, the system exists in a partially collapsed or swelled state. To start with, the variation of the normalized spectroscopic parameter (size, αsize and α as defined in eqn (1) and (2)) with temperature was plotted (Fig. 1(a)). αsize represents the ratio of the hydrodynamic diameter of the sample measured at any temperature (D) to the hydrodynamic diameter if the sample measured at room temperature (DO). On the other hand α, represents the ratio of the hydrodynamic volumes at any temperature to that at room temperature. ‘Sigmoid, 5 Parameter’ curve was thereafter fitted using SigmaPlot® version 13.0 (Fig. 1(b)). The fit provides us with the values of the 5 constant parameters (a, b, c, d and e) as shown in eqn (3). A fixed value of iteration (n) is selected to define the number of desired intervals. A MATLAB® code generates a curve utilizing the interval temperature values as the abscissa coordinates and the above obtained 5 parameters. A mean of the lowest (To) and the highest (Tn) temperature values, under study, is calculated and it acts as the starting point for the code. This mean value (Tm) divides the curve into two areas (Fig. 1(c)). Area I extends from Tm till Tn, while Area II extends from To to Tm.
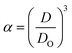 | (1) |
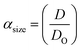 | (2) |
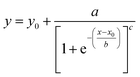 | (3) |
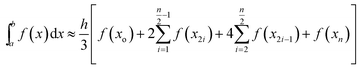 | (4) |
 | (5) |
The code calculates the areas of the two regions based on “Simpson's 1/3rd Rule” (eqn (4)) and later, equates the two obtained area values. Relative difference of the areas is calculated as shown by eqn (5). If the compared areas do not fall within the acceptable tolerance limits (defined by the user), the counter for the VPTT moves one interval towards the side of the higher area value and recalculates the areas of the newly formed regions. The final VPTT value is obtained when the relative difference of the areas falls within the tolerance limit (Fig. 1(d)).
Method I uses the above described approach. Swelling ratios, αhI and αcI are used for this method (eqn (6) and (7)). VPTT for the heating and the cooling cycles are calculated from the heating and cooling curves respectively. Same procedure is applied to both the heating as well as the cooling curves and we obtain two VPTTs for the heating (ThI) and the cooling (TcI) cycles respectively.
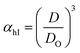 | (6) |
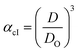 | (7) |
Method II is an extension of method I. The swelling ratio for heating cycle is defined as in method I (eqn (8)), but we use de-swelling ratio for the cooling cycle instead of the swelling ratio (eqn (9)). These swelling ratios are used in the curve fitting and parameter generation by SigmaPlot®. The intermediate values of heating (TihII) and cooling (TicII) VPTTs are calculated using the area equalization approach similar to method I. Using these two intermediate values, the corresponding α values are determined (αhII and αcII). A mean of these α values (αmII) is taken to generate the final VPTTs from the curve namely, ThII and TcII.
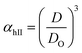 | (8) |
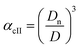 | (9) |
Method III provides a compact approach in the calculation of VPTTs. Dn is the hydrodynamic diameter of the sample at the final measurement temperature. The swelling ratios for the heating as well as the cooling cycles are defined as in method II and the curves are generated in a similar manner. Instead of calculating the intermediate values of the respective swelling ratios as in method II, an average value of the swelling and de-swelling ratios is determined from the raw data as shown by eqn (10) and (11). For the heating cycle, αho and αhn are defined as the swelling ratios using eqn (8) (similar to αhII in method II), at temperatures T0 and Tn respectively. Likewise for the cooling cycle, αcn and αco are defined as the swelling ratios at Tn and T0 respectively, using eqn (9). Heating and cooling VPTTs are then calculated using αmhIII and αmcIII, namely as ThIII and TcIII respectively. For ThIII, the temperature corresponding to αmhIII on the heating curve represents the VPTT for heating cycle, while the temperature corresponding to αmcIII on the cooling curve represents the VPTT for cooling cycle.
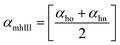 | (10) |
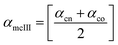 | (11) |
Calculation of mh, mc and mIII
Determination of the VPTTs might give a rough estimate of the reversibility of the systems but it is still not an absolute criterion for commenting on the reversibility of the systems. In order to define system reversibility, a general approach of hysteresis was followed. Relative hysteresis (eqn (12)) was calculated from the size vs. temperature plots for all the samples.| Areahys = |areaheat − areacool| | (12) |
In another possible approach to determine system's reversibility, a linear correlation is fitted to the size vs. temperature curves, for both the heating and the cooling cycles. The slopes of the respective fits are referred to as mh and mc respectively. These values are used for carrying out order of magnitude analysis and determination of the reversibility parameter. mIII is the slope of the fit calculated as shown by eqn (13). This parameter provides us with a qualitative approach in commenting about of the reversibility of the system under investigation. Here, VmhIII and VmcIII are the volumes calculated from hydrodynamic sizes at their corresponding α values.
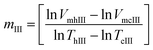 | (13) |
3. Results and discussion
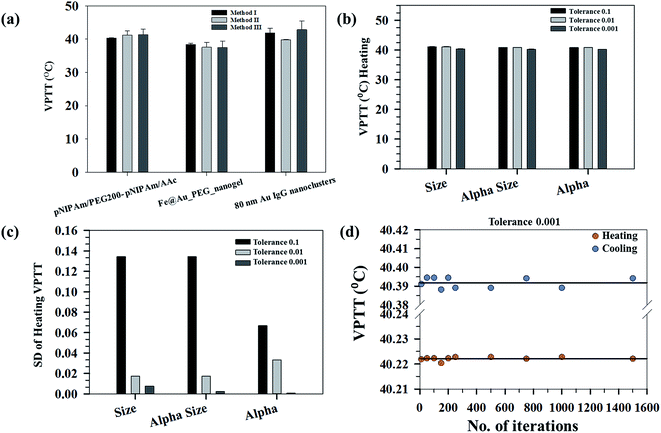
Determination of phase transition temperatures of systems undergoing swelling–collapse in response to stimuli like temperature, pH, ionic strength and so on has been mostly studied considering the end state points. However, for proper understanding of the system behavior, it is important to map the changes continuously and not bias it at specific state points. In the present study, we have developed a methodology to calculate the VPTT of phase changing systems based on the state points through which the system passes during both heating and cooling cycles. The methodology has been used to calculate the same for a wide range of samples namely; pNIPAm based nanogels, Au nanoclusters and combination of inorganic and polymeric systems. The samples studied show stimuli responsive physico-chemical properties and undergo a swelling–collapse behaviour as a function of temperature. The thermoresponsive behaviour of these systems was mapped using DLS (for pNIPAm based inorganic and polymeric systems) and UV-Vis (for Au nanoclusters), thereby covering different characterization techniques to determine the VPTTs. The VPTT values calculated for the pNIPAM based nanogels are in accordance with the experimental values of ∼39 °C as reported in our previous work.29Fig. 2(a) shows the average VPTTs for three representative samples calculated using 3 different methods. The average VPTT in this case was obtained by taking a mean of the heating and cooling VPTTs at defined tolerance value for different number of iterations. It is evident that the three methods give results in quite proximity, however, a greater variation in the three VPTTs can be seen for 80 nm Au IgG nanoclusters (irreversible systems). The standard deviation of the VPTTs also increases as we go from highly reversible samples to irreversible samples.
Fig. 2(b) shows the average heating VPTTs for a representative sample calculated at three different tolerance values for the raw data (size) and normalized properties (αsize and α) using the first method. The average VPTT in this case is obtained by taking a mean of the VPTTs at defined tolerance value for different number of iterations. It is evident that the three properties can be interchangeably used to estimate the VPTT since the values do not differ from one another. However, as explained above, α (ratio of the volumes at swollen state to ground state), bears a physical significance to the process at hand, since it represents the volumetric collapse of the system, while the other properties refer to changes in hydrodynamic diameters alone. In order to judiciously choose the best property to estimate the VPTT of such systems, the standard deviations of the VPTTs obtained using the same process are plotted in Fig. 2(c). As can be observed, the VPTTs deviate the least from the respective representative mean values (at different tolerances) when α is used as the processing property. Thus, the data discussed within the scope of this work have been interpreted using α as the independent property, obtained directly by incorporating experimental results.
The method of estimating the VPTT using the MATLAB® code employs the use of two parameters, namely the tolerance and number of iterations. Fig. 2(b) shows that a tolerance value of 0.001 gives the minimum variations of the mean VPTTs when calculated using different iteration numbers, hence, for the purpose of estimating the VPTTs, a tolerance value of 0.001 has been set for all the methods I, II and III. Although, it is customary to calculate the values at this set tolerance of 0.001 for a sample set of iteration numbers. Fig. 2(d) shows that the VPTT obtained using an iteration number of 1000 has the minimum deviation from the average VPTT obtained over the sample space. The same trend is observed both for the heating as well as the cooling cycles. Henceforth, a tolerance of 0.001 was set for all calculations and the reported VPTTs are for an iteration number 1000, unless otherwise stated.
Traditionally, VPTT for systems undergoing a phase change, have been calculated by using the average of the sigmoidal region of the size-temperature plot or defined intuitively at the inflexion point of the same plot.30–32 However, in such systems, the collapse happens over a temperature range rather than at a defined temperature since individual domains have separate VPTTs.33,34 Further, studies of such systems report one VPTT value for the whole system which is usually derived from the heating cycle data. Previous experimental results from our group have shown that there are significant differences in the properties obtained by considering heating and cooling cycles separately.24,25 This indicates that VPTT obtained using heating cycle will be different than that obtained using the cooling cycle, owing to different collapse rates of the constituting chains. In addition, system reversibility is an important property that needs detailed understanding in order to sustain physico-chemical properties over repeated cycles of heating and cooling.
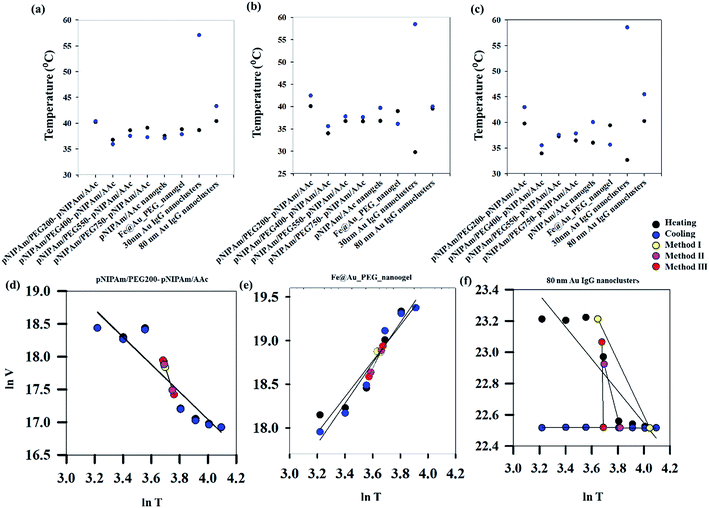
With an aim of developing a robust methodology for estimating VPTT of phase changing systems, three different approaches have been used in the present work. The first two methods (method I and II) are based on equalizing the areas of swelled and collapsed states while the third method (method III) estimates the VPTT values using mean heating and cooling swelling ratios (αmhIII, αmcIII) over the whole data range. The area equalization is based on the assumption that, at any temperature, the system exists in a two-state equilibrium comprising fractions of swelled and collapsed units.20 Fig. 3(a)–(c) show the heating and cooling VPTTs obtained by using methods I, II and III respectively for different phase transition systems. Although different approaches have been used to estimate the VPTTs using the three methods, it is worthy of mention that the VPTT values do not differ appreciably among methods. This in turn supports our hypothesis that mathematical modelling of a physical system should not alter the physical characteristics of the system at hand. In addition to incorporation of both heating and cooling cycles, the VPTT obtained from each method is a representative value as all the experimental data points have been adequately considered.
The VPTT values obtained for the different systems are discussed here to highlight the effect of composition on their physico-chemical properties. Poly(N-isopropylacrylamide) (pNIPAm) shows temperature responsiveness due to a transition from a hydrophilic state to a hydrophobic state above LCST. pNIPAm based nanogels exhibit similar transitions at and above the VPTT. Incorporation of different blocks like acrylic acid (AAc), polyethylene glycol (PEG), poly(ethylene oxide) (PEO) into the polymeric architecture affect the VPTT as a result of a change in the rigidity of the polymer structure.34–36 An increase in the VPTT is concomitant with an increase in the hydrophilic balance of the particles, whereby reducing the tendency of the hydrophobic collapse of pNIPAm.37 The VPTT is also affected by the molecular weight of the incorporated PEG – a higher molecular weight and hence higher hydrophilicity should cause an increase in the VPTT values. However, with a higher molecular weight, the steric effect imparted by the PEG blocks comes into play in the swelling–collapse behavior in addition to the size of the cavities inside the nanogels. When heated, the presence of excess water molecules in the larger voids will favour much faster collapse than the smaller voids due to the increase in shear strain caused due to pressure. Thus, although a definitive trend cannot be predicted owing to the aforementioned reasons in addition to different solubilities of the PEGDMA monomers in water phase, an obvious change in the VPTT values is however observed. (Samples pNIPAm/PEGMW-pNIPAm/AAc where MW = 200, 400, 550, 750).
On the other hand, incorporation of Fe@Au PEG NPs in pNIPAm/AAc nanogels alter the VPTT-while the heating VPTT increases upon addition of the Fe@Au PEG NPs, the cooling VPTT decreases. (Samples pNIPAm/AAc nanogel, Fe@PEG_nanogel). This happens due to the presence of the Fe@Au NPs that act as cross-linkers between the gelling units, pulling them together, leading to an increase of the size as a function of temperature, an effect opposite to that for the bare nanogels, previously observed in our work.29
The third category of samples studied here involves AuNP–immunoglobulin nanoconstructs (80 nm Au IgG nanoclusters and 30 nm Au IgG nanoclusters) that show a temperature dependent irreversible adsorption, owing to loss of protein structures at high temperatures.25 Including these two samples, further show that the methods developed herein are robust and are capable of processing both reversible and irreversible systems, independent of their swelling–collapse behaviours.
While method I employs the use of one parameter, αh, the other two methods also use the cooling swelling ratio (αc) with an intuitive search for a cross-over point defining an overall system behavior. For comparison among the three methods used in the work, a discussion is outlined here in order to assess their features. The first two methods of evaluation consider area calculations using Simpson's 1/3rd Rule, the accuracy of which is dependent on the step size and in turn the number of iterations. During the evaluation, iteration value was kept at 1000 for all the systems. This might introduce minor errors due to approximation. However, method III employs two parameters (αh and αc), but does not include the area equalization modules, meaning that, it is not as sensitive to minor variations in the curve shapes unlike the former two. Further, as explained above, the three methods provide VPTT values for both reversible and irreversible systems within the same range. Therefore, we suggest that method III is the least computationally exhaustive method with good estimations of both heating and cooling VPTTs. However, since VPTT is an undefined parameter for systems that do not undergo phase change or for systems undergoing irreversible changes, we see discrepancies in the estimated values calculated using all the three methods for the cooling VPTTs for Au-IgG samples (Fig. S1 ESI†).
Although, these methods are competent to estimate both heating and cooling VPTTs for various systems, the absolute values obtained do not give an estimate of the reversibility of these systems.
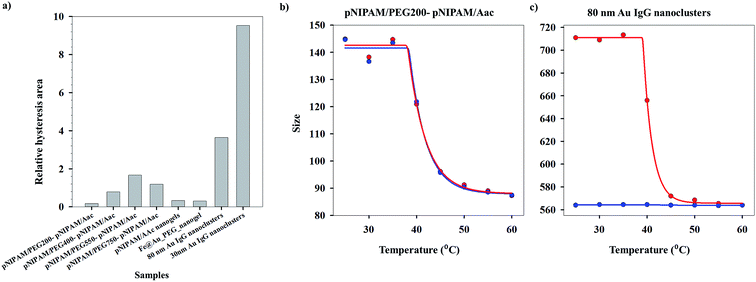
As can be seen from Fig. S1 (ESI†), the heating (40.2 °C) and cooling (40.4 °C) VPTTs obtained for pNIPAm/PEG200-pNIPAm/AAc using method I are almost equal, while this is the same scenario for 80 nm Au IgG nanoclusters (40.4 °C and 43.3 °C, heating and cooling VPTTs respectively), indicating that both the systems are equally reversible, if the criterion for reversibility is assumed to be equal heating and cooling VPTTs. However, experimental data show otherwise (Fig. 4(a)–(c)). On comparing the heating and cooling VPTT curves for pNIPAm/PEG200-pNIPAm/AAc (Fig. 4(b)) and 80 nm Au IgG nanoclusters (Fig. 4(c)), it can be observed that the latter is an irreversible sample.
This shows that the assumed criterion ‘of equal heating and cooling VPTT’ is not a suitable measure of system reversibility. Fig. 3(d)–(f) show the plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V versus ln
V versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T for three representative samples, where V represents the volume of the particles, calculated from the hydrodynamic diameter measured by DLS, and T is the temperature in K. These figures further plot the volumes obtained at the calculated VPTTs for the respective systems using all the three calculation methods. Regression lines fitted to these datasets show that an approximate measure of system reversibility is predicted by two factors – coincidence of the regression lines for heating and cooling and coincidence of the VPTTs obtained from all the methods. For pNIPAm/PEG200-pNIPAm/AAc, both the conditions are satisfied, while for Fe@Au PEG nanogels, the regression lines for heating and cooling VPTTs are not coincident and for 80 nm Au IgG nanoclusters, neither of the conditions are satisfied. Qualitatively, it is possible to ascertain irreversibility in the same order rendering pNIPAm/PEG200-pNIPAm/AAc to be the most reversible and 80 nm Au IgG nanoclusters to be the most irreversible among the selected samples. However, this is a qualitative approach to define the reversibility of phase changing systems. Similar analysis for the other samples are shown in Fig. S2 (ESI†).
T for three representative samples, where V represents the volume of the particles, calculated from the hydrodynamic diameter measured by DLS, and T is the temperature in K. These figures further plot the volumes obtained at the calculated VPTTs for the respective systems using all the three calculation methods. Regression lines fitted to these datasets show that an approximate measure of system reversibility is predicted by two factors – coincidence of the regression lines for heating and cooling and coincidence of the VPTTs obtained from all the methods. For pNIPAm/PEG200-pNIPAm/AAc, both the conditions are satisfied, while for Fe@Au PEG nanogels, the regression lines for heating and cooling VPTTs are not coincident and for 80 nm Au IgG nanoclusters, neither of the conditions are satisfied. Qualitatively, it is possible to ascertain irreversibility in the same order rendering pNIPAm/PEG200-pNIPAm/AAc to be the most reversible and 80 nm Au IgG nanoclusters to be the most irreversible among the selected samples. However, this is a qualitative approach to define the reversibility of phase changing systems. Similar analysis for the other samples are shown in Fig. S2 (ESI†).
While the approach explained takes into consideration all the experimental data points, it does not provide a quantitative description of the system reversibility. However, an order of magnitude analysis helps us to treat this semi-quantitatively as follows.
A judging criterion for reversibility can be defined in terms of the order of magnitude analysis as follows:
| O(Rmh) = O(Rmc) reversible system |
| O(Rmh) ≠ O(Rmc) irreversible system |
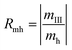 | (14) |
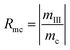 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V and ln
V and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T for heating and cooling cycles respectively. Table 1 shows the difference in the order of magnitudes of the irreversible samples as compared with other reversible ones. This falls in line with the qualitative and semi quantitative descriptions above (Fig. 3(d)–(f)). Although, this criterion defines the system reversibility, it fails to reflect the extent of reversibility of a particular system.
T for heating and cooling cycles respectively. Table 1 shows the difference in the order of magnitudes of the irreversible samples as compared with other reversible ones. This falls in line with the qualitative and semi quantitative descriptions above (Fig. 3(d)–(f)). Although, this criterion defines the system reversibility, it fails to reflect the extent of reversibility of a particular system.
| Samples | mh | mc | mIII | R2 | Order of magnitude | ||
|---|---|---|---|---|---|---|---|
| Heat | Cool | Rmh | Rmc | ||||
| pNIPAm/PEG200-pNIPAm/AAc | −2.1 | −2.1 | −6.8 | 0.88 | 0.87 | 1 | 1 |
| pNIPAm/PEG400-pNIPAm/AAc | −1.4 | −1.3 | −8.4 | 0.75 | 0.73 | 1 | 1 |
| pNIPAm/PEG550-pNIPAm/AAc | −1.9 | −1.7 | −67.9 | 0.85 | 0.79 | 2 | 2 |
| pNIPAm/PEG750-pNIPAm/AAc | −1.8 | −1.7 | −12.9 | 0.92 | 0.9 | 1 | 1 |
| pNIPAm/AAc nanogels | −5 | −4.8 | −16.1 | 0.84 | 0.86 | 1 | 1 |
| Fe@Au_PEG_nanogel | 2 | 2.3 | 3.5 | 0.92 | 0.95 | 1 | 1 |
| 30 nm Au IgG nanoclusters | −0.2 | 0 | −0.1 | 0.94 | 0.26 | 0 | 2 |
| 80 nm Au IgG nanoclusters | −1 | 0 | −1.2 | 0.84 | 0.27 | 1 | 3 |
In the search for a quantitative parameter that describes the system reversibility taking into account all the state points which the system passes through both during heating and cooling cycles, we developed the reversibility parameter (RP) defined as follows:
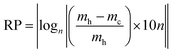 | (16) |
The condition of reversibility is defined as follows:
| RP ≤ 0.1n: reversible |
| 0.1n < RP < 0.2n: partially irreversible |
| RP = 0.2n: irreversible |
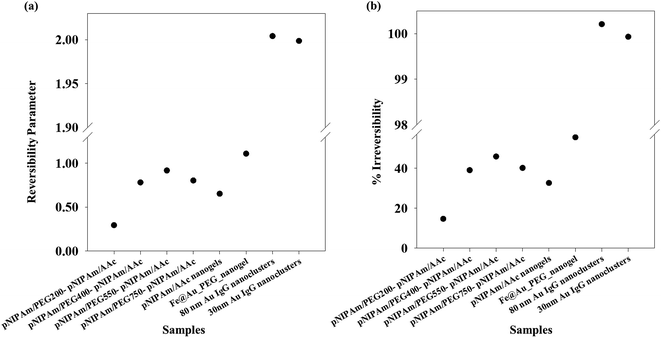
Applying the same methodology, it is possible to ascertain a system parameter to each of the samples that describes the swelling–collapse behavior. Fig. 5(a) shows the RP values for all the samples (n = 1) while Fig. 5(b) shows the percentage of irreversibility compared to the most reversible sample among those considered in this study. The RP trend follows the same trend as the relative hysteresis area curve for the samples shown in Fig. 4(a), the latter does not ascribe a definite system parameter and only gives a relative understanding of system reversibility. On the other hand, RP is also a predictive parameter that has the capability to estimate either the temporal state of the system state or its state after several cycles of operation, depending on whether RP has been calculated from time-based or cycle-based data respectively, although, in our present work the focus has been on cycle based data. This shows immediate applications of the RP in fields that require system data at defined points to optimize application. We stress that the RP could be a very important parameter for systems that lose utility over time or usage owing to fouling. In most cases, the whole system is replaced. However, utilization of RP would help design a system better from the start, since, it can effectively predict system failure. Further, for a system in operation, the whole setup need not be changed in instances of system malfunctioning, but the operation window can be changed based on previous system state values. This would not only reduce investment costs, but also reduce system down-time. One of the foreseeable situations is improved performance of various biosensors based on polymer properties. Using the RP value, it would be possible to design which polymeric system will have longer operation life. Besides, once in operation, if the system fouls due to a combination of more than one reasons, instead of replacing the sensor, it would be possible to change the detection window, based on RP. Thus, the RP not only defines accurately the system reversibility in the present conditions, it also has the functionality to define future system states with accuracy depending on the range of dataset.
4. Conclusion
Although phase changing systems have been in use for a multitude of applications, sufficient investigation to ascribe definitive values to the transition temperature have been rarely carried out. In the present study, first of its kind, three different methods have been proposed to determine the VPTTs of various systems, involving both heating and cooling cycle datasets. A wide range of samples like pNIPAm based nanogels, Au nanoclusters and combination of inorganic and polymeric systems have been studied. Although all of the three methods reveal close VPTT values, we suggest that method III is the least computation dependent and most reliable. The method can be extended to process any property that undergoes change at the phase transition. Among the samples studied, pNIPAm/PEG200-pNIPAm/AAc was found to be the most reversible while considering relative hysteresis area. In an attempt to define the overall system reversibility, a reversibility parameter was defined, taking into consideration all the system states during both heating and cooling cycles. Reversible systems were found to have RP values less than 1, while irreversible systems were observed to have RP values of 2. We predict that real systems will show RP values between 1 and 2. The RP not only explains the system behavior at each of the system states, but can also predict the system behavior at a future state. Thus, by knowing both the system's VPTT as well as its reversibility, it can be designed for a particular application in the industry such as medicine, oil and gas, water purification, etc. Further, we foresee that with the help of RP, a system can be designed or upgraded for specific uses in the industry.Conflicts of interest
There are no conflicts to declare.References
- L. C. Dong and A. S. Hoffman, Synthesis and Application of Thermally Reversible Heterogels for Drug Delivery, J. Controlled Release, 1990, 13(1), 21–31 CrossRef CAS.
- S. Bekhradnia, et al., Structure, swelling, and drug release of thermoresponsive poly(amidoamine) dendrimer-poly(N-isopropylacrylamide) hydrogels, J. Mater. Sci., 2014, 49(17), 6102–6110 CrossRef CAS.
- N. Pippa, et al., Temperature-dependent drug release from DPPC: C12H25-PNIPAM-COOH liposomes: Control of the drug loading/release by modulation of the nanocarriers' components, Int. J. Pharm., 2015, 485(1–2), 374–382 CrossRef CAS PubMed.
- J. E. Chung, et al., Thermo-responsive drug delivery from polymeric micelles constructed using block copolymers of poly(N-isopropylacrylamide) and poly(butylmethacrylate), J. Controlled Release, 1999, 62(1–2), 115–127 CrossRef CAS PubMed.
- M. Constantin, et al., Poly(N-isopropylacrylamide-co-methacrylic acid) pH/thermo-responsive porous hydrogels as self-regulated drug delivery system, Eur. J. Pharm. Sci., 2014, 62, 86–95 CrossRef CAS PubMed.
- J. Liu, et al., Thermo-responsive gold/poly(vinyl alcohol)-b-poly(N-vinylcaprolactam) core-corona nanoparticles as a drug delivery system, Polym. Chem., 2014, 5(18), 5289–5299 RSC.
- N. Adrus and M. Ulbricht, Novel hydrogel pore-filled composite membranes with tunable and temperature-responsive size-selectivity, J. Mater. Chem., 2012, 22(7), 3088–3098 RSC.
- C. Y. Tang, et al., Desalination by biomimetic aquaporin membranes: Review of status and prospects, Desalination, 2013, 308, 34–40 CrossRef CAS.
- P. F. Li, et al., Thermo-responsive membranes with cross-linked poly(N-isopropylacrylamide) hydrogels inside porous substrates, Chem. Eng. Technol., 2006, 29(11), 1333–1339 CrossRef CAS.
- W. C. Wang, et al., Thermally On-Off Switching Membranes Prepared by Pore-Filling Poly(N-isopropylacrylamide) Hydrogels, Ind. Eng. Chem. Res., 2010, 49(4), 1684–1690 CrossRef CAS.
- K. F. Arndt, D. Kuckling and A. Richter, Application of sensitive hydrogels in flow control, Polym. Adv. Technol., 2000, 11(8–12), 496–505 CrossRef CAS.
- C. Yu, et al., Flow control valves for analytical microfluidic chips without mechanical parts based on thermally responsive monolithic polymers, Anal. Chem., 2003, 75(8), 1958–1961 CrossRef CAS PubMed.
- M. R. Islam, et al., Poly(N-isopropylacrylamide) Microgel-Based Optical Devices for Sensing and Biosensing, Sensors, 2014, 14(5), 8984–8995 CrossRef CAS PubMed.
- M. Toma, et al., Active Control of SPR by Thermoresponsive Hydrogels for Biosensor Applications, J. Phys. Chem. C, 2013, 117(22), 11705–11712 CAS.
- R. M. Gant, et al., Design of a self-cleaning thermoresponsive nanocomposite hydrogel membrane for implantable biosensors, Acta Biomater., 2010, 6(8), 2903–2910 CrossRef CAS PubMed.
- X. H. Wang, X. P. Qiu and C. Wu, Comparison of the coil-to-globule and the globule-to-coil transitions of a single poly(N-isopropylacrylamide) homopolymer chain in water, Macromolecules, 1998, 31(9), 2972–2976 CrossRef CAS.
- M. Shibayama and T. Tanaka, Volume Phase-Transition and Related Phenomena of Polymer Gels, Adv. Polym. Sci., 1993, 109, 1–62 CrossRef CAS.
- M. Constantin, et al., Lower critical solution temperature versus volume phase transition temperature in thermoresponsive drug delivery systems, eXPRESS Polym. Lett., 2011, 5(10), 839–848 CrossRef CAS.
- H. Zhang and J. C. Kim, Hydroxyethyl Acrylate-Based Polymeric Amphiphiles Showing Lower Critical Solution Temperature, J. Macromol. Sci., Part A: Pure Appl.Chem., 2015, 52(2), 138–146 CrossRef CAS.
- C. Fucinos, et al., Temperature-and pH-Sensitive Nanohydrogels of Poly(N-Isopropylacrylamide) for Food Packaging Applications: Modelling the Swelling–Collapse Behaviour, PLoS One, 2014, 9(2) DOI:10.1371/journal.pone.0087190.
- K. Nomura, et al., Temperature-responsive copolymer brush constructed on a silica microparticle by atom transfer radical polymerization, Colloid Polym. Sci., 2015, 293(3), 851–859 CAS.
- U. G. Spizzirri, et al., Thermo-Responsive Albumin Hydrogels with LCST Near the Physiological Temperature, J. Appl. Polym. Sci., 2011, 121(1), 342–351 CrossRef CAS.
- X. Y. Gao, et al., pH- and thermo-responsive poly(N-isopropylacrylamide-co-acrylic acid derivative) copolymers and hydrogels with LCST dependent on pH and alkyl side groups, J. Mater. Chem. B, 2013, 1(41), 5578–5587 RSC.
- S. Volden, et al., Effect of Charge Density Matching on the Temperature Response of PNIPAAM Block Copolymer-Gold Nanoparticles, J. Phys. Chem. C, 2012, 116(23), 12844–12853 CAS.
- S. Volden, et al., Gold Nanoparticles Affect Thermoresponse and Aggregation Properties of Mesoscopic Immunoglobulin G Clusters, J. Phys. Chem. C, 2011, 115(23), 11390–11399 CAS.
- R. Raju, et al., Preparation of multiresponsive p[NIPAm-co-PEGMA](core)/p[NIPAm-co-AAc (shell)] with controlled size and monodispersity, Gels, 2017 Search PubMed , under review.
- S. Bandyopadhyay, et al., Incorporation of Fe@Au nanoparticles into multiresponsive pNIPAM-AAc colloidal gels modulates drug uptake and release, Colloid Polym. Sci., 2016, 294(12), 1929–1942 CAS.
- S. Volden, et al., Gold nanoparticles affect thermoresponse and aggregation properties of Mesoscopic immunoglobulin G clusters, J. Phys. Chem. C, 2011, 115(23), 11390–11399 CAS.
- S. Bandyopadhyay, et al., Incorporation of Fe@Au nanoparticles into multiresponsive pNIPAM-AAc colloidal gels modulates drug uptake and release, Colloid Polym. Sci., 2016, 294(12), 1929–1942 CAS.
- C. G. Wiener, R. A. Weiss and B. D. Vogt, Overcoming confinement limited swelling in hydrogel thin films using supramolecular interactions, Soft Matter, 2014, 10(35), 6705–6712 RSC.
- A. Lee, H. Y. Tsai and M. Z. Yates, Steric Stabilization of Thermally Responsive N-Isopropylacrylamide Particles by Poly(vinyl alcohol), Langmuir, 2011, 27(7), 4278 CrossRef CAS.
- M. Wolff, D. Braun and M. A. Nash, Detection of Thermoresponsive Polymer Phase Transition in Dilute Low-Volume Format by Microscale Thermophoretic Depletion, Anal. Chem., 2014, 86(14), 6797–6803 CrossRef CAS PubMed.
- E. Diez-Pena, I. Quijada-Garrido and J. M. Barrales-Rienda, On the water swelling behaviour of poly(N-isopropylacrylamide) [P(N-iPAAm)], poly(methacrylic acid) [P(MAA)], their random copolymers and sequential interpenetrating polymer networks (IPNs), Polymer, 2002, 43(16), 4341–4348 CrossRef CAS.
- M. Shibayama, S. Mizutani and S. Nomura, Thermal properties of copolymer gels containing N-isopropylacrylamide, Macromolecules, 1996, 29(6), 2019–2024 CrossRef CAS.
- J. Virtanen, C. Baron and H. Tenhu, Grafting of poly(N-isopropylacrylamide) with poly(ethylene oxide) under various reaction conditions, Macromolecules, 2000, 33(2), 336–341 CrossRef CAS.
- J. Virtanen and H. Tenhu, Thermal properties of poly(N-isopropylacrylamide)-g-poly(ethyl oxide) in aqueous solutions: Influence of the number and distribution of the grafts, Macromolecules, 2000, 33(16), 5970–5975 CrossRef CAS.
- N. Singh and L. A. Lyon, Synthesis of multifunctional nanogels using a protected macromonomer approach, Colloid Polym. Sci., 2008, 286(8–9), 1061–1069 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10258e |
| This journal is © The Royal Society of Chemistry 2017 |