Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Isomeric trimesogens exhibiting modulated nematic mesophases†
Adam Al-Janabi,
Richard J. Mandle * and
John W. Goodby
* and
John W. Goodby
Department of Chemistry, University of York, UK. E-mail: Richard.Mandle@york.ac.uk
First published on 6th October 2017
Abstract
Modulated nematic phases, in which the constituent molecules possess some form of superstructure in addition to the average orientational organization and lack positional order present in classical nematic phases, are of current fascination in liquid crystal research. Most of the recent focus has been on the twist-bend nematic phase. This phase exhibits phenomena that are of fundamental importance to science; the spontaneous formation of a helical pitch of nanometre scale in a fluid and the spontaneous breaking of mirror symmetry leading to the emergence of chiral domains in an achiral system. In this communication we report on the synthesis of two liquid-crystalline trimesogens whose structures are an extension of the known dimeric material CB6OCB. One material (A63) exhibits a nematic phase with a twist-bend modulation (NTB phase), whereas a structurally isomeric material (B63) exhibits an unusual nematic like mesophase which we believe is a candidate for being a new form of modulated nematic. Whereas the properties of dimeric LCs are somewhat indifferent to chemical composition, the stark difference in behaviour between the two materials herein shows that oligomers may exhibit an unexpected sensitivity to molecular structure.
Introduction
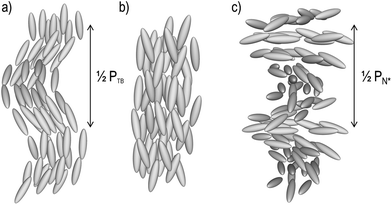
The discovery of the twist-bend phase (NTB, Fig. 1a) has given fresh impetus to the study of dimeric liquid crystals,1–13 and has been described as the missing link between the achiral nematic (N, Fig. 1b) and the helical chiral nematic phases (N*, Fig. 1c).7 Although in this case the nematic phase is transformed into the chiral nematic by the action of a chiral dopant, the NTB phase occurs spontaneously and, as a result of its locally helicoidal structure (pitch measured to be on the order of 10 nm)4,14 is chiral.13,15,16 This phase displays a number of unusual and unique optical textures.17 When the twist-bend phase is chiral other ‘nematic-like’ mesophases have been reported whose structures are as-yet-unknown,5,18 whereas a nematic-to-nematic transition has also been recently reported for a polar rod-like compound.19 A number of reviews concerning the twist-bend phase have been published recently.20–22 A relatively large number of dimeric liquid crystals are known to exhibit this state of matter,1,3,8,9,11,12,23–32 and there is a growing number of liquid crystalline oligomesogens known to exhibit the twist-bend phase.20,33–36 Additionally, this phase has been demonstrated to be exhibited by a phenylpiperazine derived bent-core liquid crystal.4In dimeric materials the twist-bend phase appears to be insensitive to the chemical composition of the mesogenic units,37 however the bend-angle between these does appear crucial.38,39 Relatively little is known about the relationship between the twist-bend phase and molecular structure within the context of oligomesogenic materials, with only a handful of examples known.33–36,40,41 One limitation to developing such a relationship is the difficulty in preparing higher oligomers. Herein we present a simple synthetic route to two isomeric trimesogens, shown in Schemes 1 and 2, which could easily be expanded to give further examples of higher oligomers with homologous structures. Examination of these two materials by POM, DSC and SAXS reveals significant differences in phase behaviour and properties.
Experimental
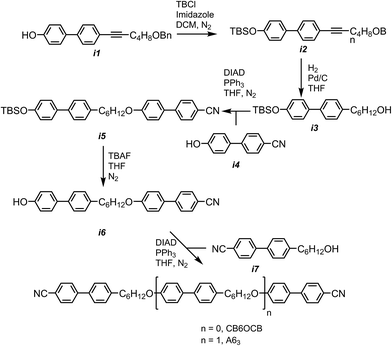
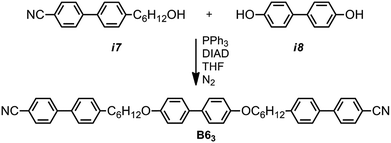
In our previous attempt to synthesis A63 we were unable to cleave the benzyl ether without accompanying nitrile reduction,40 in the present work we circumvented this issue by moving to the use of a tert butyldimethylsilyl (TBDMS) protecting group. The phenol group of the intermediate i1, synthesis reported in,40 was protected with a TBDMS group and subsequent hydrogenation saturated the alkyne and removed the benzyl ether to afford i3. Mitsunobu etherification with i4 gave i5; cleavage of the TBDMS group was achieved using TBAF. Etherification of i6 with i7 afforded the trimesogen A63.The trimesogen B63, an isomer of A63, was prepared via Mitsunobu etherification of i7 and i8 as shown in Scheme 2. Synthetic details, chemical characterisation and details of instrumentation used are given in the ESI† to this communication; both trimesogenic materials were obtained in high purity (99.4% for A63 and 99.7% for B63) as evidenced by HPLC.
Results and discussion
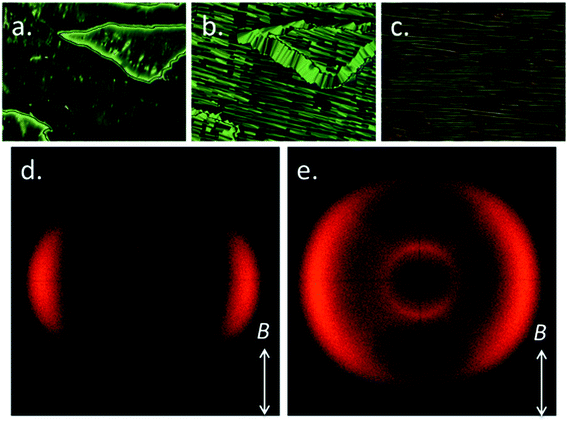
The transition temperatures of both A63 and B63 were determined using a combination of polarized optical microscopy (POM), differential scanning calorimetry (DSC) and small angle X-ray scattering (SAXS). Transition temperatures and associated enthalpies of transition for each material are presented in Table 1.The trimesogen A63 can be envisaged as an extension of the well-known liquid-crystalline dimer CB6OCB (Cr 102 NTB 110.5 N 154.2 Iso); it is unsurprising therefore that this material mirrors the behaviour of the parent compound and exhibits nematic and twist-bend phases, although we note that the trimesogen (A63) has significantly higher melting points and transition temperatures than the parent (CB6OCB), while the associated enthalpy associated with the N–NTB phase transition is an order of magnitude larger in A63. The identification of the nematic phase was trivial based on its characteristic schlieren texture (Fig. 2a), high fluidity, Brownian motion, and diffuse scattering of X-rays at small angles (Fig. 2d and SI-7†). With further cooling a transition into the twist-bend phase occurred; regions exhibiting a schlieren texture in the nematic phase exhibited a “blocky” texture (Fig. 2b), planar aligned regions transformed into the rope texture (Fig. 2c) although homeotropic regions remained optically extinct. When the rope texture was annealed for 5 minutes at a constant temperature of 125 °C we observed striations forming at an angle of ∼30° to the ‘length’ of the rope; the possibility for the formation of fibre-like structures in the NTB has been noted previously42 and recently demonstrated to have a “fish-bone” like structure from SEM imaging of photopolymerised twist-bend dimers.43
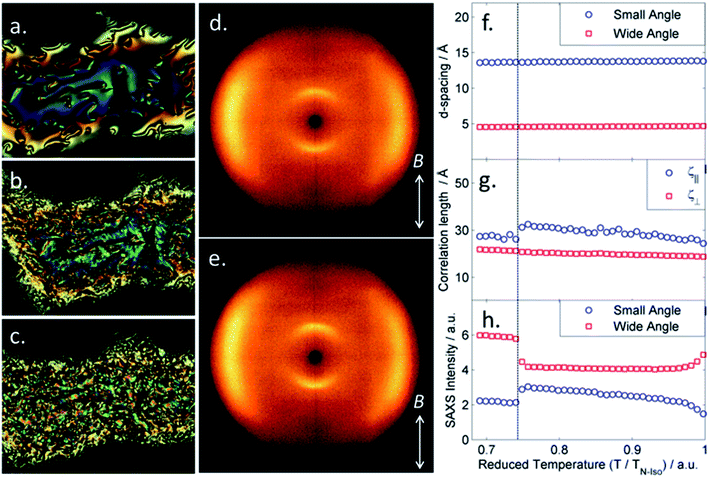
When studied by SAXS the NTB phase of A63 exhibited a diffuse scattering at small angles (Fig. 2e). The small angle scattering peak had a d-spacing value of 14.1 Å which was considered as a first approximation to be roughly 1/3 of the molecular length. DFT (B3LYP/6-31G(d)) calculations show that if the two outer mesogenic units are trans to each other then the molecular length is 43.5 Å compared with a value of 39 Å in the comparable cis geometry, however this neglects the flexibility inherent in such systems and is best considered as an approximation. The d-spacing values in both phases, taken in conjunction with the calculated molecular lengths, indicate the sub-units of the trimesogen behave essentially as free entities in both phases rather than the trimesogen behaving as one large ‘rod-like’ molecule.
As mentioned briefly, the use of a single conformer neglects the inherent flexibility afforded by the hexyloxy spacer, present in both materials. Using fully relaxed scans (at the DFT (B3LYP/6-31G(d)) level in Gaussian G09 revision e01) we studied a 1/2 fragment of both trimers. We allow each dihedral shown in Fig. 3a to rotate in 10 °C steps, giving plots of conformer energy as a function of each individual angle. For the 2nd dihedral we observe the gauche states to be lower in energy than the trans form (ΔE, 0.6 kJ mol−1), for the other dihedrals the trans form is lower than gauche by 2–6 kJ mol−1. While calculation of the full conformer distribution for both materials is too computationally expensive to be feasible, even using the RIS approximation and semi-empirical methods, the present study illustrates the flexibility inherent to these systems.
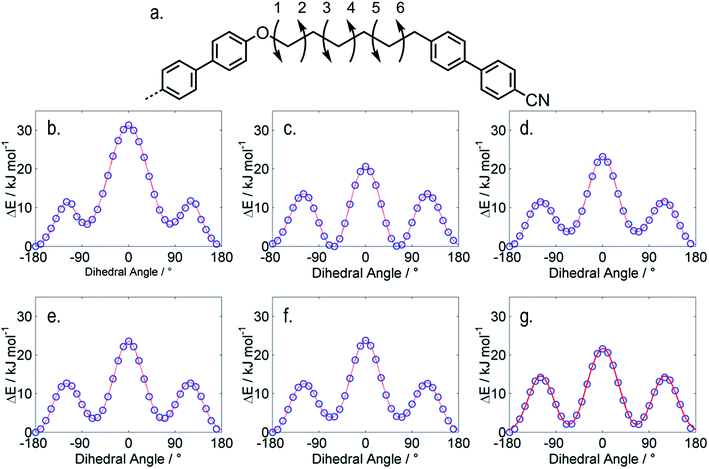 | ||
| Fig. 3 The dihedrals shown in (a) were allowed to rotate in 10 °C steps using fully relaxed scans at the B3LPY/6-31G(d) level of DFT as implemented in Gaussian G09 revision e.01,44 the plots (b–g) show the energy of as a function of each dihedral relative to that of the lowest energy conformer; (b) dihedral 1; (c) dihedral 2; (d) dihedral 3; (e) dihedral 4; (f) dihedral 5; (g) dihedral 6. | ||
Given the similarities in molecular structure it had been anticipated that B63 would exhibit similar transition temperatures and phase behaviour to A63. B63 exhibits lower transition temperatures than A63, with identification of the nematic phase being as described previously. Upon cooling into the next phase (NX) a series of unusual optical textures were observed, which we describe as follows. On an untreated glass slide we observed that regions exhibiting a schlieren texture initially take on a patchy appearance at the phase transition into the NX phase before then forming a nondescript, sand-like texture (Fig. 4a–c). We performed SAXS on B63, collecting frames on cooling in 1.2 °C intervals from the clearing point until the sample crystallised at ∼103 °C. The nematic nature of both phases, hinted at by the small enthalpy associated with the transition, was confirmed by the diffuse small angle peak in SAXS (2D patterns in Fig. 4d and e, data in Fig. 4f–h). Both the onset temperature and the enthalpy associated with the first order N–NX transition were found to be invariant with the heat/cool rate employed in DSC studies – unlike for the dimer CB11CB where the NTB–N transition appears almost second order and resolves into a small first order peak with varying scan rate,45 although this phenomenon is not repeated by either material in this present work.
Radial integration of each SAXS pattern gave scattered intensity as a function of Q; fitting the raw scattering data with a Lorentzian function gave the d-spacings of the small- (001) and wide- (100) angle peaks (Fig. 4f), which we find to be temperature invariant. The small-angle scattering peak has a d-spacing of ∼14 Å in both phases; we do not observe any scattering events at smaller angles up to the limit of our experimental setup at ∼100 Å. We obtain molecular lengths at the DFT (B3LYP/6-31G(d)) level; as with A63 we find that if the two outer mesogenic units are trans to each other the molecular length is 42.7 Å compared with a value of 38.5 Å in the comparable cis geometry, i.e. the d-spacing of the small angle peak corresponds to ∼1/3 of the molecular length. Although this neglects the flexibility of B63, but the present results indicate that, as with A63, the trimesogen does not behave as one large ‘rod-like’ molecule. The correlation lengths were determined from the FWHM of each peak; whereas the correlation length parallel to the director decreases slightly at the N–NX phase transition the perpendicular correlation length increases marginally, however we find the magnitude of both correlation lengths is consistent with a nematic-like phase. Lastly, we plot the maximum intensity of both small- and wide-angle peaks as a function of temperature, we observe that there is a decrease in the intensity small-angle scattering at the N–NX transition however there is a corresponding increase in the intensity wide-angle scattering.
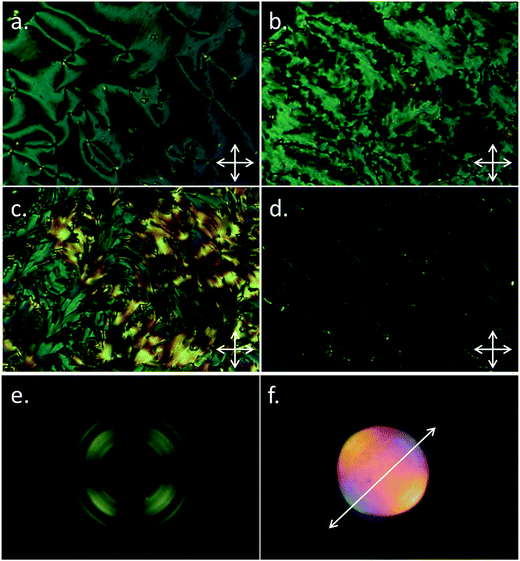
Good quality planar alignment was achieved for both compounds when filled into cells with a buffed antiparallel alignment layer (purchased from Instec thickness ∼ 5 μm). The behaviour of A63 was in keeping with our studies on CB11CB in the same confined geometry; the well aligned planar texture in the nematic phase (Fig. 5a) gives way to domains of differing handedness at the NTB transition (Fig. 5b), with further cooling giving a rope-like texture perpendicular to the rubbing direction of the cell (Fig. 5c). This behaviour is typical for the NTB phase. The isomeric trimesogen B63 also afforded a well aligned planar texture in the nematic phase, however with further cooling a blocky texture emerged (Fig. 5d) which slowly transformed into a parabolic texture (Fig. 5e). Some regions formed a quasi-planar texture featuring regions with different handed domains (Fig. 5f); this is reminiscent of the twist-bend phase, however, this texture in the twist-bend phase gives way to the rope texture (Fig. 5b and c) yet in the NX phase of B63 we did not observe a fully-fledged rope texture. Whereas the optical texture of the NTB phase changes significantly with cooling, the changes in the optical texture of the NX phase exhibited by B63 are less pronounced.
We next subjected a sample of B63 to slow cooling across the N–NX phase transition in order to obtain superior optical textures, with a view to ruling out this phase as simply being a twist-bend nematic. The typical schlieren texture of the nematic phase (Fig. 6a) is made up of disclinations, following the transition into the NX phase these lines become broken and fractal (Fig. 6b). At the N–NTB phase transition planar aligned regions adopt a blocky texture (for example Fig. 2b), whereas at the N–NX a curved, fractal texture is obtained (Fig. 6b).
Additionally the NTB phase exhibits focal-conic defects, whereas none have been observed in the optical textures of the NX phase of B63. With further cooling there is a significant change in the birefringence of the sample, with long curved domains appearing (Fig. 6c). The sample could easily be sheared to give a fairly uniform homeotropic texture (Fig. 6d). Uniform homeotropic alignment of both the nematic and NX phases of B63 was realised using glass slides treated with piranha solution (30% hydrogen peroxide and 95% sulphuric acid in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio); subsequent conoscopy demonstrates the NX phase to be optically uniaxial (Fig. 6e) and, after inserting a 1/4 waveplate into the microscope, optically positive (Fig. 6f). Lastly, a contact preparation between the two materials demonstrated them to be immiscible – while this may be due to simple chemical immiscibility we have observed previously that dimers of different structure and average gross bend tend to be miscible,38 thus, this result adds weight to the assignment of the NX phase as being something other than a ‘normal’ NTB phase.
3 ratio); subsequent conoscopy demonstrates the NX phase to be optically uniaxial (Fig. 6e) and, after inserting a 1/4 waveplate into the microscope, optically positive (Fig. 6f). Lastly, a contact preparation between the two materials demonstrated them to be immiscible – while this may be due to simple chemical immiscibility we have observed previously that dimers of different structure and average gross bend tend to be miscible,38 thus, this result adds weight to the assignment of the NX phase as being something other than a ‘normal’ NTB phase.
Conoscopy gives crucial information about the local structure of the NX phase; firstly as this phase is optically uniaxial it is implied that the modulation period (Pmod) is much shorter than the wavelength of visible light (Pmod ≪ λ). As the phase is optically positive the molecules must be tilted away from the director by less than the magic angle. Although the twist-bend phase would satisfy both of these observations, as well as the diffuse nematic-like SAXS patterns, the optical textures observed for B63 are sufficiently distinct from those of A63 and other twist-bend materials to suggest this is not the case.
If the NX phase has a structure with modulation of electron density (e.g. SmA, splay-bend nematic) Bragg scattering should be observed; as this has not been observed it raises two possibilities for the structure of the NX phase exhibited by B63: the modulation period is large enough that the corresponding Bragg scattering peak (and its harmonics) occur at larger d-spacings than those we can observe using our SAXS setup (∼100 Å). Alternatively, if there is no modulation of electron density associated with the NX phase (similar to that observed for the NTB) then non-resonant X-ray experiments are blind to the modulation period. We note the possibility that the structure may have no modulation whatsoever; we consider this unlikely given the changes in optical textures. The change in SAXS peak intensity as well as the associated enthalpy of transition of the two materials are comparable, though not identical, for both materials and to previously reported trimesogens exhibiting the twist-bend phase.34,36
In the original work on the CBnCB materials the phase now identified as being NTB was often identified as being smectic, presumably because of its smectic-like optical textures resulting from its periodic structure. We note that the trimesogen shown in Fig. 7, described 20 years ago by both Zuev and Imrie in separate publications, is reported as exhibiting nematic and smectic phases. Given the similarity of the molecular structure of this material to A63 and B63 a thorough re-examination of such materials may be warranted.
 | ||
| Fig. 7 The chemical structure of the liquid-crystalline trimesogen reported separately by Zuev46 and Imrie.47 Transition temperatures (°C) reported by Imrie and Luckhurst are Cr 173 (SmA 124) N 215 Iso. Liq. | ||
Conclusions
Two trimesogenic liquid-crystalline materials – both isomers of one another – have been prepared and characterised. The method used to prepare these materials should finally allow access to chemically stable oligomeric materials of any given length, and polydispersity approaching unity. One material (A63) exhibits nematic and twist-bend mesophases, however its counterpart material (B63) exhibits a nematic-like mesophase structure for which we have not been able to provide a definitive identity. Studies to date point to a modulated nematic phase, with a small modulation period, and although it is possible that the observed ‘NX’ phase may be simply a twist-bend nematic, the potential immiscibility of the two materials as well as the remarkably different optical textures suggest this is not the case and thus a new liquid crystal phase may be a possibility that warrants further study on this material, its analogues and higher oligomeric homologues.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
RJM would like to thank the Department of Chemistry at the University of York for funding a research placement for AAJ. The authors thank the EPSRC for funding the SAXS setup used in this work via grant EP/K039660/1.References
- D. A. Paterson, J. Xiang, G. Singh, R. Walker, D. M. Agra-Kooijman, A. Martinez-Felipe, M. Gan, J. M. D. Storey, S. Kumar, O. D. Lavrentovich and C. T. Imrie, J. Am. Chem. Soc., 2016, 138, 5283–5289 CrossRef CAS PubMed.
- Z. P. Zhang, V. P. Panov, M. Nagaraj, R. J. Mandle, J. W. Goodby, G. R. Luckhurst, J. C. Jones and H. F. Gleeson, J. Mater. Chem. C, 2015, 3, 10007–10016 RSC.
- N. Sebastian, D. O. Lopez, B. Robles-Hernandez, M. R. de la Fuente, J. Salud, M. A. Perez-Jubindo, D. A. Dunmur, G. R. Luckhurst and D. J. Jackson, Phys. Chem. Chem. Phys., 2014, 16, 21391–21406 RSC.
- D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506 CrossRef PubMed.
- A. Zep, S. Aya, K. Aihara, K. Ema, D. Pociecha, K. Madrak, P. Bernatowicz, H. Takezoe and E. Gorecka, J. Mater. Chem. C, 2013, 1, 46–49 RSC.
- D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931–15936 CrossRef CAS PubMed.
- V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jakli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CAS.
- K. Adlem, M. Copic, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88 CrossRef CAS PubMed.
- P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414 CrossRef CAS.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704 CrossRef CAS PubMed.
- M. Sepelj, A. Lesac, U. Baumeister, S. Diele, H. L. Nguyen and D. W. Bruce, J. Mater. Chem., 2007, 17, 1154–1165 RSC.
- M. Sepelj, A. Lesac, U. Baumeister, S. Diele, D. W. Bruce and Z. Hamersak, Chem. Mater., 2006, 18, 2050–2058 CrossRef CAS.
- I. Dozov, Europhys. Lett., 2001, 56, 247–253 CrossRef CAS.
- C. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803 CrossRef PubMed.
- J. W. Emsley, P. Lesot, G. R. Luckhurst, A. Meddour and D. Merlet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 040501 CrossRef PubMed.
- C. Greco, G. R. Luckhurst and A. Ferrarini, Phys. Chem. Chem. Phys., 2013, 15, 14961–14965 RSC.
- R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566 RSC.
- C. T. Archbold, E. J. Davis, R. J. Mandle, S. J. Cowling and J. W. Goodby, Soft Matter, 2015, 11, 7547–7557 RSC.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2017, 19, 11429–11435 RSC.
- R. J. Mandle, Chem.–Eur. J., 2017, 23, 8771–8779, DOI:10.1002/chem.201701167.
- R. J. Mandle, Soft Matter, 2016, 12, 7883–7901 RSC.
- V. P. Panov, J. K. Vij and G. H. Mehl, Liq. Cryst., 2017, 44, 147–159 CAS.
- T. Ivšić, U. Baumeister, I. Dokli, A. Mikleušević and A. Lesac, Liq. Cryst., 2017, 44, 93–105 Search PubMed.
- C. T. Archbold, J. L. Andrews, R. J. Mandle, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2017, 44, 84–92 CAS.
- J. P. Abberley, S. M. Jansze, R. Walker, D. A. Paterson, P. A. Henderson, A. T. M. Marcelis, J. M. D. Storey and C. T. Imrie, Liq. Cryst., 2017, 44, 68–83 CAS.
- D. A. Paterson, M. Gao, Y. K. Kim, A. Jamali, K. L. Finley, B. Robles-Hernandez, S. Diez-Berart, J. Salud, M. R. de la Fuente, B. A. Timimi, H. Zimmermann, C. Greco, A. Ferrarini, J. M. D. Storey, D. O. Lopez, O. D. Lavrentovich, G. R. Luckhurst and C. T. Imrie, Soft Matter, 2016, 12, 6827–6840 RSC.
- R. J. Mandle, C. C. A. Voll, D. J. Lewis and J. W. Goodby, Liq. Cryst., 2016, 43, 13–21 CrossRef CAS.
- R. J. Mandle and J. W. Goodby, Chem.–Eur. J., 2016, 22, 9366–9374 CrossRef CAS PubMed.
- R. J. Mandle and J. W. Goodby, Soft Matter, 2016, 12, 1436–1443 RSC.
- R. J. Mandle, E. J. Davis, C. C. A. Voll, C. T. Archbold, J. W. Goodby and S. J. Cowling, Liq. Cryst., 2015, 42, 688–703 CAS.
- R. J. Mandle, E. J. Davis, C. T. Archbold, C. C. Voll, J. L. Andrews, S. J. Cowling and J. W. Goodby, Chem.–Eur. J., 2015, 21, 8158–8167 CrossRef CAS PubMed.
- R. J. Mandle, E. J. Davis, S. A. Lobato, C. C. Vol, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2014, 16, 6907–6915 RSC.
- R. J. Mandle and J. W. Goodby, ChemPhysChem, 2016, 17, 967–970 CrossRef CAS PubMed.
- Y. Wang, G. Singh, D. M. Agra-Kooijman, M. Gao, H. K. Bisoyi, C. M. Xue, M. R. Fisch, S. Kumar and Q. Li, CrystEngComm, 2015, 17, 2778–2782 RSC.
- S. M. Jansze, A. Martinez-Felipe, J. M. Storey, A. T. Marcelis and C. T. Imrie, Angew. Chem., Int. Ed. Engl., 2015, 54, 643–646 CAS.
- R. J. Mandle and J. W. Goodby, RSC Adv., 2016, 6, 34885–34893 RSC.
- R. J. Mandle and J. W. Goodby, Chem.–Eur. J., 2016, 22, 18456–18464 CrossRef CAS PubMed.
- R. J. Mandle, C. T. Archbold, J. P. Sarju, J. L. Andrews and J. W. Goodby, Sci. Rep., 2016, 6 Search PubMed.
- C. T. Archbold, R. J. Mandle, J. L. Andrews, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2017, 1–10, DOI:10.1080/02678292.2017.1360954.
- R. J. Mandle, M. P. Stevens and J. W. Goodby, Liq. Cryst., 2017, 1–14, DOI:10.1080/02678292.2017.1343500.
- F. P. Simpson, R. J. Mandle, J. N. Moore and J. W. Goodby, J. Mater. Chem. C, 2017, 5, 5102–5110 RSC.
- J. W. Goodby, Liq. Cryst., 2017, 1–9, DOI:10.1080/02678292.2017.1347293.
- V. P. Panov, S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, C. J. Welch and G. H. Mehl, Arxiv:1708:07013, 2017, http://https://arxiv.org/pdf/1708.07013.pdf.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian G09 rev e01, 2009 Search PubMed.
- R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566 RSC.
- V. V. Zuev, Zh. Obshch. Khim., 1997, 67, 1902–1904 Search PubMed.
- C. T. Imrie and G. R. Luckhurst, J. Mater. Chem., 1998, 8, 1339–1343 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10261e |
| This journal is © The Royal Society of Chemistry 2017 |