Stacking stability and sliding mechanism in weakly bonded 2D transition metal carbides by van der Waals force

Abstract

The stability of the stacked two-dimensional (2D) transition metal carbides and their interlayered friction in different configurations are comparatively studied by means of density functional theory (DFT). At equilibrium, a larger interlayer distance corresponds to a smaller binding energy, suggesting an easier sliding between them. The oxygen-functionalized M₂CO₂ possesses much lower sliding resistance than the bare ones due to the strong metallic interactions between the stacked M₂C layers. Compared to the parallel stacking order of M₂CO₂-I, the mirror stacked M₂CO₂-II possesses better lubricant properties. At strained states, normal compression substantially enhances the sliding barrier owing to more charges transferring from the M to O atom. Furthermore, the in-plane biaxial strain may effectively hinder the interlayer sliding, while the uniaxial strain fundamentally modifies the preferred sliding pathway due to anisotropic expansion of surface electronic state. These results highlight that the functionalized MXenes with strain-controllable frictional properties are promising lubricating materials because of their low sliding energy barrier and excellent mechanical properties.

---

1. Introduction

Atomic-scale friction within nanolayered materials can depend dramatically on the weakly bonded interlayer forces and topological structure of the contact surfaces, providing insight into the atomistic mechanism of energy dissipation and superlubricity, a state with near-zero friction.^1–3 While the macroscopic-scale friction between two solids rubbing together can be readily determined in experiments, little is known about the microscopic mechanism by which the atomic-scale frictional forces are generated, especially for the newly developed 2D materials. The main challenge to explore the atomistic friction in nanolayered materials originates from the nonlocal electronic polarization and its anisotropy that is accompanied by a rather strong contribution of n-body electronic correlations to the adhesion.⁴ In the past decade, with the development of first principles methods in quantifying the weakly bonded interlayer interactions, some progress has been achieved in understanding the mechanism of interlayer sliding of the widely studied 2D materials such as graphene,^5–7 hexagonal boron nitrides,^8,9 both for elucidating their fundamental frictional and tribological properties. In the meanwhile, another distinct atomistic mechanism has also been revealed for the layered molybdenum disulfide (MoS₂), in which the friction-induced orientation of easy basal planes is responsible for sliding with the stacking of the sulphur basal plane being maintained.^10,11

With the emergence of novel 2D transition metal carbides, carbonitrides and nitrides, collectively referred as MXenes,¹² their versatile chemistry, promising stability, superior mechanical strength and flexibility, and excellent electrochemical and remarkable electronic properties have brought much interest due to their potential applications including energy storage, electromagnetic interference shielding, reinforcement for composites, water purification, gas- and biosensors, and photo-, electro- and chemical catalysis.¹³ Nevertheless, the frictional properties and its atomistic mechanism in MXenes remain unclear, which needs further investigations ranging from engineering studies of micromechanical lubrication to atomistic simulations at nano-scale. In this aspect, some preliminary works have been reported more recently for some specific MXenes. For instance, Ti₃C₂ have been explored as additives for tribological applications, and the addition of Ti₃C₂ can reduce the adhesive wear and plow friction.^14–16 Hu et al. reported the intrinsic interlayer coupling in pristine MXenes, and demonstrated that the functional terminations (OH, O, and F) weaken the interlayer coupling as compared with the bare counterparts.¹⁷

Although the equilibrium bonding characteristics have shown to play a critical role on the interface sliding of MXenes, the tunable effect of strain that was always ignored, must be included for the following reasons: (1) the profound strain effect on electrochemical and other functional properties have been widely reported. For example, Wang et al. reported a method to modify the catalytic activity by directly and continuously control the lattice strain of platinum catalyst.¹⁸ Yun et al. has revealed that the indirect to direct band gap transition of 2D materials may occur under the external strain.¹⁹ Zhao et al. studied the strain effect on the magnetic properties of monolayer MXenes and calculated the change of magnetic moment under strain for M₂C.²⁰ (2) It is generally recognized that the high pressure service environment is common for the lubricants, and therefore the frictional properties may be significantly modified in the complex strain environments. Accordingly, it is much necessary to further explore how the frictional properties and its atomistic mechanism of MXenes change under the applied strains. For this purpose, modern first principles method within framework of density functional theory has provided a unique solution to the related studies whether at equilibrium or under strains by extracting the potential energy surface (PES) associated with the interlayer sliding, providing an essential understanding of their tribological behavior.²¹

In this paper, we have firstly investigated the sliding energy barriers of the oxygen-functionalized M₂CO₂ (M = Ti, Zr, Nb, Mo, Hf, Ta, and W), and found that the Ti₂CO₂ possess the lowest barrier among them. Secondly, taking Ti₂CO₂ as a representative, we provide a comprehensive first-principles investigation on its stacking stability and interface sliding with different bilayer orientations at equilibrium by quantifying the relative adhesion energies and potential energy profile within the sliding plane. Thirdly, we extend our investigations on the variation of potential energy surfaces and minimum energy paths when the multiaxial loadings are imposed on the Ti₂CO₂. We found that the normal strain and biaxial in-plane strains increase the sliding energy barriers without changing the sliding path, while the uniaxial in-plane strain may modify the easiest sliding path by increasing the barrier parallel to the strain direction and simultaneously decreasing the barrier along the other orthogonal directions. These results suggest interestingly that a proper control of uniaxial strain may make MXenes possess the superlubricity. Finally, a comprehensive analysis of bond topologies and electronic structures is further performed to underline the atomic mechanism of the variation of energy barrier as the increasing strain. These results highlight that the functionalized MXenes are promising lubricating materials because of its low sliding energy barrier and excellent mechanical property.

2. Theoretical methods

The DFT calculations within the generalized gradient approximation (GGA)²² of Perdew, Burke and Ernzerhof (PBE)²³ and the projector augmented wave (PAW) pseudopotentials²⁴ were performed using the Vienna ab initio simulation package (VASP)²⁵ with a plane wave kinetic energy cutoff of 600 eV. Lattice parameters and atomic coordinates were optimized with an energy convergence of 10⁻⁶ eV per cell. The criterion for force convergence during the relaxation was 10⁻³ eV Å⁻¹. A Γ-centered Monkhorst–Pack grid of 12 × 20 × 3 was used to sample the Brillouin zone during the structural optimization. A vacuum layer of over 15 Å was adopted to guarantee the isolated slab boundary condition. To preserve this vacuum spacing, the z components of cell vectors remain unchanged, but atomic positions are optimized in all directions. In bilayer systems, the dispersive interaction and electrostatic interactions determine the interlayer structures and properties of the models. Thus, as a full-fledged total-energy functional, the vdW-DF2 is used to include dispersive interaction in our DFT calculations, which have also been adopted in previous studies.^26,27 To study sliding energy barriers of bilayer systems, the top layer is displaced along x and y directions within the quarter of the rectangular unit cell (Fig. 1a). Then all possible relative displacements are deduced using symmetry operation. At each displacement all atoms of the system are relaxed in z direction and fixed in x and y direction, and then the total energy of the system E (including both layers) is calculated. In addition, we have tested the effect of different functionals and k points and provided the results in Fig. S1–S3 of ESI.†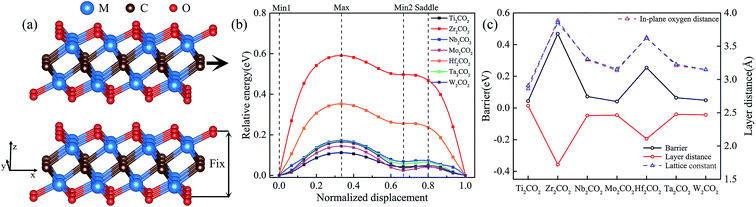

Fig. 1 Geometric arrangement (a) and potential energy profile (b) for the linear translation of upper MXenes layer above a fixed one. The x-axis sliding energy barrier, the layer distance, the in-plane oxygen distance, and lattice constant of M₂CO₂ (M = Ti, Zr, Nb, Mo, Hf, Ta, and W) (c) at Min1. Geometric arrangements for the most relevant positions (Min1, Max, Min2, and Saddle) along the profiles are shown in Fig. S4.† The schematic diagrams of the layer distance and the in-plane oxygen distance are shown in Fig. S5.†

Flexibility of 2D layered materials can be quantified by the critical strain at which the ideal strength reaches. In the case of biaxial tension strains, the equal tension strains are simultaneously applied in the zigzag and armchair directions. To be noted that the ideal strength sets up the upper limit of the material in reality, and can also be applied to many materials in experiments, especially in the 2D material.²⁸ The applied strain is defined as ε = (a − a₀)/a₀, where a and a₀ are the lattice constants of the strained and unstained materials, respectively. In the simulations of uniaxial stress, the geometry relaxation is performed for both the lattice basis vectors and the atomic coordinates by keeping the applied in-plane strain component fixed and relaxing the other in-plane strain component until their conjugate stress components, i.e., Hellmann–Feynman stresses, reach less than 0.1 GPa. For a 2D material, the dimensional length normal to the 2D layer is kept constant during the relaxation in order to keep a sufficient thickness of vacuum. Such relaxation scheme is accomplished by slightly modifying the VASP code with specific constraints of strain components. To make sure that the strain path is continuous, the starting position at each strain step must be taken from the relaxed coordinates of the previous step. Because the crystal symmetry may be changed and the Brillouin zone would significantly deform at large strain, we adopted a high energy cutoff of 600 eV and verified the convergence of tensile calculations with different k-point grids. A similar scheme for stress–strain calculation of 3D crystals has been described and thoroughly evaluated in our previous papers.^29,30

3. Results and discussion

3.1 Bilayer sliding at equilibrium

As reported in previous X-ray photoelectron spectroscopy (XPS) and Energy Dispersive Spectrometer (EDS) analyses, MXenes are generally terminated with various functional groups such as O, OH and F when they are selectively etched from the precursor MAX phases using acidic-fluoride-containing solutions.¹³ With the following three considerations, we shall focus on the oxygen-functionalized MXenes in the latter sections: (i) the majority of functional groups was determined to be oxygen during the etching process;³¹ (ii) the post-processing at high temperature or the lithiation reactions will always induce the conversion from –OH to –O functional groups;³² and (iii) the oxygen-functionalized MXenes were predicted to be thermodynamically and dynamically stable.³³

Fig. 1 shows the calculated sliding energy barriers along the x-axis direction together with the variations of the layer distances, the distance of the in-plane adjacent oxygen atoms, and the lattice constants of M₂CO₂ (M = Ti, Zr, Nb, Mo, Hf, Ta, and W). It reveals that the sliding energy profiles of M₂CO₂ can be generally characterized by two different minima (labeled as Min1 and Min2) and two maxima (labelled as Saddle and Max), and their geometric arrangements are shown in Fig. S4.† When the transition metal species changes, a significant variation of energy barriers is closely related to the variation of the lattice constants. As shown in Fig. S5,† a larger in-plane distance of adjacent oxygens leads to a larger hollow among three adjacent oxygen atoms. As for Min1, the upper oxygen atom is located at the center of the triangle which connects the lower three adjacent oxygen atoms. Because of the coulombic force between the upper and lower oxygen atoms, a larger hollow leads to a smaller interlayer distance d_S. As for Max, the interlayer distances d_U of different M₂CO₂ are almost the same. Therefore, it is hard to switch from stable position to unstable position for M₂CO₂ with a larger lattice constant because of its further movement (d_U − d_S) between the two layers. Because they show strong similarity of the calculated energy barrier profile to that of the widely studied Ti₂CO₂, we shall take it as illustrative case in the following sections for comprehensive first-principles investigations on its stacking stability and interface sliding with different bilayer orientations.

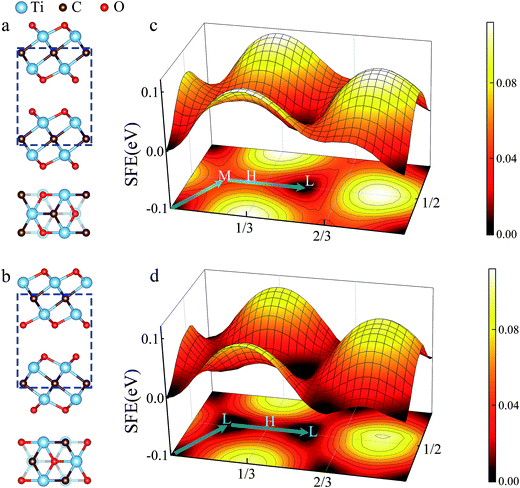
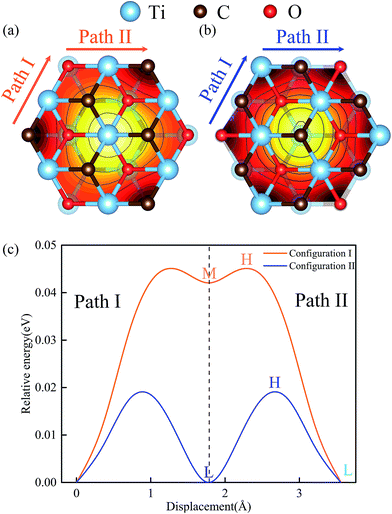
In general, two kinds of configurations were proposed for the stacked Ti₂CO₂ bilayers, i.e., configuration I is stacked with bilayers in parallel sequence (see Fig. 2a), while configuration II corresponds to the anti-parallel stacking sequence with a mirror symmetry between the top and bottom layer (see Fig. 2b). It is seen that the two configurations cannot be transformed into each other by translational operation, but a rotation of 180 degree along z axis can get the transformation between the two configurations. To show the stacking orders more clearly in Fig. 2a and b, only six atom layers surrounded by the blue dotted box are shown in both side-view plot and top-view plot. Fig. 2c and d presents the calculated PES of the Ti₂CO₂-I and Ti₂CO₂-II as a function of the relative in-plane displacement along x and y directions. It is found that along the minimum energy pathway (MEP), the position marked by symbol “L” in both Ti₂CO₂-I and Ti₂CO₂-II corresponds to the minimum stacking energy, while the position marked by symbol “H” indicates the local maxima along the MEP. The position marked by symbol “M” in Ti₂CO₂-I corresponds a local minimum, indicating the occurrence of a metastable state. Fig. 3 shows the variation of relative energies with the in-plane displacement along path I and path II for Ti₂CO₂-I and Ti₂CO₂-II. It is seen that the energy barrier of Ti₂CO₂-II (0.019 eV) is nearly half less than that of Ti₂CO₂-I (0.045 eV), indicating a larger sliding resistance for the Ti₂CO₂-I.

Fig. 2 Side and top view of bilayer Ti₂CO₂-I (a) and Ti₂CO₂-II (b). The top view just contains the atoms in the blue dotted frame. The PESs of the Ti₂CO₂-I (c) and Ti₂CO₂-I (d) as a function of relative displacement of the two layers in the x and y directions.

Fig. 3 The top view and PES of bilayer Ti₂CO₂-I (a) and Ti₂CO₂-II (b). Variation of the energies of Ti₂CO₂ of two configurations with the sliding displacement along the path I and path II marked in (c).

The binding energy (E_b) is always used to quantify the work required to remove an individual layer from a multilayered host,³⁴ providing an essential indicator for optimizing the processing procedure in the synthesis of a standalone 2D structure, as well as for understanding the underlined interlayer bonding nature. For clarity, the binding energy hereafter is referred to as the absolute value of the formation energy of a stacked multilayer from isolated monolayers by stacking in a certain ordered arrangement. The binding energy, E_b, is expressed as

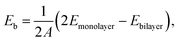where A is the area of the (0001) surface in a unit cell of the bulk structure, E_monolayer is the total energy of the optimized monolayer, and E_bilayer is the total energy of the optimized bilayer. The coefficient “2” before E_monolayer corresponds to two monolayers, and “2” in the denominator means two interface surfaces in a unit cell.

Table 1 presents the calculated binding energies E_b of Ti₂CO₂-I, Ti₂CO₂-II, Ti₂C-I, and Ti₂C-II, and compared with that of graphene, and the calculated PES of graphene and Ti₂C are compared in Fig. S6 in the ESI.† It can be generally seen that the binding energy of configuration I is greater than that of configuration II for all MXenes, resembling the relative values of the sliding energy barrier and the interlayer distance between configuration I and configuration II. Therefore, a larger interlayer distance corresponds to a smaller binding energy, suggesting a lower sliding resistance. Furthermore, the energy barrier and binding energy of Ti₂C is found to be much higher than those of Ti₂CO₂ and graphene, suggesting that the metallic bonding in the bare MXenes plays a crucial role in the enhancement of the sliding resistance.

Table 1 The energy barriers ΔE, the binding energies E_b, the lattice parameter a, and the interlayer distances d_S for the different bilayers systems

Systems	ΔE (eV per cell)	Eb (meV per Å^2 per cell)	a (Å)	dS (Å)
Ti2CO2-I	0.044	10.23	3.085	2.605
Ti2CO2-II	0.017	9.75	3.083	2.656
Ti2C-I	0.237	115.0	3.113	2.425
Ti2C-II	0.099	112.7	3.102	2.830
Graphene	0.002	9.20	2.464	3.535

---

3.2 Bilayer sliding under normal strain

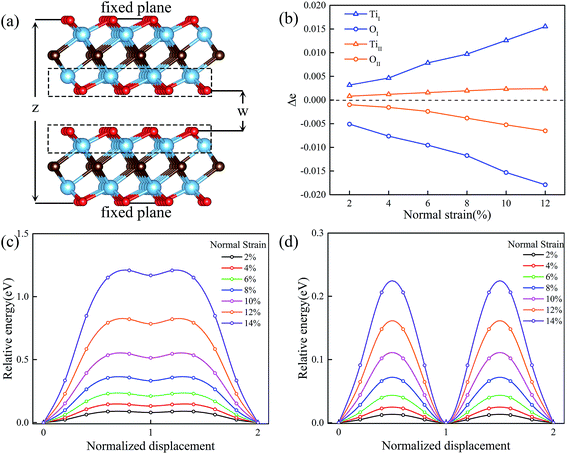
We next study the variation of potential energy surfaces and minimum energy paths of MXenes under multiaxial loadings. In order to study the effect of the normal strain on the friction property, both layers are represented by periodically repeating rectangular unit cells and the spacing z between the bottom atomic plane of the upper layer and the top atomic plane of the lower layer is fixed (see Fig. 4a). For each value of z, the fixed atomic layer at the top is displaced along x and y directions within the quarter of the rectangular unit cell. Then all possible relative displacements between fixed atomic layers are deduced using symmetry operation. At each displacement all atoms of the system except those of fixed top and bottom planes are relaxed and the total energy of the system E (comprising both layers) is calculated. The applied normal strain is defined as ε = (z − z₀)/z₀, where z and z₀ are the thickness of strained and unstained materials at the z direction, respectively. A similar scheme has been described and thoroughly evaluated in a previous paper.³⁵

Fig. 4 Two Ti₂CO₂ layers sliding over each other have the distance z between their outermost atomic planes (a). The variation of the charge difference Δe of Ti and O with normal strain (b). The variation of the energy barrier with normal strain from 2% to 14% for Ti₂CO₂-I (c) and Ti₂CO₂-II (d).

Fig. 4c and d shows the variation of the energy barrier with normal strain changing from 2% to 14% for Ti₂CO₂-I and Ti₂CO₂-II, respectively. It can be seen that the MEP under normal strain is similar to that without strain. Compared to Ti₂CO₂-II, a nearly five times higher energy barrier is found for Ti₂CO₂-I to slide at different normal strains. To be noted that a general trend is observed that normal strain will increase the energy barrier. In order to underline the physics for the variation of energy barrier, we further investigate the electronic interaction between upper and lower layers via the Bader charge analysis. We calculated the charges of Ti and O atoms at the stable site (e_S) and the transition site (e_T) of Ti₂CO₂-I and Ti₂CO₂-II, and in Fig. 4a. Fig. 4b (as indicated in the dashed box), we presented the variation of charge difference (Δe = e_S − e_T) between the stable site (e_S) and the transition site (e_T) of Ti₂CO₂-I and Ti₂CO₂-II with normal strain. It is observed that more electrons transfer from Ti atom to O atom with the increasing normal strain, and totally the Δe of Ti₂CO₂-I is larger than that of Ti₂CO₂-II. In brief, the increasing trend of energy barrier is exactly proportional to that of charge difference, suggesting that the charge difference between the stable site and the transition site provides an electronic explanation on the sliding energy barrier.

3.3 Bilayer sliding under biaxial and uniaxial in-plane strain

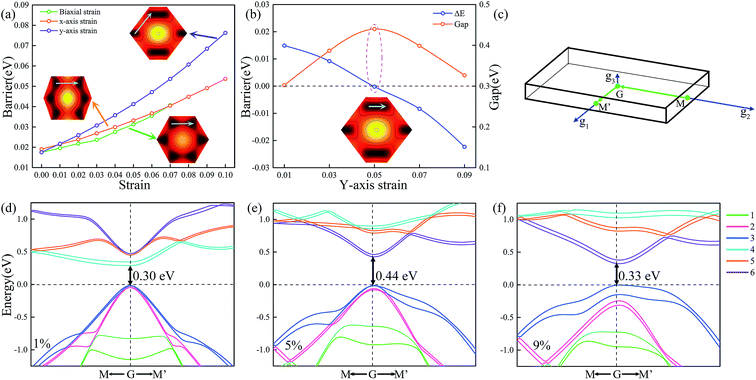
To investigate the intrinsic mechanical responses to tensile strain, we have considered three loading conditions: biaxial tension, uniaxial tension along x direction (the zigzag direction), and uniaxial tension along y direction (the armchair direction). Fig. S7 in the ESI† presents the calculated stress–strain curves for Ti₂CO₂ under both biaxial and uniaxial load conditions. It is observed that Ti₂CO₂ can sustain large strains of 19%, 24% and 29% under biaxial and uniaxial tensions along x and y directions, respectively, being obviously larger than those of graphene (15%, 20%, and 24%). Fig. 5a and b show the sliding energy barriers of Ti₂CO₂-I and Ti₂CO₂-II at biaxial tension strains, respectively. Because of the unchanged symmetry, the biaxial strain affects only the amplitude of the energy barrier but does not change the MEP. In such case, the energy profile along the path from A to B shows exactly the same feature as that along the path from B to C. As the biaxial tension strain increases, the energy barrier increases as well. Fig. 5c and d show the sliding energy barriers of Ti₂CO₂-I and Ti₂CO₂-II under the tension along x-axis, respectively. The energy barrier along the path from B to C is obviously higher than that along the path from D to C so that the MEP is firstly from E to D and then to C. For Ti₂CO₂-I, the energy barrier along the optimal sliding path increases with the increasing tension strain along x-axis, whereas the energy barrier for Ti₂CO₂-II decreases. Fig. 5e and f show the sliding energy barriers of Ti₂CO₂-I and Ti₂CO₂-II under tension along y-axis, respectively. The energy barrier along the path from B to C is less than that along the path from A to B, indicating that it is preferred to slide from B to C. For Ti₂CO₂-I, a preferred sliding path is firstly from A to B and then to C, and the relevant energy barrier increases as the strain increases along y-axis. In the case of Ti₂CO₂-II, two preferred sliding paths are observed firstly from A to B and then to C. The energy barrier from A to B increases with the increasing tension strain along y-axis, while along the path from B to C, the energy barrier decreases with the increasing strain along y-axis when the strain is less than 5%. The lowest energy barrier appears when the applied strain along y-axis is about 5%. When the strain is more than 5%, a metastable state is observed at the midpoint between B and C, and the corresponding energy barrier increases with the increasing tension strain along y-axis.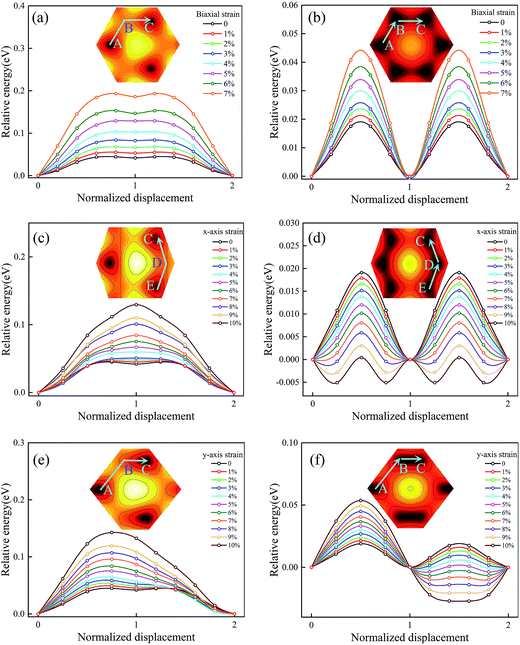

Fig. 5 The variation of the energy barrier with biaxial strain (a, b), x-axis strain (c, d), and y-axis strain (e, f) for Ti₂CO₂-I and Ti₂CO₂-II.

To gain a deeper insight into the effect of the strain, we consider the variations of energy barrier along the lengthened path and the shortened path under tension strains, respectively. In the geometrical aspect, the biaxial tension strain and tension along x-axis will lengthen the path from B to C, while the tension along y-axis will shorten that path and instead lengthen the path from A to B. As shown in Fig. 6a, the energy barrier of the corresponding lengthened path increases as the tension strain increases. Along the shortened path from B to C under tension along y-axis, it is seen that the energy barrier does not monotonically decrease as the strain along y-axis increases, but a minimum value is observed at the tension strain of 5%. To figure out why the minimum energy barrier appears at the tension strain of 5%, the deformed electronic structures are calculated at different strain states. Fig. 6d–f show the deformed band structures of Ti₂CO₂ under uniaxial tension along y direction. Because of the coupling effect between the bilayers, the upper and lower bands become much closer, and accordingly we focus on the most relevant 12 bands near the Fermi level. It can be seen that when the tension strain along y-axis is less than 5%, the gap increases with the increasing strain. As shown in Fig. 5f, the relative energy at x = 1.5 decreases as the increasing y-axial strain from 0 to 5%, which corresponds to a phase transformation accompanied by gap opening, i.e., the stable phase is gradually shifted from x = 1 to x = 1.5. The gap opening reaches the maximum and the system becomes the most stable state at the tension strain of 5%. After that, the strain leads to structural instability of the system so that its gap opening decreases and the barrier increases. Therefore, the ground state structure changes when the strain reaches a certain value under uniaxial tension in agreement with the variation of energy barrier, while the variation of gap opening shows an opposite trend before and after the structure change. In brief, the stretching of the path will increase the energy barrier along it, while the shortening of the path to a proper distance will generate the largest gap which can make the energy barrier close to 0. As shown at Fig. S8 in the ESI,† the stretching along the A–D path will produce the MEP from F to A to B. In a similar manner, the stretching along the B–E path, the MEP becomes from D to E and then to F, while the stretching along the A–D path, the MEP prefers from F to A and then to B. Therefore, the uniaxial strain may fundamentally modify the MEP due to anisotropic expansion of surface electronic state.

Fig. 6 The variation of the energy barrier of Ti₂CO₂-II with strain at the lengthened path (a). The variation of the energy barrier and band gap of Ti₂CO₂-II with y-axis strain at the lengthened path (b). The Brillouin zone is shown at (c). The energy band of Ti₂CO₂-II at 1% (d), 5% (e), and 9% (f) y-axis strain, respectively.

4. Conclusion

The stability and friction of the stacked two-dimensional transition metal carbides in different configurations are systematically studied. The key findings are summarized below:

(1) The oxygen-functionalized MXenes with larger lattice constants are more difficult to slide because the larger oxygen hollow at the surface hinders its sliding.

(2) The bare MXenes is found to possess much higher sliding resistance than the oxygen-functionalized one due to the strong metallic bonds between the stacked layers.

(3) Compared to the parallel stacked M₂CO₂-I, the mirror stacked M₂CO₂-II possesses a better lubricant property due to their much lower sliding energy barrier.

(4) Normal compression may effectively enhance the sliding barrier, while the in-plane biaxial tension may effectively hinder the interlayer sliding owing to different charges transferring from M to O atom.

(5) The uniaxial tension strain will fundamentally modify the MEP due to anisotropic expansion of surface electronic state. The in-depth analysis of deformed band structures under uniaxial tensions indicates that the gap shows an opposite variation as compared to the energy barrier, and the barrier reaches the minimum at the certain uniaxial strain.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by the National Key Research and Development Program of China (No. 2017YFB0702100 and 2016YFC1102500), National Natural Science Foundation of China (NFSC) with No. 51471018 and 51672015, the 111 Project (B17002), National Thousand Young Talents Program of China, and Fundamental Research Funds for the Central Universities. DL was supported by European Regional Development Fund in the IT4Innovations national supercomputing center – path to exascale project, project number CZ.02.1.01/0.0/0.0/16_013/0001791 within the Operational Programme Research, Development and Education and the Grant No. 17-27790S of the Czech Science Foundations and the National Programme of Sustainability (NPU II) project ‘IT4Innovations excellence in science—LQ1602’.

References

1. M. Hirano, K. Shinjo, R. Kaneko and Y. Murata, Phys. Rev. Lett., 1997, 78, 1448–1451.
2. C. M. Mate, G. M. McClelland, R. Erlandsson and S. Chiang, Phys. Rev. Lett., 1987, 59, 1942–1945.
3. M. Urbakh and E. Meyer, Nat. Mater., 2010, 9, 8–10.
4. W. Gao and A. Tkatchenko, Phys. Rev. Lett., 2015, 114, 096101.
5. M. Dienwiebel, G. S. Verhoeven, N. Pradeep, J. W. M. Frenken, J. A. Heimberg and H. W. Zandbergen, Phys. Rev. Lett., 2004, 92, 126101.
6. N. Sasaki, K. Kobayashi and M. Tsukada, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 2138–2149.
7. K. Matsushita, H. Matsukawa and N. Sasaki, Solid State Commun., 2005, 136, 51–55.
8. N. Marom, J. Bernstein, J. Garel, A. Tkatchenko, E. Joselevich, L. Kronik and O. Hod, Phys. Rev. Lett., 2010, 105, 046801.
9. C. Lee, Q. Li, W. Kalb, X.-Z. Liu, H. Berger, R. W. Carpick and J. Hone, Science, 2010, 328, 76–80.
10. J. M. Martin, C. Donnet, T. Le Mogne and T. Epicier, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10583–10586.
11. K. Miura and S. Kamiya, Europhys. Lett., 2002, 58, 610.
12. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
13. B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098.
14. H. Zhang, L. Wang, Q. Chen, P. Li, A. Zhou, X. Cao and Q. Hu, Mater. Des., 2016, 92, 682–689.
15. X. Zhang, M. Xue, X. Yang, Z. Wang, G. Luo, Z. Huang, X. Sui and C. Li, RSC Adv., 2015, 5, 2762–2767.
16. J. Yang, B. Chen, H. Song, H. Tang and C. Li, Cryst. Res. Technol., 2014, 49, 926–932.
17. T. Hu, M. Hu, Z. Li, H. Zhang, C. Zhang, J. Wang and X. Wang, Phys. Chem. Chem. Phys., 2016, 18, 20256–20260.
18. H. Wang, S. Xu, C. Tsai, Y. Li, C. Liu, J. Zhao, Y. Liu, H. Yuan, F. Abild-Pedersen, F. B. Prinz, J. K. Nørskov and Y. Cui, Science, 2016, 354, 1031–1036.
19. W. S. Yun, S. W. Han, S. C. Hong, I. G. Kim and J. D. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 033305.
20. S. Zhao, W. Kang and J. Xue, Appl. Phys. Lett., 2014, 104, 133106.
21. G. Levita, A. Cavaleiro, E. Molinari, T. Polcar and M. C. Righi, J. Phys. Chem. C, 2014, 118, 13809–13816.
22. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
26. D. Zhang, M. Ashton, A. Ostadhossein, A. C. T. van Duin, R. G. Hennig and S. B. Sinnott, ACS Appl. Mater. Interfaces, 2017, 9, 34467–34479.
27. S. Zhou, J. Han, S. Dai, J. Sun and D. J. Srolovitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155438.
28. S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703.
29. R. F. Zhang, D. Legut, Z. J. Lin, Y. S. Zhao, H. K. Mao and S. Veprek, Phys. Rev. Lett., 2012, 108, 255502.
30. Z. H. Fu, Q. F. Zhang, D. Legut, C. Si, T. C. Germann, T. Lookman, S. Y. Du, J. S. Francisco and R. F. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 104103.
31. M. A. Hope, A. C. Forse, K. J. Griffith, M. R. Lukatskaya, M. Ghidiu, Y. Gogotsi and C. P. Grey, Phys. Chem. Chem. Phys., 2016, 18, 5099–5102.
32. Y. Xie, M. Naguib, V. N. Mochalin, M. W. Barsoum, Y. Gogotsi, X. Yu, K.-W. Nam, X.-Q. Yang, A. I. Kolesnikov and P. R. Kent, J. Am. Chem. Soc., 2014, 136, 6385–6394.
33. M. Khazaei, M. Arai, T. Sasaki, C. Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192.
34. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
35. S. Cahangirov, C. Ataca, M. Topsakal, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2012, 108, 126103.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11139h

---