Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the solvation of metal ions in liquid ammonia: a molecular simulation study of M(NH2)x(NH3)y complexes as a function of pH
Dirk Zahn *
*
Lehrstuhl für Theoretische Chemie, Computer Chemie Centrum, Friedrich-Alexander Universität Erlangen-Nürnberg, Nägelsbachstraße 25, 91052 Erlangen, Germany. E-mail: dirk.zahn@fau.de
First published on 24th November 2017
Abstract
The solvation of mono-, di- and trivalent metal ions in liquid ammonia is characterized from molecular simulations. A central focus of the analyses is given by metal ion acidity within the respective solvent complexes. For this purpose, a recently developed model for estimating the pK of the auto-protolysis reaction 2NH3 → NH4+ + NH2− is transferred to assessing the ‘local’ pK of ammonia molecules coordinating a metal ion. On this basis, we identify MI/II(NH3)n+/++ complexes (M = Na+, K+, Mg2+ with n = 6 and M = Ca2+ with n = 8, respectively) as predominant species unless extremely ammono-basic conditions are imposed. On the other hand, the trivalent Al3+ and Ga3+ species were found to favor [Al(NH2)3(NH3)2]0 and [Ga(NH2)4]− complexes, respectively. The negatively charged complexes dominate over a wide range of pH for gallium ion solvation in ammonia, whilst [Al(NH2)4(NH3)2]− complexes require moderately ammono-basic solutions.
Introduction
While metal ion solvation in water has been investigated extensively,1 much less information is available for less common solvents. This situation hampers the fundamental understanding of solvothermal syntheses other than those based on water. Indeed, the hydrothermal syntheses of oxides experienced almost 200 years of development and is by now well-established in industry and their production exceeds megatons per year (mainly of Al2O3).2,3 However, solvothermal syntheses based on ammonia are currently becoming increasingly popular as potential routes to nitrides and amides.4,5Ammonothermal syntheses appear particularly interesting for aluminum and gallium nitrides which are semiconductors that are difficult to formulate as large single crystals.4,6,7 It is thus of fundamental importance to characterize the nature of Al3+ and Ga3+ ions in ammonia solution. However, also the role of di- and monovalent metal ions is of eminent interest as these species are used for mixed metal nitrides/amides.4 The larger the valence of the metal ion the more imperative it becomes to consider its effect on possible proton transfer reactions. In analogy to water, liquid ammonia also reflects a protic solvent with a pK of 32 (at 1 atm and 239 K) and 28 (at 300 K with fixed density to that at 239 K), respectively.8 Such low tendencies to solvent autoprotolysis may however change drastically for molecule coordinating a metal ion.
While hard to assess from experiment – in particular when high-pressure autoclaves are used – molecular dynamics simulations provide particularly detailed insights into atomic scale interactions accounting for ion solvation. In the present study, we use this technique to explore metal ion solvation in ammonia in combination with a recent approach to estimating the pK for the autoprotolysis of solvent molecules in bulk ammonia.8
Theory
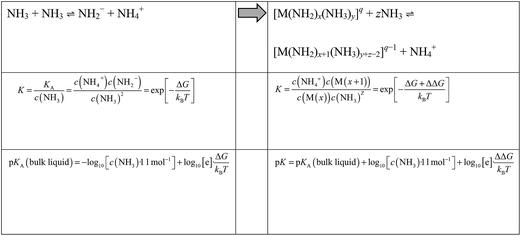
By means of Boltzmann statistics, the equilibrium constants of auto-protolyses processes may be related to the underlying free energy change ΔG. Within a recently developed quantum/molecular mechanics approach this is calculated from the quantum chemical assessment of the difference in proton affinity of the molecules in the gas phase and the change in solvation free energy as estimated from molecular dynamics simulations.8 When moving from auto-protolysis in the bulk liquid to the deprotonation of ammonia molecules within metal ion complexes, we can estimate free energy differences analogously. Thus, the pK of the bulk liquid changes to a ‘local pK’ according to Scheme 1.Where M refers to a metal ion and q to the charge of [M(NH2)x(NH3)y]q complexes. Note that K and pK refer to the overall reaction involving two NH3 molecules (one donor and one acceptor) and are thus dimensionless. Upon deprotonation of [M(NH2)x(NH3)y]q complexes, the NH4+ ion is always migrated to the solution. The resulting [M(NH2)x+1(NH3)y+z−2]q complex may change its overall coordination number by associating (z > 0) or dissociating (z < 0) ammonia molecules to/from its coordination polyhedron. This depends on the specific metal ion as discussed in the results section.
Both sides of Scheme 1 refer to idealized systems, that is pure ammonia (left side of Scheme 1) and a single metal ion M in pure ammonia (right side of Scheme 1), respectively. Note that activity coefficients used for interpreting experimental data of real solutions reflect the need to combine ammonia auto-protolyses in bulk NH3 and next to solvated ions. Using ideal solution models, our simulations however can address the respective equilibrium constants separately.
Within the metal complexes, the free energy change for auto-protolysis includes a correction term ΔΔG, which represents the change in solvation free energy upon NH3/NH2− association to the metal ion. This specific change in local interactions is clearly dominated by the electrostatics and thus the potential energy of the underlying complexes in solution. To obtain inexpensive estimates of ΔΔG we therefore use the change in potential energy (averaged over time at 300 K) of NH2− solvation in pure ammonia compared to association to the metal cluster.
Simulation details
The changes in solvation energy were assessed from molecular dynamics simulations based on molecular mechanics models. The force-fields for NH4+, NH3 and NH2− are adopted from our earlier work reported in ref. 8. For the mono- and di-valent metal ions we employed the Lennard-Jones model from Merz and coworkers.9,10 The Al3+ model could also be adopted from this group,11 while for Ga3+ the force-field of Gale and coworkers was used.12 This approach ensures formal charges for all ions, thus allowing to model complex formation/dissociation without the need of quantum mechanical calculations. The accuracy of the employed force-fields may be judged on the basis of the coordination numbers as observed from the experiment. While experimental data is still rather sparse, the coordination of alkali metal ions and of gallium ions as discussed in the results section provides a basis for such comparison.In full analogy to our earlier study,8 the simulation system is based on a cubic box of 1000 ammonia molecules imposing periodic boundary conditions to mimic an infinite liquid phase. To this, one metal ion is inserted and 2–4 ammonia are deprotonated (replaced by NH2− ions), depending on the valence of the metal ion. To also allow for possible over-compensation of the metal ion charge by amide association, we chose Na+/K+ + 2NH2− + 998NH3, Mg++/Ca++ + 2NH2− + 998NH3 and Al3+/Ga3+ + 4NH2− + 996NH3 systems which excess charge was levelled using the homogeneous, diffuse background charge approach.
Molecular dynamics simulations were run by the dlpoly package using a time-step of 1 fs and shifted-force cut-off potentials with rcut = 12 Å.13 Each model was equilibrated for 1 ns at 240 K and 1 atm within constant temperature, constant pressure runs. To mimic an autoclave scenario, the volume is fixed to maintain the average solution density at 240 K whilst further molecular dynamics are performed at elevated temperature. Production runs are performed for 0.5–1 ns at 300 K after allowing 100 ps relaxation. The quality of data sampling (i.e. the solvation energy differences) was monitored from comparing results obtained for the first half of the trajectory to that of the second part and imposing less than 1% statistical error. Average nearest-neighbor distances and coordination numbers were computed by means of the corresponding radial distribution functions.
Results
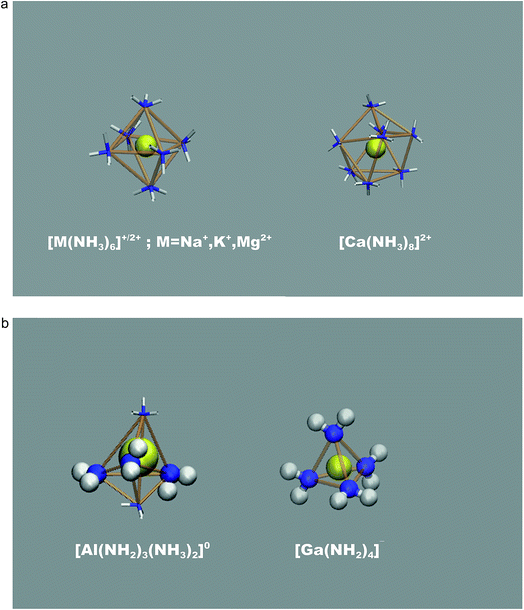
An illustration of the overall simulation model is provide by the example of Mg2+ solvation in liquid ammonia in Fig. 1. This simulation run exhibited clearly separated ionic species, each coordinated by the NH3 solvent molecules only. This picture holds for all mono- and divalent metal ions investigated (Na+, K+, Mg2+, Ca2+), however at different M(NH3)y complex arrangements. While Na+, K+ and Mg2+ ions are octahedrally coordinated, we found 8-fold coordination to be preferred for the calcium ions (Fig. 2a). The corresponding metal–nitrogen atom distances are denoted in Tables 1 and 2. Note that the observed octahedral coordination for the alkali metal ions in pure ammonia nicely agrees with the experimentally identified coordination numbers with range from 5.5 to 6.4 for Na+ and Rb+, respectively.14,15| MI(NH2)x(NH3)y1−x | x = 0 | x = 1 | x = 2 | x = 3 | x = 4 |
|---|---|---|---|---|---|
| M = Na | y = 6 | y = 4 | y = 2 | — | — |
| d(M–NH2) | — | 1 × 2.3 Å | 2 × 2.25 Å | ||
| d(M–NH3) | 6 × 2.35 Å | 4 × 2.3 Å | 2 × 2.55 Å | ||
| ΔG–ΔΔG/kJ mol−1 | G = 0 | +120 | +289 | ||
| pKa | 21 | 25 | — | ||
| M = K | y = 6 | y = 6 | y = 3 | — | — |
| d(M–NH2) | — | 1 × 2.7 Å | 2 × 2.6 Å | ||
| d(M–NH3) | 6 × 2.8 Å | 6 × 2.8 Å | 3 × 2.8 Å | ||
| ΔG–ΔΔG/kJ mol−1 | G = 0 | +201 | +343 | ||
| pKa | 35 | 36 | — |
| MII(NH2)x(NH3)y2−x | x = 0 | x = 1 | x = 2 | x = 3 | x = 4 |
|---|---|---|---|---|---|
| M = Mg | y = 6 | y = 5 | y = 2 | — | — |
| d(M–NH2) | — | 1 × 2.2 Å | 2 × 2.1 Å | ||
| d(M–NH3) | 6 × 2.2 Å | 5 × 2.2 Å | 2 × 2.3 Å | ||
| ΔG–ΔΔG/kJ mol−1 | G = 0 | +258 | +337 | ||
| pKa | 29 | Unstable | — | ||
| M = Ca | y = 8 | y = 6 | y = 3 | — | — |
| d(M–NH2) | — | 1 × 2.7 Å | 2 × 2.6 Å | ||
| d(M–NH3) | 8 × 2.7 Å | 6 × 2.8 Å | 3 × 2.8 Å | ||
| ΔG–ΔΔG/kJ mol−1 | G = 0 | +158 | +247 | ||
| pKa | 21 | Unstable | — |
While this data is in line with earlier studies on mono- and divalent metal ion coordination by NH3,16 the novel aspect of the present study is the assessment of amide formation assisted by the metal ion. For this purpose, M(NH2)x clusters in ammonia solution were prepared and subjected to relaxation. For the mono- and divalent metal ions investigated, metal clusters with x = 0, 1 and 2 were found to be sufficiently metastable to assess time averages of the corresponding solvation energy. The energy difference for NH2− desolvation from liquid ammonia and association to the (solvated) metal cluster is then taken as the ΔΔG term in Scheme 1 for assessing the change in pK with respect to the bulk liquid. The ‘local pK’ of ammonia within the M(NH2)x clusters, along with the net free energy differences ΔG–ΔΔG is provided in Tables 1–3.
| MIII(NH2)x(NH3)y3−x | x = 0 | x = 1 | x = 2 | x = 3 | x = 4 |
|---|---|---|---|---|---|
| M = Al | — | — | y = 8 | y = 2 | y = 2 |
| d(M–NH2) | 2 × 2.8 Å | 2 × 1.7 Å | 2 × 1.7 Å | ||
| d(M–NH3) | 8 × 2.9 Å | 4 × 2.3 Å | 4 × 2.3 Å | ||
| ΔG–ΔΔG/kJ mol−1 | −282 | G = 0 | +89 | ||
| pKa | −49 | 15.5 | — | ||
| M = Ga | — | — | y = 4 | y = 2 | y = 0 |
| d(M–NH2) | 2 × 1.7 Å | 3 × 1.8 Å | 4 × 1.7 Å | ||
| d(M–NH3) | 4 × 2.3 Å | 2 × 2.4 Å | — | ||
| ΔG–ΔΔG/kJ mol−1 | −361 | G = 0 | +7 | ||
| pKa | −63 | 1.2 | — |
For Na+ and K+ we find the predominant solvated species are octahedral M(NH3)6+ (M = Na, K) complexes unless extremely basic conditions are implemented. The estimated pK values of the Na(NH3)6+ and K(NH3)6+ are 21 and 35, respectively. The association of dispersed NH2− ions to the monovalent ions in liquid ammonia was found to be favored by 57 kJ mol−1 for Na+, and disfavored by 24 kJ mol−1 for K+, respectively. This implies marginal reduction of the pK as compared to the bulk liquid (28 at 300 K) upon introducing Na+ ions, whilst K+ ions do not assist the auto-protolysis at all.
In a similar fashion, the divalent ions Mg2+ and Ca2+ are also found as M(NH3)y2+ complexes (with y = 6 and 8 for M = Mg and Ca, respectively) showing weak support for ammonia deprotonation. According to our ‘local pK’ estimates, ammonia molecules next to Mg2+ ions are slightly less likely to undergo auto-protolysis compared to the bulk liquid. On the other hand, Ca2+ ions assist amide formation similarly weak as Na+, but imposing two-fold complex deprotonation and relaxation (experienced as dissociation of 3NH3 molecules) was found to lead to the neutral [Ca(NH2)2(NH3)3] species.
For the trivalent metal ions explored, we however find a strikingly different trend. The Ga3+ ion species supports NH2− association rather drastically, actually overcompensating the free energy change required for ammonia auto-protolysis. As illustrated in Fig. 2b, the predominant solvated species is given by [Ga(NH2)4]− – hence negatively charged, tetrahedral amide complexes. This was recently suggested from the experiments of Niewa and coworkers.17 Indeed, our ‘local pK’ estimate implies that rather drastic ammono-acidic conditions are required to obtain the charge neutral Ga(NH2)3(NH3)20 complex. Gallium complexes with less than 3 amide ions in the coordination shell could not be observed as stable species coexisting with dispersed NH2− in solution, thus further underlining the extreme tendency to amide formation next to the gallium ion.
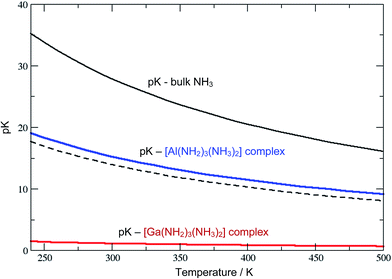
The Al3+ ions also behave ammono-acidic, but comparably weaker than Ga3+. At ammono-neutral conditions the uncharged Al(NH2)3(NH3)20 complex is most preferred. Therein the 3NH2− ions form a triangle, whilst the 2NH3 molecules constitute the top/bottom of a trigonal bi-pyramid. This unusual 5-fold coordination however reflects a pK of 15.5 which is near the pH of ammono-neutral solutions (14 at 300 K). Thus, already mildly basic conditions lead to the formation of negatively charged Al(NH2)4(NH3)2− complexes. For direct comparison, we plotted the pK of the bulk liquid and ammonia within the uncharged M(NH2)3(NH3)20 (M = Al, Ga) complexes as functions of temperature in Fig. 3.
Apart from the experimental and simulation data available for metal ion solvation in ammonia, at least some degree of comparison may be given by the different types of [M(NH3)x]q complexes in crystalline compounds. For example, 8-fold coordinated [Ca(NH3)8]2+ complexes were observed in iodine and bromide salts, however not exhibiting a square-antiprismatic coordination. Moreover, the iodide compound showed transformation to [Ca(NH3)6]I2 upon heating.18 We feel that the gap between complexes embedded in crystal structures and those dispersed in liquid solution is too large to provide robust knowledge. In analogy to our recent study on ZnO precipitation from Zn2+/2OH− solution, yet ongoing efforts will therefore address the association of larger numbers of metal and amide ions to elaborate nucleation mechanisms including de-protonation and re-organization as functions of aggregate size.19,20
Conclusion
The ‘local pK’ concept allows the inexpensive assessment of the protonation state of metal ion complexes in protic solution. Based on an earlier quantum/molecular mechanics simulation study of the auto-protolysis in liquid ammonia, we now outlined the calculation of ΔpK correction terms. For both, NH3 auto-protolysis in the bulk liquid and when assisted by a metal ion complex, the excess H+ is dispersed in the ammonia solution. The underlying ΔΔG solvation free energy is therefore given by the metal–ammonia versus metal–amide interactions, only. As these are dominated by electrostatics and van-der-Waals forces, we suggest the differences in the average potential energy as reasonable approximates to ΔΔG. Using this simulation approach, a number of ionic species and different protonation states may be screened very effectively by means of molecular mechanics simulations. Our results demonstrate the role of both, metal ion charge and ion size in promoting different coordination clusters as functions of pH.Conflicts of interest
There are no conflicts to declare.References
- The Chemical Physics of Solvation, ed. R. R. Dogonadze, Elsevier, Amsterdam, 1985 Search PubMed.
- R. Bunsen, Ann. Phys., 1839, 46, 97–103 CrossRef.
- K. Byrappa and M. Yoshimura, Handbook of Hydrothermal Technology: a Technology for Crystal Growth and Materials processing, Noyes Publications/William Andrew Publishing, LLC, Park Ridge, NY, USA, 2001 Search PubMed.
- T. M. M. Richter and R. Niewa, Inorganics, 2014, 2, 29–78 CrossRef CAS.
- H. Cao, J. Guo, F. Chang, C. Pistidda, W. Zhou, X. Zhang, A. Santoru, H. Wu, N. Schell, R. Niewa, P. Chen, T. Klassen and M. Dornheim, Chem.–Eur. J., 2017, 23, 9766–9771 CrossRef CAS PubMed.
- R. Dwilinski, A. Wysmolek, J. Baranowski, M. Kaminska, R. Doradzinski and H. Jacobs, Acta Phys. Pol., A, 1995, 88, 833–836 CrossRef CAS.
- Y. C. Lan, X. L. Chen, Y. G. Gao, Y. P. Yu, L. Xu and J. K. Liang, J. Cryst. Growth, 1999, 207, 247–250 CrossRef CAS.
- D. Zahn, Chem. Phys. Lett., 2017, 682, 55–59 CrossRef CAS.
- P. Li, L. F. Song and K. M. Merz, J. Chem. Theory Comput., 2015, 11, 1645–1657 CrossRef CAS PubMed.
- P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748 CrossRef CAS PubMed.
- P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2015, 119, 883–895 CrossRef CAS PubMed.
- P. Zapol, R. Pandey and J. D. Gale, J. Phys.: Condens. Matter, 1997, 9, 9517–9525 CrossRef CAS.
- http://www.scd.stfc.ac.uk/SCD/44516.aspx.
- J. C. Wasse, S. Hayama, S. Masmanidis, S. L. Stebbings and N. T. Skipper, J. Chem. Phys., 2003, 118, 7486–7494 CrossRef CAS.
- J. C. Wasse, S. Hayama and N. T. Skipper, J. Phys. Chem. B, 2003, 107, 14452–14456 CrossRef CAS.
- S. Hannongbua, M. Kiselev and K. Heinzinger, Condens. Matter Phys., 2000, 3, 381–392 CrossRef.
- J. Hertrampf, E. Schlücker, D. Gudat and R. Niewa, Cryst. Growth Des., 2017, 17, 4855–4863 CAS.
- P. Woidy, A. J. Karttunen, T. G. Müller and F. Kraus, Z. Naturforsch., B: J. Chem. Sci., 2014, 69, 1141–1148 CAS.
- A. Kawska, P. Duchstein, O. Hochrein and D. Zahn, Nano Lett., 2008, 8, 2336–2340 CrossRef CAS PubMed.
- J. Anwar and D. Zahn, Angew. Chem., Int. Ed., 2011, 50, 1996–2013 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |