Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the cooperative atomic motion and shape change of ultrasmall Au nanoparticles below the premelting temperature†
Ying Yang*a and
Ning Yan *b
*b
aDepartment of Mechanics and Engineering Structure, Wuhan University of Technology, 430070 Wuhan, China. E-mail: yangying@whut.edu.cn
bVan't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: n.yan@uva.nl
First published on 8th December 2017
Abstract
Surface melting is widely observed in crystalline materials, which has a significant influence on their interfacial properties. In this computational study using molecular dynamics simulations, we observed that at 50 K below the onset temperature of surface melting, the “out-shell” atoms of ultrasmall Au nanoparticles (NPs) have already undergone remarkable rearrangements. Unlike the observations in Ni ultrasmall NPs, the resulting shape change was often isotropic. Further investigations reveal that such interfacial motions are cooperative and string-like. The gold “atom strings” do not migrate through the center of the particle, behaving similarly as those in much larger particles. Therefore, the “spherical” shape was sustained during the atomic motions. This result reveals the dynamic nature of the atomic motions of Au before the commencement of premelting and sheds light on the understanding of the origin of surface melting.
Thanks to a high surface-to-volume ratio and quantum size effects, nanomaterials are playing increasingly pivotal roles in various catalytic reactions.1 Gold is a very good example: this shiny yellow metal does not tarnish at ambient conditions, and for a long time it was considered catalytically “less-active”, if not inert, compared to other metals. This empiricism completely changed when Bond discovered the superior performances of nanometric gold catalysts in olefin hydrogenation reactions in the 1970s.2 Since then, gold nanoparticles (NPs) have been showing fascinating catalytic performances in the fields of chemical industry, environmental protection and in vitro/in vivo applications.3–5 To trigger the high activity of gold, the NPs are often sufficiently small, ranging from 1–5 nm, the size- and shape-dependent performances therefore become much more prominent.6–9 In particular, Au NPs with a diameter of 1–2 nm have been reported with significantly improved catalytically activity than the larger counterparts.10–12 A classic example is the 55-atom gold cluster (∼1.4 nm) which showed superior selective oxidation activity using molecular oxygen.10
However, these ultrasmall NPs are inherently more sensitive to the surrounding environmental conditions.13–15 They often meet the energetic requirement,16 suffering shape transformation, sintering and/or surface melting below the bulk melting temperature.15,17–19 In particular, premelting phenomenon has much interested chemists and condensed matter physicists alike, and been widely documented previously in many metals and experimentally verified for Pt and Pb.19,20 Nonetheless, understanding the interfacial dynamics and the structural evolution of NPs at those states are challenging when using the conventional experimental approaches.17 In contrast, computational investigations offer a viable alternative. For example, molecular dynamics (MD) simulation has been applied to determine the surface melting temperature, revealing various interfacial effects, e.g., relaxation, reconstruction, roughening and wetting, when T approaches the melting point.18,21–23 Marzari et al. concluded that two distinct “channels” on the surface facilitated the initiation of premelting;24 Farson et al. suggested that liquid-like atoms first appeared at the vertices and edges of NPs.18 The interfacial dynamics of Ni nanoparticles was systematically investigated by Zhang et al., further elucidating the presence of string-like atomic motion in the “premelted” surface.25–27 We also observed that the collective motion led to substantial shape fluctuations of ultrasmall Ni NPs, driving Ni atom to move from the center to the surface and vice versa.28 In this work, we focused on the interfacial dynamics of an Au NP comprising of 55 atoms at 50 K below the onset temperature of surface melting and showed the nature of the remarkable atomic rearrangements.
Our MD simulations were performed using the software of LAMMPS developed at Sandia National Laboratories and the classical Sutton–Chen potential.29,30 This many-body potential provides more accurate simulation of metallic materials than the previously used two-body interaction potentials such as the Lennard-Jones interaction.22,31 It also specifically favors the FCC crystal structure and fits empirically to the properties regarding the surface, defects and grain boundaries of Au.29 The free-stand Au NP, containing 55 atoms, was constructed in the vacuum surrounding environment. Prior to all the studies, the NPs were first relaxed at room temperature (300 K) for 1.5 ns with zero angular and linear momentum values. Subsequently, the N55 NP quickly transformed into the more stable icosahedral structure. Then, the NPs were heated up at a rate of 100 K ns−1 from room temperature (T = 300 K) till 1400 K, allowing us to examine the solid–liquid phase transition of the material. To probe the interfacial dynamics as well as the atomic motions, we also performed the ‘isothermal’ studies at the fixed temperature. This isothermal simulation was performed at the designed temperatures for 3 ns after each T-jump. The melting temperature (Tm), radius of gyration (Rg) that quantify the shape characteristics of NPs, 3D distribution and dynamic positions of atoms were determined using the mathematical model reported in our previous work.28 The details were also shown in the ESI.†
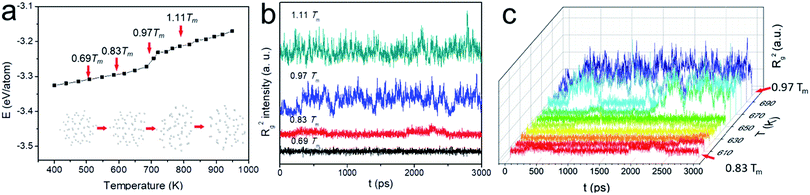
Because of the increased surface energy, the melting temperature of ultrasmall Au NP is substantially lower than that of the bulk and varied as a function of its size. We therefore determined Tm first for better dynamic study. The potential energy plot in Fig. 1a was obtained in the heating cycle. Clearly, there are three stages in the energy ramp. The middle stage with a steeper slope corresponded to the melting process, suggesting the coexistence of the liquid and solid phase. In contrast to the melting of bulk materials which occurred at a fixed temperature with an abrupt potential increase, the melting of N55 NP happened between ca. 650 K and 720 K. This was the typical observation during the surface melting of NPs.21 Tm was determined when the NP became fully liquid, i.e., 720 K. Tw (650 K) was the onset temperature of premelting, the subscript “w” denotes “wetting” which is the early stage of surface melting. This temperature was higher than the NPs consisting of >100 atoms, such abnormal size-effect was also observed when studying N55 Ni NPs.28
 | ||
| Fig. 1 (a) Potential energy plot in the heating cycle of Au NPs; (b, c) the variation of Rg2 as a function of time for N55 Au NP at different temperatures. | ||
Based on this plot, we selected four representative study temperatures as indicated by the red arrows in the figure: 0.69Tm (500 K) and 1.11Tm (800 K) suggested the full solid and liquid state, respectively; 0.97Tm (700 K) fell into the surface melting region; 0.83Tm (600 K) ensured no premelting (50 K below Tw), yet the NP is about to melt at the surface. Fig. 1b shows the spectra of Rg2 as a function of time at these temperatures. At relatively low temperatures, e.g., 0.69Tm, Rg2 seldom fluctuated, suggesting the NP was rather spherical. Because of the presence of liquid phase at sufficiently high temperature, e.g., 0.97Tm and 1.11Tm, the particle underwent significant anisotropic shape changes. 0.83Tm was however unique as heterogeneous Rg2 fluctuations were observed, possibly inferring the presence of different type of “change” of the NP. This trend well agreed with the plot of the potential energy (see Fig. S1†). To examine this “premelting incubation” state, we also had a detailed investigation from 0.83Tm to 0.97Tm (600 K to 700 K). Notwithstanding the fact that peaks were observed in all the E and Rg2 spectra below Tw, their intensities were much weaker till ∼ca. 650 K (see Fig. 1c and S2†) when wetting occurred. Therefore, 0.83Tm (600 K) was indeed suitable for studying the dynamic motions of Au NP below Tw.
In order to explore the aforementioned NPs “change”, we used various shape factors to characterize the associated shape transformations (see the ESI† for details). In brief, λi (i = 1, 2, 3) is the displacement at each axis in the transformed Cartesian coordinates, the sum of which equals to the squared radius of gyration. b, c, and k2 are asphericity, acylindricity and relative shape anisotropy, respectively. They all describe the symmetricity of the atoms in the NPs. The plot in Fig. 2a shows that, at some particular moments, each λi became unequal in value, implying that the shape change has taken place. The peaks in b and c suggested that the NP no longer held the symmetric structure, but turned into the aspherical or acylindrical shape. The spikes in the overall shape factor k2 plot further indicated that the structural evolution have led to shape anisotropy below Tw. Interestingly, such shape anisotropic variation was trivial compared to that at T > Tw and (see Fig. S3†). Further studies of the NPs' “change” are thus important.
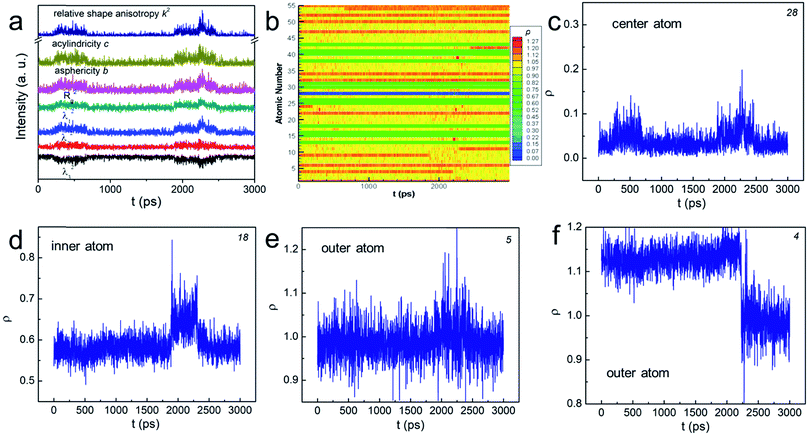 | ||
| Fig. 2 (a and b) The change of various shape factors as a function of time for N55 Au NP at 0.83Tm. The number at the corner of (c)–(f) indicates the atom number in (b). | ||
We then determined the dynamic positions (ρ, see the ESI† for the definition) of all the atoms at the radial direction. The value of 0 means that the atom occupies the central position whereas the value of 1 indicates that the atom sits on the boundary of the “sphere” (see Scheme S1†). The atom escapes from the initial “sphere” when ρ > 1. Fig. 2b plots ρ of all atoms numbered from 1 to 55 as a function of time using distinct colors. In general, the positions of “inner-core” atoms did not change significantly at the radial direction as shown by the nearly “all-blue/green” stripes. For example, atom 28, the center atom, basically remained at the center position despite two minor displacements (see Fig. 2c); atom 18's ρ stayed at ∼0.6 (Fig. 2d). Conversely, the atoms at the “outer-shell” behaved quite differently. On one hand, they could frequently move outward and inward, showing a significantly fluctuated ρ plot (see the mixed yellow-red stripes and atom 5 in Fig. 2e). On the other hand, such movements, either outward or inward, could be permanent (see Fig. 2f and S4†). Because these interfacial atoms were less-coordinated, their motions were inherently more intense. Therefore, we understood that these atoms contributed the most to the rearrangement of the NP before premelting. These gold atoms do not migrate through the center of the particle, behaving similarly as those in much larger particles. The shape change was therefore often isotropic and the “spherical” shape was sustained during the atomic rearrangement. This conclusion correlated with the previous models summarized in ref. 20.
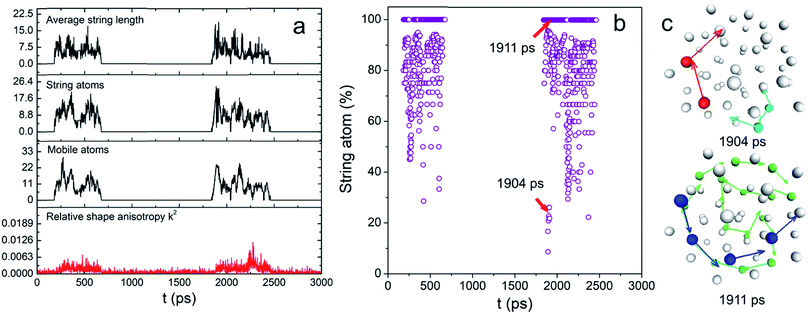
Intuitively, one would imagine how the atoms move that triggers the surface melting, causing the interfacial atomic rearrangement. Such motions might be either “diffusion-like” or cooperative and orderly. The former is the most common way of random atomic movement whereas the latter phenomenon has been observed in both liquid and solid including the glass-forming liquid and the grain boundary of metals.32 To characterize the overall dynamic motions of the atom, both radially and tangentially, we used the same mathematical models and evaluation criteria reported previously to study the stringlike motions of atom in the NP, which involves the determinations of the non-Gaussian parameter α2 and van Hove correlation function Gs (r, t).25–28 Details are also shown in the ESI†.
These two functions at 0.83Tm for N55 Au NP are plotted in Fig. S5.† The final results are shown in Fig. 3a. Remarkably, the mobile atom number is relatively small (<30) compared with that of a premelted NP.28 However, at many time points, the majority of the mobile atoms moved cooperatively (see Fig. 3b). Besides, long-chain stringlike motions dominated in this interfacial dynamics (length > 5 atoms) as shown in Fig. S6.† To have a clear view of the collective atomic motion, we depicted the atomic configuration of the NP at the time when stringlike motion prevailed in Fig. 3c. At two representative time points when the string atom ratios were 28% and 100%, we observed the sequential movement of colored atoms toward the directions shown by the arrows. Interestingly, the center atoms do not participate in the string motions and nearly all the atom strings hardly move though the center position of the particle. Because of this, the shape change of the NP was largely isotropic (see above). Besides, a short movie of the atomic motion (1950–2250 ps, see the ESI†) also shows that the center and inner atoms were essentially stable, yet the outer atoms could move aggressively. We therefore concluded that before the onset of surface melting, the interfacial atoms have already undergone substantial and cooperative rearrangement. These stringlike atomic movements might induce the local energy fluctuations and create more defects such as dislocations/grain boundaries,17 seeding the sequential nucleation of the “quasi-liquid” surface.
Conclusions
In summary, our molecular dynamics simulation indicated that ultrasmall Au NP underwent remarkable rearrangements at 50 K before the onset of surface melting temperature. The interfacial atomic motions were cooperative and string-like, yet the atom strings did not move through the center position of the nanoparticle, a phenomenon often observed in much larger particles. Thus, the resulting shape variation was largely isotropic. Our work reveals the dynamic nature of the atomic rearrangement before the commencement of premelting. It might provide a new dimension of understanding the movement of atoms at the interface and shed light on researching various physico-chemical properties of nanoparticles (e.g., sintering, reconstruction and catalytic activity).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the computing facilities and the support of WHUT under the program numbered 40120392. N. Y. also thank the support from the Netherlands Organization for Scientific Research (NWO) from NWO-GDST project (no. 729.001.022).References
- A. T. Bell, Science, 2003, 299, 1688–1691 CrossRef CAS PubMed.
- G. C. Bond, P. A. Sermon, G. Webb, D. A. Buchanan and P. B. Wells, J. Chem. Soc., Chem. Commun., 1973, 444b–445 RSC.
- M. C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936 CrossRef PubMed.
- A. Corma and H. Garcia, Chem. Soc. Rev., 2008, 37, 2096–2126 RSC.
- L. Wang, H. Wang, A. E. Rice, W. Zhang, X. Li, M. Chen, X. Meng, J. P. Lewis and F.-S. Xiao, J. Phys. Chem. Lett., 2015, 6, 2345–2349 CrossRef CAS PubMed.
- M. K. Kundu, T. Bhowmik and S. Barman, J. Mater. Chem. A, 2015, 3, 23120–23135 CAS.
- J. Y. Xiao and L. M. Qi, Nanoscale, 2011, 3, 1383–1396 RSC.
- A. Leifert, Y. Pan-Bartnek, U. Simon and W. Jahnen-Dechent, Nanoscale, 2013, 5, 6224–6242 RSC.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981 CrossRef CAS PubMed.
- H. Tsunoyama, H. Sakurai, Y. Negishi and T. Tsukuda, J. Am. Chem. Soc., 2005, 127, 9374–9375 CrossRef CAS PubMed.
- Z. Wang, Q. Zhang, D. Kuehner, A. Ivaska and L. Niu, Green Chem., 2008, 10, 907–909 RSC.
- G. Li and R. C. Jin, Acc. Chem. Res., 2013, 46, 1749–1758 CrossRef CAS PubMed.
- B. H. Kim, M. J. Hackett, J. Park and T. Hyeon, Chem. Mater., 2014, 26, 59–71 CrossRef CAS.
- S. Inasawa, M. Sugiyama and Y. Yamaguchi, J. Phys. Chem. B, 2005, 109, 3104–3111 CrossRef CAS PubMed.
- Y. Lereah, R. Kofman, J. M. Penisson, G. Deutscher, P. Cheyssac, T. Ben David and A. Bourret, Philos. Mag. B, 2001, 81, 1801–1819 CrossRef CAS.
- B. Li, F. Wang, D. Zhou, Y. Peng, R. Ni and Y. L. Han, Nature, 2016, 531, 485–488 CrossRef CAS PubMed.
- N. Y. Wang, S. I. Rokhlin and D. F. Farson, Nanotechnology, 2008, 19, 415701 CrossRef PubMed.
- Z. L. Wang, J. M. Petroski, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 6145–6151 CrossRef CAS.
- K. F. Peters, J. B. Cohen and Y. W. Chung, Phys. Rev. B, 1998, 57, 13430–13438 CrossRef CAS.
- H. A. Alarifi, M. Atiş, C. Özdoğan, A. Hu, M. Yavuz and Y. Zhou, J. Phys. Chem. C, 2013, 117, 12289–12298 CAS.
- V. Rosato, G. Ciccotti and V. Pontikis, Phys. Rev. B, 1986, 33, 1860–1870 CrossRef CAS.
- Q. S. Mei and K. Lu, Prog. Mater. Sci., 2007, 52, 1175–1262 CrossRef CAS.
- N. Marzari, D. Vanderbilt, A. De Vita and M. C. Payne, Phys. Rev. Lett., 1999, 82, 3296–3299 CrossRef CAS.
- H. Zhang and J. F. Douglas, Soft Matter, 2013, 9, 1254–1265 RSC.
- H. Zhang and J. F. Douglas, Soft Matter, 2013, 9, 1266–1280 RSC.
- H. Zhang, P. Kalvapalle and J. F. Douglas, J. Phys. Chem. B, 2011, 115, 14068–14076 CrossRef CAS PubMed.
- Y. Yang, H. Zhang and J. F. Douglas, ACS Nano, 2014, 8, 7465–7477 CrossRef CAS PubMed.
- G. J. Ackland, G. Tichy, V. Vitek and M. W. Finnis, Philos. Mag. A, 1987, 56, 735–756 CrossRef CAS.
- A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146 CrossRef.
- J. P. Vandereerden, Faraday Discuss., 1993, 95, 65–74 RSC.
- H. Zhang, D. J. Srolovitz, J. F. Douglas and J. A. Warren, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 7735–7740 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11604g |
| This journal is © The Royal Society of Chemistry 2017 |