Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Differences between the elimination of early and late transition metals: DFT mechanistic insights into the titanium-catalyzed synthesis of pyrroles from alkynes and diazenes†
Jiandong
Guo
a,
Xi
Deng
a,
Chunyu
Song
a,
Yu
Lu
a,
Shuanglin
Qu
 a,
Yanfeng
Dang
ab and
Zhi-Xiang
Wang
a,
Yanfeng
Dang
ab and
Zhi-Xiang
Wang
 *ab
*ab
aSchool of Chemistry and Chemical Engineering, University of the Chinese Academy of Sciences, Beijing 100049, China. E-mail: zxwang@ucas.ac.cn
bCollaborative Innovation Center of Chemical Science and Engineering, Tianjin 300072, China
First published on 22nd December 2016
Abstract
Early transition metals (TMs), such as titanium, generally resist undergoing reductive elimination to form C–X bonds due to their weak electronegativity. By analyzing the mechanism of the titanium-catalyzed synthesis of pyrroles from alkynes and diazenes, the present study revealed that titanium is able to promote C–N bond formation via an unconventional elimination pathway, passing through a comparatively stable masked TiII complex (i.e., IM4) rather than pyrrole directly. The formation of IM4 originates from the bilateral donation and back-donation between Ti and the pyrrole ligand. Formally, it could be considered that the two electrons resulting from the unconventional reductive elimination are temporarily buffered by back-donation to a symmetry-allowed unoccupied π-orbital of the pyrrole ring in IM4 rather than becoming a lone pair on a Ti center as adopted in the catalysis of late TMs. Because of its stability, IM4 requires additional oxidation by diazene to liberate pyrrole. The triplet counterpart (IM4T) of IM4 is more stable than IM4, but the elimination is unlikely to reach IM4T, because the process is spin-forbidden and the spin–orbit coupling is weak. Alternatively, one may consider the forming pyrrole in IM4 as a redox-active ligand, reserving the two electrons resulting from the formal reductive elimination and then releasing the electrons when IM4 is oxidized by diazene. These insights allow us to propose the conditions for early TMs to undergo a similar elimination, whereby the forming product will have symmetry-allowed frontier molecular orbitals to form donation and back-donation bonding with a TM center and a substrate possessing a comparatively strong oxidizing ability to oxidize an IM4-like intermediate for product release. These insights may provide another way of constructing C–X bonds through a similar reductive elimination pathway, using early TM catalysts.
1. Introduction
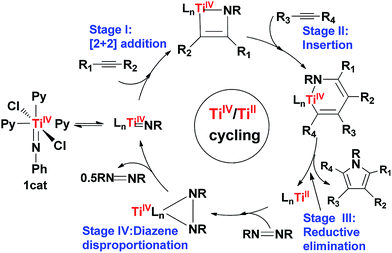
Titanium is a desirable transition metal (TM) for developing green catalytic transformations because of its abundance and non-toxicity.1 Among others, recent developments in titanium catalysis have been dominated by transformations involving hydrofunctionalization.1,2 Compared to catalysis with late TMs, such as Ru, Rh, Pd, and Ir, the variety of titanium catalysis is limited, which is commonly attributed to titanium's strong resistance to undergo redox cycling (e.g., TiIV/TiII) because of its weak electronegativity, and thus efforts have been devoted to develop redox catalysis with early TMs using redox-active ligands.3 Nevertheless, Odom et al.1a prospected that “this relative lack of diversity is largely due to the need for further development rather than an inherent lack of utility”. Indeed, Tonks et al.4 recently accomplished pyrrole synthesis from alkynes and diazenes (e.g., eqn (1)), catalyzed by a titanium imido complex 1cat.5 Intriguingly, these transformations were able to form new C–N bonds without using a redox-active ligand. It was proposed that the C–N bond formation could take place via a reductive elimination (Scheme 1). While reductive elimination is a ubiquitous elementary step in the late TM catalysis to form C–X bonds,6–9 it is rare in the early TM catalysis. Inspired by the remarkable experimental advances, we applied density functional theory (DFT) computations to gain an insight into the mechanism of the transformations, with an aim to unveil the mechanistic differences in the eliminations in the catalysis of early and late TMs. Interestingly, the study characterized that the C–N bond formation proceeds via a formal reductive elimination pathway involving donation and back-donation. Formally, one could consider that the two electrons resulting from the formal reductive elimination back-donate to a symmetry-allowed unoccupied molecular orbital of the pyrrole ring. This is different from the conventional reductive elimination in the catalysis of late TMs, where the two electrons resulting from the elimination become a lone pair located at the TM center. | (1) |
2. Computational methods
Using actual catalyst and substrates in eqn 1, all the geometries were optimized and characterized by frequency analysis calculations to be minima (without imaginary frequency) or transition states (having unique imaginary frequency) at the B3LYP/6-31G(d,p) level in the gas phase. With the optimized geometries, the energies were further refined by M06-L10/6-311++G(d,p) single-point energy calculations with solvent effects accounted for by the PCM solvent model in the experimentally used solvent (PhCF3). The refined energies were finally corrected to enthalpies and free energies at 298.15 K and 1 atm. using the gas phase B3LYP/6-31G(d,p) frequencies; only the free energies are discussed. The Wiberg bond indices (WBIs),11 natural bond orbital (NBO) charges,12 and nuclear independent chemical shift values (NICS)13 were calculated at the M06-L(PCM, solvent = PhCF3)/6-311++G(d,p)/B3LYP/6-31G(d,p) level. All the standard DFT calculations were performed using the Gaussian 09 program.14 Minimum energy crossing points (MECPs) were obtained using the MECP-location program developed by Harvey's group.15 The spin–orbit coupling (SOC) effects at the MECPs were evaluated using the MOLPRO program.163. Results and discussion
3.1 Energetic feasibility of the transformations
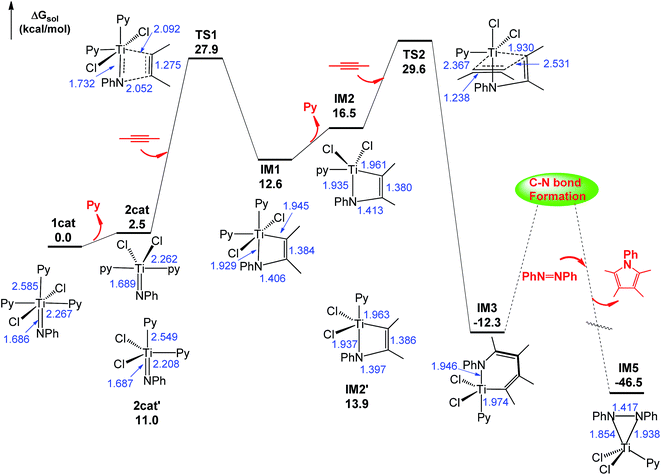
Using eqn (1) as a representative, we first examined the energetic feasibility to complete the catalytic cycle, as shown in Scheme 1. Fig. 1 illustrates the most favorable pathway from stage I to stage III of the cycle we explored. To undergo [2 + 2] addition (stage I), which often takes place in the alkyne hydroaminations catalyzed by early TM = NR imido complexes,2a–k the coordinatively saturated 16e octahedral titanium complex 1cat first releases a pyridine (Py) ligand, enabling the Ti center to interact with an alkyne substrate. In agreement with the experimental observation,17 the liberation of an axial Py ligand (Pyax) giving 2cat is 8.5 kcal mol−1 more favorable than the release of an equatorial Py ligand (Pyeq) giving 2cat′ due to the strong trans effect of the imido group on Pyax, as reflected by the longer Ti–N(Py) bond length (2.549 Å) in 2cat′ than that (2.262 Å) in 2cat (Fig. 1). Note that the barrier for convertting 2cat′ to 2catvia swinging the axial Py ligand to the equatorial position is low (4.3 kcal mol−1). Upon the active species being accessible, alkyne adds to the imido Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond. Taking both 2cat and 2cat′ into account, we located the [2 + 2] addition transition states (TSs), among which TS1 was the lowest (Fig. S2†). Relative to 1cat, the addition spans a barrier of 27.9 kcal mol−1 and is endergonic by 12.6 kcal mol−1.
N bond. Taking both 2cat and 2cat′ into account, we located the [2 + 2] addition transition states (TSs), among which TS1 was the lowest (Fig. S2†). Relative to 1cat, the addition spans a barrier of 27.9 kcal mol−1 and is endergonic by 12.6 kcal mol−1.
 | ||
| Fig. 1 Free energy profile for stages I–III of the catalytic cycle. Optimized structures of the stationary points are displayed in Fig. S1.† The values in blue are the key bond distances in angstroms. The mechanism for C–N bond formation will be discussed in Section 3.2. | ||
Subsequent to the alkyne addition forming IM1, the reaction proceeds to alkyne insertion (stage II). Since IM1 is coordinatively saturated, a Py ligand should be liberated, which gives IM2via releasing a Pyax or IM2′via releasing a Pyeq. The insertions of an alkyne into the Ti–C and Ti–N bonds of IM2 and IM2′ were considered (Fig. S3†). TS2via alkyne interaction with the π orbitals of IM2 is 4.2 kcal mol−1 lower than its TS counterpart of IM2′. Relative to IM1, the insertion giving IM3 overcomes a barrier of 17.0 kcal mol−1 and is exergonic by 24.9 kcal mol−1.
After alkyne insertion, IM3 undergoes C–N bond formation (stage III), leading to a pyrrole product and intermediate IM5. The mechanism of this stage is the focus of the study and will be discussed separately in Section 3.2.
Intermediate IM5 is not the active catalyst (2cat or 2cat′). A key for the reaction running catalytically is the use of a disproportionation reaction to close the catalytic cycle (i.e., stage IV in Scheme 1), converting IM5 to the active catalyst 2cat or 2cat′. The stage breaks the N–N single bond in IM5, but the entire catalytic cycle essentially cleaves an azobenzene N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond. The previous interest of others18 in cleaving the azobenzene N
N double bond. The previous interest of others18 in cleaving the azobenzene N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond encouraged us to characterize this stage in detail. Tonks et al. explored the disproportionation mechanism and proposed two possible mechanisms.4 In agreement with their proposal, our energetic results rule out the mechanism occurring via passing a TiII complex formed by dissociating azobenzene from IM5 (Fig. S4†). Hence, as shown below, we characterized an alternative mechanism via dimerization.
N bond encouraged us to characterize this stage in detail. Tonks et al. explored the disproportionation mechanism and proposed two possible mechanisms.4 In agreement with their proposal, our energetic results rule out the mechanism occurring via passing a TiII complex formed by dissociating azobenzene from IM5 (Fig. S4†). Hence, as shown below, we characterized an alternative mechanism via dimerization.
Pyrrole product release from IM3 gives IM5 (Fig. 1). As shown in Fig. 2, on one hand, IM5 associates with two Py ligands, giving IM6, with an energy release of 9.1 kcal mol−1. For the purpose of convenience, we used the more stable 2*IM6 as the energy reference to measure the energetics of the stage. On other hand, IM5 can dimerize by crossing TS5, resulting in a weakly bound dimer IM7. The geometric parameters given in IM7 indicate that it can be viewed as a doubly-bridged structure with one chlorine atom and one PhNNPh unit as the bridges. Subsequently, IM7 climbs TS6 to activate the N1–N2 bond. From IM7 to TS6, the N1–N2 bond is significantly elongated from 1.416 to 2.326 Å, whereas the N3–N4 bond is shortened from 1.419 to 1.382 Å. Proceeding forward, a four-membered intermediate IM8 is obtained, in which the N1–N2 bond is completely broken and a N3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N4 double bond formed. The dissociation of azobenzene from IM8viaTS7 results in IM9. After associating with two Py ligands, IM9 reaches the more stable IM10. The cleavage of two Ti–N bonds of the four-membered ring in IM10 gives two 2cat′ species that can be easily isomerized to the more stable 2catvia swinging the axial Py ligand to the equatorial position (TS9).
N4 double bond formed. The dissociation of azobenzene from IM8viaTS7 results in IM9. After associating with two Py ligands, IM9 reaches the more stable IM10. The cleavage of two Ti–N bonds of the four-membered ring in IM10 gives two 2cat′ species that can be easily isomerized to the more stable 2catvia swinging the axial Py ligand to the equatorial position (TS9).
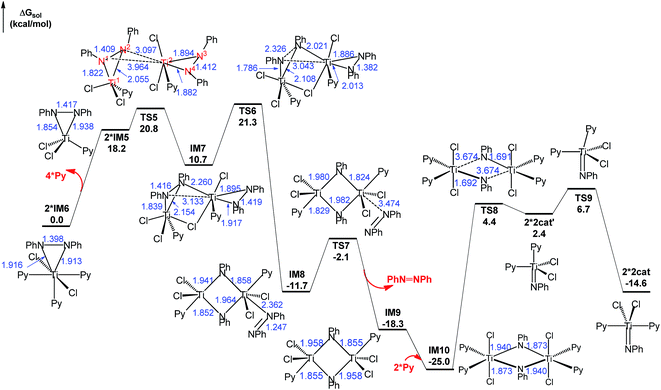 | ||
| Fig. 2 Free energy profile for regenerating the active catalysts via disproportionation, along with the optimized structures. The optimized structures of the stationary points are displayed in Fig. S5.† Key bond lengths in blue are given in angstroms. | ||
On the basis of the computed pathway, Scheme 2 simplifies our understanding of the disproportionation mechanism by tracing the electrons participating in bond formations and cleavages, using the electron-flow representation (Scheme 2). After forming the dimer IM7, among the two pairs of electrons in the two Ti–N bonds of the PhN3[Ti2]N4Ph unit, one pair flows to the N3–N4 bond, converting the single bond to a N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond, and the remaining pair, together with the pair in the N1–N2 single bond, construct new Ti2–N1 and Ti2–N2 bonds between the two units, simultaneously breaking N1–N2 bond. These electron flows result in a four-membered (TiNTiN) intermediate IM8. By breaking two of the four Ti–N single bonds in IM8, two imido titanium complexes (the active species) are formed.
N double bond, and the remaining pair, together with the pair in the N1–N2 single bond, construct new Ti2–N1 and Ti2–N2 bonds between the two units, simultaneously breaking N1–N2 bond. These electron flows result in a four-membered (TiNTiN) intermediate IM8. By breaking two of the four Ti–N single bonds in IM8, two imido titanium complexes (the active species) are formed.
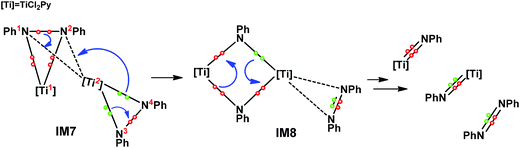 | ||
| Scheme 2 Mechanism for the bond formation and cleavage involved in IM5 disproportionation, using electron-flow representation. | ||
Examining the energetics of the pathway in Fig. 2, the barrier for the reaction to take place is 21.3 kcal mol−1 (TS6 relative to 2*IM6), which is in agreement with the experimental fact that the disproportionation could take place rapidly at elevated temperature for a similar system (PhNNPh)TiCl2(NHMe2)2. However, though the conversion of 2*IM6 to 2*2cat is thermodynamically favorable by 14.6 kcal mol−1, the reaction could not lead to 2cat′ or 2cat easily because of the high kinetic barrier (29.4 kcal mol−1) from IM10 to TS8 or 31.7 kcal mol−1 from IM10 to TS9. Thus, experimentally, one could observe the occurrence of the reaction and most likely detect IM10 but it could be difficult to detect 2cat or 2cat′. It is worth mentioning that numerous studies have reported X-ray structures featuring four-membered rings similar to that in IM10 in azobenzene cleavage by metal complexes.17
Combining the energy profiles in Fig. 1 and 2, IM10 is lowest in the catalytic cycle. Taking this into account, we estimated that the overall barrier to complete the catalytic cycle is 32.3 kcal mol−1, i.e., the energy cost from IM10 to 2cat (5.2 kcal mol−1 = (25.0 − 14.6)/2, the division by 2 is due to that the disproportionation producing two 2cat species) plus that from 2cat to TS2 (27.1 kcal mol−1, Fig. 1). This somewhat high barrier explains why these reactions needed to be performed at elevated temperatures (110.0 °C, eqn (1)).4 Briefly, our computed energetics demonstrates the feasibility of the catalytic cycle proposed by Tonks et al.4 Furthermore, we gained an insight into the mechanism for the C–N bond formation stage.
3.2 Mechanism for the C–N bond formation stage
The mechanism for the C–N bond formation stage omitted in Fig. 1 is detailed in Fig. 3A. The stage includes C–N bond formation from IM3 to IM4 and pyrrole release from IM4 to IM5. Other alternative pathways leading from IM4 to IM5 were found to be less kinetically favorable than the IM4→TS4→IM5 pathway (Fig. S6†). Fig. 3B shows the conventional reductive elimination to form a C–C bond involved in the Pd-catalyzed aerobic C–H bond functionalization of heterocycles,19 which was taken from our previous mechanistic study20 of C–H bond functionalization.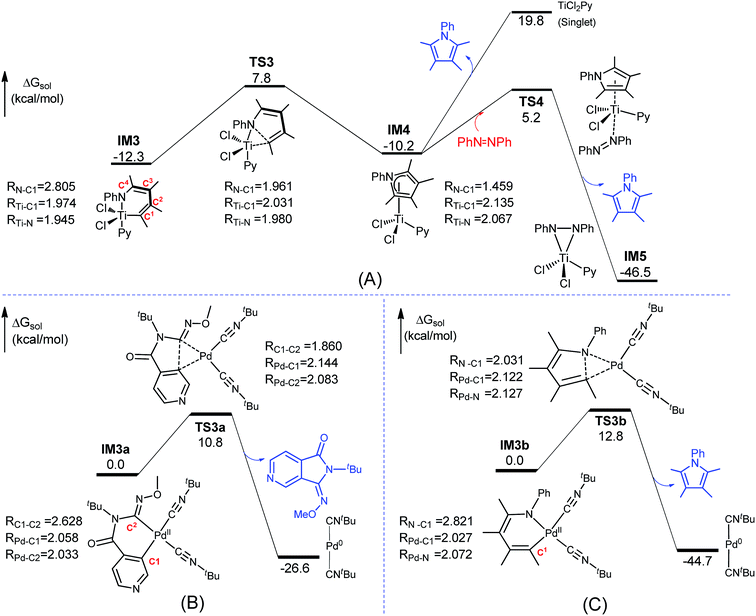 | ||
| Fig. 3 Comparisons of Ti- and Pd-eliminations. (A) Pathway for the C–N bond formation state omitted in Fig. 1(B) Pd-catalyzed C–C bond formation via reductive elimination. (C) Pd-catalyzed C–N bond formation via reductive elimination when replacing TiCl2Py in IM3 with Pd(CNtBu)2. Key bond lengths are given in angstroms. The optimized structures of all the stationary points are displayed in Fig. S7.† | ||
Compared to the elimination on the Pd center (termed as Pd-elimination hereafter), the elimination on the Ti center (termed as Ti-elimination hereafter) is different despite the geometric similarities between IM3 and IM3a, both featuring long C–X distances (X = C or N), and between TS3 and TS3a, both describing the trend to form C–X bonds. The transition state TS3a in the Pd-elimination straightforwardly leads to the product and active catalyst (Pd0(CNtBu)2), whereas TS3 in the Ti-elimination proceeds to a comparatively stable complex IM4 (which can be considered as a masked TiII complex, vide infra). The liberation of the pyrrole product from IM4via direct dissociation is not easy, costing ∼30.0 kcal mol−1. Instead, it preferentially takes place by interchanging with azobenzene, as depicted by TS4, with a much lower barrier (15.4 kcal mol−1). Geometrically, as shown by the bond length evolution of the key bonds (N–C1/Ti–C1/Ti–N) from IM3 to TS3 to IM4 (Fig. 3A), the C1–N bond is formed steadily, but the Ti–C1 and Ti–N bonds are only elongated by less than 0.2 Å. If TiCl2Py moiety in IM3 is replaced with Pd(CNtBu)2, Pd-elimination to form a C–N bond (Fig. 3C) is the same as Pd-elimination to form a C–C bond (Fig. 3B), and thus the differences between the Ti- and Pd-eliminations are not due to the different substrates but are due to the TM centers (i.e., Pd versus Ti). These differences encouraged us to characterize the Ti-elimination more deeply.
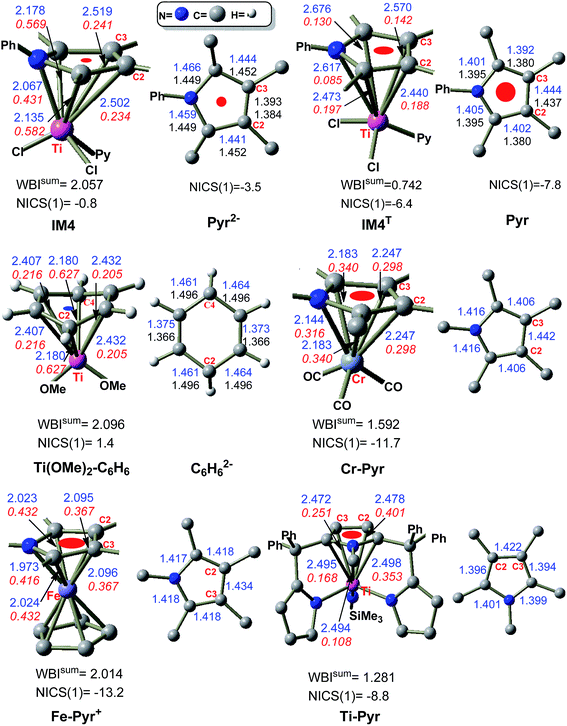
IM3 and TS3 in the Ti-elimination are similar to their counterparts (IM3a/IM3b and TS3a/TS3b) in the Pd-eliminations (Fig. 3); thereby we first focused on the abnormal complex IM4. The optimized structure of IM4 is displayed in Fig. 4. In agreement with the large dissociation energy of pyrrole from IM4, the bond lengths between Ti and the atoms (N and C1–C4) of the pyrrole ring signify a tight bonding between the pyrrole ring and Ti center. The sum of the individual Wiberg bond indices (WBIsum) of these bonds reaches 2.057, indicating a double covalent bond nature, collectively involving the five atoms of the pyrrole ring. To characterize the covalent bonding in IM4, we analyzed how the pyrrole ring interacts with TiCl2Py. As illustrated in Scheme 3A, the HOMO of IM4 originates from the symmetry-allowed interaction between the in-plane occupied dxy orbital of titanium and the LUMO+2 of pyrrole (the LUMO and LUMO+1 of pyrrole are only relevant to the phenyl group), indicating a back-donation from Ti to the pyrrole ligand. The symmetry-allowed interactions of the unoccupied perpendicular Ti dxz/dxy orbital with the occupied HOMO/HOMO−1 of the pyrrole ligand result in HOMO−1/HOMO−5 of IM4, respectively, which exemplify the donation from the pyrrole ligand to Ti. Other occupied orbitals involving less significant donation are not shown in Scheme 3A. On the basis of frontier molecular orbital interactions, we attributed the double covalent bond character between Ti and pyrrole in IM4 to bilateral donation and back-donation.
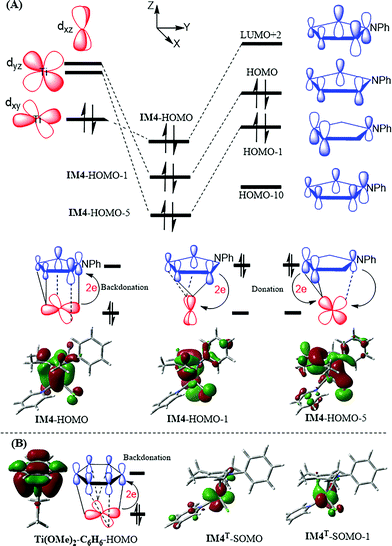 | ||
| Scheme 3 (A) Tracing the interactions of the molecular orbitals of pyrrole with those of TiCl2Py, resulting in IM4. (B) HOMO of Ti(OMe)2–C6H6 and SOMOs of IM4T. | ||
Conventionally, a reductive elimination to form a C–X bond returns two of the four electrons in the TM–C and TM–X bonds to the TM center as a lone pair, thus reducing the TM center by two oxidation numbers6–9 (for example, see Fig. 3B and C). In contrast, the MO interaction analyses unraveled that the Ti-elimination back-donates the two electrons to the nascent pyrrole product. The differences between the Ti- and Pd-eliminations intrigued us to question what may happen if the two electrons return to the Ti center as adopted in the reductive elimination in late TM catalysis. We considered the triplet counterpart of IM4. Surprisingly, the HOMO–LUMO gap of IM4 is very small (20.2 kcal mol−1, compared to 53.1 kcal mol−1 of 1cat), indicating that IM4 may have a lower triplet counterpart. Indeed, a 3.3 kcal mol−1 lower triplet (namely, IM4T) could be located, which is opposite to the cases of late TMs. For example, the triplet Pd0(CNtBu)2 is 56.4 kcal mol−1 higher than its singlet counterpart. The reliability of M06-L//B3LYP calculations in ranking the singlet and triplet was validated by computing the experimentally well-characterized TiCl2(Py)4 complex. In agreement with the experimental results,21 the ground triplet of the complex was predicted to be 9.0 kcal mol−1 more stable than its singlet (Fig. S8†). Other levels of DFT calculations also predicted that IM4T is lower than IM4 (Table S1†). In contrast to IM4, in which the two electrons resulting from the reductive elimination occupy bonding HOMO (see IM4–HOMO in Scheme 3A), the two electrons in IM4T singly occupy two MOs (see IM4T–SOMO and IM4T–SOMO−1 in Scheme 3B) dominated by Ti d orbitals, resulting in a spin density of ρα = 1.70 on the Ti center. Furthermore, the two singly occupied orbitals of IM4T are very close in orbital energy (0.67 kcal mol−1), which is in favor of a ground triplet (i.e., IM4T).
The two electrons in IM4, resulting from the elimination, form a bonding interaction via back-donation, whereas the two electrons in IM4T are the non-bonding ones. To characterize the back-donation effects, Fig. 4 compares the differences between IM4 and IM4T. It could be found that (i) the pyrrole ring in IM4 coordinates to the Ti center tighter than that in IM4T, as shown by the shorter Ti–C1/Ti–N/Ti–C4 atomic distances (2.135/2.067/2.178 Å) in IM4 than those (2.473/2.617/2.676 Å) in IM4T and the greater WBIsum (2.057) of IM4 than that (0.742) of IM4T, and (ii) the pyrrole coordination in IM4 is severely biased to the C1NC4 site and the N–C1 (1.466 Å) and N–C4 (1.459 Å) bonds in IM4 are apparently longer than those (1.401 and 1.405 Å, respectively) in IM4T, which is in line with the orbital interaction pattern of the back-donation (see IM4–HOMO in Scheme 3A).
The back-donation even affects the aromatic nature of the pyrrole ring. To demonstrate this, the dianionic (Pyr2−) and neutral (Pyr) pyrrole were optimized (Fig. 4). It could be found that the pyrrole ring in IM4 is best matched with Pyr2−, with both featuring the shortest C2–C3 bond, while the structure of Pyr is best fitted to the ring in IM4T, with both featuring the longest C2–C3 bond. These geometric matches imply that the pyrrole ring in IM4 features a dianionic character, while it is neutral in IM4T. The nuclear independent chemical shift (NICS)13 has been proven to be a good criterion to measure the aromaticity of cyclic molecules. For example, at the present calculation level, the prototypical aromatic molecule benzene has a negative NICS(1) value of −10.3 ppm (NICS(1) representing the NICS value at a point 1.0 Å above the benzene ring), whereas the antiaromatic cyclobutadiene has a positive NICS(1) value of 15.1 ppm. Neutral pyrrole (Pyr) is aromatic with an NICS(1) value of −7.8 ppm. In contrast, the NICS(1) value of the pyrrole ring in IM4 is insignificant (−0.8 ppm), indicating that the ring loses its aromaticity due to the back-donation. Because the pyrrole ring in IM4T is a neutral ligand only featuring donation, the NICS(1) value of the ring is −6.4 ppm, indicating that the ring maintains its aromaticity. It is interesting to mention that the donation does not affect the aromatic character of the ring, whereas back-donation does. The loss of aromaticity of the pyrrole ring in IM4 rationalizes why IM4, which possesses favorable back-donation bonding, is conversely 3.3 kcal mol−1 higher than IM4T without back-donation. To validate this, ethylene–TiCl2Py complex was used to avoid the interference of aromaticity stabilization. As expected, singlet C2H4–TiCl2PyS was 12.1 kcal mol−1 lower than triplet C2H4–TiCl2PyT.
While the pyrrole ligand in IM4 shows a dianionic character, pyrrole often acts as a neutral six-electron donor, forming η5-coordination TM complexes. To understand the difference and to reaffirm the dianionic character of IM4, we compared IM4 with the experimental TM complexes (see Cr–Pyr,22aFe–Pyr+,22b and Ti–Pyr22c in Fig. 4). In Cr–Pyr and Fe–Pyr+, the pyrrole ligand serves as a six-electron donor, endowing the complexes with an 18-electron count, whereas Ti-Pyr is a standard TiIV complex featuring Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NSiMe3 imido group and a 16-electron count. Geometrically, the bond length alternations in the pyrrole ligands of these experimental complexes match that in free Pyr rather than in Pyr2− (see Fig. 4). Consistently, the pyrrole ligands in these complexes have large negative NICS(1) values ranging from −8.8 to −13.3 ppm, which are significantly greater than that (−0.8 ppm) in IM4. Moreover, no occupied molecular orbital featuring significant back-donation could be found. Thus, a key difference between IM4 and these experimental complexes is the back-donation in IM4. The comparisons demonstrate that the pyrrole ligand in IM4 is indeed different from the neutral pyrrole ligand in these experimental complexes, possessing a dianionic character.
NSiMe3 imido group and a 16-electron count. Geometrically, the bond length alternations in the pyrrole ligands of these experimental complexes match that in free Pyr rather than in Pyr2− (see Fig. 4). Consistently, the pyrrole ligands in these complexes have large negative NICS(1) values ranging from −8.8 to −13.3 ppm, which are significantly greater than that (−0.8 ppm) in IM4. Moreover, no occupied molecular orbital featuring significant back-donation could be found. Thus, a key difference between IM4 and these experimental complexes is the back-donation in IM4. The comparisons demonstrate that the pyrrole ligand in IM4 is indeed different from the neutral pyrrole ligand in these experimental complexes, possessing a dianionic character.
The viability of IM4 is also supported by experimental facts. Although no low-valent titanium complex with pyrrole as a ligand has been reported to date, low-valent titanium complexes with arene as a ligand,23 as well as other low-valent early TM complexes,24 have been experimentally prepared. Most recently, Fortier et al.23a demonstrated that such a low-valent titanium complex could promote C(sp3)–H bond oxidative addition to perform transfer hydrogenation. In terms of the oxidation state of titanium in these complexes, the assignment is somewhat ambiguous, probably due to the lack of a rigorous way to assign the oxidation state of an organometallic complex, particularly for a non-classical complex. In the literature, these arene-coordinated low-valent titanium complexes have been considered as masked TiII complexes or TiII complexes with a significant TiIV character. However, Power et al.23b assigned the TiIV oxidation state to their Ti{N(H)AriPr6}2 complex because of the observed diamagnetic nature of the complex. Nevertheless, regardless of what oxidation state could be assigned properly, a common feature of these low-valent complexes was the back-donation. Scheme 3 includes the molecular orbital (see Ti(OMe)2–C6H6–HOMO) related to the back-donation in a truncated model complex of arene-coordinated low-valent titanium complexes.
IM4T is lower than IM4, and thus the Ti-elimination transition state TS3 may proceed to IM4T through spin-orbit coupling (Fig. 5),25 although the process is spin-forbidden. Fig. 5 shows the singlet-triplet potential energy surface crossing. Extensive calculations revealed that, except for IM4 and TS4, all the intermediates and transition states in Fig. 1 and 3A have triplet states significantly higher than their singlet counterparts (Fig. S9†). We located the MECPs (minimum energy crossing points) between the two surfaces, using the MECP-location program developed by Harvey's group.15 At MECP1, the RMS SOC was predicted to be 38.6 cm−1 (SI2), which is much smaller than the value (ca. 250 cm−1 at a doublet-quartet MECP) that was considered to allow hopping for a molybdenum complex.26 An SOC value of 427 cm−1 at a triplet-quintet MECP was reported for β-hydride elimination of an iron(II)–alkyl complex.27 In short, the spin–orbit coupling between the singlet and triplet in the present reaction is not strong, and thus the C–N bond formation stage may mainly proceed along the singlet energy surface. An effort was made to locate MECP2 but we could not reach a converged structure. Because the stage mainly proceeds on the singlet surface, we expect that MECP2 would not play an important role in this transformation.
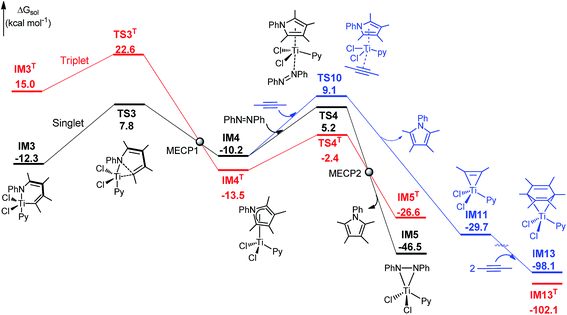 | ||
| Fig. 5 Free energy profile for C–N bond formation (stage III), with key bond lengths (in angstroms) of IM3, TS3, and IM4. For optimized structures of all the stationary points, see Fig. S1, S9 and S10.† | ||
It was assumed that azobenzene and alkyne may act as a redox-active ligand to promote the C–N bond formation. By displacing the Py ligand in IM3 with azobenzene and alkyne, as well as PhCF3 (the solvent molecule), we located the relevant pathways. The energetic results, given in Fig. S11,† show that these pathways are kinetically much less favorable than the black pathway in Fig. 3A by at least 11.0 kcal mol−1, excluding these possibilities. Therefore, azobenzene/alkyne/PhCF3 are not effective to serve as redox-active ligands to promote C–N bond formation.
Examining the favorable pathway in Fig. 1 and 3A, one or more Py ligands stay(s) coordinated to the Ti center. Given the fact that the system contains other electron donors (i.e., alkyne, azobenzene, and PhCF3), we examined whether these donors can coordinate to the Ti center to result in more stable complexes, and thus deviate the favorable pathway. As detailed in Table S2,† these possibilities can be excluded safely.
3.3 Further discussion on the difference between Ti-elimination and Pd-elimination
After characterizing the electronic structures of IM4 and IM4T, we now seek to further understand the difference between the Ti- and Pd-eliminations. Referring to Fig. 3C, the Pd-elimination from IM3b to Pd0(CNtBu)2 + free pyrrole is a two-electron reduction process, reducing the PdII(CNtBu)2 moiety in IM3b to Pd0(CNtBu)2. Referring to Fig. 3A, if the pyrrole ring in IM4 and the PhNNPh moiety in IM5 could be considered as neutral electron donors, the entire process from IM3 to IM4 to IM5 + free pyrrole would also be a two-electron reduction process, reducing the TiIVCl2Py moiety in IM3 to TiIICl2Py in IM4 and IM5. Thus, the bottom line is whether the pyrrole ring in IM4 and the PhNNPh moiety in IM5 could really be considered as neutral ligands. In Section 3.2, we demonstrated the dianionic character of the pyrrole ring in IM4 and that the PhNNPh unit in IM5 is apparently a dianionic ligand, as assigned by Tonks et al. (see Scheme 1). The difference between Ti-elimination and Pd-elimination can be attributed to the lower electronegativity of titanium than palladium. Generally, as reductive elimination proceeds, the TM moiety (e.g., the Pd(CNtBu)2 moiety in IM3b) gradually gains electron density. For the Pd-elimination, due to the great electronegativity of palladium, the Pd moiety is able to stabilize the growing electron density throughout the entire process; thus Pd-elimination leads to the pyrrole directly and, moreover, releases the active catalyst Pd0(CNtBu)2. For Ti-elimination, particularly in the early stage, because TiCl2Py is dominated by the TiIV character, it is still capable of stabilizing the gained electron density, and the elimination should proceed in a way similar to that of the Pd-elimination. As the elimination progresses further, more and more electron density accumulates on the TiCl2Py moiety. However, due to the small electronegativity of titanium, the TiCl2Py moiety is no longer able to stabilize the gained electron density and a portion of electron density must be accommodated in an energetically more favorable way. Principally, there are two ways to accommodate the excessive electron density on TiCl2Py. One way is through back-donation of the electron density to the pyrrole ring, forming a favorable bonding interaction, which is the role of IM4. Another way is to become a triplet by taking advantage of the stabilization effect of exchange correlation energy, which is one of the reasons why IM4T is more stable than IM4. Because the spin–orbit coupling is not strong, the latter way is not feasible (vide supra) and the former way is thus adopted. To complete the two-electron reduction for eventually releasing pyrrole product from IM4, one way is to enforce the pyrrole ring to dissociate from IM4; however, this is energetically unfavorable, costing about 30.0 kcal mol−1 due to the bonding interactions of donation and back-donation. A mild way is to use an oxidant to pull the back-donated electrons back, which is the role of azobenzene, oxidizing the masked TiII intermediate (IM4) to a genuine TiIV complex (IM5), while simultaneously, the back-donated electrons are withdrawn to the Ti center.The stronger ability of Pd(CNtBu)2 than TiCl2Py in stabilizing the gained electron density is also reflected by the fact that the singlet Pd0(CNtBu)2 is 58.0 kcal mol−1 lower than its triplet counterpart, whereas the singlet TiIICl2Py species is 18.1 kcal mol−1 higher than its triplet counterpart. To stabilize the two non-bonding electrons in TiCl2Py, the two electrons have to singly occupy two molecular orbitals in order to take advantage of the stabilization effect of exchange correlation.
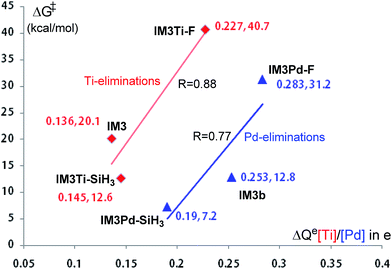
It should be noted that although the Ti-elimination features back-donation and donation, the general trend of two-electron reduction cannot be altered. Thus, the substitution effect on the elimination barrier of Ti-elimination is similar to that in Pd-elimination. For example, the Ti-elimination barriers of IM3Ti–F, IM3, and IM3Ti–SiH3 (see Scheme 3) are 40.7, 20.1, and 12.6 kcal mol−1, respectively and are in the same order as that of Pd-elimination barriers of IM3Pd–F, IM3b, and IM3Pd–SiH3 being 31.2, 12.8, and 7.2 kcal mol−1, respectively. The high barriers in the case of X = F can be attributed to the strong electron-withdrawing nature of fluorine atoms, which hinders the tendency of electron transfer to the TM moiety (i.e., Pd(CNtBu)2 or TiCl2Py) before reaching the transition states. Fig. 6 correlates the electron gains of the TM moieties from the IM3/IM3b analogs to the TS3/TS3b analogs with the elimination barriers. Similar to Hammond's postulation, for Ti-eliminations and Pd-eliminations, it is generally true that more the electrons the TM moiety gains, the higher the elimination barrier. It is interesting to mention that IM4Ti–F should possess stronger back-donation than IM4 and IM4Ti–SiH3, but the elimination barrier of IM3Ti–F is higher than that of the others, indicating that the back-donation is only one of the factors determining the barrier for Ti-elimination. Other factors include the intrinsic effects (TMn/TMn−2 reduction) like in conventional reductive elimination and donation. In the case of X = F, as the back-donation is relatively strong, the donation should be relatively weak.
In Ti-elimination, both donation and back-donation bonding interactions favor the stabilization of the system, thus facilitating the elimination. To prove this, we saturated one of the remote double bonds in IM3, resulting in IM3Ti–HMe (see Scheme 4). We did not saturate another C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond because the elimination would form a C(sp3)–N bond, which is not comparable with IM3 elimination to form C(sp2)–N. As expected, its elimination barrier (25.5 kcal mol−1) is higher than the 20.1 kcal mol−1 of IM3 elimination.
C double bond because the elimination would form a C(sp3)–N bond, which is not comparable with IM3 elimination to form C(sp2)–N. As expected, its elimination barrier (25.5 kcal mol−1) is higher than the 20.1 kcal mol−1 of IM3 elimination.
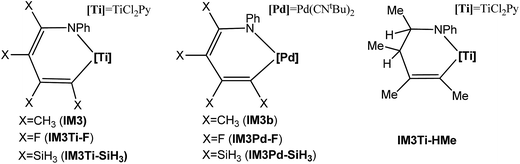 | ||
| Scheme 4 Hypothesized molecules used to study the substitution effect of the substituents. The optimized structures of the IM3/IM3b, TS3/TS3b and IM4/IM4b analogs are displayed in Fig. S12.† | ||
In an alternative/formal way, Scheme 5 compares conventional reductive elimination with the present reductive elimination by focusing on how the two pairs of electrons in the TM–C and TM–X/N bond in A/IM3 flow. As the C–X/N bond formation proceeds, a pair of electrons (in green) would be used to form a new C–X/N bond. The competition to pull electrons between TM and the forming product determines the destination where the remaining pair of electrons (in red) ultimately goes. For late TMs with strong electronegativity (the left cycle), the pair of electrons prefers migrating to the TM center to become a lone pair, reducing TMn in A to TMn−2 in B. We denote this way of reductive elimination as RELP in Scheme 5. In Ti-elimination (the right cycle), due to the small electronegativity of titanium, the pair of electrons prefer back-donating to a symmetry-allowed unoccupied orbital of the pyrrole ring (see IM4–HOMO in Fig. 4). We call this way of reductive elimination as REBD in Scheme 5. Note that in addition to the back-donation, IM4 also features donation from pyrrole to the Ti center. As compared in Fig. 3, the barrier (20.1 kcal mol−1, TS3 relative to IM3) for Ti-elimination is higher than that (12.8 kcal mol−1, TS3b relative to IM3b) for Pd-elimination, implying that the RELP adopted by late TMs is more effective to stabilize the two electrons than the REBD used by early TMs. The remaining pair of electrons could migrate to the Ti center in IM4T, but requires spin-flipping. Because the spin–orbit coupling to enable the spin-flip is weak, the process from IM3 to IM4TviaTS3 is unlikely.
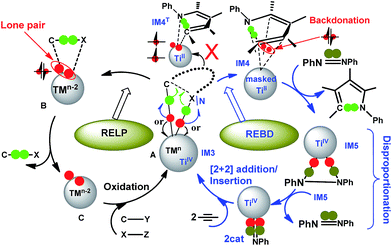 | ||
| Scheme 5 Comparisons of conventional reductive elimination via forming a lone pair on the TM center (RELP, left) with the present reductive elimination via back-donation (REBD, right). Note that B generally involves weakly bound complexes and may not exist in some cases (e.g., those in Fig. 3B and C). | ||
The process from IM4 to IM5 takes place via the oxidation of azobenzene, which oxidizes the masked TiII to TiIV and, moreover, pulls the two back-donated electrons back to the Ti center, forming two Ti–N bonds with the PhNNPh unit in IM5. This is why the pyrrole release from IM4 prefers to undergo an interchange mechanism rather than a dissociative route (see Fig. 3A). On the basis of the mechanistic understanding of the Ti-elimination, we were able to conceive the necessary requirements for early TMs to undergo REBD elimination, including that (i) the product has symmetry-allowed empty orbitals to accommodate the two electrons from the elimination via back-donation and (ii) the substrate (i.e., azobenzene) should possess a comparatively strong oxidizing ability to oxidize the electron-buffering intermediate (e.g., IM4) for product release. To some extent, the pyrrole product acts like a redox-active ligand, reserving electrons during the process of forming a C–N bond from IM3 to IM4 and liberating the reserved electrons when reacting with an oxidant (azobenzene) from IM4 to IM5.
Experimentally, it was reported that a trace amount of alkyne trimerization product (i.e., hexamethylbenzene) could be obtained.4 Our predicted mechanism is able to explain this experimental observation. Referring to Fig. 5, as an alternative to azobenzene attacking IM4 and giving IM5, the alkyne, serving as an oxidant, can also attack IM4viaTS10 (the blue pathway in Fig. 5), leading to the IM5 analog (i.e., IM11). As detailed in Fig. S9,†IM11 can readily react with two alkynes, resulting in hexamethylbenzene after azobenzene or alkyne attacks IM13. Because of the weaker oxidizing ability of alkyne than azobenzene, TS10 is 3.9 kcal mol−1 higher than TS4. The barrier difference (3.9 kcal mol−1) rationalizes why trace and only trace amounts of alkyne trimerization product (i.e., hexamethylbenzene) could be produced (eqn (1)).
As discussed above, the essence of REBD is that the two electrons resulting from the elimination are stabilized by a back-donation bonding interaction. There are other ways to stabilize the two electrons, such as the strategy of using a redox-active ligand. Herein, we show that a negative hyperconjugation28 can also stabilize the two electrons. We replaced the phenyl group in IM3 with a F atom, resulting in IM3Ti-NF (see Fig. 7), and then calculated the elimination pathway from IM3Ti-NF to TS3Ti-NF to IM4Ti-NF. As compared in Fig. 7, IM4Ti-NF has a N–F bond length (1.858 Å) much longer than that (1.409 Å) in IM3Ti-NF, indicating the negative hyperconjugation described by IM4Ti-NF–HOMO. By comparing the five-membered ring in IM4Ti-NF with free C4Me4N− in terms of NICS(1) values (both having a NICS (1) value of ca. −9.0 ppm) and the bond length alternation pattern of the rings, we assigned the Lewis structure (Lewis–IM4Ti-NF) to IM4Ti-NF. Therefore, one difference between IM3 and IM3Ti-NF eliminations is that the two electrons in the former elimination are stabilized by the back-donation bonding, whereas the two electrons in the latter elimination are stabilized by the negative hyperconjugation. The occurrence of the negative hyperconjugation further supports the dianionic character of the pyrrole ring in IM4 and IM4Ti-NF. Thus, a more general principle for early TM catalysts to undergo reductive elimination is that the two electrons resulting from elimination must be stabilized, no matter what favorable interactions (e.g., back-donation and negative hyperconjugation) could be used, rather than becoming a lone pair located at the TM center, as adopted in the late TM catalysis systems.
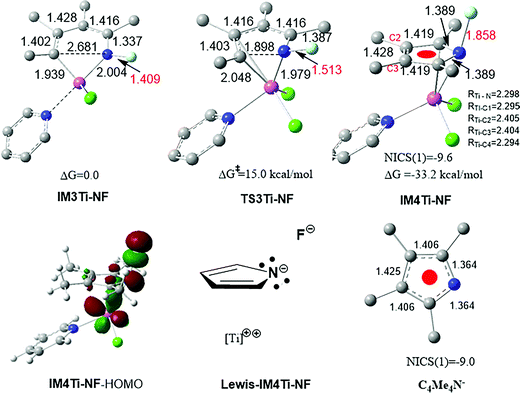 | ||
| Fig. 7 Optimized structures, together with the key bond lengths in angstroms. NICS(1) is the NICS value (in ppm) at a point 1.0 Å above the ring center. | ||
4. Conclusion
In summary, the present study reveals that the C–N bond formation in the titanium(IV)-catalyzed pyrrole synthesis from alkynes and diazenes takes place via an elimination pathway featuring donation and back-donation. Different from the conventional reductive elimination adopted by late TMs, where the two electrons resulting from elimination are stabilized by the TM center as a lone pair, the two electrons in the present reductive elimination are stabilized by donating to a symmetry-allowed unoccupied orbital of the forming pyrrole product. Because of the back-donation and donation, the elimination leads to a comparatively stable masked TiII complex (IM4) rather than the pyrrole product directly. IM4 requires undergoing an additional oxidation step by azobenzene to liberate the pyrrole product. The triplet counterpart (IM4T) of IM4 is more stable than IM4; however, the elimination is unlikely to lead to IM4T because it is spin-forbidden and the spin–orbit coupling to enable the hopping from the singlet to triplet energy surfaces is weak. The study provides an insight into the unconventional elimination mechanism. Although the weak electronegativity of titanium does not favor stabilizing the two formal electrons resulting from the reductive elimination, the same feature favors back-donation to allow the two electrons to donate to the nascent product easier. Alternatively, one may consider the pyrrole product as a redox-active ligand, reserving electrons resulting from the formal reductive elimination and releasing electrons when reacting with an oxidant. On the basis of the mechanistic understanding of the reaction, we conceived two requirements for early TMs to undergo similar elimination, including that (i) the forming product has a symmetry-allowed unoccupied orbital to accommodate the two electrons resulting from the elimination, which as a lone pair cannot be stabilized by early TMs and (ii) a comparatively strong oxidizing reagent (e.g., azobenzene in the present case) is important to pull the back-donated electrons back, thus releasing the product. It should be noted that back-donation is one way to stabilize the two electrons resulting from the reductive elimination; these two electrons can also be stabilized via other ways, such as a negative hyperconjugation. The insights from the present study could provide another way to construct C–X bonds using early TM catalysts.Acknowledgements
We thank the anonymous reviewers for providing insightful comments and helping us to improve the study, and Professor Tonks for helpful discussion. We acknowledge the financial support from the National Science Foundation of China (Grant Nos. 21573263 and 21373216).Notes and references
- Selected reviews on titanium catalysis: (a) A. L. Odom and T. J. McDaniel, Acc. Chem. Res., 2015, 48, 2822–2833 CrossRef CAS PubMed; (b) S. A. Ryken and L. L. Schafer, Acc. Chem. Res., 2015, 48, 2576–2586 CrossRef CAS PubMed; (c) N. Hazari and P. Mountford, Acc. Chem. Res., 2005, 38, 839–849 CrossRef CAS PubMed; (d) C. Lorber, Coord. Chem. Rev., 2016, 308, 76–96 CrossRef CAS; (e) T. E. Müller, K. C. Hultzsch, M. Yus, F. Foubelo and M. Tada, Chem. Rev., 2008, 108, 3795–3892 CrossRef PubMed; (f) V. Estévez, M. Villacampa and J. C. Menéndez, Chem. Soc. Rev., 2010, 39, 4402–4421 RSC; (g) O. G. Kulinkovich, Chem. Rev., 2003, 103, 2597–2632 CrossRef CAS PubMed; (h) A. L. Odom, Dalton Trans., 2005, 225–233 RSC.
- Selected papers on titanium catalysis: (a) E. Haak, I. Bytschkov and S. Doye, Angew. Chem., Int. Ed., 1999, 38, 3389–3391 CrossRef CAS; (b) B. F. Straub and R. G. Bergman, Angew. Chem., Int. Ed., 2001, 40, 4632–4635 CrossRef CAS; (c) C. Cao, Y. Shi and A. L. Odom, Org. Lett., 2002, 4, 2853–2856 CrossRef CAS PubMed; (d) V. Khedkar, A. Tillack and M. Beller, Org. Lett., 2003, 5, 4767–4770 CrossRef CAS PubMed; (e) Y. Li, Y. Shi and A. L. Odom, J. Am. Chem. Soc., 2004, 126, 1794–1803 CrossRef CAS PubMed; (f) C. Lorber, R. Choukroun and L. Vendier, Organometallics, 2004, 23, 1845–1850 CrossRef CAS; (g) E. Smolensky, M. Kapon and M. S. Eisen, Organometallics, 2007, 26, 4510–4527 CrossRef CAS; (h) E. Chong, S. Qayyum, L. L. Schafer and R. Kempe, Organometallics, 2013, 32, 1858–1865 CrossRef CAS; (i) I. A. Tonks, J. C. Meier and J. E. Bercaw, Organometallics, 2013, 32, 3451–3457 CrossRef CAS; (j) J. C.-H. Yim, J. A. Bexrud, R. O. Ayinla, D. C. Leitch and L. L. Schafer, J. Org. Chem., 2014, 79, 2015–2028 CrossRef CAS PubMed; (k) L. H. Lühning, C. Brahms, J. P. Nimoth, M. Schmidtmann and S. Doye, Z. Anorg. Allg. Chem., 2015, 641, 2071–2082 CrossRef; (l) L. Bareille, S. Becht, J. L. Cui, P. L. Gendre and C. Moïse, Organometallics, 2005, 24, 5802–5806 CrossRef CAS; (m) S. Banerjee, E. Barnea and A. L. Odom, Organometallics, 2008, 27, 1005–1014 CrossRef CAS; (n) E. Barnea, S. Majumder, R. J. Staples and A. L. Odom, Organometallics, 2009, 28, 3876–3881 CrossRef CAS; (o) J. A. Bexrud, P. Eisenberger, D. C. Leitch, P. R. Payne and L. L. Schafer, J. Am. Chem. Soc., 2009, 131, 2116–2118 CrossRef CAS PubMed; (p) I. A. Tonks, L. M. Henling, M. W. Day and J. E. Bercaw, Inorg. Chem., 2009, 48, 5096–5105 CrossRef CAS PubMed; (q) E. Chong and L. L. Schafer, Org. Lett., 2013, 15, 6002–6005 CrossRef CAS PubMed; (r) J. Dörfler, T. Preuß, A. Schischko, M. Schmidtmann and S. Doye, Angew. Chem., Int. Ed., 2014, 53, 7918–7922 CrossRef PubMed; (s) L. C. Stevenson, S. Mellino, E. Clot and P. Mountford, J. Am. Chem. Soc., 2015, 137, 10140–10143 CrossRef CAS PubMed; (t) M. Manßen, N. Lauterbach, J. Dörfler, M. Schmidtmann, W. Saak, S. Doye and R. Beckhaus, Angew. Chem., Int. Ed., 2015, 54, 4383–4387 CrossRef PubMed; (u) J. Schlüter, M. Blazejak, F. Boeck and L. Hintermann, Angew. Chem., Int. Ed., 2015, 54, 4014–4017 CrossRef PubMed.
- Selected papers for using redox-active ligand to promote C–X bond formation in early TM catalysis: (a) M. R. Haneline and A. F. Heyduk, J. Am. Chem. Soc., 2006, 128, 8410–8411 CrossRef CAS PubMed; (b) N. A. Ketterer, H. Fan, K. J. Blackmore, X. Yang, J. W. Ziller, M.-H. Baik and A. F. Heyduk, J. Am. Chem. Soc., 2008, 130, 4364–4374 CrossRef CAS PubMed; (c) D. C. Ashley and M.-H. Baik, Chem.–Eur. J, 2015, 21, 4308–4314 CrossRef CAS PubMed.
- Z. W. Gilbert, R. J. Hue and I. A. Tonks, Nat. Chem., 2016, 8, 63–68 CrossRef CAS PubMed.
- N. Adams, H. R. Bigmore, T. L. Blundell, C. L. Boyd, S. R. Dubberley, A. J. Sealey, A. J. Cowley, M. E. G. Skinner and M. Mountford, Inorg. Chem., 2005, 44, 2882–2894 CrossRef CAS PubMed.
- R. H. Crabtree, The organometallic chemistry of the transition metals, Wiley-Interscience, A John Wiley & Sons, Inc, Hoboken New Jersey, 4th edn, 2005 Search PubMed.
- J. F. Hartwig, Organotransition metal chemistry: from bonding to catalysis, University Science Book, Mill Valley, CA, 2010 Search PubMed.
- Representative reviews see: (a) J. F. Hartwig, Acc. Chem. Res., 1998, 31, 852–860 CrossRef CAS; (b) B. M. Trost, F. D. Toste and A. B. Pinkerton, Chem. Rev., 2001, 101, 2067–2096 CrossRef CAS PubMed; (c) D. A. Culkin and J. F. Hartwig, Acc. Chem. Res., 2003, 36, 234–245 CrossRef CAS PubMed; (d) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169 CrossRef CAS PubMed; (e) L. McMurray, F. O'Hara and M. J. Gaunt, Chem. Soc. Rev., 2011, 40, 1885–1898 RSC; (f) K. M. Engle, T.-S. Mei, X. Wang and J.-Q. Yu, Angew. Chem., Int. Ed., 2011, 50, 1478–1491 CrossRef CAS PubMed; (g) I. D. G. Watson and F. D. Toste, Chem. Sci., 2012, 3, 2899–2919 RSC; (h) S. R. Neufeldt and M. S. Sanford, Acc. Chem. Res., 2012, 45, 936–946 CrossRef CAS PubMed; (i) C. S. Yeung and V. M. Dong, Chem. Rev., 2011, 111, 1215–1292 CrossRef CAS PubMed; (j) D. A. Petrone, J. Ye and M. Lautens, Chem. Rev., 2016, 116, 8003–8104 CrossRef CAS PubMed; (k) T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed; (l) A. Vigalok, Acc. Chem. Res., 2015, 48, 238–247 CrossRef CAS PubMed; (m) K. M. Engle, T.-S. Mei, M. Wasa and J.-Q. Yu, Acc. Chem. Res., 2012, 45, 788–802 CrossRef CAS PubMed; (n) T. Gensch, M. N. Hopkinson, F. Glorius and J. Wencel-Delord, Chem. Soc. Rev., 2016, 45, 2900–2936 RSC.
- Representative mechanistic studies involving reductive elimination: (a) Y. F. Yang, K. N. Houk and Y. D. Wu, J. Am. Chem. Soc., 2016, 138, 6861–6868 CrossRef CAS PubMed; (b) I. M. Pendleton, M. H. Perez-Temprano, M. S. Sanford and P. M. Zimmerman, J. Am. Chem. Soc., 2016, 138, 6049–6060 CrossRef CAS PubMed; (c) P. Gao, W. Guo, J. Xue, Y. Zhao, Y. Yuan, Y. Xia and Z. Shi, J. Am. Chem. Soc., 2015, 137, 12231–12240 CrossRef CAS PubMed; (d) G. Lu, C. Fang, T. Xu, G. Dong and P. Liu, J. Am. Chem. Soc., 2015, 137, 8274–8283 CrossRef CAS PubMed; (e) Q. Lu, H. Yu and Y. Fu, J. Am. Chem. Soc., 2014, 136, 8252–8260 CrossRef CAS PubMed; (f) B. E. Haines, H. Xu, P. Verma, X.-C. Wang, J.-Q. Yu and D. G. Musaev, J. Am. Chem. Soc., 2015, 137, 9022–9031 CrossRef CAS PubMed; (g) T. M. Figg, M. Wasa, J.-Q. Yu and D. G. Musaev, J. Am. Chem. Soc., 2013, 135, 14206–14214 CrossRef CAS PubMed; (h) J. Chen, W. Guo and Y. Xia, J. Org. Chem., 2016, 81, 2635–2638 CrossRef CAS PubMed; (i) G. Huang and P. Liu, ACS Catal., 2016, 6, 809–820 CrossRef CAS; (j) X.-K. Guo, L.-B. Zhang, D. Wei and J.-L. Niu, Chem. Sci., 2015, 6, 7059–7071 RSC; (k) Y. Mi, T. Zhou, K.-P. Wang, D. Lee and Y. Xia, Chem.–Eur. J., 2015, 21, 17256–17268 CrossRef CAS PubMed; (l) Q. Lu, B. Wang, H. Yu and Y. Fu, ACS Catal., 2015, 5, 4881–4889 CrossRef CAS; (m) Y. Dang, S. Qu, Y. Tao, X. Deng and Z.-X. Wang, J. Am. Chem. Soc., 2015, 137, 6279–6291 CrossRef CAS PubMed; (n) Z. Xing, F. Huang, C. Sun, X. Zhao, J. Liu and D. Chen, Inorg. Chem., 2015, 54, 3958–3969 CrossRef CAS PubMed; (o) S. E. Denmark, W. T. T. Chang, K. N. Houk and P. Liu, J. Org. Chem., 2015, 80, 313–366 CrossRef CAS PubMed; (p) M. J. Hilton, L.-P. Xu, P. O. Norrby, Y.-D. Wu, O. Wiest and M.-S. Sigman, J. Org. Chem., 2014, 79, 11841–11850 CrossRef CAS PubMed; (q) M. C. Nielsen, E. Lyngvi and F. Schoenebeck, J. Am. Chem. Soc., 2013, 135, 1978–1985 CrossRef CAS PubMed.
- (a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed; (b) A. D. Kulkarni and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 2325–2332 CrossRef CAS PubMed; (c) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 324–333 CrossRef CAS PubMed.
- (a) K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS; (c) F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- (a) J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS; (b) A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS; (c) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- (a) P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. E. Homes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS; (b) Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox. Gaussian 09, revision A.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, G. Hetzer, T. Hrenar, G. Knizia, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang, A. Wolf, MOLPRO, version 2008.1, a package of ab initio programs, see http://www.molpro.net.
- A. J. Blake, P. E. Collier, S. C. Dunn, W.-S. Li, M. Mountford and O. V. Shishkin, J. Chem. Soc., Dalton Trans., 1997, 1549–1558 RSC.
- (a) S. M. Bellows, N. A. Arnet, P. M. Gurubasavaraj, W. W. Brennessel, E. Bill, T. R. Cundari and P. L. Holland, J. Am. Chem. Soc., 2016, 138, 12112–12123 CrossRef CAS PubMed; (b) T. M. Powers and T. A. Betley, J. Am. Chem. Soc., 2013, 135, 12289–12296 CrossRef CAS PubMed; (c) Y. Zhao, Y. Liu, L. Yang, J.-G. Yu, S. Li, B. Wu and X.-J. Yang, Chem.–Eur. J., 2012, 18, 6022–6030 CrossRef CAS PubMed; (d) K. Kaleta, P. Arndt, T. Beweries, A. Spannenberg and O. Theilmann, Organometallics, 2010, 29, 2604–2609 CrossRef CAS; (e) Y.-C. Tsai, P.-Y. Wang, S.-A. Chen and J.-M. Chen, J. Am. Chem. Soc., 2007, 129, 8066–8067 CrossRef CAS PubMed; (f) Y. Ohki, Y. Takikawa, T. Hatanaka and K. Tatsumi, Organometallics, 2006, 25, 3111–3113 CrossRef CAS; (g) U. J. Kilgore, X. Yang, J. Tomaszewski, J. C. Huffman and D. J. Mindiola, Inorg. Chem., 2006, 45, 10712–10721 CrossRef CAS PubMed.
- Y.-J. Liu, H. Xu, W.-J. Kong, M. Shang, H.-X. Dai and J.-Q. Yu, Nature, 2014, 515, 389–393 CrossRef CAS PubMed.
- Y. Dang, X. Deng, J. Guo, C. Song, W. Hu and Z.-X. Wang, J. Am. Chem. Soc., 2016, 138, 2712–2723 CrossRef CAS PubMed.
- (a) G. B. Wijeratne, E. M. Zolnhofer, S. Fortier, L. N. Grant, P. J. Carroll, C.-H. Chen, K. Meyer, J. Krzystek, A. Ozarowski, T. A. Jackson, D. J. Mindiola and J. Telser, Inorg. Chem., 2015, 54, 10380–10397 CrossRef CAS PubMed; (b) M. A. Araya, F. A. Cotton, J. H. Matonic and C. A. Murillo, Inorg. Chem., 1995, 34, 5424–5428 CrossRef CAS.
- (a) N. Kuhn, J. Kreutzberg, E.-M. Lampe, D. Blaser and R. Boese, J. Organomet. Chem., 1993, 458, 125–129 CrossRef CAS; (b) N. Kuhn, E.-M. Horn, R. Boese and N. Augart, Angew. Chem., Int. Ed., 1988, 27, 579–580 CrossRef; (c) G. B. Nikiforov, I. Vidyaratne, S. Gambarotta and I. Korobkov, Angew. Chem., Int. Ed., 2009, 48, 7415–7419 CrossRef CAS PubMed.
- (a) J. R. Aguilar-Calderon, A. J. Metta-Magana, B. Noll and S. Fortier, Angew. Chem., Int. Ed., 2016, 55, 14101–14105 CrossRef CAS PubMed; (b) J. N. Boynton, J.-D. Guo, F. Grandjean, J. C. Fettinger, S. Nagase, G. J. Long and P. P. Power, Inorg. Chem., 2013, 52, 14216–14223 CrossRef CAS PubMed; (c) O. V. Ozerov, B. O. Patrick and F. T. Ladip, J. Am. Chem. Soc., 2000, 122, 6423–6431 CrossRef CAS; (d) J. R. Hagadorn and J. Arnold, Angew. Chem., Int. Ed., 1998, 37, 1729–1731 CrossRef CAS.
- (a) F. Reiß, K. Altenburger, L. Becker, K. Schubert, H. J. Jiao, A. Spannenberg, D. Hollmann, P. Arndt and U. Rosenthal, Chem.–Eur. J., 2016, 22, 3361–3369 CrossRef PubMed; (b) G. Tomaschun, K. Altenburger, F. Reiß, L. Becker, A. Spannenberg, P. Arndt, H. J. Jiao and U. Rosenthal, Eur. J. Inorg. Chem., 2016, 272–280 CrossRef CAS; (c) K. Altenburger, F. Reisß, K. Schubert, W. Baumann, A. Spannenberg, P. Arndt and U. Rosenthal, Eur. J. Inorg. Chem., 2015, 1709–1715 CrossRef CAS; (d) K. Altenburger, P. Arndt, A. Spannenberg and U. Rosenthal, Z. Anorg. Allg. Chem., 2015, 641, 2047–2050 CrossRef CAS; (e) K. Altenburger, W. Baumann, A. Spannenberg, P. Arndt and U. Rosenthal, Eur. J. Inorg. Chem., 2014, 5948–5957 CrossRef CAS; (f) M. Kamitani, B. Pinter, K. Searles, M. G. Crestani, A. Hickey, B. C. Manor, P. J. Carroll and D. J. Mindiola, J. Am. Chem. Soc., 2015, 137, 11872–11875 CrossRef CAS PubMed; (g) M. Horáček, P. Štěpnička, J. Kubišta, I. Císařová, L. Petrusová and K. Mach, J. Organomet. Chem., 2003, 667, 154–166 CrossRef; (h) J. Y. Chen, I. A. Guzei and L. K. Woo, Inorg. Chem., 2000, 39, 3715–3717 CrossRef CAS PubMed; (i) P. Štěpnička, R. Gyepes, I. Císařová, V. Varga, M. Polášek, M. Horáček and K. Mach, Organometallics, 1999, 18, 627–633 CrossRef; (j) M. Horáček, K. V. U. Thewalt, P. Štěpnička, M. Polášek and K. Mach, Organometallics, 1999, 18, 3572–3578 CrossRef.
- (a) D. Danovich and S. Shaik, J. Am. Chem. Soc., 1997, 119, 1773–1786 CrossRef CAS; (b) D. Schroder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145 CrossRef CAS PubMed; (c) J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1–14 CrossRef CAS; (d) P. L. Holland, Acc. Chem. Res., 2015, 48, 1696–1702 CrossRef CAS PubMed.
- K. M. Smith, R. Poli and J. N. Harvey, New J. Chem., 2000, 24, 77–80 RSC.
- S. M. Bellows, T. R. Cundari and P. L. Holland, Organometallics, 2013, 32, 4741–4751 CrossRef CAS.
- (a) P. v. R. Schleyer and A. J. Kos, Tetrahedron, 1983, 39, 1141–1150 CrossRef CAS; (b) A. E. Reed and P. v. R. Schleyer, J. Am. Chem. Soc., 1990, 112, 1434–1445 CrossRef CAS; (c) O. Exner and S. Böhm, New J. Chem., 2008, 32, 1449–1453 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational results, energies, and Cartesian coordinates of the optimized structures. See DOI: 10.1039/c6sc04456e |
| This journal is © The Royal Society of Chemistry 2017 |