Coevolution and ratiometric behaviour in metal cation-driven dynamic covalent systems

Abstract

Dynamic Covalent Libraries (DCLs) have been used to demonstrate coevolution behaviour on a molecular level using dynamic covalent molecules such as imines and hydrazones. Two systems are presented: the first system is based on a dialdehyde and two diamines in combination with Zn(II) and Hg(II) to form a 2 × 2 Constitutional Dynamic Network (CDN) of four complexes of macrocyclic bis-imines. Whereas the two metal ions, when reacted separately form a complex with each macrocycle with low selectivity, when applied together, each cation yields selectively a complex with one of the two macrocycles. Thus, the simultaneous application of both cations, where one might have expected the formation of four different complexes, results in the synergistic evolution (co-evolution) towards a simpler, more selective outcome under agonist amplification. The second system of 4 components, 2 amines and 2 aldehydes displays metalloselection together with a correlated evolution in distribution on complexation of Zn(II) and Cu(I) with the dynamic ligand constituents and exhibits a dynamic ratiometry process related to the antagonistic behaviour of a pair of ligand constituents.

---

Introduction

Coevolution can be defined as the correlated changes of structurally and/or functionally connected entities.¹ In a broader context, the concept of coevolution may concern biological and biochemical systems (such as host-parasite^2a or predator–prey relationships^2b or chemical networks^2c,d), as well as other disciplines such as computer science,¹ sociology³ and astronomy.⁴ Processes of a related conceptual nature may take place in chemistry within the realm of constitutional dynamic chemistry (CDC), where dynamic molecular and supramolecular chemical entities exchange their reversibly linked components within a constitutional dynamic network (CDN).^5,6

Thermodynamically-driven molecular or supramolecular self-sorting may be considered to also imply a coevolution behavior inasmuch as it displays parallel generation of well-defined dynamic entities from a mixture based on molecular recognition/information features.⁷ We have previously described a constitutional coevolution process, based on dynamic imine bonds, in the generation of macrocyclic ligands by component selection between two different diamines and a single dialdehyde in response to two different metal cations.⁸ We here extend these observations within the framework of agonistic amplification, simultaneous up-regulation of two constituents, in the corresponding CDN.^5c,d

On the other hand, a single effector acting on a constitutional dynamic system produces simultaneous up- and down-regulation of two antagonistically-related constituents.⁵ As a consequence, two different effectors applied in different ratios may produce opposite effects on two dynamically-linked constituents, in a combined agonist/antagonist manner which is in principle inherently of coevolution type and may be termed dynamic ratiometry. Indeed, it is reminiscent of the ratiometric analytical method, whereby an effector produces an opposite effect on two sensors, usually displayed by a change in a given macroscopic observable such as an optical effect, like a change in fluorescence.⁹ This methodology was also applied to pH measurements using ¹H NMR, where the ratio between two peaks of different species (protonated and deprotonated) was used to determine the pH of an aqueous solution with high precision.¹⁰

We herewith describe both types of coevolution processes, based on dynamic covalent chemistry (DCC) involving ligand constituents generated from components linked by reversibly forming C=N covalent bonds.

Agonistic coevolution of a dynamic system under effector competition

The first system examined here (system I, Scheme 1; see also ESI for details†) is based on a previously described morphological switch that has been integrated into covalent dynamic systems through formation of reversible imine bonds.⁸ It involves the condensation of the dialdehyde (1-Me), based on a pyridine–hydrazone–pyridine scaffold, with two different diamines, 1,3-diaminopropane (N2C3) and 1,4-diaminobutane (N2C4), in the presence of different metal ions, Zn(II) and Hg(II), either separately or both together, to give the corresponding four macrocyclic complexes Zn·1-Me·N2C3, Zn·1-Me·N2C4, Hg·1-Me·N2C3 and Hg·1-Me·N2C4.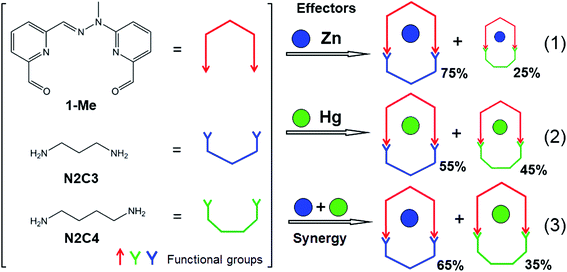

Scheme 1 Schematic representation of the coevolution process in system I (see also ESI†) involving the four constituents (right) generated from the three components (left) and displaying the outcome of the competition experiments (1)–(3). The red double arrow represents the dialdehyde 1-Me, shown in its U shape for simplicity, the free dialdehyde being in a W conformation.¹¹ The green and blue graphics represent respectively the N2C3 and N2C4 diamine components. Blue and green dots represent Zn(II) ion and Hg(II) ion, respectively.

The competition experiments have been designed so as to reveal the operation of coevolution in determining the constituents predominantly formed under simultaneous application of the two metal cation effectors cooperation as compared to the effect of each cation taken separately. To this end, all experiments were conducted with a 1 : 1 ratio of all the components. Reacting first the dialdehyde 1-Me with the two diamines N2C3 and N2C4, and Zn(II), (1 equivalent (3 μmol) each, in 0.6 mL CDCl₃/CD₃CN: 1/1) (Scheme 1; competition experiment (1)) yielded both macrocyclic complexes Zn·1-Me·N2C3, Zn·1-Me·N2C4 in 75% and 25% proportions respectively (determined using ¹H NMR integration). The same experiment was repeated with Hg(II), giving also a mixture of complexes (Scheme 1; competition experiment (2)), with again the complex incorporating the diamine N2C3, Hg·1-Me·N2C3 formed predominantly (55 and 45%, respectively). Note that the ¹H–¹⁹⁹Hg spin–spin coupling can be observed in the ¹H NMR spectra (Fig. S1, ESI†). Both experiments thus gave a mixture of products. The third experiment (Scheme 1; competition experiment (3)) was conducted using both Zn(II) and Hg(II), with again 1 equivalent of all the components. Out of the four possible macrocyclic complexes, only two compounds were observed (Fig. 1). The Zn(II) metal ion formed exclusively the macrocyclic complex Zn·1-Me·N2C3, containing the diamine N2C3, whereas the Hg(II) cation gave exclusively the agonistic macrocyclic complex, Hg·1-Me·N2C4 involving the diamine N2C4 (65 and 35%, respectively).

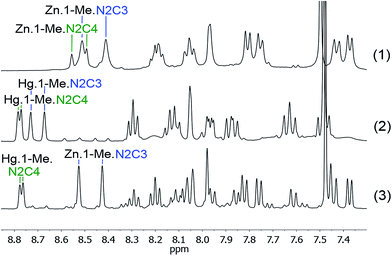Fig. 1 ¹H NMR competition experiments between the components 1-Me, N2C3 and N2C4, in presence of Zn(OTf)₂ (1) or Hg(OTf)₂ (2) and of a 1 : 1 mixture of Hg(OTf)₂ and Zn(OTf)₂ (3).

It is interesting to see that the Hg(II) macrocycle obtained in this double competition experiment involving both cations is that which was less favored in the competition experiment (2) where Hg(II) was alone (Scheme 1). Based on the complementary competition experiments, it is clearly the Zn(II) ion which forced the Hg(II) ion to choose the N2C4 diamine, as Zn(II) has a very strong preference for binding to the 1-Me·N2C3 macrocycle (Fig. S2–S4, ESI†).

The present results illustrate in a simple fashion three attractive features of CDC: (1) coevolution of constituents subjected to two different effectors; (2) agonist amplification whereby the amplification of one constituent enforces the amplification of its agonist which otherwise would not form predominantly (see also ref. 12); (3) competition-driven selection by which a more complex system (i.e. here containing one more component, the second metal cation) results in a simpler outcome (here only two products out of four possible, Scheme 1; see also ref. 13). All three features result from the fact that the system operates within a CDN (Scheme 2).

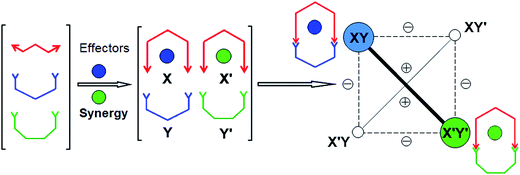Scheme 2 Graphical representation of the coevolution of system I (Scheme 1) resulting from the synergistic selection operated by effector competition within the dynamic constitutional network formed by the four constituents XY, X′Y, XY′ and X′Y′. (−) and (+) indicate respectively an antagonistic and an agonistic relationship between constituents.

The operation of the present system represents a competitive coevolution behavior (see also point (3) above). It bears some analogy to evolutionary biology which addresses the evolution of species that have a negative or positive effect on each other, like predators and preys (see for instance ref. 2b). It illustrates analogies between dynamic molecular constitutional coevolution and the occurrence of natural selection of chemical entities.

Agonistic/antagonistic competitive coevolution and dynamic ratiometry in a DCL

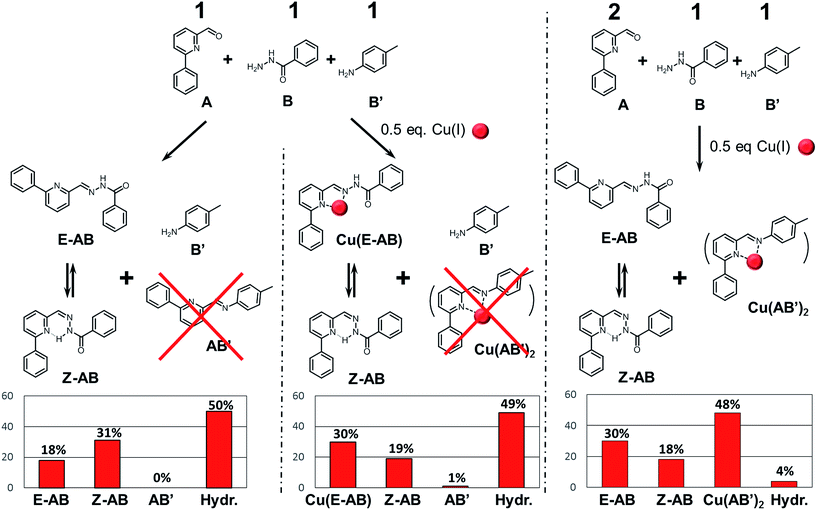
The second system (system II, Scheme 3 top; see also ESI for details†) studied in this work has been implemented previously for other purposes.¹⁴ It serves here to illustrate a competitive agonist/antagonist coevolution process exhibiting a ratiometry effect with the effectors used. It was generated from 4 components, 2 amines (A, A′) and 2 aldehydes (B; B′), which were mixed in deuterated acetonitrile (1.25 × 10⁻⁵ mol, 25 mM each) to give the four library constituents AB, A′B, AB′ and A′B′ (see also ref. 14; Fig. S5–S9, ESI†).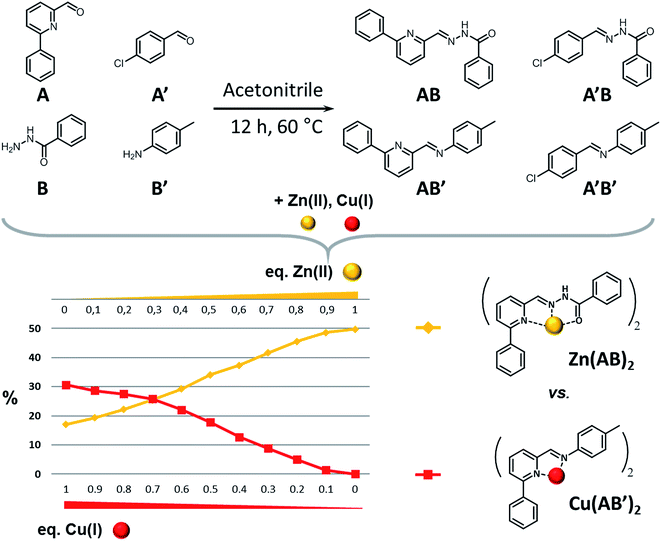

Scheme 3 (Top) Generation of the CDL AB, A′B, AB′ and A′B′ from components A, B, A′ and B′. (Bottom) Constitutional dynamic ratiometry: graph representing the evolution of the relative amounts of the antagonists AB and AB′ against the Cu(I)/Zn(II) ratio. Similar results are obtained when the metal ions are added either to the components or to the preformed constituents. The other 50% of constituents is formed by A′B′ and A′B plus hydrolysis products (see Fig. S8†). For a graph displaying the evolution of all four constituents, see Table S1 and Fig. S9 in ESI.†

As previously observed, addition of Cu(I) or Zn(II) to this DCL gave respective CDLs containing preferentially the complexes Cu(AB′)₂, and Zn(AB)₂. Furthermore, it was found that addition of Zn(II) to the Cu(I) CDL, converted it into the same CDL as that obtained when Zn(II) alone was added.

The adaptability of this dynamic system can be implemented to probe mixtures of the two effectors (Scheme 3 bottom). Indeed, the ratio between the two antagonists AB and AB′ in the DCL of the four constituents directly correlates with the ratio between the Zn(II) and Cu(I) in the test mixture, as was shown by addition of mixtures of Cu(I) and Zn(II) in different proportions containing a total amount of 0.5 eq. of metal cations (0.62 × 10⁻⁵ mol, 12.5 mM each) to the DCL. To this end, a series of samples was prepared, where the amount of Cu(I) gradually decreased from 0.5 eq. to 0 eq. and the amount of Zn(II) correspondingly increased from 0 eq. to 0.5 eq. All samples were heated at 60 °C for 12 h to achieve thermodynamic equilibration. Thereafter the ratio of antagonists AB and AB′ was calculated from the integrations of all the species (free, complexed) of a given constituent (see Fig. S5 to S9 in ESI†). Adding the metals ions either to the components or to the preformed constituents gives similar results. The other 50% of constituents is formed by A′B′ and A′B plus hydrolysis products.

The changes observed result from the differential amplification effects of these two effectors onto the antagonists AB and AB′, containing both the aldehyde A, and their direct competition for this component, each metal cation in the mixture favoring the opposite antagonist (Scheme 3). Increasing the ratio of Zn(II) in the Cu(I)/Zn(II) mixture enhances also the formation of AB, but as long as there is some Cu(I) in the mixture its antagonist (AB′) will not disappear. This correlation is shown on the graph of Scheme 3, exemplifying further the concept of coevolution in this case in opposite fashion. It is possible to directly relate the ratio of antagonists to the ratio of the metals (Cu/Zn) present, hence use this system as a way to titrate mixtures of the metal cation. In view of the dynamic component exchange between the cation sensors AB and AB′, the behaviour observed can be described as a constitutional dynamic ratiometry, referring to the analytical method called ratiometry where an effector produces an opposite effect on two sensors usually displayed by a change in a given macroscopic observable (like an optical effect). Two significant points can be seen on the graph: the 0.7 : 0.3 Cu/Zn ratio which gives a 1/1 ratio of AB and AB′ (25% each) and the 0.5 : 0.5 Cu/Zn ratio giving a 0.33 : 0.17 AB/AB′ ratio (Table S1, ESI†). This clearly indicates that formation of the Zn(II) complex favoured over that of the Cu(I) complex. One may also note, that this approach requires to work under overall stoichiometric ratios between components of the mixture in order to obtain a linear response.¹⁵

Coevolution: synergism of pairs of agonists in a balanced full network

Another important question concerns the requirements for coevolution to occur. Indeed, the constituents AB, A′B, AB′ and A′B′ of the DCL consist in two acylhydrazones and two imines of very different thermodynamics of C=N bond formation, the former being preferentially formed in competition.¹⁶ The effect of this factor for the occurrence of the present coevolution processes was investigated by performing competition experiments with “subsystems” of only three components. Thus, using a three-component system A, B and B′ instead of four, the two amino partners B and B′ compete for the same aldehyde A (Scheme 4). When these components were mixed in 1 : 1 : 1 ratio and heated for 12 h at 60 °C, the only formed constituent was as expected AB present as its E and Z isomers in 1 : 1.8 ratio (Scheme 4, left).^6a,17 It is worth noting the effect of p-toluidine¹⁸ and aniline^6a,19 as nucleophilic catalyst of acylhydrazone and hydrazone formation. Indeed, the formation of the acylhydrazone AB in the mixture of A, B and B′ is considerably faster than when just A and B are mixed under the same conditions.

Scheme 4 (Left) Subsystem A : B : B′ (1 : 1 : 1) equilibrated without metal cation (acetonitrile, 12 h, 60 °C) – only AB (E and Z) is formed; (middle) subsystem A : B : B′ (1 : 1 : 1) equilibrated (acetonitrile, 12 h, 60 °C) in presence of Cu(I) cation, leading to a change in E/Z ratio for AB, presumably due to coordination to the E form of AB; (right) subsystem A : B : B′ (2 : 1 : 1) equilibrated (acetonitrile, 12 h, 60 °C) in a presence of 0.5 eq. of Cu⁺ cation; AB and AB′ form in 1 : 1 ratio, the latter in its expected Cu(I) complex; the E/Z ratio is similar to that observed in the case in the middle due to the presence of Cu(I) ions in the medium (see also text). The error of the experiment is ±2%.

Thereafter, the impact of the presence of the Zn(II) or Cu(I) cations was studied. One could assume that each metal would amplify its respective ligand constituent, AB for Zn(II) and AB′ for Cu(I). While Zn(II) provided the expected result, giving Zn(AB)₂ as a sole product (see ESI†), the addition of Cu(I) did not give the expected Cu(AB′)₂. The only product observed after equilibration of this subsystem was again AB with a reversed E : Z ratio 1.6 : 1, indicating that potential Cu(I) coordination was not sufficient to enforce the formation of AB′. In addition, the reversed E : Z ratio can be attributed to the partial coordination of the Cu(I) cations to the E-AB isomer (Scheme 4, middle). However, the absence of full amplification of the E isomer and persisting presence of the Z isomer indicated that the coordination of Cu(I) to AB cannot be solely responsible for the biased evolution of the subsystem.

To ascertain the coordination preference of the Cu(I) for binding either to AB or AB′ a mixture of A/B/B′ in 2 : 1 : 1 ratio was studied. This set up also takes into account possible kinetic and thermodynamic aspects of complex/constituent formation (slow formation, hydrolysis, coordination to components, etc.). After equilibration at 60 °C for 12 h in acetonitrile in presence of 0.5 eq. Cu(I) the Cu(AB′)₂/AB/hydrolysis = 48/48/4% distribution was observed with AB being present in 1.6 : 1 E : Z ratio. This ratio is similar to that obtained in the case above (Scheme 4, middle), indicating that the observed library composition was caused by Cu(I) ions from the labile complex Cu(AB′)₂ (Scheme 4, right; Table S2 and Fig. S10 and S11 in ESI†). This result only confirms the strong preference of Cu(I) cation for coordination of AB′ over the acylhydrazone AB when both are present.

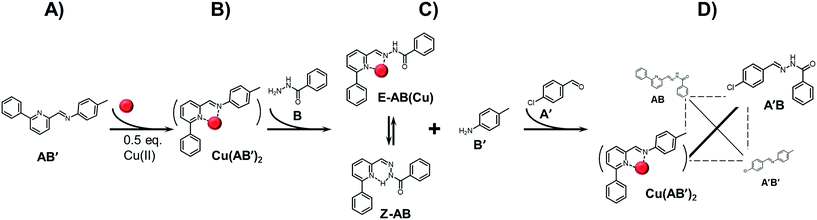
In order to get a better insight into the behaviour of the present system, a series of consecutive reactions was conducted (Scheme 5, as well as Fig. S12 and Table S3 in ESI†). The sequence starts with the clean and quantitative formation of imine complex Cu(AB′)₂ (step A to B in Scheme 5). The introduction of benzhydrazide (component B) leads to the exchange of components and almost quantitative formation of AB as a mixture of both E and Z isomers (step B to C in Scheme 5). The complex Cu(AB′)₂ reappears only after introduction of components A′ which, via formation of non-complexing acylhydrazone A′B, energetically balances the difference in bond formation preference of the imine/acylhydrazone agonist pairs (step C to D in Scheme 5). As a result, AB′/A′B pair is amplified as observed in the previously studied system¹⁵ as well as in the above described dynamic ratiometry.

Scheme 5 Sequential reactions leading to a thermodynamically balanced system comprising the four components A, A′, B and B′ and resulting in a fully formed 2D dynamic network of four constituents AB, A′B, AB′ and A′B′, with amplification of the agonist constituents AB′ and A′B in response to addition of Cu(I) ions (the former as its Cu(I) complex). See also text.

These experiments point to the reason behind the one-sided evolution of the A, B, B′ mixture both as such and in the presence of Cu(I) ions (see above): in the case of a large difference in thermodynamic stability of individual dynamic bonds (here acylhydrazone vs. imine), the effect of metal cation coordination to the less stable ligand may just not be sufficient to significantly affect/invert the constituent distribution in the absence of cation. Thus, all four components A, A′, B, B′ are required in order for the system to behave as observed above so that one imine C=N bond and one acylhydrazone C=N bond are formed at each side of the balance represented here as the opposite diagonals/agonist pairs. Only when the agonists pairs of constituents, AB, A′B′ on one hand and AB′, A′B on the other, bear similar overall thermodynamic stability, the coordination of the metal ion Cu(I) to the less stable constituent (imine AB′) paired with the more stable agonist partner (acylhydrazone A′B) is strong enough to tilt the balance in favour of the formation of Cu(AB′)₂ and enforce the observed constituent distribution.

Conclusion

Constitutional dynamic coevolution based on reversible covalent bonds has been implemented in two complementary systems involving the operation of agonistic and antagonistic relationships in the CDN of the system. The results obtained lead to three main conclusions: (i) increasing the complexity of a CDL by addition of a further component reduces the number of output entities, yielding a more selective output through dynamic competition;¹³ (ii) agonist/antagonist competition allows for a process that may be described as dynamic ratiometry, making it possible to directly relate the ratio of antagonists to the ratio of two different effectors (here the Cu(I)/Zn(II) ratio) by means of a calibration curve; (iii) most significantly, a generally important factor in the behaviour of CDNs and in the outcome of coevolution is that the full CDN, i.e. the system of higher complexity, is required so as to allow for the concerted operation of both agonists in a pair acting in synergy.

Acknowledgements

The authors thank the ERC (Advanced Research Grant SUPRADAPT 290585) and the University of Strasbourg for post-doctoral (SD) and doctoral (JH) fellowships and financial support.

References

1. K. Y. Yip, P. Patel, P. M. Kim, D. M. Engelman, D. McDermott and M. Gerstein, Bioinformatics, 2008, 24, 290–292.
2. (a) R. M. Anderson, Parasitology, 1982, 85, 411–426; (b) T. Fujii and Y. Rondelez, ACS Nano, 2013, 7, 27–34; (c) For competition and cooperation in chemical networks, see: Z. Dadon, N. Wagner, S. Alasibi, M. Samiappan, R. Mukherjee and G. Ashkenasy, Chem.–Eur. J., 2015, 21, 648–654; (d) For systems chemistry, see for instance: R. F. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101–108; V. del Amo and D. Philp, Chem.–Eur. J., 2010, 16, 13304–13318; S. Ghosh, P. Mukhopadhyay and L. Isaacs, J. Syst. Chem., 2010, 1, 1–13; R. A. R. Hunt and S. Otto, Chem. Commun., 2011, 47, 847–858; B. Grzybowski, S. Otto and D. Philp, Systems chemistry: a web themed issue, Chem. Commun., 2014, 50, 14924–14925.
3. A. Bandura, Annu. Rev. Psychol., 2001, 52, 1–26.
4. G. L. Granato, G. De Zotti, L. Silva, A. Bressan and L. Danese, Astrophys. J., 2004, 600, 580.
5. (a) J.-M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160; (b) J.-M. Lehn, in Constitutional Dynamic Chemistry, Topics Curr. Chem., ed. M. Barboiu, 2012, vol. 322, pp. 1–32; (c) J.-M. Lehn, Angew. Chem., Int. Ed., 2013, 52, 2836–2850; (d) J.-M. Lehn, Angew. Chem., Int. Ed., 2015, 54, 3276–3289.
6. For two specific recent examples, see: (a) G. Vantomme, S. Jiang and J.-M. Lehn, J. Am. Chem. Soc., 2014, 136, 9509–9518; (b) G. Vantomme, N. Hafezi and J.-M. Lehn, Chem. Sci., 2014, 5, 1475–1483.
7. (a) R. Krämer, J.-M. Lehn and A. Marquis-Rigault, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 5394–5398; (b) P. Mukhopadhyay, P. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2006, 128, 14093–14102; (c) J. R. Nitschke, Acc. Chem. Res., 2007, 40, 103–112; (d) M. M. Safont-Sempere, G. Fernandez and F. Würthner, Chem. Rev., 2011, 111, 5784–5814; (e) M. Schmittel, Chem. Commun., 2015, 51, 14956–14968; (f) Z. He, W. Jiang and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 779–789.
8. (a) S. Ulrich, E. Buhler and J.-M. Lehn, New J. Chem., 2009, 33, 271–292; (b) S. Ulrich and J.-M. Lehn, J. Am. Chem. Soc., 2009, 131, 5546–5559.
9. (a) A. P. Demchenko, A. S. Klymchenko, V. G. Pivovarenko and S. Ercelen, Ratiometric Probes: Design and Applications, in Fluorescence Spectroscopy, Imaging and Probes, Springer: Verlag, 2nd edn, 2002, pp. 101–110; (b) P. Carol, S. Sreejith and A. Ajayaghosh, Chem.–Asian J., 2007, 2, 338–348; (c) H. M. Lee, J. S. Kim and J. L. Sessler, Chem. Soc. Rev., 2015, 44, 4185–4191; (d) D. Fan, J. Zhu, Q. Zhai, E. Wang and S. Dong, Chem. Commun., 2016, 52, 3766–3769.
10. (a) P. K. Senanayake, A. M. Kenwright, D. Parker and S. K. van der Hoorn, Chem. Commun., 2007, 2923–2925; (b) L. H. Perruchoud, M. D. Jones, A. Sutrisno, D. B. Zamble, A. J. Simpson and X.-A. Zhang, Chem. Sci., 2015, 6, 6305–6311.
11. (a) S. Ulrich and J.-M. Lehn, Chem.–Eur. J., 2009, 15, 5640–5645; (b) L. Ratjen, G. Vantomme and J.-M. Lehn, Chem.–Eur. J., 2015, 27, 10070–10081.
12. S. Ulrich and J.-M. Lehn, Angew. Chem., Int. Ed., 2008, 47, 2240–2243.
13. For a related process concerning organic reactional selectivity, see: P. Kovaříček, A. C. Meister, K. Flídrová, R. Cabot, K. Kovaříčková and J.-M. Lehn, Chem. Sci., 2016, 7, 3215–3226.
14. J. Holub, G. Vantomme and J.-M. Lehn, J. Am. Chem. Soc., 2016, 138, 11783–11791.
15. For a related case of self-sensing of Zn(II) in a dynamic system, see: N. Giuseppone and J.-M. Lehn, J. Am. Chem. Soc., 2004, 126, 11448–11449.
16. (a) A.-M. Stadler, Isr. J. Chem., 2013, 53, 113–121; (b) S. Kulchat, PhD thesis, Université de Strasbourg, 2015, manuscript in preparation.
17. (a) P. Hope and L. A. Wiles, J. Chem. Soc. C, 1966, 283–285; (b) G. Palla, G. Predieri and P. Domiano, Tetrahedron, 1986, 42, 2649–3654; (c) M. N. Chaur, D. Collado and J.-M. Lehn, Chem.–Eur. J., 2011, 17, 248–258; (d) D. J. van Dijken, P. Kovaříček, S. P. Ihrig and S. Hecht, J. Am. Chem. Soc., 2015, 137, 14982–14991.
18. P. Crisalli and E. T. Kool, J. Org. Chem., 2013, 78, 1184–1189.
19. (a) E. H. Cordes and W. P. Jencks, J. Am. Chem. Soc., 1962, 84, 826–831; (b) A. Dirksen, S. Dirksen, T. M. Hackeng and P. E. Dawson, J. Am. Chem. Soc., 2006, 128, 15602–15603.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc04662b

---