Open Access Article
Open Access ArticlePrediction of superconducting iron–bismuth intermetallic compounds at high pressure
Maximilian
Amsler
,
S. Shahab
Naghavi
and
Chris
Wolverton
*
Department of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA. E-mail: c-wolverton@northwestern.edu; Tel: +1 847 467 0593
First published on 7th December 2016
Abstract
The synthesis of materials in high-pressure experiments has recently attracted increasing attention, especially since the discovery of record breaking superconducting temperatures in the sulfur–hydrogen and other hydrogen-rich systems. Commonly, the initial precursor in a high pressure experiment contains constituent elements that are known to form compounds at ambient conditions, however the discovery of high-pressure phases in systems immiscible under ambient conditions poses an additional materials design challenge. We performed an extensive multi component ab initio structural search in the immiscible Fe–Bi system at high pressure and report on the surprising discovery of two stable compounds at pressures above ≈36 GPa, FeBi2 and FeBi3. According to our predictions, FeBi2 is a metal at the border of magnetism with a conventional electron–phonon mediated superconducting transition temperature of Tc = 1.3 K at 40 GPa.
1 Introduction
Improved strategies to discover energy materials are called for to tackle the inevitable global environmental challenges due to limited fossil fuels and climate change. Recent advances in materials science have not only been aimed at exploring uncharted chemical space, but has also brought forward novel synthesis pathways to design materials at non-ambient conditions. In addition to composition and temperature, pressure constitutes an accessible degree of freedom to be sampled in the search for novel materials. Significant progress has been made in high-pressure techniques such that several hundred GPa can be meanwhile readily achieved in diamond anvil cells (DAC).Often, materials design rules based on chemical intuition derived at ambient conditions cannot be directly applied at high pressure, where unexpected physical phenomena can lead to surprising discoveries in novel compositions, bonding and electronic structures. Ab initio calculations have proven to provide crucial insight in understanding and predicting new phases at these conditions. The discovery of an ionic form of boron for example was first predicted from evolutionary structural search and later confirmed by experiments,1 and similarly the metal–insulator transition in elemental sodium was initially predicted from density functional theory (DFT) calculations.2 Recently, a range of unexpected stoichiometries was found in the Na–Cl system at high pressure with compositions ranging from NaCl3 to Na3Cl,3 radically defeating chemical intuition for ionic materials.
Many high pressure studies, including the examples above, are commonly performed with precursors (i.e. crystals or molecules) containing constituent elements that are known to form some compound at ambient condition. This choice is well justified due to two reasons: first, it is easier and hence preferable to place a sample into a DAC which already exhibits the targeted interatomic bonds. Second, the risk of elemental decomposition can be expected to be lower if the constituent elements form stable compounds at some known condition. Studying alloy systems at high pressures with severe immiscibility at ambient pressure (i.e. not forming compounds over any range of composition and temperature) therefore poses a significant additional materials discovery challenge. In fact, bismuth is well known for its notorious solid-state immiscibility, which has precluded the formation of binaries with a wide range of elements,4 leading to various high pressure attempts to synthesize novel bismuth containing intermetallics.5–8 In particular, the ambient phase diagram of the Fe–Bi intermetallic system shows essentially no solubility of Fe in Bi (or vice versa)4 and thus constitutes an excellent example of a system possibly containing unexpected high-pressure phases awaiting discovery.
Superconductivity has been the main focus of many recent theoretical and experimental high-pressure studies, with an increasing interest in hydrogen-rich materials since the discovery of record-breaking transition temperatures in the range of 100–200 K in sulfur- and phosphorus-hydrides.9–35 Similarly, iron based superconductors have recently been intensely studied36,37 in so called 1111,38,39 122,40 111,41 and 11 (ref. 42) compounds. Ferro pnictides such as LiFeAs41,43,44 and Sr0.5Sm0.5FeAsF45 exhibit high transition temperatures at ambient condition of Tc = 18 K and Tc = 56 K, respectively, while other compounds such as NaFeAs44,46,47 and FeSe42,48 show a strong increase in Tc at high pressure (e.g. from 8 to 36.7 K in FeSe). The superconducting mechanism in all these iron-based compounds is unconventional and thus not based on electron–phonon coupling,49–51 instead the proximity to magnetism suggests that magnetic (spin) fluctuations play a key role in mediating superconductivity.49–52 Furthermore, many phosphide, arsenide and antimonide superconductors have been discovered, also reviving intense investigations in bismuth containing compounds. The intermetallic compound Ca11Bi10−x was found to be superconducting with Tc = 2.2 K, and several other Ca–Bi binaries were predicted to have Tcs in the range of 2.27–5.25 K in high pressure phases.53 The nickel–bismuth binaries, NiBi54 and NiBi3,55,56 are both superconductors with Tc values of 4.25 K (ref. 57) and 4.06 K,58,59 respectively. Similarly, the CoBi3 high pressure compound is a superconductor with Tc = 0.48 K,6–8 as well as the copper–bismuth binary Cu11Bi7 which forms at high-pressure with a Tc of 1.36 K.5
Here we report on the prediction of two stable high-pressure compounds, FeBi2 and FeBi3, in the completely immiscible Fe–Bi system by performing an extensive multi-component ab initio structural search. The Fe–Bi system not only shows no stable compounds in its ambient-pressure phase diagram,4 but there is virtually no solubility of either solid-state element in the other. Thus, the prediction of stable compounds in this system is particularly surprising. In contrast to FeSb2 and FeAs2, which are both semiconductors with promising thermoelectric properties, FeBi2 is metallic in a wide pressure range. The ferromagnetic and antiferromagnetic order in FeBi2 is suppressed by pressure, leading to a superconducting behavior with a conventional Tc of 1.3 K in the non magnetic state at 40 GPa. Due to its proximity to magnetism, FeBi2 is possibly a new member in the family of unconventional iron-pnictide superconductors.51
2 Method
Density functional theory (DFT) calculations were carried out to predict the composition, structure, and properties of novel binary Fe–Bi compounds. The minima hopping structure prediction method (MHM) as implemented in the Minhocao package60,61 was employed to perform a multi-component search for stable phases at high pressure. The MHM implements a reliable algorithm to identify the ground state structure of any compound by efficiently sampling low lying phases on the enthalpy landscape, based solely on the information of the chemical composition.31,62,63 Consecutive short molecular dynamics escape steps are performed to overcome enthalpy barriers followed by local geometry optimizations, while exploiting the Bell–Evans–Polanyi principle in order to accelerate the search.64,65The energies, forces and stresses were evaluated from DFT calculations within the projector augmented wave (PAW) formalism66 as implemented in the VASP67–69 code together with the Perdew–Burke–Ernzerhof (PBE) approximation70 to the exchange–correlation potential. A plane-wave cutoff energy of 400 eV was used in conjunction with a sufficiently dense k-point mesh to ensure a convergence of the total energy to within 1 meV per atom. Geometries were fully relaxed with a tight convergence criterion of less than 4 meV Å−1 for the maximal force components.
The magnetic properties for the estimation of the Stoner parameter were evaluated with the full potential linearized augmented plane wave (FLAPW) method as implemented in the WIEN2k code.71 The number of plane waves was restricted by RMTkmax = 9. All self-consistent calculations were performed with 6000 k-points in the irreducible wedge of the Brillouin zone, based on a mesh of 18 × 18 × 18 k-points. The convergence criteria were set to 10−5 Ry for the energies and simultaneously to 10−3 e for charges.
Superconducting properties were computed with the Quantum Espresso package72 together with ultra-soft pseudopotentials and a plane-wave cutoff energy of 60 Ry. The phonon-mediated superconducting temperature was estimated using the Allan-Dynes modified McMillan's approximation of the Eliashberg equation73 according to
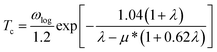 | (1) |
3 Results and discussion
We employed the MHM within the DFT framework to fully assess the stability of high-pressure phases of the Fe–Bi system. A pre-screening of only few compositions showed that Fe-rich compositions were overall less stable, such that the Bi-rich region was more densely sampled. Overall, structural searches were conducted in the compositional space of FexBi1−x for x = (0.2, 0.![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) , 0.25, 0.3, 0.
, 0.25, 0.3, 0.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , 0.375, 0.4,
, 0.375, 0.4,  , 0.
, 0.![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) , 0.5, 0.6, 0.
, 0.5, 0.6, 0.![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) , 0.75) with up to 4 formula units per cell at 50 GPa, scanning several thousand different structures. The initial seeds were randomly generated or taken from already known bismuth intermetallics whenever available in structural databases. A range of the lowest energy structures at each compositions were subsequently relaxed with refined parameters at pressures between 0 and 100 GPa to obtain the complete pressure-composition phase diagram.
, 0.75) with up to 4 formula units per cell at 50 GPa, scanning several thousand different structures. The initial seeds were randomly generated or taken from already known bismuth intermetallics whenever available in structural databases. A range of the lowest energy structures at each compositions were subsequently relaxed with refined parameters at pressures between 0 and 100 GPa to obtain the complete pressure-composition phase diagram.
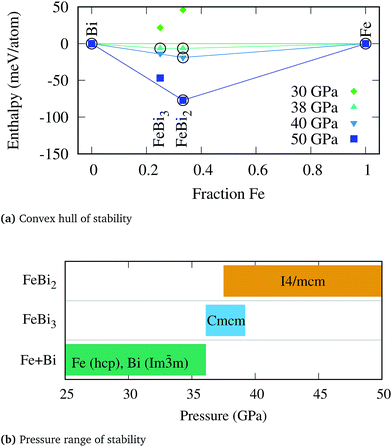
No thermodynamically stable compound was found up to around 36 GPa, at which point two binary phases, FeBi2 and FeBi3, exhibit negative formation enthalpies. The pressure range for which the compounds are thermodynamically stable are shown in Fig. 1 together with the evolution of the convex hull of stability as a function of pressure. The range of stability for the FeBi3 phase is rather narrow, merely between 36.1 and 39.2 GPa, whereas FeBi2 remains thermodynamically stable from 37.5 up to at least 100 GPa. In fact, the magnitude by which the formation enthalpy of FeBi3 is negative is very small, as shown in panel (a) of Fig. 1, such that the driving force for forming this phase is weak and it might be hard to experimentally synthesize it from elements. The FeBi2 phase was predicted to crystallize in the Al2Cu structure with space group I4/mcm. The lattice parameters at 40 GPa are a = 6.12 Å and c = 5.46 Å, respectively, with Fe and Bi at the Wyckoff positions 4a(0, 0, 0.250) and 8h(0.333, 0.833, 0), respectively. The FeBi3 phase crystallizes in the PuBr3 structure74 with space group Cmcm and lattice parameters a = 3.15 Å, b = 11.39 Å, and c = 7.93 Å, with Fe at the Wyckoff positions 4c(0, 0.733, 0.250), and two Bi at 8f(0, 0.359, 0.440) and 4c(0, 0.059, 0.250).
During the structural search the well known marcasite phase of FeBi2 with space group Pnnm was also recovered, which is the ground state structure of many iron-pnictides systems such as FeSb2.75 In fact, the ICSD contains only two early transition metal–antimonides, TiSb2 (ref. 76) and VSb2,76 which crystallize directly in the Al2Cu structure (I4/mcm), but 9 further 3d transition metal pnictides MPn2 which attain the marcasite structure under ambient condition, namely CrSb2,77 FeP2,78 FeAs2,79 FeSb2,80 CoAs2,81 CoSb2,82 NiAs2,83 NiSb2,84 and CuAs2.85 Two of above Pnnm compounds, CrSb2 and FeSb2, have been shown experimentally to undergo a pressure-induced phase transition into the Al2Cu structure at around 5.5 GPa (ref. 86) and 14.3 GPa,87 respectively. While these structural transitions have also been confirmed computationally,88 the transition pressure in FeSb2 is slightly overestimated (38 GPa).89 In analogy to these two compounds, the formation enthalpy of the marcasite structure in FeBi2 becomes lower than the Al2Cu phase at pressures below 11 GPa, however it remains positive at all pressures and this phase is therefore thermodynamically unstable at any condition. Similarly, for the FeBi3 compound the RhBi3-type structure with space group Pnma, which has also been reported in NiBi3,90 is thermodynamically favored with respect to the PuBr3 phase at pressures below 32 GPa but retains a positive formation enthalpy.
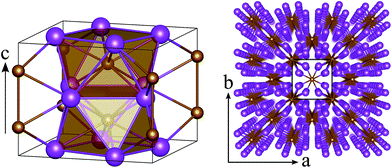
Since the composition with the largest range of stability is FeBi2, we will henceforth focus on this compound in the Al2Cu structure. Although there are many different interpretations of this structure,91 K. Schubert describes it as a stacking of square antiprisms along the c-direction of the conventional cell.92 Each antiprism consists of an iron atom which is surrounded by eight symmetrically equivalent bismuth atoms at identical interatomic distances of 2.99 Å at 0 GPa (see left panel in Fig. 2). These antiprisms are stacked on top of each other by sharing their square faces, forming columns along the c-direction and leading to Fe–Fe distances of 2.85 Å at 0 GPa. These columns themselves are arranged in a square lattice within the ab-plane (Fig. 2, right panel) by sharing the edges of the antiprisms. The three unique Bi–Bi bonds in FeBi2 form the edges of the square faces (3.72 Å), the sides of the triangular faces (3.66 Å), and the inter-column bonds in the ab-plane (3.26 Å).
We carried out a detailed theoretical investigation of the FeBi2 phase with respect to the chemical bonding, magnetic and superconducting properties based on ab initio calculations. Unusual magnetism is prevalent in several iron containing intermetallics with the Al2Cu structure: FeGe2 was for example initially reported to be antiferromagnetic and ferromagnetic above and below 190 K,93 respectively, but later studies could not reproduce the ferromagnetic state, reporting temperature dependent transitions from the paramagnetic state to spin spiral and collinear antiferromagnetism (see ref. 94 and 95 and references therein). Similarly, FeSn2 was reported to exhibit temperature dependent collinear and non-collinear antiferromagnetism.96 Iron pnictides were found to exhibit temperature or pressure induced transitions from semiconductor to metal, accompanied with strong magnetic fluctuations.97–99 Although these compounds crystallize in the marcasite phase, theoretical result predicts that FeP2, FeAs2 and FeSb2 transform into the Al2Cu structure at pressures of above 108, 92 and 38 GPa, respectively,89 and experimental observations report that the phase transition in FeSb2 indeed occurs at 14.3 GPa.87
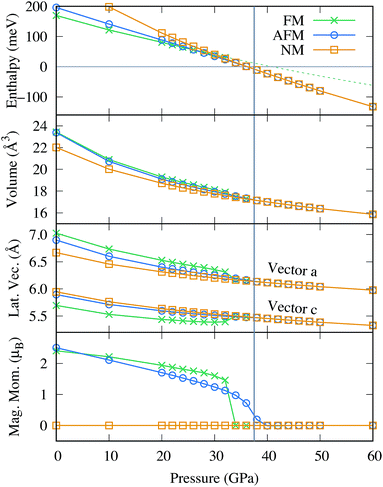
To account for the various reported magnetic properties, we considered the closed shell non magnetic (NM) and two collinear magnetic states in this work: the ferromagnetic (FM) and one anti-ferromagnetic (AFM) configuration, where neighboring Fe atoms carry alternating spins as illustrated in Fig. 2 of ref. 93. Fig. 3 shows how various materials properties vary as a function of pressure for the three different magnetic states. The thermodynamically most stable state at ambient condition is FM although it has a positive formation enthalpy, as illustrated in the top panel. Upon compression, the formation enthalpies of all three magnetic states gradually decreases, until at around 26 GPa AFM becomes the energetically most favorable state. Similarly, the AFM configuration competes with the NM state until at above 38 GPa when the NM state becomes the most stable. The magnetic moments as a function of pressure is shown in the bottom panel of Fig. 3. At ambient pressure, the magnetic moment in the FM configuration is 2.41 μB per Fe, whereas it is 2.51 μB per Fe for the AFM configuration. In both cases, the absolute value of the magnetic moment decreases monotonically as a function of pressure. At a critical pressure of 32 GPa for FM and 40 GPa for AFM, respectively, the magnetic spin polarization collapses, leading to the NM configuration. In contrast to AFM where the magnetic moment decreases smoothly, the spin collapse occurs discontinuously for the FM configuration, accompanied with a sudden decrease in the atomic volume and change in the cell parameters as illustrated in the two middle panels of Fig. 3.
In fact, this reduction in volume plays a crucial role for the stability of FeBi2. The dashed line in the top panel of Fig. 3 was obtained through a quadratic fit within the range of 0 to 30 GPa of the FM state and shows how the formation enthalpy would evolve if the magnetic collapse didn't occur. The formation enthalpy would stay positive until slightly above 40 GPa, and retains a slope with a magnitude much lower compared to the NM configuration. Consequently, the FeBi3 compound would compete with FeBi2 up to a much higher pressure than shown in Fig. 1, leading to a larger stability range of FeBi3 (and a smaller stability range of FeBi2). Therefore, the reduction in volume due to the magnetic collapse is the main driving force that stabilizes FeBi2 since the pressure term pV in the enthalpy, H = E + pV, increasingly dominates the formation enthalpy at high pressure. Its decrease is essentially responsible for the thermodynamic stability of FeBi2.
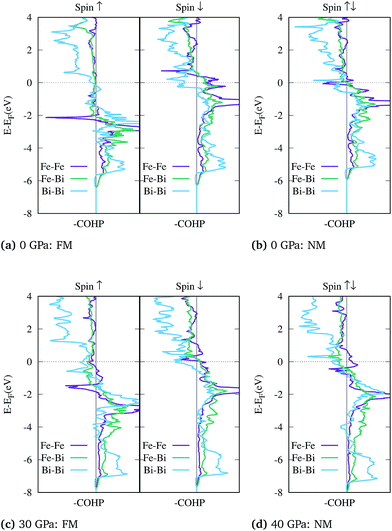
Based on above observations, the collapse of the magnetic state is evidently accompanied by a change in the bonding properties of FeBi2. To analyze the interatomic bonding the crystal orbital Hamilton overlap population (COHP) was computed using the LOBSTER package.100–102 The bonding and antibonding states for the shortest Fe–Fe, Fe–Bi and the Bi–Bi bonds are plotted in Fig. 4. For the NM configuration at 0 GPa shown in panel (b), where the two spin channels are equal (closed shell), the Fermi level falls in the antibonding region of both the Fe–Fe and Bi–Bi interactions, leading to an electronic instability. This unfavorable bonding is relieved in the spin polarized FM configuration shown in (a), where the antibonding states at the Fermi level for the ↑-spin channel are completely removed. When the structure is compressed, the Fermi level is gradually pushed into the antibonding region of both spin channels as shown in Fig. 4(c) for 30 GPa. At this point, the NM configuration becomes favorable and the system is driven towards a closed shell system where the Fermi level does not lie in the Fe–Fe antibonding states, as shown in Fig. 4(d) at 40 GPa.
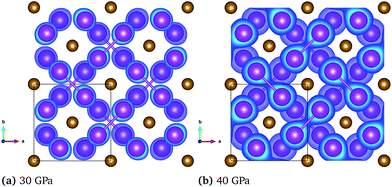
This change in the bonding properties can also be observed when analyzing the electron localization function (ELF). Fig. 5 shows the ELF within the Bi layers of the FM and NM configuration at 30 and 40 GPa, respectively. The electrons, which are initially localized on the individual atoms (see panel (a)), are transferred to the Bi layers to form Bi–Bi dumbbells with strongly covalent character and electrons localized between the Bi atoms. Simultaneously, the Fe–Fe bond is weakened as evident by the increasing lattice constant in the c-direction (Fig. 3, panel 3). This behavior is in good agreement with the COHP shown in Fig. 4, where the Bi–Bi antibonding states at the Fermi level are reduced upon compression. The transition in the bonding character is also reflected in a significant change of the interatomic bond lengths. At a pressure of 30 GPa, the change of the FM to the NM state leads to a decrease in the Bi–Bi and Fe–Bi bonds from 2.95 Å to 2.92 Å and from 2.73 Å to 2.69 Å, respectively, while the Fe–Fe bond increases from 2.69 Å to 2.77 Å.
For isostructural compounds with lighter pnictogen elements Pn = {P, As, Sb}, the formation of Pn-dimers essentially leads to Zintl phases with semiconducting behavior.103 In contrast, FeBi2 remains metallic although similar Bi dumbbells are formed. The Bi–Bi bond length of 2.92 Å is slightly larger than the isolated double-bonded dianion [Bi![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Bi]2−,104 which is about 2.84 Å. This discrepancy can be attributed to extra electronic charge delocalized over the cations, in agreement with the antibonding states at the Fermi level of the dimers shown in Fig. 4(d). Therefore, the expected charge state is [Fe](2−δ)+[Bi2](2+δ)−, where δ > 0. This non-integer charge can readily account for the metallic behavior of FeBi2 as opposed to the Zintl compounds where the octet rule implies a finite band gap as observed in FeAs2.105 Hence, despite the similarities in the main characteristics with other FePn2 compounds, metallic FeBi2 cannot be classified as a traditional Zintl phase.
Bi]2−,104 which is about 2.84 Å. This discrepancy can be attributed to extra electronic charge delocalized over the cations, in agreement with the antibonding states at the Fermi level of the dimers shown in Fig. 4(d). Therefore, the expected charge state is [Fe](2−δ)+[Bi2](2+δ)−, where δ > 0. This non-integer charge can readily account for the metallic behavior of FeBi2 as opposed to the Zintl compounds where the octet rule implies a finite band gap as observed in FeAs2.105 Hence, despite the similarities in the main characteristics with other FePn2 compounds, metallic FeBi2 cannot be classified as a traditional Zintl phase.
Fig. 6 shows the evolution of the simulated X-ray diffraction (XRD) spectra as a function of pressure between 0 and 100 GPa. The change in bonding and the unit cell volume is reflected in the evolution of the XRD pattern, and the relative diffraction angles of the low index peaks could therefore serve as a fingerprint to indirectly distinguish the competing magnetic states. Specifically the pairs of reflections from hkl = (002)/(211), (112)/(221) and (213)/(411) exhibit distinct changes in their relative positions around 30 GPa. In fact, preliminary XRD data has been recently collected with in situ high pressure synchrotron experiments in excellent agreement with our predictions, confirming the formation of the FeBi2 phase at high pressure. A detailed analysis of the experimental results will be published elsewhere.
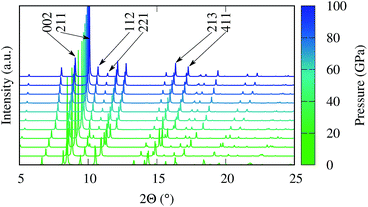 | ||
| Fig. 6 Simulated XRD pattern of FeBi2 at various pressures for synchrotron radiation at a wavelength of 0.40663 Å. | ||
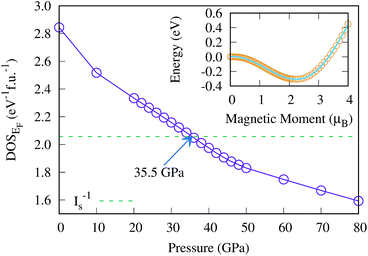
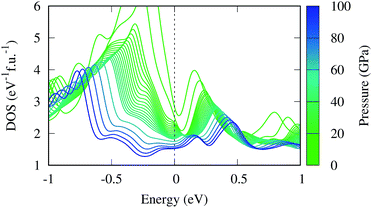
The magnetic collapse in FeBi2 upon compression can be readily explained by the Stoner model,106 which is valid in the context of materials with itinerant magnetism.107–110 According to this model, FM is favored if the gain in exchange energy is larger than the loss in kinetic energy.111 The Stoner criterion serves as an indicator for this magnetic transition, which occurs if DOSEF > Is−1, where DOSEF is the density of states at the Fermi level, and Is is the Stoner parameter which only weakly depends on the inter atomic distances.112 The Stoner parameter can be obtained from a polynomial expansion of the energy as a function of the magnetic moment: E(M) = E0 + a2M2 + a4M4…, where 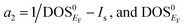 is the non magnetic DOSEF (ref. 111, 113 and 114) (see inset in Fig. 7). With increasing pressure the value of DOSEF gradually decreases (see Fig. 8), and at pc = 35.5 GPa the Stoner criterion is not satisfied anymore as shown in Fig. 7, where DOSEF < Is−1, and thus the NM state is preferred for pressures above pc. This result is in good agreement with the enthalpy plot shown in the top panel of Fig. 3, where NM becomes thermodynamically more favorable than FM above a pressure of 30 GPa, a value close to pc.
is the non magnetic DOSEF (ref. 111, 113 and 114) (see inset in Fig. 7). With increasing pressure the value of DOSEF gradually decreases (see Fig. 8), and at pc = 35.5 GPa the Stoner criterion is not satisfied anymore as shown in Fig. 7, where DOSEF < Is−1, and thus the NM state is preferred for pressures above pc. This result is in good agreement with the enthalpy plot shown in the top panel of Fig. 3, where NM becomes thermodynamically more favorable than FM above a pressure of 30 GPa, a value close to pc.
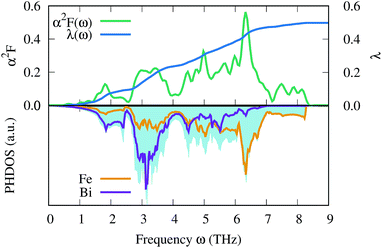
Finally, we estimate the superconducting temperature of FeBi2 in its NM state at 40 GPa within the Bardeen–Cooper–Schrieffer (BCS) theory. The Eliashberg spectral function, the coupling constant λ and the phonon density of states (PHDOS) are shown in Fig. 9. According to our calculations, FeBi2 is a superconductor with Tc = 1.3 K and a moderate electron–phonon coupling constant of λ = 0.50. The lower panel in Fig. 9 shows the total PHDOS together with the partial, atom projected PHDOS. By comparing the spectral function α2F(ω) and the frequency dependent coupling constant λ(ω) with the partial PHDOS we conclude that the electron–phonon coupling is almost evenly distributed over the whole energy range, but two features contribute more then average to the final value of λ. First, there is a strong increase in λ(ω) at a frequency of around ω = 3 THz, which arises mainly from the Bi vibrations. Second, there is an additional strong contribution to λ(ω) in a frequency range between ω = 4.5–7 THz, which can be attributed to the Fe dominated region of the PHDOS. Table 1 contains the results of the electron–phonon coupling calculations at two additional pressures, 60 and 80 GPa. The electron–phonon coupling strength decreases with increasing pressure, leading to a suppression of the superconducting transition temperatures, a behavior also observed in other bismuth superconductors (e.g. CaBi3 (ref. 53)). This trend in Tc can be readily explained by the decreasing DOSEF shown in Fig. 7, since mainly electrons at the Fermi surface contribute to the electron–phonon coupling.
| Pressure (GPa) | λ | ω log (K) | T c (K) |
|---|---|---|---|
| 40 | 0.50 | 184.6 | 1.3 |
| 60 | 0.41 | 217.9 | 0.5 |
| 80 | 0.35 | 244.3 | 0.1 |
Although it is in principle possible for any metal to attain superconductivity at low temperatures, superconducting behavior is usually suppressed in ordered ferromagnetic materials and only few examples have been reported where superconductivity coexists with intrinsic magnetism.115–117 On the other hand, suppressed magnetism, for example through pressure, can induce (unconventional) superconductivity in iron-based materials:51 elemental, non magnetic hcp-iron shows superconductivity above 13 GPa with a maximum Tc = 2 K at 20 GPa,118 and superconductivity in other iron containing materials at the border of magnetism such as FeSe42,119 cannot be fully explained by conventional BCS theory, where the conventional Tc is about one order of magnitude lower than the experimental values.50,120,121 Similarly, LiFeAs was found to superconduct at 18 K, while the Tc from BCS theory is less than 1 K.122 Since electron–phonon coupling cannot fully account for the observed superconducting behavior in above materials, spin fluctuation has been considered as a possible coupling mechanism,50,51,123 but the role of magnetic fluctuations on superconductivity still remains the subject of ongoing research. Our calculations show that FeBi2 is at the verge of FM and AFM order, indicating that it could possibly exhibit unconventional superconductivity, in which case the computed Tc is merely a probable lower limit of the real value. Future experimental efforts are thus called for to fully assess the magnetic and superconducting properties of FeBi2.
4 Conclusion
In summary, we have successfully predicted the stability and superconducting properties of the first binary compound in the ambient-immiscible Fe–Bi system at high pressure, FeBi2. It crystallizes in the Al2Cu structure with space group I4/mcm, is thermodynamically stable above 37.5 GPa and undergoes a series of magnetic transitions upon compression: from ferromagnetic ordering at ambient pressure to an anti-ferromagnetic state and finally to a non magnetic configuration at pressures above 38 GPa. These magnetic transitions are accompanied by structural changes, where short, covalent Bi–Bi bonds are formed in the non magnetic state at high pressure, leading to a significant decrease in the unit cell volume. The resulting low pV term in the enthalpy is thus the main driving force responsible for the formation of FeBi2. Electron–phonon coupling calculations show that FeBi2 is a potential superconductor with a moderate coupling constant and a critical temperature of Tc = 1.3 K at 40 GPa. However, the magnetic frustration in FeBi2 might be an indication of non-conventional superconductivity with a higher value of Tc.Acknowledgements
We thank J. A. Flores-Livas and V. Hegde for valuable discussions. M. A. acknowledges support from the Novartis Universität Basel Excellence Scholarship for Life Sciences and the Swiss National Science Foundation (P300P2-158407). S. S. N. and C. W. acknowledge support by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Grant DE-FG02-07ER46433. The Swiss National Supercomputing Center in Lugano (Project s499, s621 and s700), the Extreme Science and Engineering Discovery Environment (XSEDE) (which is supported by National Science Foundation grant number OCI-1053575), the Bridges system at the Pittsburgh Supercomputing Center (PSC) (which is supported by NSF award number ACI-1445606), the Quest high performance computing facility at Northwestern University, and the National Energy Research Scientific Computing Center (DOE: DE-AC02-05CH11231), are gratefully acknowledged.References
- A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867 CrossRef CAS PubMed.
- Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182–185 CrossRef CAS PubMed.
- W. Zhang, A. R. Oganov, A. F. Goncharov, Q. Zhu, S. E. Boulfelfel, A. O. Lyakhov, E. Stavrou, M. Somayazulu, V. B. Prakapenka and Z. Konôpková, Science, 2013, 342, 1502–1505 CrossRef CAS PubMed.
- D. Boa, S. Hassam, G. Kra, K. P. Kotchi and J. Rogez, CALPHAD, 2008, 32, 227–239 CrossRef CAS.
- S. M. Clarke, J. P. S. Walsh, M. Amsler, C. D. Malliakas, T. Yu, S. Goedecker, Y. Wang, C. Wolverton and D. E. Freedman, Angew. Chem., Int. Ed., 2016, 55, 13446 CrossRef CAS PubMed.
- B. T. Matthias, A. Jayaraman, T. H. Geballe, K. Andres and E. Corenzwit, Phys. Rev. Lett., 1966, 17, 640–643 CrossRef CAS.
- U. Schwarz, S. Tencé, O. Janson, C. Koz, C. Krellner, U. Burkhardt, H. Rosner, F. Steglich and Y. Grin, Angew. Chem., Int. Ed., 2013, 52, 9853–9857 CrossRef CAS PubMed.
- S. Tencé, O. Janson, C. Krellner, H. Rosner, U. Schwarz, Y. Grin and F. Steglich, J. Phys.: Condens. Matter, 2014, 26, 395701 CrossRef PubMed.
- N. Ashcroft, Phys. Rev. Lett., 1968, 21, 1748–1749 CrossRef CAS.
- N. Ashcroft, Phys. Rev. Lett., 2004, 92, 187002 CrossRef CAS PubMed.
- P. Cudazzo, G. Profeta, A. Sanna, A. Floris, A. Continenza, S. Massidda and E. Gross, Phys. Rev. Lett., 2008, 100, 257001 CrossRef CAS PubMed.
- J. M. McMahon and D. M. Ceperley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 144515 CrossRef.
- R. Szczȩśniak and M. Jarosik, Solid State Commun., 2009, 149, 2053–2057 CrossRef.
- J. S. Tse, Y. Yao and K. Tanaka, Phys. Rev. Lett., 2007, 98, 117004 CrossRef CAS PubMed.
- X.-J. Chen, V. V. Struzhkin, Y. Song, A. F. Goncharov, M. Ahart, Z. Liu, H.-k. Mao and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20–23 CrossRef CAS PubMed.
- D. Y. Kim, R. H. Scheicher, S. Lebègue, J. Prasongkit, B. Arnaud, M. Alouani and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16454–16459 CrossRef CAS PubMed.
- J. Feng, R. G. Hennig, N. W. Ashcroft and R. Hoffmann, Nature, 2008, 451, 445–448 CrossRef CAS PubMed.
- S. Wang, H.-k. Mao, X.-J. Chen and W. L. Mao, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14763–14767 CrossRef CAS PubMed.
- Y. Yao and D. D. Klug, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20893–20898 CrossRef CAS PubMed.
- G. Gao, A. R. Oganov, P. Li, Z. Li, H. Wang, T. Cui, Y. Ma, A. Bergara, A. O. Lyakhov, T. Iitaka and G. Zou, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1317–1320 CrossRef CAS PubMed.
- D. Y. Kim, R. H. Scheicher, H.-k. Mao, T. W. Kang and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2793–2796 CrossRef CAS PubMed.
- Y. Li, G. Gao, Y. Xie, Y. Ma, T. Cui and G. Zou, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15708–15711 CrossRef CAS PubMed.
- D. Zhou, X. Jin, X. Meng, G. Bao, Y. Ma, B. Liu and T. Cui, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014118 CrossRef.
- J. Hooper, T. Terpstra, A. Shamp and E. Zurek, J. Phys. Chem. C, 2014, 118, 6433–6447 CAS.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968 CrossRef CAS PubMed.
- N. Bernstein, C. S. Hellberg, M. D. Johannes, I. I. Mazin and M. J. Mehl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 060511 CrossRef.
- I. Errea, M. Calandra, C. J. Pickard, J. Nelson, R. J. Needs, Y. Li, H. Liu, Y. Zhang, Y. Ma and F. Mauri, Phys. Rev. Lett., 2015, 114, 157004 CrossRef PubMed.
- D. Duan, X. Huang, F. Tian, D. Li, H. Yu, Y. Liu, Y. Ma, B. Liu and T. Cui, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 180502 CrossRef.
- R. Akashi, M. Kawamura, S. Tsuneyuki, Y. Nomura and R. Arita, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224513 CrossRef.
- T. Muramatsu, W. K. Wanene, M. Somayazulu, E. Vinitsky, D. Chandra, T. A. Strobel, V. V. Struzhkin and R. J. Hemley, J. Phys. Chem. C, 2015, 119, 18007–18013 CAS.
- J. A. Flores-Livas, M. Amsler, T. J. Lenosky, L. Lehtovaara, S. Botti, M. A. L. Marques and S. Goedecker, Phys. Rev. Lett., 2012, 108, 117004 CrossRef PubMed.
- A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73–76 CrossRef CAS PubMed.
- J. A. Flores-Livas, A. Sanna and E. K. U. Gross, Eur. Phys. J. B, 2016, 89, 63 CrossRef.
- A. P. Drozdov, M. I. Eremets and I. A. Troyan, 2015, arXiv:1508.06224 [cond-mat].
- J. A. Flores-Livas, M. Amsler, C. Heil, A. Sanna, L. Boeri, G. Profeta, C. Wolverton, S. Goedecker and E. K. U. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 020508 CrossRef.
- G. R. Stewart, Rev. Mod. Phys., 2011, 83, 1589–1652 CrossRef CAS.
- P. D. Johnson, G. Xu and W.-G. Yin, Iron-based superconductivity, Springer, 2015 Search PubMed.
- Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297 CrossRef CAS PubMed.
- F. Han, X. Zhu, G. Mu, P. Cheng and H.-H. Wen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 180503 CrossRef.
- A. D. Christianson, E. A. Goremychkin, R. Osborn, S. Rosenkranz, M. D. Lumsden, C. D. Malliakas, I. S. Todorov, H. Claus, D. Y. Chung, M. G. Kanatzidis, R. I. Bewley and T. Guidi, Nature, 2008, 456, 930–932 CrossRef CAS PubMed.
- J. H. Tapp, Z. Tang, B. Lv, K. Sasmal, B. Lorenz, P. C. W. Chu and A. M. Guloy, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 060505 CrossRef.
- F.-C. Hsu, J.-Y. Luo, K.-W. Yeh, T.-K. Chen, T.-W. Huang, P. M. Wu, Y.-C. Lee, Y.-L. Huang, Y.-Y. Chu, D.-C. Yan and M.-K. Wu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14262–14264 CrossRef CAS PubMed.
- X. C. Wang, Q. Q. Liu, Y. X. Lv, W. B. Gao, L. X. Yang, R. C. Yu, F. Y. Li and C. Q. Jin, Solid State Commun., 2008, 148, 538–540 CrossRef CAS.
- C. W. Chu, F. Chen, M. Gooch, A. M. Guloy, B. Lorenz, B. Lv, K. Sasmal, Z. J. Tang, J. H. Tapp and Y. Y. Xue, Phys. C, 2009, 469, 326–331 CrossRef CAS.
- G. Wu, Y. L. Xie, H. Chen, M. Zhong, R. H. Liu, B. C. Shi, Q. J. Li, X. F. Wang, T. Wu, Y. J. Yan, J. J. Ying and X. H. Chen, J. Phys.: Condens. Matter, 2009, 21, 142203 CrossRef CAS PubMed.
- D. R. Parker, M. J. Pitcher, P. J. Baker, I. Franke, T. Lancaster, S. J. Blundell and S. J. Clarke, Chem. Commun., 2009, 2189–2191 RSC.
- S. J. Zhang, X. C. Wang, Q. Q. Liu, Y. X. Lv, X. H. Yu, Z. J. Lin, Y. S. Zhao, L. Wang, Y. Ding, H. K. Mao and C. Q. Jin, EPL, 2009, 88, 47008 CrossRef.
- S. Medvedev, T. M. McQueen, I. A. Troyan, T. Palasyuk, M. I. Eremets, R. J. Cava, S. Naghavi, F. Casper, V. Ksenofontov, G. Wortmann and C. Felser, Nat. Mater., 2009, 8, 630–633 CrossRef CAS PubMed.
- K. Haule, J. H. Shim and G. Kotliar, Phys. Rev. Lett., 2008, 100, 226402 CrossRef CAS PubMed.
- I. I. Mazin, D. J. Singh, M. D. Johannes and M. H. Du, Phys. Rev. Lett., 2008, 101, 057003 CrossRef CAS PubMed.
- I. I. Mazin, Nature, 2010, 464, 183–186 CrossRef CAS PubMed.
- P. Dai, J. Hu and E. Dagotto, Nat. Phys., 2012, 8, 709–718 CrossRef CAS.
- X. Dong and C. Fan, Sci. Rep., 2015, 5, 9326 CrossRef CAS PubMed.
- G. Haegg and G. Funke, Z. Phys. Chem., Abt. B, 1929, 6, 272–283 Search PubMed.
- V. P. Glagoleva and G. S. Zhdanov, Zh. Eksp. Teor. Fiz., 1954, 26, 337–344 CAS.
- M. Ruck and T. Söhnel, Z. Naturforsch., B: J. Chem. Sci., 2006, 61, 785–791 CAS.
- N. Alekseevskii, N. Brandt and T. Kostina, Izv. Akad. Nauk SSSR, 1952, 16, 233 CAS.
- N. Alekseevskii, Zh. Eksp. Teor. Fiz., 1948, 18, 101–102 CAS.
- T. Herrmannsdörfer, R. Skrotzki, J. Wosnitza, D. Köhler, R. Boldt and M. Ruck, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 140501 CrossRef.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911 CrossRef CAS PubMed.
- M. Amsler and S. Goedecker, J. Chem. Phys., 2010, 133, 224104 CrossRef PubMed.
- M. Amsler, J. A. Flores-Livas, L. Lehtovaara, F. Balima, S. A. Ghasemi, D. Machon, S. Pailhès, A. Willand, D. Caliste, S. Botti, A. San Miguel, S. Goedecker and M. A. L. Marques, Phys. Rev. Lett., 2012, 108, 065501 CrossRef PubMed.
- M. Amsler, J. A. Flores-Livas, T. D. Huan, S. Botti, M. A. L. Marques and S. Goedecker, Phys. Rev. Lett., 2012, 108, 205505 CrossRef PubMed.
- S. Roy, S. Goedecker and V. Hellmann, Phys. Rev. E, 2008, 77, 056707 CrossRef PubMed.
- M. Sicher, S. Mohr and S. Goedecker, J. Chem. Phys., 2011, 134, 044106 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse, J. Non-Cryst. Solids, 1995, 193, 222–229 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Comput. Phys. Commun., 1990, 59, 399–415 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- W. H. Zachariasen, Acta Crystallogr., 1948, 1, 265–268 CrossRef CAS.
- F. Hulliger, Nature, 1963, 198, 1081–1082 CrossRef.
- H. Nowotny, R. Funk and J. Pesl, Monatsh. Chem., 1951, 82, 513–525 CrossRef CAS.
- H. Haraldsen, F. Grönvold and T. Rosenqvist, Arch. Math. Naturvidensk., 1949, 50, 95–135 Search PubMed.
- K. Meisel, Z. Anorg. Allg. Chem., 1934, 218, 360–364 CrossRef CAS.
- M. J. Buerger, Z. Kristallogr.–Cryst. Mater., 1932, 82, 165–187 CAS.
- G. Hägg, Z. Kristallogr., 1928, 68, 470–472 Search PubMed.
- E. H. Roseboom, Am. Mineral., 1963, 48, 271 CAS.
- U. Furst and F. Halla, Z. Phys. Chem., Abt. B, 1938, 40, 285–307 Search PubMed.
- S. Kaiman, Univ. Toronto Stud., Geol. Ser., 1947, 51, 49–58 Search PubMed.
- T. Rosenqvist, Acta Metall., 1953, 1, 761–763 CrossRef.
- M. A. Peacock and A. S. Dadson, Am. Mineral., 1940, 25, 561–577 CAS.
- H. Takizawa, K. Uheda and T. Endo, J. Alloys Compd., 1999, 287, 145–149 CrossRef CAS.
- C. M. Poffo, S. M. Souza, D. M. Trichês, J. C. de Lima, T. A. Grandi, A. Polian and M. Gauthier, Phys. B, 2012, 407, 4686–4694 CrossRef CAS.
- G. Kuhn, S. Mankovsky, H. Ebert, M. Regus and W. Bensch, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085113 CrossRef.
- X. Wu, G. Steinle-Neumann, S. Qin, M. Kanzaki and L. Dubrovinsky, J. Phys.: Condens. Matter, 2009, 21, 185403 CrossRef CAS PubMed.
- H. Fjellvåg and S. Furuseth, J. Less-Common Met., 1987, 128, 177–183 CrossRef.
- M. Armbrüster, Bindungsmodelle für intermetallische Verbindungen mit der Struktur des CuAl2-Typs, Cuvillier Verlag, 2005 Search PubMed.
- K. Schubert, Kristallstrukturen zweikomponentiger Phasen, Springer, Berlin, Heidelberg, 1964, vol. 17 Search PubMed.
- K. Yasukōchi, K. Kanematsu and T. Ohoyama, J. Phys. Soc. Jpn., 1961, 16, 429–433 CrossRef.
- L. M. Corliss, J. M. Hastings, W. Kunnmann, R. Thomas, J. Zhuang, R. Butera and D. Mukamel, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 4337–4346 CrossRef CAS.
- T. Jeong, Solid State Commun., 2007, 141, 329–331 CrossRef CAS.
- G. Venturini, D. Fruchart, J. Hubsch, G. L. Caer, B. Malaman and B. Roques, J. Phys. F: Met. Phys., 1985, 15, 427 CrossRef CAS.
- C. Petrovic, J. W. Kim, S. L. Budko, A. I. Goldman, P. C. Canfield, W. Choe and G. J. Miller, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155205 CrossRef.
- A. V. Lukoyanov, V. V. Mazurenko, V. I. Anisimov, M. Sigrist and T. M. Rice, Eur. Phys. J. B, 2006, 53, 205–207 CrossRef CAS.
- A. Perucchi, L. Degiorgi, R. Hu, C. Petrovic and V. F. Mitrovi, Eur. Phys. J. B, 2006, 54, 175–183 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- M. Armbrüster, W. Schnelle, U. Schwarz and Y. Grin, Inorg. Chem., 2007, 46, 6319–6328 CrossRef PubMed.
- L. Xu, S. Bobev, J. El-Bahraoui and S. C. Sevov, J. Am. Chem. Soc., 2000, 122, 1838–1839 CrossRef CAS.
- V. J. Yannello and D. C. Fredrickson, Inorg. Chem., 2015, 54, 11385–11398 CrossRef CAS PubMed.
- E. C. Stoner, Proc. R. Soc. A, 1938, 165, 372–414 CrossRef.
- R. E. Cohen, I. I. Mazin and D. G. Isaak, Science, 1997, 275, 654–657 CrossRef CAS PubMed.
- L. Ortenzi, I. I. Mazin, P. Blaha and L. Boeri, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 064437 CrossRef.
- C.-Q. Jin, J.-S. Zhou, J. B. Goodenough, Q. Q. Liu, J. G. Zhao, L. X. Yang, Y. Yu, R. C. Yu, T. Katsura, A. Shatskiy and E. Ito, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7115–7119 CrossRef CAS PubMed.
- M. Sieberer, S. Khmelevskyi and P. Mohn, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 014416 CrossRef.
- P. James, O. Eriksson, B. Johansson and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 419–430 CrossRef CAS.
- W. Zhang and W. Zhang, J. Magn. Magn. Mater., 2016, 404, 83–90 CrossRef CAS.
- J. Kübler, Theory of itinerant electron magnetism, Oxford University Press, 2000, vol. 106 Search PubMed.
- R. J. Hemley, G. L. Chiarotti and G. Chiarotti, et al., High Pressure Phenomena, Varenna on Como Lake, Villa Monastero, 3–13 July 2001, 2002 Search PubMed.
- S. S. Saxena, P. Agarwal, K. Ahilan, F. M. Grosche, R. K. W. Haselwimmer, M. J. Steiner, E. Pugh, I. R. Walker, S. R. Julian, P. Monthoux, G. G. Lonzarich, A. Huxley, I. Sheikin, D. Braithwaite and J. Flouquet, Nature, 2000, 406, 587–592 CrossRef CAS PubMed.
- D. Aoki, A. Huxley, E. Ressouche, D. Braithwaite, J. Flouquet, J.-P. Brison, E. Lhotel and C. Paulsen, Nature, 2001, 413, 613–616 CrossRef CAS PubMed.
- N. T. Huy, A. Gasparini, D. E. de Nijs, Y. Huang, J. C. P. Klaasse, T. Gortenmulder, A. de Visser, A. Hamann, T. Görlach and H. v. Löhneysen, Phys. Rev. Lett., 2007, 99, 067006 CrossRef CAS PubMed.
- K. Shimizu, T. Kimura, S. Furomoto, K. Takeda, K. Kontani, Y. Onuki and K. Amaya, Nature, 2001, 412, 316–318 CrossRef CAS PubMed.
- Y. Mizuguchi, F. Tomioka, S. Tsuda, T. Yamaguchi and Y. Takano, Appl. Phys. Lett., 2008, 93, 152505 CrossRef.
- A. Subedi, L. Zhang, D. J. Singh and M. H. Du, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134514 CrossRef.
- L. Boeri, O. V. Dolgov and A. A. Golubov, Phys. Rev. Lett., 2008, 101, 026403 CrossRef CAS PubMed.
- R. A. Jishi and H. M. Alyahyaei, Adv. Condens. Matter Phys., 2009, 2010, e804343 Search PubMed.
- T. Jarlborg, Phys. Lett. A, 2002, 300, 518–523 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |