Open Access Article
Open Access ArticleConcentration gradient driven molecular dynamics: a new method for simulations of membrane permeation and separation†
Aydin
Ozcan
a,
Claudio
Perego
bc,
Matteo
Salvalaglio
a,
Michele
Parrinello
bc and
Ozgur
Yazaydin
 *a
*a
aDepartment of Chemical Engineering, University College London, London, WC1E 7JE, UK. E-mail: ozgur.yazaydin@ucl.ac.uk
bDepartment of Chemistry and Applied Biosciences, ETH Zurich, Zurich, Switzerland
cInstitute of Computational Science, Università della Svizzera Italiana, Lugano, Switzerland
First published on 20th March 2017
Abstract
In this study, we introduce a new non-equilibrium molecular dynamics simulation method to perform simulations of concentration driven membrane permeation processes. The methodology is based on the application of a non-conservative bias force controlling the concentration of species at the inlet and outlet of a membrane. We demonstrate our method for pure methane, ethane and ethylene permeation and for ethane/ethylene separation through a flexible ZIF-8 membrane. Results show that a stationary concentration gradient is maintained across the membrane, realistically simulating an out-of-equilibrium diffusive process, and the computed permeabilities and selectivity are in good agreement with experimental results.
Introduction
Membrane separations of mixtures are economically significant processes widely used in petrochemical, pharmaceutical, biomedical, food and water treatment industries.1 Water desalination technology, for example, is one of the major application areas of industrial membranes. Worldwide water desalination plants process nearly 70 million cubic meters per day2 and membrane-based processes account for more than 60% of the entire water desalination market.3 Another application area for membranes is gas separation. Hydrogen recovery, air separation, CO2 separation, natural gas sweetening, alkane–alkene separation are examples of important industrial processes where membrane based separation technologies are eminently utilized.4,5 A significant example of commercial application of membranes in gas separation is an 830![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Nm3 h−1 system provided by Cynara-NATCO for the separation of CO2 from natural gas operating on an offshore platform located in the Gulf of Thailand.6
000 Nm3 h−1 system provided by Cynara-NATCO for the separation of CO2 from natural gas operating on an offshore platform located in the Gulf of Thailand.6
Polymers, carbon molecular sieves and zeolites are materials commonly used in commercial membranes.4,5 On the other hand, ongoing research in materials science and chemistry have provided new candidate materials to manufacture membranes; such as metal–organic frameworks (MOFs),7 carbon nanotubes8 (CNTs) and graphene oxide.9
Developing novel membranes for a specific separation is a challenging task and requires a detailed understanding of the complex transport mechanisms down at the nanometer scale. Molecular dynamics (MD) is a simulation method which can be used to understand such complexities with atomic resolution. Classical MD simulations unveils the interactions between molecules at the atomistic level by exploiting empirical force fields.10
Membrane separations are peculiarly a non-equilibrium process and this should be considered in membrane simulations. A variety of approaches have been used to impose non-equilibrium conditions in MD simulations to investigate membrane separations. In principle, an exact solution to impose non-equilibrium conditions during an MD simulation of a membrane process is the so-called dual control volume grand canonical molecular dynamics (DCV-GCMD) technique.11 This is a hybrid Monte-Carlo (MC) and MD method which defines two control volumes at the feed and permeate sides of the membrane and keeps the chemical potential in these control volumes fixed by employing insertion and deletion of the fluid molecules. This simulation technique was utilized in many studies of different membrane systems; such as simple slit-shaped micropore,12 porous silica membranes13 and carbon molecular sieve membranes.14 However, DCV-GCMD method doesn't work efficiently for dense fluids due to the extremely low acceptance rates for the insertion and deletion of the molecules. Moreover, according to Ható et al.15 coupling MC moves with MD can be problematic since the ratio of insertion/deletion steps vs. MD steps should be optimized in order to perform a reliable simulation.
Another common approach for imposing non-equilibrium conditions in MD simulations is placing impermeable moving walls in a simulation box and exerting a constant force on them to create a piston effect. For instance, Wang et al.16 studied water transport through CNT membranes by placing two moving walls at opposite ends of the simulation box. By applying two forces in opposite directions, a larger force on the feed side wall and a smaller force on the permeate side wall, they created a pressure gradient and pushed the water molecules through pores of the CNT membrane. The same authors applied a similar approach for polyamide membranes17 to study water transport. In another recent study, Shen et al.18 applied the moving wall approach to explore the potential of polymeric FT-30 membranes for reverse osmosis. Hu et al.19 and Gupta et al.20 used the moving wall approach to investigate water desalination in zeolitic imidazolate frameworks (ZIFs). In another study, Gupta et al.21 used a modified moving wall approach to investigate desalination in five different ZIFs in a pervaporation membrane setting. On the feed side, a force was applied on an impermeable wall to push the saline water through the membrane, and at the end of the permeate side of the simulation box a fixed wall was placed to create a vacuum effect which interacted with the fluid molecules through a strong attractive force. In non-equilibrium MD (NEMD) simulations which use one or more moving impermeable walls, a disadvantage is that the simulation length is limited by the number of molecules placed on the feed side. This is because the simulation practically generates no information once all the fluid molecules which can diffuse through the membrane are pushed to the permeate side by the moving wall. We will call this a “feed depletion” problem. Another shortcoming of using an impermeable wall to push fluid molecules through a membrane is that it is not possible to keep the concentration of species fixed if the simulation involves a mixture. This is because the concentration of the less diffusive species will increase on the feed side as the mixture is pushed towards the membrane by the impermeable wall. In order to address the feed depletion problem in an NEMD membrane simulation which uses impermeable walls, Cabrales-Navarro et al.22 considered deleting a certain number of molecules from the permeate side and adding them to the feed side at regular intervals (every 50 ps in their work). While this approach addressed the feed depletion issue, the transfer of molecules from one side to another side essentially precludes the possibility of running a steady state simulation.
Another way of imposing non-equilibrium conditions for an MD membrane simulation is to apply a continuous external force on the molecules (steered-molecular dynamics) along the direction perpendicular to the membrane and with periodic boundary conditions in all directions so that feed depletion can be avoided. Using this method Zhu et al.23 investigated the transport of water through a biological membrane. This ensured the circulation of molecules in the permeate side back to the feed side through the periodic boundary. Ding et al.24 used a similar approach to investigate the water desalination performance of a polyamide polymer membrane. On the other hand, this method does not provide a way for controlling the concentration of species in the case of a mixture simulation. Moreover, applying an external force all over the simulation box requires care because if the bias exceeds a critical level then thermostat or barostat algorithms can fail to do their job due to fictional increase of particle velocities.15 To address this concern, in their study of gas permeation through slit pores, Frentrup et al.25 restricted the external force in to a considerably small region in the simulation box (boundary-driven NEMD) in attribution to the position of the small force region placed at the boundary of the simulation box. The same authors extended their method to investigate single gas permeation of CO2 and He through a PIM-1 polymer membrane.26 Even though their methodology allows the circulation of fluid molecules between the permeate and feed sides to ensure a continuous simulation, it does not provide any control over the density of fluids at the inlet and outlet of the membrane. To address the shortcomings of previous methods Ható et al.15 proposed a methodology which was essentially a combination of the method of Frentrup et al.25 and of the DCV-GCMD method of Heffelfinger et al.,11 thus again requiring the coupling of MC and MD algorithms. All the methods we summarized above served to the purposes they were developed for and deserve credit; however, none of them provide a platform for running a steady state and continuous simulation for a mixture across a membrane without involving a hybrid MC and MD approach.
In this study, we present a new NEMD method which allows the simulation of permeation of a mixture kept at a fixed composition through a membrane and avoids the feed depletion issue without the need for coupling an MC scheme. The proposed method builds on CμMD, a recent technique developed to model crystal growth in solutions at constant chemical potential by using a nonconservative force.27 In our new NEMD method we use self-adjusting bias forces to control the mixture composition in selected regions of the simulation box in order to continuously enforce a concentration difference between the inlet and outlet of the membrane. This method has two main advantages over the previously implemented methodologies; first, it is completely deterministic since no stochastic move like particle insertion–deletion is needed, and second, it allows us to perform simulations of mixture permeation through membranes at fixed feed composition.
We first explain the new methodology and then demonstrate it by simulating permeation of pure methane (CH4), ethylene (C2H4) and ethane (C2H6) through a zeolitic imidazolate framework-8 (ZIF-8)28 membrane, and by applying it for the separation of an equimolar ethylene/ethane mixture, again in a ZIF-8 membrane. We chose the separation of ethylene from ethane due its paramount importance. Market data confirm the necessity of this separation; the demand of ethylene as feedstock in chemical industry for production of rubbers, plastics and other valuable chemical products is almost 25 trillion tons per annum and the biggest portion of ethylene comes as by-product of oil refineries in the form of a mixture of ethane/ethylene.29 On the other hand, this is an extremely difficult separation due to the fact that the kinetic diameters of ethylene (4.16 Å) and ethane (4.44 Å) are very close to each other.30
Models & computational details
Concentration gradient driven molecular dynamics
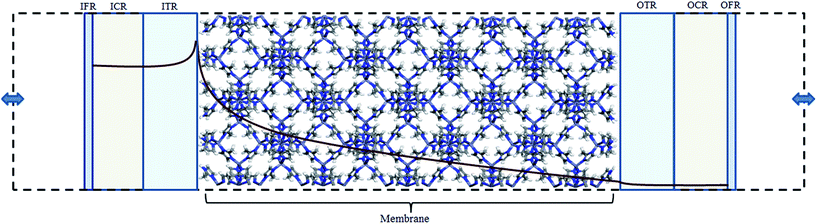
The diffusive transport of fluids across membranes is an intrinsically non-equilibrium process. To faithfully reproduce this fact in our modelling, we aim to carry out simulations in which a steady state concentration gradient is maintained between the two sides of the membrane surrounded by a fluid, pure or a mixture. To this aim here we introduce two separate control regions, inlet control region (ICR), located on the feed side of the membrane, and the outlet control region (OCR), on the permeate side of the membrane (Fig. 1). The control regions and the membrane are separated by two transitions regions; inlet transition region (ITR) and the outlet transition region (OTR). The concentrations in the ICR and OCR are controlled by applying on the fluid molecules two separate external forces which are localized in two regions, the inlet force region (IFR) and outlet force region (OFR), which are adjacent to ICR and OCR, respectively. The external forces are perpendicular to the membrane surface and regulate the flux of molecules across the IFR (and OFR) in order to restrain the concentration in the ICR (and OCR) to a selected target value. This makes it possible to impose two different concentrations in the inlet and outlet control region, where the forces are defined by the following equations:| FIi = kIi(nT,Ii − nICRi)GI(z − ZIF,w) | (1) |
| FOi = kOi(nT,Oi − nOCRi)GO(z − ZOF,w) | (2) |
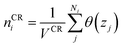 | (3) |
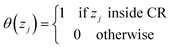 | (4) |
Simulation details
In order to demonstrate our method ZIF-8 was chosen to construct the membrane model in our simulations. ZIF-8 is formed by the assembly of Zn metal atoms and methyl imidazole bridging ligands. It has a sodalite topology with unit cell dimensions a = b = c = 16.991 Å, a pore diameter of 11.6 Å, and a pore aperture of 3.4 Å. The membrane was constructed by replicating the ZIF-8 unit cell by 2 × 2 × 5 in the x, y, and z directions, respectively. Zinc atoms at both ends of the membrane were removed and dangling nitrogen atoms were terminated by hydrogens. The dimensions of the resulting membrane were Lx = Ly = 3.3982 and Lz = 8.4955 nm (Fig. 2). The membrane was placed in the centre of a simulation box which is 28.4955 nm in the z directions and with dimensions equal to the membrane in the x and y directions.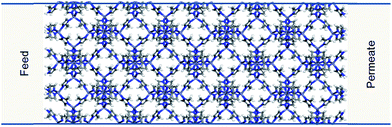 | ||
| Fig. 2 ZIF-8 membrane model used in the simulations. Carbon, nitrogen, hydrogen and zinc atoms are represented in grey, blue, white and purple, respectively. | ||
ZIF-8 membrane was modelled as a flexible structure using the force field recently developed by Krokidas et al.31 Since in their work a continuous periodic structure of ZIF-8 was studied partial atomic charges for surface atoms were not present. We calculated the charges for the dangling nitrogen atoms and the hydrogens used for terminations by performing quantum chemical calculations on a cluster isolated from ZIF-8 and scaling the charges reported by Krokidas et al.31 accordingly. Bond stretching, bond bending and torsional energy parameters for these surface atoms were taken from GAFF32 force field. In order to prevent drifting of membrane in the z direction due to the concentration gradient, membrane atoms within the first 4 Å of the membrane at both ends were tethered to their initial positions.
Methane, ethylene and ethane were modelled using the TraPPE force field.33 In this force field a carbon atom and the hydrogens bonded are treated as a united atom. Hence, methane was represented as a single united atom (CH4), ethylene consisted two CH2 united atoms and ethane two CH3 united atoms. The bond between the united atoms in ethylene and the ethane were rigid as defined in the TraPPE force field. Lorentz–Berthelot mixing rules were applied between unlike atoms. The cut-off distance for Lenard-Jones interactions was set at 12 Å. The electrostatic interactions were computed using the particle mesh Ewald (PME) method and for the real part of the Ewald sum the cut-off distance was set to 12 Å.
The permeations of 4 different systems through the ZIF-8 membrane were simulated. These were pure methane, ethylene and ethane, and an equimolar mixture of ethylene and ethane. MD simulations were performed with GROMACS 5.1.2 software34 in the NVT ensemble. Temperature was kept constant at 300 K using a Nose–Hoover thermostat. A time step of 1 fs was used and PBCs were applied in all directions. Simulations were first equilibrated for at least 10 ns followed by 40 ns production runs. Simulation data including the trajectory were saved every 500 steps (0.5 ps). Standard deviations of the ensemble averages were computed by breaking the production runs into 5 blocks.
A private version of PLUMED 2.2.2 plugin35 was used to apply the bias forces, FIi and FOi, in order to control concentrations in ICR and OCR. Target concentration in the ICR was set to a molecular density which corresponds to the total feed pressure (which varied between 2 to 40 bars in our simulations) based on the pressure/density data from the NIST database.36 The target concentration in the OCR was set to 0 to create a vacuum effect on the permeate side in all simulations. Here we note that in MD simulations of membranes creating a vacuum effect is a challenging task as also mentioned by others.15,21 To create the vacuum effect, a larger outlet force constant, kOi, was used compared to the inlet force constant, kIi. The values of parameters used in eqn (1) & (2) and the locations of the force and control regions are given in Table S2.†
The flux due to concentration difference in the z direction, Jz, was calculated by counting the number of molecules which passed through a plane at the centre of the membrane and dividing that by the production simulation time, t, and the cross sectional area of the membrane, Axy,25
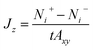 | (5) |
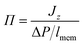 | (6) |
In order to generate initial configurations of the fluid molecules in the simulation box, prior to an MD run we simulated the adsorption of fluid molecules by performing grand canonical Monte Carlo (GCMC) simulations using RASPA37 molecular simulation package. In the grand canonical ensemble temperature, volume and chemical potential of the species are fixed. GCMC simulations were performed at 300 K and at a total pressure which is the average of pressures corresponding to the target densities of the fluid in the ICR and OCR of the MD simulation box. For instance, for 40 bar feed pressure and 0 bar permeate pressure GCMC simulation was performed at 20 bar. We found that this provides a good starting configuration for MD simulations to reach steady state quickly (Fig. S2†). GCMC simulations included 105 cycles for initialization and 105 cycles for production, where each cycle is N steps. N is equal to the number of molecules present in the system. For single component methane GCMC simulations, swap moves (insertion/deletion) between the bulk and adsorbed phases, translation and reinsertion moves were sampled. For ethylene and ethane simulations a rotation move was added to the above list. For the ethylene–ethane mixture simulation an identity exchange move between the species was also sampled. All moves were sampled with equal probability.
Results and discussion
Permeation of pure methane, ethylene and ethane
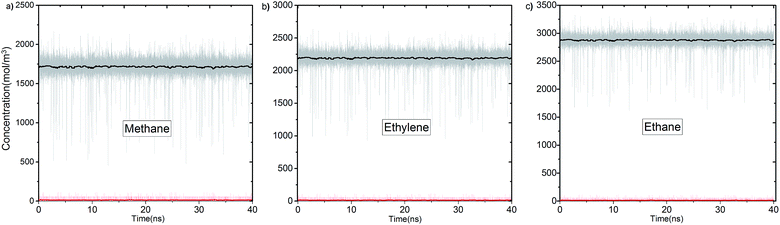
In Fig. 3 we report the variation of concentrations in ICR and OCR for pure methane, ethylene and ethane as a function of simulation time. In these simulations the target concentrations in ICR were set to the molecular density of the fluid at 40 bar (feed pressure). In all cases concentration of the species are stable and fluctuate around an average value. The average concentrations calculated for ICR and OCR are given in Table 1 for each fluid. For the inlet the standard deviations are very small in comparison to the average concentrations, which demonstrate excellent control of the concentration in ICR. The relatively high fluctuations in OCR with respect to the average values indicates the difficulty of controlling the concentration at very low target values (see Fig. S3† for OCR concentration data plotted on a smaller scale). However, such fluctuations are actually insignificant because the number of molecules present in the OCR at any time is extremely small due to the vacuum effect. For instance, for methane, 14.7 mol m−3 (Table 1) corresponds to only 0.26 molecules in the whole ICR volume (28.9 nm3).The number densities of methane, ethylene and ethane are plotted against the z coordinate of the simulation box in Fig. 4 and it demonstrates how the concentration gradient works along the membrane. These density profiles were obtained by averaging data over the 40 ns production runs. The density of fluid molecules decreases through membrane in an almost linear fashion. Density is higher at the entrance of the membrane (molecules adsorbed by ZIF-8) and it decreases along the z direction of membrane (molecules inhaled by vacuum).
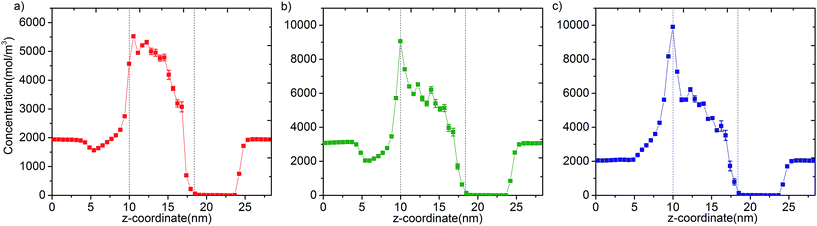 | ||
| Fig. 4 Concentration profiles of (a) methane, (b) ethylene and (c) ethane molecules along the z coordinate of the simulation box. Dashed lines show entrance and exit points of the membrane (see Fig. S5† for larger figures and the location of FRs, CRs and TRs). | ||
Overall, data for single component permeation simulations shows that our methodology controls the concentration of fluid molecules around a targeted value in specified regions to remarkable accuracy (Fig. 3). We highlight that the bias force acts in a localized region out of the membrane. Permeation is purely due to the diffusive transfer of molecules, driven by the steady difference in concentration maintained across the two sides of the membrane (Fig. 4). It is also apparent from the variation of temperature data that the bias forces applied do not overwhelm the thermostat during the course of the simulations (Fig. S4†).24
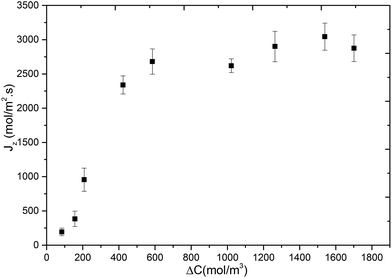
In Fig. 5, we show the variation of methane flux (Jz) with respect to concentration difference across the membrane. This was obtained by performing additional MD simulations of methane permeation at 300 K where target concentrations in the ICR were set to molecular densities corresponding to 36 bar, 30 bar, 24 bar, 14 bar, 10 bar, 5 bar, 4 bar and 2 bar, and in the OCR was set to 0. Again the initial positions for the methane molecules were obtained from GCMC simulations which were performed at half of the pressure values given above. The flux initially increases rapidly with increasing concentration difference but then starts levelling-off after about 500 mol m−3 and then reaches a plateau. The initial part is known as the pressure/concentration difference controlled region and the final part where a plateau is observed is known as the mass transfer controlled region.1 Such behaviour was reported experimentally for propane and propylene permeation in ZIF-8 based membranes.38,39
In Table 2, permeabilities of methane, ethane and ethylene from simulations, in which target concentration in ICR for each fluid was set to a density corresponding to 4 bar, are compared against experimental data. Simulated permeabilities are about one or two orders of magnitude larger than those reported by Pan et al.,40 who reported the permeabilities for all three fluids, and those reported by Bux et al.,41,42 in two different studies. But most importantly simulated permeabilities match with the order of experimentally measured permeabilities, that is, Πethylene> Πmethane> Πethane, which is the most important outcome in a computational screening study. Given the simulations were conducted in the molecular scale; the agreement with the order of the experimental results is remarkable.
| Simulationa | Experimental | |||
|---|---|---|---|---|
| a Feed pressures corresponding to the average ICR concentrations obtained from simulations are 3.9 bar for methane, 4.8 bar for ethylene and 4.8 bar for ethane. b Feed pressure = 1 bar, Pan et al.;40. c Feed pressure = 1 bar, Bux et al.;42. d Feed pressure = 6 bar, Bux et al.41 (see Table S3 for the computed fluxes used for the calculation of permeabilities). | ||||
| Methane | 97.5 | 1.56b | 2.7c | — |
| Ethylene | 152.5 | 2.8b | — | 4.5d |
| Ethane | 67.5 | 1.38b | — | 1.63d |
Equimolar ethylene/ethane mixture separation
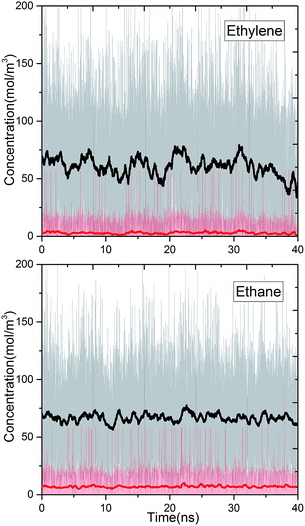
We studied the separation of an equimolar ethylene/ethane mixture with a ZIF-8 membrane in order to demonstrate the applicability of the new method for mixture simulations. Besides, to the best of our knowledge, present work is the first simulation study reporting the separation of ethylene/ethane mixture in a flexible ZIF-8 membrane. The target concentrations of ethylene and ethane in the ICR were set to molecular densities so that the corresponding total pressure is 2 bar. Fig. 6 shows the variation of the concentrations of ethylene and ethane in ICR and OCR. Similar to the single component simulations, the concentrations fluctuates around the target values. The average concentrations are given in Table 3. For the inlet side, these correspond to ethylene and ethane mole fractions of 0.48 and 0.52, respectively. Despite the difficulty in controlling concentrations at low target values our method successfully keeps the mixture very close to the equimolar target composition (see Fig. S6† for histogram analyses of instantaneous concentration of ethylene and ethane molecules). Furthermore, we calculated the permeation selectivity, S, for the equimolar ethylene/ethane separation simulation as follows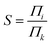 | (7) |
Conclusions
In this study, we presented a new non-equilibrium MD method, concentration gradient driven MD (CGD-MD), in order to simulate the permeation of pure fluids and mixtures through membranes. The new method works by using bias forces to fix the concentration of fluids at target values at the inlet and outlet of a membrane. This in turn creates a concentration gradient which drives the diffusion of the molecules through the membrane. CGD-MD addresses two main shortcomings of previous NEMD methods used for simulating membrane separation processes in the molecular scale. First, it avoids the feed depletion issue and allows running, in principal, an infinitely long simulation. Second, it maintains the feed composition without the need of any complex MC-MD coupling. We successfully demonstrated our new method for the permeation of pure methane, ethylene and ethane and for the separation of an equimolar ethylene/ethane mixture in a ZIF-8 membrane by predicting the methane, ethylene and ethane permeabilities, and the ethylene/ethane selectivity in very good agreement with the experimental data. Given its predictive success, CGD-MD can be an invaluable tool to computationally screen new and existing materials for membrane separation processes.In our simulations, pure or mixture, CGD-MD maintained the concentration of species at their target values in the denser feed side to a remarkable accuracy. Based on this, we expect that CGD-MD will perform very well for dense phases. Indeed, a preliminary simulation of pure liquid water permeation through the ZIF-8 membrane clearly demonstrates that our method works for such systems with a great accuracy (Fig. S7, Table S4†). Therefore, our future work will include separations in liquid phase where DCV-GCMD method is known to struggle.
Acknowledgements
A. O. has been supported by the Scientific and Technological Research Council of Turkey (TUBITAK). The authors acknowledge the use of the University College London Legion High Performance Computing Facility (Legion@UCL), and associated support services, in the completion of this work. M. P. and C. P. acknowledge the VARMET European Union Grant ERC-2014-ADG-670227 and the National Centre of Competence in Research MARVEL.References
- R. W. Baker, Membrane technology, Wiley Online Library, 2000 Search PubMed.
- H. Sakai, T. Ueyama, M. Irie, K. Matsuyama, A. Tanioka, K. Saito and A. Kumano, Desalination, 2016, 389, 52–57 CrossRef CAS.
- V. G. Gude, Renewable Sustainable Energy Rev., 2016, 57, 1038–1065 CrossRef.
- E. D. P. Bernardo and G. Golemme, Ind. Eng. Chem. Res., 2009, 48, 4638–4663 CrossRef.
- R. P. Lively and D. S. Sholl, Nature, 2016, 532, 435–437 CrossRef PubMed.
- A. Callison and G. Davidson, Oil Gas J., 2007, 105, 56 CAS.
- S. Qiu, M. Xue and G. Zhu, Chem. Soc. Rev., 2014, 43, 6116–6140 RSC.
- B. J. Hinds, N. Chopra, T. Rantell, R. Andrews, V. Gavalas and L. G. Bachas, Science, 2004, 303, 62–65 CrossRef CAS PubMed.
- P. C. R. K. Joshi, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Science, 2014, 343, 752–754 CrossRef PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 1989 Search PubMed.
- G. S. Heffelfinger and F. V. Swol, J. Chem. Phys., 1994, 100, 7548 CrossRef CAS.
- R. F. Cracknell, D. Nicholson and N. Quirke, Phys. Rev. Lett., 1995, 74, 2463–2466 CrossRef CAS PubMed.
- P. I. Pohl and G.S. Heffelfinger, J. Membr. Sci., 1999, 155, 1–7 CrossRef CAS.
- L. Xu, M.G. Sedigh, M. Sahimi and T. T. Tsotsis, Phys. Rev. Lett., 1998, 80, 3511–3514 CrossRef CAS.
- Z. Ható, Á. Kaviczki and T. Kristóf, Mol. Simul., 2015, 42, 71–80 CrossRef.
- L. Wang, R. S. Dumont and J. M. Dickson, J. Chem. Phys., 2013, 138, 124701 CrossRef PubMed.
- L. Wang, R. S. Dumont and J. M. Dickson, RSC Adv., 2016, 6, 63586–63596 RSC.
- M. Shen, S. Keten and R. M. Lueptow, J. Membr. Sci., 2016, 506, 95–108 CrossRef CAS.
- Z. Hu, Y. Chen and J. Jiang, J. Chem. Phys., 2011, 134, 134705 CrossRef PubMed.
- K. M. Gupta, K. Zhang and J. Jiang, Langmuir, 2015, 31, 13230–13237 CrossRef CAS PubMed.
- K. M. Gupta, Z. Qiao, K. Zhang and J. Jiang, ACS Appl. Mater. Interfaces, 2016, 8, 13392–13399 CAS.
- F. A. Cabrales-Navarro, J. L. Gómez-Ballesteros and P. B. Balbuena, J. Membr. Sci., 2013, 428, 241–250 CrossRef CAS.
- F. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2002, 83, 154–160 CrossRef CAS PubMed.
- M. Ding, A. Szymczyk and A. Ghoufi, Desalination, 2015, 368, 76–80 CrossRef CAS.
- H. Frentrup, C. Avendaño, M. Horsch, A. Salih and E. A. Müller, Mol. Simul., 2012, 38, 540–553 CrossRef CAS.
- H. Frentrup, K. E. Hart, C. M. Colina and E. A. Muller, Membranes, 2015, 5, 99–119 CrossRef CAS PubMed.
- C. Perego, M. Salvalaglio and M. Parrinello, J. Chem. Phys., 2015, 142, 144113 CrossRef CAS PubMed.
- K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS PubMed.
- A. Van Miltenburg, W. Zhu, F. Kapteijn and J. A. Moulijn, Chem. Eng. Res. Des., 2006, 84, 350–354 CrossRef CAS.
- M. Rungta, C. Zhang, W. J. Koros and L. Xu, AIChE J., 2013, 59, 3475–3489 CrossRef CAS.
- P. Krokidas, M. Castier, S. Moncho, E. Brothers and I. G. Economou, J. Phys. Chem. C, 2015, 119, 27028–27037 CAS.
- Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 2569–2577 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- E. Lemmon, M. McLinden and D. Friend, NIST chemistry webbook, NIST standard reference database, 2005, vol. 69 Search PubMed.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2015, 42, 81–101 CrossRef.
- M. Fang, C. Wu, Z. Yang, T. Wang, Y. Xia and J. Li, J. Membr. Sci., 2015, 474, 103–113 CrossRef CAS.
- K. Eum, C. Ma, A. Rownaghi, C. W. Jones and S. Nair, ACS Appl. Mater. Interfaces, 2016, 8, 25337–25342 CAS.
- Y. Pan and Z. Lai, Chem. Commun., 2011, 47, 10275–10277 RSC.
- H. Bux, C. Chmelik, R. Krishna and J. Caro, J. Membr. Sci., 2011, 369, 284–289 CrossRef CAS.
- H. Bux, C. Chmelik, J. M. van Baten, R. Krishna and J. Caro, Adv. Mater., 2010, 22, 4741–4743 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional simulation settings, results and snapshots. See DOI: 10.1039/c6sc04978h |
| This journal is © The Royal Society of Chemistry 2017 |