Open Access Article
Open Access ArticleHeterospin biradicals provide insight into molecular conductance and rectification†
Martin L.
Kirk
 *a,
David A.
Shultz
*b,
Jinyuan
Zhang
b,
Ranjana
Dangi
a,
Laura
Ingersol
a,
Jing
Yang
a,
Nathaniel S.
Finney
c,
Roger D.
Sommer
b and
Lukasz
Wojtas
d
*a,
David A.
Shultz
*b,
Jinyuan
Zhang
b,
Ranjana
Dangi
a,
Laura
Ingersol
a,
Jing
Yang
a,
Nathaniel S.
Finney
c,
Roger D.
Sommer
b and
Lukasz
Wojtas
d
aThe University of New Mexico, MSC03 2060, 1 University of New Mexico, Albuquerque, New Mexico 87131-0001, USA. E-mail: mkirk@unm.edu
bDepartment of Chemistry, North Carolina State University, Raleigh, North Carolina 27695-8204, USA. E-mail: shultz@ncsu.edu
cSchool of Pharmaceutical Science and Technology, Tianjin University, 505/Building 24, 92 Weijin Road, Nankai District, Tianjin, 300072, P. R. China
dDepartment of Chemistry, University of South Florida, 4202 E. Fowler Avenue, CHE 205 Tampa, FL 33620-5250, USA
First published on 1st June 2017
Abstract
The correlation of electron transfer with molecular conductance (g: electron transport through single molecules) by Nitzan and others has contributed to a fundamental understanding of single-molecule electronic materials. When an unsymmetric, dipolar molecule spans two electrodes, the possibility exists for different conductance values at equal, but opposite electrode biases. In the device configuration, these molecules serve as rectifiers of the current and the efficiency of the device is given by the rectification ratio (RR = gforward/greverse). Experimental determination of the RR is challenging since the orientation of the rectifying molecule with respect to the electrodes and with respect to the electrode bias direction is difficult to establish. Thus, while two different values of g can be measured and a RR calculated, one cannot easily assign each conductance value as being aligned with or opposed to the molecular dipole, and calculations are often required to resolve the uncertainty. Herein, we describe the properties of two isomeric, triplet ground state biradical molecules that serve as constant-bias analogs of single-molecule electronic devices. Through established theoretical relationships between g and electronic coupling, H2, and between H2 and magnetic exchange coupling, J (g ∝ H2 ∝ J), we use the ratio of experimental J-values for our two isomers to calculate a RR for an unsymmetric bridge molecule with known geometry relative to the two radical fragments of the molecule and at a spectroscopically-defined potential bias. Our experimental results are compared with device transport calculations.
Introduction
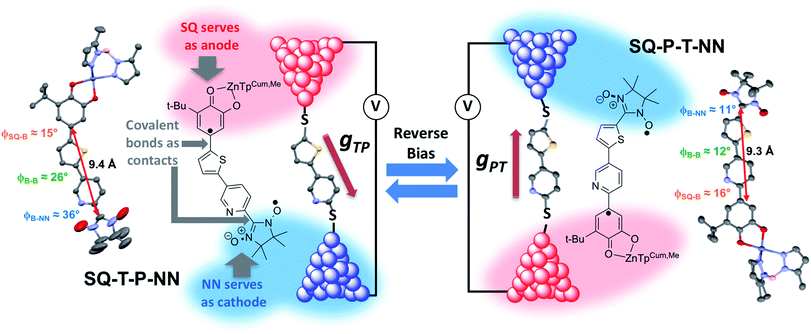
Over 40 years ago, Aviram and Ratner1 proposed a design strategy for a unimolecular organic rectifier that employed aromatic π-system donor (D) and acceptor (A) moieties connected to one another by the σ-orbitals of a saturated bridge (B) fragment. To date, true molecular rectification2 has been difficult to achieve3,4 with molecular rectification ratios (RRs), defined as the ratio of the electrical current propagated through the molecular junction in the forward and reverse bias directions, rarely exceeding 10.4–7 Although the D–B–A rectifier concept allows for remarkable design and control of the active rectifying component, a critical problem remains regarding the nature of the D–B–A coupling with metallic electrodes. Namely, the contact geometry of the molecule sandwiched between the metallic electrodes is generally unknown. This requires the construction of conductance histograms consisting of thousands of individual measurements8 in order to assess the conductance properties of single molecules. In these experiments, it is difficult to assess the productive geometry(ies) of the molecule relative to the electrodes and, for rectifying molecules, the geometry responsible for the preferred current direction. The geometric relationship between a rectifying molecule and the conductance under forward and reverse bias is generally assessed with quantum chemical computations that provide transmission probabilities using a precise device geometry.In the present work, we remove these ambiguities entirely by replacing the metallic electrodes with molecular electrode equivalents. These electrode equivalents are spin-bearing organic radicals poised at spectroscopically defined chemical potentials, vide infra, which are covalently attached to the D–A rectifying fragment. As shown in Fig. 1, semiquinone (SQ) and nitronylnitroxide (NN) radicals9 serve as biased electrodes with covalent chemical bonds as the contacts. The pyridine–thiophene/thiophene–pyridine (P–T/T–P) bridges serve as the molecule spanning the electrodes of a break-junction device and the two constitutional isomers SQ-P-T-NN and SQ-T-P-NN model the effect of reversing the bias direction. The large bridge dipole moment (μcalc = 1.94 D, see ESI†) satisfies one of the requirements for unimolecular rectification as previously proposed by Aviram and Ratner.1 Intrinsic unimolecular rectification, where the energy levels of the molecule shift as a function of the applied bias direction, is of interest since this is an inherent property of the molecule. Herein, we evaluate the results of single-molecule electron transport calculations, which have found broad utility in the molecular electronics community, with experimental observables derived from electronic absorption, magnetic susceptibility, and molecular electronic structure computations on structurally well-defined small molecule analogs of molecular break-junction and STM devices.
Experimental
Synthesis and characterization
Molecules have been synthesized and characterized according to established procedures that have been published in the literature.10–19 Synthetic methods, characterization, and X-ray crystallographic material is given in the ESI.†Transport calculations
Transport calculations were performed using ATK 2016.0 v16.0.20–22 The device configuration consists of the left Au electrode, the molecular bridge (scattering region), and the right Au electrode. Both the left and right gold electrodes consist of nine layers with each layer comprised of a 3 × 3 array of Au(111) atoms, for a total of 81 gold atoms per electrode. For the electrodes, the C or z direction is periodic in the system. This is also the direction of electron transport. Initial geometry optimizations of the T–P molecular bridge were performed using Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 with 6-31g(d′,p′) basis set and a B3LYP functional. Electrode surfaces were constructed by cleaving the bulk crystal, and using a copy of this to form the second electrode. The T–P molecule was then placed on the surface of the left electrode and subsequently connected to the right electrode through terminal sulfur atoms to create the final device geometry. Prior to creating the final device geometry, the bulk configuration was optimized using a single-zeta basis set for the gold atoms (to save computational time) and a double zeta basis set for all other atoms. The optimization was performed using ATK-DFT with a Perdew Zunger local density approximation (LDA-PZ) exchange correlation. After this bulk optimization, the configuration was converted into a final device geometry for all subsequent calculations. The 5 × 5 × 51 K-point sampling has been used in x, y, z-directions, respectively.
23 with 6-31g(d′,p′) basis set and a B3LYP functional. Electrode surfaces were constructed by cleaving the bulk crystal, and using a copy of this to form the second electrode. The T–P molecule was then placed on the surface of the left electrode and subsequently connected to the right electrode through terminal sulfur atoms to create the final device geometry. Prior to creating the final device geometry, the bulk configuration was optimized using a single-zeta basis set for the gold atoms (to save computational time) and a double zeta basis set for all other atoms. The optimization was performed using ATK-DFT with a Perdew Zunger local density approximation (LDA-PZ) exchange correlation. After this bulk optimization, the configuration was converted into a final device geometry for all subsequent calculations. The 5 × 5 × 51 K-point sampling has been used in x, y, z-directions, respectively.
The boundary conditions were Dirichlet (fixed boundary condition) in the z direction, which is the direction of transport. The boundary conditions in the x and y directions were disabled so they could not be changed but the default parameterization is periodic for the x and y directions. The NEGF formalism was used to calculate the non-equilibrium electron density of the central region of the device.
The Landauer–Büttiker formula24 relates transmission probabilities to conductance, g (g = I/V). This formula is used to calculate the voltage dependent current, I(V), across a molecular junction, which is determined by integrating the transmission function, T(E,V), according to eqn (1).
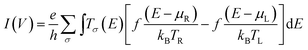 | (1) |
Here, e is the charge of the electron, h is Planck's constant, eVbias is the bias window equivalent to μR − μL (with Vbias = VL − VR), Tσ(E) is the aforementioned transmission coefficient for the spin component, σ, that describes the junction at an energy E and at a given bias voltage, Vbias. The Fermi-Dirac distribution functions are given by f(E − μR)/kBTR and f(E − μL)/kBTL and the right and left electrodes, respectively, with associated chemical potentials of μR for the right electrode and μL for the left electrode. All electron transport properties were computed using the ATK software package that includes virtual nanolab associated analysis modules. We have used the MPSH technique4,25 to understand the molecular orbital origin of the resonant peaks in the transmission spectra. The transmission eigenstates have been directly compared to the associated molecular orbitals of the isolated T–P molecule to understand the molecular orbital origin of a given transmission peak, including how the transmission peaks are modified with the application of an external bias across the left and right electrodes.
Results and discussion
We use torsionally-rotated D (thiophene) and A (pyridine) fragments connected by a σ-bond to partially decouple the D and A bridge fragments, in analogy with Aviram and Ratner's use of a cycloalkane bridge. We recently evaluated both σ- and torsionally restricted π contributions to electronic coupling at parity of D and A and showed that the σ contribution to the electronic coupling is ∼13 times weaker than a planar, conjugated π-contribution,19 in agreement with theoretical predictions.26,27 Given that HDA2 is proportional to the molecular conductance (g), it can be anticipated that there will be an ∼200 fold decrease in the transport mediated by the σ-system relative to a π-bridge at parity of bridge distance. Thus, although σ bonds may be used to effectively create tunnelling barriers between D and A, this effect will occur at the expense of attenuated conductance in both forward and reverse bias directions, and will limit the utility of the rectifier.Molecular design, structure, couplings and rectification ratios
Biradical ligand complexes SQ-P-T-NN and SQ-T-P-NN have been synthesized by standard procedures (see ESI for synthetic details†) used for the preparation of other SQ-B-NN biradical molecules.10–14,16,17,19,28–30 Bond line drawings and X-ray structures for SQ-P-T-NN and SQ-T-P-NN are given in Fig. 1 along with relevant SQ-B, B-B, and B-NN torsion angles. While the SQ to NN distances are within 0.1 Å, the torsion angles are quite different. For SQ-T-P-NN, the torsion angles are 15°, 26° and 36° for the SQ-T, T–P and P-NN torsion angles, respectively. The corresponding torsion angles for SQ-P-T-NN are 16°, 12° and 11°.Since both the SQ and NN are S = 1/2 spin-bearing units, the relative magnitudes of the bridge-mediated SQ-NN electronic coupling (HSQ-B-NN) in SQ-P-T-NN and SQ-T-P-NN can be conveniently determined at high resolution by measuring the relative magnitudes of their respective bridge-mediated SQ-NN magnetic exchange interactions, JSQ-B-NN.13,14,31–34 This can be accomplished using temperature- or magnetic field-dependent spectroscopies (e.g., electronic absorption spectroscopy14,35 or EPR,36) or magnetic susceptibility measurements with the singlet–triplet exchange splitting being equal to 2JSQ-B-NN according to the Heisenberg exchange Hamiltonian, eqn (2):
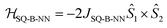 | (2) |
Magnetic susceptibility data, plotted as χpara · T products vs. temperature are displayed in Fig. 2A and B (see ESI for additional magnetic data†). Fits (derived from eqn (2)) to the data give JSQ-TP-NN = +51.2 ± 0.6 cm−1 and JSQ-PT-NN = +56.5 ± 0.5 cm−1.
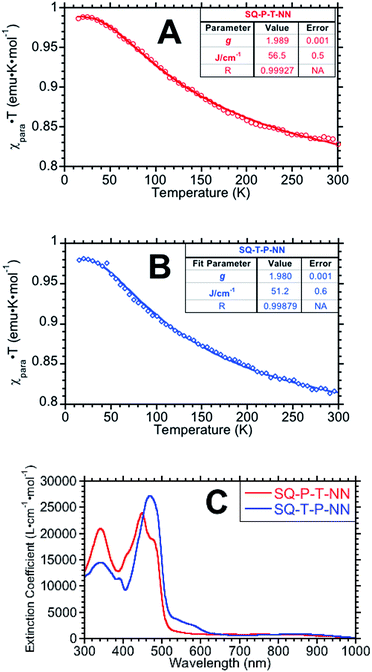 | ||
| Fig. 2 χ para · T vs. temperature plots for SQ-P-T-NN (A) and SQ-T-P-NN (B). (C) Electronic absorption spectra for SQ-T-P-NN and SQ-P-T-NN. SQ → B-NN ILCT bands appear ∼475 nm and closely approximates Δ in eqn (3), (5), (6a) and (6b). | ||
In terms of molecular design principles, it is desirable to explicitly relate the magnetic exchange, JSQ-NN, to the total-, SQ-B, and B-NN electronic couplings (HSQ-NN,HSQ-B, and HB-NN, respectively) and the molecular conductance (g) according to the relationship described by eqn (3) based on theories developed by Anderson,37 McConnell,38 and by Nitzan:39
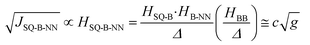 | (3) |
Thus, magnetic exchange is proportional to conductance (J ∝ g; where c is a proportionality constant), and eqn (3) is the electronic coupling theory complement to models for molecular rectification in terms of the experimental observables for the SQ-B-NN biradical complexes SQ-P-T-NN and SQ-T-P-NN, the SQ → B-A charge transfer energy, Δ; and the biradical magnetic exchange coupling, JSQ-B-NN. Here, the relative magnitudes of electronic couplings HSQ-B and HB-NN (as well as the SQ → B-NN charge transfer energy, vide infra) describe how strongly the unsymmetrical SQ and NN π-systems (which serve as biased electrode equivalents) interact with those of the unsymmetric bridge fragment. The magnitude of HBB quantifies the degree of coupling between the π systems of the unsymmetric, n bridge fragments.38
Electronic absorption spectra for the two isomeric biradicals are shown in Fig. 2C. The spectra are characterized by absorption bands of the constituent chromophores (SQ ∼ 840 nm and NN ∼ 580 nm), and an intense intraligand charge transfer (ILCT) band at ∼475 nm. TD-DFT calculations and analogy with other SQ-B-NN species allows assignment of the ILCT band in SQ-P-T-NN and SQ-T-P-NN as possessing dominant SQ(SOMO) → B-NN(LUMO) character with a minor contribution from the B-NN(HOMO) → SQ(SOMO) one-electron promotion (Fig. S3†). The ILCT transition is important, since the excited state configurations involved directly contribute to the magnitude of the observed ground state ferromagnetic exchange by configurational mixing with the ground state. This configurational mixing has been quantified in the context of a valence bond configuration interaction (VBCI) model, which has been successfully used to evaluate the electronic structure of SQ-B-NN heterospin biradical complexes.13,14 The ILCT band energy can be used to approximate Δ in eqn (3) and (4), where Δ also represents the intrinsic molecular bias between SQ and NN.15,17 Given the small ∼900 cm−1 energy difference in the two ILCT band maxima, we can make the approximation that ΔSQTPNN ≊ ΔSQPTNN.
With ΔSQTPNN ≊ ΔSQPTNN ≡ Δ and the J-values for the two constitutional isomers, eqn (3) relates the exchange coupling to the conductance. Thus eqn (3) can be recast in terms of ratios with JSQ-TP-NN/JSQ-PT-NN equating to an effective RR, gTP/gPT, using this unsymmetric bridge, eqn (4):
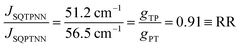 | (4) |
The effects of molecular conformation can be accounted for by modifying eqn (3) with the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ values determined by X-ray heterospin biradical complexes. These bond torsions control the degree to which the π-orbitals of nearest neighbor fragments become decoupled by torsional rotation. In addition to the decoupling between fragments, the torsional rotations affect the degree of unsymmetric orbital alignment between the bridge and the SQ/NN electrode equivalents. Thus, the magnitude of JSQ-TP-NN/JSQ-PT-NN, and the associated RRs, can be modulated by changes in the torsion angles between nearest neighbors (ϕSQ-P, ϕSQ-T, ϕT-P, ϕP-NN and ϕT-NN, Fig. 1) as shown in eqn (5):
φ values determined by X-ray heterospin biradical complexes. These bond torsions control the degree to which the π-orbitals of nearest neighbor fragments become decoupled by torsional rotation. In addition to the decoupling between fragments, the torsional rotations affect the degree of unsymmetric orbital alignment between the bridge and the SQ/NN electrode equivalents. Thus, the magnitude of JSQ-TP-NN/JSQ-PT-NN, and the associated RRs, can be modulated by changes in the torsion angles between nearest neighbors (ϕSQ-P, ϕSQ-T, ϕT-P, ϕP-NN and ϕT-NN, Fig. 1) as shown in eqn (5):
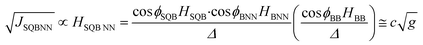 | (5) |
Recently, we demonstrated that HSQ-B-NN (∼√JSQ-B-NN. eqn (3)) varies smoothly as products of cosines of the SQ-B and B-NN torsion angles.19 This product (including cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕBB) is 0.70 for SQ-T-P-NN, while for the SQ-P-T-NN isomer, the product of cosines is 0.93. Substituting these cos
ϕBB) is 0.70 for SQ-T-P-NN, while for the SQ-P-T-NN isomer, the product of cosines is 0.93. Substituting these cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ products into eqn (5), gives eqn (6a) and (b). Squaring eqn (6a) and (6b) and taking the ratio gives eqn (7).
ϕ products into eqn (5), gives eqn (6a) and (b). Squaring eqn (6a) and (6b) and taking the ratio gives eqn (7).
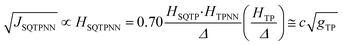 | (6a) |
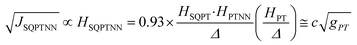 | (6b) |
 | (7) |
Thus, when the bridge molecule is planar (all cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φij = 1) and at parity of the individual Hij and SQ → B-NN charge transfer energies (Δ) we expect the intrinsic RR0 for planar T–P to be 1.58 times greater than that of planar P–T,
φij = 1) and at parity of the individual Hij and SQ → B-NN charge transfer energies (Δ) we expect the intrinsic RR0 for planar T–P to be 1.58 times greater than that of planar P–T, 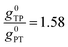 . Clearly, this value indicates a switch in the preferred direction of conductance compared to the “experimental” value, since the experimental JSQ-TP-NN/JSQ-PT-NN = ratio is 0.91, corresponding to a gTP/gPT RR of 0.91. The 0.70 and 0.93 rotational prefactors in eqn (6a) and (6b) suggest that greater intrinsic coupling is achieved in planar SQ-T-P-NN compared to SQ-P-T-NN (∼+104 and +66 cm−1, respectively, eqn (7)) allowing for a greater (and inverted) RR0.
. Clearly, this value indicates a switch in the preferred direction of conductance compared to the “experimental” value, since the experimental JSQ-TP-NN/JSQ-PT-NN = ratio is 0.91, corresponding to a gTP/gPT RR of 0.91. The 0.70 and 0.93 rotational prefactors in eqn (6a) and (6b) suggest that greater intrinsic coupling is achieved in planar SQ-T-P-NN compared to SQ-P-T-NN (∼+104 and +66 cm−1, respectively, eqn (7)) allowing for a greater (and inverted) RR0.
Superexchange/orbital pathway for coupling and the mechanism for rectification in T–P bridges
Within the context of our VBCI model, the topology of the T–P bridge HOMO and LUMO can be used to explain why the SQ-T-P-NN and SQ-P-T-NN magnetic exchange interactions and ILCT transitions are so similar, and provide a rationale for why the T–P unsymmetric bridge may be ineffective at promoting large RRs. Despite strong D–A character in the T–P bridge, both the bridge HOMO and LUMO that are responsible for the ILCT energy/intensity, magnetic superexchange coupling, and electronic transport are highly symmetric (Fig. 3).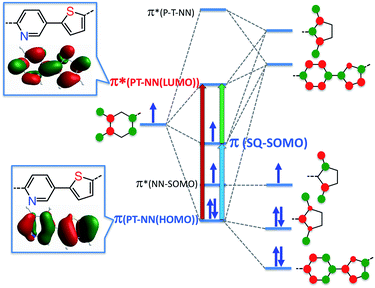 | ||
| Fig. 3 VBCI model for SQ-P-T-NN illustrating bridge HOMO and LUMO mirror plane-like symmetry: nearly identical p-orbital coefficients on T and P rings at the atoms of attachment to NN and SQ radicals renders the T–P bridge ineffective at both exchange coupling and rectification. Red, green and blue arrows indicate dominant one-electron contributions to the intraligand CT band. The blue and red transitions probe dominant CT contributions to magnetic superexchange pathways. Insets: DFT computed T–P LUMO and NN HOMO wave functions (see ESI†) that mix with frontier NN orbitals. | ||
Consequently, the magnitude of the P–T bridge torsion angle is insufficient to reduce the π-coupling in the D–A bridge. Thus, a critical component of an unsymmetric bridge necessary for unimolecular rectification is lost, highlighting the importance of understanding conductance orbital topology and excited state electronic structure contributions to molecular rectification. The intrabridge bond torsion effectively serves as an analog of the σ tunnelling barrier as was originally proposed by Aviram and Ratner.1 Maximum bridge localization occurs when the P and T bridge components are oriented perpendicular to each other. Although this would result in the elimination of π-coupling between the T–P bridge components and simulate a tunnel junction, this decoupling occurs with a marked reduction in conductance under both forward and reverse bias. This effect has been keenly illustrated and quantitated by our recent studies on bond torsion modulation of electronic coupling in an SQ-[(CH3)nphenylene]-NN series.19 Thus, a key component to increased rectification while maintaining a relatively high degree of conductance along a single bias direction resides in increasing the magnitude of the intrabridge T-P torsion just enough to partially decouple and localize the donor (thiophene) and acceptor (pyridine) components of the bridge fragment.
Computational assessment of molecular electron transport mediated by T–P
Our electronic absorption, magnetic susceptibility, and electronic structure calculations show that the electronic coupling matrix element that couples the T–P bridge to the SQ and NN radical electrode equivalents must be very similar for both SQ-P-T-NN and SQ-T-P-NN. Furthermore, this electronic coupling is primarily mediated by the T–P bridge LUMO and HOMO wavefunctions.Here, we employ a computational approach utilizing an electrode-molecule-electrode (two-probe Au electrode) construct to compute molecular electron transport properties of the unsymmetric dipolar T–P molecule under forward and reverse bias directions in a device setup. Our primary goal here is to evaluate the results of electron transport calculations in the context of experimentally determined SQ-P-T-NN and SQ-T-P-NN electronic and geometric structure, since bridge-mediated magnetic exchange couplings are related to conductance through the electronic coupling matrix element.39 The results of our transport calculations on Au(L)-S-T-P-S-Au(R) constructs with the T–P molecule bond torsion, ϕT–P, equal to 20° (≈the average of the T–P torsion angles in the biradicals determined from X-ray crystallography, see Fig. 1) are displayed in Fig. 4. The current (I) vs. bias potential (V) curve (I–V curve) in Fig. 4A shows that the computed bias dependent RRs are small. This is to be expected due to the small ϕT–P torsion angle and the concomitant high degree of delocalization in the bridge HOMO and LUMO wavefunctions, and fully in line with our experimentally determined exchange coupling ratios using SQ and NN radicals as biased molecular electrode analogs. The effective bias between SQ and NN in our SQ-P-T-NN and SQ-T-P-NN biradicals can be approximated by the energy (∼2.6 eV) of the SQ(SOMO) → B-NN(LUMO) ILCT band in Fig. 2C (= Δ in eqn (3)). We determine a RR = 1.24 at ±2.56 V in the I–V curve of Fig. 4A. This can be directly compared to our experimental results for SQ-P-T-NN and SQ-T-P-NN, where we observe a magnetic exchange determined RR0 of 1.58, a value that is in remarkably good agreement with the RR computed for the unsymmetrical T–P bridge in the device configuration using Au electrodes. This further illustrates the utility of using unsymmetrical bridge fragments to relate the results of transport calculations and experimental magnetic exchange coupling constants at geometric parity of the bridge contact geometry. Furthermore, the direct comparison of ratioed current values at a fixed bias potential (i.e. RRs) with JSQ-TP-NN/JSQ-PT-NN values eliminates complications associated with an unknown proportionality constant (c, eqn (3)) that relates the two measurable quantities; magnetic exchange couplings and current.
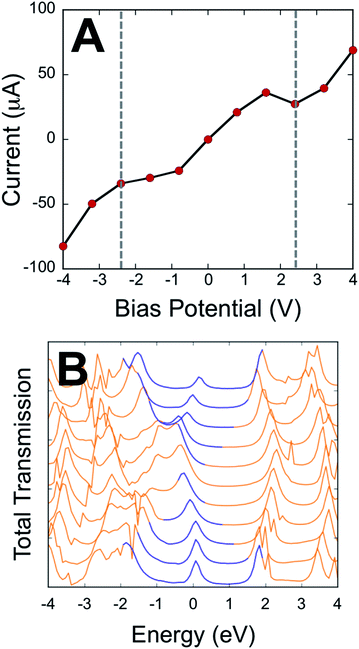 | ||
| Fig. 4 Results of transport calculations for the T–P bridge fragment under forward and reverse bias. (A) The I–V curve. Dashed, vertical lines indicate the intrinsic bias of SQ-PT-NN and SQ-TP-NN = Δ (2C, eqn (3)). (B) Bias-dependent transmission spectrum (note that the bias window is shown in blue). Transmission spectra correspond to the applied bias voltages in A, with −4 V at the bottom and +4 V at the top of the plot. The rectification ratio at ±2.56 V is observed to be RR = 1.3. A plot of RR vs. bias is shown in Fig. S3.† | ||
Further analysis of this system can be obtained by understanding the electronic origins of the transmission in the context of a tight-binding model.40,41 Under this approximation, the transmission function, T(E,V), can be cast as eqn (8).
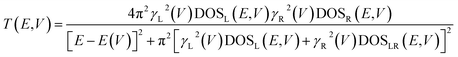 | (8) |
Here, the electrode density of states is given by DOSL,R(V), the molecule-electrode coupling parameters for the left and right contacts are γL(V) and γR(V), and the E(V) are the molecular energy levels that are affected by the Stark effect under forward or reverse bias. We note that DOSL,R(V), γL(V) and γR(V), and E(V) are all voltage dependent parameters that contribute to the current through the transmission function. Since our focus here is on intrinsic unimolecular rectification, we have used Au for both the left and right electrodes, and identical thiol anchoring groups to these electrodes. Thus, the dominant contributions to differences in the transmission function under forward and reverse bias are primarily determined by the bias dependent energy levels of the T–P molecule sandwiched between the two Au electrodes.
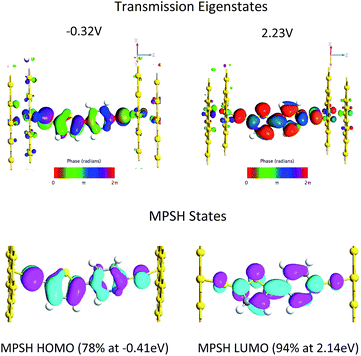
Fig. 4B displays the computed transmission as a function of bias voltage. At small applied voltages, |V| ≤ 1.0 V, a single transmission peak is found in the bias window. The dominant molecular orbital contribution to the transmission is obtained by evaluating the molecular projected self-consistent Hamiltonian (MPSH) states associated with a given transmission peak. These MPSH states are the S-T-P-S molecular orbitals that are modified through bonding to the Au electrodes. The MPSH state that contributes to the −0.32 V transmission eigenstate is the MPSH HOMO (78%), which is virtually identical to the free T–P molecular HOMO. At applied potentials lower than −1.5 V, another transmission peak begins to enter the bias window that is also dominantly MPSH HOMO in nature. Conversely, applied voltages greater than +1.5 V result in a transmission peak of different electronic origin beginning to enter into the bias window. The zero bias transmission peak at +2.23 V possesses dominant MPSH LUMO character that mirrors the LUMO of free T–P. Thus, both the T–P HOMO and LUMO contribute to conductance in the device geometry depicted in Fig. 5, with the T–P HOMO contributing prominently at low bias voltages due, presumably, to the known pinning effect of molecular HOMOs to the electrode Fermi level.4,42,43
The T–P HOMO and LUMO molecular orbitals that are responsible for transmission are the same as those that contribute to the ground state magnetic exchange coupling in SQ-P-T-NN and SQ-T-P-NN. The thiol groups in the transmission calculations increases the degree to which the molecular eigenstates can couple with those of the Au electrodes. As such, bridge molecular orbitals that possess large S contributions in the bias window dominate the conductance. The same effect is true for the SQ-bridge-NN systems. Here the S atom contact analogs are the bridgehead carbons of the NN and SQ radicals. In a Hückel approximation, magnetic exchange is maximized when the bridge MOs admix with the bridgehead carbons, and magnetic exchange is minimized for bridge MOs that do not possess NN and SQ bridgehead carbon character.
Interestingly, the T–P(LUMO) MPSH state enters the bias window at potentials near the energy of the SQ(SOMO) → B-NN(LUMO) ILCT band. The T–P bridge HOMO plays a dominant role in conduction at low bias voltages, but it plays a minor role in magnetic exchange coupling (∼14% contribution to the ILCT transition). The relative importance of a highly delocalized HOMO orbital for molecular conduction is increased when the MPSH HOMO is pinned to the electrode Fermi level in the device construct.4 Thus, a key difference in bridge-mediated electronic communication emerges as a result of using molecular electrode equivalents as opposed to metallic electrodes. While the T–P(HOMO) is pinned to the electrode Fermi level in the device construct and contributes to conduction at low bias voltages, orbital contributions to enhanced electronic coupling using molecular contact analogs can be different. In SQ-P-T-NN and SQ-T-P-NN this effectively favors the B-NN(LUMO). This is due to different resonance interactions between the bridge molecular orbital energy levels and those of the SQ(SOMO) and the NN(LUMO). In general, using other molecular contact analogs that possess different reduction potentials and orbital topologies will further modulate the bridge mediated electronic coupling. Future device constructs may be able to make more extensive use of molecular electrodes in order to make more reliable contacts44 and to enhance specific bridge orbitals for conductance and enhanced molecular rectification.
Conclusions
The biradical approach can be used to estimate RRs for nearly any bridge at any conformation observed in X-ray crystal structures and provide critical bridge electronic structure information from spectroscopy and magnetic measurements. Our work shows that the exchange coupling ratio is close to 1 for SQ-P-T-NN and SQ-T-P-NN. When understood in the context of transport calculations, small RRs are indeed expected for the P–T bridge in near planar conformations. This is exemplified by P–T bridge HOMO and LUMO mediated transmission in a near planar bridge geometry. Here, both the bridge HOMO and LUMO wavefunctions are observed to be highly symmetric with respect to a plane that bisects the SQ and NN fragments of the bridge, leading to contact invariance with respect to transmission through these orbitals. Despite the small degree of unsymmetric coupling promoted by the T–P bridge, increasing the intrabridge bond torsion should dramatically enhance RRs. Surprisingly, these results also show that bond torsions can potentially reverse the intrinsic RR through a given bridge fragment.In addition, this approach provides an important link that connects transport calculations that determine conductance, and spectroscopic/magnetic data that determine magnetic exchange couplings to an effective electronic coupling matrix element. Further efforts at understanding the electronic structure origins of molecular conductance and rectification, as well as optimizing molecular rectification using this approach are currently underway.
Acknowledgements
No competing financial interests have been declared. D. A. Shultz thanks the National Science Foundation (CHE-1464085 and CHE-1213269) for financial support. M. L. Kirk acknowledges the National Science Foundation (NSF CHE 1565930 and NSF #IIA-1301346) for financial assistance.Notes and references
- A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283 CrossRef CAS.
- B. Capozzi, J. Xia, O. Adak, E. J. Dell, Z.-F. Liu, J. C. Taylor, J. B. Neaton, L. M. Campos and L. Venkataraman, Nat. Nanotechnol., 2015, 10, 522–527 CrossRef CAS PubMed.
- V. Mujica, M. A. Ratner and A. Nitzan, Chem. Phys., 2002, 281, 147–150 CrossRef CAS.
- C. Van Dyck and M. A. Ratner, Nano Lett., 2015, 15, 1577–1584 CrossRef CAS PubMed.
- R. M. Metzger, Chem. Phys., 2006, 326, 176–187 CrossRef CAS.
- C. L. Guo, K. Wang, E. Zerah-Harush, J. Hamill, B. Wang, Y. Dubi and B. Q. Xu, Nat. Chem., 2016, 8, 484–490 CrossRef CAS PubMed.
- M. L. Perrin, E. Galan, R. Eelkema, J. M. Thijssen, F. Grozema and H. S. J. van der Zant, Nanoscale, 2016, 8, 8919–8923 RSC.
- B. Q. Xu and N. J. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- Y. Tsujia, R. Hoffmann, M. Strange and G. C. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E413–E419 CrossRef PubMed.
- E. C. Depperman, S. H. Bodnar, K. E. Vostrikova, D. A. Shultz and M. L. Kirk, J. Am. Chem. Soc., 2001, 123, 3133 CrossRef CAS PubMed.
- M. L. Kirk and D. A. Shultz, Coord. Chem. Rev., 2013, 257, 218–233 CrossRef CAS.
- M. L. Kirk, D. A. Shultz and E. C. Depperman, Polyhedron, 2005, 24, 2880–2884 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, E. C. Depperman and C. L. Brannen, J. Am. Chem. Soc., 2007, 129, 1937–1943 CrossRef CAS PubMed.
- M. L. Kirk, D. A. Shultz, E. C. Depperman, D. Habel-Rodriguez and R. D. Schmidt, J. Am. Chem. Soc., 2012, 134, 7812–7819 CrossRef CAS PubMed.
- M. L. Kirk, D. A. Shultz, D. Habel-Rodriguez, R. D. Schmidt and U. Sullivan, J. Phys. Chem. B, 2010, 114, 14712–14716 CrossRef CAS PubMed.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, D. Habel-Rodriguez, B. Stein and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 14713–14725 CrossRef CAS PubMed.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, G. F. Lewis, G. B. Wang, C. L. Brannen, R. D. Sommer and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 17144–17154 CrossRef CAS PubMed.
- D. A. Shultz, K. E. Vostrikova, S. H. Bodnar, H. J. Koo, M. H. Whangbo, M. L. Kirk, E. C. Depperman and J. W. Kampf, J. Am. Chem. Soc., 2003, 125, 1607–1617 CrossRef CAS PubMed.
- D. E. Stasiw, J. Y. Zhang, G. B. Wang, R. Dangi, B. W. Stein, D. A. Shultz, M. L. Kirk, L. Wojtas and R. D. Sommer, J. Am. Chem. Soc., 2015, 137, 9222–9225 CrossRef CAS PubMed.
- Atomistix ToolKit 2016.0 version 16.0, QuantumWise A/S, http://www.quantumwise.com.
- M. Brandbyge, J. L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- Gaussian 09, R. C. G., Inc., Pittsburgh, PA, 2009 Search PubMed.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B Condens. Matter, 1985, 31, 6207–6215 CrossRef.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B, 2001, 63, 245407 CrossRef.
- G. C. Solomon, D. Q. Andrews, R. R. Van Duyne and M. A. Ratner, ChemPhysChem, 2009, 10, 257–264 CrossRef CAS PubMed.
- G. C. Solomon, J. P. Bergfield, C. A. Stafford and M. A. Ratner, Beilstein J. Nanotechnol., 2011, 2, 862–871 CrossRef CAS PubMed.
- D. A. Shultz, K. E. Vostrikova, S. H. Bodnar, H. J. Koo, M. H. Whangbo, M. L. Kirk, E. C. Depperman and J. W. Kampf, J. Am. Chem. Soc., 2003, 125, 1607 CrossRef CAS PubMed.
- M. L. Kirk, D. A. Shultz, R. D. Schmidt, D. Habel-Rodriguez, H. Lee and J. Lee, J. Am. Chem. Soc., 2009, 131, 18304–18313 CrossRef CAS PubMed.
- J. Yang, D. K. Kersi, L. J. Giles, B. W. Stein, C. J. Feng, C. R. Tichnell, D. A. Shultz and M. L. Kirk, Inorg. Chem., 2014, 53, 4791–4793 CrossRef CAS PubMed.
- G. Blondin and J. J. Girerd, Chem. Rev., 1990, 90, 1359–1376 CrossRef CAS.
- P. Bertrand, Chem. Phys. Lett., 1985, 113, 104–107 CrossRef CAS.
- C. Herrmann and J. Elmisz, Chem. Commun., 2013, 49, 10456–10458 RSC.
- T. C. Brunold, D. R. Gamelin and E. I. Solomon, J. Am. Chem. Soc., 2000, 122, 8511–8523 CrossRef CAS.
- J. Hankache and O. S. Wenger, Chem. Rev., 2011, 111, 5138–5178 CrossRef CAS PubMed.
- A. S. Lukas, P. J. Bushard, E. A. Weiss and M. R. Wasielewski, J. Am. Chem. Soc., 2003, 125, 3921–3930 CrossRef CAS PubMed.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- H. M. McConnell, J. Chem. Phys., 1961, 35, 508–515 CrossRef CAS.
- A. Nitzan, J. Phys. Chem. A, 2001, 105, 2677–2679 CrossRef CAS.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2010 Search PubMed.
- W. D. Ding, M. Koepf, C. Koenigsmann, A. Batra, L. Venkataraman, C. F. A. Negre, G. W. Brudvig, R. H. Crabtree, C. A. Schmuttenmaer and V. S. Batista, J. Chem. Theory Comput., 2015, 11, 5888–5896 CrossRef CAS PubMed.
- C. Van Dyck, V. Geskin, A. J. Kronemeijer, D. M. de Leeuw and J. Cornil, Phys. Chem. Chem. Phys., 2013, 15, 4392–4404 RSC.
- C. Van Dyck, V. Geskin and J. Cornil, Adv. Funct. Mater., 2014, 24, 6154–6165 CrossRef CAS.
- K. W. Hipps, Science, 2001, 294, 536–537 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1526005 and 1526006. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc00073a |
| This journal is © The Royal Society of Chemistry 2017 |