Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of a complex crystal structure in the absence of single crystals: analysis of powder X-ray diffraction data, guided by solid-state NMR and periodic DFT calculations, reveals a new 2′-deoxyguanosine structural motif†‡
Colan E.
Hughes
a,
G. N. Manjunatha
Reddy
b,
Stefano
Masiero
 c,
Steven P.
Brown
c,
Steven P.
Brown
 b,
P. Andrew
Williams
a and
Kenneth D. M.
Harris
b,
P. Andrew
Williams
a and
Kenneth D. M.
Harris
 *a
*a
aSchool of Chemistry, Cardiff University, Park Place, Cardiff, CF10 3AT, UK. E-mail: HarrisKDM@cardiff.ac.uk
bDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK
cDipartimento di Chimica “G. Ciamician”, Alma Mater Studiorum – Università di Bologna, via San Giacomo, 11-40126 Bologna, Italy
First published on 16th March 2017
Abstract
Derivatives of guanine exhibit diverse supramolecular chemistry, with a variety of distinct hydrogen-bonding motifs reported in the solid state, including ribbons and quartets, which resemble the G-quadruplex found in nucleic acids with sequences rich in guanine. Reflecting this diversity, the solid-state structural properties of 3′,5′-bis-O-decanoyl-2′-deoxyguanosine, reported in this paper, reveal a hydrogen-bonded guanine ribbon motif that has not been observed previously for 2′-deoxyguanosine derivatives. In this case, structure determination was carried out directly from powder XRD data, representing one of the most challenging organic molecular structures (a 90-atom molecule) that has been solved to date by this technique. While specific challenges were encountered in the structure determination process, a successful outcome was achieved by augmenting the powder XRD analysis with information derived from solid-state NMR data and with dispersion-corrected periodic DFT calculations for structure optimization. The synergy of experimental and computational methodologies demonstrated in the present work is likely to be an essential feature of strategies to further expand the application of powder XRD as a technique for structure determination of organic molecular materials of even greater complexity in the future.
Introduction
Powder X-ray diffraction (XRD) and solid-state NMR spectroscopy are both rich sources of structural data for polycrystalline materials. While successful crystal structure determination of organic molecular solids can now (since the early 1990s) be carried out directly from powder XRD data alone,1–8 the structure determination process is often enhanced significantly by consideration of solid-state NMR data for the same material, allowing specific structural details to be established or validated. In general, solid-state NMR data are used in two ways to assist the process of structure determination from powder XRD data.9First, after completing structure refinement (the final stage of structure determination from diffraction data), periodic DFT calculations employing the GIPAW (Gauge Including Projector Augmented Wave) method10–15 (for example in the CASTEP program16) can be used to calculate solid-state NMR data (e.g., isotropic chemical shifts) for the crystal structure, which may then be compared with the corresponding experimental solid-state NMR data. Clearly, an acceptable level of agreement between calculated and experimental solid-state NMR data can provide strong validation of the crystal structure, augmenting the validation that is already provided by the rigorous assessment17 of the quality of fit between experimental and calculated powder XRD patterns in the final Rietveld refinement. This strategy is becoming an increasingly popular way of enhancing the scrutiny and validation of the results obtained in structure determination from powder XRD data.18–25
Second, measurements of internuclear couplings from solid-state NMR experiments have the potential to yield information on specific internuclear distances, molecular conformations and/or bonding arrangements in the material. For example, measurement of direct (through-space) dipole–dipole interactions can be used to determine specific internuclear distances in the crystal structure. Measurement of indirect (electron-coupled) dipole–dipole interactions (i.e., J-couplings) can also provide useful structural insights that may be utilized in the structure determination process. In this regard, J-coupling through hydrogen bonds26,27 (e.g., 15N⋯15N J-coupling in N–H⋯N hydrogen bonds) can allow the specific functional groups engaged in hydrogen-bonding interactions to be identified. Clearly, such knowledge is particularly valuable in the context of structure determination from powder XRD data, as it may allow plausible structural motifs to be identified in trial structures during the structure solution process or may allow trial structures containing incorrect motifs to be modified or rejected.
This paper is focused on structure determination directly from powder XRD data in tandem with consideration of solid-state NMR data, specifically to elucidate the structure of 3′,5′-bis-O-decanoyl-2′-deoxyguanosine [denoted dG(C10)2; Fig. 1]. This material is believed to be polymorphic, as two distinct solid forms have been identified on crystallization from ethanol. In previous work, Pham et al.28 referred to these two forms as 2q and 2r. The material studied in the present work corresponds to 2q, as the powder XRD data matches the powder XRD data for 2q published previously.29 We note that 2q appears to be more readily obtained, as 2r has only been reported once.28 In order to introduce a systematic nomenclature, we define polymorph I of dG(C10)2 as 2q and we define polymorph II of dG(C10)2 as 2r.
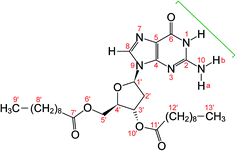 | ||
| Fig. 1 Molecular structure of dG(C10)2 showing the atom numbering scheme. The green bracket indicates the Watson–Crick hydrogen-bonding groups. The non-hydrogen atoms of the guanine moiety are labelled 1 to 10 and the non-hydrogen atoms of the 2′-deoxyribose moiety are labelled 1′ to 6′ and 10′. Note that the atom labelled here as N10 was labelled N2 or NH2 in previous publications28–30 on dG(C10)2. | ||
The dG(C10)2 molecule has found applications in the context of photoelectric devices, including photoconductive materials,31–33 biphotonic quantum dots34 and photodetectors with rectifying properties.35 It has also been shown36 that dG(C10)2 can reversibly interconvert between quartets and ribbons, using a cryptand for cation capture and addition of acid to release the cation. In all these applications, the hydrogen bonding of the guanine moieties is a key factor, emphasizing the importance of understanding the preferred structural properties of dG(C10)2 in the solid state. Among 3′,5′-bis-O-alkanoyl derivatives of 2′-deoxyguanosine, crystal structures have been reported previously only for 3′,5′-bis-O-acetyl-2′-deoxyguanosine [dG(C2)2]37 and 3′,5′-bis-O-propanoyl-2′-deoxyguanosine [dG(C3)2],38 although several 3′,5′-bis-O-silyl derivatives have also been studied39,40 and self-assembly of 2′-deoxyguanosine derivatives in solution has been investigated.41–44
Guanine derivatives are known for their rich supramolecular chemistry.47–49 In the solid state, a variety of distinct hydrogen-bonding motifs have been reported, including ribbons and quartets, which resemble the G-quadruplex50 found in nucleic acids with sequences rich in guanine. Most reported ribbon motifs are the so-called “narrow” form (Fig. 2a), in which neighbouring guanine moieties are linked by two hydrogen bonds (N–H⋯N and N–H⋯O), with each pair of guanines forming a hydrogen-bonded ring designated as R22(9) in graph-set notation.45,46 A less common motif, described as a “wide” ribbon (Fig. 2b), has been observed in two structures [2′,3′-O-bis(tri-isopropylsilyl)guanosine40 and 9-(2,3-bis(hydroxymethyl)cyclobutyl)-guanine51] and contains three distinct hydrogen bonds: two N–H⋯O hydrogen bonds between the O atom of one guanine moiety and two different N atoms of a neighbouring guanine moiety [forming a ring with graph set R12(6)], and an N–H⋯N hydrogen bond which, together with the two N–H⋯O hydrogen bonds, forms a ring involving three guanine moieties with graph set R33(11). Another ribbon motif has been observed in the solution state41,43 and in a number of salts of 7-methylguanine52 in which two distinct hydrogen-bonded rings alternate along the ribbon. Among the reported quartet motifs, there are only two cases53,54 in which the quartet is not formed around a metal cation.
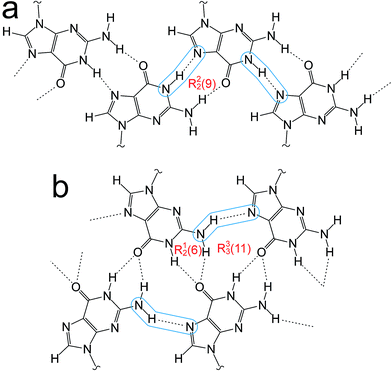 | ||
| Fig. 2 (a) The “narrow” guanine ribbon and (b) the “wide” guanine ribbon. In each case, the N–H⋯N hydrogen bonds are highlighted and the graph sets45,46 for the hydrogen-bonded rings are indicated. | ||
As dG(C10)2 was obtained in our work only as a fine powder (by crystallization from ethanol), powder XRD provides the only viable approach for structure determination. As demonstrated over the past 20 years or so,1–8 crystal structure determination of organic materials directly from powder XRD data has become a relatively mature field. Nevertheless, challenges in structure determination can be encountered in specific cases, which can be greatly facilitated by incorporating other sources of information (i.e., other experimental data and/or computational insights) within the structure determination process. As illustrated by the present study of structure determination of dG(C10)2 – a molecule with 90 atoms – the successful application of techniques for structure determination from powder XRD data is not just limited to the case of relatively small molecules.
Methods
The sample of dG(C10)2 was prepared using the method described previously28 and crystallized from ethanol. Powder XRD data confirmed that the sample was polymorph I, as defined above. High-quality powder XRD data suitable for structure determination were recorded (at 21 °C), for a powder sample contained in two flame-sealed capillaries, using a Bruker D8 Diffractometer (Ge-monochromated CuKα1 radiation) operating in transmission mode with a Våntec detector covering 3° in 2θ. The data were recorded in the 2θ range from 3° to 50° (step size 0.017°) with a total data collection time of 57 h. A two-dimensional powder XRD pattern was also recorded at ambient temperature using an Agilent SuperNova Dual Atlas diffractometer (CuKα radiation, λ = 1.54180 Å) in order to assess the extent of “preferred orientation” in the powder sample.55Periodic DFT calculations for geometry optimization and calculation of NMR parameters were carried out using the CASTEP program16 (Academic Release version 8.0). Geometry optimization used ultrasoft pseudopotentials,56 PBE functional,57 semiempirical dispersion corrections (TS correction scheme58), fixed unit cell, preserved space group symmetry and periodic boundary conditions. Isotropic NMR chemical shifts were calculated using the GIPAW approach,10–14 while J-coupling values were calculated at the scalar-relativistic level of theory using the ZORA method.59–61 All calculations used a basis set cut-off energy of 700 eV and a Monkhorst–Pack grid62 of minimum sample spacing 0.05 × 2π Å−1. In the first instance, chemical shifts are referenced using the formula
| δiso(calc) = σref − σiso(calc) | (1) |
| δiso(calc) = σ0 − m σiso(calc) | (2) |
Structure determination
The powder XRD pattern of polymorph I of dG(C10)2 was indexed using the DICVOL91 algorithm63 in the program Crysfire,64 giving the following unit cell with monoclinic metric symmetry: a = 8.33 Å, b = 7.82 Å, c = 25.79 Å, β = 97.5°. However, in the subsequent profile-fitting stage of the structure determination process, progress was hampered significantly by two specific features of the powder XRD pattern of dG(C10)2, which introduced challenges in achieving an acceptable quality of profile fitting (Fig. 3). First, the powder XRD pattern of dG(C10)2 contains a very intense peak at low diffraction angle (2θ = 3.4°), which is substantially more intense than any of the other peaks. The presence of one peak of dominant intensity initially raised the possibility that the powder XRD data may be strongly affected by preferred orientation of the crystallites in the sample. However, the powder XRD pattern (see Fig. S1 in ESI‡) recorded using a two-dimensional detector (for one of the two capillaries used to record the one-dimensional powder XRD data in Fig. 3) exhibited uniform intensity around the Debye–Scherrer rings, indicating that the distribution of crystallite orientations in the powder sample was essentially random and hence that there was no significant preferred orientation.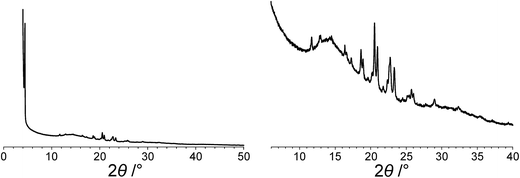 | ||
| Fig. 3 The experimental powder XRD pattern for polymorph I of dG(C10)2. The full powder XRD pattern is shown on the left; the expanded region from 2θ = 6° to 40° is shown on the right. | ||
The second challenging aspect concerns the very high background in the low-angle region of the powder XRD pattern, arising from a significant amount of X-ray scattering from air in the region of the peak at 2θ = 3.4°. To achieve a high quality of fit in the profile-fitting stage, which was carried out using the Le Bail technique65 in the GSAS program,66 it was necessary first to fit the baseline of the low-angle region (2θ = 3° to 5°) using a polynomial, which was then subtracted from the experimental data. Although this procedure introduced some artefacts to the baseline, these artefacts were fitted successfully by the shifted Chebyshev polynomials67 used for baseline correction in the Le Bail fitting procedure in GSAS. We note that attempts to fit the original baseline using this method were not successful.
The modified powder XRD data were then subjected to Le Bail fitting (Fig. 4a; due to the high intensity of the first peak relative to all other peaks, the data between 2θ = 6° and 40° are shown separately with an expanded intensity scale in Fig. 4b). The lineshape of the first peak is rather poorly fitted as a consequence of the double baseline fitting described above. Nevertheless, the overall quality of fit obtained in the Le Bail fitting is considered acceptable (Fig. 4a; Rp = 0.93%, Rwp = 1.23%).
Density considerations suggest that there are two molecules of dG(C10)2 in the unit cell and, given the fact that the dG(C10)2 molecule is chiral, the only plausible space groups are P2 and P21. As these space groups could not be distinguished definitively on the basis of systematic absences in the powder XRD data [although the absence of the (010) peak may point towards P21], each of these space groups was considered in independent structure-solution calculations using the direct-space genetic algorithm technique68–70 in the program EAGER.71–76 Structure-solution calculations for space group P2 did not generate any plausible trial structures and only space group P21 was considered further.
Previous solid-state NMR studies of dG(C10)2 provide direct structural insights concerning the hydrogen-bonding between guanine moieties. Pham et al.28,30 determined the 15N chemical shifts and J-couplings for polymorph I of dG(C10)2 (see Table 1), including a 2hJN7N10 coupling of 5.9 Hz, while Webber et al.29 reported 1H and 13C chemical shifts and found evidence for several H⋯H short contacts. The value of 2hJN7N10 provides a strong indication that there is a relatively strong N–H⋯N hydrogen bond involving N7 and N10, which provided a robust criterion for acceptance or rejection of trial structures obtained in the structure solution from powder XRD data reported here (particularly as a basis for rejecting trial structures that clearly do not contain this hydrogen bond, as discussed in more detail below). Furthermore, comparison of the chemical shifts and J-couplings calculated for the final refined crystal structure with the chemical shifts and J-couplings measured experimentally provides additional scrutiny and validation of the crystal structure following the final Rietveld refinement.
In setting up the structural model to be used in the direct-space genetic algorithm structure solution calculations, the dG(C10)2 molecule was constructed as follows. The geometry of the guanine moiety was modelled on the structure of one of the molecules in the reported crystal structure77 of guanosine dihydrate (CCDC ref. code GUANSH10) and the geometry of the 2′-deoxyribose ring was modelled on that in the reported crystal structure38 of dG(C3)2 (CCDC ref. code MOFBUE). The two C10 chains were constructed using the average bond lengths and bond angles for similar moieties determined using the program Mogul version 1.7.1 (for bonds not involving hydrogen) and from Allen et al.78 (for bonds involving hydrogen). The conformation of the 2′-deoxyribose ring was kept fixed during the structure solution calculation. As the position along the b-axis can be fixed arbitrarily for space group P21, each trial structure was defined by a total of 27 structural variables (2 positional, 3 orientational and 22 torsional variables). The 22 torsional variables are specified in Fig. S2.‡
With this model, the structure solution calculations in space group P21 generated trial structures that were considered plausible, including a geometric relation between N7 and N10 consistent with N–H⋯N hydrogen bonding. In contrast, structure solution calculations using other models for the dG(C10)2 molecule (e.g., with the geometry of the 2′-deoxyribose ring based on the average bond lengths and bond angles for similar moieties) led to trial structures that were considered implausible as they did not contain hydrogen bonding between N7 and N10.
The genetic algorithm structure solution calculations in space group P21 involved the evolution of 32 independent populations of 500 structures, with 50 mating operations and 250 mutation operations carried out per generation, and a total of 500 generations in each calculation. In two of the calculations, the trial structure giving the best quality of fit between calculated and experimental powder XRD data was essentially the same structure, and the quality of fit was significantly better than the best-fit structure obtained in any of the other calculations (see ESI‡ for more details). The trial structure giving the best quality of fit from all the structure-solution calculations was used as the initial structural model for Rietveld refinement,79 which was carried out using the GSAS program.66 In the Rietveld refinement, restraints were applied to bond lengths and bond angles based on the initial molecular model (discussed above) and planar restraints were applied to the guanine moiety and the two carbonyl moieties. These restraints were relaxed over the course of the refinement. A common isotropic atomic displacement parameter was refined for all non-hydrogen atoms and the value for hydrogen atoms was set equal to 1.2 times the refined value for non-hydrogen atoms. No corrections were applied for preferred orientation. The Rietveld refinement at this stage gave a reasonably good fit to the powder XRD data (Fig. 4c; Rp = 1.35%, Rwp = 1.86%).
The structure obtained in this Rietveld refinement was then subjected to geometry optimization using the CASTEP program, leading to small shifts in atomic positions with an average atomic displacement of 0.65 Å. The most significant structural changes concerned the orientations of the two carbonyl moieties in the decanoyl chains. The structure obtained following geometry optimization was then used as the starting structural model for a final Rietveld refinement, which gave an improved fit (Fig. 4e; Rp = 1.15%, Rwp = 1.56%) compared to the first Rietveld refinement discussed above. The final refined unit cell parameters were: a = 8.3072(7) Å, b = 7.8052(10) Å, c = 25.7246(27) Å, β = 97.491(4), V = 1653.73(31) Å3 (2θ range, 3–50°; 2755 profile points; 289 refined variables). Overall, the combination of geometry optimization followed by further Rietveld refinement led to an average atomic displacement of 0.71 Å, with significant changes in the conformations of the decanoyl chains (particularly in the region of the carbonyl moieties) and a small shift of the 2′-deoxyguanosine moiety, which led to an improvement in geometrical aspects of the hydrogen bonding between guanine moieties in neighbouring molecules.
Discussion
The crystal structure from the final Rietveld refinement is shown in Fig. 5 and 6. Viewed along the b-axis (Fig. 5), it is clear that the structure comprises hydrogen-bonded ribbons constructed from the guanine moieties (the view in Fig. 5 is parallel to the plane of the ribbons). The ribbons run parallel to the b-axis and the guanine moieties within a given ribbon are related by the 21 screw axis. The 2′-deoxyribose moiety and alkyl chains occupy the space between adjacent ribbons. The ribbons involve three distinct hydrogen bonds: two N–H⋯O hydrogen bonds involving N–H10b and N–H1 of a given molecule as donors and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group of a neighbouring guanine moiety as the acceptor, and an N–H⋯N hydrogen bond involving N–H10a as the donor and the N7 atom of a neighbouring guanine moiety as the acceptor (geometric data for these hydrogen bonds are given in Table S1 in ESI‡). The ribbons in dG(C10)2 are unambiguously identified (compare Fig. 6 and 2b) as the “wide” ribbon motif,40,51 which has not been observed previously for any 2′-deoxyguanosine derivative. A C–H⋯O hydrogen bond is also identified (see Fig. 6) between C8 of the guanine moiety as the C–H donor and the C
O group of a neighbouring guanine moiety as the acceptor, and an N–H⋯N hydrogen bond involving N–H10a as the donor and the N7 atom of a neighbouring guanine moiety as the acceptor (geometric data for these hydrogen bonds are given in Table S1 in ESI‡). The ribbons in dG(C10)2 are unambiguously identified (compare Fig. 6 and 2b) as the “wide” ribbon motif,40,51 which has not been observed previously for any 2′-deoxyguanosine derivative. A C–H⋯O hydrogen bond is also identified (see Fig. 6) between C8 of the guanine moiety as the C–H donor and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group containing C11′ of a neighbouring molecule as the acceptor.
O group containing C11′ of a neighbouring molecule as the acceptor.
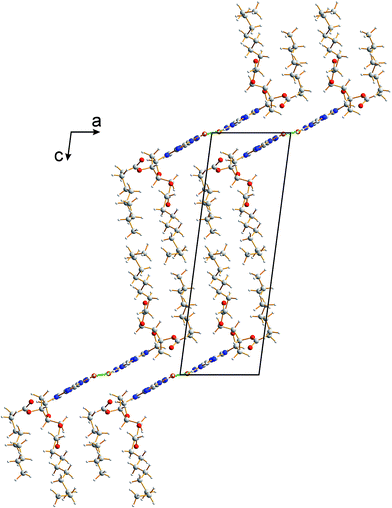 | ||
| Fig. 5 Crystal structure of polymorph I of dG(C10)2 viewed along the b-axis (parallel to the direction of the hydrogen-bonded ribbons). | ||
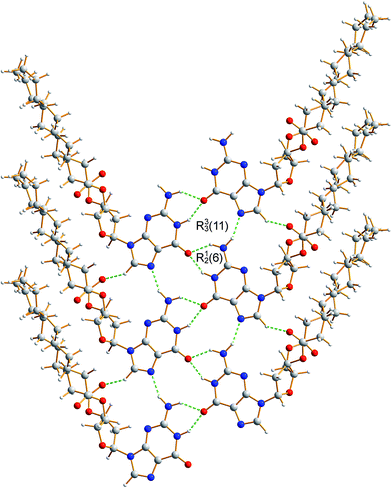 | ||
| Fig. 6 Crystal structure of polymorph I of dG(C10)2 showing the hydrogen-bonded ribbon of the guanine moieties. In this view, the b-axis is vertical. | ||
There is also evidence for π⋯π interactions between guanine moieties in adjacent ribbons in the crystal structure of dG(C10)2, as the distances from the N3, C2 and N10 atoms of one guanine moiety to the N7, C8 and N9 atoms, respectively, of a neighbouring molecule are all ca. 3.5 Å (Fig. 7). Such π⋯π interactions are not observed in the two previously reported crystal structures40,51 containing the “wide” ribbon motif.
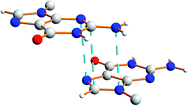 | ||
| Fig. 7 Illustration of π⋯π interactions between guanine moieties in the crystal structure of polymorph I of dG(C10)2. The dashed lines represent distances of ca. 3.5 Å. | ||
The relative arrangement of the 2′-deoxyribose and guanine moieties around the N-glycosidic bond (N9–C1′) corresponds to the syn conformation, with the Watson–Crick hydrogen-bonding groups (see Fig. 1) directed towards the 2′-deoxyribose ring.80 Significantly, Webber et al.29 predicted that the crystal structure of dG(C10)2 should exhibit this structural feature, based on the high values of isotropic 13C chemical shift for C8 and C1′, which are characteristic of the syn conformation. It is noteworthy that the only guanosine derivative that forms the “wide” ribbon motif in its crystal structure also has the syn conformation.40
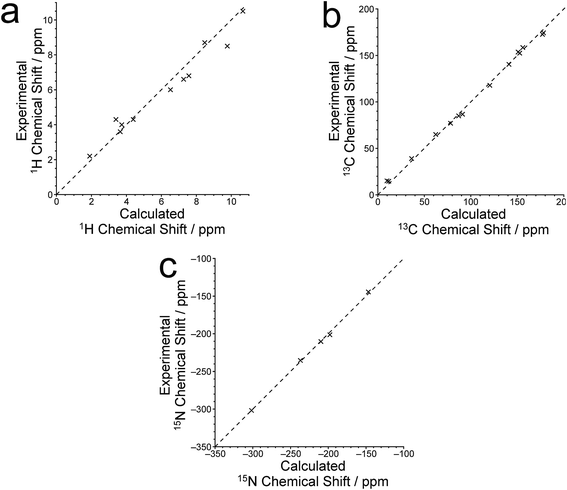
The isotropic 1H, 13C and 15N chemical shifts calculated using the CASTEP program for the crystal structure of polymorph I of dG(C10)2 determined here are compared with the experimental values29,30 in Fig. 8 (see also Tables S2–S4‡). The calculated (using eqn (1)) and experimental data are in very good agreement, with RMS deviations of 0.57 ppm, 3.02 ppm and 2.01 ppm for the 1H, 13C and 15N chemical shifts, respectively. From Fig. 8b, it is evident that the calculated 13C chemical shifts are higher than the experimental data for the resonances at high ppm and lower than the experimental data for the resonances at low ppm. This phenomenon is well known and can be addressed empirically either by establishing the calculated chemical shifts using eqn (2) and the least-squares fitting procedure (in which the gradient m may deviate from unity) described in the Methods section, or by using different reference shieldings for the high-ppm region and the low-ppm region of the spectrum.11,23,81 As shown in Fig. S3,‡ when the calculated 13C chemical shifts are established using eqn (2), the RMS deviation between calculated and experimental 13C chemical shifts is decreased to 2.51 ppm. Using the same procedure (based on eqn (2)) to establish the calculated 1H and 15N chemical shifts, the RMS deviations between calculated and experimental data are decreased to 0.39 ppm and 1.99 ppm, respectively.
Hartman et al.82 have reported that GIPAW calculations of 13C chemical shifts across a range of small organic molecules give an RMS deviation of 2.12 ppm when using the procedure based on eqn (2). Although this deviation is slightly lower than that obtained for our results, it is important to note that the dG(C10)2 molecule is significantly larger and more flexible than any of the molecules considered by Hartman et al. Furthermore, the slightly higher RMS deviation observed for dG(C10)2 may be caused, in part, by the fact that 13C chemical shifts for the CH2 moieties were not included in our analysis as the 13C resonances for individual CH2 moieties are not resolved in the experimental 13C NMR spectrum.
Three 15N⋯15N J-couplings across N–H⋯N hydrogen bonds between guanine moieties were also calculated (see Table 1), specifically the intramolecular couplings 3JN3N10 and 3JN3N9, and the intermolecular coupling 2hJN7N10. In each case, the calculated J-coupling is higher, to a greater or lesser extent, than the experimental value, but the calculated values successfully reflect the correct trend.
Concluding remarks
Several aspects of the structure determination of dG(C10)2 from powder XRD data reported in this paper presented challenges, including the presence of the very intense (001) peak at low angle in the powder XRD pattern on a very steeply sloping baseline. This peak represents more than 45% of the total diffraction intensity across the 2θ range recorded and it was essential to ensure that the method applied for baseline correction did not significantly distort this peak. This factor, combined with the complexity of the direct-space search involved in the structure-solution calculation (a consequence of the large size and flexibility of the dG(C10)2 molecule), led to a large number of distinct trial structures giving similar fits to the data. In order to identify the correct structure solution, information obtained in previous solid-state NMR studies of dG(C10)2 proved to be vital, in particular the knowledge that a strong intermolecular N–H⋯N hydrogen bond exists between N7 and N10. After initial Rietveld refinement, geometry optimization using periodic DFT calculations (with fixed unit cell) generated a structure which, upon further Rietveld refinement, gave an improved fit to the experimental powder XRD data, illustrating the utility of introducing geometry optimization as a key step in the overall structure elucidation process. Clearly, the fact that a wide range of solid-state NMR parameters calculated from the final refined crystal structure are in good agreement with the corresponding experimental solid-state NMR parameters gives additional support to the veracity of the structure determined from powder XRD data. The synergy of experimental and computational methodologies demonstrated in the present work is likely to be an essential feature of strategies to further expand the application of powder XRD as a technique for structure determination of organic molecular materials of even greater complexity in the future.Acknowledgements
We are grateful to Cardiff University for financial support. CASTEP calculations were carried out on the Cardiff University supercomputer, Raven, run by Advanced Research Computing @ Cardiff. This research was carried out within the framework of the EPSRC funded Collaborative Computational Project for NMR Crystallography CCP-NC (EP/M022501/1). GNMR and SPB acknowledge funding from EPSRC (EP/K003674/1). SM acknowledges the University of Bologna and the European Community (EC FP7 ICT-MOLARNET project 318516).References
- P. Lightfoot, M. Tremayne, K. D. M. Harris and P. G. Bruce, J. Chem. Soc., Chem. Commun., 1992, 1012–1013 RSC.
- K. D. M. Harris, M. Tremayne, P. Lightfoot and P. G. Bruce, J. Am. Chem. Soc., 1994, 116, 3543–3547 CrossRef CAS.
- V. V. Chernyshev, Russ. Chem. Bull., 2001, 50, 2273–2292 CrossRef CAS.
- K. D. M. Harris, M. Tremayne and B. M. Kariuki, Angew. Chem., Int. Ed., 2001, 40, 1626–1651 CrossRef CAS PubMed.
- Structure Determination from Powder Diffraction Data, ed. W. I. F. David, K. Shankland, L. B. McCusker and C. Baerlocher, IUCr/OUP, 2002 Search PubMed.
- H. Tsue, M. Horiguchi, R. Tamura, K. Fujii and H. Uekusa, J. Synth. Org. Chem. Jpn., 2007, 65, 1203–1212 CrossRef CAS.
- W. I. F. David and K. Shankland, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 52–64 CrossRef CAS PubMed.
- K. D. M. Harris, Top. Curr. Chem., 2012, 315, 133–178 CrossRef CAS PubMed.
- K. D. M. Harris and M. Xu, in NMR Crystallography, ed. R. K. Harris, R. Wasylishen and M. J. Duer, 2009, ch. 19, pp. 275–287 Search PubMed.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–S186 CrossRef CAS PubMed.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS PubMed.
- S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204 RSC.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- Z. Pan, E. Y. Cheung, K. D. M. Harris, E. C. Constable and C. E. Housecroft, Cryst. Growth Des., 2005, 5, 2084–2090 CAS.
- M. Tremayne, B. M. Kariuki and K. D. M. Harris, Angew. Chem., Int. Ed. Engl., 1997, 36, 770–772 CrossRef CAS.
- X. Filip, G. Borodi and C. Filip, Phys. Chem. Chem. Phys., 2011, 13, 17978–17986 RSC.
- D. V. Dudenko, P. A. Williams, C. E. Hughes, O. N. Antzutkin, S. P. Velaga, S. P. Brown and K. D. M. Harris, J. Phys. Chem. C, 2013, 117, 12258–12265 CAS.
- P. Li, Y. Chu, L. Wang, R. M. Wenslow Jr, K. Yu, H. Zhang and Z. Deng, CrystEngComm, 2014, 16, 3141–3147 RSC.
- X. Li, A. D. Bond, K. E. Johansson and J. Van de Streek, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 784–789 CAS.
- G. N. M. Reddy, D. S. Cook, D. Iuga, R. I. Walton, A. Marsh and S. P. Brown, Solid State Nucl. Magn. Reson., 2015, 65, 41–48 CrossRef CAS PubMed.
- M. Sardo, S. M. Santos, A. A. Babaryk, C. López, I. Alkorta, J. Elguero, R. M. Claramunt and L. Mafra, Solid State Nucl. Magn. Reson., 2015, 65, 49–63 CrossRef CAS PubMed.
- A. E. Watts, K. Maruyoshi, C. E. Hughes, S. P. Brown and K. D. M. Harris, Cryst. Growth Des., 2016, 16, 1798–1804 CAS.
- A. J. Dingley and S. Grzesiek, J. Am. Chem. Soc., 1998, 120, 54–64 CrossRef.
- I. G. Shenderovich, S. N. Smirnov, G. S. Denisov, V. A. Gindin, N. S. Golubev, A. Dunger, R. Reibke, S. Kirpekar, O. L. Malkina and H.-H. Limbach, Ber. Bunsen-Ges. Phys. Chem., 1998, 102, 422–428 CrossRef CAS.
- T. N. Pham, S. Masiero, G. Gottarelli and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 16018–16019 CrossRef CAS PubMed.
- A. L. Webber, S. Masiero, S. Pieraccini, J. C. Burley, A. S. Tatton, D. Iuga, T. N. Pham, G. P. Spada and S. P. Brown, J. Am. Chem. Soc., 2011, 133, 19777–19795 CrossRef CAS PubMed.
- T. N. Pham, J. M. Griffin, S. Masiero, S. Lena, G. Gottarelli, P. Hodgkinson, C. Filipe and S. P. Brown, Phys. Chem. Chem. Phys., 2007, 9, 3416–3423 RSC.
- R. Rinaldi, E. Branca, R. Cingolani, S. Masiero, G. P. Spada and G. Gottarelli, Appl. Phys. Lett., 2001, 78, 3541–3543 CrossRef CAS.
- G. Maruccio, P. Visconti, V. Arima, S. D'Amico, A. Biasco, E. D'Amone, R. Cingolani, R. Rinaldi, S. Masiero, T. Giorgi and G. Gottarelli, Nano Lett., 2003, 3, 479–483 CrossRef CAS.
- R. Rinaldi, G. Maruccio, A. Biasco, V. Arima, R. Cingolani, T. Giorgi, S. Masiero, G. P. Spada and G. Gottarelli, Nanotechnology, 2002, 13, 398–403 CrossRef CAS.
- A. Neogi, J. Li, P. B. Neogi, A. Sarkar and H. Morkoc, Electron. Lett., 2004, 40, 1605–1606 CrossRef CAS.
- H. Liddar, J. Li, A. Neogi, P. B. Neogi, A. Sarkar, S. Cho and H. Morkoç, Appl. Phys. Lett., 2008, 92, 013309 CrossRef.
- S. Pieraccini, S. Masiero, O. Pandoli, P. Samorì and G. P. Spada, Org. Lett., 2006, 8, 3125–3128 CrossRef CAS PubMed.
- L. H. Koole, H. M. Buck, J. A. Kanters and A. Schouten, Can. J. Chem., 1988, 66, 2634–2639 CrossRef CAS.
- T. Giorgi, F. Grepioni, I. Manet, P. Mariani, S. Masiero, E. Mezzina, S. Pieraccini, L. Saturni, G. P. Spada and G. Gottarelli, Chem.–Eur. J., 2002, 8, 2143–2152 CrossRef CAS.
- T. Sato, M. Seko, R. Takasawa, I. Yoshikawa and K. Araki, J. Mater. Chem., 2001, 11, 3018–3022 RSC.
- R. Takasawa, I. Yoshikawa and K. Araki, Org. Biomol. Chem., 2004, 2, 1125–1132 CAS.
- G. Gottarelli, S. Masiero, E. Mezzina, G. P. Spada, P. Mariani and M. Recanatini, Helv. Chim. Acta, 1998, 81, 2078–2092 CrossRef CAS.
- A. L. Marlow, E. Mezzina, G. P. Spada, S. Masiero, J. T. Davis and G. Gottarelli, J. Org. Chem., 1999, 64, 5116–5123 CrossRef CAS.
- G. Gottarelli, S. Masiero, E. Mezzina, S. Pieraccini, J. P. Rabe, P. Samorí and G. P. Spada, Chem.–Eur. J., 2000, 6, 3242–3248 CrossRef CAS.
- E. Mezzina, P. Mariani, R. Itri, S. Masiero, S. Pieraccini, G. P. Spada, F. Spinozzi, J. T. Davis and G. Gottarelli, Chem.–Eur. J., 2001, 7, 388–395 CrossRef CAS.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126 CrossRef CAS.
- M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262 CrossRef.
- J. T. Davis, Angew. Chem., Int. Ed., 2004, 43, 668–698 CrossRef CAS PubMed.
- J. T. Davis and G. P. Spada, Chem. Soc. Rev., 2007, 36, 296–313 RSC.
- S. Lena, S. Masiero, S. Pieraccini and G. P. Spada, Chem.–Eur. J., 2009, 15, 7792–7806 CrossRef CAS PubMed.
- M. Gellert, M. N. Lipsett and D. R. Davies, Proc. Natl. Acad. Sci. U. S. A., 1962, 48, 2013–2018 CrossRef CAS.
- G. S. Bisacchi, J. Singh, J. J. D. Godfrey, T. P. Kissick, T. Mitt, M. F. Malley, J. D. D. Marco, J. Z. Gougoutas, R. H. Mueller and R. Zahler, J. Org. Chem., 1995, 60, 2902–2905 CrossRef CAS.
- Á. Kozma, S. Ibáñez, R. Silaghi-Dumitrescu, P. J. S. Miguel, D. Guptaa and B. Lippert, Dalton Trans., 2012, 41, 6094–6103 RSC.
- Y. Inui, M. Shiro, S. Fukuzumi and T. Kojima, Org. Biomol. Chem., 2013, 11, 758–764 CAS.
- J. L. Sessler, M. Sathiosatham, K. Doerr, V. Lynch and K. A. Abboud, Angew. Chem., Int. Ed., 2000, 39, 1300–1303 CrossRef CAS PubMed.
- E. Y. Cheung, K. D. M. Harris and B. M. Foxman, Cryst. Growth Des., 2003, 3, 705–710 CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892–7895 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 71, 3865–3868 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- S. A. Joyce, J. R. Yates, C. J. Pickard and F. Mauri, J. Chem. Phys., 2007, 127, 204107 CrossRef PubMed.
- S. A. Joyce, J. R. Yates, C. J. Pickard and S. P. Brown, J. Am. Chem. Soc., 2008, 130, 12663–12670 CrossRef CAS PubMed.
- T. F. G. Green and J. R. Yates, J. Chem. Phys., 2014, 140, 234106 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Boultif and D. Louër, J. Appl. Crystallogr., 1991, 24, 987–993 CAS.
- R. Shirley, The CRYSFIRE System for Automatic Powder Indexing: User's Manual, The Lattice Press, Guildford, U.K., 1999 Search PubMed.
- A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452 CrossRef CAS.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report, LAUR, 2004, pp. 86–748 Search PubMed.
- J. C. Mason and D. C. Handscomb, Chebyshev Polynomials, Chapman & Hall/CRC, Boca Raton, Florida, 2003 Search PubMed.
- B. M. Kariuki, H. Serrano-González, R. L. Johnston and K. D. M. Harris, Chem. Phys. Lett., 1997, 280, 189–195 CrossRef CAS.
- K. D. M. Harris, R. L. Johnston and B. M. Kariuki, Acta Crystallogr., Sect. A: Found. Crystallogr., 1998, 54, 632–645 CrossRef.
- K. D. M. Harris, S. Habershon, E. Y. Cheung and R. L. Johnston, Z. Kristallogr., 2004, 219, 838–846 CAS.
- B. M. Kariuki, P. Calcagno, K. D. M. Harris, D. Philp and R. L. Johnston, Angew. Chem., Int. Ed., 1999, 38, 831–835 CrossRef CAS.
- B. M. Kariuki, K. Psallidas, K. D. M. Harris, R. L. Johnston, R. W. Lancaster, S. E. Staniforth and S. M. Cooper, Chem. Commun., 1999, 1677–1678 RSC.
- E. Tedesco, G. W. Turner, K. D. M. Harris, R. L. Johnston and B. M. Kariuki, Angew. Chem., Int. Ed., 2000, 39, 4488–4491 CrossRef CAS PubMed.
- D. Albesa-Jové, B. M. Kariuki, S. J. Kitchin, L. Grice, E. Y. Cheung and K. D. M. Harris, ChemPhysChem, 2004, 5, 414–418 CrossRef PubMed.
- K. Fujii, A. Lazuen Garay, J. Hill, E. Sbircea, Z. Pan, M. Xu, D. C. Apperley, S. L. James and K. D. M. Harris, Chem. Commun., 2010, 46, 7572–7574 RSC.
- P. A. Williams, C. E. Hughes and K. D. M. Harris, Angew. Chem., Int. Ed., 2015, 54, 3973–3977 CrossRef CAS PubMed.
- U. Thewalt, C. E. Bugg and R. E. Marsh, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1089–1101 CrossRef CAS PubMed.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19 RSC.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- S. Neidle, Principles of Nucleic Acid Structure, Elsevier, Amsterdam, 2008 Search PubMed.
- A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, J. Phys. Chem. A, 2010, 114, 10435–10442 CrossRef CAS PubMed.
- J. D. Hartman, S. Monaco, B. Schatschneider and G. J. O. Beran, J. Chem. Phys., 2015, 143, 102809 CrossRef PubMed.
Footnotes |
| † The experimental datasets for this study and the magres output (.magres) files from the CASTEP calculations are available from the Cardiff University data catalogue at http://doi.org/10.17035/d.2017.0031643370 |
| ‡ Electronic supplementary information (ESI) available. CCDC 1535685. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc00587c |
| This journal is © The Royal Society of Chemistry 2017 |