Open Access Article
Open Access ArticleChemistry with semi-classical electrons: reaction trajectories auto-generated by sub-atomistic force fields
Chen
Bai
 ,
Seyit
Kale†
,
Seyit
Kale†
 and
Judith
Herzfeld
and
Judith
Herzfeld
 *
*
Department of Chemistry, Brandeis University, Waltham, MA 02454, USA. E-mail: herzfeld@brandeis.edu
First published on 19th April 2017
Abstract
For a century now, “Lewis dots” have been a mainstay of chemical thinking, teaching and communication. However, chemists have assumed that this semi-classical picture of electrons needs to be abandoned for quantitative work, and the recourse in computational simulations has been to the extremes of first principles treatments of electrons on the one hand and force fields that avoid explicit electrons on the other hand. Given both the successes and limitations of these highly divergent approaches, it seems worth considering whether the Lewis dot picture might be made quantitative after all. Here we review progress to that end, including variations that have been implemented and examples of applications, specifically the acid–base behavior of water, several organic reactions, and electron dynamics in silicon fracture. In each case, the semi-classical approach is highly efficient and generates reasonable and readily interpreted reaction trajectories in turnkey fashion (i.e., without any input about products). Avenues for further progress are also discussed.
Introduction
Despite the importance of the non-classical behavior of electrons, the semi-classical picture that Lewis proposed in 1916 (ref. 1) continues to serve chemists as an essential and user-friendly tool for imagining molecular structures and reaction mechanisms, and for representing them in textbooks and journal articles. Lewis' electrons are “classical” in that they are conceived as particles that repel one another, but only “semi” in that they fail to stick to nuclei, have spin and tend to form pairs. Within these rules, the “Lewis dot” picture admirably informs chemical intuition and communication.At the same time, the limitations of the Lewis dot picture are obvious. It is qualitative and does not speak to the wave-like nature of electrons, including their quantized energies. On the other hand, wave features are expensive to access and not always of interest. In fact, where excited states are not relevant, the expense of first principles methods (whether ab initio or density functional) is often avoided by using molecular mechanics where electrons are only acknowledged implicitly in the forms of atomistic force fields that describe the influence of the atoms on one another. However, since the behavior and effects of the underlying electrons vary among chemical groups, the force fields for atoms of each element need to be laboriously re-parameterized for these different contexts. Furthermore, the complexity of parameterization and the computational expense increase when atomic multipoles and polarizability (as in e.g. AMOEBA2) or bond making and breaking (as in e.g. ReaxFF3) are considered. This seems a high price to pay for trying to ignore electrons and it raises the question of whether we have overreached in that respect.
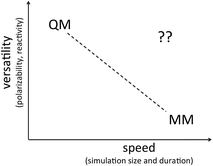
In this brief review we consider whether the Lewis dot picture is as irredeemably qualitative as has been supposed and whether its qualitative strengths can be translated into quantitative strengths. Because explicit, independently mobile electrons naturally confer context dependent behavior, only one set of force field parameters might be required for each element. In addition, explicit, independently mobile electrons naturally confer polarizability and reactivity. Thus, although explicit electrons increase the number of particles in play, the expectation is that sub-atomistic force fields will be able to avoid the need for multi-particle terms such as those required in atomistic force fields for torsion, polarizability and reactivity. Furthermore, during bond rearrangements, the easily visualized trajectories of semi-classical electrons can readily inform our understanding of reaction mechanisms. Indeed, one can imagine that sub-atomistic force fields based on semi-classical electrons could have a versatility approaching that of first principles methods with a speed, user-friendliness and efficiency approaching that of atomistic force fields (see Fig. 1).
We are aware of two groups working on sub-atomistic force fields, ours and the Goddard group at the California Institute of Technology. In our group, the first generation force field is LEWIS4,5 and the second generation is LEWIS˙.6–8 In the Caltech group the first generation force field is eFF9,10 and the second generation is eFF–ECP11,12 (where eFF stands for “electron force field” and ECP for “effective core potential”). Until well into these projects, neither of these groups was aware of the work of the other and the models from the two groups differ significantly. In the next section, we will summarize these and other possible variations.
In subsequent sections, we will present a sampling of applications that illustrates what these models are capable of. First, applications to the acid–base behavior of water show that a thoroughly optimized LEWIS force field predicts experimentally observed behavior that has eluded extensive density functional theory (DFT) studies. Second, applications to organic reactions show that even a coarsely optimized LEWIS force field can efficiently generate non-trivial reaction trajectories without prior knowledge of the products. Finally, applications under extreme conditions show that eFF–ECP can provide trajectories for material breakdown with electron ejection. Following these examples, we will conclude with some comments about prospects.
Variations
The first step in developing a sub-atomistic force field is the choice of particles. The most comprehensive is to make all electrons explicit and this is the approach initially taken in eFF. However, we know that core electrons have little influence on chemistry. Thus, for many purposes it would suffice, as Lewis pointed out, to explicitly consider only the valence electrons and to bundle core electrons in a “kernel” with the corresponding nucleus. This path, which is analogous to the “frozen cores” often used in first principles calculations, has been taken in LEWIS, LEWIS˙ and eFF–ECP.Another consideration is whether to model the electrons singly, with two possible spins, or in pairs (where spin is not an issue). While the latter is clearly more efficient, it is far less versatile in that it cannot describe free radicals or fractional bond order. While the eFF series has always opted for single electrons, LEWIS explored the capabilities of electron pairs before LEWIS˙ tackled single electrons.
To take the wave properties of electrons into account, it is clearly necessary to assign a “spread” to each electron. In principle, this “cloud size” will depend on the environment of the electron. However, approximating it as fixed improves efficiency. While the eFF series has always opted for variable cloud sizes, LEWIS explored the capabilities of fixed cloud sizes before LEWIS˙ tackled variable cloud sizes.
Having defined the particles in the system, the great challenge is to define the interactions between them in a fashion that results in molecules with correct structures and thermodynamics. The expectation is that by taking explicit account of electrons, sub-atomistic force fields will have less need for multi-particle interactions than atomistic force fields. Both the LEWIS and eFF series of force fields have considered only pairwise interactions with the sorts of promising results shown below. However, a recent analysis suggests that properly accounting for the exchange effects arising from the anti-symmetry of electron wave functions will require three-particle terms.13 Still, this is less than the four-particle torsion terms required in conventional atomistic force fields and the higher order terms required in atomistic force fields that incorporate polarizability or reactivity.
What we can say for sure about the interactions, is that
(i) the potentials must be smoothly differentiable in order to produce trajectories that are energy conserving,
(ii) at long distances, pair interactions must be asymptotically coulombic and multi-body interactions must go to zero faster than coulombic, and
(iii) at short distances, the interactions of electrons with other particles must not diverge in a manner that depends on the electron cloud size.
Within these constraints there are many possible functions to consider, a challenge that is analogous to the decades-long quest for the correct functional for density functional theory. Furthermore, the details of the functions are critical because molecular behavior is dictated by relatively small differences between very strong repulsions and very strong attractions.
Two approaches can be taken to exploring the space of possible potential functions. The heuristic approach tries different functional forms to see which perform best, choosing successive forms that would seem to address the deficits of those already considered. The theoretical approach derives potential functions from approximate wave functions for localized electrons and then adds some flexibility to compensate for the approximations. The two approaches are not mutually exclusive, but the development of LEWIS potentials has relied more heavily on the heuristic approach and the development of eFF potentials has relied more heavily on the theoretical approach. As a result, although LEWIS˙ and eFF–ECP have converged in focusing on valence electrons modeled singly with variable cloud sizes, they continue to use different forms for the interactions of the electrons with each other and with atomic kernels.
Trial potential functions typically have adjustable parameters that need to be optimized to best reproduce training data. These data can be either from experimental measurements or quantum calculations. In either case, attention has to be paid to the quality of the data and its adequacy to constrain the potential functions over the range of distances required. For these purposes the LEWIS effort has emphasized experimental training data while the eFF effort has emphasized quantum training data.
Because sub-atomistic force fields are similar in spirit to conventional force fields (albeit with a different choice of particles and a different set of functional forms for interactions between them), the new force fields can be implemented in standard molecular dynamics packages. For molecular dynamics simulations, LEWIS has been implemented in GROMACS as an add-on (see http://people.brandeis.edu/%7Eherzfeld/LEWIS/) and eFF has been implemented in LAMMPS.
Although, the LEWIS and eFF series of force fields have taken rather different approaches, they have similar goals and have each achieved significant successes as illustrated below.
LEWIS simulations of the acid–base behavior of water
Water is arguably the most interesting molecule that comprises just two elements. In the LEWIS construct, water is described by just three types of particles: protons, oxygen kernels and electron pairs. Among these three particles, there are six types of pair interactions, three between like particles and three between unlike particles. Among the many combinations of potential energy forms considered for these six interactions, one was found to be exceptionally good at fitting a training set comprised of structural and thermodynamic data for monomers and dimers in all of their protonation states, complimented by the density of water at 1 atmosphere and room temperature.4An important feature of LEWIS is its efficiency. Compared to density functional theory in the relatively simple generalized gradient approximation (DFT/GGA), LEWIS readily accommodates 10-fold larger systems for 100-fold longer simulation times. The former allows the examination of ion behavior at relevant concentrations and at suitable distances from surfaces or periodic images. The latter allows extensive sampling for good statistics.
The LEWIS force field for water has been validated by predictions of both molecular and bulk properties, including radial distribution functions for water in all three of its protonation states, the dielectric constant, and the molecular polarizability.4,14 The importance of getting the molecular polarizability right has been underscored by a recent comparison between MP2 and DFT/GGA results.15 As shown in Fig. 2, LEWIS predicts dipole moments in the bulk phase that are centered around ∼2.6 D, which is the close to the reported MP2 value of 2.67 D. In contrast, reported DFT/GGA values of 2.95–3.24 D are deep in the high-end tail of the LEWIS distribution.
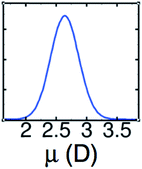 | ||
| Fig. 2 LEWIS prediction for the distribution of dipole moments of water molecules in the neat liquid under ambient conditions. | ||
The molecular polarizability is particularly important because it affects the solvation of water self-ions. As illustrated in Fig. 3, LEWIS reproduces the general accepted picture of excess protons residing primarily in “Eigen complexes” (i.e., hydronium donating three hydrogen bonds to neighboring water molecules) that break symmetry to form “Zundel complexes” where the excess proton is shared between two water molecules and can transfer between them. With the same potentials, LEWIS also predicts the expected “mirror” solvation of missing protons (a.k.a., proton holes), with a dominant Eigen-like complex in which hydroxide accepts three hydrogen bonds from neighboring water molecules and symmetry breaking to form Zundel-like special pairs where the proton deficit is shared between two water molecules and can transfer between them. In contrast, DFT/GGA, with its overestimation of the polarizability of water,15 predicts that hydroxide is generally over-coordinated, with four hydrogen bonds donated by neighboring water molecules, a configuration seen only rarely in LEWIS.14
The difference in hydroxide solvation is significant for understanding the surface charge of water. Although it was noted already in the middle of the 19th century,16–19 and confirmed by more exacting experiments in recent years,20–25 that the surface of pure water is negatively charged, LEWIS is the first model of water that obtains that result.26 In LEWIS simulations of water slabs, hydroxide is found at the surface with its proton pointing outward and its oxygen accepting hydrogen bonds from three water molecules. As a result, when hydroxide displaces a water molecule from the surface, the water gains more hydrogen bonds than the hydroxide loses (see Fig. 4). On the other hand, because it would be difficult to organize an additional hydrogen bond donor to over-coordinate a hydroxide at the surface, DFT/GGA fails to predict the propensity of hydroxide for the surface of water.
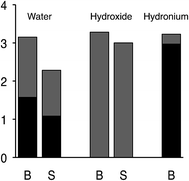 | ||
| Fig. 4 Statistics from LEWIS simulations of slabs of 1000 molecules for the average number of H-bonds accepted (gray) and donated (black) by the indicated species, in the slab surface (S) vs. in the bulk (B) at ambient temperature and pressure.26 | ||
The story for hydronium is more complicated. For H3O+(H2O)20 clusters, LEWIS agrees with high level first principles calculations27 that the lowest energy is achieved in configurations with hydronium at the surface, pointing its lone pair outward. As illustrated in Fig. 5, this is because (a) dimpling of the cluster allows the internal water to participate in four hydrogen bonds and (b) a tight surface curvature provides a full set of H-bond acceptors for the hydronium. Once again, when the ion displaces a water from the surface, the water gains more hydrogen bonds than the ion loses. However, in slabs of water under ambient conditions, LEWIS finds that hydronium avoids the surface.26 Here a water displaced from the surface gains fewer hydrogen bonds (see Fig. 4) and this more modest gain is evidently outweighed by poorer accommodation of hydronium at the flatter surface.
The dynamics of the self-ions of water involve bond making and breaking, for which the semi-classical approach provides a natural, intuitive and efficient description. Compared to the self-diffusion of water, an excess proton diffuses rapidly because a proton can hop from hydronium to a neighboring water (via a Zundel type intermediate). A proton hole can also diffuse by proton hops, but less easily because it requires that a proton leave a water molecule to join a neighboring hydroxide. Thus the diffusion constant for hydroxide is intermediate between that of water and that of hydronium. The corresponding predictions from DFT/GGA vary wildly, with one functional predicting that hydroxide diffuses faster than hydronium, another that hydroxide diffuses slower than water, and another with the correct trend. In contrast, LEWIS unambiguously predicts the correct trend, with reasonable diffusion constants for all three species.14
Dynamics are of particular interest in auto-ionization and neutralization events. Auto-ionization is a rare event that is difficult to sample. A DFT/GGA study using transition path sampling suggested that electric field fluctuations are responsible for ionization events followed by rapid ion separation.28 Meanwhile, DFT/GGA simulations of neutralization produce trajectories in bulk water that are almost 100-fold faster than are seen experimentally.29 In both cases, the rapid dynamics are very likely another consequence of having overestimated the polarizability of water. In contrast, LEWIS predicts more difficult proton transfer, dependent on the occurrence of unusually short hydrogen bonds. Present at ∼1 M under ambient conditions, these special pairs are sufficiently common to be responsible for the Debye relaxation of water (a strong absorption band in the dielectric spectrum of water at 2 × 1010 Hz)30–33 and sufficiently rare to result in time scales for neutralization that are consistent with experiment.34 The dependence on ultra-short hydrogen bonds for proton transfer, suggests that density fluctuations may be a greater factor in ionization events than electric field fluctuations. In addition, the dependence on ultra-short hydrogen bonds explains why proton diffusion is faster in water chains than in bulk water. In the 1D hydrogen bonded “wire” of a water chain, ultra-short hydrogen bonds are readily formed by chain contraction. However, ultra-short hydrogen bonds are much more difficult to form under the constraints of the 3D hydrogen bonded network that prevails in bulk water. The result is that proton transfer is concerted in chains and diffusive in the bulk liquid.34
Simulations of organic reactions with coarsely tuned LEWIS potentials
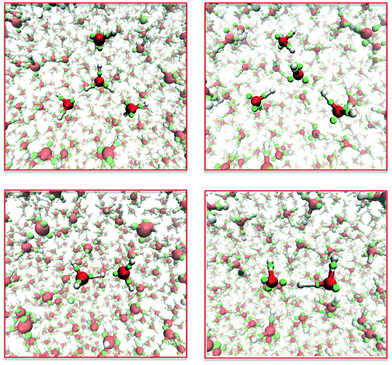
To be broadly effective, the interactions between the semi-classical electrons need to be independent of context. Therefore, adding another element to the model should require new potentials only for the interactions of kernels of the new element with each other, with electrons, and with the kernels of other elements. This step has been partially successful in extending LEWIS to include carbon as well as hydrogen and oxygen. The training set included the structures and thermodynamics of molecules with up to two heavy atoms (e.g., methanol and ethene) and dimers of molecules with one heavy atom (e.g., water–methane). Functional forms for electron–kernel and kernel–kernel interactions that were successful for water yielded fits to the training data that were not as good as had been obtained for water. Such weak transferability is not surprising for a first generation force field. Nevertheless, it turns out that this relatively crude force field suffices to provide remarkable reaction trajectories for a range of organic reactions. Here we show three examples.Dimethyl ether is produced commercially by the acid-catalyzed dehydration of methanol at 400 K. Fig. 6 shows snapshots from a LEWIS simulation of this process. Most of the time, the excess proton (placed initially on a methanol) is shared between hydroxyl groups (as at 3.6 ps and 14.9 ps). However, when the excess proton re-localizes on one molecule, that methyloxonium is subject to nucleophilic attack by another methanol (as at 11.2 ps). The resulting transition state (at 11.4 ps) is over-coordinated at three atoms. The first resolution is release of water, a good leaving group (at 13.1 ps). This is followed by release of the excess proton from the ether oxygen, making it available for further catalysis. Note that the simulation does not depend on prior knowledge of the reaction product. In fact, there was no ether molecule in the LEWIS training set.
Also outside the training set were epoxide rings. Since these are highly strained, it is significant that they are stable under the LEWIS force field, with the expected bent “banana” bonds shown in the first frames of Fig. 7. On the other hand, given this stability, it is also significant that they open appropriately when attacked by a base, as shown in last frames of Fig. 7.
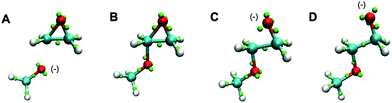 | ||
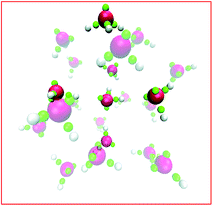
| Fig. 7 Snapshots of a Monte Carlo simulation of base catalyzed epoxide ring opening in the gas-phase. A negatively charged methoxide (A) attacks one of the epoxy carbons to form a short-lived carbanion state (B). The epoxide ring opens and the charge is now on the newly formed terminal oxide (C). The product then assumes a more favorable configuration (D). The color scheme is the same as in Fig. 6. | ||
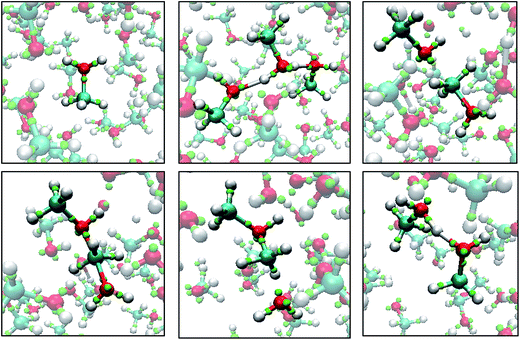
Fig. 8 shows snapshots from a LEWIS simulation of formaldehyde hydration. In this case, both reactants were in the training set, but the product was not. A significant feature of this turnkey simulation is that proton transfer occurs spontaneously via two accessory water molecules that close a hydrogen bonded ring that acts as a proton transfer pathway. This pathway was surmised in 1983 (ref. 35) but was not accessible to even rudimentary first principles calculations until 1995.36 Also notable is that the nucleophilic attack on the formaldehyde occurs at the Bürgi–Dunitz angle37 even though the LEWIS construct has no knowledge of the first principles molecular orbitals according to which the geometry of attack is usually predicted.
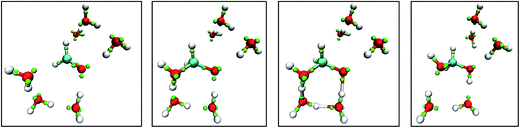 | ||
| Fig. 8 Snapshots from a Monte Carlo simulation of formaldehyde hydration in the gas phase. Left to right: formaldehyde with six water molecules; nucleophilic attack by one water molecule; water mediated proton transfer; and relaxation of the methanediol product. Note that, in LEWIS, double and triple bonds comprise “banana bonds”. The color scheme is the same as in Fig. 6. | ||
eFF–ECP simulations of electron dynamics in silicon fracture
Silicon fracture is a non-adiabatic process that is beyond the reach of first principles modeling. The eFF–ECP approach has provided an opportunity to follow the behavior of the valence electrons on useful time and length scales.11 Silicon parameters for eFF–ECP potentials were trained by first principle calculations for small silicon hydrides. In simulations, cracking was induced by applying a one dimensional load to a seed crack in the fracture plane. The resulting crack tip velocity showed an approximately step-function dependence on the normalized energy release rate, behavior that compares well with experiment and with previous results from ReaxFF and a multi-scale approach.The unique contribution of the eFF–ECP simulations is to describe the mechanism of electron excitation and release during fracture. The details of the simulations show that voltages, due to heterolytic breaking of Si–Si bonds, are responsible more often than heat. A simulated potential difference of 1.02 V between the two crack faces, is reasonably consistent with potentials of up to 0.39 V observed experimentally. In addition, the electron yields of 5.3 × 1011 to 1.6 × 1012 cm−2 predicted by eFF–ECP are similar to the 1011 cm−2 observed experimentally for faster cracks. These fracture-induced mobile charge carriers provide an explanation for the fracture-induced currents that are observed experimentally.
Summary and outlook
Although these are still early days for sub-atomistic force fields, several variations have already demonstrated the ability to efficiently auto-generate non-trivial reaction trajectories with observables that compare well with experiment.Limitations in first generation force fields have been partially addressed in the second generation. In eFF–ECP, new electron–kernel potentials have improved transferability among elements. However, it remains that potentials trained on molecular structures and enthalpies give poor estimates of bulk properties and vice versa.11 In LEWIS˙, transferability for ionization and spin states has been demonstrated for monoatomic and diatomic species across all the reactive 2p and 3p elements. However, the resulting potential is rugged with problematic local minima.8
The present limitations of LEWIS and eFF are likely due to the fact that both have relied exclusively on pairwise potentials. A recent study of the exchange integrals for simple localized wave functions has shown that 3-body contributions are important.13 Preliminary work on a third generation of LEWIS suggests that these contributions will “fill” the spurious local minima in the second generation force field.
In summary, tremendous progress has been made in developing a quantitative version of the Lewis dots picture. Despite the limitations of the present force fields, they have generated informative reaction trajectories, including some that improve significantly upon those obtained by DFT/GGA. Further improvements can be expected from third generation potentials based on new insights into exchange contributions.
References
- G. N. Lewis, The Atom and the Molecule, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- Y. Shi, Z. Xia, J. Zhang, R. B. Best, C. Wu, J. W. Ponder and P. Ren, Polarizable Atomic Multipole-Based Amoeba Force Field for Proteins, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik and H. M. Aktulga, et al., The ReaxFF Reactive Force-Field: Development, Applications and Future Directions, npj Computational Materials, 2016, 2, 15011 CrossRef CAS.
- S. Kale and J. Herzfeld, Natural Polarizability and Flexibility Via Explicit Valency: The Case of Water, J. Chem. Phys., 2012, 136, 084109 CrossRef PubMed.
- S. Kale, J. Herzfeld, S. Dai and M. Blank, Lewis-Inspired Representation of Dissociable Water in Clusters and Grotthuss Chains, J. Biol. Phys., 2012, 38, 49–60 CrossRef CAS PubMed.
- S. Ekesan and J. Herzfeld, Pointillist Rendering of Electron Charge and Spin Density Suffices to Replicate Trends in Atomic Properties, Proc. R. Soc. A, 2015, 471, 20150370 CrossRef.
- S. Ekesan, S. Kale and J. Herzfeld, Transferable Pseudoclassical Electrons for Aufbau of Atomic Ions, J. Comput. Chem., 2014, 35, 1159–1164 CrossRef CAS PubMed.
- S. Ekesan, D. Y. Lin and J. Herzfeld, Magnetism and Bond Order in Diatomic Molecules Described by Semi-Classical Electrons, J. Phys. Chem. B, 2016, 120, 6264–6269 CrossRef CAS PubMed.
- J. T. Su and W. A. Goddard, Excited Electron Dynamics Modeling of Warm Dense Matter, Phys. Rev. Lett., 2007, 99, 185003 CrossRef PubMed.
- J. T. Su and W. A. Goddard, The Dynamics of Highly Excited Electronic Systems: Applications of the Electron Force Field, J. Chem. Phys., 2009, 131, 244501 CrossRef PubMed.
- P. L. Theofanis, A. Jaramillo-Botero, W. A. Goddard III and H. Xiao, Nonadiabatic Study of Dynamic Electronic Effects During Brittle Fracture of Silicon, Phys. Rev. Lett., 2012, 108, 045501 CrossRef PubMed.
- H. Xiao, A. Jaramillo-Botero, P. L. Theofanis and W. A. Goddard III, Non-Adiabatic Dynamics Modeling Framework for Materials in Extreme Conditions, Mech. Mater., 2015, 90, 243–252 CrossRef.
- J. Herzfeld and S. Ekesan, Exchange Potentials for Semi-Classical Electrons, Phys. Chem. Chem. Phys., 2016, 18, 30748–30753 RSC.
- S. Kale and J. Herzfeld, Proton Defect Solvation and Dynamics in Aqueous Acid and Base, Angew. Chem., Int. Ed., 2012, 51, 11029–11032 CrossRef CAS PubMed.
- S. Y. Willow, X. C. Zeng, S. S. Xantheas, K. S. Kim and S. Hirata, Why Is MP2-Water “Cooler” and “Denser” Than DFT-Water?, J. Phys. Chem. Lett., 2016, 7, 680–684 CrossRef CAS PubMed.
- J. C. Carruthers, The Electrophoresis of Certain Hydrocarbons and Their Simple Derivatives as a Function of pH, Trans. Faraday Soc., 1938, 34, 300–307 RSC.
- P. Lenard, Über Die Electricitat Der Wasserfälle, Ann. Phys. Chem., 1892, 282, 584–586 CrossRef.
- P. Lenard, Über Wasserfallelektrizität Und ÜBer Die Oberflächenbeschafenheit Der Flüssigkeiten, Ann. Phys. Chem., 1915, 352, 463–524 CrossRef.
- G. Quincke, Über Die Fortführung Materieller Theilchen Durch Strömende Elektricität (on the Continuation of Material Particles by the Flow of Electricity), Ann. Phys., 1861, 189, 513–598 CrossRef.
- J. K. Beattie and A. M. Djerdjev, The Pristine Oil/Water Interface: Surfactant-Free Hydroxide-Charged Emulsions, Angew. Chem., Int. Ed., 2004, 43, 3568–3571 CrossRef CAS PubMed.
- A. J. Colussi and S. Enami, Comment on “Surface Acidity of Water Probed by Free Energy Calculation for Trimethylamine Protonation”, J. Phys. Chem. C, 2014, 118, 2894–2894 CAS.
- P. Creux, J. Lachaise, A. Graciaa, J. K. Beattie and A. M. Djerdjev, Strong Specific Hydroxide Ion Binding at the Pristine Oil/Water and Air/Water Interfaces, J. Phys. Chem. B, 2009, 113, 14146–14150 CrossRef CAS PubMed.
- A. Graciaa, P. Creux, C. Dicharry and J. Lachaise, Measurement of the Zeta Potential of Oil Drops with the Spinning Tube Zetameter, J. Dispersion Sci. Technol., 2002, 23, 301–307 CrossRef CAS.
- A. Graciaa, G. Morel, P. Saulner, J. Lachaise and R. S. Schechter, The Z-Potential of Gas Bubbles, J. Colloid Interface Sci., 1995, 172, 131–136 CrossRef CAS.
- H. Mishra, S. Enami, R. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard III and A. J. Colussi, Brønsted Basicity of the Air–Water Interface, PNAS, 2012, 109, 18679–18683 CrossRef CAS PubMed.
- C. Bai and J. Herzfeld, Surface Propensities of the Self-Ions of Water, ACS Cent. Sci., 2016, 2, 225–231 CrossRef CAS PubMed.
- S. S. Xantheas, Low-Lying Energy Isomers and Global Minima of Aqueous Nanoclusters: Structures and Spectroscopic Features of the Pentagonal Dodecahedron (H2O)20 and (H3O)+(H2O)20, Can. J. Chem. Eng., 2012, 90, 843–851 CrossRef CAS.
- P. L. Geissler, C. Dellago, D. Chandler, J. Hutter and M. Parrinello, Autoionization in Liquid Water, Science, 2001, 291, 2121–2124 CrossRef CAS PubMed.
- A. Hassanali, M. K. Prakash, H. Eshet and M. Parrinello, On the Recombination of Hydronium and Hydroxide Ions in Water, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20410–20415 CrossRef CAS PubMed.
- A. A. Volkov, V. G. Artemov and A. V. Pronin, A Radically New Suggestion About the Electrodynamics of Water: Can the pH Index and the Debye Relaxation Be of a Common Origin?, EPL, 2014, 106, 46004 CrossRef.
- A. A. Volkov, V. G. Artemov and A. V. Pronin, On the Origin of Dielectric Properties of Water, Dokl. Phys., 2014, 59, 111–114 CrossRef CAS.
- V. G. Artemov, A. A. Volkov, N. N. Sysoev and A. A. Volkov, Conductivity of Aqueous HCl, NaOH and NaCl Solutions: Is Water Just a Substrate?, EPL, 2015, 109, 26002 CrossRef.
- V. G. Artemov, A. A. Volkov and N. N. Sysoev, On Autoionization and pH of Liquid Water, Dokl. Phys., 2016, 61, 1–4 CrossRef CAS.
- C. Bai and J. Herzfeld, Special Pairs Are Decisive in the Autoionization and Re-Combination of Water, J. Phys. Chem. B, 2017 DOI:10.1021/acs.jpcb.7b02110.
- I. H. Williams, D. Spangler, D. A. Femec, G. M. Maggiora and R. L. Schowen, Theoretical Models for Solvation and Catalysis in Carbonyl Addition, J. Am. Chem. Soc., 1983, 105, 31–40 CrossRef CAS.
- S. Wolfe, C. K. Kim, K. Yang, N. Weinberg and Z. Shi, Hydration of the Carbonyl Group. A Theoretical Study of the Cooperative Mechanism, J. Am. Chem. Soc., 1995, 117, 4240–4260 CrossRef CAS.
- H. B. Bürgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Stereochemistry of Reaction Paths at Carbonyl Centres, Tetrahedron, 1974, 30, 1563–1572 CrossRef.
Footnote |
| † Present address: Laboratory of Theoretical Cellular Physics, Biochemistry and Biophysics Center, National Heart, Lung and Blood Institute, 50 South Drive, Bethesda, MD, 20814. |
| This journal is © The Royal Society of Chemistry 2017 |