Open Access Article
Open Access ArticleElectronic delocalization, charge transfer and hypochromism in the UV absorption spectrum of polyadenine unravelled by multiscale computations and quantitative wavefunction analysis†
Juan J.
Nogueira‡
 *,
Felix
Plasser‡
*,
Felix
Plasser‡
 * and
Leticia
González
* and
Leticia
González
 *
*
Institute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria. E-mail: nogueira.perez.juanjose@univie.ac.at; felix.plasser@univie.ac.at; leticia.gonzalez@univie.ac.at
First published on 13th June 2017
Abstract
The characterization of the electronically excited states of DNA strands populated upon solar UV light absorption is essential to unveil light-induced DNA damage and repair processes. We report a comprehensive analysis of the electronic properties of the UV spectrum of single-stranded polyadenine based on theoretical calculations that include excitations over eight nucleobases of the DNA strand and environmental effects by a multiscale quantum mechanics/molecular mechanics scheme, conformational sampling by molecular dynamics, and a meaningful interpretation of the electronic structure by quantitative wavefunction analysis. We show that electronic excitations are extended mainly over two nucleobases with additional important contributions of monomer-like excitations and excitons delocalized over three monomers. Half of the spectral intensity derives from locally excited and Frenkel exciton states, while states with partial charge-transfer character account for the other half and pure charge-transfer states represent only a minor contribution. The hypochromism observed when going from the isolated monomer to the strand occurs independently from delocalization and charge transfer and is instead explained by long-range environmental perturbations of the monomer states.
1 Introduction
Absorption of UV light by DNA initiates a series of photochemical events that can lead to lethal genetic modifications.1,2 Although it is challenging, the characterization of the electronically excited states involved in these photoinduced events is unavoidable to understand the mechanisms of DNA photodamage. In particular, the question of whether the UV absorption spectrum of DNA is dominated by monomer-like excitations or by collective excitations has intrigued researchers for over 50 years.3–9 The initial extent of the exciton over the DNA strand is of fundamental significance as it decides whether the early electronically excited-state dynamics of DNA is dominated by delocalized excitons undergoing intraband scattering and energy transfer,10 by dimer excitations paving the way for excimer formation11–13 and dimerization,14–17 or by monomer-like processes.18,19 Furthermore, delocalization of UV energy over several nucleobases has been invoked as a self-protection mechanism of DNA against radiation.20,21 The initial discussion of electronic delocalization in DNA strands was dominated by two seemingly contradictory observations:22 on the one hand, the strong hypochromism observed upon helix formation was interpreted in terms of delocalized states;8 on the other hand, the fact that no significant energy shifts were observed was seen as an indication of strictly localized states.5 To resolve this paradox, the extent of electronic delocalization along stacked nucleobases has been further investigated in the last decade with involved spectroscopic experiments3,6,20,23 and theoretical calculations.9,24–32 However, no consensus has been reached so far as quite different electronic degrees of delocalization ranging from localized states23 to delocalization over more than six bases27 have been reported.Another intriguing question intensively discussed in the literature is the role of charge-transfer (CT) states in the UV absorption spectrum. These states are relevant to DNA damage because their radical character may induce photochemical reactions after Franck–Condon excitation.17 Additionally, they play a crucial role in some DNA repair mechanisms.33 However, the energetic position of these states is under dispute. Some authors argue that CT states constitute the red tail28,32,34 of the spectrum, which is absent in the monomer, while other authors contend that all CT states are at least similar in energy or higher than the bright electronic states.31,35–38 Additional complications arise from the mixing between CT and local states. Such mixing is not only important from a methodological viewpoint, as it determines whether a Frenkel exciton model is appropriate to describe the absorption spectrum, but it can also give a first indication whether interconversion between local and CT states17 plays a role in the dynamical processes following UV absorption.
Discrepancies between different delocalization lengths and the position of CT states originate from the difficulty to study these phenomena experimentally and computationally. In the first case, the challenge is due to the fact that electronic delocalization3,6,20,23 and CT11 can only be deduced indirectly. The difficulty in the calculations comes from the extended system size, the importance of environmental interactions and structural disorder, as well as the fact that the resulting wavefunctions have to be analyzed in a meaningful and consistent way.22,39
This paper is the first calculation of the lowest-energy UV absorption band of adenosine monophosphate (AMP) and single stranded polyadenine (dA)20 including eight nucleobases at quantum mechanical level and taking into account conformational sampling and environmental effects. Through a skilled wavefunction analysis we also provide the most rigorous to date quantitative characterization of the electronic excitations classified in terms of delocalization length and CT character. Further, we clarify the origin of the hypochromism when going from the monomer to the polymer and unveil the nature of the excitations involved in the red tail of the polymer spectrum.
2 Theory
Our computational protocol is based on a multiscale approach that combines molecular dynamics simulations with extensive quantum mechanics/molecular mechanics (QM/MM) calculations and a comprehensive wavefunction analysis.Classical molecular dynamics simulations were performed by NVIDIA graphical processing units (GPUs) using the module pmem40 implemented in Amber14 (ref. 41) to sample the Franck–Condon region in the electronic ground state of solvated AMP and (dA)20, represented in Fig. 1a and b, respectively. Both systems were first minimized and heated at 300 K in the canonical ensemble. Then, a production run was evolved in the isothermal–isobaric ensemble during 5 and 50 ns for AMP and (dA)20, respectively. Both the monomeric and polymeric systems were described by a force field42,43 during the dynamics. An ensemble of 100 equidistant snapshots from the dynamics was selected for each system. For each snapshot of the ensemble, the electronic excitation energies of the lowest 60 singlet states of (dA)20 and the lowest 10 singlet states of AMP were computed using an electrostatic embedding QM/MM scheme. The QM region comprises eight nucleobases located in the middle of the (dA)20 strand and the single nucleobase of AMP. They are described by time-dependent density functional theory (TD-DFT) using the CAM-B3LYP functional and the Ahlrichs SV(P) basis set.44,45 The large size of the QM region is possible thanks to the use of the NVIDIA GPU-based Terachem code.46,47 The resulting 6000 (1000) excitation energies of (dA)20 (AMP) were convoluted with Gaussian functions to obtain the UV absorption spectra discussed in Section 3.1. More details can be found in Sections S1 and S2 of the ESI.†
An exhaustive and meaningful analysis of the excited-state wavefunctions of (dA)20 (AMP) obtained from the 6000 (1000) states was performed using the analysis toolbox described in ref. 31, 48 and 49. The electronic states with primary contributions on nucleobases located at the edge of the QM region were discarded to avoid artefacts due to the proximity of MM nucleobases (see Section S2 of the ESI†). For the analysis of the results, the CT numbers (cf.ref. 50) are computed as
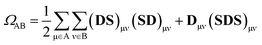 | (1) |
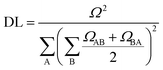 | (2) |
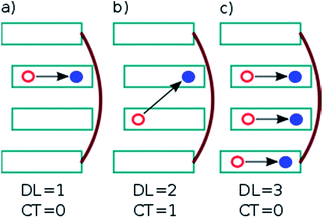
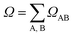 . In this case, since eight nucleobases were considered in the analyses, the delocalization length value ranges from one to eight. A value of one denotes a completely localized state (Fig. 2a), while higher values indicate collective behavior between the bases, either in the form of CT (Fig. 2b) or exciton delocalization (Fig. 2c). The delocalization length analysis will be discussed in Section 3.2.
. In this case, since eight nucleobases were considered in the analyses, the delocalization length value ranges from one to eight. A value of one denotes a completely localized state (Fig. 2a), while higher values indicate collective behavior between the bases, either in the form of CT (Fig. 2b) or exciton delocalization (Fig. 2c). The delocalization length analysis will be discussed in Section 3.2.
We have also calculated the CT contribution to the absorption band by analysing the excited-state wavefunctions of (dA)20. To quantify the contribution of CT states to each individual excited state, we use the formula
 | (3) |
3 Results and discussion
3.1 Absorption spectra of AMP and (dA)20
The calculated and experimental32 absorption spectra for both solvated AMP and (dA)20 are plotted in Fig. 3a and b, respectively. The experimental spectrum of (dA)20 (black line) peaks at 4.85 eV.32,51 For ease of comparison, the maximum of the calculated spectrum for (dA)20 obtained from the ensemble of 100 geometries has been red-shifted by 0.70 eV. This shift can be attributed to the basis set, as it is known52 that larger basis sets place the spectrum at lower energies. Unfortunately, the use of eight nucleobases in the QM region and the large number of snapshots precludes the use of more extended basis sets. However, a larger basis set does not change significantly the character of the excited-state wavefunctions (see Section S3 of the ESI†). | ||
| Fig. 3 (a) Calculated lowest-energy band of the UV absorption spectrum for AMP (red line) and (dA)20 (black line) considering 100 geometries (solid lines) or the optimized geometry (dashed lines). The spectra are red shifted by 0.70 eV to facilitate the comparison with experiments. (b) Experimental UV absorption spectra of AMP (red line) and (dA)20 (black line) taken from ref. 32. | ||
The experimental absorption spectrum of the polynucleotide (black line in Fig. 3b) presents three important differences with respect to the spectrum of the mononucleotide (red line). Upon formation of a stacked helix, the most dramatic effect is the hypochromism observed7,8 – the integrated absorption coefficient decreases by 35%. Furthermore, the spectrum is blue-shifted by 0.04 eV and a low-intensity red tail appears.51 The calculations based on the ensemble (solid lines in Fig. 3a) reproduce properly the hypochromism of the polymer (integrated intensity decreases by 36%) and the red tail of the polymer spectrum, which crosses with the AMP spectrum at 4.5 eV. The blue shift of 0.04 eV when going from AMP to (dA)20 is not described by the calculations; instead, a redshift of 0.03 eV is obtained –similar to the redshift of 0.05 eV obtained in previous TD-DFT calculations.9 Whereas this erroneous behavior has been attributed to the underestimation of excitation energies of CT states in TD-DFT,53 we want to point out here that such a small change in energy is well beyond the accuracy of TD-DFT (and any current quantum mechanical method for excited states) and any agreement is due to fortuitous coincidence. Overall, we conclude that our calculations provide a good description of the experimental absorption spectrum of AMP and (dA)20, which is a prerequisite for the forthcoming analysis.
For methodological reasons we found interesting to analyze the effect of conformational sampling on the absorption spectra. Thus, excited-state calculations were also performed on a single geometry, i.e. the optimized geometries of AMP and (dA)20 (dashed lines in Fig. 3a). The geometry optimization was performed classically using the same force field employed in the dynamics42,43 (more details in Section S3†), and the same redshift of 0.70 eV was applied. Conspicuously, the spectra of AMP and (dA)20 for the optimized geometries are narrowed against those from the ensembles due temperature effects (0 K for optimized geometries vs. 300 K for molecular dynamics ensembles). In addition, the maximum of the spectra for the optimized monomer and polymer are blue-shifted by 0.15 eV with respect to the ensemble spectra. Intra- and intermolecular motion thus decreases the energy of the absorption band providing a closer agreement with the experiment. Fair enough, the calculations on the optimized geometries reproduce well the appearance of the red tail when going from the monomer to the polymer. Moreover, the hypochromism is reasonably well described, with a 30% decrease of the integrated absorption coefficient vs. the 35% and 36% decrease obtained experimentally and with the ensemble calculations, respectively. However, as it will be seen below, conformational sampling is mandatory to properly describe other crucial electronic features of the UV absorption band.
3.2 Delocalization length
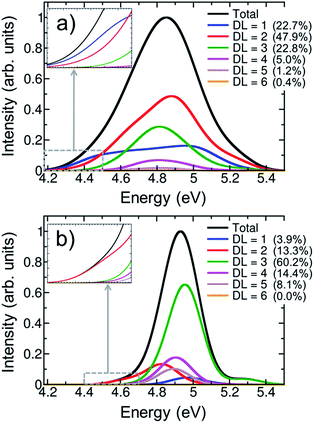
One of the most intensively debated questions related to the electronically excited states of DNA strands is the number of nucleobases, or delocalization length, involved in Franck-Condon excitations.3,9,20,24–32 Exciton theory calculations on double strands (dA)20(dT)20 and (dAdT)10(dAdT)10 concluded that electronically excited states are delocalized over the whole length of the helix when the model relies on an idealized B-DNA geometry,24 over four to eight nucleobases when conformational motion is considered by molecular dynamics,25 or over only one to two nucleobases when the exciton Hamilton matrix is refined.26 The results obtained by exciton theory are also quite dependent on the approximation employed to compute the electronic coupling between nucleobases; thus, depending whether the ideal dipole or the transition density cube approximation is used electronic delocalization lengths of 4.5 to 7.1 or 3.7 to 8.2 nucleobases have been obtained for the double strand (dA)12(dT)12.27 Quantum mechanical calculations have also been employed to investigate the size of exciton states.9,28,29,31 TD-DFT computations on an adenine trimer (A)3 with a geometry restrained to mimic an idealized B-DNA conformation showed delocalization over the three nucleobases.28 The same result was obtained when conformational motion was taken into account for a single strand (dA)4.9 However, a larger degree of delocalization of five to six nucleobases was reported when the single-stranded (dA)9 and (dA)11 oligomers were built by considering a B-DNA arrangement.9 The impact of conformational sampling was also discussed based on semiempirical calculations combined with a QM/MM approach, in which the double strand (A)6(T)6 was included in the QM region. Delocalization lengths of two to three and four to five nucleobases were computed for molecular dynamics structures and an idealized B-DNA geometry, respectively.29 Higher-level QM/MM calculations, using the second-order algebraic diagrammatic construction (ADC(2)) to compute electronic excitations of four stacked bases, (TA)2 and (CG)2, concluded that most electronically excited states are monomer-like excitations or are delocalized over two monomers.31 Experimental measurements also dissent about electronic delocalization. The general importance of excited-state collectivity was illustrated by transient fluorescence anisotropy experiments.6 Femtosecond time-resolved broadband spectra of a series of single-stranded (dA)n and double-stranded (dA)n(dT)n oligomers invoked delocalization lengths of three nucleobases for the single strand, while exciton extensions larger than four nucleobases were attributed to the double strand.3 Circular dichroism experiments on single strands (dA)n showed that only nearest neighbor interactions play a crucial role on the excitation for excitation wavelengths above 200 nm, and thus the exciton is extended over only two monomers.20 In contrast, the results of Kerr-gated time-resolved fluorescence and transient absorption experiments were interpreted in terms of local absorbing states.23In order to provide a clear-cut answer on the delocalization length, the first band of the UV absorption spectrum, calculated for the ensemble of 100 (dA)20 geometries has been decomposed according to eqn (2). The different delocalization length contributions are displayed in Fig. 4a. The delocalization length can acquire any real value from 1 to 8. In order to simplify the analysis, and directly relate delocalization with the number of nucleobases, the computed delocalization length of each electronic state was rounded to the closest integer value.
The analyses show that most of electronic transitions are delocalized over two nucleobases (47.9%). Delocalization length of three nucleobases (22.8%) and monomer-like excitations (22.7%) also contribute significantly to the absorption band. Excited states delocalized over four nucleobases are much less relevant, but not negligible (5.0%). In conclusion, virtually the whole UV lowest-energy band (98.4%) is composed by excitations involving at most four monomers. The average delocalization length is 2.2 nucleobases, which agrees well with the delocalization lengths of two and three nucleobases obtained from circular dichroism20 and femtosecond time-resolved broad band spectroscopies,3 respectively.
It is intriguing that the shape of the spectrum of monomer-like excitations in the polymer is very different from that in AMP: the pronounced maximum in the center of the band in AMP (solid red line in Fig. 3a) is flattened in the polymer (blue line in Fig. 4a). This flattening indicates that the formation of exciton states in the polymer occurs by combination of monomeric states that lie mostly in the center of the absorption band. The inspection of the density of states of AMP (Fig. S1†) corroborates that a larger number of energetically degenerated states, which are prone to form exciton states in the polymer, is found in the center of the band. As a consequence the monomer-like spectrum of the strand is depleted in this area.
In order to appreciate the impact of structural disorder on the absorbing states, the contributions of different delocalization lengths were also calculated for the optimized single-stranded geometry. As seen from Fig. 4b, the delocalization length is dramatically overestimated when sampling is omitted. Electronic excitations distributed over three nucleobases are the most significant ones (60.2%), and delocalization over five nucleobases still contributes notably (8.1%) to the absorption band. Moreover, monomer-like excitations are erroneously underestimated, with a contribution of only 3.9%. This overestimation of the delocalization length for the optimized (and unrealistic) structure is a consequence of the stronger stacking between neighboring nucleobases that favors electronic delocalization over the strand. Contrary, when thermal motion is considered, structural disorder is introduced, leading to localization of the excited states. The decrease of delocalization length induced by conformational sampling has been previously shown by exciton theory25 and quantum mechanical calculations9,29 performed on geometrical ensembles and idealized B-DNA structures. It has been pointed out that the relevant degrees of freedom responsible for this effect are intramolecular motions rather than large scale fluctuations.29
The hyperchromism observed in the low-energy region of the UV absorption band is a singular feature of DNA strands. As discussed above, both the calculations on the optimized geometry and the ensemble correctly reproduce this red tail. A closer inspection of the delocalization length decomposition around the low-energy tail of the ensemble spectrum (inset of Fig. 4a) reveals that the electronically excited states in this energy range are mainly monomer-like excitations, while the contribution of excitations delocalized over two or more nucleobases is significantly reduced when compared to the remaining spectrum. Specifically, the average delocalization length of the states located in the red tail is 1.4, i.e., it is smaller than the delocalization length of 2.2 computed for the whole spectrum. Thus, we are led to conclude that the energy lowering of these states is mainly caused by electrostatic interactions and polarization effects with the rest of the strand, while excited-state delocalization plays a minor role. This means that these electronic states can be seen as perturbed monomer-like excitations. Our analysis stands in contrast to previous theoretical studies that concluded that the low-energy states derive from exciton coupling.38,54 However, in these studies,38,54 the conclusion could be strongly influenced by the choice of a small QM region, which only included two adenine residues. Moreover, a statistically significant statement can only be made after performing sampling. It has also been argued that the electronic states that are involved in the red tail are CT excitations.28,34 Although a comprehensive CT analysis is discussed in the next section, we anticipate here that CT states are not relevant in the red tail since only one nucleobase is involved in most of excitations. The delocalization length analysis around the red tail performed on the optimized structure (inset of Fig. 4b) leads mistakenly to the conclusion that the red tail for the optimized strand is completely dominated by excitations involving two nucleobases, instead of one.
Finally, it is interesting to discuss our results in the context of time-resolved experimental measurements. A delocalization length of two nucleobases for the initial states serves as a natural precursor for excimer formation as has been invoked to explain the experimental transients of interacting adenine molecules.11 More specifically, the dominance of delocalization over two nucleobases observed here, agrees with the observation that the bleach recovery signals for ApA are basically identical to those of longer adenine strands.11 Our results also underline the importance of collective excited-state behavior. The degree of delocalization extracted from the calculations, together with a general high density of states, is certainly consistent with rapid energy transfer occurring during the initial dynamics, as was observed experimentally.6
3.3 Charge transfer states
A proper characterization of CT electronic states after Franck–Condon excitation is vital to understand DNA damage and repair.17,33 The formation of CT states between two nucleobases involves charge separation, generating cation and anion radicals. On the one hand, these radical species can initiate a series of reactions leading to DNA damage; for example, CT states between two pyrimidines may result in the formation of 6–4 adducts.17 On the other hand, nucleobases with radical character may play a role in DNA repair mechanisms. It has recently been shown that cyclobutane pyrimidine dimer lesions can be repaired when a CT state in a guanine-adenine stacked pair adjacent to the lesion is generated.33 The formation of cyclobutane pyrimidine dimers can be quenched by the formation of a CT state as a result of electron transfer from guanine to one of the reactive thymines.55,56 Furthermore, mixed local and CT states have been connected to long-lived high-energy fluorescence in DNA.57Despite the importance of CT states in the photophysics of DNA strands, the extent and energy range in which CT states contribute to Franck–Condon excitations has generated controversy in the literature. While several studies argued that low-energy CT states are present in the UV absorption band of DNA strands, including in the red tail,28,32,34 others have concluded that CT states are higher or at least similar in energy to the bright electronic states.31,35–38
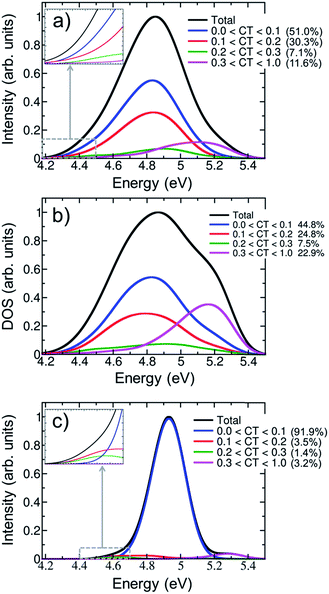
Fig. 5a shows the contribution of CT electronic states to the first absorption band calculated for the ensemble of (dA)20. In agreement with a previous study on alternating duplexes,31 we find that only about half of the spectral intensity (51%) derives from states with CT character below 0.1. These states can be justifiably termed pure Frenkel excitons or pure local excitations. The remaining half of the spectral intensity is carried by states with non-negligible CT admixture. The strong interactions between CT and Frenkel states can be explained58 in terms of orbital overlap between the different nucleobases. It has been indeed concluded from experiment that orbital overlap plays an important role in the excited-state dynamics.59 Furthermore, the strong mixing between Frenkel and CT states stands in agreement with the hypothesis of interconversion between these types of states during the dynamical processes following UV absorption17 and the formation of exciplexes with CT character.11,13,32,56,60,61
The CT decomposition of the density of states, in which the intensity of the electronic transitions is not considered so that every state contributes equally, is analysed and plotted in Fig. 5b. As can be seen, pure Frenkel excitons and pure local excitations represent almost half of the states (44.8%), as in the absorption spectrum, and the other half is composed of states with CT admixture. The most notable difference between the absorption spectrum and the density of states is the appearance of a shoulder in the blue side of the latter. This shoulder can be ascribed to a high density of states with significant CT character (CT > 0.3). These states are rather dark and, thus, do not contribute significantly to the initial photon absorption. Due to their high energy it is also not expected that they play an important role in the early dynamics. Additionally, it is interesting to analyse whether CT occurs only between nearest neighbour nucleobases or whether long-range CT takes place. This can be analysed by computing the net CT distance (CTnet),48 which is defined as the difference between the center of charge of the electron and the center of charge of the hole involved in the process. A value of CTnet lower than 1.5 indicates that CT takes place between adjacent nucleobases, while a value larger than 1.5 indicates long-range CT. According to this definition only 1.3% of the CT states in the first absorption band are long-range CT states and in all other cases nearest neighbour interactions dominate. This fact can be understood by considering that long-range CT imposes a severe energetic penalty through the Coulomb energy that is needed for separating the charges.
The effect of conformational sampling on the CT character of the absorption band is reflected in Fig. 5c, where only the optimized geometry is considered. As in the delocalization length analysis, the differences on the CT decomposition are extreme. Using a single geometry leads to incorrectly interpreting the excitation band as a combination of Frenkel and monomer-like excitations, since the majority of electronic states (91.9%) has insignificant CT contribution (lower than 0.1). Only a small amount (3.2%) of electronic states with important CT contribution (higher than 0.3) appears in the blue tail of the absorption band. Therefore, the lack of conformational sampling clearly underestimates the contribution of CT states. This indicates that anisotropy of the environment as well as intra- and intermolecular motion of the DNA strand change the amount of mixing between CT, Frenkel and local states.
The contribution of electronic states with different amount of CT character in the energy range of the red tail can be seen in the insets of Fig. 5a and c for the thermal ensemble and optimized geometry, respectively. In case of the ensemble (Fig. 5a), most of electronic states do not present an important CT contribution. This was already expected considering that the red tail is dominated by monomer-like excitations, as was discussed in Section 3.2. The absence of CT states in the red tail of the spectrum is in contradiction to results reported by previous theoretical studies; therefore, it is worth investigating these discrepancies in more detail. The initial claim28 of the presence of low-energy CT states derives from calculations using the PBE0 functional on an adenine trimer (A)3 restrained to the idealized B-DNA conformation. Later, QM/MM calculations on solvated adenine and thymine monomers and dimers using PBE0, long-range corrected density functionals and wavefunction-based methods on B-DNA structures showed36 that PBE0 is not capable of describing CT states properly due to the absence of long-range Hartree–Fock exchange. In a second study, CT states were found to be above the bright states, while they were transferred to the red tail only through the application of inhomogeneous broadening to the computed energies of optimized stacked adenine clusters of different sizes.32 Many-body Green function theory calculations performed for different solvated single-stranded adenine and thymine oligomers, and double-stranded adenine-thymine pair oligomers predicted low-energy CT states.34 It seems therefore that the employed computational model and method strongly affects the position of CT states, which can be then found in the red tail, close to the band maximum or in the high-energy region of the band. Clearly, a definitive conclusion cannot be drawn based on the available literature results as these previous calculations28,32,34 used small cluster models without including the effect of a DNA strand. This means that explicit water molecules34 or the continuum solvent model28,32 are in direct contact with the excited nucleobases, and thus solvation effects are likely overestimated. Additionally, conformational sampling was not performed, and the lack of vibrational motion strongly affects the computations, as was discussed above. All these issues have been considered in the present study and, thus, our conclusions rely on a more realistic theoretical model.
For completeness, the CT decomposition of the red tail of the spectrum for the optimized geometry is shown in the inset of Fig. 5c. Since the overall absorption band does not present significant CT character, so is found in the red tail. However, it is curious to note that electronic states with CT contribution smaller than 0.1 only appear in the high-energy part of the red tail. Thus, while the contribution of CT states to the entire absorption band is underestimated without conformational sampling, it is overestimated in the red tail, leading once more to an incorrect interpretation of the spectrum.
3.4 Hypochromism
The most remarkable fingerprint of the UV absorption spectra of DNA strands, when compared to the spectra of isolated nucleobases, is a pronounced hypochromism of the first UV absorption band7,8 (cf.Fig. 3b). It was early recognized that this hypochromism stands in contrast to a “zeroth-order” exciton model.7 Therefore, a number of different quite involved models for hypochromism were developed, including orientation-specific dipole interactions,8 dispersion–force interactions,7 local field effects,62 and mutual shielding of chromophores.63 More recently, CT admixture due to orbital overlap interactions was also invoked to explain hypochromism.57,64,65The basic starting point for the present discussion is the Frenkel exciton model.22,24,66 In its standard form,24 this model is based on two elementary steps. First, the zeroth-order functions are constructed as products of monomer wavefunctions. Second, linear combinations of the zeroth-order functions are formed to construct delocalized exciton wavefunctions. Step one is based on two important restrictions: (i) there is no orbital overlap between the monomer wavefunctions and (ii) the wavefunctions of the monomers are not perturbed by environmental interactions. Under these assumptions, it is assured that the squares of the transition dipole moments are conserved upon polymer formation.24 Unless there is a significant shift in energy, this means that also the total oscillator strength and, hence, the spectral intensity is unaffected. Thus, a Frenkel exciton model cannot explain uniform hypochromism but can only account for a redistribution of intensity between different parts of the spectrum. Hypochromism in one band could occur only if “one band steals intensity from the other”.7 Interestingly, evidence for such a second band with increased intensity has never been provided.
The occurrence of uniform hypochromism is thus in contradiction to the Frenkel exciton model described above. Orbital overlap interactions58 and consequent interactions between Frenkel and CT states have been considered as one possible reason for hypochromism.57,64,65 As we showed in Section 3.3, mixing between CT states and Frenkel excitons certainly plays an important role in UV absorption, accounting for about half of the total spectral intensity. However, it is not clear whether this mixing can be responsible for the pronounced hypochromism present in DNA. Therefore, here we also want to evaluate a different hypothesis that has not received much attention so far: the perturbation of monomer-like excitations by environmental effects. This endeavour is motivated by the well-known fact that the surrounding medium can have a strong impact on the excited-state properties of chromophores, including hypochromism.67
To summarize the above discussion, there are three different hypotheses to explain DNA hypochromism: (i) redistribution of the oscillator strength to higher energy bands, (ii) orbital overlap interactions, and (iii) perturbation of monomer-like excitations. We shall investigate first hypothesis (i). To that aim, we calculated the lowest six bands of the absorption spectrum of (dA)20 using only four nucleobases in the QM region of the optimized solvated (dA)20 geometry and 200 states. Unfortunately, the calculation of the six bands is unaffordable using the previous level of theory and setup. Although the employed model is not quantitative, it is sufficient to obtain a qualitative picture of the intensity of the absorption bands, see Fig. 6. For comparison, the lowest six absorption bands of solvated AMP calculated from the lowest 20 excited states were also computed for the optimized geometry. A general hypochromism along the entire spectrum when going from AMP to (dA)20 can be appreciated. Only the fifth band is more intense in the strand than in the monomer, but clearly the hyperchromism of this band does not compensate the hypochromism of the remaining bands. We conclude therefore, that the hypochromism of the lowest-energy UV absorption band is not a consequence of absorption intensity transfer between different absorption bands due to formation of exciton states.
 | ||
| Fig. 6 Calculated six lowest-energy bands of the absorption spectrum for AMP (red line) and (dA)20 (black line) at the optimized geometries. | ||
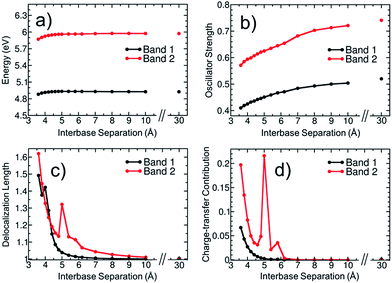
To elucidate then the factors leading to hypochromism, we construct a model that allows discriminating between hypothesis (ii) and (iii). For this purpose, additional calculations for the adenine dimer (A)2 in the gas phase were carried out. This simplified model, which was constructed following arguments made in ref. 68, retains the main physics behind electronic excitation while it allows for a clearer picture of the electronic properties. In order to partially retain the effect of conformational sampling, the dimer was built based on two structures randomly selected from the thermal ensemble of AMP (see more details in Section S4 of the ESI†). The variation of excitation energy, absorption intensity, delocalization length and CT contribution of the two lowest absorption bands with the interbase separation was calculated and plotted in Fig. 7. The separation between the two adenine monomers goes from 30 Å, where interactions between monomers are negligible, to 3.6 Å, which is the average interbase separation obtained from the classical molecular dynamics simulation.
The average excitation energy (Fig. 7a) of both absorption bands is virtually constant with the interbase distance, with only a small red shift of 0.05 and 0.1 eV for bands 1 and 2, respectively, when the separation between monomers is lower than 4.5 Å. The oscillator strength (Fig. 7b) shows a strikingly different behaviour. The intensity starts decreasing for both bands already at large distances and decreases significantly when the nucleobases approach each other. The oscillator strength of the lowest-energy band goes from 0.52 to 0.41, i.e., the absorption intensity decreases by 21.2%. As discussed in Section 3.1, the hypochromism of the absorption spectrum calculated for the thermal ensemble of (dA)20 is 36%. Thus, the employed dimer model already accounts for more than half of the hypochromism of the strand. Similar results were obtained in a previous theoretical study,38 which concluded that adenine dimer takes into account half of the hypochromism of the polymer. In a more general sense Fig. 7a and b reflect the effect of helix formation in the total absorption spectrum shown in Fig. 3a: whereas interbase interactions induce only small shifts on the energies, the oscillator strengths are affected dramatically. This indicates that the dimer model is a reasonable qualitative model to describe the hypochromism.
To investigate whether orbital overlap and/or collective excitation character is involved in the observed hypochromism of the two lowest absorption bands, the delocalization length and CT contribution (Fig. 7c and d) are analysed next. We start with the discussion of band 1. The important observation is that neither delocalization nor CT play any important role until the two bases approach each other quite closely. Taken, as an example, a separation of 5.0 Å, it is observed that all states of the first band are completely localized with a maximum delocalization length of 1.07 bases and a maximum CT of 0.003 a.u. Nonetheless, at this geometry already a hypochromism of 13.6% is observed. This shows that long-range interactions between the nucleobases are the main factor responsible for the hypochromism and that collective excitation character is not required. An analysis of band 2 is somewhat more involved due to the presence of CT states at this energy range. However, also in this case it is apparent that the onset of hypochromism largely happens without either delocalization or CT. Note that the spike in the values occurring at 5.0 Å derives from an accidental degeneracy between a local state and a CT state and has no further physical implication.
We therefore conclude that hypochromism can be explained by the perturbation of monomer-like excitations, induced by long-range interactions between nucleobases, and it does not require delocalization or participation of CT states. This observation opens a number of new questions regarding the properties of the perturbed wavefunctions, the nature of the relevant long-range interactions (electrostatic, induced dipoles, dispersion), and the cumulative effect when several surrounding nucleobases are considered. In addition, it would be of interest to investigate the cumulative effect of monomer-state perturbations and exciton or CT effects. The answer to these detailed mechanistic questions can be the subject of future investigations.
4 Conclusions
In summary, we have shown that conformational sampling by molecular dynamics simulations and a QM/MM scheme that takes into account environmental effects and includes eight nucleobases at quantum mechanical level is able to resolve a number of open questions regarding the electronic properties of the lowest-energy UV absorption band of single-stranded polyadenine. Specifically, electronic delocalization, charge transfer and hypochromism have been investigated and the following conclusions are obtained. (i) Exciton states delocalized over two nucleobases represent about half of the lowest UV absorption band, while the remaining intensity is almost equally distributed between monomer-like excitations and states delocalized over three monomers. The red tail present in the absorption spectrum of the strand, but absent in the monomer one, is formed by states with a reduced delocalization degree as opposed to the spectral maximum. It is dominated by monomer-like excitations, which are perturbed by interactions with the rest of the strand. (ii) The occurrence of CT states only happens in the blue side of the spectrum and represents a very small contribution to the intensity. Thus, direct population of CT states upon UV radiation is unlikely. However, we note that a significant fraction of the states do possess non-negligible CT admixture and only about 50% of the spectral intensity can be explained by pure Frenkel excitons and local excitations. (iii) Finally, the hypochromism of the lowest-energy absorption band observed when going from the monomer to the polymer is explained by perturbed monomer-like excitations induced by long-range interactions between the nucleobases.Our study also shows unequivocally that conformational sampling is crucial to describe the electronic properties of the absorption band. A model based on a single optimized geometry is able to qualitatively describe the hypochromism and the appearance of the red tail of the spectrum, but the lack of sampling strongly overestimates electronic delocalization and underestimates the contribution of CT states.
This theoretical work thus provides a clear-cut picture on three excited-state properties largely debated in the DNA community: electronic delocalization, charge transfer, and hypochromism. The conclusions drawn here for polyadenine have important consequences on the current notions of photoinduced DNA damage and repair. The dominance of delocalization over two adjacent bases highlights the importance of collective excitation character but also suggests that monomer-like processes play an important role in the early dynamics. Pure CT states do not play an important role in the initial absorption process. However, due to strong mixing between locally excited and CT states the formation of charged exciplexes and radicals in the ensuing dynamical processes can be expected. This study also sheds new light on hypochromism, the most prominent spectral signature of the absorption spectrum of the stack. As opposed to previous speculations, hypochromism does not require either collective excitation character or CT, but it occurs through the perturbation of monomeric states. Generalization of these conclusions needs further calculations on additional single and double DNA strands with different nucleobase sequences.
Acknowledgements
We thank Philipp Schilling for performing preliminary calculations. This material is based upon work supported by the VSC Research Center funded by the Austrian Federal Ministry of Science, Research and Economy (bmwfw). We also thank the University of Vienna.Notes and references
- A. Besaratinia, T. W. Synold, H. H. Chen, C. Chang, B. Xi, A. D. Riggs and G. P. Pfeifer, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10058–10063 CrossRef CAS PubMed
.
- R. P. Sinha and D. P. Häder, Photochem. Photobiol. Sci., 2002, 1, 225–236 CAS
.
- I. Buchvarov, Q. Wang, M. Raytchev, A. Trifonov and T. Fiebig, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4794–4797 CrossRef CAS PubMed
.
- C. E. Crespo-Hernández, B. Cohen and B. Kohler, Nature, 2005, 436, 1141–1144 CrossRef PubMed
.
- J. Eisinger and R. G. Shulman, Science, 1968, 161, 1311–1319 CAS
.
- D. Markovitsi, D. Onidas, T. Gustavsson, F. Talbot and E. Lazzarotto, J. Am. Chem. Soc., 2005, 127, 17130–17131 CrossRef CAS PubMed
.
- W. Rhodes, J. Am. Chem. Soc., 1961, 83, 3609–3617 CrossRef CAS
.
- I. Tinoco Jr, J. Am. Chem. Soc., 1960, 82, 4785–4790 CrossRef
.
- S. Tonzani and G. C. Schatz, J. Am. Chem. Soc., 2008, 130, 7607–7612 CrossRef PubMed
.
- D. Onidas, T. Gustavsson, E. Lazzarotto and D. Markovitsi, Phys. Chem. Chem. Phys., 2007, 9, 5143–5148 RSC
.
- T. Takaya, C. Su, K. De La Harpe, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10285–10290 CrossRef CAS PubMed
.
- G. Olaso-González, M. Merchán and L. Serrano-Andrés, J. Am. Chem. Soc., 2009, 131, 4368–4377 CrossRef PubMed
.
- F. Plasser and H. Lischka, Photochem. Photobiol. Sci., 2013, 12, 1440–1452 CAS
.
- W. J. Schreier, T. E. Schrader, F. O. Koller, P. Gilch, C. E. Crespo-Hernández, V. N. Swaminathan, T. Carell, W. Zinth and B. Kohler, Science, 2007, 315, 625–629 CrossRef CAS PubMed
.
- M. Boggio-Pasqua, G. Groenhof, L. V. Schäfer, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2007, 129, 10996–10997 CrossRef CAS PubMed
.
- C. Rauer, J. J. Nogueira, P. Marquetand and L. González, J. Am. Chem. Soc., 2016, 138, 15911–15916 CrossRef CAS PubMed
.
- D. Markovitsi, Photochem. Photobiol., 2016, 92, 45–51 CrossRef CAS PubMed
.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef CAS PubMed
.
- I. Conti, P. Altoè, M. Stenta, M. Garavelli and G. Orlandi, Phys. Chem. Chem. Phys., 2010, 12, 5016–5023 RSC
.
- U. Kadhane, A. I. S. Holm, S. V. Hoffmann and S. B. Nielsen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021901 CrossRef PubMed
.
- H. H. Ritze, P. Hobza and D. Nachtigallová, Phys. Chem. Chem. Phys., 2007, 9, 1672–1675 RSC
.
- F. Plasser, A. J. A. Aquino, H. Lischka and D. Nachtigallová, Top. Curr. Chem., 2015, 356, 1–38 CrossRef CAS PubMed
.
- W. M. Kwok, C. Ma and D. L. Phillips, J. Am. Chem. Soc., 2006, 128, 11894–11905 CrossRef CAS PubMed
.
- B. Bouvier, T. Gustavsson, D. Markovitsi and P. Millié, Chem. Phys., 2002, 275, 75–92 CrossRef CAS
.
- B. Bouvier, J. P. Dognon, R. Lavery, D. Markovitsi, P. Millié, D. Onidas and K. Zakrzewska, J. Phys. Chem. B, 2003, 107, 13512–13522 CrossRef CAS
.
- E. Emanuele, D. Markovitsi, P. Millié and K. Zakrzewska, ChemPhysChem, 2005, 6, 1387–1392 CrossRef CAS PubMed
.
- A. Czader and E. R. Bittner, J. Chem. Phys., 2008, 128, 035101 CrossRef PubMed
.
- F. Santoro, V. Barone and R. Improta, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9931–9936 CrossRef CAS PubMed
.
- A. A. Voityuk, Photochem. Photobiol. Sci., 2013, 12, 1303–1309 CAS
.
- Z. Benda and P. G. Szalay, Phys. Chem. Chem. Phys., 2016, 18, 23596–23606 RSC
.
- F. Plasser, A. J. A. Aquino, W. L. Hase and H. Lischka, J. Phys. Chem. A, 2012, 116, 11151–11160 CrossRef CAS PubMed
.
- A. Banyasz, T. Gustavsson, D. Onidas, P. Changenet-Barret, D. Markovitsi and R. Improta, Chem.–Eur. J., 2013, 19, 3762–3774 CrossRef CAS PubMed
.
- D. B. Bucher, C. L. Kufner, A. Schlueter, T. Carell and W. Zinth, J. Am. Chem. Soc., 2016, 138, 186–190 CrossRef CAS PubMed
.
- H. Yin, Y. Ma, J. Mu, C. Liu and M. Rohlfing, Phys. Rev. Lett., 2014, 112, 228301 CrossRef PubMed
.
- E. B. Starikov, G. Cuniberti and S. Tanaka, J. Phys. Chem. B, 2009, 113, 10428–10435 CrossRef CAS PubMed
.
- A. W. Lange and J. M. Herbert, J. Am. Chem. Soc., 2009, 131, 3913–3922 CrossRef CAS PubMed
.
- A. J. A. Aquino, D. Nachtigallova, P. Hobza, D. G. Truhlar, C. Hättig and H. Lischka, J. Comput. Chem., 2011, 32, 1217–1227 CrossRef CAS PubMed
.
- V. A. Spata and S. Matsika, J. Phys. Chem. A, 2014, 118, 12021–12030 CrossRef CAS PubMed
.
- P. Marquetand, J. J. Nogueira, S. Mai, F. Plasser and L. González, Molecules, 2017, 22, 49 CrossRef
.
- R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed
.
-
D. A. Case, J. T. Berryman, R. M. Betz, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke and A. W. Goetz, et al., AMBER 2015, University of California, San Francisco, 2015 Search PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed
.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef
.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS
.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed
.
-
TeraChem v. 1.9, PetaChem, LLC, 2015 Search PubMed
.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed
.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed
.
- A. V. Luzanov and O. A. Zhikol, Int. J. Quantum Chem., 2010, 110, 902–924 CAS
.
- A. Banyasz, I. Vayá, P. Changenet-Barret, T. Gustavsson, T. Douki and D. Markovitsi, J. Am. Chem. Soc., 2011, 133, 5163–5165 CrossRef CAS PubMed
.
- P. Caruso, M. Causà, P. Cimino, O. Crescenzi, M. D'Amore, R. Improta, M. Pavone and N. Rega, Theor. Chem. Acc., 2012, 131, 1–12 CrossRef CAS
.
- L. Hu, Y. Zhao, F. Wang, G. Chen, C. Ma, W. M. Kwok and D. L. Phillips, J. Phys. Chem. B, 2007, 111, 11812–11816 CrossRef CAS PubMed
.
- R. R. Ramazanov, D. A. Maksimov and A. I. Kononov, J. Am. Chem. Soc., 2015, 137, 11656–11665 CrossRef CAS PubMed
.
- W. Lee and S. Matsika, Phys. Chem. Chem. Phys., 2015, 17, 9927–9935 RSC
.
- V. A. Spata, W. Lee and S. Matsika, J. Phys. Chem. Lett., 2016, 7, 976–984 CrossRef CAS PubMed
.
- I. Vayá, J. Brazard, M. Huix-Rotllant, A. K. Thazhathveetil, F. D. Lewis, T. Gustavsson, I. Burghardt, R. Improta and D. Markovitsi, Chem.–Eur. J., 2016, 22, 4904–4914 CrossRef PubMed
.
- G. D. Scholes and K. P. Ghiggino, J. Phys. Chem., 1994, 98, 4580–4590 CrossRef CAS
.
- J. Chen and B. Kohler, J. Am. Chem. Soc., 2014, 136, 6362–6372 CrossRef CAS PubMed
.
- R. Improta and V. Barone, Angew. Chem., Int. Ed., 2011, 50, 12016–12019 CrossRef CAS PubMed
.
- F. Santoro, V. Barone and R. Improta, J. Am. Chem. Soc., 2009, 131, 15232–15245 CrossRef CAS PubMed
.
- A. D. McLachlan and M. A. Ball, Mol. Phys., 1964, 8, 581–595 CrossRef CAS
.
- N. L. Vekshin, J. Biol. Phys., 1999, 25, 339–354 CrossRef CAS PubMed
.
- D. Markovitsi, T. Gustavsson and F. Talbot, Photochem. Photobiol. Sci., 2007, 6, 717–724 CAS
.
- A. Banyasz, S. Karpati, E. Lazzarotto, D. Markovitsi and T. Douki, J. Phys. Chem. C, 2009, 113, 11747–11750 CAS
.
- J. Frenkel, Phys. Rev., 1931, 37, 1276–1294 CrossRef
.
- A. B. Myers and R. R. Birge, J. Chem. Phys., 1980, 73, 5314–5321 CrossRef CAS
.
- G. D. Scholes, J. Phys. Chem., 1996, 100, 18731–18739 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc01600j |
| ‡ Authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |