Open Access Article
Open Access ArticleFormation and decay of negative ion states up to 11 eV above the ionization energy of the nanofabrication precursor HFeCo3(CO)12†
Ragesh Kumar
T P
a,
Ragnar
Bjornsson
 a,
Sven
Barth
a,
Sven
Barth
 b and
Oddur
Ingólfsson
b and
Oddur
Ingólfsson
 *a
*a
aScience Institute, University of Iceland, Dunhagi 3, 107 Reykjavík, Iceland. E-mail: odduring@hi.is
bInstitute of Materials Chemistry, Vienna University of Technology, Getreidemarkt 9/BC/02, 1060 Vienna, Austria
First published on 23rd June 2017
Abstract
In single electron collisions with the heteronuclear metal carbonyl compound HFeCo3(CO)12 we observe the formation of long-lived negative ion states up to about 20 eV, 11 eV above its ionization energy. These transient negative ions (TNIs) relax through dissociation (dissociative electron attachment, DEA), losing up to all 12 CO ligands, demonstrating their resilience towards reemission of the captured electron – even at such very high energies. This is unique in DEA and we hypothesize that this phenomenon is rooted in the orbital structure enabling a scaffold of multi-particle, electronically excited resonances. We support this with calculated MO-diagrams revealing dense bands of energy levels near the HOMO–LUMO gap. HFeCo3(CO)12 is a promising focused electron beam induced deposition (FEBID) precursor and we argue that its unusual DEA behavior relates to its exceptional performance in FEBID. This may be general to a class of molecules with high potential for nano-fabrication by FEBID.
Introduction
The understanding of low energy electron interaction with molecules of different constellation is fundamental to a broad spectrum of processes. These include industrially relevant areas such as plasma physics1 and nanofabrication2–4 as well as natural phenomena in atmospheric and astro-chemistry5,6 and in radiation damage to biologically relevant molecules.7–9 The formation of transient negative ions (TNIs) through electron capture and their subsequent relaxation through fragmentation, i.e., dissociative electron attachment (DEA),10,11 is an important aspect of such low energy electron-induced chemistry. This is a resonant process, where electron capture can generally be understood as a vertical transition from the initial neutral molecular state to the resulting negative ion state. The TNI formed may constitute a single particle resonance or a two-particle, core-excited resonance, where the attachment process is concomitant with an electronic excitation within the molecule, i.e., a two-particle-one-hole resonance with two electrons occupying previously vacant orbitals and a single electron vacancy in a lower lying orbital. A relaxation of such a resonance to the neutral ground state through electron emission (autodetachment, AD) is a two-particle process and thus inefficient. Furthermore, when the electronically excited parent state of the neutral is energetically above the TNI state formed, AD leading to the electronically excited parent state cannot proceed without additional energy in the respective AD coordinate. Such resonances, referred to as Feshbach or closed-channel resonances, may thus have comparatively long lifetimes with regards to AD, favoring their relaxation through dissociation, i.e., DEA.Focused electron beam induced deposition (FEBID)12,13 is a direct-write nano-fabrication approach where high resolution metal structures may be achieved through a continuous supply of organometallic precursor molecules at a surface being exposed to a tightly focused high energy electron beam. Ideally such precursors fully decompose under the electron beam, leaving a pure metal deposit while the ligands are pumped away. However, incomplete decomposition and deposit broadening is the rule rather than the exception2,12 and it is generally recognized that the dominant decomposition processes are induced through the interaction of the precursor molecules with low energy secondary electrons produced through the interaction of the high energy beam with the solid substrate, rather than through interaction with the primary beam.3 Along with dissociative ionization (DI), neutral dissociation (ND) upon electron excitation and dipolar dissociation (DD),14,15 DEA is an important mechanism of such low energy secondary electron induced decomposition and can proceed with very high cross-sections.16–18
HFeCo3(CO)12, a heteronuclear carbonyl-cluster compound, is an emerging FEBID precursor, allowing high purity deposits (>80%) of a Fe/Co metal alloy with potential for controllable magnetic properties.19 It is thus a very promising candidate for the fabrication of well-defined functional nanostructures.
In this context, we have studied low energy electron interaction with this precursor, and we find that with regards to DEA it shows extraordinary behavior, for which we offer an explanation and we argue that this phenomenon should be general for a class of molecules with potential as high performing FEBID precursors.
Results and discussion
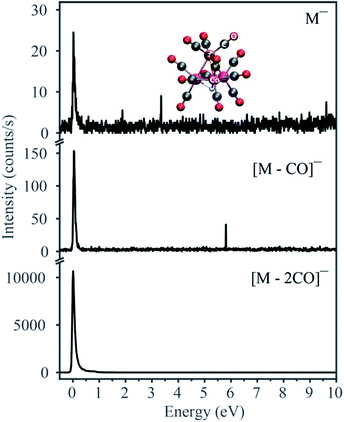
Fig. 1 displays the negative ion yield curves for the molecular anion and the loss of 1 and 2 CO ligands from HFeCo3(CO)12 at around 0 eV incident electron energy, while Fig. 2 combines the ion yield curves for sequential loss of 3–12 CO ligands upon electron attachment in the energy range from 0 to about 27 eV. In principle, negative ion fragments may also arise from DD, however, the threshold for the respective DD processes is shifted to higher energies by the ionization energy (IE) of the neutral counterpart in the DEA process. Hence, in the current case, DD should appear about 14 eV (IE of CO) above the respective DEA processes.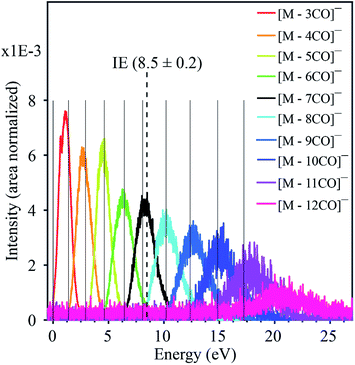 | ||
| Fig. 2 Combined negative ion yield curves for [M − nCO]− (n = 3–12) formed by DEA to HFeCo3(CO)12 in the energy range 0–27 eV. Solid vertical lines represent the appearance energies of negative ions, i.e. the onset of the respective channels. The dotted vertical line shows the molecular ionization energy (IE).21 | ||
As electron attachment is most efficient at very low incident energies, i.e. close to 0 eV,20 it is not surprising that the most efficient channel, the loss of 2 CO, is observed at this energy. In this context, it is important to keep in mind the detection window of the current instrument. Here the extraction time from the ionization region is around 10 μs and the flight time through the quadrupole mass filter about 50 μs. Negative ions that fragment during the flight through the mass filter will not maintain stable trajectories and will not be detected. Thus, we only observe ions that are formed within the first 10 μs after electron capture, but are stable against further fragmentation during their flight through the mass filter. This is reflected in the low yield of the molecular ion and [M − 1CO]− at 0 eV as compared to [M − 2CO]−. The adiabatic electron affinity of HFeCo3(CO)12 calculated at the PBE0 level of theory is 2.77 eV.21 This excess energy has to be efficiently distributed within the respective molecular anions for them to be detected in the current experiment. Further, the loss of 1 CO is exothermic by 3.13 eV and the loss of 2 CO by 1.74 eV. This is reflected in the dominating loss of the second CO, as the 3.13 eV available after the loss of one CO result in further dissociation. The 1.74 eV excess energy remaining after the second CO loss is probably lower or close to the threshold for further CO loss and may be distributed as internal and kinetic energy of the departing fragments, increasing the survival probability of [M − 2CO]− (this fragment has 69 vibrational degrees of freedom).
This reflection of the formation probability of the TNI and its decay probability in the ion yields is general to DEA experiments, and readily explainable. However, the further progression of CO loss from the initially formed TNI is extraordinary for four main reasons:
(i) it requires the formation of the TNI more than 11 eV above the ionization limit of the molecule (8.5 eV (ref. 21)),
(ii) the respective TNI must be sufficiently stable with respect to AD to survive the time it takes for dissociation of up to 12 CO units. This is especially intriguing as the energy dependency of the CO loss channels substantiates that this is sequential loss as is discussed here below,
(iii) each fragment shows a distinct energy dependence appearing through a “resonant-like” structure shifted by about 2 eV to higher energy for every CO lost, and
(iv) the attachment of a single electron can trigger the complete decomposition of the ligand structure through loss of all 12 CO.
The formation of negative ion resonances above the ionization limit of the respective molecule is not unheard of, but such resonances are usually only few eV above their IE, and may be explained by inner-shell excitations and high-lying Rydberg states.17 An exceptional case is the fullerene C60, where the intact TNI is observed up to 14 eV.22 This is ascribed to electronically excited Feshbach resonances associated with π to π* transitions and plasmon excitations. For the current molecule, however, the observed ion yields would require a series of two-particle-one-hole resonances extending from the lowest lying HOMO–LUMO transitions up to inner shell excitations extending up to about 20 eV. Furthermore, a close look at the apparent “resonant-like” structure of the ion yields for the individual fragments reveals that the maximum intensity of each fragment, [M − nCO]−, coincides with the onset of the next CO loss, [M − (n + 1)CO]−. This is typical for sequential loss, where [M − nCO]− is the precursor of [M − (n + 1)CO]−. This is further substantiated by the approximate 2 eV spacing between the respective contributions, reflecting the expected bond dissociation energy of the CO units.21 This picture, however, requires a quasi-continuous electron attachment extending from few eV up to about 20 eV. Moreover, the corresponding TNIs formed must be sufficiently stable with regards to AD to allow time for sequential loss of up to 12 CO units, and we emphasize that this is at about 11 eV above the ionization limit of this molecule.
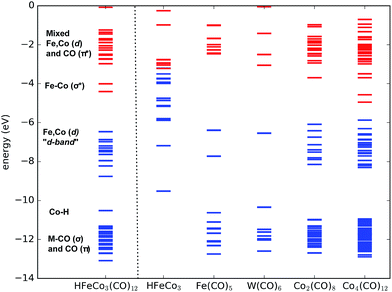
With this in mind we expect that there is a large density of fairly long-lived excited states involved in the initial formation of the TNIs. Direct ab initio calculations of the anionic excited states would be ideal to explore these. However, this is impractical, as a proper theoretical description to account for anion states, formed via multiple orbital excitations of the neutral molecule, requires a multiconfigurational wave function treatment, which is not currently feasible for such large molecules. Furthermore, calculations of metastable states require inclusion of coupling to the free electron continuum.23 Instead, we present molecular orbital diagrams from DFT calculations of the neutral HFeCo3(CO)12 at the BP86 level of theory. Though these do not reveal the actual anionic state densities, they do present the molecular orbital structure available to support TNI states in the relevant energy range. For comparison we have calculated MO energy diagrams for the HFeCo3 metal core along with those for the metal carbonyls Fe(CO)5, W(CO)6 and Co2(CO)8, and the hypothetical, linear carbonyl compound Co4(CO)12 (6 bridging COs). The linear form of Co4(CO)12 was calculated instead of the real cluster form in order to compare to a molecule of similar size as HFeCo3(CO)12 but without metal–metal bonding and featuring more bridging carbonyls. Fig. 3 shows the respective MO energy level diagrams. It is clear that HFeCo3(CO)12 shows dense “bands” of occupied/unoccupied molecular orbitals close to the HOMO–LUMO gap, while the MO structure of Fe(CO)5 and W(CO)6 is much more discrete in this region. Co2(CO)8, on the other hand, already shows increased density of occupied/unoccupied molecular orbitals close to the HOMO–LUMO gap and the MO diagram for the hypothetical, linear Co4(CO)12 is very similar to that of HFeCo3(CO)12. The metal core alone shows what can be interpreted as an emerging metallic structure with increased density of occupied valence orbitals in close proximity to an emerging “conduction band”.
In HFeCo3(CO)12 the highest occupied MOs are mostly metal-based σ-bonding d-orbitals and d-orbitals with some ligand mixing due to metal–carbonyl back-bonding. Below this band there is the bonding Co–H orbital, the metal–carbonyl σ orbitals and the π orbitals within the CO ligands. The unoccupied orbitals include the metal–metal σ* d-orbitals followed by a dense “band” of ligand CO π* orbitals. We note that the covalency in the compound results in considerable mixing of the metal d-orbitals and ligand CO π* orbitals, making orbital excitations between them likely to occur. Further, the poly-nuclear nature of this compound gives rise to a dense constellation of occupied metal d-orbitals, a “d-band” at the HOMO–LUMO gap. This is absent in the mono-nuclear carbonyls Fe(CO)5 and W(CO)6, but starts emerging in the di-nuclear Co2(CO)8 and is fully fledged in the hypothetical linear Co4(CO)12. We further note that HFeCo3(CO)12, Co4(CO)12 and Co2(CO)8 contain 3, 6 and 2 bridging carbonyls, favorably contributing to the mixing of the metal d-orbitals and ligand π* orbitals.
We note in this context that Co2(CO)8 has shown good performance in FEBID and Co deposits of purity higher than 90% have been achieved with this precursor24 (see also ref. 25 and references therein). Similarly, depositions of 75–80 at% in Fe have been achieved with Fe2(CO)9,26 a precursor with 3 bridging and 6 terminal carbonyls.
Turning back to Fig. 1 and 2, it is clear that the loss of 1 and 2 CO proceeds through a single particle 0 eV resonance. This is also the case for the low energy side of the [M − 3CO]− yield, apparent through the double structure of the ion yield curve (see ESI S1†). Below the transition energy between the “d-band” and the dense metal–ligand π* orbitals, single-particle shape resonances are likely to dominate (loss of 3 and 4 CO). At higher energies, i.e., above about 3–4 eV, core-excited resonances constituting transitions between the “d-band” and the dense metal–ligand π* orbitals are bound to play an increasing role. Moreover, these may include multiple electron excitations already at around 7 eV and such multi-particle-multi-hole resonances will dominate at higher energies. At an electron incident energy of about 20 eV, the excess energy is sufficient to induce the transition of 5–6 electrons.
Conclusions
In conclusion, we attribute the unusual DEA behavior of HFeCo3(CO)12 to the combination of the poly-nuclear structure of this organometallic compound and the high number and different nature of carbonyl ligands (bridging and terminal). The former gives rise to a high density of metal-based HOMOs, while the latter gives rise to a high density of unoccupied ligand CO π* orbitals close to the HOMO–LUMO gap. This and the substantial mixing of these orbitals allows for multiple electronic excitations in conjunction with the electron attachment process, giving rise to long-lived multi-particle-multi-hole resonances at high energies. In conjunction with sub-excitation single-particle resonances at low energies and two-particle-one-hole resonances at intermediate energies, this allows for a quasi-continuous electron attachment from about 1 eV up to about 20 eV – i.e., about 11 eV above the IE of this molecule. This in turn provides sufficient energy for sequential loss of all 12 CO ligands upon attachment of a single electron. Considering the exceptional performance of HFeCo3(CO)12 in FEBID,19 we argue that its molecular structure and the resulting MO constellation may offer guidance for the design of FEBID precursors allowing high purity metal deposition.Acknowledgements
This work was supported by the Icelandic Center of Research (RANNIS) Grant No. 13049305(1-3) and the University of Iceland Research Fund. RKTP acknowledges a doctoral grant from the University of Iceland Research Fund and financial support from the COST Action CM1301; CELINA, for short term scientific missions (STSMs). R. B. acknowledges support from the Icelandic Research Fund, Grant No. 141218051.References
- L. G. Christophoru, Electron-Molecule Interactions and their Applications, Academic Press, Orlando, Florida, 1984 Search PubMed.
- R. M. Thorman, R. K. T P, D. H. Fairbrother and O. Ingólfsson, Beilstein J. Nanotechnol., 2015, 6, 1904–1926 CrossRef CAS PubMed.
- N. Silvis-Cividjian, C. Hagen, L. Leunissen and P. Kruit, Microelectron. Eng., 2002, 61, 693–699 CrossRef.
- S. Bhattarai, A. R. Neureuther and P. P. Naulleau, Advances in Patterning Materials and Processes XXXIII, Proc. SPIE, 2016, 9779, 97790B–97791B CrossRef.
- Q.-B. Lu, Phys. Rep., 2010, 487, 141–167 CrossRef CAS.
- F. Carelli, M. Satta, T. Grassi and F. Gianturco, Astrophys. J., 2013, 774, 97 CrossRef.
- B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef.
- I. Baccarelli, I. Bald, F. A. Gianturco, E. Illenberger and J. Kopyra, Phys. Rep., 2011, 508, 1–44 CrossRef CAS.
- L. Sanche, Eur. Phys. J. D, 2005, 35, 367–390 CrossRef CAS.
- I. Bald, J. Langer, P. Tegeder and O. Ingólfsson, Int. J. Mater. Sci., 2008, 277, 4–25 CAS.
- O. Ingólfsson, F. Weik and E. Illenberger, Int. J. Mass Spectrom. Ion Processes, 1996, 155, 1–68 CrossRef.
- I. Utke, P. Hoffmann and J. Melngailis, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2008, 26, 1197–1276 CrossRef CAS.
- W. Van Dorp and C. Hagen, J. Appl. Phys., 2008, 104, 081301 CrossRef.
- E. Böhler, J. Warneke and P. Swiderek, Chem. Soc. Rev., 2013, 42, 9219–9231 RSC.
- C. R. Arumainayagam, H.-L. Lee, R. B. Nelson, D. R. Haines and R. P. Gunawardane, Surf. Sci. Rep., 2010, 65, 1–44 CrossRef CAS.
- S. Engmann, M. Stano, Š. Matejčík and O. Ingólfsson, Angew. Chem., Int. Ed., 2011, 50, 9475–9477 CrossRef CAS PubMed.
- O. May, D. Kubala and M. Allan, Phys. Chem. Chem. Phys., 2012, 14, 2979–2982 RSC.
- K. Wnorowski, M. Stano, C. Matias, S. Denifl, W. Barszczewska and Š. Matejčík, Rapid Commun. Mass Spectrom., 2012, 26, 2093–2098 CrossRef CAS PubMed.
- F. Porrati, M. Pohlit, J. Müller, S. Barth, F. Biegger, C. Gspan, H. Plank and M. Huth, Nanotechnology, 2015, 26, 475701 CrossRef CAS PubMed.
- E. P. Wigner, Phys. Rev., 1948, 73, 1002 CrossRef CAS.
- R. K. T P, S. Barth, R. Bjornsson and O. Ingólfsson, Eur. Phys. J. D, 2016, 70, 163 CrossRef.
- M. Lezius, P. Scheier and T. Märk, Chem. Phys. Lett., 1993, 203, 232–236 CrossRef CAS.
- I. I. Fabrikant, S. Eden, N. J. Mason and J. Fedor, in Advances In Atomic, Molecular, and Optical Physics, ed. C. C. L. Ennio Arimondo and F. Y. Susanne, Academic Press, 2017, vol. 66, pp. 545–657 Search PubMed.
- L. Serrano-Ramón, R. Córdoba, L. A. Rodríguez, C. s. Magén, E. Snoeck, C. Gatel, I. s. Serrano, M. R. Ibarra and J. M. De Teresa, ACS Nano, 2011, 5, 7781–7787 CrossRef PubMed.
- E. Begun, O. V. Dobrovolskiy, M. Kompaniiets, R. Sachser, C. Gspan, H. Plank and M. Huth, Nanotechnology, 2015, 26, 075301 CrossRef CAS PubMed.
- R. Córdoba, D.-S. Han and B. Koopmans, Microelectron. Eng., 2016, 153, 60–65 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and computational details. See DOI: 10.1039/c7sc01927k |
| This journal is © The Royal Society of Chemistry 2017 |