Open Access Article
Open Access ArticleDiscrimination of supramolecular chirality using a protein nanopore†
James A.
Cooper
,
Stefan
Borsley
,
Paul J.
Lusby
 and
Scott L.
Cockroft
and
Scott L.
Cockroft
 *
*
EaStCHEM School of Chemistry, University of Edinburgh, Joseph Black Building, David Brewster Road, Edinburgh EH9 3FJ, UK. E-mail: scott.cockroft@ed.ac.uk
First published on 11th May 2017
Abstract
Supramolecular chirality may emerge from self-assembly processes to yield architectures that differ only in the topological arrangement of their constituent parts. Since the properties of the resulting enantiomeric assemblies are identical, purification and characterisation can be challenging. Here, we have examined the hypothesis that the intrinsic chirality of a protein nanopore can be exploited to detect supramolecular chirality. Transient blockages in the ion current flowing through a single membrane-spanning α-haemolysin nanopore were shown to discriminate between M4L6 tetrahedral coordination cages of opposing chiralities. The single-molecule nature of the approach facilitated direct access to the rates of association and dissociation with the nanopore, which allowed the concentrations of the enantiomeric supramolecular assemblies to be determined in situ. Thus, we have established that a protein nanopore can be used to discriminate the chiral topologies of supramolecular assemblies, even when they are too large to fully enter the nanopore.
Introduction
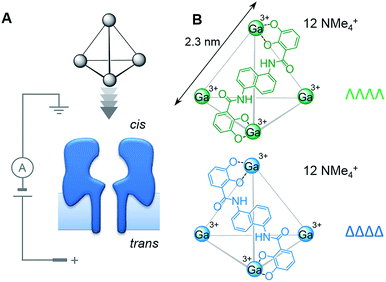
Chirality is ubiquitous in chemistry and biology. As such, the discrimination and separation of stereoisomers is vital. Diastereotopic relationships have long been exploited to discriminate between stereoisomers. For example, covalent derivatisation with chiral reagents can be used to distinguish between chiral centres that are identical in every other regard. Diastereotopic relationships can also be manifested in a non-covalent supramolecular context, as illustrated by stereoselective synthesis,1 chiral HPLC2 and the use of chiral shift agents in NMR spectroscopy.3,4 However, the control and characterisation of supramolecular chirality in self-assembled systems5,6 becomes more challenging as chemists seek to construct increasingly complicated assemblies.7,8 Indeed, the expression, recognition and control of supramolecular chirality is essential for life.9–12 Bringing together these biological and synthetic supramolecular aspects,13 we reasoned that intrinsically chiral transmembrane protein nanopores might be utilised as detectors of supramolecular chirality.Here we have examined the utility of an α-haemolysin (α-HL) protein nanopore to discriminate the supramolecular chirality of tetrahedral coordination cages (Fig. 1). Enantiopure cages, and mixtures thereof, were interrogated at the single-molecule level by monitoring changes in the transmembrane ion current passing through a single protein pore under an applied potential (Fig. 2). Differences between the magnitudes of the ion current blockages (Fig. 2 and 5), and the kinetics and thermodynamics of binding (Fig. 3) were evaluated for both chiral forms of the supramolecular cage and discussed in the context of the relative dimensions of the cage complex and the nanopore (Fig. 4).
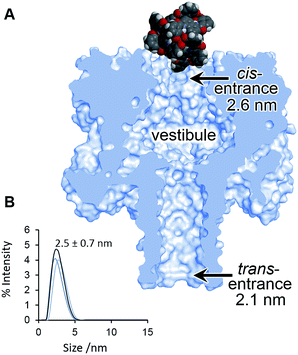 | ||
| Fig. 4 (A) Scaled model of a Ga(III) cage complex overlaid with the crystal structure of α-HL.44 (B) Dynamic light scattering measurement of a racemic sample of the Ga(III) cage complex in D2O 293 ± 2 K. | ||
Chirality is a key aspect in biological signal transduction14,15 that has inspired synthetic transmembrane messengers.16,17 Similarly, the chiral discrimination of molecules small enough to enter membrane-spanning nanopores has been previously demonstrated.18–27 To date, it is not yet known whether nanopore-based chiral sensors are amenable to the study of larger supramolecular assemblies, particularly those that are too large to enter the nanopore. Furthermore, the advantage of using atomically precise protein nanopores in the enantio-detection of small molecules has been counterbalanced by the need to employ genetically modified proteins.18–20
Results and discussion
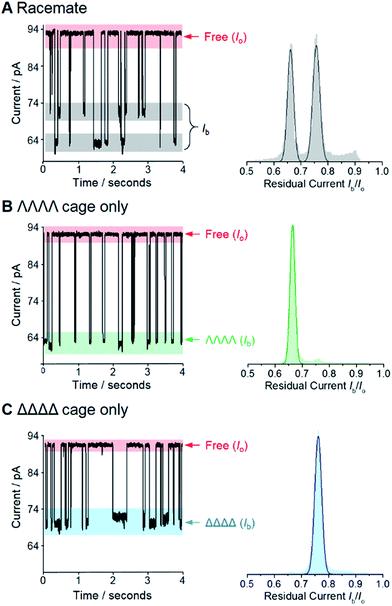
We selected the pairing of the transmembrane protein nanopore, wild-type α-haemolysin (α-HL), and a previously reported chiral Ga(III) cage for our investigation of supramolecular enantiodiscrimination (Fig. 1).28 These coordination cages possess supramolecular chirality due to the two possible propeller-like arrangements of the ligands around each metal centre (ΛΛΛΛ and ΔΔΔΔ, Fig. 1B). Like many other cages constructed from rigid bis(bidentate) ligands and octahedral metal ions, these complexes assemble exclusively as the homochiral racemate at the expense of the other possible diastereoisomers.29–36 It has previously been established that the selected Ga(III) tetrahedral cages are water soluble, and that conversion between the homochiral forms is negligible under basic conditions.37 The cages bear twelve negative charges meaning that they can be driven towards the nanopore under an applied electric field.38 Furthermore, the dimensions of the tetrahedral cage and the cis-opening of α-HL nanopore are similar (∼2.3 nm vs. ∼2.6 nm).At the start of our investigations we synthesised a racemic mixture of the tetrahedral cages28 for nanopore analysis. In the initial nanopore experiments, a planar lipid bilayer was painted across a 100 µm aperture separating two wells of buffered solution (1 M KCl, 30 mM Tris–DCl, pD 7.6 in D2O‡). A single α-HL nanopore was introduced into the bilayer,39 as indicated by the characteristic ionic current flowing through the nanopore at an applied transmembrane voltage of +100 mV (Io, Fig. 2, left). Upon the addition of ∼100 nM of a racemic mixture of the tetrahedral cage to the cis-side of the bilayer (Fig. 1A), temporal blockages of the ion current were observed at two discrete levels (Ib, grey bars in Fig. 2A). Data collated from multiple experiments that consisted of several thousand blockage events revealed two Gaussian distributions in the residual ion current (Ib/Io), consistent with two distinct classes of blockage event. The possibility that these two classes arose from multiple cages interacting with the pore simultaneously was ruled out, since the ratio of the two events was independent of the overall cage concentration (Fig. S15, ESI†). Thus, the two classes of blockage in the presence of a racemic mixture of the ΛΛΛΛ and ΔΔΔΔ tetrahedral cages was consistent with our initial hypothesis that a protein nanopore may be able to discriminate supramolecular chirality at the single-molecule level.
Encouraged by these preliminary findings, we set out to confirm the ability of the approach to discriminate the chirality of tetrahedral cages. Enantiopure samples of both the ΛΛΛΛ and ΔΔΔΔ cages were obtained using established procedures.37,40 Pleasingly, only one discrete blockage event class was observed for each enantiopure ΛΛΛΛ and ΔΔΔΔ cage sample (Fig. 2B and C). Moreover, the residual currents of these individual peaks were coincident with the two classes of event observed for the racemic mixture (Fig. 2B and C cf. A). Hence, we confirmed that α-HL is capable of discriminating the opposing supramolecular chirality of two otherwise chemically identical Ga(III) tetrahedral cages.
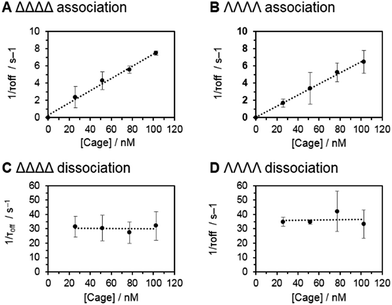
Having established that the discrimination of supramolecular chirality was possible based on the current blockage, we sought to examine the underlying kinetics and thermodynamics of the recognition process, which might be expected to significantly differ between enantiomers. Indeed, single-molecule methods allow the direct observation of association/dissociation kinetics.41 A series of nanopore analyses were performed in which the concentration of each chiral form of the tetrahedral cage was varied between 25 and 100 nM. Each nanopore analysis was performed at least three times at each concentration. Event durations and inter-event durations (τoff and τon respectively) were plotted as frequency-count histograms and fitted to single exponential decay functions (Fig. S20 and 21, ESI†). For both enantiomers, τoff was found to be independent of cage concentration, whereas τon was linearly dependent on concentration (Fig. 3). These concentration dependencies confirmed the bimolecular nature of the interaction between each tetrahedral cage and the nanopore.18,42 Thus, the rate constants of dissociation, koff = 1/τoff, and association, kon = 1/τon[cage], could be determined for each enantiomer (Table 1). Intuitively, the intrinsic diastereotopic nature of the α-HL·cage complex might be expected to result in markedly different binding characteristics. However, only marginally different kon, koff and Ka values were observed (Table 1). Thus, unambiguous assignment of cage chirality was only possible using ion current blockages that result from electrostatic and steric factors, which are difficult to predict.43
| ΔΔΔΔ cage | ΛΛΛΛ cage | |
|---|---|---|
| Residual current, Ib/Io | 0.76 ± 0.013 | 0.66 ± 0.011 |
| Rate of association, kon/M−1 s−1 | 7.5 ± 0.3 × 107 | 6.5 ± 0.1 × 107 |
| Rate of dissociation, koff/s−1 | 31 ± 3 | 35 ± 6 |
| Association constant, Ka/M−1 | 2.4 ± 0.3 × 106 | 1.8 ± 0.3 × 106 |
Although the geometry and dynamics of the α-HL·cage complex are not known, the relatively small magnitudes (Ib/Io) and durations (<200 ms) of the blockage events, combined with the marginal differences in the rates of association and dissociation (Table 1), indicate that the coordination cages interact transiently with the cis-opening of the nanopore without completely entering or translocating.45–47 The scaled diagram shown in Fig. 4A shows that the longest diameter of the cage (2.3 nm) is slightly narrower than the cis-opening of the pore (2.6 nm), but wider than the trans-opening (2.1 nm). However, the space filling model does not take into account the solvation shell surrounding both the protein and the highly-charged cage. Indeed, dynamic light scattering experiments gave a hydrodynamic diameter of 2.5 ± 0.7 nm for the cage in D2O (Fig. 4B). Thus, the size analysis and the characteristics of the blockage events indicate that entry of the cage into the wider vestibule of the pore is largely occluded. Nonetheless, deeper current blockages were occasionally observed that often lasted for tens of seconds under a continued applied potential. Such deeper events were distinct from non-specific gating events and showed a qualitative concentration dependence, suggesting that they may have arisen from inclusion of the cage within the vestibule of the pore (Fig. S10–13, ESI†). In contrast, no significant current blockages were observed when cages were added to the opposite side of the membrane that contained the even narrower trans-opening of the α-HL pore (Fig. 4 and S14, ESI†). Interestingly, the ability of ion current to discriminate the supramolecular chirality of a proportionally large cage species during transient interactions with the cis-entrance of the pore, rather than inclusion within the pore, raises the intriguing possibility that protein nanopores may provide a platform for the analysis of even larger constructs at the single-molecule level.
Significantly, the single-molecule nature of the approach enables facile in situ determination of enantiopurities. Since the kon of each enantiomer can be determined from a racemic mixture of enantiomers that populate discrete current levels, then the concentration of each enantiomer can be determined by simply counting events. Eqn (1) describes the general relationship between the event counts and the concentration of an individual enantiomer (see ESI† Section 4 for derivation).
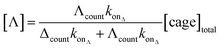 | (1) |
We demonstrated the validity of this approach by determining the absolute concentrations of known mixtures of enantio-enriched samples (Fig. 5, Table 2 and ESI† Section 4). Furthermore, the technique proved useful during our own investigation by revealing that a sample that was intended to be enantiopure was, in fact, contaminated with 22% of the other enantiomer (Table 2, “Unknown” column). It is important to emphasise that the nanopore-based approach can determine the enantiopurity of a sample without a 100% pure reference sample, as required by ensemble analytical methods. Thus, we have established nanopore analysis as a complementary approach to existing methods such as circular dichroism48,49 for the detection of supramolecular chirality.
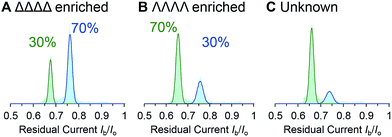 | ||
| Fig. 5 (A–C) Event distributions generated for enantio-enriched samples. Experiments were performed in 1 M KCl, 30 mM Tris–DCl, pD 7.6 in D2O at 293 ± 2 K with an applied potential of +100 mV. | ||
| a Determined by 1H NMR spectroscopy. | |||||
|---|---|---|---|---|---|
Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λactuala Λactuala |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 70 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 70 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
Unknown |
| [cage]totala/nM | 77 | 102 | 77 | 102 | 50 |
| Δcount | 1715 | 501 | 4763 | 3148 | 1723 |
| Λcount | 3753 | 1060 | 2411 | 1565 | 425 |
| [Δ]obs/nM | 22 ± 2 | 30 ± 3 | 47 ± 5 | 65 ± 7 | 39 ± 4 |
| [Λ]obs/nM | 55 ± 6 | 72 ± 7 | 28 ± 3 | 37 ± 4 | 11 ± 1 |
Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λobs Λobs |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 71 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36 36 |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
Conclusions
In conclusion, we have demonstrated the general principle that an intrinsically chiral protein nanopore can serve as a detection element to discriminate the chirality of otherwise identical supramolecular entities. More specifically, we showed the magnitude of the ion current blockages arising from the transient association of tetrahedral Ga(III) cages with an α-haemolysin nanopore provided unambiguous assignment of the individual enantiomers. The single-molecule nature of the approach presents a distinct advantage over traditional ensemble-averaged techniques that cannot easily determine whether a sample is enantiopure or enantio-enriched, thus side-stepping the challenges associated with enantiopurification.37,50–53 Direct access to kinetic parameters relating to the association/dissociation of individual cages with the nanopore allowed the concentrations of cage enantiomers to be determined from a single experiment on a timescale of minutes. Thus, such an approach may be amenable to the in situ analysis of dynamic supramolecular systems,18,54 such as those associated with chiral amplification phenomena.55–57 Significantly, the small magnitude of the observed current blockages was consistent with transient interactions with the pore opening rather than inclusion within the pore. As such, this preliminary study should encourage the future interrogation of even larger supramolecular architectures using nanopores.Acknowledgements
We thank the Edinburgh Protein Purification Facility for equipment access and ERC Starting Grant 336935, “Transmembrane molecular machines” for funding.Notes and references
- E. M. Carreira and L. Kvaerno, Classics in Stereoseletive Synthesis, Wiley-VCH, 2008 Search PubMed.
- Y. Okamoto and T. Ikai, Chem. Soc. Rev., 2008, 37, 2593–2608 RSC.
- K. Tanaka and N. Fukuda, Tetrahedron: Asymmetry, 2009, 20, 111–114 CrossRef CAS.
- L. Yang, T. Wenzel, R. T. Williamson, M. Christensen, W. Schafer and C. J. Welch, ACS Cent. Sci., 2016, 2, 332–340 CrossRef CAS PubMed.
- M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397 CrossRef CAS PubMed.
- M. A. Mateos-Timoneda, M. Crego-Calama and D. N. Reinhoudt, Chem. Soc. Rev., 2004, 33, 363–372 RSC.
- A. Sorrenti, R. Rodriguez-Trujillo, D. B. Amabilino and J. Puigmartí-Luis, J. Am. Chem. Soc., 2016, 138, 6920–6923 CrossRef CAS PubMed.
- Q.-F. Sun, J. Iwasa, D. Ogawa, Y. Ishido, S. Sato, T. Ozeki, Y. Sei, K. Yamaguchi and M. Fujita, Science, 2010, 328, 1144–1147 CrossRef CAS PubMed.
- R. Dickerson, H. Drew, B. Conner, R. Wing, A. Fratini and M. Kopka, Science, 1982, 216, 475–485 CAS.
- A. J. Wilson, Chem. Soc. Rev., 2009, 38, 3289–3300 RSC.
- D. G. Blackmond, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5732–5736 CrossRef CAS PubMed.
- P. L. Luisi, The Emergence of Life: From Chemical Origins to Synthetic Biology, Cambridge University Press, Cambridge, 2006 Search PubMed.
- J. Buratto, C. Colombo, M. Stupfel, S. J. Dawson, C. Dolain, B. Langlois d'Estaintot, L. Fischer, T. Granier, M. Laguerre, B. Gallois and I. Huc, Angew. Chem., Int. Ed., 2014, 53, 883–887 CrossRef CAS PubMed.
- M. Simon, M. Strathmann and N. Gautam, Science, 1991, 252, 802–808 CrossRef CAS PubMed.
- A. Miyazawa, Y. Fujiyoshi and N. Unwin, Nature, 2003, 423, 949–955 CrossRef CAS PubMed.
- M. De Poli, W. Zawodny, O. Quinonero, M. Lorch, S. J. Webb and J. Clayden, Science, 2016, 352, 575–580 CrossRef CAS PubMed.
- F. G. A. Lister, B. A. F. Le Bailly, S. J. Webb and J. Clayden, Nat. Chem., 2017, 9, 420–425 CrossRef CAS.
- X.-f. Kang, S. Cheley, X. Guan and H. Bayley, J. Am. Chem. Soc., 2006, 128, 10684–10685 CrossRef CAS PubMed.
- A. J. Boersma and H. Bayley, Angew. Chem., Int. Ed., 2012, 51, 9606–9609 CrossRef CAS PubMed.
- M. B. Steffensen, D. Rotem and H. Bayley, Nat. Chem., 2014, 6, 603–607 CrossRef CAS PubMed.
- S.-H. Shin, M. B. Steffensen, T. D. W. Claridge and H. Bayley, Angew. Chem., Int. Ed., 2007, 46, 7412–7416 CrossRef CAS PubMed.
- L. Chen, W. Si, L. Zhang, G. Tang, Z.-T. Li and J.-L. Hou, J. Am. Chem. Soc., 2013, 135, 2152–2155 CrossRef CAS PubMed.
- B. B. Lakshmi and C. R. Martin, Nature, 1997, 388, 758–760 CrossRef CAS PubMed.
- M. Ali, S. Nasir and W. Ensinger, Electrochim. Acta, 2016, 215, 231–237 CrossRef CAS.
- Z. Sun, F. Zhang, X. Zhang, D. Tian, L. Jiang and H. Li, Chem. Commun., 2015, 51, 4823–4826 RSC.
- C. Han, X. Hou, H. Zhang, W. Guo, H. Li and L. Jiang, J. Am. Chem. Soc., 2011, 133, 7644–7647 CrossRef CAS PubMed.
- C. Gao, S. Ding, Q. Tan and L.-Q. Gu, Anal. Chem., 2009, 81, 80–86 CrossRef CAS PubMed.
- D. L. Caulder, R. E. Powers, T. N. Parac and K. N. Raymond, Angew. Chem., Int. Ed., 1998, 37, 1840–1843 CrossRef CAS.
- L.-J. Chen, H.-B. Yang and M. Shionoya, Chem. Soc. Rev., 2017, 46, 2555–2576 RSC.
- N. Ousaka, S. Grunder, A. M. Castilla, A. C. Whalley, J. F. Stoddart and J. R. Nitschke, J. Am. Chem. Soc., 2012, 134, 15528–15537 CrossRef CAS PubMed.
- A. M. Castilla, W. J. Ramsay and J. R. Nitschke, Acc. Chem. Res., 2014, 47, 2063–2073 CrossRef CAS PubMed.
- P. J. Stang, B. Olenyuk, D. C. Muddiman and R. D. Smith, Organometallics, 1997, 16, 3094–3096 CrossRef CAS.
- S. P. Argent, T. Riis-Johannessen, J. C. Jeffery, L. P. Harding and M. D. Ward, Chem. Commun., 2005, 4647–4649 RSC.
- M. J. Burke, G. S. Nichol and P. J. Lusby, J. Am. Chem. Soc., 2016, 138, 9308–9315 CrossRef CAS PubMed.
- S. R. Seidel and P. J. Stang, Acc. Chem. Res., 2002, 35, 972–983 CrossRef CAS PubMed.
- T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001–7045 CrossRef CAS PubMed.
- A. V. Davis, D. Fiedler, M. Ziegler, A. Terpin and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 15354–15363 CrossRef CAS PubMed.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS.
- M. A. Holden and H. Bayley, J. Am. Chem. Soc., 2005, 127, 6502–6503 CrossRef CAS PubMed.
- A. J. Terpin, M. Ziegler, D. W. Johnson and K. N. Raymond, Angew. Chem., Int. Ed., 2001, 40, 157–160 CrossRef CAS PubMed.
- L. Ma and S. L. Cockroft, ChemBioChem, 2010, 11, 25–34 CrossRef CAS PubMed.
- O. Braha, J. Webb, L.-Q. Gu, K. Kim and H. Bayley, ChemPhysChem, 2005, 6, 889–892 CrossRef CAS PubMed.
- S. F. Buchsbaum, N. Mitchell, H. Martin, M. Wiggin, A. Marziali, P. V. Coveney, Z. Siwy and S. Howorka, Nano Lett., 2013, 13, 3890–3896 CrossRef CAS PubMed.
- L. Song, M. R. Hobaugh, C. Shustak, S. Cheley, H. Bayley and J. E. Gouaux, Science, 1996, 274, 1859–1865 CrossRef CAS PubMed.
- L.-Q. Gu, O. Braha, S. Conlan, S. Cheley and H. Bayley, Nature, 1999, 398, 686–690 CrossRef CAS PubMed.
- J. Sánchez-Quesada, A. Saghatelian, S. Cheley, H. Bayley and M. R. Ghadiri, Angew. Chem., Int. Ed., 2004, 43, 3063–3067 CrossRef PubMed.
- M. A. Watson and S. L. Cockroft, Chem. Commun., 2015, 51, 12243–12246 RSC.
- L. A. Joyce, M. S. Maynor, J. M. Dragna, G. M. da Cruz, V. M. Lynch, J. W. Canary and E. V. Anslyn, J. Am. Chem. Soc., 2011, 133, 13746–13752 CrossRef CAS PubMed.
- D. Leung and E. V. Anslyn, Org. Lett., 2011, 13, 2298–2301 CrossRef CAS PubMed.
- K. Wu, K. Li, Y.-J. Hou, M. Pan, L.-Y. Zhang, L. Chen and C.-Y. Su, Nat. Commun., 2016, 7, 10487 CrossRef CAS PubMed.
- S. Wan, L.-R. Lin, L. Zeng, Y. Lin and H. Zhang, Chem. Commun., 2014, 50, 15301–15304 RSC.
- C. Zhao, Q.-F. Sun, W. M. Hart-Cooper, A. G. DiPasquale, F. D. Toste, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2013, 135, 18802–18805 CrossRef CAS PubMed.
- J. L. Bolliger, A. M. Belenguer and J. R. Nitschke, Angew. Chem., Int. Ed., 2013, 52, 7958–7962 CrossRef CAS PubMed.
- N. Ousaka, J. K. Clegg and J. R. Nitschke, Angew. Chem., Int. Ed., 2012, 51, 1464–1468 CrossRef CAS PubMed.
- F. Helmich, C. C. Lee, A. P. H. J. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2010, 132, 16753–16755 CrossRef CAS PubMed.
- Y. Zhang, S. Li, M. Ma, M. Yang, Y. Wang, A. Hao and P. Xing, New J. Chem., 2016, 40, 5568–5576 RSC.
- A. R. A. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2007, 46, 8948–8968 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, characterisation, methods and supplementary data. See DOI: 10.1039/c7sc01940h |
| ‡ D2O was used to enable NMR characterisation at all stages of the experiments. |
| This journal is © The Royal Society of Chemistry 2017 |