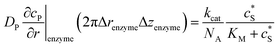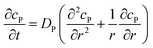Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding single enzyme activity via the nano-impact technique†
Chuhong
Lin
,
Enno
Kätelhön
,
Lior
Sepunaru
and
Richard G.
Compton
 *
*
Department of Chemistry, Physical and Theoretical Chemistry Laboratory, Oxford University, South Parks Road, Oxford OX1 3QZ, UK. E-mail: richard.compton@chem.ox.ac.uk; Fax: +44 (0)1865 275410; Tel: +44 (0)1865 275957
First published on 19th July 2017
Abstract
To evaluate the possible detection of single enzyme activity via electrochemical methods, a combined finite difference and random walk simulation is used to model individual enzyme-electrode collisions where such events are monitored amperometrically via the measurement of products formed by the enzyme in solution. It is found that the observed signal is highly sensitive to both the enzyme turnover number, the size of the electrode and the bandwidth of the electronics. Taking single catalase impacts as an example, simulation results are compared with experimental data. Our work shows the requirement for the detection of electrochemically active product formed by individual enzymes and gives guidance for the design of experiments.
1 Introduction
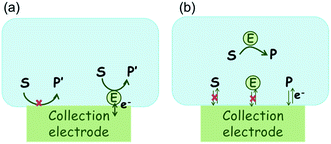
The nano-impact technique investigates stochastic current signals (“spikes”) that reflect the approach of individual nanoparticles to an electrode and has evolved to become a powerful tool in the analysis of the physical properties as well as the catalytic activity of individual nano-scale particles or macromolecules.1–6 In the latter case, a catalyst particle collides with the electrode or is located at or close to the electrode surface and a reaction involving electron transfer is detected, from which the catalytic ability of the particle can be inferred.7–11 In the study of enzyme catalysis, the nano-impact technique in principle might enable the observation of enzyme activity at the single-molecule scale while the target enzyme is investigated in its natural environment preserving its original activity and reactivity during the detection.12–16 In this respect, the electrochemical method potentially holds an advantage over the conventional spectroscopic methods17,18 for studying single enzyme activity, since no enzyme modification is needed. The latter methods, can resolve single catalytic turnover using a single photon counting apparatus. In the ‘nano-impacts’ method the current is the observable. Although electrochemical single electron counting is currently far from realization, information on the flux of charge at variable time scales (in the range μs–s) can be gained, limited by the noise level of the system and the time resolution.In the investigation of the activity of an enzyme via the nano-impact technique, the detection approach can be classified into two categories: as illustrated in Fig. 1, on the one hand the enzyme activity is measured via electron transfer when the enzyme collides with the electrode (Fig. 1a) and on the other it is detected via the electrochemical reaction of redox species generated by the enzyme's catalytic reaction in the solution (Fig. 1b). In the first case of an enzyme collision, the catalytic reaction is mediated probably via the active site of the enzyme, and the enzyme effectively works as a “nano-electrode” attached to the supporting substrate.14,19 The mechanism of the whole process then follows:
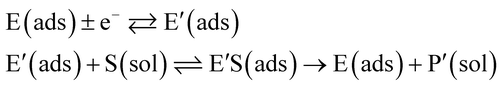 | (1) |
 | (2) |
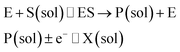 | (3) |
Although current signals corresponding to enzyme activities were observed via both methods,14,16 the second is probably more suitable for exploring the activity of authentic solution-phase enzyme catalysis as the enzyme does not interact with the electrode surface and any influence of the electrode potential on its active sites can be avoided. Moreover, the product P′ formed by the direct electron transfer to the active site can at least in principle be quite different to that of the solution-phase catalysis P. As the enzyme catalysis was reported to significantly rely on the dynamics of the enzyme and the surrounding reaction environment,21,22 it is important to understand the kinetics of the process as otherwise the analysis of corresponding stochastic signals recorded from the electrode remains obstructed and results concluded can at best be exclusively of a qualitative nature.
In this work, a two-dimensional simulation is developed to describe the solution-phase catalysis of the single enzyme. Stochastic current signals (“spikes”) of the detection of the activity of a single diffusing enzyme are simulated. Through comparison of different enzyme-electrode systems, the key factors influencing the measured signal are explored and it is determined under which experimental conditions such experiments may succeed.
2 Theory and simulation
The enzyme and electrode are simulated to understand the characteristics of the electrochemical detection of single enzyme activity. To this end and following a short general discussion of enzyme activity (2.1), enzyme catalysis is investigated for a stationary enzyme via the finite difference method (2.2), of which the results are then combined with a random walk model for the simulation of the enzyme movement in the solution (2.3) to simulate the electrode response (2.4).2.1 Theoretical model of the enzyme catalysis
The reactions involved in the detection of the solution-phase catalytic reaction of a single enzyme are expressed in eqn (3), where the catalytic activity is examined via the reduction or oxidation of the product at the electrode. To simplify the problem, the amount of the substrate S in solution is herein always assumed to be present in excess. The product P is generated from S and the reaction is assumed to follow the Michaelis–Menten kinetics as shown in eqn (5).20 The amount of product generated per single enzyme nP (mol) is determined by the turnover number kcat of the enzyme (s−1), the Michaelis–Menten constant KM (M), the concentration of the substrate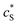 (M), and the reaction time t (s). It is noted that Michaelis–Menten kinetics relate to enzyme ensembles dispersed in the solution and expressed as:
(M), and the reaction time t (s). It is noted that Michaelis–Menten kinetics relate to enzyme ensembles dispersed in the solution and expressed as: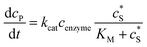 | (4) |
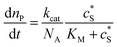 | (5) |
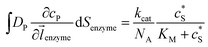 | (6) |
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) enzyme is the unit vector pointing from the enzyme surface,
enzyme is the unit vector pointing from the enzyme surface, 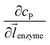 is the concentration gradient (M m−1) of P on and perpendicular to the enzyme surface, and Senzyme is the surface area of the enzyme (m2).
is the concentration gradient (M m−1) of P on and perpendicular to the enzyme surface, and Senzyme is the surface area of the enzyme (m2).
If the reaction environment contains enough supporting electrolyte and the detection time is relatively short, only diffusion needs to be considered when modelling the mass transport.24,25 Here we assume that a single enzyme generates enough product so that the distribution of product molecules can be properly described as a concentration rather than individual molecule positions. The diffusion of the product is then described via Fick's second law:26
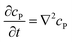 | (7) |
Assuming the over- or under-potential applied at the collection electrode is high enough to immediately consume all product species reaching the electrode surface, the concentration of P at the electrode surface is regarded to be effectively zero during the experiment. The current arising from the reduction or oxidation of P can then be calculated from the concentration gradient at the electrode surface:
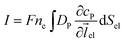 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 F mol−1), ne is the number of electrons transferred per product (in this work, ne is set to be 1),
485 F mol−1), ne is the number of electrons transferred per product (in this work, ne is set to be 1), ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) el is the unit vector pointing from the electrode surface, and Sel is the surface area of the electrode.
el is the unit vector pointing from the electrode surface, and Sel is the surface area of the electrode.
2.2 Simulation of the electrode response to a stationary enzyme
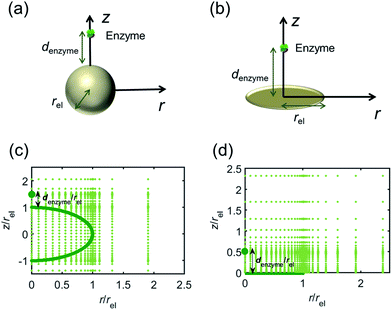
For simulating the catalysis of a stationary enzyme, the finite difference approach is applied. As the size of the enzyme is small compared to the size of the detecting electrode, the enzyme is treated as a point in the simulation space. To simplify the problem, the orientation of the enzyme is not taken into consideration and a micro-size spherical electrode is first selected as the detecting electrode. The simulation space can then be described in two-dimensional cylindrical coordinates (r, z). As shown in Fig. 2a, the z axis is located on the line linking the enzyme and the centre of the spherical electrode, and the r axis is set perpendicular to the z axis. In addition and to further simplify the enzyme-electrode system as explained below, in a second simulation the spherical electrode is replaced by a disc electrode in the same coordinate system, as illustrated in Fig. 2b.For the numerical simulation via the finite difference method, meshes of both the sphere- and the disc model are built, of which two examples are shown in the Fig. 2c and d and on which more details can be found in the ESI.† The conditions and equations used to describe the enzyme-electrode system are listed in Table 1.
To numerically simulate the enzyme catalysis based on the theoretical model described by eqn (6), the enzyme is treated as a point and the process can be described as:
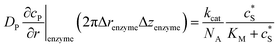 | (9) |
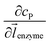 can be approximated to be
can be approximated to be 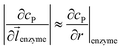 and only one direction is evaluated as shown in eqn (9).
and only one direction is evaluated as shown in eqn (9).
Through the finite difference method, the enzyme catalysis can be expressed as:
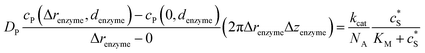 | (10) |
With the above definition the simulation is convergent as the choice of Δrenzyme and Δzenzyme does not influence the results (the corresponding convergence tests can be found in the ESI†).
In this work, we define three dimensionless properties to characterise the single-enzyme catalysis: the flux at the electrode J, the total amount of product generated by the enzyme NP, and the “collection efficiency” of the electrode σ:
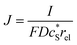 | (11) |
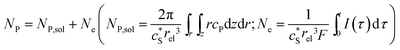 | (12) |
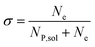 | (13) |
2.3 Simulation of the enzyme diffusion
In the above finite difference model, which focusses on the diffusion of the product, the enzyme is treated as a stationary point at a fixed distance denzyme from the electrode. However, due to its Brownian motion, the enzyme does not remain at a fixed position but randomly moves in solution. The enzyme is therefore treated as a random walker when modelling its movement in the electrolyte. When the it enters the region close to the electrode, the enzyme can be detected via its catalytic product, which partly diffuses towards to the electrode where it may be oxidised or reduced, and a corresponding current “spike” may be observed in the chronoamperogram.15,16 The diffusion of the enzyme is herein dependent on the distance between the enzyme and the electrode surface, which is due to the effect of near-wall hindered diffusion.27–30If we only consider the diffusion of the enzyme perpendicular to the electrode surface, the random walk of the enzyme can be simulated in one direction x, defined as the dimension perpendicular to the electrode surface. In the hindered diffusion theory, the distance-dependent diffusion coefficient of the enzyme can be expressed as:31
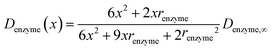 | (14) |
The diffusion of the enzyme follows Fick's second law:
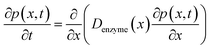 | (15) |
| p(x) = δ(x − x0) | (16) |
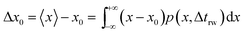 | (17) |
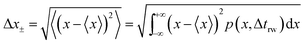 | (18) |
The direction of the movement after each random walk is herein set randomly and the total displacement hence:
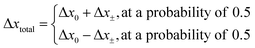 | (19) |
The location of the enzyme after the kth random walk step is then determined as:
| x0k = x0k−1 + Δxtotal | (20) |
However, although the random walk step length Δxtotal can be calculated via solving the mass transport equation eqn (15), the simulation is very time-consuming, especially when the level of accuracy required is high and the modelled time interval is long. Therefore, in order to optimise the simulation procedure, an approximation to the random walk is used.
If the diffusion is homogeneous, that is D(x) = Denzyme,∞, the probability distribution after each random walk step is a Gaussian function and the step length of each random step is  .Taking hindered diffusion into account, the Gaussian step length for the one-dimensional random walk however needs to be corrected. It is reported in the literature that the corrected Gaussian step length Δxtotal for the case of anisotropic diffusion can be expressed as:32,33
.Taking hindered diffusion into account, the Gaussian step length for the one-dimensional random walk however needs to be corrected. It is reported in the literature that the corrected Gaussian step length Δxtotal for the case of anisotropic diffusion can be expressed as:32,33
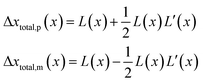 | (21) |
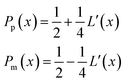 | (22) |
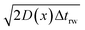 is the uncorrected step length and L′(x) = dL(x)/dx.
is the uncorrected step length and L′(x) = dL(x)/dx.
2.4 Simulation of the electrode response to a diffusing enzyme
For a time series of enzyme locations {denzymei} = {dmin, … dmax}, the corresponding catalytic currents {ienyzmei(denzymei, t)} can be calculated from the enzyme catalysis model introduced in Section 2.1, where the discretised ienzyme signify the average current between two sampling points. For each ienyzmei(denzymei, t), which is the current arising from an enzyme located at a fixed position and being active within the time interval [0, Δtrw], the catalytic reaction is modelled, while significantly longer time interval are considered as the electrode response to the product generated within this time interval is at least partly observed after t = Δtrw. On the basis of these {ienyzmei(denzymei, t), denzyme ∈ [dmin, dmax]}, the current contribution of each random walk step can be approximated via: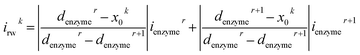 | (23) |
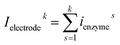 | (24) |
It is herein noted that the recorded spike shape is also determined by the measurement sampling frequency and the filter built into the potentiostat.34 The filter is of particular relevance as it may lower the height of the observed peak currents if the electrode signal exceeds the filter bandwidth. Measured currents hence represent a lower limit for the actual electrode currents if the measured spike shape is similar to the filter's impulse response, which for instance is the case in our previous work.16 To model a more realistic experimental condition, the current calculated from the random walk of the enzyme is therefore filtered via a first-order Butterworth filter.35
The finite difference problem is solved numerically by means of the Newton–Raphson method and the alternating direction implicit (ADI) method.36 The simulation is written in Matlab R2016a and run on an Intel(R) Xeon(R) 3.60G CPU. The validation of the simulation program is examined via the convergence tests which can be found in the ESI.†37
3 Results and discussion
This section studies the catalysis of a single enzyme near a micro-electrode and explores the possibility of its detection via the electrochemical reaction of the product molecules. We herein first investigate the electrode response to a stationary enzyme (3.1) before we model amperometric currents resulting from a freely-diffusing enzyme (3.2). The latter is accompanied by experimental data of catalase and signals originating from both experiments and simulations are compared (3.3). Finally, we provide a discussion of the implications of our findings on the design of experimental set-ups.3.1 Electrode response to a stationary enzyme
Fig. 2 illustrates the two microelectrode geometries that are considered in the simulation of the enzyme-electrode system. Numerical results reveal that, although absolute values of the currents collected from the two microelectrodes are not identical; their responses are similar as illustrated in the ESI.† The computationally more efficient enzyme-microdisc system can therefore be treated as an excellent approximation for the enzyme-microsphere electrode and, in the following, all simulation results are based on the enzyme-microdisc model, while similar conclusions can be drawn with regard to the enzyme-microsphere system.We characterise the enzyme-electrode system by the flux J (defined in eqn (11)), the total amount of product generated by the enzyme NP (eqn (12)), and the collection efficiency of the electrode σ (eqn (13)). To illustrate the catalysis-collection process, three dimensionless quantities affecting the current collected by the electrode are further introduced: the enzyme catalytic ability, Kcat, the relative distance between the enzyme and the centre of the electrode d, and the normalized reaction time T. The dimensionless parameter Kcat is defined as:
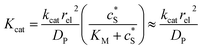 | (25) |
In this paper, where it is assumed that the enzyme is always exposed to an excess concentration of the substrate, 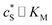 and thus
and thus 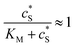 . The relative distance between the enzyme and the centre of the microdisc electrode is normalized with respect to the size of the electrode:
. The relative distance between the enzyme and the centre of the microdisc electrode is normalized with respect to the size of the electrode:
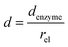 | (26) |
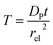 | (27) |
The advantage of using these “combined” parameters is that all variables, such as rel, 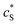 and DP, are grouped according to their influence on the enzyme-electrode system. It is then clearer to describe the characteristics of the whole process.
and DP, are grouped according to their influence on the enzyme-electrode system. It is then clearer to describe the characteristics of the whole process.
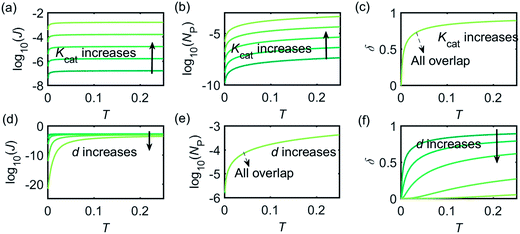
Fig. 3 illustrates how the enzyme-electrode system is affected by these factors. Fig. 3a–c show the flux J, the amount of product NP, and the collection efficiency σ varying as a function of T at different enzyme catalytic abilities Kcat. It can be seen that J and NP are determined by Kcat while σ is independent on the value of Kcat. In Fig. 3d–f, the influence of the relative enzyme location d is examined. J and σ are found to be affected by the value of d while NP remains constant when the enzyme changes its location. When the reaction time is long enough, the enzyme-electrode system is able to reach steady state, where the flux no longer increases with time. The total amount of the enzyme product NP at the steady state is determined only by the catalytic ability NP = f(Kcat), the collection efficiency is only related to the enzyme location σ = f(d), and the reaction flux is a function of both factors J = f(Kcat, d).
Fig. 4 shows a working curve of the normalized current at the steady state varying as a function of d and Kcat. For clarity, the steady-state current Iss, which is defined as the current value at T = 0.25, is normalized by Imax. Imax is the maximum current that can be collected by the electrode and is limited by enzyme catalysis, corresponding to the case where the enzyme locates exactly at the electrode surface and each product molecule generated is immediately consumed by the electrode. Thus Imax can be predicted by the turnover number of the enzyme:
| Imax = kcate0 | (28) |
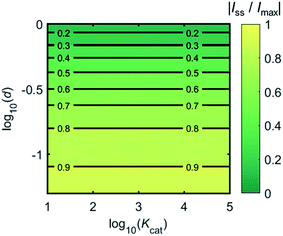 | ||
| Fig. 4 Normalized steady-state current (defined as the current at T = 0.25) as a function of d and Kcat for the enzyme-microdisc system. | ||
3.2 Electrode response to a freely-diffusing enzyme
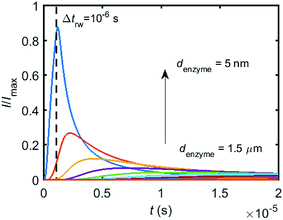
When the enzyme movement is additionally taken into consideration, the generated product does not fully reach the electrode before the enzyme moves on to its next position and both processes, the product diffusion and the enzyme movement, are modelled separately. The enzyme is herein treated as a random walker, while the step length Δtrw of the random walk is determined by convergence tests to ensure that Δtrw is small enough in comparison with the bandwidth of the simulated measurement electronics (1/fcutoff). Please note that below dimensional variables (i.e. rel, DP, denzyme) are depicted in the modelling of real nano-impact experiments, while the above Fig. 3 and 4 employ dimensionless parameters (i.e. J, Kcat, d) to better illustrate the kinetics of the stationary enzyme.To simulate the chronoamperogram for a diffusing enzyme, the electrode's current responses to stationary enzymes are collected for a series of enzyme locations as discussed in Section 2.4 and exemplarily shown Fig. 5 where the current responses to an enzyme at locations denzyme ranging from 0.05 to 1.5 μm are modelled. The enzyme herein features a size renzyme of 5 nm and a bulk diffusion coefficient Denzyme,∞ of 5 × 10−11 m2 s−1, while the microdisc radius is set to 0.5 μm and the diffusion coefficient of the product DP is set to 10−9 m2 s−1. To generalise the results, the collected current is normalized to the maximum catalytic current Imax. For each current response in Fig. 5, the catalytic reaction only occurs within the time period 0 < t ≤ Δtrw in which the enzyme is stationary. The current at t > Δtrw is caused by the fraction of the product which is not fully consumed during the time 0 < t ≤ Δtrw. It can be found in Fig. 5 that the closer the enzyme is located to the electrode, the larger is the catalytic current and the sharper is the drop of the current amplitude after Δtrw is reached. For all further simulations the stationary current response was modelled in a time interval tmax of 10−4 s via the finite difference simulation, while the response in the range tmax < t < 2tmax is interpolated linearly to ienzyme (2tmax) = 0. The convergence tests of tmax can be found in the ESI.†
Based on the normalized current–time responses shown in Fig. 5, the chronoamperogram of the diffusing enzyme is simulated in Fig. 6 and the corresponding pathway of its movement is presented. Two current “spikes” can be observed, while each spike indicates an approach of the enzyme towards the electrode and the spike shape infers the details of each approach. When the enzyme immediately leaves the electrode after an approach, a sharp spike is measured in the chronoamperogram such as that at around 1.1 s in Fig. 6. On the other hand, if the enzyme moves forward and backward several times near the electrode, a long spike with noisy current fluctuations will be recorded, such as the one at 0–0.1 s.
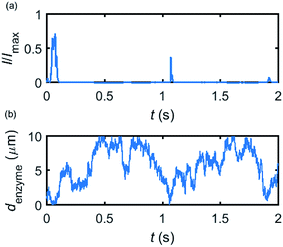 | ||
| Fig. 6 Example of a simulated random walk current (a) and the corresponding pathway in the solution (b). The space, in which the enzyme moves freely, ranges from 5 nm to 10 μm. Other simulation parameters are the same as applied in Fig. 5. | ||
Fig. 6 proves that the solution-phase enzyme catalysis can in principle be observed experimentally. It is also shown that each approach of the enzyme can be distinguished as the current is very sensitive to changes in the distance between the enzyme and the electrode, which enables a further analysis of the spike data and the extraction of information on both the enzyme catalysis and the enzyme diffusion. This two dimensional result differs significantly from the one-dimension case discussed in the previous work:15 in the two-dimensional case, convergent diffusion leads to a collection efficiency that depends sharply on the distance between the enzyme and the electrode. When the enzyme diffuses towards or away from the microelectrode, sharp current on- and offsets can be observed in the chronoamperometry that are due to the dependency of the collection efficiency on the enzyme location as shown in Fig. 3 and 4. This sensitivity of the microelectrode in principle enables the detection of single enzyme activity via its product in the nano-impact technique, which is obscured in the case of a macroelectrode. The semi-infinite diffusion field at the macroelectrode resulting from linear diffusion and coupled to the marked mismatch of the diffusion coefficients of the enzyme and its product means that the 'collection' of the product is much less sensitive to the motion of the enzyme.
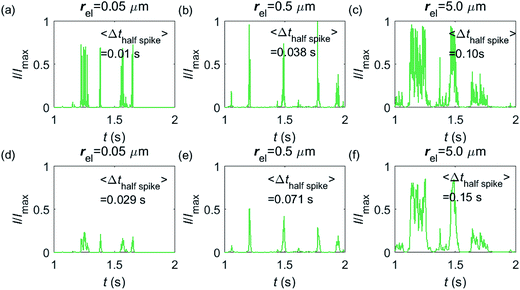
Having shown that spikes can only be observed at micro-sized electrodes, the influence of the electrode size needs to be taken into consideration. Fig. 7 shows the current responses to a freely-diffusing enzyme at microdisc electrodes of various radii. Fig. 7a–c are the chronoamperograms (normalized to the maximum possible current, Imax) at electrodes featuring radii of 0.05, 0.5 and 5.0 μm and the cut-off frequency of the measurement filter is set to 4 kHz; (d–f) are the same simulations as shown in (a–c) but with a different cut-off frequency of 50 Hz. The spike durations in each chronoamperogram are analysed and indicated in the corresponding figure. The spikes are recognized via a threshold value that is set to distinguish a spike from the background. In the analysis in Fig. 7, the threshold value for spike duration is selected to be 0.5% of the maximum spike current. In addition, considering the noise level in the real experiment, spikes featuring a small current height are unrecognizable and are here removed if the peak current is less than 10% of the maximum spike current. To avoid any influence from the background noise, the spike duration is characterised by the width at half of the spike height Δthalf-spike.
From Fig. 7a–c, it is found that the spike features a height close to the maximum possible current Imax at the electrodes with 0.05, 0.5 and 5.0 μm radii. The current signal at the 0.05 μm is slightly smaller than the other two due to the finite closest approach of the enzyme applied in the simulation. The closest approach dmin is defined as the radius of the enzyme (5 nm) for all the three electrode systems but the magnitude of the current spike is determined by the relative closest approach dmin/rel as explained in Fig. 3 and 4. Therefore, the spikes recorded at the 0.05 μm electrode (dmin/rel = 0.1) are slightly lower than that at the 5.0 μm one (dmin/rel = 0.001). More discussion on the selection of the simulation space can be found in the ESI.† It is also found in (a–c) that the spike length varies significantly with the electrode size. The average half-spike widths of 0.05, 0.5 and 5.0 μm electrodes are 0.01, 0.038 and 0.10 s under the 4 kHz cut-off frequency. Sharper spikes are observed at the 0.05 μm electrode than the 5.0 μm electrode, reflected by a 5 fold decreases in the spike duration. This is because the current is more sensitive to the variation of the enzyme location at the smaller electrode. The spikes last for longer at larger electrodes, showing the transition from the two-dimensional to the one-dimensional system as discussed above.
In Fig. 7d–f, with a 50 Hz cut-off frequency, a similar dependency of the current signal on the electrode size is still observed as shown in (a–c). The spikes recorded at larger electrodes have longer duration time. However, the spike height in (d–f) is smaller than Imax, especially at the smallest 0.05 μm electrode. This is because that a low cut-off frequency is employed and the current response recorded from the electrode is largely distorted. Comparison of the chronoamperograms in (a–c) and (d–f) reveals that the spike currents in (a–c) are larger than those in (d–f) and the spikes are sharper, as a low-pass filter with higher cut-off frequency retains more information of the original current recorded.
3.3 On the possible electrochemical detection of single catalase enzymes
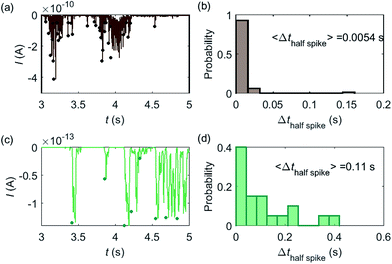
Based on the model developed in this work, the electrochemical detection of single catalase enzymes is simulated. To this end, the experimental parameters of the catalase-microdisc system are modelled: DP(O2) = 10−9 m2 s−1,38rel = 5 μm,15Denzyme(catalase) = 5 × 10−11 m2 s−1,39kcat(catalase) = 106 s−1,40renzyme(catalase) = 5 nm,41fcutoff = 4 kHz.15 In reported work of this group, single catalase impact experiments were conducted in a 9 pM catalase solution with chronoamperograms recorded at a 5 μm radius microdisc electrode.15 The reason for choosing catalase is mainly due to its high turnover number40 which is at the upper limit of known enzymatic catalytic rates. In addition, the oxygen product is easy to detect electrically.Some typical current spikes collected from the experiment are shown in Fig. 8a and the analysis of the spikes is presented in Fig. 8b. The control experiment (see Fig. S8 in the ESI†) relating to Fig. 8a in the absence of catalase does not show any spikes in the chronoamperometric measurements, indicating that the spikes relate to the catalase catalysis. From the experimental results, the magnitude of the spike height is approximately 10−10 A and the average half-spike width is 0.0054 s. For direct comparison, a simulation of the same catalase-microdisc system is shown in Fig. 8c and d. The simulated spikes feature a height of ca. 10−13 A and an average half-spike width of 0.11 s. To compare the experimental and the simulated current responses, we consider both the duration and shape of the spike. First, the simulated half-spike width Δthalf-spike is significantly longer than that of the experiment. According to the simulation in Fig. 7, only broad spikes are anticipated to be observed at the relatively large 5 μm electrode, which contradicts experiment. Secondly, as the magnitude of the spike height is mainly determined by the turnover number and the reported turnover number (106 s−1) measured from an ensemble of catalases40 leads to spike heights of the order of 10−13 A, the simulated spikes are much too small to be distinguished from the background noise in any real experiment using broad bandwidth. That said, in contrast to the kinetics averaged over an ensemble as reflected in the classical Michaelis–Menten kinetics, single enzyme activity is thought to be dynamically fluctuating and the turnover number for individual enzymes can deviate from the average value.22,42 Hypothetically, if the turnover number of a single catalase is temporarily near 109 s−1 at the moment of detection, a current spike of 10−10 A can be observed, which is experimentally feasible to measure. However, the activity of single catalase is yet to be reported by optical or other experimental means and the fact that the enzyme contains four catalytic heme centres probably slightly averages any dynamic disorder of the enzyme catalytic rate. Comparison of the experimentally measured current (Fig. 8a) and the theoretical calculated current spikes (Fig. 8c) reveals a three orders of magnitude difference in the current magnitude. This discrepancy might be explained by experimental artefacts such the formation of electrochemically active oxygen bubbles.15 Alternatively, the experimental spikes may reflect enzymatic activity operating ‘transiently’ at catalytic rates that are three orders of magnitude higher than the ensemble averaged rate and consequently with substantially lower observed “impact” frequency. However, this process can be further complicated by contribution from surface adsorbed enzymes and is out of the scope of this theoretical investigation. In either case, full information on the enzyme turn-over rate cannot be gained.
3.4 Implications for the design of experiments
The possibility of experimentally detecting the activity of an individual enzyme in solution is mainly determined by the maximum current and the duration time of the signal. If under experimental conditions a 10 pA current spike is the minimum current that can still be observed at a microelectrode, according to eqn (28), the turnover number needs to be of the order of magnitude of 108 s−1 in the case of one electron being transferred per consumed substrate molecules, which means the detection of the activity for an individual enzyme is feasible for enzymes exhibiting a fast turnover number or an agglomerate or aggregate of enzymes.16 In addition, the spike duration determines whether a signal can be distinguished from the background noise. Only sharp spike onsets can be identified, while slow spike on- and off-sets will be indistinguishable from (the typically slow) changes in the background current. Although the electrical signal attributed to the enzyme activity can be observed at both micro- and macro-electrodes, the spikes can be only identified at nano- and micro-electrodes, as the sensitivity of the current to the variation of the enzyme distance is related to the size of the detection electrode. At macroelectrodes, the spike is too broad to be identified and hence it is difficult to observe spikes from the background.In addition, the characterisation of the spikes is also influenced by the bandwidth of the measurement electronics. Fig. 7a–f are calculated for different filter models, i.e. different potentiostats, which feature different transfer characteristics and different bandwidths. If the same series of impact events was recorded simultaneously with both potentiostats, different current responses would hence be observed and the average spike duration and the number of spikes detected may alter between the measurements. The filter response to signals in the high frequency regime is herein particularly interesting as series of signal fluctuations in this regime may be resolved through some potentiostats and then be identified as individual spikes, while a different potentiostat may show the same series of fluctuations as a single longer spike. The application of a low-pass filter operated at a cut-off frequency of 4 kHz therefore leads to a shorter average spike length and a larger number of spikes being detected if compared to a measurement using a low-pass filter set at 50 Hz.
4 Conclusions
It is computationally shown that in principle the nano-impact method enables the electrochemical characterisation of freely-diffusing enzymes if a small electrode is used, the potentiostats bandwidth is sufficient, and the enzyme features a large average turnover number. These findings apply to an enzyme operating at a constant turnover number, while fluctuations in the enzyme activity will further enhance its detectability. The model presented provides understanding of the enzyme-electrode system and useful predictions for experimentalists: we demonstrate that current responses corresponding to single catalase activity can in principle be observed at electrodes with radii varying from a few nanometres to a few micrometres. However, the simulated current spikes are too small to be distinguished from the background noise in any real experiment using a broad bandwidth. Enzymes with faster turnover numbers than catalase lead to larger current signals that can be experimentally observed and electrodes with smaller sizes better detect the signals. Again, the influence of the measurement electronics cannot be ignored. The electronics with a short bandwidth keeps more information than that of a broad bandwidth and is more favourable in the detection of the single enzyme activity.The model is applied to simulate current signals that could possibly be attributed to single catalase at a 5.0 μm electrode measured at a cut-off frequency of 4 kHz. The simulation and the experiment show however significant discrepancy in the magnitude and the duration time of the current signal, revealing that without further consideration of the enzyme catalysis kinetics and the influence of the experiment environment, the experimental phenomena cannot be explained as the detection of product generated by the activity of a single catalase enzyme in solution.
Acknowledgements
The research is sponsored by funding from the European Research Council under the European Union Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. [320403].References
- X. Xiao, F.-R. F. Fan, J. Zhou and A. J. Bard, J. Am. Chem. Soc., 2008, 130, 16669–16677 CrossRef CAS PubMed.
- W. Cheng and R. G. Compton, TrAC, Trends Anal. Chem., 2014, 58, 79–89 CrossRef CAS.
- N. V. Rees, Electrochem. Commun., 2014, 43, 83–86 CrossRef CAS.
- S. V. Sokolov, S. Eloul, E. Kätelhön, C. Batchelor-McAuley and R. G. Compton, Phys. Chem. Chem. Phys., 2017, 19, 28–43 RSC.
- M. Pumera, ACS Nano, 2014, 8, 7555–7558 CrossRef CAS PubMed.
- P. H. Robbs and N. V. Rees, Phys. Chem. Chem. Phys., 2016, 18, 24812–24819 RSC.
- X. Xiao, S. Pan, J. S. Jang, F. R. F. Fan and A. J. Bard, J. Phys. Chem. C, 2009, 113, 14978–14982 CAS.
- J. Kim, B.-K. Kim, S. K. Cho and A. J. Bard, J. Am. Chem. Soc., 2014, 136, 8173–8176 CrossRef CAS PubMed.
- J. M. Kahk, N. V. Rees, J. Pillay, R. Tshikhudo, S. Vilakazi and R. G. Compton, Nano Today, 2012, 7, 174–179 CrossRef CAS.
- X. Jiao, C. Lin, N. P. Young, C. Batchelor-McAuley and R. G. Compton, J. Phys. Chem. C, 2016, 120, 13148–13158 CAS.
- Q. Lin, C. Lin, H. Wu, C. Batchelor-McAuley and R. G. Compton, J. Phys. Chem. C, 2016, 120, 20216–20223 CAS.
- J. E. Dick, C. Renault and A. J. Bard, J. Am. Chem. Soc., 2015, 137, 8376–8379 CrossRef CAS PubMed.
- A. N. Sekretaryova, M. Y. Vagin, A. P. F. Turner and M. Eriksson, J. Am. Chem. Soc., 2016, 138, 2504–2507 CrossRef CAS PubMed.
- L. Han, W. Wang, J. Nsabimana, J.-W. Yan, B. Ren and D. Zhan, Faraday Discuss., 2016, 193, 133–139 RSC.
- E. Kätelhön, L. Sepunaru, A. A. Karyakin and R. G. Compton, ACS Catal., 2016, 6, 8313–8320 CrossRef.
- C. Chan, L. Sepunaru, S. V. Sokolov, E. Kätelhön, N. P. Young and R. G. Compton, Chem. Sci., 2017, 8, 2303–2308 RSC.
- X. S. Xie, Acc. Chem. Res., 1996, 29, 598–606 CrossRef CAS.
- S. Weiss, Science, 1999, 283, 1676–1683 CrossRef CAS PubMed.
- J. A. Cracknell, K. A. Vincent and F. A. Armstrong, Chem. Rev., 2008, 108, 2439–2461 CrossRef CAS PubMed.
- L. Michaelis and M. M. L. Menten, FEBS Lett., 2013, 587, 2712–2720 CrossRef CAS PubMed.
- R. M. Daniel, R. V. Dunn, J. L. Finney and J. C. Smith, Annu. Rev. Biophys. Biomol. Struct., 2003, 32, 69–92 CrossRef CAS PubMed.
- B. P. English, W. Min, A. M. van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. C. Kou and X. S. Xie, Nat. Chem. Biol., 2006, 2, 87–94 CrossRef CAS PubMed.
- S. C. Kou, B. J. Cherayil, W. Min, B. P. English and X. S. Xie, J. Phys. Chem. B, 2005, 109, 19068–19081 CrossRef CAS PubMed.
- E. J. F. Dickinson, J. G. Limon-Petersen, N. V. Rees and R. G. Compton, J. Phys. Chem. C, 2009, 113, 11157–11171 CAS.
- K. Ngamchuea, S. Eloul, K. Tschulik and R. G. Compton, Anal. Chem., 2015, 87, 7226–7234 CrossRef CAS PubMed.
- R. G. Compton and C. E. Banks, Understanding Voltammetry, Imperial College Press, 2nd edn, 2011 Search PubMed.
- E. Kätelhön and R. G. Compton, Chem. Sci., 2014, 5, 4592–4598 RSC.
- E. Kätelhön, S. V. Sokolov and R. G. Compton, Sens. Actuators, B, 2016, 234, 420–425 CrossRef.
- S. Eloul, E. Kätelhön and R. G. Compton, Phys. Chem. Chem. Phys., 2016, 18, 26539–26549 RSC.
- S. Eloul and R. G. Compton, J. Phys. Chem. Lett., 2016, 7, 4317–4321 CrossRef CAS PubMed.
- M. A. Bevan and D. C. Prieve, J. Chem. Phys., 2000, 113, 1228–1236 CrossRef CAS.
- L. Farnell and W. G. Gibson, J. Comput. Phys., 2004, 198, 65–79 CrossRef.
- L. Farnell and W. G. Gibson, J. Comput. Phys., 2005, 208, 253–265 CrossRef.
- E. Kätelhön, E. E. L. Tanner, C. Batchelor-McAuley and R. G. Compton, Electrochim. Acta, 2016, 199, 297–304 CrossRef.
- S. Butterworth, Experimental Wireless & Wireless Engineer, 1930, 7, 536–541 Search PubMed.
- R. G. Compton, E. Laborda and K. R. Ward, Understanding Voltammetry: Simulation of Electrode Processes, Imperial College Press, 2013 Search PubMed.
- E. Kätelhön and R. G. Compton, Analyst, 2015, 140, 2592–2598 RSC.
- R. T. Ferrell and D. M. Himmelblau, J. Chem. Eng. Data, 1967, 12, 111–115 CrossRef CAS.
- S. Sengupta, K. K. Dey, H. S. Muddana, T. Tabouillot, M. E. Ibele, P. J. Butler and A. Sen, J. Am. Chem. Soc., 2013, 135, 1406–1414 CrossRef CAS PubMed.
- J. Switala and P. C. Loewen, Arch. Biochem. Biophys., 2002, 401, 145–154 CrossRef CAS PubMed.
- E. Sim and R. B. Sim, Eur. J. Biochem., 1979, 97, 119–126 CrossRef CAS PubMed.
- R. B. Liebherr, M. Renner and H. H. Gorris, J. Am. Chem. Soc., 2014, 136, 5949–5955 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc02084h |
| This journal is © The Royal Society of Chemistry 2017 |