Open Access Article
Open Access ArticleDynamic studies of the interaction of a pH responsive, amphiphilic polymer with a DOPC lipid membrane†
Sivaramakrishnan
Ramadurai
a,
Marco
Werner
b,
Nigel K. H.
Slater
c,
Aaron
Martin
a,
Vladimir A.
Baulin
*b and
Tia E.
Keyes
 *a
*a
aNational Centre for Sensor Research, Dublin City University, Glasnevin, Dublin 9, Ireland. E-mail: tia.keyes@dcu.ie
bDepartament d'Enginyeria Química, Universitat Rovira i Virgili, Tarragona 43007, Spain. E-mail: vladimir.baulin@urv.cat
cDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Cambridge CB2 3RA, UK
First published on 28th February 2017
Abstract
Deeper understanding of the molecular interactions between polymeric materials and the lipid membrane is important across a range of applications from permeation for drug delivery to encapsulation for immuno-evasion. Using highly fluidic microcavity supported lipid bilayers, we studied the interactions between amphiphilic polymer PP50 and a DOPC lipid bilayer. As the PP50 polymer is pH responsive the studies were carried out at pH 6.5, 7.05 and 7.5, corresponding to fully, partly protonated (pH = pKa = 7.05) and fully ionized states of the polymer, respectively. Fluorescence correlation spectroscopy (FCS) using both labelled lipid and polymer revealed the PP50 associates with the bilayer interface across all pHs where its diffusion along the interface is impeded. Both FCS and electrochemical impedance spectroscopy (EIS) data indicate that the PP50 does not penetrate fully into the bilayer core but rather forms a layer at the bilayer aqueous interface reflected in increased resistance and decreased capacitance of the bilayer on PP50 binding. The extent of these effects and the dynamics of binding are influenced by pH, increasing with decreasing pH. These experimental trends concurred with coarse grained Monte Carlo simulations of polymer–bilayer interactions wherein a model hydrophilic polymer backbone grafted with side chains of varying hydrophobicity, to mimic the effect of varying pH, was simulated based on the bond fluctuation model with explicit solvent. Simulation results showed that with increasing hydrophobicity, the polymer penetrated deeper into the contacting bilayer leaflet of the membrane suppressing, consistent with EIS data, solvent permeation and that a full insertion of the polymer into the bilayer core is not necessary for suppression of permeability.
Introduction
Biodegradable and biocompatible (bio)polymers are an important class of low toxicity drug delivery vectors and efficient membrane-active agents.1–6 Amongst this class of materials, amphiphilic polymers are particularly important as drug carriers due to their high affinity for lipid membranes and because on membrane binding they can modulate membrane permeability, solubilise the membrane, stabilise membrane proteins or haemolyse red blood cells.3,7–9 Hydrophobicity, hydrophilicity, and surface charge of the polymer each influence polymer–membrane interactions, the challenge is often to balance these interactions through modification of polymer structure to achieve the desired interaction. Cell membranes play a central role in selectively transporting solutes and various small molecules into and out of cells. The transport of low molecular weight solutes and membrane association of macromolecules are important in cryo-protection of cells and in protecting cells from osmotic and haemolytic conditions.10 In nature, membrane disruption by amphiphilic peptides is a critical step in viral and bacterial toxin infection progression and also central to the mechanism of action of antimicrobial peptides.11One approach to design biodegradable and biocompatible polymers with pronounced membrane activity is to use, as polymer blocks, natural cell components such as peptides that mimic the pH mediated membrane-lytic properties of naturally occurring viral peptides.8,12,13 A class of such membrane active amphiphilic polymers has been reported comprised of blocks composed of biodegradable polyamide poly(L-lysine iso-phthalamide) (PLP) grafted with L-phenylalanine at a degree of grafting of 46.2%.14,15 The co-polymer (PP50) is pH-responsive. A modification of PP50 obtained by copolymerization of PLP polymer with the fluorescent probes Cy3 and Cy5 was investigated as a pH mediated molecular probe for biomedical imaging specifically applied to diagnosing solid tumors.16,17 PP50, Scheme 1, has been found to enhance the uptake of trehalose a membrane-impermeable disaccharide, natural anti-oxidant and desiccation protection agent for erythrocytes. Trehalose uptake into erythrocytes mediated by PP50 exceeded 250 mM at pH 7.05 whereas with more commonly used methods trehalose uptake does not exceed concentrations beyond 60 mM.15 It was also shown that PP50 can be used along with other cryoprotectants such as DMSO for protection of freeze-dried red blood cells.12 However, the mechanism by which PP50 interacts with the cell membrane has not been explored in detail to date.
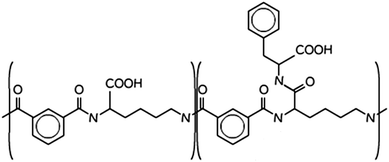 | ||
| Scheme 1 Molecular structure of PP50, the “50” pertains to the fact that 50% of the carboxylic acids are functionalised in the structure.14 | ||
Artificial membrane model systems are widely used to study biomolecular interactions with membranes as they are easy to access and manipulate using biophysical techniques and systematic studies can provide detailed insight into interaction of polymers with the membrane. Commonly employed models such as giant unilamellar vesicles (GUVs) and supported lipid bilayers (SLB) have been successfully used to study changes in membrane fluidity18–20 resulting from interaction of antimicrobial peptides and polymer8,21,22 on the membrane including membrane curvature stress.23 Furthermore, such model membrane systems are used to study mobility of proteins and lipids in the membrane24,25 and lipid bilayer resistivity.26,27 However, control and stability of free standing vesicles in solution and frictional substrate–membrane interactions are key limitations of liposomes and SLBs respectively.28 Recently, we reported that microcavity supported lipid bilayer (MSLB) substrates offer a versatile, highly fluidic membrane model that overcomes issues of stability and substrate–membrane interactions.26,29 In MSLBs, lipid bilayers are suspended across aqueous buffer filled microcavities providing bilayers with lipid fluidity analogous to that of a liposome combined with the stability and versatility of a supported lipid bilayer. The deep aqueous wells incident at both sides of the bilayer provides for lipid lateral diffusion unaffected by frictional effects arising from substrate–lipid interactions prevalent in SLBs. This is important in this study as we examine the impact of polymer on the lateral diffusion of the lipid bilayer.
In this contribution, we examine the impact of pH-responsive PP50 polymer on lipid lateral diffusion in a DOPC bilayer supported at an aqueous filled microcavity array using fluorescence correlation spectroscopy (FCS). FCS is a single molecule method used to measure the mobility of the fluorescent molecules in an observation volume defined by confocal optics, typically a femtolitre volume. As the geometry of the observation volume is known, precise concentration and diffusion coefficients of the molecules can be calculated. FCS is widely used to study the diffusion of fluorescently labelled proteins in the cellular membrane, cytosol, nucleus in living cells and in synthetic membranes.30–33 It has also been applied to study the aggregation state and critical micelle concentration of peptides and polymers in solution.33,34 Here, changes in lateral diffusion of lipids in a cavity supported DOPC bilayer were studied by fluorescent lifetime correlation spectroscopy (FLCS), an adaptation of FCS in which the FCS is time gated permitting removal of background noise, after-pulse from the detectors. This approach provides FCS curves along with fluorescent lifetime data of the probes.22,30,35
The lipid diffusivity studies are supported by electrochemical impedance measurements to investigate changes to the permeability of the membrane.26,36 Electrochemical impedance spectroscopy (EIS) is used to measure the complex impedance properties of a material and has been widely used to study interfacial interactions, such as antigen–antibody interaction, and cancer cell capture as well as for evaluation of biomembranes.27,37–39 EIS was implemented here at gold microcavity array substrates analogous in structure to the optically transparent PDMS arrays used for FCS. The combination of FLCS and EIS provides new insights into the dynamics of the membrane and impact of PP50 polymer on lipid membrane lateral packing and integrity in real time. The experimental data is supported by theoretical studies which provide insights into a possible molecular origin of the optical and electrochemical changes elicited at the DOPC bilayer membrane by PP50 as a function of pH.
Combined, the data suggests that PP50 polymers significantly perturb the lipid membrane leading to local changes in lipid packing and that the extent of interaction is pH dependent, originating from change induced in the hydrophobicity of the polymer with its ionization.
Materials and methods
Lipids
1,2-Dioleyl-sn-glycerophosphocholine (DOPC) in powder form was purchased from Avanti polar lipids (Delfzijl, The Netherlands). Phosphate buffer saline (PBS) tablets were purchased from Sigma-Aldrich (Wicklow, Ireland), β-BODIPY-C5-HPC (2-(4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine) (530/550 nm) was purchased from Thermofisher (Ireland) and fluorescent probe Atto-655 with an NH2 functional group was purchased from Atto-tech GmbH (Siegen, Germany). All other chemicals were of HPLC grade and were used as purchased. The buffers were prepared from MilliQ water (>18 MΩ).Polymer
PP50 was synthesized in house according to a reported procedure15 and Atto-655-NH2 was coupled to the PP50-COOH using a previously reported standard DCC/DMAP mediated coupling procedure.14 The labelled product was confirmed by TLC which showed the disappearance of the Atto-655-NH2 starting material and a single spot corresponding to the dye labelled PP 50, Rf 0.4 (CHCl3/MeOH/H2O 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26) on silica. The crude material was purified via silica gel chromatography.
26) on silica. The crude material was purified via silica gel chromatography.
PP50 polymer and Atto-655 labelled PP50 were dissolved in PBS buffer at the required pH and left overnight on a shaker. The dissolved polymers were diluted to the required concentration and used for further measurements. DOPC and β-BODIPY-C5-HPC stock solutions were prepared using chloroform. Lipid mixtures were prepared by mixing ratios of unlabelled (DOPC) and labelled β-BODIPY-C5-HPC lipid (5000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol/mol) into of stock solution in a glass tube. The organic solvents were removed by gentle stream of nitrogen gas and then placed under vacuum for 2 h to 12 h to remove residual solvents. The resultant dry lipid films were used for experimental measurements.
1 mol/mol) into of stock solution in a glass tube. The organic solvents were removed by gentle stream of nitrogen gas and then placed under vacuum for 2 h to 12 h to remove residual solvents. The resultant dry lipid films were used for experimental measurements.
Vesicle preparation
The lipid thin films were rehydrated in 1 ml of phosphate buffer saline (PBS) and vortexed for a period of 30–60 seconds. Next, the lipid suspensions were extruded 11 times through a 100 nm polycarbonate filter using a mini-extruder (Avanti Polar Lipids) to form large unilamellar vesicles (LUV) and diluted to final concentration of 0.25 mg ml−1.Microcavity arrays supported lipid bilayers
Lipid bilayers were assembled across aqueous filled microcavity arrays according to protocols modified slightly from previous reports.29 For fluorescence studies the microcavity arrays were prepared from polydimethylsiloxane (PDMS) [Sylgard 184 base and curing kit, Dow Corning] according to a microsphere templating method previously described.29 Briefly, PDMS was cast onto a dried film of polystyrene spheres of 3 μm diameter, formed on freshly cleaved mica, and cured. The PDMS was peeled off the mica and the spheres were removed to form open spherical cavities embedded in PDMS. The planar PDMS was plasma cleaned, followed by 1 h of sonication in PBS buffer to ensure the cavities were filled with the aqueous solution.Following filling a Langmuir monolayer of DOPC was spread across the aqueous filled array. This was achieved using a Model 102M from Nima Technology, lipid bilayer trough. DOPC was prepared in chloroform at a concentration of 50 mg ml−1 and 100 μl of this solution was suspended on the water sub-phase. Fifteen minutes were allocated for evaporation of the solvent, prior to lipid monolayer compression. The rate of compression was 30 cm2 min−1 and a constant surface pressure of 35 mN m−1 was maintained for the transfer of a probe labelled (β-BODIPY-C5-HPC) DOPC monolayer from the water–air interface to the aqueous filled microcavity array.
During lipid bilayer transfer, the rate of the dipper motion was maintained at 5 mm min−1 to ensure adequate transfer. The monolayer coated template was incorporated into the flow chamber by sticking the edges of the PDMS to the microscope cover slip using adhesive (Araldite, UK). DOPC lipid vesicles also containing the lipid probe were injected into the flow chamber where they spontaneously disrupt to form a free-spanning lipid bilayer across the lipid bilayer monolayer. After 10 minutes, the flow chamber was flushed with 1 ml of PBS buffer to remove excess vesicles and to maintain the fluid above the bilayer. Lipid bilayers formed in this way were found from FLCS to be stable for 3 to 5 days, but experiments on a given substrate were always completed within 8 hours.
The microcavity arrays for EIS measurements were prepared in gold from gold coated silicon wafers as reported previously.40 In brief, silicon wafers coated with 100 nm gold on 50 nm titanium were purchased from AMS biotechnology, UK. The wafer were cut to 2 × 1 cm and polystyrene spheres of 2.88 μm were drop cast on the wafers for and left to dry overnight. The sphere modified wafers were dipped into commercial gold deposition solution and gold was deposited around the spheres using electrodeposition. The spheres were removed and top surface was treated with 1 mM mercaptoethanol. The quality and uniformity of the microcavity array was confirmed by scanning electron microscopy as reported previously.26,36 The microcavity array was sonicated for 15 minutes with the PBS buffer before the DOPC bilayer by lipid bilayer/vesicle fusion deposition as described above. The suspension and homogeneity of the bilayer film across the array was confirmed by confocal microscopy.26,36 The aqueous filled lipid bilayer coated gold cavity array was placed inside glass cell containing PBS buffer along with the reference and auxiliary electrodes and electrochemical impedance spectroscopy was measured as described below.
Fluorescence lifetime correlation spectroscopy (FLCS)
FLCS experiments were performed using a Microtime 200 system (PicoQuant GmBH, Germany) consisting of FCS module, dual SPD detection unit, time correlated single photon counting (TCSPC), and inverted microscope model Olympus X1-71 with a Olympus UPlanSApo 60×/1.2 water immersion objective. The lipid labelled fluorophores β-BODIPY-C5-HPC and Atto-655 labelled PP50 were excited by pulsed picosecond lasers at 532 nm laser PicoTA from Toptica (Picoquant) and 640 nm LDH-P-C-640B Picoquant, respectively. A single mode optical fibre guides the two lasers to the main unit and provides a homogeneous Gaussian profile for the both excitations. The lasers were pulsed at 20 MHz, corresponding to an interval of 50 ns. The emitted fluorescence was collected through the microscope objective and dichroic mirror z532/635rpc blocked the backscattered light and HQ550lp AHF/Chroma for 532 nm and HQ670lp AHF/Chroma for 640 nm filters were used to clean up the signal. A 50 μm pinhole was used to confine the volume of detection in the axial direction. Fluorescence was detected using a single photon avalanche diode (SPAD) from MPD (Picoquant). The time-correlated single photon counting system (PicoHarp 300 from Picoquant), enabled simultaneous assessment of the lifetime in a nanosecond range along with the time of diffusion in the millisecond range.41To calibrate the FCS confocal volume, rhodamine 6G (532 nm) and Atto-655 (640 nm) dyes with known diffusion coefficients, were used as standards. The volume was determined at the start of each set of experiments and at least 15 data points were collected from each sample, across different individual pores and each data point was measured for 30 s. The time-dependent fluctuations of the fluorescence intensity dI(t) were recorded and analysed by an autocorrelation function G(t) = I + 〈dI(t′)dI(t′ + t)〉/〈I(t′)〉2. As has been shown theoretically for freely diffusing molecules, G(t) has following analytical form:31
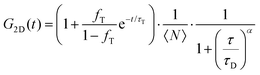 | (1) |
Electrochemical impedance spectroscopy (EIS)
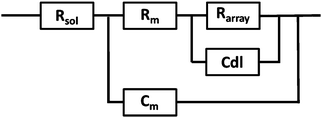
EIS was performed on a CH660A potentiostat (CH Instruments, Germany). A standard 3-electrode cell was employed consisting of an Ag/AgCl reference electrode, a platinum auxiliary electrode and the gold microcavity array which constituted the working electrode. The EI spectra were measured over a frequency range of 1 MHz to 0.01 Hz with an AC modulation amplitude of 5 mV at a potential bias of 0 V (vs. Ag/AgCl). All measurements were carried out in a 3 ml glass cell in PBS buffer adjusted to the desired pH. The EIS of the aqueous filled microcavity array coated with the DOPC lipid bilayer was measured initially prior to addition of PP50 to ensure signal stability and then, 0.4 mg ml−1 concentration of polymer was added to the glass cell containing PBS buffer separately at each pH. The electrochemical impedance response of the lipid bilayer following PP50 introduction was then measured over 4 h. Each measurement takes approximately 10 minutes and measurements were carried out at room temperature (20 °C).The measured data were analysed using Z-View software using the fitting model (Scheme 2) to calculate the change in membrane resistivity and capacitance as reported previously for these arrays.26 Where, Rsol is the solution resistance, Rarray is resistance of cavity array, Cdl is the electrode double layer capacitance and Rm and Cm is the resistance and capacitance of the lipid membrane. The model circuit provided an excellent fit of the EIS data over the full frequency range and was used to estimate the change in membrane resistivity and conductance of the bilayer in response to PP50. The quality of fit was determined from plotted residuals and reduced χ2 value.
Furthermore, in fitting the impedance response, the only elements which underwent a significant response on addition of the PP50 to the bilayer was Rm and Cm, which suggests the model is valid.
Coarse grained Monte Carlo simulation
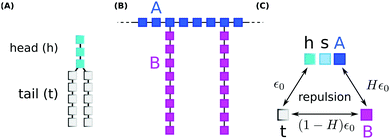
We performed coarse grained Monte Carlo simulations based on the bond fluctuation model43,44 with explicit solvent45,46 in order to investigate the interaction of a lipid membrane with an amphiphilic polymer with grafted side chains under variation of the hydrophobicity of the side chains.As shown in Scheme 3(A), coarse grained phospholipids are composed of three head (h) monomers and two tails (t) of five monomers each. A model polymer consists in a backbone of N = 32 A-type monomers, with grafted side chains containing 8 B-type monomers connected to every 4th backbone monomer. The polymer architecture is sketched in Scheme 3(B). Lipids and polymer are embedded into an explicit solvent of s-type monomers.
The solvent interaction model employed is visualized in Scheme 3(C). It is defined as
| εt,(h,s,A) = ε0; εB,(h,s,A) = Hε0; εt,B = (1 − H)ε0 | (2) |
As described in previous studies, we initially locate 300 lipids such that a stable self-assembled membrane is spanned parallel to the x,y-plane and perpendicular to the z-direction of a periodic simulation box of 64 × 64 × 64 lattice units.46 The polymer backbone (A-type monomers) is generated as a self-avoiding random walk in the vicinity of the upper leaflet of the membrane followed by the grafting of the side chains (B-type monomers) (Scheme 3(B)). Both polymer and lipid chains are fully flexible. We select three side chain hydrophobicity namely H = 0.8, H = 0.9, and H = 1.0 which mimics the effect of increasing hydrophobicity of the PP50 side chains with decreasing pH on coarse grained level. Note that the three chosen values of H do not necessarily map to specific pH values, but correspond to a systematic variation of hydrophobicity in the coarse grained model. For each side chain hydrophobicity, we run a set of 8 independent simulations for 10 million Monte Carlo Steps (MCS) for initial relaxation, and another 100 million MCS for production.
The polymer PP50 is a complex structure that beside pH-sensitive carboxyl groups comprises hydrophobic phenyl groups, aliphatic backbones as well as hydrophilic carbonyl groups (Scheme 1). A systematic coarse graining of the polymer on the basis of atomistic models, or the translation into an existing system of coarse grained force fields such as MARTINI,47 will be a field of research by itself (see G. Rossi et al.48 for polystyrene as an example). Instead of an exact mapping of the structure, we use a generic coarse grained model for the polymer (Scheme 3(B)), which captures essential features of PP50 relevant for this work: its amphiphilic character, the branched architecture, the hydrophobic character of L-phenylalanine end group, and a variation of hydrophobicity mediated by changes of pH. The degree of hydrophobicity of B-type monomers will be variable as described above. Variations of hydrophobicity of the backbone as well as the random sequence of bound and unbound grafting sites are not included in the model. The model does not resolve amphiphilic features on atomic scale such as seen by phenyl groups neighbouring carbonyl groups on the backbone in Scheme 1, but reflects the amphiphilic character of the polymer by means of A- and B-species on a global scale. When comparing Schemes 1 and 3(B), one sees that a typical PP50 repeat unit is mapped to units of 12 statistical segments in the model, and one segment represents 3 to 4 carbons plus the contribution of other elements. This ratio is in the order of a typical value of 5 carbons per monomer found for systematic coarse graining of polyethylene.49 In turn, a mass of 23 kDa15 corresponds to a total of 300 to 500 monomers. The size of 96 monomer cubes is a compromise between matching this order of magnitude and the computational cost for the necessary box size to embed the polymer in order to obtain significant permeability signals.
The coarse grained model allows to analyse polymer-induced variations of long-time statistical membrane properties such as permeability within accessible computational time. Results do not depend on the chemical details of the components and do not allow for an exact quantitative mapping, but reflect universal static and dynamic properties of the polymer–membrane interaction.
Results and discussion
FLCS studies on the effect of PP50 on PDMS microcavity arrays
Fig. 1(A) shows a back-reflectance image of a DOPC bilayer modified PDMS microcavity array. The refractive index mismatch between the PDMS (n ∼ 1.45) and the buffer (n ∼ 1.33) causes the liquid filled cavities to appear as intensely reflective spots making selection of filled microcavities for study facile. For FLCS measurement, the observation volume was positioned at the centre of a filled micropore and the bilayer located by z scanning until the most intense fluorescence point is identified from where the autocorrelation function (ACF) trace is collected. β-BODIPY-C5-HPC was used as the lipid probe in these studies and the PP50 was labelled with Atto-655. The structures of both probes are shown ESI† (Fig. S1 and S2). Time traces were acquired for 30 s at room temperature (20 °C) and Symphotime 64 software was used to acquire and analyse the time traces. Representative ACF curves for labelled lipid diffusion in a DOPC MSLB and Atto-655 labelled PP50 at the membrane surface are shown in Fig. 1(B) along with their fits to the 2D-diffusion model (eqn (1)). The arrayed nature of the micropores, permits independent collection of ACFs from multiple pores across a single substrate to obtain an average diffusion coefficient. The calculated average diffusion coefficient of lipid probe in DOPC lipid membrane at the pore aperture is 11.7 ± 1.6 μm2 s−1. This value is consistent with previous reported literature on MSLB lipid diffusion coefficients29 and with values reported for giant unilamellar vesicles (GUVs) of DOPC,25 and reflects the high degree of fluidity of the lipids in this format.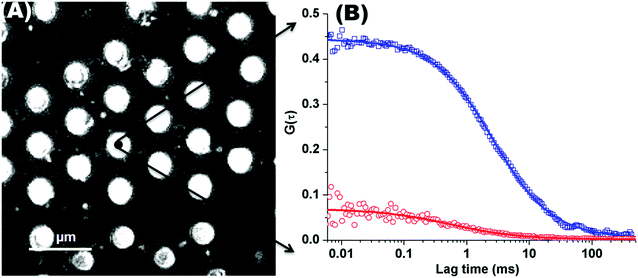 | ||
Fig. 1 (A) Representative back reflectance image of a microcavity array made from PDMS. The white circles are the buffer filled cavities and the dark regions are the planar regions of the array and non-filled PDMS cavities. The cavity diameters are 2.5 ± 0.5 μm. The DOPC lipid bilayer labelled with fluorescent marker β-BODIPY-C5-HPC (5000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol/mol) and in contact with PBS buffer at defined pH, was formed at the microcavity array by Langmuir–Blodgett technique combined with vesicle disruption. The black spot on the microcavity indicates the positioning of a typical observation volume, where the fluorophore fluctuation over the time was measured using FLCS. (B) shows typical FLCS curves obtained after normalising the fluctuation signal and fluorescence lifetime signature to calculated true autocorrelation curve. The square box represents the experimental data for the lipid marker in the membrane and solid line correspond to the model in eqn (1), from which the diffusion time and number of molecules in the observation volume are obtained. The red circles represent the experimental ACF curve for Atto-655-PP50 at the lipid membrane and solid line corresponds to the fitted model (eqn (1)). 1 mol/mol) and in contact with PBS buffer at defined pH, was formed at the microcavity array by Langmuir–Blodgett technique combined with vesicle disruption. The black spot on the microcavity indicates the positioning of a typical observation volume, where the fluorophore fluctuation over the time was measured using FLCS. (B) shows typical FLCS curves obtained after normalising the fluctuation signal and fluorescence lifetime signature to calculated true autocorrelation curve. The square box represents the experimental data for the lipid marker in the membrane and solid line correspond to the model in eqn (1), from which the diffusion time and number of molecules in the observation volume are obtained. The red circles represent the experimental ACF curve for Atto-655-PP50 at the lipid membrane and solid line corresponds to the fitted model (eqn (1)). | ||
The PP50 is a pH responsive biopolymer15 wherein the carboxyl functionalities on the polymer are expected to be deprotonated at pH 7.5, partly and fully protonated at pH 7.05 (pKa) and 6.5 respectively. Where, at these latter two pHs, the lipophilicity of the polymer is expected to increase promoting lipid interaction. In order to evaluate if the PP50 associates with the lipid bilayer across all protonation states, we compared the diffusion coefficient of the polymer in free solution and then following contact of a solution of the polymer with the bilayer at pH 7.5, 7.05 and 6.5. In these experiments 0.4 mg ml−1 of the polymer containing a small fraction of labelled polymer (1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol/vol) Atto-655-PP50, was dissolved in the PBS buffer and injected into the flow chamber and into contact with the DOPC MSLB and the ACF was collected periodically after polymer introduction. The data collected from the fits of the ACF at each pH is summarised in Table 1 (detailed analysis is provided as ESI,† Tables S1–S3).
1 vol/vol) Atto-655-PP50, was dissolved in the PBS buffer and injected into the flow chamber and into contact with the DOPC MSLB and the ACF was collected periodically after polymer introduction. The data collected from the fits of the ACF at each pH is summarised in Table 1 (detailed analysis is provided as ESI,† Tables S1–S3).
| Time (h) | pH 6.5 | pH 7.05 | pH 7.5 | |||
|---|---|---|---|---|---|---|
| D L (μm2 s−1) | D P (μm2 s−1) | D L (μm2 s−1) | D P (μm2 s−1) | D L (μm2 s−1) | D P (μm2 s−1) | |
| D L and DP are diffusion coefficient of lipid and polymer. All time points were repeated a minimum of twice on different days and standard deviations calculated from at least 20 ACFs for a given substrate. | ||||||
| 0 | 11.7 ± 1.6 | 11.7 ± 1.6 | 11.7 ± 1.6 | |||
| 0.05 | 9.3 ± 0.4 | 79.7 ± 19.3 | 7.8 ± 0.4 | 66.85 ± 25.0 | 9.5 ± 1.1 | 79.6 ± 19.6 |
| 0.30 | 9.0 ± 0.3 | 83.5 ± 20.2 | 10.1 ± 1.0 | 61.75 ± 20.2 | 10.0 ± 1.0 | 93.5 ± 20.5 |
| 1 | 8.63 ± 0.5 | 78.7 ± 14.0 | 10.1 ± 1.0 | 83.0 ± 18.2 | 11.2 ± 1.4 | 87.6 ± 21.0 |
| 2 | 8.06 ± 0.5 | 71.0 ± 19 | 10.1 ± 0.9 | 71.75 ± 18.2 | 11.7 ± 1.5 | 84.5 ± 18.0 |
| 4 | 8.68 ± 1.0 | 71.4 ± 25 | 9.4 ± 0.8 | 80.0 ± 29.0 | 10.2 ± 1.3 | 81.65 ± 22.0 |
The diffusion coefficient, D, of Atto-655 labelled PP50 in PBS solution was determined from FLCS to be 235 ± 5 μm2 s−1 (the corresponding ACF curve is provided in ESI,† Fig. S3). Following introduction of the PP50 to the lipid membrane contacting solution, D of the polymer at the bilayer interface reduced to approximately 80 ± 20 μm2 s−1 (Table 1) and the diffusion coefficient was within the experimental error, constant across all the pHs explored. The reduction of the diffusion coefficient indicates increased friction for the polymer upon interaction with the membrane although the diffusion coefficients observed are significantly greater than the lipid diffusion.
This observation suggests that the polymer is surface associated and diffusing along the lipid membrane aqueous interface. The anomalous exponent, which is approximately unity for PP50 in solution, decreased to 0.85 ± 0.1 for PP50 at the membrane interface (ESI,† Tables S1–S3). This value indicates that the polymer at the interface is undergoing anomalous sub-diffusion consistent again with PP50 association with the membrane wherein diffusion is impeded by obstacles,50 which can be imposed by other adsorbed polymers or lipids. It is important to note that the standard deviation on the diffusion coefficient of the membrane bound PP50 is large, rendering any pH dependent trends difficult to appreciate (approx. 25%). This may be due to the molecular weight distribution of the polymer and variation in the geometry of absorption of polymer on to the bilayer surface (Table 1). The fluorescence lifetime of Atto-655-PP50 was 3.0 ± 0.03 ns and this value remained unchanged on membrane association.
To investigate the impact of PP50 membrane binding on lipid diffusion within the suspended bilayer, the diffusion coefficient of the β-BODIPY-C5-HPC probe within the DOPC bilayer was evaluated before and after PP50 introduction and as a function of pH. Interestingly, the impact was pH and time dependent, wherein at all but the highest pH, PP50 was observed to retard lipid diffusion. The most dramatic impact was observed for the fully protonated polymer at pH 6.5 where the diffusion coefficient (DL) of the lipid probe in the PP50 treated DOPC lipid bilayer was reduced from 11.7 ± 1.6 to 9.3 ± 0.4 μm2 s−1 at 0.05 h and this value remained unchanged within experimental error over 4 hours after PP50 introduction. At pH 7.05, DL decreased to 7.8 ± 0.4 μm2 s−1 immediately after addition of PP50 polymer, but then recovered to 10.1 ± 1.0 μm2 s−1 after 30 minutes where it remained constant throughout the experiment. Finally, DL of the lipid probe was reduced initially to 9.5 ± 1.1 μm2 s−1 after introduction of PP50 polymer at pH 7.5. However, the coefficient fully recovered to 11.7 ± 1.5 μm2 s−1 after 4 hours. Overall, significant and irreversible decrease in lipid diffusion coefficient is induced by adsorption of PP50 at the bilayer at pH 7.05 but particularly at pH 6.5 where relatively strong retardation of lipid diffusion was observed, conversely at pH 7.5, the influence of PP50 is weaker and temporary. Retardation of lipid lateral diffusion has been similarly reported for triblock copolymers interacting with SLBs of POPC. Here, retardation was dependent on the temperature of the system, with increasing lipid retardation observed with increasing temperature, attributed to increasing penetration of the co-polymer into the bilayer at higher temperatures.48 The effect here is analogous with increased retardation observed at pHs at which the polymer contains the higher proportion of hydrophobic moiety which promotes penetration of the polymer into the bilayer. The β-BODIPY-C5-HPC is a tail labelled probe in the membrane hydrophobic core reflecting changes induced by deep penetration of the polymer into the bilayer, if this occurred. For example, anomalous lipid diffusion has been observed for polymer tethered lipid bilayers where the bound lipids present obstacles to diffusion.49
In the present study, the penetration of the PP50 into the bilayer seems not to affect normal character of lipid diffusion in the bilayer: the exponent α for the β-BODIPY-C5-HPC lipid probe was recorded within experimental error as 1 (0.97 ± 0.05) reflecting normal diffusion of the lipid probe at the micropore on interaction with PP50 across all pHs explored. The lifetime of the β-BODIPY-C5-HPC probe was also not influenced by the presence of PP50 where it was determined to be 5.9 ± 0.2 ns over the pH range used here irrespective of the presence of the polymer, which is consistent with its reported value.53 This observation, combined with the retardation of the diffusion rate but retention of Brownian diffusion suggests the PP50, particularly at pH 6.5 in its most hydrophobic form, binds at and modifies the membrane fluidity but does not penetrate fully into the hydrophobic core.
To investigate the impact of PP50 on the electrical properties of the lipid bilayer we then investigated the electrochemical impedance of the bilayer on PP50 binding.
Electrochemical impedance studies on the effect of PP50 on gold microcavity arrays
To assess changes to the structural integrity and permeability of the lipid membrane, the electrochemical impedance spectroscopy (EIS) of the DOPC MSLB was compared before and after introduction of PP50 to the contacting solution. EIS studies the electrodynamic response of a surface under application of an sinusoidally varying potential field and the phase shift in impedance response to this field can provide insights into the capacitance and resistance of the membrane film.26 First, the impedance of the lipid bilayer coated electrode was measured at an applied potential of 0 V.Then, without disturbing the setup, PP50 polymer was introduced to the cell contacting solution to a final concentration of 0.4 mg ml−1 and the complex impedance of the bilayer was measured periodically over a 4 hour window. The absolute impedance values are similar to those reported previously for MSLBs and vary from electrode to electrode due to variation in electrode area and surface coverage from substrate to substrate.26 Therefore, the relative changes to the electrochemical impedance are presented here as ΔR and ΔC (changes in resistance and capacitance of the films) and these values, found to be highly reproducible across all experiments, were evaluated from the fit to the equivalent circuit given in Scheme 1 and are summarized in Table 2.
| Time (min) | pH 6.5 | pH 7.05 | pH 7.5 | |||
|---|---|---|---|---|---|---|
| ΔR (MΩ cm2) | ΔC (μF cm−2) | ΔR (MΩ cm2) | ΔC (μF cm−2) | ΔR (MΩ cm2) | ΔC (μF cm−2) | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2.45 ± 1.22 | −0.72 ± 0.18 | 2.42 ± 0.23 | −0.48 ± 0.06 | 0.70 ± 0.46 | 1.45 ± 0.45 |
| 30 | 6.10 ± 0.19 | −1.54 ± 0.45 | 3.39 ± 0.96 | −1.13 ± 0.13 | 1.06 ± 0.10 | 1.63 ± 0.40 |
| 60 | 6.19 ± 0.88 | −1.70 ± 0.56 | 3.46 ± 1.64 | −1.36 ± 0.05 | 1.41 ± 0.10 | 0.93 ± 0.43 |
| 120 | 7.43 ± 2.00 | −1.88 ± 0.61 | 3.26 ± 2.00 | −1.62 ± 0.12 | 1.52 ± 0.20 | 0.72 ± 0.31 |
| 240 | 7.40 ± 2.50 | −1.94 ± 0.54 | 3.02 ± 2.08 | −1.80 ± 0.15 | 2.41 ± 0.42 | 0.57 ± 0.25 |
Fig. 2(A)–(C) shows a representative Nyquist plot of the complex impedance data collected over 4 hours for different pHs. Addition of PP50 across all pHs induces an increase in film impedance reflected in a upward curvature of the Nyquist plots. As observed from FLCS studies, PP50 exerts the greatest impact on the bilayer at pH 6.5 and there is a temporal component to the interaction. On addition of PP50 there is an immediate increase in bilayer resistance which continues to increase over 2 hours after which time it stabilises at a resistance value which has increased by 7.40 ± 2.50 MΩ cm2 compared with the DOPC bilayer alone (Table 2). At pH 7.05 the resistance again immediately increases on introduction of PP50 to the contacting solution but stabilizes at a resistance which has increased to 3.26 ± 2.00 MΩ cm2 compared with the untreated bilayer. At pH 7.5, the resistance change is weakest and the change more gradual (Fig. 2(C)). The dynamic changes in resistance accompanying PP50 incubation with the bilayer are plotted in Fig. 2(D). Accompanying the increasing resistance is a decrease in membrane capacitance, again, the magnitude of the change is greatest at pH 6.5 and weakest at pH 7.5. The capacitance decreases and resistance increases indicate that the membrane has become less permeable to ion species and solvent on PP50 binding. This trend suggests the bilayer is thickened indicating the PP50 blankets the bilayer interface. EIS data is consistent with the FLCS data which indicates that PP50 is binding at the external leaflet with some shallow penetration into the bilayer hydrophobic core. The resistance of the film increases most significantly at pH 6.5 suggesting (a) that more of the polymer binds at this pH and/or (b) the extent of interaction, e.g. spreading of the polymer along the bilayer is greatest at this pH.
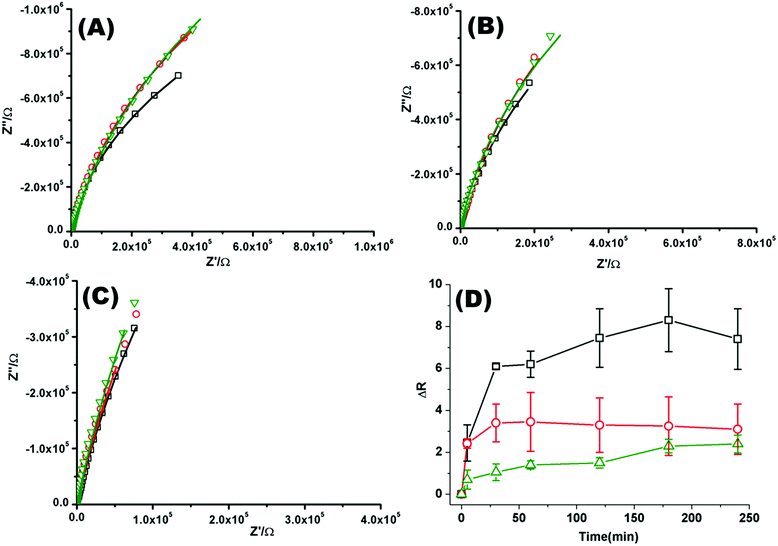 | ||
| Fig. 2 Nyquist plots of EIS data for DOPC lipid bilayers formed on a 1 cm diameter gold microcavity array electrode. (A) pH 6.5, (B) pH 7.05, and (C) pH 7.5. (A–C) Black squares correspond to EIS experimental data and the solid line represents the ECM model fit (Scheme 2), circles correspond to EIS data collected 30 minutes after introducing PP50 polymer and solid line represents the fit, triangles represent the EIS data 4 h after PP50 polymer introduction and the solid line represents the fit. The frequency range is 0.01 Hz to 1 × 105 Hz. The glass cell was filled with PBS buffer, at the desired pH. The gold microcavities act as working electrode along with reference electrode (Ag/AgCl) and counter electrode (platinum). The EIS data was collected over 4 h, following addition of PP50 polymer (concentration 0.4 mg ml−1) and changes were recorded over time. (D) Impact of the PP50 polymer on DOPC lipid bilayer resistance at pH 6.5 (□), 7.05 (○), 7.5 (Δ). The bilayer resistance was calculated and the change in the resistivity after introducing the PP50 against untreated DOPC lipid bilayer was plotted against the time. Values shown are experimental means and standard error on mean. | ||
Whereas cationic polymers such as poly-L-lysine, polyethylenimine, and diethylaminoethyl-dextran (DEAE-DEX) have been reported to cause defects within both model and cell membranes, increasing permeation.51,54 PP50 bilayer interactions appear here to be similar to those reported for chitosan at a DMPA layer where AFM studies indicated that polymer binding resulted in thickening and roughening of a bilayer surface.55 The results are also consistent with previous reports on PP50 at cell surfaces where they were found to form surface aggregates.52
The kinetic response of the impedance data is also affected by pH wherein the rate at which the polymer adsorption onto the membrane reaches equilibrium and the overall magnitude of impedance change once bound are strongly impacted by pH. This is again consistent with the increased lipophilicity of the polymer at pH 6.5 which is below its pKa. For 7.5 and 7.05, the final impedance change at 4 hours incubation with the polymer is approximately the same. However, the kinetics of binding is slower at higher pH.
Coarse grained Monte Carlo simulation
Previous simulation studies on linear homopolymers45,46 and amphiphilic copolymers56 showed that a polymer suppresses permeability when fully embedded in the bilayer's core in the limit large hydrophobicity. Experimental data on PP50, however, indicate that full insertion of amphiphilic branched polymer is not necessary for suppression of permeability, if anchoring side groups are sufficiently hydrophobic. In order to test this hypothesis, we performed coarse grained Monte Carlo simulations by means of the bond fluctuation model with explicit solvent45,46 according to the coarse grained representation given in Scheme 3.Typical simulation snapshots of equilibrated configurations are shown in Fig. 3. The permeability of the membrane with respect to solvent was analysed by direct counting of solvent translocation events as a function of the distance, R, from the polymer centre of mass as projected into the bilayer's mid-plane. The results of the simulation are shown in Fig. 4. For the lowest hydrophobicity shown, the polymer induces an increase of solvent permeability while for increasing hydrophobicity, permeability is suppressed by the presence of the polymer. This result is consistent with the EIS data which indicates that most especially at pH 6.5 the polymer forms a layer at the DOPC interface which reduces capacitance and increases resistance.
 | ||
| Fig. 3 Top view (A) and side view (B) simulation snapshots of a coarse grained lipid bilayer interacting with a hydrophilic A-type polymer backbone (blue) of length N = 32 grafted by hydrophobic B-type groups (red) for a value of hydrophobicity H = 1.0 according to Scheme 3(B). | ||
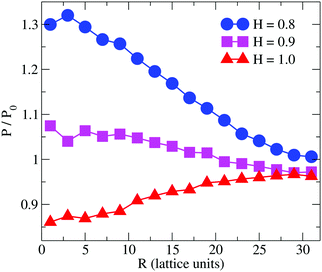 | ||
| Fig. 4 Simulation result for the relative permeability change induced by a branched polymer as shown in Scheme 2 for various values of hydrophobicity, H, of the side chains (B-type). Results are shown as a function of distance, R, from the polymer centre of mass projected to the bilayer's mid-plane. | ||
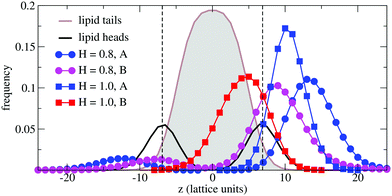
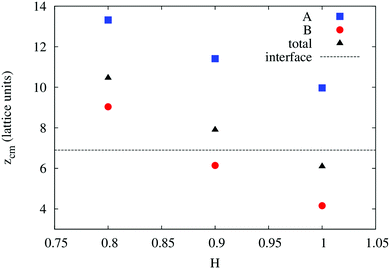
In order to understand the result based on the structural configuration of the polymer with respect to the membrane, in Fig. 5 we plot the frequency of observing A-type and B-type monomers as a function of the distance, z, from the bilayer's mid-plane. Since the polymer is amphiphilic, the interface region of the membrane is attractive, and we observe the polymer in an adsorbed state at the bilayer–solvent interface. Consequently, the two monomer distributions A and B are split into a hydrophobic fraction B embedded into the adjacent leaflet of tails, and hydrophilic loops (A) within the hydrophilic solvent/head environment. When comparing the two values of side chain hydrophobicity H = 0.8 and H = 1.0, we see that monomers of both species A and B enter the leaflet more deeply with increasing hydrophobicity, where they hinder solvent molecules from passing through the membrane. Note that the polymer causes a decrease of permeability, although the side chains are not fully inserted into the bilayer's mid-plane, but incorporated into one leaflet. As illustrated in Fig. 6 by the mean absolute center of mass positions, zcm, of the polymer, we observe that permeability starts to get suppressed with increasing hydrophobicity near a point, where the polymer center of mass crosses the bilayer–solvent interface. This result is consistent with the pH dependent studies described above. In particular, the increasing resistance and decreased capacitance of the film in contact with the PP50 at pH 6.5 indicated that the lipid bilayer permeability is reduced by the polymer binding.
The observation that the least hydrophobic polymer (H = 0.8) enhances solvent permeability (Fig. 4) indicates that the chosen window of side group hydrophobicity reflects a wider range of polymer hydrophobicity as compared to the effects seen for PP50 by variation of pH. By decreasing the value of H to H = 0.8, the hydrophobicity of the side chains gets close to a point of balanced hydrophobicity, where a polymer-induced increase of permeability has been seen for homopolymers45,46 as well as random amphiphilic copolymers.56
Conclusions
The pH dependent interactions of amphiphilic co-polymer PP50 with a DOPC bilayer was investigated by fluorescence correlation spectroscopy and electrochemical impedance spectroscopy at microcavity supported lipid bilayers. Three pHs; 6.5, 7.05 and 7.5 were explored corresponding to fully, and partly protonated (pH = pKa = 7.05) states and the ionized polymer respectively. To better understand the polymer–membrane interactions coarse-grained Monto-Carlo simulation of the interaction over three hydrophilic–hydrophobic co-polymer ratios was also performed.FLCS using fluorescently labelled polymer confirmed that the PP50 associated with the membrane over the three pHs explored. At the bilayer–aqueous interface the polymer displayed sub-diffusion attributed to formation of barriers at the lipid membrane interface due to the adsorbed polymer. The polymer association was found to retard the diffusion of the lipid probe with greatest retardation observed at pH 6.5, corresponding to the most lipophilic state of the polymer. Whereas lipid diffusion slowed, its diffusion remained Brownian and there was no evidence for alteration of the photophysics of the lipid tail labelled probe. Electrochemical impedance spectroscopy showed large and systematic increases to lipid membrane resistance with concomitant decreases in capacitance on addition of PP50, the magnitude of the changes was pH dependent.
Overall, both polymer diffusion coefficient and EIS data indicate that the PP50 adsorbs at the bilayer–aqueous interface. The most extensive binding indicated from EIS and lipid diffusion coefficient occurs at pH = 6.5 when the polymer is fully protonated suggesting that adsorption proceeds via hydrophobic anchoring of lipophilic units from the amphiphilic chain into lipid bilayer. Absence of changes to the emission lifetime or induction of anomalous diffusion in the lipid, along with the relatively fast diffusion of the polymer at the interface, suggests that the penetration of the polymer into the hydrophobic core is relatively shallow. Monte Carlo simulations of coarse grained amphiphilic polymers with hydrophobic side chains reproduce a localized state around bilayer–solvent interfaces and, consistent with EIS data, demonstrate the suppression of lipid membrane solvent permeability for the most hydrophobic polymer. Simulation results indicate that for suppression of permeability it is sufficient that hydrophobic units enter one leaflet, while the amphiphilic polymer as a whole is adsorbed at one bilayer–solvent interface. Therefore consistent with previous studies which showed that the amphiphilic polymer forms fibres at cell membrane interfaces our studies confirm the polymer adsorbs onto and penetrates but does not span the bilayer, the extent of penetration depending on the extent of ionization of the polymer which is controlled by pH.
Furthermore, the very high fluidity of the bilayers at the MSLBs makes them valuable platforms for studying dynamic impact of polymers at bilayer interfaces as complicating support substrate–membrane are not a consideration.
Acknowledgements
This material is based upon work supported by the Science Foundation Ireland under Grant No. [14/IA/2488]. T. E. K. and S. R. are grateful to the Irish Research Council for a Government of Ireland postdoctoral fellowship (GOIPD/2014/322). M. W. and V. A. B. gratefully thank the European Union's funding of the Initial Training Network SNAL (grant agreement no. 608184) under the 7th Framework programme.References
- W. B. Liechty, D. R. Kryscio, B. V. Slaughter and N. A. Peppas, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 149–173 CrossRef CAS PubMed.
- C. G. Palivan, R. Goers, A. Najer, X. Zhang, A. Car and W. Meier, Chem. Soc. Rev., 2016, 45, 377–411 RSC.
- A. A. Strömstedt, L. Ringstad, A. Schmidtchen and M. Malmsten, Curr. Opin. Colloid Interface Sci., 2010, 15, 467–478 CrossRef.
- C. Peetla, A. Stine and V. Labhasetwar, Mol. Pharmacol., 2009, 6, 1264–1276 CrossRef CAS PubMed.
- C. Chen, C. Yang, Y. Chen, F. Wang, Q. Mu, J. Zhang, Z. Li, F. Pan, H. Xu and J. R. Lu, ACS Appl. Mater. Interfaces, 2016, 8, 26501–26510 CAS.
- N. B. Leite, A. Aufderhorst-Roberts, M. S. Palma, S. D. Connell, J. R. Neto and P. A. Beales, Biophys. J., 2015, 109, 936–947 CrossRef CAS PubMed.
- M. Hara, M. Miyake, S. Iijima, Q. Yang, T. Arai, H. Yuan and J. Miyake, Supramol. Sci., 1998, 5, 777–781 CrossRef CAS.
- D. R. Nogueira, M. Mitjans, M. C. Morán, L. Pérez and M. P. Vinardell, Amino Acids, 2011, 43, 1203–1215 CrossRef PubMed.
- E. Marie, S. Sagan, S. Cribier and C. Tribet, J. Membr. Biol., 2014, 247, 861–881 CrossRef CAS PubMed.
- C. Stoll and W. F. Wolkers, Transfus. Med. Hemother., 2011, 38, 89–97 CrossRef PubMed.
- M. Zasloff, Nature, 2002, 415, 389–395 CrossRef CAS PubMed.
- A. L. Lynch, R. Chen, P. J. Dominowski, E. Y. Shalaev, R. J. Yancey Jr. and N. K. H. Slater, Biomaterials, 2010, 31, 6096–6103 CrossRef CAS PubMed.
- Z. Yue, M. E. Eccleston and N. K. H. Slater, Biomaterials, 2005, 26, 6357–6366 CrossRef CAS PubMed.
- R. Chen, S. Khormaee, M. E. Eccleston and N. K. H. Slater, Biomaterials, 2009, 30, 1954–1961 CrossRef CAS PubMed.
- A. L. Lynch, R. Chen and N. K. H. Slater, Biomaterials, 2011, 32, 4443–4449 CrossRef CAS PubMed.
- X. Dai, M. E. Eccleston, Z. Yue, N. K. H. Slater and C. F. Kaminski, Polymer, 2006, 47, 2689–2698 CrossRef CAS.
- M. Eccleston, J. Lee, F. Gilchrist, N. Slater and C. F. Kaminski, Laser Applications to Chemical and Environmental Analysis (2004), paper TuF10, Optical Society of America, 2004, p. TuF10 Search PubMed.
- S. Ramadurai, A. Holt, L. V. Schäfer, V. V. Krasnikov, D. T. S. Rijkers, S. J. Marrink, J. A. Killian and B. Poolman, Biophys. J., 2010, 99, 1447–1454 CrossRef CAS PubMed.
- S. Ramadurai, R. Duurkens, V. V. Krasnikov and B. Poolman, Biophys. J., 2010, 99, 1482–1489 CrossRef CAS PubMed.
- D. Scherfeld, N. Kahya and P. Schwille, Biophys. J., 2003, 85, 3758–3768 CrossRef CAS PubMed.
- C. Ladavière, C. Tribet and S. Cribier, Langmuir, 2002, 18, 7320–7327 CrossRef.
- T. Tabarin, A. Martin, R. J. Forster and T. E. Keyes, Soft Matter, 2012, 8, 8743–8751 RSC.
- K. Bacia, P. Schwille and T. Kurzchalia, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3272–3277 CrossRef CAS PubMed.
- R. Macháň and M. Hof, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1377–1391 CrossRef PubMed.
- S. Ramadurai, A. Holt, V. Krasnikov, G. van den Bogaart, J. A. Killian and B. Poolman, J. Am. Chem. Soc., 2009, 131, 12650–12656 CrossRef CAS PubMed.
- S. Maher, H. Basit, R. J. Forster and T. E. Keyes, Bioelectrochemistry, 2016, 112, 16–23 CrossRef CAS PubMed.
- M. Naumowicz and Z. A. Figaszewski, Biophys. J., 2005, 89, 3174–3182 CrossRef CAS PubMed.
- Y.-H. M. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef CAS PubMed.
- H. Basit, V. Gaul, S. Maher, R. J. Forster and T. E. Keyes, Analyst, 2015, 140, 3012–3018 RSC.
- H. Basit, S. G. Lopez and T. E. Keyes, Methods, 2014, 68, 286–299 CrossRef CAS PubMed.
- E. Haustein and P. Schwille, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 151–169 CrossRef CAS PubMed.
- K. Kristensen, J. R. Henriksen and T. L. Andresen, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2994–3002 CrossRef CAS PubMed.
- D. Wöll, RSC Adv., 2013, 4, 2447–2465 RSC.
- A. Orte, M. J. Ruedas-Rama, J. M. Paredes, L. Crovetto and J. M. Alvarez-Pez, Langmuir, 2011, 27, 12792–12799 CrossRef CAS PubMed.
- P. Kapusta, R. Macháň, A. Benda and M. Hof, Int. J. Mol. Sci., 2012, 13, 12890–12910 CrossRef CAS PubMed.
- B. Jose, C. T. Mallon, R. J. Forster, C. Blackledge and T. E. Keyes, Chem. Commun., 2011, 47, 12530–12532 RSC.
- H. Basit, A. Van der Heyden, C. Gondran, B. Nysten, P. Dumy and P. Labbé, Langmuir, 2011, 27, 14317–14328 CrossRef CAS PubMed.
- E. Diamanti, D. Gregurec, M. J. Rodríguez-Presa, C. A. Gervasi, O. Azzaroni and S. E. Moya, Langmuir, 2016, 32, 6263–6271 CrossRef CAS PubMed.
- J. Lin, J. Motylinski, A. J. Krauson, W. C. Wimley, P. C. Searson and K. Hristova, Langmuir, 2012, 28, 6088–6096 CrossRef CAS PubMed.
- S. Maher, H. Basit, R. J. Forster and T. E. Keyes, Bioelectrochemistry, 2016, 112, 16–23 CrossRef CAS PubMed.
- M. Böhmer, M. Wahl, H.-J. Rahn, R. Erdmann and J. Enderlein, Chem. Phys. Lett., 2002, 353, 439–445 CrossRef.
- P. Schwille, J. Korlach and W. W. Webb, Cytometry, 1999, 36, 176–182 CrossRef CAS PubMed.
- I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823 CrossRef CAS.
- H. P. Deutsch and K. Binder, J. Chem. Phys., 1991, 94, 2294–2304 CrossRef CAS.
- M. Werner, J.-U. Sommer and V. A. Baulin, Soft Matter, 2012, 8, 11714–11722 RSC.
- J.-U. Sommer, M. Werner and V. A. Baulin, Europhys. Lett., 2012, 98, 18003 CrossRef.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Soft Matter, 2011, 7, 698–708 RSC.
- V. Tries, W. Paul, J. Baschnagel and K. Binder, J. Chem. Phys., 1997, 106, 738–748 CrossRef CAS.
- A. Baumgärtner, Europhys. Lett., 1987, 4, 1221 CrossRef.
- J. Wang, L. Segatori and S. L. Biswal, Soft Matter, 2014, 10, 6417–6424 RSC.
- M. A. Deverall, E. Gindl, E.-K. Sinner, H. Besir, J. Ruehe, M. J. Saxton and C. A. Naumann, Biophys. J., 2005, 88, 1875–1886 CrossRef CAS PubMed.
- A. Benda, V. Fagul'ová, A. Deyneka, J. Enderlein and M. Hof, Langmuir, 2006, 22, 9580–9585 CrossRef CAS PubMed.
- S. Hong, P. R. Leroueil, E. K. Janus, J. L. Peters, M.-M. Kober, M. T. Islam, B. G. Orr, J. R. Baker and M. M. Banaszak Holl, Bioconjugate Chem., 2006, 17, 728–734 CrossRef CAS PubMed.
- F. J. Pavinatto, L. Caseli, A. Pavinatto, D. S. dos Santos, T. M. Nobre, M. E. D. Zaniquelli, H. S. Silva, P. B. Miranda and O. N. de Oliveira, Langmuir, 2007, 23, 7666–7671 CrossRef CAS PubMed.
- M. Werner and J.-U. Sommer, Biomacromolecules, 2015, 16, 125–135 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm02645a |
| This journal is © The Royal Society of Chemistry 2017 |