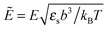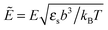DOI:
10.1039/C7SM00417F
(Paper)
Soft Matter, 2017,
13, 4363-4369
Statistical theory of polarizable target compound impregnation into a polymer coil under the influence of an electric field
Received
27th February 2017
, Accepted 24th April 2017
First published on 25th April 2017
Abstract
The paper presents a theoretical approach for describing the influence of an electric field on the conformation of an electrically neutral dielectric polymer chain dissolved in a dielectric solvent with an admixture of a target compound. Each monomer and each molecule of the target compound carries positive excess polarizability and the solvent is described as a continuous dielectric medium. The model is based on the Flory-type mean-field theory. We demonstrate non-monotonic dependences of the expansion factor and the concentration of the target compound on the strength of the electric field and molecular polarizability. Namely, the target compound concentration in the internal polymer volume as a function of electric field strength has pronounced maxima if the molecules are polarizable. In addition, the expansion factor of the non-polarizable polymer chain can be controlled by the electric field. The dependences of the expansion factor and target compound concentration on the monomer polarizability exhibit minima and intersection points. The intersection points correspond to the equality of dielectric permittivities in the bulk solution and in the internal polymer volume.
1 Introduction
It is well known that there are numerous external stimuli such as temperature, pressure, pH, composition, etc., which may affect the thermodynamic and structural properties of polymer solutions. These external stimuli are particularly important for the description of the so-called ‘smart’ or ‘environmentally sensitive’ polymers.1,2 These polymers are called smart because their properties can be changed by minor changes in the polymer surroundings. The abovementioned stimuli can produce changes in one or several properties such as shape, volume, solubility, surface characteristics, etc.3 Moreover, the reversibility of these changes is the peculiarity of ‘smart’ materials. An electric field is one of the stimuli, despite its nature, which can be both artificial (a pair of electrodes) and natural (electric fields of biological membranes, for instance). It is also one of the possible stimuli for a controlled drug release system.2,4 The mechanism is based on the motion of electrically charged molecules under the influence of an electric field. The electric field affects both particles carrying a net electric charge and dielectric particles carrying permanent or induced dipole moments. The application of an electric field to dielectrics may lead to different effects, for instance, electrostriction and dielectrophoresis (electrostriction is the deformation of a dielectric medium under an electric field, and dielectrophoresis is the motion of particles in an inhomogeneous electric field5,6).
The theoretical physics of dielectric polymers still remains a terra incognita. Indeed, there are several works devoted to the thermodynamic properties of dielectric polymer solutions and polymer brushes. Kumar et al. described the influence of monomer permanent dipole moments on the polymer mixture phase diagram shape.7 Dean and Podgornik formulated the theory of anisotropic van der Waals interactions of semi-flexible polymers and their influence on ordering.8 Podgornik also presented a theory describing the influence of electrostatic interactions of permanent dipoles on persistence length.9 Lu et al. analyzed static van der Waals interactions between two polarizable rigid polymers within the field-theoretic approach.10 In ref. 11, the authors formulated a statistical field theory of dielectric soft matter. In ref. 12, the authors developed a self-consistent field theory of polar polymer brushes and analyzed its phase behavior depending on dipolar monomer interactions.
Theoretically, the electric field influence on various polymer properties has been studied mostly for polyelectrolyte solutions13–21 and polyelectrolyte-based electrically responsive hydrogels as delivery systems (see, for instance, ref. 22–24). Under an electric field, polyelectrolyte chains and electrically responsive hydrogels are strongly deformable, which makes them perfect systems for drug delivery or creation of artificial muscles.19–21,25–27 Their response to the electric field is achieved by the presence of an electric charge on the polymer backbone. However, there is a wide class of neutral dielectric polymers with permanent dipoles and/or molecular polarizability of monomers that are exposed to an electric field. Nevertheless, dielectric polymeric materials under an electric field have theoretically been studied even much less extensively than the mentioned bulky dielectric polymers. Shkel and Klingenberg formulated generic models of solid material electrostriction.28 Suo suggested theoretical models of dielectric elastomers which are strongly deformable under an applied electric field.29 There are some works on the electrostriction of polymeric gels30,31 and copolymer melts.32,33 Recent papers34,35 have shown that the application of a homogeneous constant electric field leads to dielectric polymer expansion, regardless of the conformation (coil or globule). Moreover, these studies have investigated the influence of the many-body electrostatic dipole correlations of monomers on the conformational behavior of polymer chains.35,36 These papers have demonstrated that when the excess polarizability is positive, the application of an electric field to a polymer solution always leads to electrostriction swelling of the polymer chain. In recent papers,37,38 the authors theoretically studied the influence of co-solvent polarizability on the differential capacitance of electric double layers. Using a local density functional approach, a modified Poisson–Boltzmann theory with an explicit account of polarizable co-solvent and excluded volume of the ions and the co-solvent was formulated.
The polymer coil swelling under the constant homogeneous electric field makes it reasonable to question: how will electrostriction affect the impregnation of some polarizable target compound (TC) inside a polarizable polymer coil? To the best of our knowledge, dilute solutions of dielectric polymers in the presence of the dielectric TC under an electric field have not been investigated systematically even at the level of the mean-field theory. A theoretical description of the TC concentration inside the polymer volume and polymer conformational behavior under an electric field is the main focus of the paper.
The paper is organized as follows: Section 2 presents the model and Section 3 the numerical results and discussion, followed by conclusions in Section 4.
2 Model
Now we will consider a simple model of a dilute polymer solution with an admixture of polarizable TC molecules. The solvent is treated as a dielectric medium with constant dielectric permittivity εs. As in our previous papers,39–42 the whole volume of the solution is divided into two parts: the volume of the polymer chain (assessed by the polymer chain gyration volume) and the volume of the bulk solution. The impregnation process is described as a thermodynamic equilibrium between the bulk volume and the gyration volume of the polymer chain in terms of target compound concentration and polymer volume. The aim of this paper is to consider such a system under a static electric field taking into account the static positive excess polarizability of monomers and TC molecules. To reach our goal, we simplify the model, which assumes a linear and isotropic response of all molecules in the solution to the electric field. The latter assumption allows us to consider the grand thermodynamic potential for the gyration volume in the simplest form. Moreover, the effects discussed in this paper in general are independent of the polymer form and determined by the difference in dielectric permittivities in the gyration volume and bulk solution. We would like to stress that only our assumption of the isotropic dielectric response of the solution species makes it possible to consider the theory in terms of pressure instead of a stress tensor.43
2.1 Model: bulk volume
We start from the free energy per particle of the TC in the bulk solution, which can be written as follows:| | 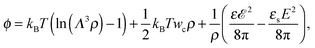 | (1) |
where the concentration ρ of TC molecules and the temperature T are determined. The first contribution on the right hand side of (1) is the ideal gas free energy of the target compound, the second one is the interaction energy between the particles at the level of the second virial term and the third one is the electrostatic energy of the solution. Also, kB is the Boltzmann constant, Λ is the thermal de Broglie wavelength, wc is the second virial coefficient of the effective interactions between the TC molecules in the solvent medium, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is the strength of the electric field in the pure solvent, is the strength of the electric field in the solution (see below), εs is the dielectric permittivity of the solvent medium, and ε is the dielectric permittivity in the bulk solution:37,38where the polarizability of the TC (γc) is introduced. The third term on the right hand side of (1) describes the excess electrostatic free energy of the TC relative to the pure solvent. The electric field strength in the solution can be evaluated as follows:43
is the strength of the electric field in the pure solvent, is the strength of the electric field in the solution (see below), εs is the dielectric permittivity of the solvent medium, and ε is the dielectric permittivity in the bulk solution:37,38where the polarizability of the TC (γc) is introduced. The third term on the right hand side of (1) describes the excess electrostatic free energy of the TC relative to the pure solvent. The electric field strength in the solution can be evaluated as follows:43| | 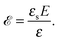 | (3) |
Using these notations, the chemical potential and partial pressure of the TC molecules take the following form:| | 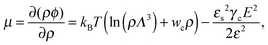 | (4) |
and| | 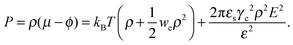 | (5) |
2.2 Model: internal polymer volume
Now let us discuss the model of a mixture in the gyration volume. We choose two independent order parameters: the gyration radius (Rg) of the polymer chain and the average number of the TC molecules (Nc) in the gyration volume. We consider the configurational entropy of the polymer chain at the level of the well-known Fixman's approximation,44–46 which has been successfully used to describe the coil–globule transitions induced by different external stimuli.39–42 The volume interactions between the molecules in the solution are described by the second virial coefficients (monomer–monomer, TC–TC, monomer–TC interactions). Thus, bearing in mind all the above factors, one can construct the Gibbs thermodynamic potential as follows:| | | ΔG(Nc, Rg) = Fid(Rg, Nc) + Fvol(Rg, Nc) + Fel(Rg, Nc) − μNc + PVg, | (6) |
Here| | 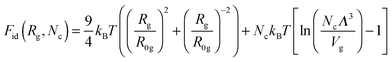 | (7) |
is the ideal part of the free energy, where the first term is the conformation free energy of the Gaussian polymer chain within Fixman's approximation and the second term is the free energy of the ideal gas confined in the volume Vg; the contribution of the effective interactions between the species can be written as follows:47| | 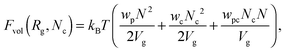 | (8) |
where N is the degree of polymerization, and wp, wc, and wpc are the second virial coefficients for monomer–monomer, TC–TC and monomer–TC interactions, respectively. It should be noted that in our consideration we assume that the degrees of freedom of the solvent molecules are integrated out, so the above mentioned second virial coefficients are renormalized with respect to the “bare” virial coefficients by the presence of the solvent. In other words, in accordance with the classical McMillan–Mayer theory,48 all the considered second virial coefficients are related to the potentials of mean-force of the interaction between the species in the solvent medium. Thus, following the logic mentioned above (McMillan–Mayer theory), one can construct the solvation free energy of the polymer using partial pressure instead the total pressure. The total electrostatic free energy within the mean-field approximation consists of two terms: where Fex,p is the excess free energy of the mixture in the gyration volume relative to the bulk solution, and Fex,c is the excess free energy of the bulk solution in the gyration volume relative to the pure solvent. These contributions can be assessed within the mean-field approximation as follows:49| | 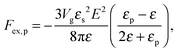 | (10) |
and| | 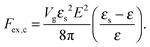 | (11) |
We would like to emphasize that the polymer is modeled as a polarizable sphere with the dielectric permittivity εp immersed in the dielectric medium with the dielectric permittivity ε. Thus, the total electrostatic free energy is calculated as the excess electrostatic energy of the monomers together with the TC molecules contained in the gyration volume relative to the pure solvent occupying the same volume. μ and P are, respectively, the chemical potential and partial pressure of the TC in the bulk solution satisfying expressions (4) and (5). Now, let us clarify the symbolic notations: R0g2 = Nb2/6 is the mean-square radius of gyration of the Gaussian polymer chain with the Kuhn length b, and E is the strength of the electric field. The gyration volume of the polymer chain is expressed through the gyration radius as:| | 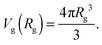 | (12) |
The dielectric permittivity of the solution in the gyration volume is expressed as:37| | 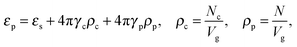 | (13) |
where γc is the polarizability of one TC molecule, γp is the polarizability of monomers, ρc is the TC concentration in the gyration volume, and ρp is the concentration of monomers in the gyration volume. Now minimizing eqn (6) relative to the expansion factor of the polymer chain and the concentration of TC molecules in the gyration volume, one can obtain the following system of two coupled equations:| | 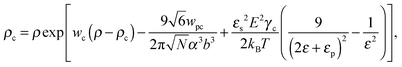 | (14) |
| | 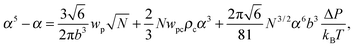 | (15) |
where the expansion factor α = Rg/R0g is introduced. The latter system describes the behavior of the expansion factor α and concentration ρc of the TC molecules near the polymer backbone depending on the electric field strength E, polarizabilities of the solution species γp and γc, second virial coefficients wp, wc and wpc, and the index of polymerization N. In eqn (15), the difference ΔP between the partial TC pressure inside the gyration volume which is expressed as:| | 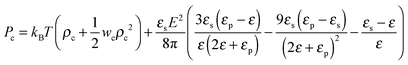 | (16) |
and the bulk pressure (5) is determined. The pressure difference ΔP consists of three parts: the first is the ideal contribution, the second is the contribution of the interactions between the target compound and the third is the electrostatic contribution. The exact form of the electrostatic contribution depends on the geometrical description of the polymer chain, while the first two terms hold the standard form of the virial expression.47 When the dielectric permittivity in the gyration volume is equal to the bulk permittivity εp = ε, the electrostatic contributions in eqn (14) and (15) vanish. Let us now consider the limiting case of the expanded coil, i.e., when α ≫ 1 and (ρc − ρ)/ρ ≪ 1. In the present limit, we obtain the following equation:| | 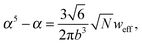 | (17) |
where| | 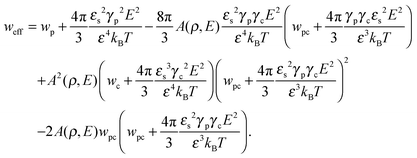 | (18) |
is the effective second virial coefficient of monomers in the solution under the electric field and the auxiliary function| | 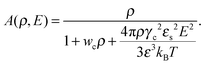 | (19) |
is also introduced.
The results recently obtained by Budkov et al.34,35 can be derived from eqn (17) by deleting the terms produced by the presence of TC molecules in the solution, i.e., when ρ = 0. Thus, in the absence of TC molecules in the solution, monomer polarizability is the only driving force for polymer chain swelling in the electric field. As we shall show below, an admixture of the TC molecules leads to non-monotonic dependences of both the expansion factor and TC concentration on the electric field and polarizability of the TC molecules.
3 Numerical results
For numerical calculations the following set of dimensionless parameters has been introduced: ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = wp/b3,
p = wp/b3, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = wc/b3,
c = wc/b3, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = wpc/b3,
pc = wpc/b3, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs),
p = γp/(b3εs), ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs), and
c = γc/(b3εs), and 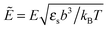 . The calculations have been made for the polymer chain with repulsive interactions between the monomers and TC molecules, that is to say
. The calculations have been made for the polymer chain with repulsive interactions between the monomers and TC molecules, that is to say ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc > 0. The numerical results are divided into two parts:
pc > 0. The numerical results are divided into two parts: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c and
c and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c.
c.
3.1 Regime I: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) c
c
The expansion factor α and the dimensionless concentration of TC molecules ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = ρcb−3 in the gyration volume were plotted as functions of the electric field strength to demonstrate the influence of TC polarizability on them. The other parameters were fixed: N = 102,
c = ρcb−3 in the gyration volume were plotted as functions of the electric field strength to demonstrate the influence of TC polarizability on them. The other parameters were fixed: N = 102, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = 0.5,
p = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 0.5,
c = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = 1.5, and
pc = 1.5, and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = 0.15. This combination of virial coefficients results in a collapsed conformation of the polymer coil at E → 0 due to the polymer “solvophobicity” relative to the TC molecules.
c = 0.15. This combination of virial coefficients results in a collapsed conformation of the polymer coil at E → 0 due to the polymer “solvophobicity” relative to the TC molecules.
The TC concentration ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c in the gyration volume and the expansion factor α of the polymer coil as functions of electric field strength are shown in Fig. 1 and 2. These calculations were done for the following set of TC polarizabilities
c in the gyration volume and the expansion factor α of the polymer coil as functions of electric field strength are shown in Fig. 1 and 2. These calculations were done for the following set of TC polarizabilities ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0,
c = 0, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.2, and
c = 0.2, and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.4 and fixed monomer polarizability
c = 0.4 and fixed monomer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0.8. As mentioned above, in the absence of an electric field the polymer coil exists in a collapsed conformation, whereas its application expands the coil. Such behavior is in agreement with our previous results.34,35 If the TC molecules are non-polarizable, then ρc tends to the bulk value as the electric field strength increases. However, in the case of polarizable TC molecules, the picture changes. Namely, with an increase in the polarizability of TC molecules, their concentration in the gyration volume monotonically decreases as the electric field strength increases. Moreover, at the non-zero polarizability of the TC molecules, the dependence of the TC concentration on the electric field strength has pronounced maxima in the vicinity of E ≈ 2. These extrema are caused by introducing TC polarizability into the model. Now let us consider the behavior of ρc with the increase in the degree of polymerization N, analyzing eqn (14). It is evident that with N → ∞ the second term in the exponent of eqn (14) vanishes. Thus, in the limit of infinite chain solution, eqn (14) results in ρc = ρ. To illustrate that, Fig. 3 presents the dependence of TC concentration ρc on the electric field for N = 100, 600, and 1000. As one can see, with the increase in the polymerization index the abovementioned non-monotonic behavior of TC concentration disappears.
p = 0.8. As mentioned above, in the absence of an electric field the polymer coil exists in a collapsed conformation, whereas its application expands the coil. Such behavior is in agreement with our previous results.34,35 If the TC molecules are non-polarizable, then ρc tends to the bulk value as the electric field strength increases. However, in the case of polarizable TC molecules, the picture changes. Namely, with an increase in the polarizability of TC molecules, their concentration in the gyration volume monotonically decreases as the electric field strength increases. Moreover, at the non-zero polarizability of the TC molecules, the dependence of the TC concentration on the electric field strength has pronounced maxima in the vicinity of E ≈ 2. These extrema are caused by introducing TC polarizability into the model. Now let us consider the behavior of ρc with the increase in the degree of polymerization N, analyzing eqn (14). It is evident that with N → ∞ the second term in the exponent of eqn (14) vanishes. Thus, in the limit of infinite chain solution, eqn (14) results in ρc = ρ. To illustrate that, Fig. 3 presents the dependence of TC concentration ρc on the electric field for N = 100, 600, and 1000. As one can see, with the increase in the polymerization index the abovementioned non-monotonic behavior of TC concentration disappears.
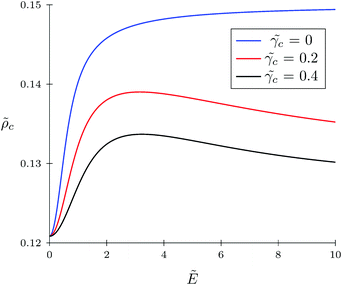 |
| | Fig. 1 Dependence of target compound concentration ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = ρcb−3 on electric field strength c = ρcb−3 on electric field strength 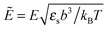 in the gyration volume at constant polymer polarizability in the gyration volume at constant polymer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities. p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities. | |
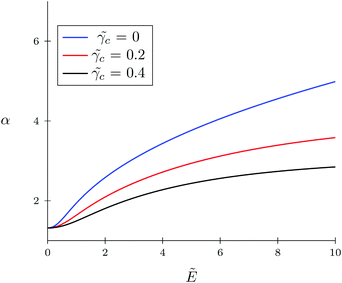 |
| | Fig. 2 Dependence of expansion parameter α on electric field strength 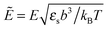 of the polymer coil at constant polymer polarizability of the polymer coil at constant polymer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities. p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities. | |
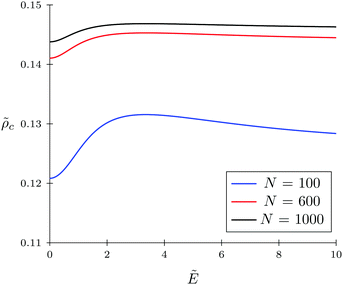 |
| | Fig. 3 Dependence of target compound concentration ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = ρb−3 on the electric field strength c = ρb−3 on the electric field strength 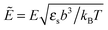 in the gyration volume at constant polymer in the gyration volume at constant polymer ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) = 0.8 and target compound p = γp/(b3εs) = 0.8 and target compound ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs) = 0.5 polarizabilities. c = γc/(b3εs) = 0.5 polarizabilities. | |
3.2 Regime II: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) c
c
Firstly, let us look at the dependence of α and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c on polymer polarizability at fixed electric field strength and other parameters. Fig. 4 and 5 show the concentration of TC molecules
c on polymer polarizability at fixed electric field strength and other parameters. Fig. 4 and 5 show the concentration of TC molecules ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c and expansion factor α as functions of
c and expansion factor α as functions of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p monomer polarizability at different electric field strengths with fixed TC polarizability
p monomer polarizability at different electric field strengths with fixed TC polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.5.
c = 0.5.
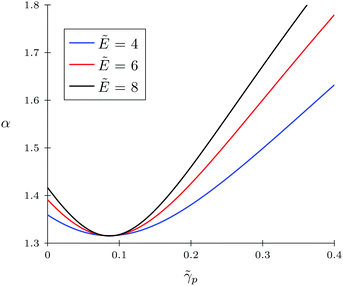 |
| | Fig. 4 Expansion factor α as a function of monomer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) for the solvophobic polymer at fixed values of electric field strength; target compound polarizability p = γp/(b3εs) for the solvophobic polymer at fixed values of electric field strength; target compound polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs) = 0.5. c = γc/(b3εs) = 0.5. | |
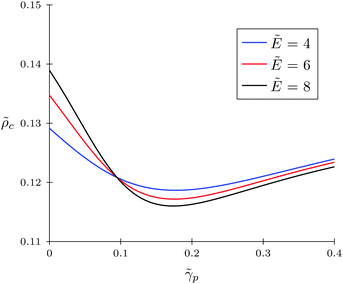 |
| | Fig. 5 Concentration of target compound molecules in the gyration volume ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c as a function of monomer polarizability c as a function of monomer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) for the solvophobic polymer at fixed values of electric field strength; target compound polarizability p = γp/(b3εs) for the solvophobic polymer at fixed values of electric field strength; target compound polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs) = 0.5. c = γc/(b3εs) = 0.5. | |
Both functions have minima at non-zero monomeric polarizability. There is another interesting feature – these functions have intersection points that correspond to the equality of the dielectric permittivities in the bulk solution and the gyration volume. In order to prove this statement, we put ε = εp. This substitution slightly changes the system of coupled equations. The only differences are: in eqn (14) the third term in the exponent is absent and in eqn (15) the third term is modified with ΔP = Pc − P = kBT(ρc − ρ + 1/2wc(ρc2 − ρ2)). Following these changes, let us write down:
| | 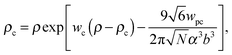 | (20) |
| | 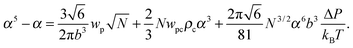 | (21) |
Using the new system, we obtain numerical values of
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p
p ≈ 0.09,
α ≈ 1.31 and
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c
c ≈ 0.12 which correspond to the intersections on the graphs. So,
eqn (20) and (21) describe the case when neither the expansion factor nor the TC concentration depends on the electric field strength.
Now let us discuss the case of a non-polarizable polymer chain, i.e. ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0, as opposed to TC molecules. Thus, it can be the case of a highly ‘solvophobic’ polymer relative to the TC molecules. The virial coefficients
p = 0, as opposed to TC molecules. Thus, it can be the case of a highly ‘solvophobic’ polymer relative to the TC molecules. The virial coefficients ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = 0.5,
p = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 0.5, and
c = 0.5, and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = 3 are chosen in order to make this regime more pronounced. In Fig. 6, we present the behavior of the expansion factor with different values of TC polarizability, namely,
pc = 3 are chosen in order to make this regime more pronounced. In Fig. 6, we present the behavior of the expansion factor with different values of TC polarizability, namely, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.2,
c = 0.2, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.4 and
c = 0.4 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.6. Also, in Fig. 7, the TC concentration behavior inside the gyration volume is presented at the same TC polarizabilities.
c = 0.6. Also, in Fig. 7, the TC concentration behavior inside the gyration volume is presented at the same TC polarizabilities.
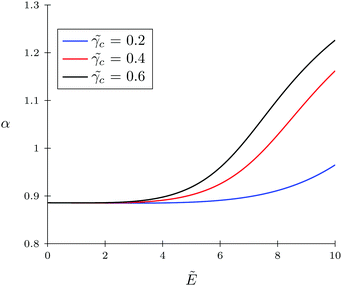 |
| | Fig. 6 Behavior of the solvophobic polymer with zero polarizability (![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0) in the presence of the polarizable target compound under an electric field. The polarizabilities of target compound molecules are taken as p = 0) in the presence of the polarizable target compound under an electric field. The polarizabilities of target compound molecules are taken as ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs) = 0.2, 0.4, and 0.6. c = γc/(b3εs) = 0.2, 0.4, and 0.6. | |
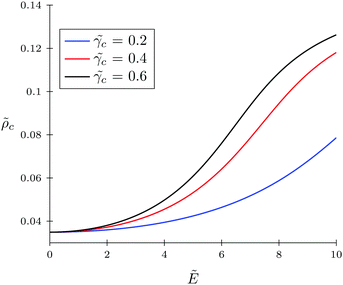 |
| | Fig. 7 Behavior of TC concentration inside the gyration volume of the solvophobic polymer with zero polarizability (![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0) under an electric field. The polarizabilities of target compound molecules are taken as p = 0) under an electric field. The polarizabilities of target compound molecules are taken as ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs) = 0.2, 0.4, and 0.6. c = γc/(b3εs) = 0.2, 0.4, and 0.6. | |
Under low electric fields, the expansion factor remains nearly constant and then begins to increase monotonically. This regime can be described as follows. Due to the high ‘solvophobicity’ of the polymer chain the concentration of TC molecules inside the gyration volume is much lower compared to the bulk value, which leads to polymeric coil compression. The electric field application tends to increase the TC concentration in the gyration volume, which, in turn, expands the polymer coil. It is worth noting that the TC molecule concentration in the gyration volume is always lower than the bulk value even at zero polymer solvophobicity (wpc = 0). That is due to the fact that the electric field in the gyration volume is weaker than its bulk value, so the TC molecules – carrying induced dipoles – prefer to be in the bulk solution rather than in the gyration volume.
4 Conclusions
In this work we have extended the theoretical description of internal and external stimuli for a polymer coil as a ‘smart’ polymer. We have described the impregnation of a polarizable solvophobic polymer coil with an additional amount of the polarizable target compound.
We tested two regimes: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c and
c and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c. The first regime has shown (1) a monotonic increase in the expansion factor of the polymer coil with the increase of the electric field strength and (2) a maximum for the dependence of the target compound concentration in the gyration volume on the electric field. This maximum becomes more pronounced with the target compound polarizability growth. In the second regime, non-monotonic dependences of the expansion factor and the TC concentration on the polymer polarizability were demonstrated.
c. The first regime has shown (1) a monotonic increase in the expansion factor of the polymer coil with the increase of the electric field strength and (2) a maximum for the dependence of the target compound concentration in the gyration volume on the electric field. This maximum becomes more pronounced with the target compound polarizability growth. In the second regime, non-monotonic dependences of the expansion factor and the TC concentration on the polymer polarizability were demonstrated.
We also stress that the results described above were provided with the assumption of an isotropic dielectric response to the electric field, which allowed us to use the simple level of theoretical description. We assume that the effects related to the change in the coil shape should be important at a high strength of the electric field. In any case, our aim was to show the very possibility of controlling the polymer and the target compound concentration inside the polymer volume. We believe that all this information can contribute to a better understanding of the dielectric polymer behavior under an electric field.
We would like to stress that in this study we have neglected the contribution of the dipole correlations (for details see ref. 35) of the solution species. It can be shown that this contribution cannot qualitatively change the final outcomes of the present pure mean-field theory. The suggested theory also has an obvious limitation. Namely, it can be applied to polymer chains whose monomers are isotropically polarizable. In other words, in order to apply this theory, monomers and target compound molecules must have small non-diagonal components of polarizability tensors. The second limitation of the present theory is that it cannot describe the change in the polymer shape under an electric field. Indeed, we have introduced only one geometric parameter – radius of gyration – that makes it possible to control changes in the polymer volume as a whole, but it does not allow us to describe the polymer coil shape change. Nevertheless, in our opinion, this limitation is not crucial in the case, when small enough polymer coil deformations or electric field strengths (compared to the internal molecular electric field) are considered. The latter assumption is always satisfied under the experimentally accessible conditions.
Acknowledgements
YAB and MGK are grateful for the financial support from the Russian Scientific Foundation (grant no. 14-33-00017).
References
- P. Bawa, V. Pillay, Y. E. Choonara and L. C. Du Toit, Biomed. Mater., 2009, 4, 022001 CrossRef PubMed.
- A. Bajpai, S. K. Shukla, S. Bhanu and S. Kankane, Prog. Polym. Sci., 2008, 33, 1088–1118 CrossRef CAS.
- A. Kumar, A. Srivastava, I. Y. Galaev and B. Mattiasson, Prog. Polym. Sci., 2007, 32, 1205–1237 CrossRef CAS.
- J. Ge, E. Neofytou, T. J. Cahill III, R. E. Beygui and R. N. Zare, ACS Nano, 2011, 6, 227–233 CrossRef PubMed.
- H. A. Pohl, J. Appl. Phys., 1951, 22, 869 CrossRef CAS.
- R. Pethig, Adv. Drug Delivery Rev., 2013, 65, 1589–1599 CrossRef CAS PubMed.
- R. Kumar, B. G. Sumpter and M. Muthukumar, Macromolecules, 2014, 47, 6491–6502 CrossRef CAS.
- D. S. Dean and R. Podgornik, J. Chem. Phys., 2012, 136, 154905 CrossRef PubMed.
- R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 031801 CrossRef PubMed.
- B.-S. Lu, A. Naji and R. Podgornik, J. Chem. Phys., 2015, 142, 214904 CrossRef PubMed.
- J. M. Martin, W. Li, K. T. Delaney and G. H. Fredrickson, J. Chem. Phys., 2016, 145, 154104 CrossRef PubMed.
- J. P. Mahalik, B. G. Sumpter and R. Kumar, Macromolecules, 2016, 49, 7096–7107 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 1987, 86, 7230–7235 CrossRef CAS.
- R. Podgornik and B. Jönsson, EPL, 1993, 24, 501 CrossRef CAS.
- O. Borisov, E. Zhulina and T. Birshtein, Macromolecules, 1994, 27, 4795–4803 CrossRef CAS.
- X. Châtellier and J.-F. Joanny, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6923 CrossRef.
- R. Netz, J. Phys. Chem. B, 2003, 107, 8208–8217 CrossRef CAS.
- N. Brilliantov and C. Seidel, EPL, 2012, 97, 28006 CrossRef.
- C. Seidel, Y. A. Budkov and N. V. Brilliantov, Proc. Inst. Mech. Eng., Part N, 2013, 174034 Search PubMed.
- N. Brilliantov, Y. A. Budkov and C. Seidel, Philos. Trans. R. Soc., A, 2016, 374, 20160143 CrossRef PubMed.
- N. V. Brilliantov, Y. A. Budkov and C. Seidel, Phys. Rev. E, 2016, 93, 032505 CrossRef CAS PubMed.
- M. Jensen, P. B. Hansen, S. Murdan, S. Frokjaer and A. T. Florence, Eur. J. Pharm. Sci., 2002, 15, 139–148 CrossRef CAS PubMed.
- S. J. Kim, S. J. Park, I. Y. Kim, M.-S. Shin and S. I. Kim, J. Appl. Polym. Sci., 2002, 86, 2285–2289 CrossRef CAS.
- A. K. Anal, Recent Pat. Endocr., Metab. Immune Drug Discovery, 2007, 1, 83–90 CrossRef CAS.
- Y. Qiu and K. Park, Adv. Drug Delivery Rev., 2012, 64, 49–60 CrossRef.
- T. Hirai, H. Nemoto, M. Hirai and S. Hayashi, J. Appl. Polym. Sci., 1994, 53, 79–85 CrossRef CAS.
- N. V. Brilliantov, Yu. A. Budkov and C. Seideld, Theoretical and numerical analysis of nano-actuators based on grafted polyelectrolytes in an electric field, Faraday Discuss. 10.1039/c6fd00240d.
- Y. M. Shkel and D. J. Klingenberg, J. Appl. Phys., 1998, 83, 7834–7843 CrossRef CAS.
- Z. Suo, Acta Mechanica Solida Sinica, 2010, 23, 549–578 CrossRef.
- G. Filipcsei, J. Feher and M. Zrnyi, J. Mol. Struct., 2000, 554, 109–117 CrossRef CAS.
- J. Fehér, G. Filipcsei, J. Szalma and M. Zrinyi, Colloids Surf., A, 2001, 183, 505–515 CrossRef.
- E. Gurovich, Macromolecules, 1994, 27, 7339–7362 CrossRef CAS.
- E. Gurovich, Macromolecules, 1995, 28, 6078–6083 CrossRef CAS.
- Y. A. Budkov, A. Kolesnikov and M. Kiselev, J. Chem. Phys., 2015, 143, 201102 CrossRef PubMed.
- Y. A. Budkov and A. Kolesnikov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 110 CrossRef PubMed.
- Y. A. Budkov, A. Kolesnikov and M. Kiselev, EPL, 2015, 111, 28002 CrossRef.
- Yu. A. Budkov, N. N. Kalikin and A. L. Kolesnikov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 47 CrossRef PubMed.
- Y. A. Budkov, A. Kolesnikov and M. Kiselev, J. Chem. Phys., 2016, 144, 184703 CrossRef PubMed.
- Y. A. Budkov, A. Kolesnikov, N. Georgi and M. Kiselev, J. Chem. Phys., 2014, 141, 014902 CrossRef PubMed.
- Y. A. Budkov, I. Vyalov, A. Kolesnikov, N. Georgi, G. Chuev and M. Kiselev, J. Chem. Phys., 2014, 141, 204904 CrossRef PubMed.
- Y. A. Budkov, A. Kolesnikov, N. Georgi and M. Kiselev, EPL, 2015, 109, 36005 CrossRef.
- Y. A. Budkov, A. Kolesnikov, N. Kalikin and M. Kiselev, EPL, 2016, 114, 46004 CrossRef.
-
L. Landau and E. Lifshitz, Electrodynamics of Continuous Media V.8, A Course of Theoretical Physics, Pergamon Press, Oxford, 1960 Search PubMed.
- M. Fixman, J. Chem. Phys., 1962, 36, 306–310 CrossRef CAS.
- A. Y. Grosberg and D. Kuznetsov, Macromolecules, 1992, 25, 1970–1979 CrossRef CAS.
- Y. A. Budkov and A. Kolesnikov, J. Stat. Mech.: Theory Exp., 2016, 2016, 103211 CrossRef.
-
L. D. Landau, E. Lifshitz and L. Pitaevskii, Statistical physics, part I, Pergamon, Oxford, 1980 Search PubMed.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids: With Applications to Soft Matter, Academic Press, 2013 Search PubMed.
-
L. Landau and M. Lifshitz, Electrodynamics of continuous media, Pergamon Press, Oxford, 1960 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Yu. A.
Budkov
b,
E. A.
Basharova
c and
M. G.
Kiselev
d
*a,
Yu. A.
Budkov
b,
E. A.
Basharova
c and
M. G.
Kiselev
d
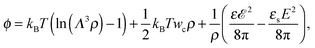
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is the strength of the electric field in the pure solvent, is the strength of the electric field in the solution (see below), εs is the dielectric permittivity of the solvent medium, and ε is the dielectric permittivity in the bulk solution:37,38
is the strength of the electric field in the pure solvent, is the strength of the electric field in the solution (see below), εs is the dielectric permittivity of the solvent medium, and ε is the dielectric permittivity in the bulk solution:37,38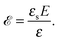
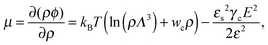
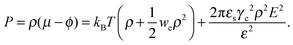
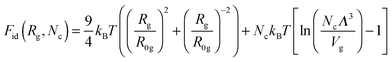
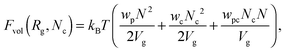
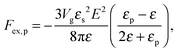
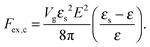
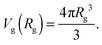
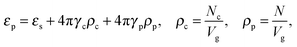
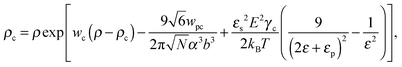
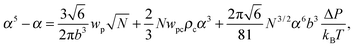
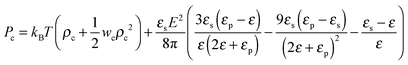
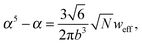
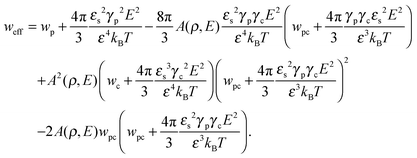
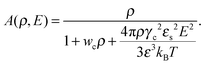
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = wp/b3,
p = wp/b3, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = wc/b3,
c = wc/b3, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = wpc/b3,
pc = wpc/b3, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs),
p = γp/(b3εs), ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = γc/(b3εs), and
c = γc/(b3εs), and 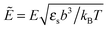 . The calculations have been made for the polymer chain with repulsive interactions between the monomers and TC molecules, that is to say
. The calculations have been made for the polymer chain with repulsive interactions between the monomers and TC molecules, that is to say ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc > 0. The numerical results are divided into two parts:
pc > 0. The numerical results are divided into two parts: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c and
c and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c.
c.
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) c
c![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = ρcb−3 in the gyration volume were plotted as functions of the electric field strength to demonstrate the influence of TC polarizability on them. The other parameters were fixed: N = 102,
c = ρcb−3 in the gyration volume were plotted as functions of the electric field strength to demonstrate the influence of TC polarizability on them. The other parameters were fixed: N = 102, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = 0.5,
p = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 0.5,
c = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = 1.5, and
pc = 1.5, and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c = 0.15. This combination of virial coefficients results in a collapsed conformation of the polymer coil at E → 0 due to the polymer “solvophobicity” relative to the TC molecules.
c = 0.15. This combination of virial coefficients results in a collapsed conformation of the polymer coil at E → 0 due to the polymer “solvophobicity” relative to the TC molecules.
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c in the gyration volume and the expansion factor α of the polymer coil as functions of electric field strength are shown in Fig. 1 and 2. These calculations were done for the following set of TC polarizabilities
c in the gyration volume and the expansion factor α of the polymer coil as functions of electric field strength are shown in Fig. 1 and 2. These calculations were done for the following set of TC polarizabilities ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0,
c = 0, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.2, and
c = 0.2, and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.4 and fixed monomer polarizability
c = 0.4 and fixed monomer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0.8. As mentioned above, in the absence of an electric field the polymer coil exists in a collapsed conformation, whereas its application expands the coil. Such behavior is in agreement with our previous results.34,35 If the TC molecules are non-polarizable, then ρc tends to the bulk value as the electric field strength increases. However, in the case of polarizable TC molecules, the picture changes. Namely, with an increase in the polarizability of TC molecules, their concentration in the gyration volume monotonically decreases as the electric field strength increases. Moreover, at the non-zero polarizability of the TC molecules, the dependence of the TC concentration on the electric field strength has pronounced maxima in the vicinity of E ≈ 2. These extrema are caused by introducing TC polarizability into the model. Now let us consider the behavior of ρc with the increase in the degree of polymerization N, analyzing eqn (14). It is evident that with N → ∞ the second term in the exponent of eqn (14) vanishes. Thus, in the limit of infinite chain solution, eqn (14) results in ρc = ρ. To illustrate that, Fig. 3 presents the dependence of TC concentration ρc on the electric field for N = 100, 600, and 1000. As one can see, with the increase in the polymerization index the abovementioned non-monotonic behavior of TC concentration disappears.
p = 0.8. As mentioned above, in the absence of an electric field the polymer coil exists in a collapsed conformation, whereas its application expands the coil. Such behavior is in agreement with our previous results.34,35 If the TC molecules are non-polarizable, then ρc tends to the bulk value as the electric field strength increases. However, in the case of polarizable TC molecules, the picture changes. Namely, with an increase in the polarizability of TC molecules, their concentration in the gyration volume monotonically decreases as the electric field strength increases. Moreover, at the non-zero polarizability of the TC molecules, the dependence of the TC concentration on the electric field strength has pronounced maxima in the vicinity of E ≈ 2. These extrema are caused by introducing TC polarizability into the model. Now let us consider the behavior of ρc with the increase in the degree of polymerization N, analyzing eqn (14). It is evident that with N → ∞ the second term in the exponent of eqn (14) vanishes. Thus, in the limit of infinite chain solution, eqn (14) results in ρc = ρ. To illustrate that, Fig. 3 presents the dependence of TC concentration ρc on the electric field for N = 100, 600, and 1000. As one can see, with the increase in the polymerization index the abovementioned non-monotonic behavior of TC concentration disappears.
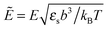 of the polymer coil at constant polymer polarizability
of the polymer coil at constant polymer polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities.
p = γp/(b3εs) = 0.8 and different co-solvent polarizabilities.![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e0dd.gif) c
c![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c on polymer polarizability at fixed electric field strength and other parameters. Fig. 4 and 5 show the concentration of TC molecules
c on polymer polarizability at fixed electric field strength and other parameters. Fig. 4 and 5 show the concentration of TC molecules ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c and expansion factor α as functions of
c and expansion factor α as functions of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p monomer polarizability at different electric field strengths with fixed TC polarizability
p monomer polarizability at different electric field strengths with fixed TC polarizability ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.5.
c = 0.5.
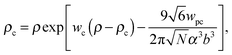
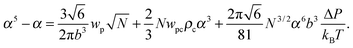
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p ≈ 0.09, α ≈ 1.31 and
p ≈ 0.09, α ≈ 1.31 and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) c ≈ 0.12 which correspond to the intersections on the graphs. So, eqn (20) and (21) describe the case when neither the expansion factor nor the TC concentration depends on the electric field strength.
c ≈ 0.12 which correspond to the intersections on the graphs. So, eqn (20) and (21) describe the case when neither the expansion factor nor the TC concentration depends on the electric field strength.
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p = 0, as opposed to TC molecules. Thus, it can be the case of a highly ‘solvophobic’ polymer relative to the TC molecules. The virial coefficients
p = 0, as opposed to TC molecules. Thus, it can be the case of a highly ‘solvophobic’ polymer relative to the TC molecules. The virial coefficients ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) p = 0.5,
p = 0.5, ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) c = 0.5, and
c = 0.5, and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) pc = 3 are chosen in order to make this regime more pronounced. In Fig. 6, we present the behavior of the expansion factor with different values of TC polarizability, namely,
pc = 3 are chosen in order to make this regime more pronounced. In Fig. 6, we present the behavior of the expansion factor with different values of TC polarizability, namely, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.2,
c = 0.2, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.4 and
c = 0.4 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c = 0.6. Also, in Fig. 7, the TC concentration behavior inside the gyration volume is presented at the same TC polarizabilities.
c = 0.6. Also, in Fig. 7, the TC concentration behavior inside the gyration volume is presented at the same TC polarizabilities.![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p <
p < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c and
c and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) p >
p > ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) c. The first regime has shown (1) a monotonic increase in the expansion factor of the polymer coil with the increase of the electric field strength and (2) a maximum for the dependence of the target compound concentration in the gyration volume on the electric field. This maximum becomes more pronounced with the target compound polarizability growth. In the second regime, non-monotonic dependences of the expansion factor and the TC concentration on the polymer polarizability were demonstrated.
c. The first regime has shown (1) a monotonic increase in the expansion factor of the polymer coil with the increase of the electric field strength and (2) a maximum for the dependence of the target compound concentration in the gyration volume on the electric field. This maximum becomes more pronounced with the target compound polarizability growth. In the second regime, non-monotonic dependences of the expansion factor and the TC concentration on the polymer polarizability were demonstrated.