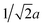Structure and magnetism of the solid solution GexFe4−xNy (0 ≤ x ≤ 1): from a ferromagnet to a spin glass
T.
Scholz
and
R.
Dronskowski
 *
*
Institute of Inorganic Chemistry, RWTH Aachen University, 52056 Aachen, Germany. E-mail: drons@HAL9000.ac.rwth-aachen.de; Fax: (+49) 241-80-92642
First published on 22nd November 2016
Abstract
We present an experimental and theoretical study of the solid solution GexFe4−xNy (0 ≤ x ≤ 1). A two-step ammonolytic reaction gives access to the compounds with phase-pure quality. The GexFe4−xNy nitrides show a transition from an antiperovskite-like to a tetragonally distorted structure with increasing germanium concentration. Various experimental and theoretical methods evidence that the iron substitution by germanium exclusively takes place at the cubic Wyckoff position 1a. Despite the phase transition, one observes a Vegard-type decrease of the lattice parameter over the entire compositional range. In addition, the nitrides have a limited nitrogen capacity: incorporating germanium drastically reduces the nitrogen content in the cubic structure, but increases it again in the tetragonal structure. Combined HT-XRD and TG-DSC measurements evidence that the germanium-richest nitrides are highly expanding materials. They first show a transition to a cubic structure before they decompose by releasing nitrogen. Magnetic measurements reveal that the gradual germanium incorporation is accompanied by a drastic weakening of the ferromagnetic interactions leading to a frustrated iron spin system. Ge0.97Fe3.03N0.56 is identified as a canonical spin glass with the characteristic parameters Tg = 36.68(5) K, τ* = 10−13.8(2) s, zν = 7.2(1) and ΔTm/(Tm·Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω) = 0.012.
ω) = 0.012.
1. Introduction
In recent years, transition-metal based ternary nitrides and carbides with a simple antiperovskite-like structure have been studied extensively because they feature remarkable physical properties such as superconductivity in MgNi3C,1 a giant magnetoresistance effect in GaMn3C,2 and the negative thermal expansion of Ge-doped MMn3N (M = Cu, Zn, Ga),3 to only name a few. Thus, it seems rewarding to focus on ternary nitrides with the general formula MxFe4−xN in order to obtain new materials. These nitrides are derived from ferromagnetic γ′-Fe4N that exhibits exceptional magnetic properties, namely a large saturation magnetisation of 208 emu g−1 and a low coercivity of 460 A m−1.4,5 Furthermore, γ′-Fe4N has high mechanical hardness and large corrosion resistance.A recently developed two-step ammonolytic synthesis6 combining a high-temperature sintering reaction (1000–1200 °C) and a low-temperature nitriding step (300–800 °C) was proven to be the most effective method to yield ternary iron nitrides MxFe4−xN (M = Rh,6 Pd,7 Ga,8,9 In,10 Sn,11,12etc.) with phase-pure quality. To date, the nitrides can be divided into two groups with regard to their magnetic properties: upon substitution they either remain ferromagnetic, as is the case in transition-metal iron nitrides, or lose the long-range magnetic order resulting in a frustrated spin system. Candidates of the second class of compounds include Sn0.9Fe3.1N, the first ternary iron nitride spin glass,12 and Ga0.9Fe3.1N with a postulated “cluster magnetism”.9 Germanium's proximity to Sn in the periodic table suggests that the Ge-substituted nitride might be related to those frustrated magnetic systems as well.
GexFe4−xNy was first studied by Stadelmaier and Fraker in 1962.13 They applied a classical NH3/H2 ammonolytic reaction to Fe–Ge precursor alloys to synthesize the ternary phase, and they also reported a cubic antiperovskite-like structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Fig. 1(a)) as well as a tetragonally distorted structure (I4/mcm, Fig. 1(b)). The relationship between the two structures can clearly be seen when considering the cuboids of Ge atoms. The very centre of a cuboid is occupied by a nitrogen atom that is surrounded by an octahedron of iron atoms. In the tetragonal structure, these octahedra are then twisted against each other. In the cubic nitride, the Ge–Ge distances are equal and correspond to the lattice parameter a. In the tetragonal structure, however, there are short and long Ge–Ge distances. To compare both structures in the later discussion, we will refer to an equivalent parameter aeq expressing an average Ge–Ge distance in the tetragonal case. Furthermore, Stadelmaier and Fraker found, in contrast to γ′-Fe4N and many ternary iron nitrides, a limited nitrogen concentration.
m, Fig. 1(a)) as well as a tetragonally distorted structure (I4/mcm, Fig. 1(b)). The relationship between the two structures can clearly be seen when considering the cuboids of Ge atoms. The very centre of a cuboid is occupied by a nitrogen atom that is surrounded by an octahedron of iron atoms. In the tetragonal structure, these octahedra are then twisted against each other. In the cubic nitride, the Ge–Ge distances are equal and correspond to the lattice parameter a. In the tetragonal structure, however, there are short and long Ge–Ge distances. To compare both structures in the later discussion, we will refer to an equivalent parameter aeq expressing an average Ge–Ge distance in the tetragonal case. Furthermore, Stadelmaier and Fraker found, in contrast to γ′-Fe4N and many ternary iron nitrides, a limited nitrogen concentration.
In another study by Sankar et al., the magnetic properties of the daltonide phase GeFe3Ny were investigated.14 Depending on the nitrogen concentration they found either a cubic nitride with a ferromagnetic (FM) ground state or a tetragonal nitride, for which they claimed antiferromagnetic (AFM) properties with a Néel temperature of 80 K. Experience with Ga0.9Fe3.1N8,9 suggests that a frustrated magnetic ground state can be easily misinterpreted as antiferromagnetism which is why we decided to re-examine the magnetic properties of germanium-rich iron nitride.
In this article, we present a comprehensive study of the entire solid solution GexFe4−xNy (0 ≤ x ≤ 1) regarding their two-step ammonolytic synthesis from the oxides, the determination of their structures and composition, the stability at elevated temperatures and, finally, the magnetic characterisation. Extensive density-functional theory (DFT) calculations were utilised to guide the experiments and to validate the results.
2. Experimental and computational methods
2.1. Synthesis of GexFe4−xNy
Phase-pure, polycrystalline GexFe4−xNy was synthesised by a recently introduced two-step ammonolytic reaction6 starting from the powdered oxides GeO2 and Fe2O3 that were mixed and finely ground using the desired ratio of the metal atoms. For an optimised reaction, the following conditions were used: 1 min at 1150 °C (sintering reaction), 17.3 K min−1 to the nitriding temperature in the range of 500–800 °C, 10 h at the nitriding temperature (nitriding reaction), 30 K min−1 to room temperature. The ammonolysis gas was a NH3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 mixture with a 1
H2 mixture with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and a flow rate of 14 mL min−1.
1 ratio and a flow rate of 14 mL min−1.
2.2. XRPD and Rietveld refinement
X-ray diffraction of GexFe4−xNy at room temperature was performed using a calibrated STADI MP (STOE Darmstadt) powder diffractometer with Mo Kα1 radiation (λ = 0.70932 Å) and a PSD detector (5° ≤ 2θ ≤ 90°, step rate 0.01° in 2θ). The flat samples were measured in transmission mode. Rietveld refinements were carried out with the program FullProf15 using a pseudo-Voigt profile function for which the axial divergence asymmetry was accounted for up to 30° in 2θ. The patterns were refined either in the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 221) with the Wyckoff positions 1a for Ge, 1b for N and 1a/3c for Fe or in the space group I4/mcm (no. 140) with 4b for Ge, 4c for N and 4a/4b/8h for Fe. The mixed occupations of Ge and Fe atoms on 1a or 4b were constrained to unity, as were the full occupations of Fe on its other positions. The experimentally determined occupation was used for N. The refinement parameters and the residual values are listed in Table 3.
m (no. 221) with the Wyckoff positions 1a for Ge, 1b for N and 1a/3c for Fe or in the space group I4/mcm (no. 140) with 4b for Ge, 4c for N and 4a/4b/8h for Fe. The mixed occupations of Ge and Fe atoms on 1a or 4b were constrained to unity, as were the full occupations of Fe on its other positions. The experimentally determined occupation was used for N. The refinement parameters and the residual values are listed in Table 3.
The high-temperature X-ray diffraction of Ge0.97Fe3.03N0.56 in a 0.3 mm quartz capillary was performed using a G644 diffractometer with Cu Kα1 radiation (λ = 1.54059 Å) and a PSD detector (38° ≤ 2θ ≤ 52°, step rate 0.02° in 2θ) from room temperature to the maximum temperature of 720 °C with temperature steps ΔT = 20 K.
2.3. TG-DSC measurements
Thermal decomposition and phase transitions were recorded by simultaneous Thermogravimetry–Differential Scanning Calorimetry using a Netzsch STA 449 C calorimeter. The experiments were conducted in an argon flow (25 mL min−1) from room temperature to 1000 °C and back to room temperature with heating and cooling rates of 20 K min−1.2.4. Magnetometry
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz such as to cover a large timescale for studying the spin-glass dynamics.
000 Hz such as to cover a large timescale for studying the spin-glass dynamics.
2.5. Computational details
Theoretical calculations of the structural and electronic properties were carried out using the Vienna ab initio simulation package (VASP)16–18 based on density-functional theory (DFT) using projector-augmented-wave (PAW) potentials19,20 for core and valence electron separation. Exchange and correlation contributions were treated with the generalised gradient approximation as parametrised by Perdew, Burke and Ernzerhof (GGA-PBE).21 An 8 × 8 × 8 Monkhorst–Pack22k-point grid for one supercell containing eight formula units was used for Brillouin-zone integration while the energy cutoff was set to 500 eV. Because of the structural similarities, the tetragonal cells were also calculated in 2 × 2 × 2 primitive supercells derived from the cubic structure but allowing for the tetragonal distortion of the Fe atoms. Spin-polarised calculations for FM and AFM cases were performed with integer starting values for all local magnetic moments, namely 3 for all magnetically active elements and 0 for all other elements. Forces, stress tensors, atomic positions, unit-cell shapes and unit-cell volumes of the crystal structures were allowed to relax during optimisation. Because of the expected small energy differences, the convergence criterion of the electronic structure calculation was set to a rather strict 10−6 eV.3. Results and discussion
3.1. Stability of GeFe3N
Prior to the synthesis and characterisation of the GexFe4−xNy series, we theoretically investigated the stability of the end member GeFe3Ny (with y = 1) to better understand the compound's structure and thermochemistry. Hence, first-principles (DFT) total-energy calculations were carried out to quantify the energies of GeFe3N at absolute zero temperature.When studying the structure of ternary iron nitrides MxFe4−xN, the first question concerns the Wyckoff position at which the substitution of Fe by a metal or metalloid M takes place. The M atom can either substitute Fe exclusively on one or on both positions simultaneously (1a and/or 3c). This depends on the covalent or metallic radius and, furthermore, on the metal's affinity to the central nitrogen atom. Generally speaking, larger M atoms prefer the larger cuboctahedral 1a environment (an approximated sphere with r = 1.42 Å) over the smaller 3c position (1.28 Å).8 The metallic radius of Ge (rM = 1.37 Å) is larger than that of Fe (rM = 1.26 Å)23, but the covalent radius of Ge (rcov = 1.20 Å) is smaller than that of Fe (l.s., rcov = 1.32 Å).24 These very different radii make the decision difficult if not impossible, and we therefore calculated the Ge distribution over both Wyckoff positions in cubic and tetragonal GeFe3N. The Ge atoms can either occupy 1a or 3c resulting in ordered phases 1a(Ge)3c(Fe3)1b(N) and 1a(Fe)3c(GeFe2)1b(N) when applying the cubic nomenclature. Furthermore, they can be statistically disordered as given in 1a(Ge1/4Fe3/4)3c(Ge3/4Fe9/4)1b(N). From the energetic results in Table 1, it is all too obvious that the Ge atoms will exclusively occupy the larger corner position – that scenario is energetically favoured by an enormous 97 or 110 kJ mol−1 over the statistically disordered arrangement. Furthermore, the theoretical calculations predict a preferred formation of tetragonal over cubic GeFe3N by an also significant 28 kJ mol−1. This is in good agreement with the only experimental results on GeFe3Ny in the literature.13,14 Since cubic γ′-Fe4N and tetragonal GeFe3N are the end members of the GexFe4−xNy series, experiments will show at which composition the tetragonal distortion arises.
| Atomic arrangement in the cubic nomenclature | Cubic GeFe3N | Tetragonal GeFe3N | ||
|---|---|---|---|---|
| ΔE (kJ mol−1) | a (Å) | ΔE (kJ mol−1) | a eq (Å) | |
| 1a(Ge)3c(Fe3)1b(N) | +28 | 3.83 | 0 | 3.75 |
| 1a(Ge1/4Fe3/4)3c(Ge3/4Fe9/4)1b(N) | +138 | 3.97 | +97 | 3.92 |
| 1a(Fe)3c(GeFe2)1b(N) | +171 | 3.96 | +122 | 3.89 |
Prior to synthesis, the compound's theoretical thermochemistry is also worth studying. Hence, we compare GeFe3N to the elements and nitrides that are the most likely competing phases in the reaction. It is important to note that the metal oxides (GeO2 and Fe2O3) are used as starting materials in the later synthesis, but it is correct to refer to elemental Ge and Fe in the theoretical sets of reactants because they are instantly formed through reduction in the hydrogen flow. Furthermore, these thermochemical calculations are restricted to an FM ordering. An AFM ordering is considered in the later sections, but the energy differences introduced by different magnetic states are very small (cf. Section 3.5.2).
Table 2 shows two possible reaction schemes assuming that GeFe3N may adopt both structures, the cubic and the tetragonal. The first reaction can be understood as the incorporation of Ge into ε-Fe3N, while the second one describes the substitution of Fe in γ′-Fe4N by Ge. Both reaction schemes are exothermic, showing that the ternary compound is preferred over the binary nitrides and that the synthesis should be feasible over a wide range of reaction temperatures. However, it is well known from the binary Fe–N system that γ′-Fe4N decomposes to ε-Fe3N1+x at elevated temperatures (680 °C).25 Since this temperature is comparable to the usual nitriding temperatures, special attention needs to be paid to ε-Fe3N1+x as a possible side phase.
| ΔHR (kJ mol−1) | Cubic GeFe3N | Tetragonal GeFe3N |
|---|---|---|
| (1) Ge + ε-Fe3N → GeFe3N | −3.9 | −31.9 |
| (2) Ge + γ′-Fe4N → GeFe3N + α-Fe | −12.4 | −40.4 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m or I4/mcm: the nitriding reaction temperature ϑ, the intended composition xint, the refined Ge occupation xocc(Ge)R, the N occupation determined gravimetrically yocc(N)G, the refined lattice parameter a or the Ge–Ge distance, the related profile and Bragg residual values RP and RB, the molar mass M and the X-ray density ρ
m or I4/mcm: the nitriding reaction temperature ϑ, the intended composition xint, the refined Ge occupation xocc(Ge)R, the N occupation determined gravimetrically yocc(N)G, the refined lattice parameter a or the Ge–Ge distance, the related profile and Bragg residual values RP and RB, the molar mass M and the X-ray density ρ
| ϑ (°C) | x int | x occ(Ge)R | y occ(N)G | a or Ge–Ge (Å) | R P (%) | R B (%) | M (g mol−1) | ρ (g cm−3) |
|---|---|---|---|---|---|---|---|---|
| 650 | 0.25 | 0.247(3) | 0.87 | 3.7909(1) | 3.41 | 3.11 | 239.71 | 7.31 |
| 650 | 0.50 | 0.492(3) | 0.61 | 3.7811(1) | 4.49 | 5.24 | 240.19 | 7.38 |
| 650 | 0.75 | 0.731(3) | 0.34 | 3.7638(1) | 3.38 | 3.43 | 240.42 | 7.49 |
| 650 | 1.00 | 0.975(5) | 0.54 | 3.7306(3)/3.8156(5) | 3.40 | 8.59 | 247.32 | 7.73 |
| 700 | 0.25 | 0.249(3) | 0.88 | 3.7916(1) | 3.30 | 3.24 | 239.89 | 7.31 |
| 700 | 0.50 | 0.485(2) | 0.64 | 3.7823(1) | 3.48 | 4.34 | 240.49 | 7.38 |
| 700 | 0.75 | 0.761(3) | 0.44 | 3.7696(1) | 3.61 | 2.83 | 242.32 | 7.51 |
| 700 | 1.00 | 0.974(3) | 0.56 | 3.7345(3)/3.8197(5) | 3.85 | 9.52 | 247.58 | 7.76 |
3.2. Synthesis of GexFe4−xNy
The entire series of germanium iron nitrides GexFe4−xNy (0 ≤ x ≤ 1) was synthesised as single-phase powders via a two-step ammonolytic reaction that already gave access to RhxFe4−xN,6 PdFe3N,7 GaxFe4−xN,8,9 InxFe4−xN,10 and SnxFe4−xN.11,12 The reactants, ground iron(III) oxide and germanium(IV) oxide, were placed in the furnace at an elevated temperature and were transformed in a high-temperature sintering step at 1150 °C and in a subsequent nitriding step in the range of 500–800 °C to avoid competing side phases like binary nitrides, especially ε-Fe3N1+x, and intermetallic Fe–Ge compounds. Phase-pure GexFe4−xNy of best crystallinity was achieved at nitriding temperatures of 650 °C and 700 °C, so only those products will be considered.3.3. Structure and composition
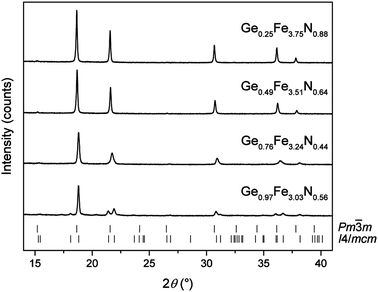
The structure of GexFe4−xNy was characterised by powder X-ray diffraction using Mo Kα1 radiation (λ = 0.70932 Å). The two major advantages over commonly used Cu Kα1 radiation (λ = 1.54059 Å) are a drastically improved intensity-to-background ratio by suppressing the high fluorescence background of iron as well as a larger accessible reciprocal space in the same 2θ angular range of the detector. The quality of the X-ray powder patterns is exemplarily shown in Fig. 2 for four different compositions GexFe4−xNy. The analysis revealed single-phase powders just up to x ≤ 1 composition. Therefore, the cubic structure of γ′-Fe4N is corroborated in almost all GexFe4−xNy compounds. With increasing Ge content, the powder patterns evidence a shift of the reflections to higher 2θ values as well as a broadening of the individual reflections. For reasons of brevity, more in-between compositions are not shown here but were also studied in detail. The tetragonal structure was only observed for GexFe4−xNy with x ≥ 0.97.To deduce the lattice parameters and the mixed occupations from these powder patterns, Rietveld refinements were carried out whose results are summarised in Table 3. The Rietveld refinements were only successful if a Ge occupation was considered at the cubic corner position (1a) or at the equivalent tetragonal position (4b). Thus, both experimental and theoretical (cf. Section 3.1) results clearly point towards this position. Also, the Rietveld results match the intended metal ratios very well so that a metal loss during the reaction can be ruled out. But how about the nitrogen content? It is well known that GexFe4−xNy has a limited nitrogen capacity (y ≪ 1)13,14 but the nitrogen content is not accessible from Rietveld refinements because site-occupation refinements of light elements are hardly reliable from powder XRD data. Therefore, we determined the nitrogen content gravimetrically for several identical reactions. We consider this approach legitimate because it gave a satisfactory result for the synthesis of γ′-Fe4N which has only a small phase width regarding the nitrogen content;25 in addition, the constant metal ratio has already been established. The nitrogen content of four different germanium iron nitrides, each synthesised at 650 °C and 700 °C (all from Table 3), is illustrated in the ternary phase diagram in Fig. 3. The nitrogen occupation varies between 88% and 34% and, as Stadelmeier and Fraker already suggested,13 it decreases with increasing Ge content for the cubic nitrides along a curve from binary γ′-Fe4N to intermetallic Fe3Ge. Interestingly, the nitrogen content increases again when the structure distorts tetragonally at the highest Ge content. The data further indicate that the higher nitriding temperature of 700 °C leads to slightly higher nitrogen contents in the sample, all else equal.
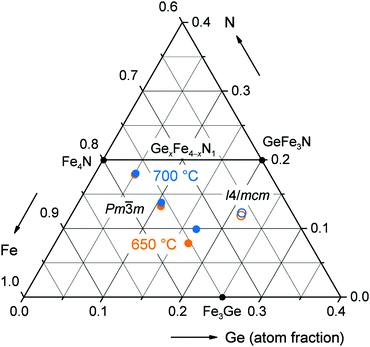 | ||
| Fig. 3 Excerpt from the Fe–Ge–N phase diagram with compounds GexFe4−xNy synthesised at nitriding temperatures of 650 °C (orange) and 700 °C (blue). The compositional and structural parameters of these eight compounds are listed in Table 3. | ||
For the nitrides GexFe4−xNy synthesised at 700 °C and 650 °C, the structural parameters are shown in Fig. 4(a) either as the cubic lattice parameter a or as the equivalent parameter aeq in the tetragonal case. Substituting Fe by Ge atoms leads to a Vegard-type decrease. Even though the nitrides richest in Ge, namely Ge0.97Fe3.03N0.56 (700 °C) and Ge0.98Fe3.02N0.54 (650 °C), exhibit a tetragonal structure and have a relatively high nitrogen content, the averaged Ge–Ge distances (aeq) perfectly fit the Vegard lines of each series. The nitrides synthesised at the lower nitriding temperature and, therefore, with the lower nitrogen content result in slightly smaller unit cells. Compared to the nitride γ′-Fe4N, the unit cell contraction is 3.0% (700 °C) or 3.3% (650 °C). We also note that the contraction throughout the series does not fit the larger metallic radius of Ge (cf. Section 3.1) but the smaller covalent radius of Ge. This clearly suggests the importance of covalent bonding in this series. The tetragonal lattice parameters of Ge0.97Fe3.03N0.56 (700 °C) and Ge0.98Fe3.02N0.54 (650 °C) are a = 5.2814(7) Å, c = 7.6394(10) Å and a = 5.2759(7) Å, c = 7.6311(10) Å, respectively. Similar lattice parameters were reported in the literature.13,14
In addition, theoretical lattice parameters were calculated assuming different magnetic ground states. Supercells were filled random-like with different ratios of Fe and Ge atoms on 1a, either preserving the cubic metric or allowing the tetragonal distortion of Fe atoms. For a given composition only the supercells with the lowest energy were included in the final analysis (Fig. 4(b)). We reiterate that in contrast to experiment, the nitrogen position was fully occupied in these supercells.
For a cubic FM model the lattice parameter a does not reproduce the entire Vegard-like behaviour of the experimental data but it fits to the shrinking of the unit cell up to Ge0.375Fe3.625N, especially since the DFT parameterisation (GGA) underestimates the bond length. For higher substitutions the lattice parameter a significantly increases and deviates from the experimental trend. The calculated non-linear behaviour was actually observed in GaxFe4−xN, and it was understood as a magnetic effect.8
Jumping to the highest substitutions, it is not at all surprising that a cubic FM model is an inadequate description for GeFe3N, and so tetragonally distorted FM and AFM supercells were calculated. Both tetragonal FM and AFM models result in similar splittings of the Ge–Ge distances that slightly overestimate the experimental splitting. Nevertheless, the averaged distances aeq in theory and experiment fit nicely. The energetically more favourable tetragonal model for GeFe3N arrives, not surprisingly, at a better structural description than the cubic model (cf. Section 3.1).
Experimentally, the phases with intermediate substitutional grades show a linear shrinking of the lattice parameter a that cannot be described by just one theoretical model. It can rather be understood as a transition from a cubic FM cell to a tetragonal cell with FM and AFM interactions (discussed in Section 3.5.2). It may also be the case that the transition to the tetragonal phase is gradual, starting early and leading to broad reflections and changes in magnetic interactions of Fe spins.
In addition to FM and AFM ground states, a cubic non-magnetic (NM) model was used. The calculations yield much smaller lattice parameters and an expanding Vegard-like behaviour from 3.67 Å for γ′-Fe4N to 3.74 Å for GeFe3N. Hence, these clearly do not reproduce the experimental results.
3.4. High-temperature behaviour of Ge0.97Fe3.03N0.56
Ternary iron nitrides are often subject to nitrogen loss at elevated temperatures where they undergo decomposition to binary metal iron alloys or decay like cubic γ′-Fe4N to ε-Fe3N1+x. Herein, the high-temperature behaviour of Ge0.97Fe3.03N0.56 having an already limited nitrogen concentration is studied using X-ray diffraction and thermal analysis.The high-temperature X-ray diffraction pattern in Fig. 5(a) reveals a transition from the tetragonal Ge0.97Fe3.03N0.56 to a cubic primitive cell by a simple distortion (comparable to Fig. 1) setting in between 560 °C and 640 °C. Structural parameters like the Ge–Ge distances and the volume per formula unit Vf.u. were deduced from the positions of the reflections (202), (004) and (220) and are shown in Fig. 5(b). Up to 480 °C the Ge–Ge distances and the volume of tetragonal Ge0.97Fe3.03N0.56 expand linearly. The corresponding thermal expansion coefficients α in different directions are around 21–25 × 10−6 K−1, the expansion in the ab plane being larger than that along the c axis (Table 4). Given these values, Ge0.97Fe3.03N0.56 belongs to the group of highly expanding materials.26 In comparison, γ′-Fe4N has a value of 7.6 × 10−6 K−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 and is a candidate of the intermediate group (2 × 10−6 K−1 ≤ α ≤ 8 × 10−6 K−1).26 Above 480 °C the shorter Ge–Ge distance, mirroring what happens in the ab plane, is shrinking while the larger Ge–Ge distance, along the c direction, is still expanding. At 560 °C, reflections of the cubic structure appear, and in the range up to 580 °C reflections of the tetragonal and the cubic structures were fitted side-by-side showing a smooth transition especially for the shorter Ge–Ge distance. The volume of the cubic structure is shrinking up to 640 °C, the temperature at which the transition is complete, and a subsequent thermal expansion is absent.
27 and is a candidate of the intermediate group (2 × 10−6 K−1 ≤ α ≤ 8 × 10−6 K−1).26 Above 480 °C the shorter Ge–Ge distance, mirroring what happens in the ab plane, is shrinking while the larger Ge–Ge distance, along the c direction, is still expanding. At 560 °C, reflections of the cubic structure appear, and in the range up to 580 °C reflections of the tetragonal and the cubic structures were fitted side-by-side showing a smooth transition especially for the shorter Ge–Ge distance. The volume of the cubic structure is shrinking up to 640 °C, the temperature at which the transition is complete, and a subsequent thermal expansion is absent.
| Direction | α (10−6 K−1) |
|---|---|
| Short Ge–Ge distance | 23.7(6) |
| Tetragonal axis a | 24.3(7) |
| Long Ge–Ge distance | 21.3(8) |
| Tetragonal axis c | 21.7(7) |
| Deduced from Vf.u. (averaged) | 22.5(4) |
The high-temperature behaviour of Ge0.97Fe3.03N0.56 hints at a nitrogen loss upon shrinkage of the shorter Ge–Ge distance at 480 °C and a subsequent transition to the cubic structure. Nitrogen-free Fe3Ge itself crystallizes in the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (with a phase transition to a hexagonal structure at 700 °C).28
m (with a phase transition to a hexagonal structure at 700 °C).28
Although a thermogravimetric measurement showed a step in the mass loss curve from 480 °C to 640 °C, it was only −0.2%, not a sign of nitrogen loss. A more significant step of −3.8% is from 640 °C to 970 °C. This corresponds to the entire nitrogen in the sample. To conclude, the sample does not decompose ahead of the structural transition. Ge0.97Fe3.03N0.56 rather shows a transition from the tetragonal to the cubic structure and a subsequent loss of nitrogen with increasing temperature. This may be the reason why the capillary for the high-temperature X-ray diffraction broke above 720 °C and an examination at higher temperatures was impossible.
3.5. Magnetic characterisation
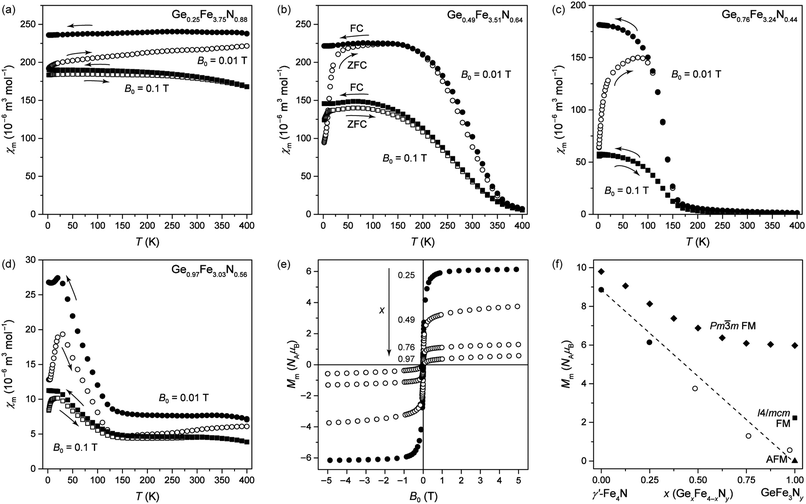
The molar DC susceptibilities of four different GexFe4−xNy nitrides were measured in the temperature range 2–400 K in field-cooled (FC) and zero-field-cooled (ZFC) modes (Fig. 6(a)–(d)). The course of the susceptibilities suggests that an increase in Fe substitution by Ge leads to FM compounds with decreasing Curie temperatures from above room temperature to about 160 K for Ge0.76Fe3.24N0.44. The nitride with the highest germanium concentration shows a pronounced maximum at low temperatures (ca. 30–40 K for Ge0.97Fe3.03N0.56). Atomic substitution affects the magnetic properties continuously so that intermediate substitutional degrees have broad susceptibility maxima.
We further note that FC and ZFC susceptibilities diverge at low temperatures especially for the lower probing field of B0 = 0.01 T. Such a divergence indicates a collective spin behaviour like spin-glass behaviour, mictomagnetism, superparamagnetism, etc.29 Ge-substituted γ′-Fe4N therefore belongs to the latter class of ternary nitrides mentioned above. This divergence is demonstrated by a nearly constant FC susceptibility value at low temperatures, whereas the ZFC susceptibility increases with increasing temperature, approaching the FC susceptibility. These are characteristic features of a spin glass in which the magnetic moments are figuratively frozen below the spin-freezing temperature in case of a FC measurement; this results in a constant value for the susceptibility. Without a magnetic field, frozen clusters of magnetic moments are orientated anisotropically at low temperatures. In a subsequent ZFC measurement, the energy supplied by increasing temperature enables the alignment of these clusters with respect to the external field to eventually reach magnetic saturation. The energy barrier for rotation can also be overcome by higher external magnetic fields so that FC and ZFC susceptibilities converge already at lower temperatures and the characteristic features of a spin glass can be suppressed (cf. B0 = 0.1 T measurements).
To further investigate the magnetic properties of GexFe4−xNy, hysteretic loops were recorded at 5 K which is below the maximum-susceptibility temperature (Fig. 6(e)). The hysteretic loops have S-shapes and small coercivities. Clearly, the magnetisation decreases with increasing Ge concentration. The hysteretic loop of Ge0.25Fe3.75N0.88 is saturated, whereas those phases with higher Ge concentration only approach the magnetic saturation within the range of the applied field (B0 = ±5 T). This unsaturated behaviour is typical for a magnetically frustrated system because full saturation is never attained in these systems even at the lowest temperatures and highest magnetic fields. Spin glasses lack long-range magnetic order, and the highly degenerate ground state prevents the external field from fully aligning the frozen moments into its directions.29 Nonetheless, the experimental saturated and unsaturated magnetisation at B0 = ±5 T shows a linear behaviour decreasing from 8.96 NAμB for γ′-Fe4N to 0.57 NAμB for Ge0.97Fe3.03N0.56 (Fig. 6(f)). Substituting Fe by Ge atoms obviously weakens the ferromagnetic coupling and even suggests a zero overall magnetisation for daltonide GeFe3Ny when assuming a linear trend over the entire substitutional range. Upon comparing experimental data with theoretical saturation moments, a cubic FM model fits best the range from γ′-Fe4N to Ge0.375Fe3.625N with the slight overestimation going back to the chosen GGA parametrisation. The unsaturated magnetisation of Ge0.97Fe3.03N0.56, however, agrees with a tetragonal FM or even better with an AFM model. This trend was already observed when comparing the experimental lattice parameter to theoretical ones.
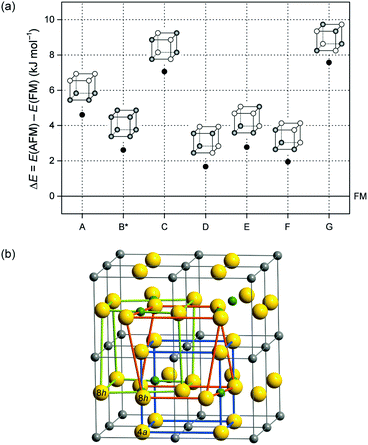 | ||
| Fig. 7 (a) Energy difference between different AFM spin arrangements (A–G) and the FM ordering in tetragonally distorted GeFe3N. Primitive cells illustrate the different spin arrangements of Fe atoms in which empty and filled circles relate to opposite directions of spins. (b) A cell of GeFe3N with tetragonal distortion (deduced from a cubic 2 × 2 × 2 cell) contains three of these primitive iron sublattices, one undistorted (blue, Fe(4a)) and two distorted (green and orange, Fe(8h)). Note: the B*-type cell is constructed from two B-type sublattices with opposite spin alignments and one A-type sublattice. For a more detailed explanation of the concept see ref. 8. | ||
Fig. 7(a) shows the comparison of the energies of different AFM spin arrangements using the tetragonal FM model of GeFe3N as a reference. All AFM arrangements differ from each other by less than 6 kJ mol−1 and they even have about the same energy as the FM reference. More precisely, the FM model is more stable than all AFM cells (indicated by positive energy differences) but the amount of less than 2 kJ mol−1 for the D and F models more or less equals the DFT internal accuracy. Thus, the narrow energy distribution reflects the importance of AFM interactions in GexFe4−xNy with high Ge contents despite an overall FM ground state for the idealised composition.
A closer look at the different AFM arrangements A–G shows that the energetically most favourable D- and F-type cells exhibit an equivalent number of both FM and AFM interactions between the neighbouring iron atoms along all spatial directions. In contrast, the highest-energy G-type structure has predominantly AFM interactions, and the A-type cell with mainly FM interactions is also more unstable. It seems that in an AFM ordering neither FM nor AFM interactions alone are preferred, and indeed a well-balanced, or better said, a statistical arrangement of iron spins is favoured. These findings support the idea of a spin-glass behaviour in Ge-rich iron nitrides.
 at frequencies from 100 Hz to 10 kHz is plotted in Fig. 8. The pronounced maximum in the DC magnetisation at 30–40 K appears here as a broad peak at around 37 K and exhibits a frequency dispersion which always accompanies magnetic glassy transitions. As the frequency increases, the temperature Tm at the maximum shifts to higher values. This dependency was used to fit the data to the critical power law
at frequencies from 100 Hz to 10 kHz is plotted in Fig. 8. The pronounced maximum in the DC magnetisation at 30–40 K appears here as a broad peak at around 37 K and exhibits a frequency dispersion which always accompanies magnetic glassy transitions. As the frequency increases, the temperature Tm at the maximum shifts to higher values. This dependency was used to fit the data to the critical power lawwith τ = (2πf)−1 (the inset of Fig. 8).29,31 Its fit evidences the spin-glass-like transition and characterises the spin glass with a static glassy transition temperature Tg = 36.68(5) K, a relaxation time of the individual particle moment τ* = 10−13.8(2) s and a dynamical critical exponent zν = 7.2(1). Tg corresponds well to the DC (equilibrium) value, and τ* and zν have values suitable for a canonical spin glass characterised by RKKY indirect-exchange interactions.29,31 When comparing Ge0.97Fe3.03N0.56 with the first iron nitride spin glass Sn0.9Fe3.1N, the tin compound has a lower transition temperature Tg of 12.8 K, a slower relaxation time τ* of 10−12 s and a smaller exponent zν of 5.6.12
The frequency shift of the temperature Tm, which is particularly important for a magnetic glassy transition, can further be quantified as (ΔTm/Tm) per decade of the angular frequency ω as ΔTm/(Tm·Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω).29 The shift of Ge0.97Fe3.03N0.56 was estimated to be about 0.012, which falls in the range of known canonical spin glasses (0.005–0.018) and which is also close to the value of Sn0.9Fe3.1N (0.015).12 Both ternary iron nitrides can be distinguished from semiconducting and insulating spin glasses (0.06–0.08) and superparamagnets (0.3).29
ω).29 The shift of Ge0.97Fe3.03N0.56 was estimated to be about 0.012, which falls in the range of known canonical spin glasses (0.005–0.018) and which is also close to the value of Sn0.9Fe3.1N (0.015).12 Both ternary iron nitrides can be distinguished from semiconducting and insulating spin glasses (0.06–0.08) and superparamagnets (0.3).29
All these experimental findings clearly show that the magnetic transition at low temperatures in the DC and real AC susceptibilities arises from a spin-glass freezing of the magnetic moments in the sample so that Ge0.97Fe3.03N0.56 is a canonical spin glass. The reason for the spin-glass behaviour of highly diluted iron nitrides is that FM and AFM exchange interactions of comparable size play important roles, as exemplified from first-principles calculations.
4. Conclusions
The GexFe4−xNy (0 ≤ x ≤ 1) series of compounds was studied experimentally and theoretically. Calculations prior to synthesis showed that, first, the Fe substitution by Ge takes place exclusively at the cubic Wyckoff position 1a. Second, for GeFe3N, the tetragonally distorted structure (I4/mcm) is more stable than an antiperovskite-like structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Third, the ternary compound GeFe3N is preferred over the binary nitrides ε-Fe3N and γ′-Fe4N, the common decomposition products in iron nitride chemistry.
m). Third, the ternary compound GeFe3N is preferred over the binary nitrides ε-Fe3N and γ′-Fe4N, the common decomposition products in iron nitride chemistry.
A two-step ammonolytic reaction gave access to GexFe4−xNy. The nitrides adopt an antiperovskite-like structure nearly throughout the compositional range for which the cubic lattice parameter continuously decreases with a Vegard-type behaviour. Only the nitrides richest in Ge have tetragonally distorted structures with, for example, lattice parameters a = 5.2814(7) Å and c = 7.6394(10) Å for Ge0.97Fe3.03N0.56. In experiment, germanium iron nitrides have a limited nitrogen capacity, and the nitrogen content decreases with increasing Ge incorporation for the cubic nitrides; the tetragonal nitrides have a significantly higher nitrogen concentration. Combined high-temperature XRD and TG-DSC experiments evidence that Ge0.97Fe3.03N0.56 is a highly expanding material and it first shows a transition to a cubic structure before it loses its already limited nitrogen.
DC susceptibility and saturation magnetisation of GexFe4−xNy compounds reveal a linear weakening of FM interactions with increasing Ge concentration. Theoretical investigations of different AFM orderings show that neither FM nor AFM Fe spin orientations alone are preferred; instead, a statistical arrangement is favoured. Combined DC and AC magnetometry confirms a magnetically frustrated ground state and a spin-glass behaviour of Ge0.97Fe3.03N0.56. The temperature dependence of the real component of the AC susceptibility at different frequencies classifies Ge0.97Fe3.03N0.56 as a canonical spin glass (Tg = 36.68(5) K, τ* = 10−13.8(2) s, zν = 7.2(1), and ΔTm/(Tm·Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω) = 0.012) with RKKY indirect-exchange interactions.
ω) = 0.012) with RKKY indirect-exchange interactions.
Acknowledgements
The authors thank Dr P. Müller for the X-ray measurements, Ch. Houben and Dr J. van Leusen for the SQUID data and Dr K. Chang for the TG-DSC analysis (all RWTH Aachen University). The Peter Grünberg Institut PGI-4/JCNS-2 at FZ Jülich is gratefully acknowledged for the measurement time on the PPMS, and we thank B. Schmitz for his support during the measurements. The IT Center of RWTH Aachen University is gratefully acknowledged for providing us with their supercomputing facilities. The financial support from Deutsche Forschungsgemeinschaft and RWTH Graduiertenförderung (scholarship to T. S.) is gratefully acknowledged.References
- T. He, Q. Huang, A. P. Ramirez, Y. Wang, K. A. Regan, N. Rogado, M. A. Hayward, M. K. Haas, J. S. Slusky, K. Inumara, H. W. Zandbergen, N. P. Ong and R. J. Cava, Nature, 2001, 411, 54–56 CrossRef CAS PubMed.
- K. Kamishima, T. Goto, H. Nakagawa, N. Miura, M. Ohashi, N. Mori, T. Sasaki and T. Kanomata, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024426 CrossRef.
- K. Takenaka and H. Takagi, Appl. Phys. Lett., 2005, 87, 261902 CrossRef.
- S. K. Chen, S. Jin, T. H. Tiefel, Y. F. Hsieh, E. M. Gyorgy and D. W. Johnson, J. Appl. Phys., 1991, 70, 6247–6249 CrossRef CAS.
- C. Guillard and H. Creveaux, C. R. Hebd. Seances Acad. Sci., 1946, 222, 1170–1172 Search PubMed.
- A. Houben, V. Šepelák, K.-D. Becker and R. Dronskowski, Chem. Mater., 2009, 21, 784–788 CrossRef CAS.
- D. Music, J. Burghaus, T. Takahashi, R. Dronskowski and J. M. Schneider, Eur. Phys. J. B, 2010, 77, 401–406 CrossRef CAS.
- J. Burghaus, M. Wessel, A. Houben and R. Dronskowski, Inorg. Chem., 2010, 49, 10148–10155 CrossRef CAS PubMed.
- J. Burghaus, M. T. Sougrati, A. Möchel, A. Houben, R. P. Hermann and R. Dronskowski, J. Solid State Chem., 2011, 184, 2315–2321 CrossRef CAS.
- J. Burghaus, J. Kleemann and R. Dronskowski, Z. Anorg. Allg. Chem., 2011, 637, 935–939 CrossRef CAS.
- T. Scholz and R. Dronskowski, Inorg. Chem., 2015, 54, 8800–8807 CrossRef CAS PubMed.
- T. Scholz and R. Dronskowski, AIP Adv., 2016, 6, 055107 CrossRef.
- H. H. Stadelmaier and A. C. Fraker, Z. Metallkd., 1962, 53, 48–51 CAS.
- Y. Xu, J. M. Elbicki, W. E. Wallace, S. Simizu and S. G. Sankar, IEEE Trans. Magn., 1992, 28, 2569–2571 CrossRef CAS.
- J. Rodriguez-Carvajal, FULLPROF Version 5.60, ILL, 2015 Search PubMed.
- S. Liu, Phys. Rev. B: Solid State, 1977, 15, 4281–4287 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L. Pauling, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- H. A. Wriedt, N. A. Gokcen and R. H. Nafziger, Bull. Alloy Phase Diagrams, 1987, 8, 355–377 CrossRef CAS.
- R. Roy, D. K. Agrawal and H. A. McKinstry, Annu. Rev. Mater. Sci., 1989, 19, 59–81 CrossRef CAS.
- M. A. J. Somers, N. M. van der Pers, D. Schalkoord and E. J. Mittemeijer, Metall. Mater. Trans. A, 1989, 20, 1533–1539 CrossRef.
- J.-P. Turbil, Y. Billiet and A. Michel, C. R. Acad. Sci. Paris, Série C, 1969, 269, 309–311 CAS.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, Washington DC, 1996 Search PubMed.
- E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545–563 CrossRef CAS.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435–479 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |