Open Access Article
Open Access ArticlePrediction of morphological changes of catalyst materials under reaction conditions by combined ab initio thermodynamics and microkinetic modelling†
Raffaele
Cheula
 a,
Aloysius
Soon
a,
Aloysius
Soon
 b and
Matteo
Maestri
b and
Matteo
Maestri
 *a
*a
aLaboratory of Catalysis and Catalytic Processes, Dipartimento di Energia, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy. E-mail: matteo.maestri@polimi.it
bDepartment of Materials Science and Engineering, Yonsei University, Seoul, Korea
First published on 1st June 2018
Abstract
In this article, we couple microkinetic modelling, ab initio thermodynamics and Wulff–Kaishew construction to describe the structural variation of catalyst materials as a function of the chemical potential in the reactor. We focus specifically on experiments of catalytic partial oxidation (CPO) of methane on Rh/α-Al2O3. We employ a detailed structureless microkinetic model to calculate the profiles of the gaseous species molar fractions along the reactor coordinate and to select the most abundant reaction intermediates (MARIs) populating the catalyst surfaces in different zones of the reactor. Then, we calculate the most stable bulk and surface structures of the catalyst under different conditions of the reaction environment with density functional theory (DFT) calculations and ab initio thermodynamics, considering the presence of the MARIs on the catalyst surface in thermodynamic equilibrium with the partial pressures of their reservoirs in the gas phase surrounding the catalyst. Finally, we exploit the Wulff–Kaishew construction method to estimate the three-dimensional shape of the catalyst nanoparticles and the distribution of the active sites along the reactor coordinate. We find that the catalyst drastically modifies its morphology during CPO reaction by undergoing phase transition, in agreement with spectroscopy studies reported in the literature. The framework is also successfully applied for the analysis and interpretation of chemisorption experiments for catalyst characterization. These results demonstrate the crucial importance of rigorously accounting for the structural effect in microkinetic modeling simulations and pave the way towards the development of structure-dependent microkinetic analysis of catalytic processes.
Introduction
Heterogeneous catalysts are dynamic systems in the sense that they can be seen as “smart materials”, which adapt their structure under the specific reaction conditions locally experienced in the reactor.1 Such “living character” of the catalyst within the reaction environment strongly affects the surface structure, which is a crucial component in determining the observed activity and selectivity in very important metal-supported catalytic processes of industrial relevance (e.g., NH3 synthesis, Fisher–Tropsch, hydrocarbon reforming).2 Considering the complex nature of these phenomena, multiscale analysis based on microkinetic modelling is acknowledged to be the key tool for the interpretation of the experimental evidence for gaining fundamental information on the relation between the structure and the activity of heterogeneous catalysts.3,4 However, despite the fact that the surface structure has been considered an important factor in catalysis science since the discovery of structure sensitive reactions,5,6 the effect of the structure of the catalyst on reactivity and selectivity is at present neglected in state-of-the-art microkinetic modelling. As such, these models strongly rely on an abstract and static concept of the “catalyst material”, which is often modelled as a generic free site “*”, without explicitly accounting for the effect of the actual orientation and positioning of the atoms at the surface and their dependence on the operating conditions. All the structural effects are typically accounted for by means of fine-tuning and refinement of the kinetic parameters based on selected experimental data. This approach can lead to a satisfactory description of conversion and selectivity trends and, thus, it is a very valuable tool for the description of the macroscopic kinetic behaviour of a catalytic process. However, the material gap in the modelling of the active site intrinsically precludes the detailed analysis and understanding of the underlying mechanisms at the atomic-scale level.A catalyst under reaction conditions generally shows numerous types of active sites, each with different activity. For instance, catalyst nanoparticles are characterized by crystal facets, edges, corners and defects, which interact differently with the reaction intermediates, yielding different reactivities. In particular, low-coordinated catalyst atoms are generally more active than high-coordinated ones, and in some conditions they give a predominant contribution to the catalytic process.2,7 Moreover, adsorption, phase transitions and sintering processes can modify the morphology (e.g., shape and size) of the catalyst nanoparticles and consequently change the nature and the relative amount of their active sites.8,9
An example of a system in which the catalyst undergoes drastic morphological modifications under reaction conditions is the catalytic partial oxidation (CPO) of CH4 on a Rh/Al2O3 catalyst.10,11 Grunwaldt et al. performed a 2D-mapping of the Rh oxidation state in a catalyst bed by means of X-ray absorption near edge structure (XANES) spectroscopy and a charged coupled device (CCD) camera,12 and observed that the catalyst changes its oxidation state as a function of the O2 chemical potential in the reactor. At the steady state, the reactor turns out to be stratified in two distinct zones: in the first zone, Rh is highly oxidized, whereas, in the second zone, Rh nanoparticles are reduced. The variation in structure observed between the two zones of the catalytic bed is sharp and it is accompanied by a drastic change in the selectivity of the process: when the catalyst is oxidized, total oxidation is observed, whereas, when Rh is in its metallic form, syngas is produced.
The modelling of the crystal habit of the catalyst material under reaction conditions and its effect on the activity easily result in a high level of complexity.13 This is related to the necessity of both (i) building microkinetic models not only for one facet, but for several facets (potentially including corners, edges, and defects), and (ii) coupling the prediction of the structure and shape of the nanoparticle to the local variation of the chemical potential in the reactor. In this situation, however, the first-principles description of the whole set of possible phenomena is beyond the limit of complexity accessible to even the most efficient implementation of first-principles calculations.13
A first step towards filling the material gap in microkinetic modelling can be achieved by decoupling the calculations of the distribution of the chemical potential in the reactor and its effect on the structure of the catalyst. We first employ a structureless microkinetic model to calculate the distribution of the chemical potential in the reactor. Structureless models allow for a reliable and detailed analysis of the macroscopic kinetic behaviour of the catalytic process. However, they do not provide any information about the catalyst structure and how it is modified by the gas phase. These phenomena are lumped together in effective kinetic parameters of the elementary steps that reflect the fine-tuning of the kinetic parameters with various experimental data. Then, at the specific conditions of the chemical potential calculated with the microkinetic model, we study how the reaction environment induces morphological changes in the catalyst structure. The description of the catalyst structural changes is achieved by using ab initio thermodynamics and Wulff–Kaishew construction.
In particular, here we focus our analysis on the CPO of CH4 on Rh/α-Al2O3, for which well-established microkinetic models are reported in the literature. The structureless microkinetic model by Maestri et al.14,15 is used for calculating the profiles of the gaseous species along the reactor coordinate and to identify the most abundant reaction intermediates (MARIs) at the catalyst surface. Then, with ab initio thermodynamics and Wulff–Kaishew construction, we calculate how the morphology of the catalyst changes when exposed to the calculated chemical potential of the gaseous species, in agreement with the experimental evidence.16 In particular, density functional theory (DFT) calculations and ab initio thermodynamics are employed to calculate the most stable bulk and surface structures of catalyst materials under different conditions of the reaction environment. For each crystal facet of the catalyst, the thermodynamically most stable surface structure (e.g. ordered or disordered adsorbate configurations, surface reconstructions) in equilibrium with the surrounding gas is selected. Then, the adhesion energy between the catalyst and the support is calculated and the 3D shape of the nanoparticles along the reactor coordinate is estimated by the Wulff–Kaishew construction method.
Methods
In this section we provide the description of the different methods employed in the analysis of the CH4 CPO experiments on Rh catalysts.Microkinetic modelling
The reaction environment inside the chemical reactor for CH4 CPO experiments on Rh/α-Al2O3 is characterized in terms of profiles of gaseous species partial pressures and adsorbate coverages, by numerically solving mass balance equations under isothermal conditions as reported in ref. 17. Details are provided in the ESI† (section 1). The reaction rates are calculated with the detailed, thermodynamically consistent microkinetic model developed by Maestri et al.14,15 The model is structureless, in the sense that it does not contain any explicit information about the catalyst structure and how it evolves during reaction. It consists of 82 surface reactions between 13 single-site adsorbate species and includes the effect of adsorbate–adsorbate interactions on activation energies of surface kinetics. It was derived using a hierarchical multiscale methodology based on the UBI-QEP framework and it was refined with first principles calculations to correctly account for the relevant pathways involved in water-gas shift (WGS) and reverse water-gas shift reactions.15 The resulting scheme can describe several reaction systems on a Rh/α-Al2O3 catalyst: CH4 pyrolysis and oxidation, steam reforming, H2 and CO-rich oxidation, WGS and reverse WGS.18,19Electronic-structure calculations
Electronic-structure calculations are performed using density-functional theory (DFT), as implemented in the Quantum Espresso20 suite of codes, with PBE (Perdew, Burke, and Ernzerhof21) GGA ultrasoft pseudopotentials and a plane wave basis set. Rh oxide systems are described using a DFT+U approach, to correct electron self-interaction, which can be relevant for these systems.22 The value of the U parameter is selected by testing different values and comparing the band gap of the relaxed bulk Rh2O3 with its experimental value. A value of U of 3.5 eV is applied to the Rh atoms in order to match the experimental value of the band gap of Rh2O3 (1.20 eV (ref. 23)). Metallic Rh surface structures are instead described taking into account the contributions of van der Waals interactions (with the vdW-DF2 functional24–27), which can play an important role in the description of CO* adsorption on Rh surfaces.28 Further considerations on the selection of the U parameter and the employed functionals are reported in the ESI† (section 2).Periodic surface slabs with inversion symmetry are used to characterize the catalyst surfaces in terms of specific surface free energy (per unit of area) and binding energies of adsorbates, which are positioned on both sides of the slabs. The top three and bottom three slab layers are fully relaxed until all force components acting on the atoms are below 2.6 × 10−2 eV Å−1 and the difference in energy between two calculations is lower than 1.36 × 10−3 eV. Convergence tests have been performed with respect to the specific surface energy, with a threshold value of 10−3 eV Å−2. The resulting converged parameters are: a kinetic energy cut-off for wave functions of 35 Ry and for charge density and potential of 280 Ry, a grid of 12 × 12 × 12 k-points for bulk Rh and of 6 × 6 × 2 for bulk Rh2O3, 6 × 6 × 6 for bulk RhO2, a slab height of about 12 Å and 10 Å of vacuum. For surface supercells, correspondingly smaller k-points grids are used to ensure an equivalent sampling of reciprocal space. All the parameters have been selected to achieve convergence with the different functionals or calculation set-ups herein employed. Gas phase calculations have been performed in a cubic supercell. The size of the supercell (14 Å) was selected to avoid interactions between the atoms of two neighbouring periodic cells.
The lattice constant of Rh was 3.85 Å (3.96 Å with vdW-DF2), in agreement with the experimental value (3.80 Å).29 The lattice parameters of the hexagonal cell of corundum Rh2O3, i.e. the length of the basis vectors and the height of the cell, were 5.17 Å and 13.96 Å, respectively, consistent with the experimental values (5.21 Å and 14.15 Å).30 The lattice constants of rutile RhO2 were 4.51 Å and 3.06 Å, in good agreement with the experimental values (4.59 Å and 3.15 Å).30 The geometric parameters of Rh oxides did not change after the application of Hubbard U corrections. The lattice parameters of α-Al2O3 were 4.80 Å and 13.09 Å, in good agreement with the experimental values (4.76 Å and 12.99 Å)31 and with previous theoretical studies.32
Ab initio thermodynamics
The changes in the structure of the catalyst are predicted by means of ab initio thermodynamics33 calculations. This method consists of selecting the most stable configuration of a system of atoms in equilibrium with a reservoir by comparison of specific thermodynamic quantities – e.g. the surface free energy – calculated by means of first-principle techniques. The main assumption is that the system is in thermodynamic equilibrium with the surrounding environment, which can be characterized by both experimental observation and microkinetic modelling.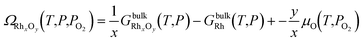 | (1) |
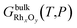 and GbulkRh(T,P) are the Gibbs free energy of the bulk structure RhxOy and the bulk Rh, respectively. μO is the chemical potential of an oxygen atom in the catalyst structure, assumed to be equal to the chemical potential of an oxygen atom in the reservoir of the system, typically oxygen molecules in the gas phase.
and GbulkRh(T,P) are the Gibbs free energy of the bulk structure RhxOy and the bulk Rh, respectively. μO is the chemical potential of an oxygen atom in the catalyst structure, assumed to be equal to the chemical potential of an oxygen atom in the reservoir of the system, typically oxygen molecules in the gas phase.
The chemical potential of gaseous species is calculated in the ideal gas approximation as:
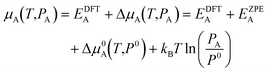 | (2) |
The Gibbs free energy of crystalline solid bulk systems is calculated as:
| Gsolid(T,P) = EDFTsolid + Fvibsolid(T,P) | (3) |
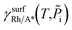 :
: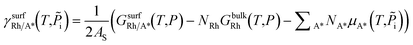 | (4) |
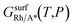 is the Gibbs free energy of the surface structure supercell, GbulkRh is the energy of an atom in Rh bulk, NRh and NA* are the number of Rh atoms and of the adsorbate molecules in the supercell, respectively. μA* is the chemical potential of the adsorbate present in the surface structure, assumed to be equal to the chemical potential of its reservoir (in the gas phase) and AS is the area of the supercell base.
is the Gibbs free energy of the surface structure supercell, GbulkRh is the energy of an atom in Rh bulk, NRh and NA* are the number of Rh atoms and of the adsorbate molecules in the supercell, respectively. μA* is the chemical potential of the adsorbate present in the surface structure, assumed to be equal to the chemical potential of its reservoir (in the gas phase) and AS is the area of the supercell base.
The specific surface energies of the different terminations that Rh2O3 can expose in equilibrium with the oxygen in the surrounding environment are calculated as:
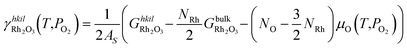 | (5) |
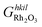 is the Gibbs free energy of the slab that represents the (hkil) surface termination, made of NRh Rh atoms and NO oxygen atoms,
is the Gibbs free energy of the slab that represents the (hkil) surface termination, made of NRh Rh atoms and NO oxygen atoms, 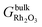 is the energy of 2 metal atoms and 3 oxygen atoms in the bulk phase and μO is half of the chemical potential of an oxygen molecule in the gas phase.
is the energy of 2 metal atoms and 3 oxygen atoms in the bulk phase and μO is half of the chemical potential of an oxygen molecule in the gas phase.
Neglecting the contribution of the PV term,33 we calculate the Gibbs free energy of Rh systems in the presence of adsorbates on the surfaces as:
| GsurfRh/A = EDFT,surfRh/A + Fvib,surfRh/A − TSconf,surfRh/A | (6) |
The vibration contributions to the systems containing adsorbates on the Rh surfaces are calculated in the harmonic oscillator approximation, from a finite difference approximation of the Hessian matrix. The contribution of the vibrational modes of the Rh atoms below the top layer of the slabs is neglected. The configurational entropy of disordered surface structures is calculated in the lattice 2D gas approximation,35 considering the adsorbates as indistinguishable, as a function of the coverages of adsorbates (ϑA*):
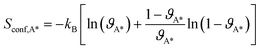 | (7) |
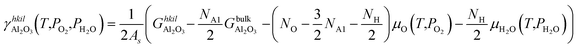 | (8) |
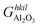 is the Gibbs free energy of the termination, made of NAl aluminium atoms, NO oxygen atoms and NH hydrogen atoms, and
is the Gibbs free energy of the termination, made of NAl aluminium atoms, NO oxygen atoms and NH hydrogen atoms, and 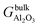 is the energy of 2 metal atoms and 3 oxygen atoms in the bulk phase.
is the energy of 2 metal atoms and 3 oxygen atoms in the bulk phase.
Sandwich-like symmetric slabs (shown in section 3 of the ESI†) characterized by inversion symmetry are employed to calculate the adhesion energy between the catalyst and the support surfaces. In the case of Rh and Al2O3 facets:
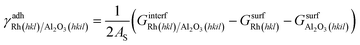 | (9) |
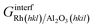 is the Gibbs free energy of the sandwich-like slab, and 2AS is the total contact area between the two phases, equal to twice the area of the supercell base. The supercell is constructed by ensuring that the periodicities of the two different structures (support and catalyst surfaces) are preserved (details in section 3 of the ESI†).
is the Gibbs free energy of the sandwich-like slab, and 2AS is the total contact area between the two phases, equal to twice the area of the supercell base. The supercell is constructed by ensuring that the periodicities of the two different structures (support and catalyst surfaces) are preserved (details in section 3 of the ESI†).
Wulff–Kaishew construction
The size-independent 3D shape of catalyst nanoparticles under reaction is drawn with the Wulff–Kaishew construction method. The minimum surface energy for a given volume of a crystal polyhedron is achieved if the distances of its faces from one given point are proportional to their specific surface energies:| hhkl = λγhkl | (10) |
| hsupport = λγadh | (11) |
The space that lies inside all these planes defines the equilibrium shape for the nanoparticle in the considered conditions. The thermodynamic shape is size-independent, except in cases of exceptionally large strain effects or counting effects related to edge and corner atoms.37
Results and discussion
In this section, the methods described above are employed to study the morphological changes of a 4% Rh/α-Al2O3 catalyst induced by the variation of chemical potential in the reactor. We focus our analysis on the experiments of Donazzi et al. in an annular reactor.38Microkinetic modelling
Microkinetic modelling is employed to calculate the gas phase composition inside the reactor and to identify the MARIs present at the catalyst surfaces. We employ a steady-state 1D heterogeneous model and the kinetics of the microkinetic model by Maestri et al.14 The geometric parameters of the reactor and the operating conditions are reported in Table 1.| Temperature | 773 K | GHSV | 2 × 106 Nl kgcat−1 h−1 |
| Pressure | 1 atm | Inlet molar fractions | |
| Reactor length | 2.2 cm | CH4 | 0.01 |
| Inner diameter | 0.4 cm | O2 | 0.01 |
| Outer diameter | 0.5 cm | N2 | 0.98 |
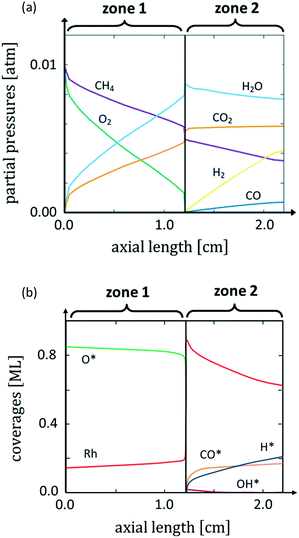
Fig. 1a shows the calculated axial profiles of partial pressures of the gaseous species that come into contact with the Rh catalyst in the reactor. The concomitant surface coverages are reported in Fig. 1b.
In agreement with previous experimental findings,12 we observe a sharp change in the reactive environment that divides the reactor into two different zones: at a distance from the reactor inlet of about 1.2 cm, a sharp drop of O* coverage at the catalyst and of O2 partial pressure in the gas phase occur. This drastic variation in the chemical potential of O2 in the reactor is accompanied by a change in the selectivity of the process: syngas formation – absent in the presence of O2 at the catalyst interface – starts to occur as soon as the amount of O2 drops to very low values at the catalyst surface. Thus, the reactor becomes stratified in two distinct zones. In the first zone, no syngas production is observed and O* is the most abundant adsorbate at the catalyst surface. In the second zone of the reactor, syngas production is observed and CO* and H* are the MARIs. This dependence on the selectivity to syngas is in agreement with the experimental observation.10 The structureless microkinetic model relates this selectivity change to the oxygen coverage dependence of the H* and CO* oxidation pathways, which are faster at high O* coverages than their desorption, thus leading to CH4 total oxidation.18 The experiments of Grunwaldt et al.,10,16 however, suggest that this selectivity change is related to a change of the morphology of the catalyst in an O-rich environment. To account for this structural variation, here we associate the chemical potential of gaseous species along the reactor coordinate calculated by microkinetic modelling with particular morphologies of the catalyst. This allows us to study how the reaction environment induces changes in the catalyst structure during reaction.
Bulk phase stability
In the aim of modelling how the catalyst morphology changes as a function of the chemical potential in the reactor, we first investigate which is the thermodynamically stable bulk phase of the catalyst when it is in contact with the gaseous environment.In their experimental work, Grunwaldt et al.12 observed that temperature induced oxidations and reductions of the catalyst are very fast: during the stabilization period of their tests (250 °C < T < 350 °C, duration = 2 hour) they made the temperature rise and decrease multiple times and they observed that the catalyst got fully reduced at high temperatures and fully oxidized at low temperatures. Then, the oxidation state of the catalyst remained stable with time. Thus, it can be assumed that for Rh/α-Al2O3 systems, the morphological transformation at relatively high temperatures (T > 250 °C) is reversible and it is not hindered by metastable structures.
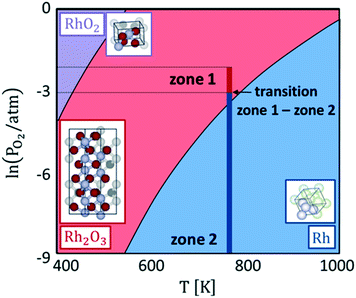
Hence, with eqn (1), we calculate the oxygen chemical potential at which the phase transition between Rh, Rh2O3 and RhO2 bulk phases occurs. Explicating the dependence of μO from temperature and oxygen partial pressure with eqn (2), we derive the bulk phase diagram of Rh and its oxides, represented in Fig. 2. Under the inlet conditions of the CPO reactor (T = 773 K and PO2 = 0.01 atm), the stable catalyst bulk phase is Rh2O3. At the same temperature, when the oxygen partial pressure drops below 1.2 × 10−3 atm, metallic Rh becomes the most thermodynamically stable bulk structure. This value of oxygen partial pressure is close to the critical value at which the sharp change in the reactive environment is predicted by reactor modelling. Therefore, the sharp variation of the selectivity of the process (no syngas vs. syngas production) is associated with a concomitant change of the oxidation state of the catalyst. In zone 2 of the reactor, where the oxygen content in the system is very low, metallic Rh remains the most stable bulk phase. RhO2 does not become thermodynamically stable in the range of conditions of our simulation.
Our calculations agree with the experimental observations of Grunwaldt et al.12 and show a modification of the structure of the catalyst as a function of the chemical potential, which is not accounted for by the microkinetic model. Thus, the structureless microkinetic model, although able to well reproduce the kinetic macroscopic behaviour of the process, cannot give insights into the underlying atomistic details at the active site.
Catalyst morphology in zone 1
After modelling how the bulk phase changes with the change of reactive environment, we now aim at predicting the morphology of the catalyst surface and its relationship with the reaction environment. We use two different models to describe the catalyst in the two regimes found in the annular reactor. In the first zone, the catalyst is oxidized, and the reservoir of oxygen atoms is gaseous oxygen in contact with the catalyst surfaces. The O2 adsorption/desorption elementary step is at quasi-equilibrium.Therefore, we calculate the chemical potential of O* as a function of μO2 as:
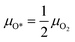 | (12) |
With the aim of calculating the catalyst morphology in the first zone of the CPO reactor, the stability of eight crystalline facets of Rh2O3 are investigated: (0001), (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02), (11
02), (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3), (1
3), (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01), (10
01), (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1), (11
1), (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), (10
0), (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), and (10
0), and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2), selected because they are the most stable surfaces of α-Al2O3,39 which has the same bulk structure as Rh2O3. For each (hkil) surface, different terminations, obtained from cleaving the bulk with parallel planes, are considered. Their specific surface free energies are calculated with eqn (5), neglecting the vibrational energy and the entropy contributions, because we calculated that at reasonably low temperatures (T < 1000 K) the error introduced remains lower than 0.001 eV Å−2.
2), selected because they are the most stable surfaces of α-Al2O3,39 which has the same bulk structure as Rh2O3. For each (hkil) surface, different terminations, obtained from cleaving the bulk with parallel planes, are considered. Their specific surface free energies are calculated with eqn (5), neglecting the vibrational energy and the entropy contributions, because we calculated that at reasonably low temperatures (T < 1000 K) the error introduced remains lower than 0.001 eV Å−2.
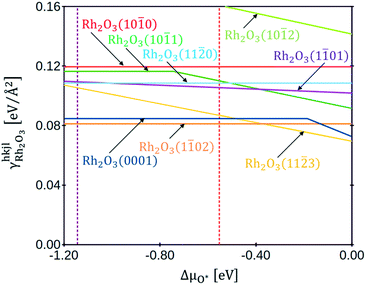
Fig. 3 shows the plot of the specific surface energies of the Rh2O3 facets as a function of the oxygen chemical potential. With dashed lines are underlined the chemical potentials at which the transition to metallic Rh (ΔμO* = −1.15 eV, in brown) and to RhO2 (ΔμO* = −0.55 eV, in red) occur. In the whole range of stability of bulk Rh2O3, the most stable surface is Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02), and the second is Rh2O3(0001), both exposing stoichiometric terminations, in agreement with the findings of Scherson et al.23 Rh2O3(11
02), and the second is Rh2O3(0001), both exposing stoichiometric terminations, in agreement with the findings of Scherson et al.23 Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3) turns out to be very stable at high values of oxygen chemical potential: it exposes an over-stoichiometric termination (with an excess of oxygen atoms with respect to the stoichiometric value of NO/NRh = 3/2), which reduces its surface energy with the increase of oxygen chemical potential. The most stable terminations of Rh2O3(11
3) turns out to be very stable at high values of oxygen chemical potential: it exposes an over-stoichiometric termination (with an excess of oxygen atoms with respect to the stoichiometric value of NO/NRh = 3/2), which reduces its surface energy with the increase of oxygen chemical potential. The most stable terminations of Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and Rh2O3(10
0) and Rh2O3(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) are stoichiometric, whereas the most stable termination of Rh2O3(1
0) are stoichiometric, whereas the most stable termination of Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) has an excess of oxygens with respect to the stoichiometric ratio. Rh2O3(10
01) has an excess of oxygens with respect to the stoichiometric ratio. Rh2O3(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) shows a stoichiometric termination for ΔμO* < −0.75 eV, then an over-stoichiometric one. Rh2O3(10
1) shows a stoichiometric termination for ΔμO* < −0.75 eV, then an over-stoichiometric one. Rh2O3(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) presents an over-stoichiometric termination with very high specific surface energy. Under-stoichiometric terminations are not stable at any value of ΔμO* at which Rh2O3 is thermodynamically preferred. Representations of the structures are provided in section 4 of the ESI.†
2) presents an over-stoichiometric termination with very high specific surface energy. Under-stoichiometric terminations are not stable at any value of ΔμO* at which Rh2O3 is thermodynamically preferred. Representations of the structures are provided in section 4 of the ESI.†
The effect of the support on the three-dimensional shape of the catalyst is taken into account by calculating the specific adhesion energy of Rh2O3(0001) and Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) facets in contact with Al2O3(0001) and Al2O3(1
02) facets in contact with Al2O3(0001) and Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02), which are the two most exposed facets of α-Al2O3.32,40 First, we characterize the Al2O3 surface structures: exploiting eqn (8), we investigate the stability of different terminations of the Al2O3 facets, with Al, O or OH as terminal groups. The stoichiometric terminations are the most stable over the entire considered range of oxygen chemical potentials, whereas hydroxylated terminations become stable for high water chemical potential (ΔμH2O = −1.475 eV, i.e. PH2O = 100 bar at 773 K), in agreement with the data of García-Mota et al.32 and Marmier et al.40 The specific adhesion energy between Rh2O3 and α-Al2O3 is evaluated with eqn (9). Independent from the combination of facets, the resulting value of adhesion energy is about 0.02 eV Å−2 (details are provided in section 3 of the ESI†). This value is very small compared to the surface free energies of the Rh2O3 facets, yielding Wulff plots with a large contact area between the catalyst and the support.
02), which are the two most exposed facets of α-Al2O3.32,40 First, we characterize the Al2O3 surface structures: exploiting eqn (8), we investigate the stability of different terminations of the Al2O3 facets, with Al, O or OH as terminal groups. The stoichiometric terminations are the most stable over the entire considered range of oxygen chemical potentials, whereas hydroxylated terminations become stable for high water chemical potential (ΔμH2O = −1.475 eV, i.e. PH2O = 100 bar at 773 K), in agreement with the data of García-Mota et al.32 and Marmier et al.40 The specific adhesion energy between Rh2O3 and α-Al2O3 is evaluated with eqn (9). Independent from the combination of facets, the resulting value of adhesion energy is about 0.02 eV Å−2 (details are provided in section 3 of the ESI†). This value is very small compared to the surface free energies of the Rh2O3 facets, yielding Wulff plots with a large contact area between the catalyst and the support.
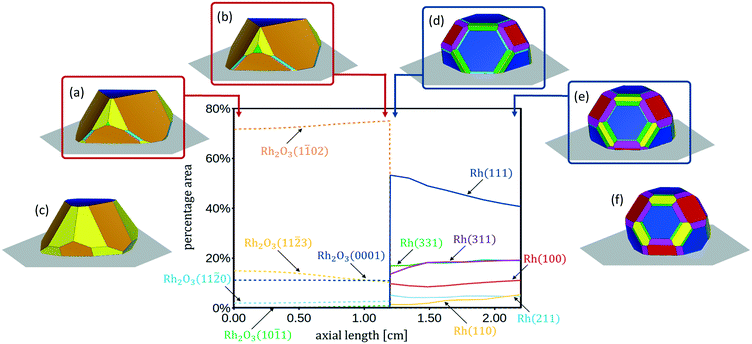
In Fig. 4 the 3D shapes of Rh2O3 nanoparticles at different values of ΔμO*, obtained with the Wulff–Kaishew construction method (eqn (10) and (11)), are represented. At the inlet of the reactor (Fig. 1), when ΔμO* = −1.01 eV, the most exposed surfaces are Rh2O3(0001), Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) and Rh2O3(11
02) and Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3), whereas the facets Rh2O3(11
3), whereas the facets Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and Rh2O3(10
0) and Rh2O3(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) appear in the Wulff plot, even with very small areas (Fig. 4, panel a). Close to the phase transition to reduced Rh bulk, at ΔμO = −1.11 eV, the surface area of Rh2O3(11
1) appear in the Wulff plot, even with very small areas (Fig. 4, panel a). Close to the phase transition to reduced Rh bulk, at ΔμO = −1.11 eV, the surface area of Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3) is smaller, whereas that of Rh2O3(1
3) is smaller, whereas that of Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02), Rh2O3(11
02), Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and Rh2O3(10
0) and Rh2O3(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) is slightly wider (Fig. 4, panel b). Considering now conditions characterized by higher oxygen chemical potential in the system, when ΔμO = −0.55 eV (close to the bulk phase transformation to RhO2), we find that the nanoparticle exposes only the Rh2O3(0001), Rh2O3(1
1) is slightly wider (Fig. 4, panel b). Considering now conditions characterized by higher oxygen chemical potential in the system, when ΔμO = −0.55 eV (close to the bulk phase transformation to RhO2), we find that the nanoparticle exposes only the Rh2O3(0001), Rh2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) and Rh2O3(11
02) and Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3) surfaces, with a high amount of Rh2O3(11
3) surfaces, with a high amount of Rh2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3). The catalyst shape in these conditions is represented in Fig. 4, panel c.
3). The catalyst shape in these conditions is represented in Fig. 4, panel c.
Catalyst morphology in zone 2
As reported in Fig. 2, in the second zone of the reactor, the catalyst nanoparticles are reduced; CO* and H* are the MARIs, with coverages lower than 0.20 ML. The gas phase is not at the thermodynamic equilibrium composition, and it contains different gaseous species reservoirs of CO* and H*: H2O, CO2, CH4, CO and H2. However, only the reactions of adsorption/desorption of gaseous CO and H2 to CO* and H* turn out to be quasi-equilibrated from the microkinetic analysis. Therefore, we calculate the chemical potentials of CO* and H* as functions of μCO and μH2:| μCO* = μCO | (13) |
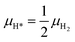 | (14) |
The presence of other adsorbates does not affect the stability of Rh surfaces, as a consequence to the fact that their coverage is calculated to be lower than 0.01 ML.
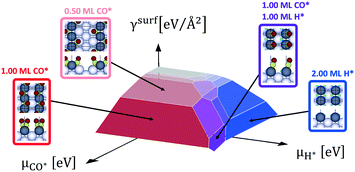
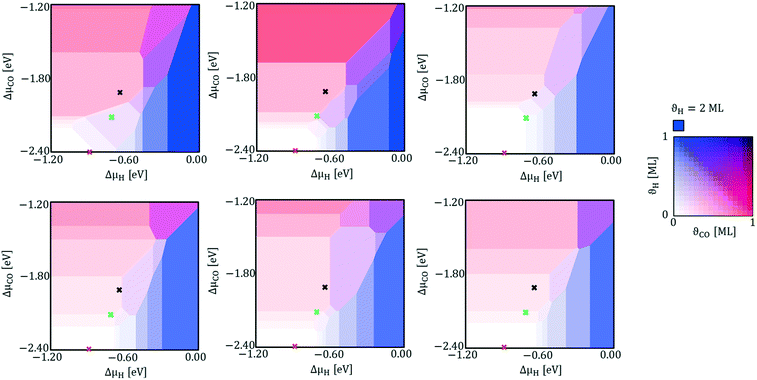
With eqn (4) we calculate the specific surface free energy of all clean Rh facets characterized by Miller indices lower than 4. Then, with the Wulff construction method (eqn (10)) we calculate the equilibrium shape of clean Rh nanoparticles under vacuum and we find that the exposed facets are only six: (100), (110) (111), (211), (311) and (331). We select these six facets for the following study, as a good compromise between computational time and accuracy of results. Exploiting eqn (4), we calculate the thermodynamically stable surface structures of the six selected facets of Rh, in the presence of CO*, H* or both the adsorbates on the surfaces. Fig. 5 shows an example of a double chemical potential plot of specific surface free energy (that of the Rh(110) facet). The specific surface free energy of the facet decreases with the increase of both chemical potentials. Fig. 6 shows the double chemical potential phase diagrams of several ordered and disordered surface structures that we calculated to be the most stable on the six considered surfaces at different values of CO* and H* chemical potentials. On all the facets there are regions in which co-adsorption is preferred.
Our simulation of the CPO annular reactor at 773 K and 1 atm shows that, at the beginning of zone 2 (see Fig. 1), the partial pressures of CO and H2 are 4 × 10−6 atm (ΔμCO* = −2.40 eV) and 2 × 10−5 atm (ΔμH* = −0.87 eV), respectively. Under these conditions, the coverage on all the facets is very low (ϑCO* < 0.01 ML and ϑH* < 0.01 ML). At the outlet of the reactor, the CO partial pressure increases to 7 × 10−4 atm (ΔμCO* = −2.06 eV), and the H2 partial pressure is 4.2 × 10−3 atm (ΔμH* = −0.70 eV). Under these conditions, co-adsorption of CO* and H* is preferred on Rh(100). On Rh(110), Rh(211) and Rh(311), structures with adsorbed CO* and H* have similar energy to structures with only CO* adsorbed. On Rh(111), the coverages predicted are very low, with H* found to remain adsorbed more favourably than CO*. On Rh(331), CO* alone is the most stable. Considering now the conditions of the equilibrium composition of the gas phase at 773 K (PCO = 6 × 10−3 atm and PH2 = 1.4 × 10−2 atm), we calculate that ΔμCO* = −1.91 eV and ΔμH* = −0.66 eV. Under these conditions, we find that CO* is the favoured adsorbate on Rh(100), Rh(110) and Rh(331). Meanwhile, on Rh(111), Rh(211) and Rh(311) the co-adsorption competes with CO* adsorbed alone. Details on the tested surface structures are reported in section 4 of the ESI.†
The effect of the support is taken into account by calculating the specific adhesion energy of Rh(100), Rh(110) and Rh(111) in contact with Al2O3(0001) and Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surfaces. The adhesion energy is calculated with eqn (14), assuming non-coherent epitaxy between Rh and Al2O3 facets. Rh(111) is calculated to be the most favourable facet with which the catalyst is in contact with the support, and similar adhesion energies are obtained with the two investigated Al2O3 facets (0.025 eV A−2 for Al2O3(0001) and 0.029 eV A−2 for Al2O3(1
02) surfaces. The adhesion energy is calculated with eqn (14), assuming non-coherent epitaxy between Rh and Al2O3 facets. Rh(111) is calculated to be the most favourable facet with which the catalyst is in contact with the support, and similar adhesion energies are obtained with the two investigated Al2O3 facets (0.025 eV A−2 for Al2O3(0001) and 0.029 eV A−2 for Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)). Details are provided in section 3 of the ESI.†
02)). Details are provided in section 3 of the ESI.†
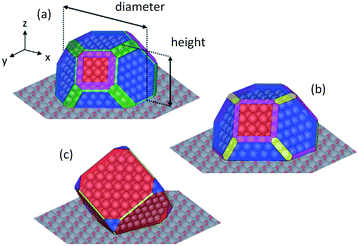
With the Wulff–Kaishew construction method (eqn (10) and (11)) we eventually calculate the equilibrium shape of the Rh catalyst nanoparticles as a function of the reactive environment. When syngas starts to be produced in the reactor, the catalyst nanoparticles (represented in Fig. 4, panel d) show a highly faceted shape, where the close-packed Rh(111) surface prevails. Rh(311) is the second most exposed surface structure, followed by Rh(331) and Rh(100). Rh(211) and Rh(110), on the other hand, present very small areas in the Wulff plot. At the reactor outlet, the exposed areas of Rh(111), Rh(211) and Rh(331) are reduced, while those of Rh(100), Rh(110) and Rh(331) are enlarged (Fig. 4, panel e). When the gas phase is at thermodynamic equilibrium, the catalyst nanoparticle is more spherical and the height to diameter ratio is increased (Fig. 4, panel f).
In Fig. 4 the profiles of the relative areas of the crystal facets exposed by the catalyst nanoparticles along the reactor coordinate are also reported. In the first zone of the CPO reactor the catalyst morphology changes with the variation of the oxygen partial pressure in the reactive environment. In particular, over-stoichiometric terminations are more abundant when the oxygen content is high. In the second zone of the reactor, the amount of stepped surfaces and Rh(110) increases with the increase of the chemical potential of H2 and CO, whereas the relative area of Rh(111) is reduced. This clearly shows that the relative abundance of the possible active sites is influenced by the reaction environment and thus changes as a function of the chemical potential.
Comparison with chemisorption analysis
The previous analysis has been performed irrespective of the actual size of the nanoparticle, since the Wulff–Kaishew construction is size-independent. Here, we aim at testing the ability of the framework for given values of catalyst nanoparticle size. At this scope, we report an analysis and interpretation of catalyst characterization experiments on a 0.5% Rh/α-Al2O3 catalyst prepared by chemical vapor deposition (CVD) of Rh(acac)(CO)2 by Beretta et al.41 These experimental data include HRTEM images obtained after aging under CPO conditions at 850 °C and H2 and CO chemisorption experiments. HRTEM allowed for the calculation of the particle size distribution of the catalyst under the conditions of the HRTEM analysis (vacuum, room temperature). Chemisorption data are used for estimating the ratio between the number of adsorbed molecules (NA*) and the catalyst total number of atoms (NRh,tot). This quantity can be employed to calculate the catalyst dispersion (Rh atoms which constitute the catalyst surfaces, NRh,surf, divided by NRh,tot), if the adsorption stoichiometry (the ratio between NA* and NRh,surf) is known. Thus, the catalyst dispersion can be calculated as follows: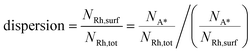 | (15) |
Here, using as an input the particle size distribution from HRTEM analysis, we test the ability of our thermodynamic model to estimate the catalyst dispersion. In particular, we calculate the structure of the catalyst and the adsorption stoichiometry under the chemisorption conditions and we compare the resulting catalyst dispersion with the data of chemisorption. In order to input the information regarding the size we proceed as follows. We assume that the number of atoms in the nanoparticles is the same under both HRTEM and chemisorption conditions. This assumption implies that sintering phenomena do not occur (room temperature), but the shape can undergo modifications induced by adsorption of probe molecules.
To this aim, with ab initio thermodynamics (eqn (4)) and Wulff–Kaishew construction (eqn (10) and (11)) we calculate the catalyst shape in equilibrium with the environment of the HRTEM analysis. We assume that the catalyst surfaces are adsorbate-free under vacuum conditions. Then, for each diameter of the particle size distribution we calculate the number of atoms in each nanoparticle by filling a Wulff–Kaishew plot with the considered diameter and counting the resulting amount of Rh atoms inside the Wulff–Kaishew plot. We consider the Wulff–Kaishew plot diameter as the distance between the closest two sides of the Wulff–Kaishew plot projected in the xy plane.
An example of a nanoparticle with a diameter of 2 nm is shown in Fig. 7 (panel a). The corresponding height from Wulff–Kaishew construction turns out to be 1.18 nm, thus leading to a catalyst height/diameter ratio of 0.59. This ratio is in agreement with the qualitative observation of Beretta et al.41 based on HRTEM images (height/diameter = 2/3).
After calculating the distribution of number of atoms of the sample, we study the catalyst structure under chemisorption conditions. With ab initio thermodynamics we calculate the specific surface free energy of the Rh facets in equilibrium with the chemical potential of CO and H2 in the gas phase. Then, with Wulff–Kaishew construction we calculate the equilibrium shape of the catalyst under the conditions at which the chemisorption pulses are performed. For each group of the distribution of number of atoms, we fill a Wulff–Kaishew plot with the corresponding number of atoms and we count the resulting Rh atoms that form the catalyst surfaces (the ones with a coordination number lower than 11). Weighting the number of surface atoms by the percentage amounts of atoms of the groups, we calculate the dispersion of the entire population of nanoparticles.
Under H2 chemisorption conditions (PH2 = 4.78 × 10−2 atm, room temperature), the H* chemical potential is ΔμH* = −0.39 eV (eqn (2) and (14)). The corresponding catalyst shape under H2 chemisorption conditions is shown in Fig. 7 (panel b) and allows for the direct calculation of the catalyst dispersion (atoms at the surfaces divided by the total number of atoms: 0.45 Rhsurf/Rhtot). We perform the same analysis for CO chemisorption conditions (PCO = 5.04 × 10−2 atm, room temperature). Under these conditions the CO* chemical potential is equal to ΔμCO* = −0.60 eV (eqn (2) and (13)). As a result of the different chemical potential, the catalyst shape is different from the one predicted under H2 chemisorption conditions (Fig. 7, panel e), and leads to a value of dispersion of 0.46 Rhsurf/Rhtot.
Next, we compare the values of catalyst dispersion calculated with our thermodynamic model with the ones obtained experimentally through uptake measurements.41 A crucial information for the interpretation of such experiments is the stoichiometry of chemisorption, which can be deduced by the H2 and CO coverages at equilibrium (ϑH*, ϑCO*). Thus, the adsorption stoichiometry can be expressed as:
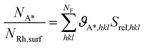 | (16) |
Under H2 chemisorption conditions, the H* coverage on the facets that the catalyst exposes to the environment is 1.00 ML (see Table 2). Therefore, the 0.47 H*/Rhtot uptake measurement leads to the following value of dispersion:
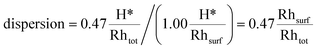 | (17) |
| hkl | H2 chemisorption | CO chemisorption | ||
|---|---|---|---|---|
| S rel [%] | ϑ H* [ML] | S rel [%] | ϑ CO* [ML] | |
| 100 | 15.68 | 1.00 | 91.35 | 0.83 |
| 110 | 9.32 | 1.00 | 3.01 | 1.00 |
| 111 | 58.60 | 1.00 | 5.65 | 0.75 |
| 211 | 0.00 | 0.67 | 0.00 | 0.67 |
| 311 | 16.41 | 1.00 | 0.00 | 0.75 |
| 331 | 0.00 | 0.67 | 0.00 | 0.67 |
This value is found to be in very good agreement with the one obtained using our thermodynamic model (0.45 Rhsurf/Rhtot).
Concerning CO chemisorption, the surface coverage for each facet is given in Table 2, and results in a CO* adsorption stoichiometry of 0.83 CO*/Rhsurf. As such, by analogy to H2 chemisorption, the resulting dispersion is:
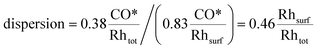 | (18) |
Conclusions
In this work, we investigated how the reactor environment influences the morphology of a catalyst, in the context of CH4 CPO over Rh. In agreement with previous analysis, we find that the reactor is stratified in two distinct zones. The first zone is characterized by a high amount of oxygen in the gas phase in contact with the catalyst, whereas in the second zone the oxygen in the gas phase is very low. We predict that the change from the oxidized zone to the reduced zone of the reactor is accompanied by a change in the structure and morphology of the catalyst. These theoretical findings agree with previously reported operando spectroscopic data. In particular, we found Rh2O3 to be the thermodynamically stable bulk phase in the first zone of the reactor, whereas in the second zone, where the amount of O2 drops to very low values at the catalyst interface, metallic Rh turns out to be the most stable bulk structure. We analysed the catalyst morphology along the reactor coordinate using Wulff–Kaishew constructions, and thus obtained 3D representations of the catalyst nanoparticles. This allowed us to estimate the relative amount of catalyst active sites that was found to change significantly along the reactor coordinate. The proposed framework was also validated via the interpretation of characterization data on a conditioned 0.5% Rh/α-Al2O3 catalyst and led to calculated values of catalyst dispersion that are in very good agreement with the experimental estimation via H2 and CO chemisorption.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project leading to this work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Project SHAPE – grant agreement No. 677423). Computational time at CINECA, Bologna (Italy) is gratefully acknowledged.References
- R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465–3520 CrossRef PubMed.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef PubMed.
- D. G. Vlachos, A. B. Mhadeshwar and N. S. Kaisare, Comput. Chem. Eng., 2006, 30, 1712–1724 CrossRef.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef.
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef PubMed.
- G. A. Somorjai and J. Y. Park, J. Chem. Phys., 2008, 128, 182504 CrossRef PubMed.
- L. Foppa, C. Copéret and A. Comas-Vives, J. Am. Chem. Soc., 2016, 138, 16655–16668 CrossRef PubMed.
- A. Berkó and F. Solymosi, J. Catal., 1999, 183, 91–101 CrossRef.
- T. Avanesian, S. Dai, M. J. Kale, G. W. Graham, X. Pan and P. Christopher, J. Am. Chem. Soc., 2017, 139, 4551–4558 CrossRef PubMed.
- S. Hannemann, J. D. Grunwaldt, N. van Vegten, A. Baiker, P. Boye and C. G. Schroer, Catal. Today, 2007, 126, 54–63 CrossRef.
- J. Grunwaldt, J. Catal., 2001, 200, 321–329 CrossRef.
- J. D. Grunwaldt, S. Hannemann, C. G. Schroer and A. Baiker, J. Phys. Chem. B, 2006, 110, 8674 CrossRef PubMed.
- M. Maestri, Chem. Commun., 2017, 53, 10244–10254 RSC.
- M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, AIChE J., 2009, 55, 993–1008 CrossRef.
- M. Maestri, D. Livio, A. Beretta and G. Groppi, Ind. Eng. Chem. Res., 2014, 53, 10914–10928 CrossRef.
- J. D. Grunwaldt, S. Hannemann, C. G. Schroer and A. Baiker, J. Phys. Chem. B, 2006, 110, 8674–8680 CrossRef PubMed.
- M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, J. Catal., 2008, 259, 211–222 CrossRef.
- M. Maestri, D. G. Vlachos, A. Beretta, P. Forzatti, G. Groppi and E. Tronconi, Top. Catal., 2009, 52, 1983–1988 CrossRef.
- A. Donazzi, M. Maestri, B. C. Michael, A. Beretta, P. Forzatti, G. Groppi, E. Tronconi, L. D. Schmidt and D. G. Vlachos, J. Catal., 2010, 275, 270–279 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef.
- Y. D. Scherson, S. J. Aboud, J. Wilcox and B. J. Cantwell, J. Phys. Chem. C, 2011, 115, 11036–11044 Search PubMed.
- T. Thonhauser, S. Zuluaga, C. A. Arter, K. Berland, E. Schröder and P. Hyldgaard, Phys. Rev. Lett., 2015, 115, 1–6 CrossRef PubMed.
- T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–11 CrossRef.
- K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 66501 CrossRef PubMed.
- D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 84203 CrossRef PubMed.
- P. Lazić, M. Alaei, N. Atodiresei, V. Caciuc, R. Brako and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 1–6 Search PubMed.
- P. Villars and L. D. Calvert, Pearson's Handbook of Crystallographic Data for Intermediate Phases, American Society of Metals, 1986, p. 3258 Search PubMed.
- M. E. Grillo, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–6 CrossRef.
- R. G. Munro, J. Am. Ceram. Soc., 1997, 80, 1919–1928 CrossRef.
- M. García-Mota, M. Rieger and K. Reuter, J. Catal., 2015, 321, 1–6 CrossRef.
- J. Rogal and K. Reuter, Exp. Model. Simul. Gas-Surface Interact. React. Flows Hypersonic Flights, 2007, pp. 1–18 Search PubMed.
- J. Malcolm and W. Chase, NIST-JANAF thermochemical tables, American Chemical Society, American Institute of Physics for the National Institute of Standards and Technology, Washington, DC, New York, 4th edn, 1998 Search PubMed.
- C. T. Campbell, L. H. Sprowl and L. Árnadóttir, J. Phys. Chem. C, 2016, 120, 10283–10297 Search PubMed.
- P. Muller and R. Kern, Surf. Sci., 2000, 457, 229–253 CrossRef.
- E. Ringe, R. P. Van Duyne and L. D. Marks, Nano Lett., 2011, 11, 3399–3403 CrossRef PubMed.
- A. Donazzi, A. Beretta, G. Groppi and P. Forzatti, J. Catal., 2008, 255, 259–268 CrossRef.
- M. Kitayama and A. M. Glaeser, J. Am. Ceram. Soc., 2002, 85, 611–622 CrossRef.
- A. Marmier and S. C. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115409 CrossRef.
- A. Beretta, A. Donazzi, G. Groppi, P. Forzatti, V. Dal Santo, L. Sordelli, V. De Grandi and R. Psaro, Appl. Catal., B, 2008, 83, 96–109 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Modelling of the annular reactor; details of the calculations of the morphology of Rh and Rh2O3 nanoparticles; details of the calculation of the interfacial energy between the catalyst and the support; surface structures of Rh2O3 and Rh. See DOI: 10.1039/c8cy00583d |
| This journal is © The Royal Society of Chemistry 2018 |