Direct visualization of sulfur cathodes: new insights into Li–S batteries via operando X-ray based methods

Abstract

As the need for the development of “beyond lithium” ion battery technologies continues unabated, lithium sulfur batteries have attracted widespread attention due to their very high theoretical energy density of 2600 W h kg⁻¹. However, despite much effort, the detailed reaction mechanism remains poorly understood. In this study, we have combined operando X-ray diffraction and X-ray microscopy along with X-ray tomography, to visualize the evolution of both the morphology and crystal structure of the materials during the entire battery cycling (discharging/charging) process. The dissolution and reformation of sulfur clusters is clearly observed during cycling. In addition, we demonstrate, for the first time, the critical role of current density and temperature in determining the size of both the resulting sulfur clusters and Li₂S particles. This study provides new insights about promising avenues for the continued development of lithium sulfur batteries, which we believe may lead to their broad deployment and application.

---

Broader context

Lithium–sulfur (Li–S) batteries represent one of the most attractive candidates to replace state-of-art Li-ion batteries due to their high theoretical energy density. However, a remaining challenge relates to the complex reaction mechanism which involves the formation, dissolution and precipitation/nucleation of sulfur and lithium sulfides. In this work, we present an operando study on the evolution of the morphology and crystal structure of sulfur cathodes during operation in Li–S batteries via synchrotron-based X-ray diffraction, microscopy and tomography. We visualized dissolution and reformation of sulfur. Sulfur is completely dissolved during discharge, and reformed near the end of the re-charge. The size of both lithium sulfides and sulfur, formed during the discharge and re-charge, respectively, were strongly dependent on experimental conditions including current density and temperature. At higher current densities, both the sulfur and lithium sulfide tended to form smaller clusters with a more uniform distribution, which we ascribe to a higher nucleation density. At lower temperatures, lithium sulfide also formed smaller clusters. This study provides new insights about promising avenues for the continued development of lithium sulfur batteries, which we believe may lead to their broad deployment and application.

1. Introduction

The development of novel high performance electrical energy storage systems (EES) with energy densities surpassing those of state-of-the-art lithium ion batteries (LIBs) has become increasingly important, due to the dramatic increase in their applications, especially in transportation.^1–4 Lithium sulfur (Li–S) batteries are an especially promising option because elemental sulfur has a high theoretical capacity of 1672 mA h g⁻¹, is abundant, inexpensive and environmentally benign.^5–9 However, there are several road blocks hindering the practical deployment of Li–S batteries including the formation of highly soluble, as well as insoluble, species during cycling, and the fact that both sulfur and lithium sulfide (Li₂S) are electrical insulators. In addition, some of the long-chain polysulfide intermediates are soluble in the electrolyte (vide supra), causing the loss of active material and leading to rapid capacity fade. Moreover, dissolved polysulfides can be reduced and re-oxidized between the anode and cathode, resulting in the self-discharge process known as the “shuttle mechanism”.

Since Nazar group's initial work on the preparation of sulfur electrodes by infiltrating sulfur into mesoporous carbons, which yielded cycling stability enhancements,¹⁰ significant efforts have been made to develop other alternatives for high performance sulfur-based cathode materials.^11–14 These efforts have resulted in significant improvements in overall performance. Concurrently, numerous experimental probes have been developed and employed in an effort to unravel the reaction mechanism, while the battery is under operation (“operando methods”).^15–23 Despite these efforts, there is still no consensus on the mechanistic details. For example, recent work by Waluś et al. using operando X-ray diffraction (XRD) found that the diffraction signal from sulfur completely disappeared at the end of the upper plateau during the discharge, and that monoclinic sulfur (β-S₈) formed during the recharge step.¹⁵ Contrary to that, using operando X-ray microscopy (XRM), Nelson et al. found that the sulfur particles did not dissolve significantly in the discharge and they did not observe changes in the morphology during the re-charge process.¹⁶

In an effort to obtain a more complete understanding of the reaction mechanism, we have carried out both operando XRD and XRM during battery operation along with X-ray tomography. In our case, we obtain excellent agreement from all three techniques. By characterizing the battery over its entire (discharge/recharge) cycle, we have observed, in real time, significant changes in both morphology and diffraction features (structure). Additionally, we demonstrate, for the first time, the role that current density and temperature play in determining the size of sulfur clusters and Li₂S particles.

2. Experimental

2.1. Electrochemical characterization

Sulfur electrodes were prepared by coating a homogeneous slurry onto carbon paper (AvCarb EP40, Fuelcell Store). The slurry was made of sulfur (Aldrich), super P carbon, and polyvinylidene fluoride (60 : 25 : 15 wt%) dissolved in N-methyl-2-pyrrolidinone (NMP) solvent. A 3 mm diameter hole was made in the center of a 2032-type coin cell and sealed with Kapton film (30 μm) and Torr Seal epoxy to serve as an X-ray transmissive window. The electrolyte consisted of 1.0 M lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) in 1,3-dioxolane (DOL)/1,2-dimethoxyethane (DME) solvent with 0.2 M LiNO₃ additive. The coin cells, with affixed X-ray windows, were assembled in an argon-filled glove box. Lithium metal was used as both reference and counter electrodes, while the sulfur electrode was used as the working electrode. Unless otherwise noted, the cells were cycled at a rate of 0.1C (1C = 1672 mA h g⁻¹) at room temperature, with a potentiostat (Biologic SP-200).

In the lithium/polysulfide battery experiment, a polysulfide (0.5 M Li₂S₈) catholyte with carbon paper was used. Stoichiometric amounts of Li₂S and sulfur were added to the electrolyte mentioned above and mixed by stirring at 60 °C overnight in the glove box. For cycling, the current density was fixed at 0.1 mA for discharging and variable, between 0.05 and 0.5 mA, for charging during 5 cycles.

2.2. Operando XRD

Operando XRD experiments were performed at the A-1 station of the Cornell High Energy Synchrotron Sources (CHESS) at an X-ray energy of 19.8 keV. The diffraction signal was collected using an area detector (Dexela 2923) with a pixel size of 74.8 μm and a total area of 290 × 230 mm². The distance between sample and detector was 66 cm. The diffraction signal was collected every 4 min. For temperature controlled experiments, the cells were mounted in a home-made coin cell holder, with coolant liquid running through the holder to maintain constant temperature. The temperature was controlled and monitored with a water bath circulator (Thermo Scientific NESLAB).

2.3. Operando XRM

Operando XRM was performed at the F-3 station of CHESS using an incident X-ray energy of 10.0 keV. XRM was conducted in a transmission geometry, in which the X-ray beam penetrates through the whole cell (about 3.2 mm), including Li anode (∼750 μm), sulfur cathode on carbon paper (∼100 μm) and electrolyte, making the XRM images reflect the morphology of the whole electrode. Images were collected using a Scintillator-coupled Andor camera (Neo 5.5 sCMOS), with a resolution of about 2 μm. The distance between the sample and detector was between 2.0 and 23.2 cm. For absorption contrast imaging without phase enhancement, a distance of about 2 cm was chosen. For phase contrast imaging, the distance chosen was 23.2 cm.

2.4. X-ray tomography

Tomography was performed at the F-3 station of CHESS. A setup similar to that used for operando XRM was employed, except the sample stage was on an air bearing rotation stage enabling the acquisition of projected images of the sample at different angles. In total, 900 projected images were taken within 180 degrees, with acquisition time of 15 seconds for each image.

2.5. Computational details

Density Functional Theory calculations were carried out using the JDFTx code,²⁴ with the generalized-gradient approximation PBE,²⁵ GBRV ultrasoft pseudopotentials²⁶ with the recommended wavefunction and charge-density kinetic energy cutoffs (20 Eh and 100 Eh, respectively). A set of sulfur anions (and neutral S₈) were geometrically relaxed in a 20 Bohr square box, in the presence of the continuum fluid “glyme”,²⁷ with a 1.2 M concentration of ions. The anionic species considered were: S¹⁻, S²⁻, S₂²⁻, S₃¹⁻, S₃²⁻, S₄¹⁻, S₄²⁻, S₅¹⁻, S₅²⁻, S₆¹⁻, S₆²⁻, S₇¹⁻, S₇²⁻, S₈, S₈¹⁻, S₈²⁻, S₉²⁻, S₉³⁻, S₁₀²⁻. The sulfur species were solvated by a linear continuum fluid with a dielectric constant of 7.2, closely approximating the dielectric of the 1,3-dioxolane (DOL)/1,2-dimethoxyethane (DME).

Solution free energies from these calculations were combined with a statistical mechanics calculation to predict the equilibrium concentration of each sulfur anion or molecule, at a given amount of excess negative charge, (or equivalently, the number of lithium cations needed to screen the negative charges). These statistical mechanics calculations were performed for 1 mM sulfur solutions, with variable lithium ion concentrations. Within the grand canonical ensemble, we determined the chemical potentials, at given net sulfur and lithium concentrations, and subsequently used those to find the concentration of each sulfur anion/molecule.

3. Results and discussion

3.1. Evolution in morphology and crystal structure during cell discharge

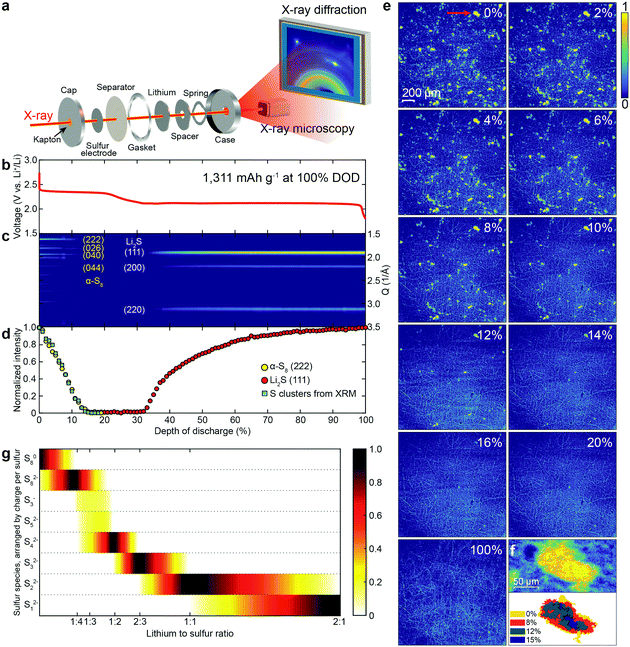
Fig. 1a presents a combined schematic of the experimental set-ups for operando XRD and XRM. Both XRD and XRM were performed in real time, with the battery under operation (operando). The morphology of the sulfur electrode was measured via XRM. For XRD, the diffraction signals from the electrode were collected with a large area detector in a transmission geometry. A CR-2032 coin cell, with X-ray transparent windows (30 μm Kapton), was galvanostatically charged and discharged. 1.0 M LiTFSI bis(trifluoromethanesulfonyl)imide in 1,3-dioxolane (DOL)/1,2-dimethoxyethane (DME) solvent with 0.2 M LiNO₃ additive was used as the supporting electrolyte. The voltage profile during the first discharge, at a rate of 0.1C (1C = 1672 mA h g⁻¹, the initial discharge capacity was 1311 mA h g⁻¹), is shown in Fig. 1b. Two distinct voltage plateaus were observed at about 2.4 and 2.1 V, which is consistent with the reported initial discharge profiles of the Li/S system in ether-based electrolytes.^21–23,28

Fig. 1 Operando X-ray microscopy and diffraction for Li–S batteries during the initial discharge. (a) Combined schematic illustration of the experimental set-ups for X-ray microscopy and diffraction. (b) Voltage profile, (c) operando X-ray diffraction pattern and (d) normalized intensity of α-S₈ and Li₂S of the sulfur electrode at a rate of 0.1C (1C = 1672 mA h g⁻¹) during discharge. Yellow and red circles in (d) indicate normalized X-ray diffraction intensities of α-S₈(222) and Li₂S(111), respectively. The sky blue squares are the normalized amount of all sulfur clusters calculated based on the total integrated signal from X-ray microscopy. (e) Operando X-ray microscopy images of a sulfur electrode at different depths of discharge (DODs) indicated as a %. (f) Enlarged image of a single sulfur cluster in the region indicated by a red arrow at 0% DOD (top) and area changes of the same cluster at different DODs (bottom). (g) Computed equilibrium fraction of total sulfur for a given sulfur species, with varying lithium concentration, from statistical mechanics calculations using DFT energies of solvated sulfur species.

Fig. 1c presents the powder diffraction patterns of the sulfur electrode at different depths of discharge (DODs). The initial structure of sulfur is orthorhombic α-S₈ (see Fig. S1 for the crystal structures and Fig. S2 for diffraction patterns, ESI†). The intensity of the α-S₈ diffraction peaks decreased rapidly until about 13% DOD, with only 6% of the initial intensity remaining. The α-S₈ diffraction peak intensity continued to slowly decrease, disappearing completely near end of the upper voltage plateau. The Li₂S diffraction peaks appeared at the start of the lower voltage plateau, and increased, asymptotically approaching their maximum value at the end of the discharge, as can be clearly observed in Fig. 1d. Fig. 1d presents the integrated intensities of both the α-S₈(222) and the Li₂S(111) diffraction peaks, shown as yellow and red circles, respectively. There have been conflicting reports as to when the Li₂S peaks appear in the discharge. Some reports have claimed that Li₂S is not observed until the middle of the lower voltage plateau,²⁰ while others suggest that the formation of Li₂S starts at the beginning of the lower plateau.^15,19 Our results clearly agree with the latter.

In XRM, two types of contrast information are available, absorption and phase. Phase contrast sharpens the edges of objects. Experimentally, the distance between the sample and the detector modulates the level of phase contrast. In the XRM images (Fig. 1e and Fig. S3, ESI†), the bright yellow clusters are sulfur, while the thread-like features arise from the carbon fibers, used as the current collector. While the sulfur particles can be readily observed using only absorption contrast (Fig. S3b, ESI†), the carbon fibers are difficult to resolve. However, by increasing the phase contrast (see Fig. S3d–f, and S4 for simulation concerning phase enhancement, ESI†), the carbon fibers become clearly visible. Fig. 1e shows the XRM of a sulfur electrode at different DODs (see Movie S1, ESI†), and clearly illustrates the disappearance of sulfur clusters. In order to identify the location and morphology of both the sulfur and carbon fibers simultaneously, we employed the enhanced phase contrast experimental configuration. From Fig. 1e, one can surmise that the initial sulfur clusters are randomly distributed on the carbon current collector and that their size distribution is inhomogeneous with some clusters having a projected area as large as 4000 μm². The sulfur clusters begin to dissolve concomitantly with the start of the cell discharge. At 20% DOD, all the sulfur clusters have disappeared, and no other resolvable features emerge during the rest of the discharge. This indicates that the size of the Li₂S formed, which will be discussed in Fig. 2, is below the resolution limit of XRM. Fig. 1f (top panel) shows a single sulfur cluster, which is marked by a red arrow, at 0% DOD (top left panel) in Fig. 1e. Fig. 1f (bottom panel) shows the change in area, of the same cluster, at different DODs. It is evident that the dissolution of the cluster is from the edges to the center.

Fig. 2 Operando X-ray diffraction for Li–S batteries during the initial discharge at different temperatures. (a) Schematic depiction of the temperature controlled experiment. (b) Voltage profiles, (c) normalized intensity of X-ray diffraction from α-S₈ and Li₂S of the sulfur electrodes at a rate of 0.2C (1C = 1672 mA h g⁻¹) during discharge at different temperatures. (d) Voltage profiles, (e) operando X-ray diffraction pattern and (f) particle size of Li₂S calculated from the Li₂S(111) Bragg peak of the sulfur electrodes during the lower plateau at different temperatures, after shifting the capacity to be zero at the beginning of the lower plateau.

In order to obtain a more detailed understanding of sulfur dissolution, the change in area of all of the observed sulfur clusters was further analyzed. The integrated intensity of all of the sulfur clusters in the XRM image is plotted as blue squares in Fig. 1d. The XRM data closely track the integrated intensity of the diffraction peak from α-S₈(222), strongly supporting the identification of these XRM features as sulfur in the crystalline alpha phase (α-S₈). Fig. 1g presents results from DFT calculations of the equilibrium state among various sulfur species at different lithium to sulfur ratios. For S₈, the calculated DFT profile decreases linearly as the lithium level increases, matching our XRD and XRM results (see Fig. 1d) in which signals from crystalline sulfur decrease linearly. However, it is worth noting that the calculated profile for Li₂S increases linearly with lithium, starting at a ratio of 1 : 1 between lithium and sulfur, which does not match the XRD results. In Fig. 1d, the increase in diffraction intensity from Li₂S slows down during the discharge, which might be due to the increasing coverage of Li₂S (an insulator) on the surface of the carbon fiber current collector.^15,29

3.2. Temperature effects on discharge and the formation of Li₂S particles

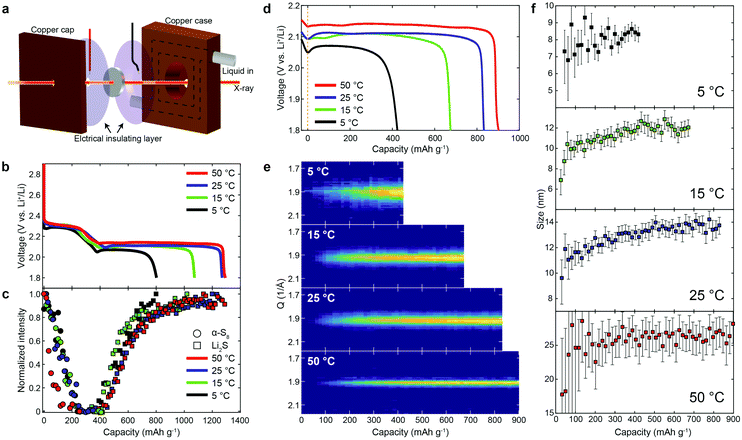
To further understand the mechanism during discharge, we discharged lithium/sulfur cells at a rate of 0.2C at different temperatures, while conducting operando XRD. Fig. 2a shows the experimental setup of operando X-ray measurements with a temperature-controlled home-made cell holder. Fig. 2b and c show the voltage profiles during the first discharge at 5, 15, 25 and 50 °C, and the corresponding X-ray intensity. It is evident that both the upper and lower plateaus were affected by temperature. The capacity delivered at the upper plateau increased slightly as the temperature increased (except at 50 °C, Fig. 2b and Fig. S5, ESI†), which we ascribe to increased kinetics at higher temperatures. The capacity decreased at 50 °C, and the diffraction intensity of α-S₈ dropped much faster (Fig. 2c) as well, which we believe is due, at least in part, to an increase in the rate of dissolution of α-S₈ at the higher temperature (50 °C) (by forming polysulfides and/or through chemical reactions, see Fig. S6, ESI†).

However, the upper plateau was less significantly influenced than the lower plateau. This arises from the fact that the first process in the discharge is related to the breakage of the S₈ rings of solid sulfur, and their subsequent dissolution as polysulfides, and such processes are likely to be minimally affected by temperature (assuming that the temperature is well below the melting temperature of sulfur, which was the case in these studies). To clearly compare the effect of temperature on the lower plateau, we shifted the capacity to be zero at the beginning of the lower plateau (in a consistent manner, from the first derivative of the voltage profiles, see Fig. S5, ESI†). As is evident, the overpotential for the formation of Li₂S increases as the temperature decreases, suggesting an activation process. A similar trend in the overpotential could also be observed during the recharging processes (see Fig. S7, ESI†). Fig. 2e shows the diffraction pattern of Li₂S(111) at different temperatures as a function of capacity for the lower plateau. The Li₂S particle size (obtained via the Scherrer equation) is plotted in Fig. 2f (see Fig. S8 for Li₂S particle size at different current rates, ESI†). It is evident that the Li₂S particle size is smaller at lower temperatures/high current rates (Fig. 2f and Fig. S8, ESI†), which might be due, at least in part, to the higher number of nuclei induced by the larger overpotential as well as to lower transport rates.

3.3. Evolution in morphology and crystal structure during re-charge

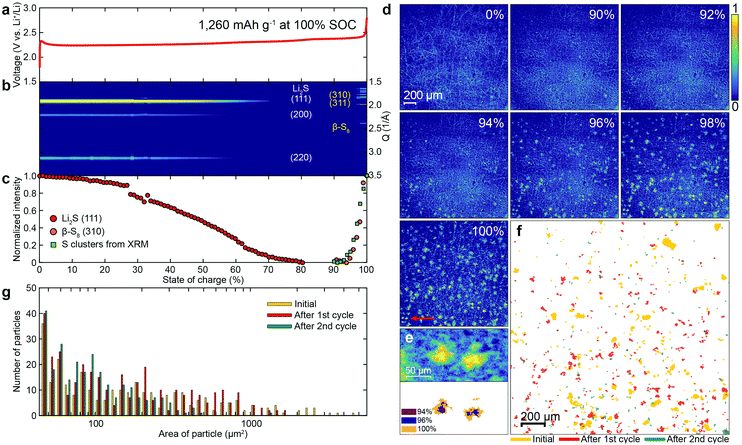
The voltage profile, operando XRD patterns and XRM images of the sulfur electrode during re-charging are shown in Fig. 3a–e and Movie S2 (ESI†). In the voltage profile (Fig. 3a), a potential barrier is observed at the very early stages of charging, likely due to the activation energy required to oxidize the insoluble (and insulating) Li₂S to polysulfides.³⁰ Subsequently, the potential increased continuously until reaching a plateau at about 2.4 V. From the XRD pattern of the sulfur electrode during charging (Fig. 3b), the intensity of the diffraction peaks of Li₂S decreased and disappeared at about 80% state of charge (SOC). After the plateau at 2.4 V (around 90% SOC), the diffraction peaks of β-S₈ emerged. The normalized intensities of the diffraction peaks of Li₂S(111) and β-S₈(310) are plotted as red and orange circles in Fig. 3c, respectively.

Fig. 3 Operando X-ray microscopy and diffraction for Li–S batteries during charge in the initial cycle and comparison of sulfur cluster size and location between cycles. (a) Voltage profile, (b) operando X-ray diffraction pattern and (c) normalized intensity of Li₂S and β-S₈ of sulfur electrode at a rate of 0.1C during charge. The red and orange circles in (c) are the normalized X-ray diffraction intensities of Li₂S(111) and β-S₈(310), respectively. The green squares represent the normalized amount of all sulfur clusters calculated based on the total integrated signal from X-ray microscopy. (d) Operando X-ray microscopy images of a sulfur electrode at different states of charge (SOCs). (e) Enlarged image of sulfur clusters formed in the region indicated by the red arrow at 100% SOC (top) and area changes of the clusters at different SOCs (bottom). (f) Shapes of sulfur clusters on the electrode before cycling (yellow), overlapped with reformed clusters after the first (red) and second (green) cycles. Images were taken at identical locations on the cathode. (g) Size histograms of sulfur clusters on the electrode before cycling (yellow), after the first cycle (red), and second cycle (green).

Fig. 3d presents XRM images of a sulfur electrode at different SOCs. Initially, no sulfur clusters are observed. At approximately 90% SOC, the sulfur clusters emerge. The size distribution of the sulfur clusters, grown during recharge, is more homogeneous than the initial distribution. These results clearly illustrate the differences between the dissolution and reformation of sulfur clusters under operando conditions during full discharge/re-charge cycles (see Fig. S9 for voltage profiles during the 2nd cycle; see Fig. S10 and S11, and Movies S3 and S4 for corresponding XRM images and movies of the sulfur cathode, respectively, ESI†). Fig. 3e shows two sulfur clusters formed, marked by a red arrow at 100% SOC in Fig. 3d, and their growth. The integrated intensity from all the sulfur clusters in the XRM experiment was plotted as the green squares in Fig. 3c, and compared with the intensity of β-S₈(310). The very good agreement between the two, suggests that the sulfur clusters shown in the XRM are, in fact, β-S₈. Fig. 3f presents the contour changes of the sulfur clusters on the electrode before cycling (yellow), and reformed after the 1st (red) and 2nd cycles (green). As can be seen, the locations of the pristine sulfur and reformed sulfur after the 1st and 2nd cycles are different, indicating that the sulfur particles are completely dissolved during the discharge, so that the sulfur nucleation sites are “refreshed” in every cycle.

A histogram of the projected area of the sulfur clusters in Fig. 3f is presented in Fig. 3g. The area of the sulfur clusters becomes smaller after each cycle, including the initial one. After the 2nd cycle, the percentage of clusters with an area larger than 1000 μm² is only 0.4%, which is much less than the initial value (8.2%) as well as the value after the 1st cycle (3.9%) (see Table S1 for details, ESI†). The decrease in cluster size with cycle number is mainly attributed to the loss of active material by polysulfide dissolution into the electrolyte.

3.4. Tomography of sulfur electrodes

In order to further analyze the three-dimensional morphology of the electrode, X-ray tomography was performed. Fig. 4 presents the reconstructed image of the pristine sulfur electrode (Fig. 4a, b and Movie S5, ESI†), the electrode after discharge (Fig. 4c, d and Movie S6, ESI†) and after re-charge (Fig. 4e, f and Movie S7, ESI†). The difference in the attenuation lengths of sulfur and carbon makes the respective features clearly distinguishable. The yellow features represent the sulfur clusters, and the grey, the carbon species. In general, the grey network structure is from the carbon fibers. However, note that on the pristine samples (Fig. 4a and b), grey shells cover the sulfur clusters. These shells are from the carbon additive and/or binder. After discharge, only the carbon fibers remain (Fig. 4c and d). After re-charge, the clusters are uniformly dispersed and their sizes are smaller and more homogeneous in size when compared to the pristine sample (Fig. 4e and f). The reformed sulfur clusters are no longer covered with a (carbon) shell, as was initially observed in the pristine sample (vide supra).

Fig. 4 X-ray tomography of sulfur electrode before and after battery test. Front and perspective views of (a and b) pristine electrode, (c and d) after the first discharge, and (e and f) charge, respectively. Yellow represents sulfur particles, and grey represents carbon species.

3.5. The effect of current density on the formation and distribution of sulfur clusters

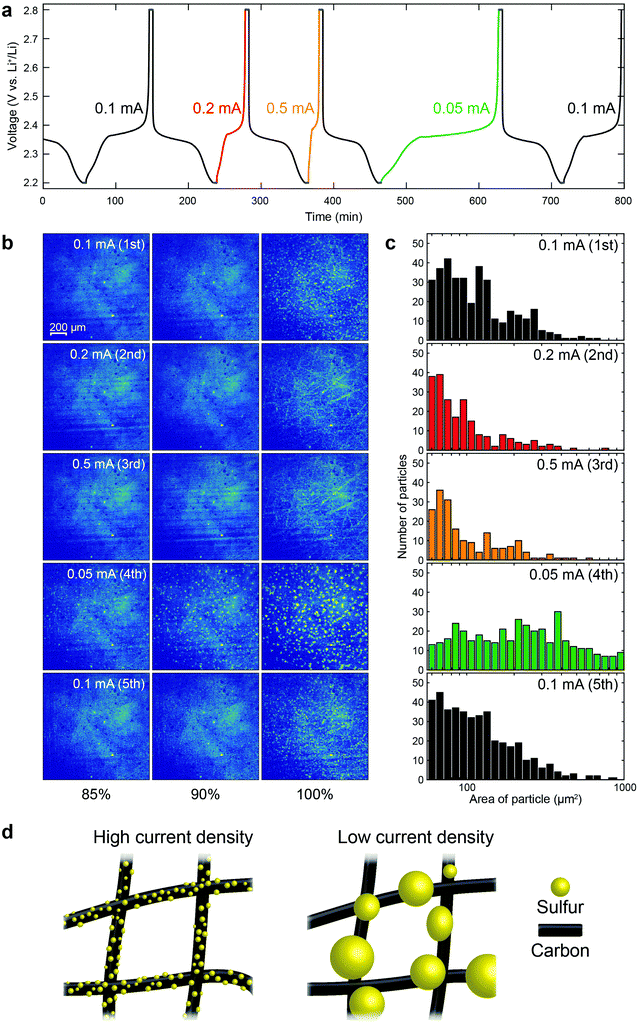
From the above results, it is evident that the size of the sulfur clusters is strongly affected by the cycle number. In order to elucidate the effects of the current density on the formation of sulfur clusters in a single cell, we needed to mitigate (or account for) the cycle number effect. Therefore, a polysulfide catholyte, without sulfur on the electrode, was chosen, since it has been observed that a lithium/polysulfide battery can better retain capacity with cycling.^31,32 The voltage profiles of a lithium/polysulfide (Li₂S₈) cell during the first 5 cycles are shown in Fig. 5a. While the discharging current density was held constant at 0.1 mA, the charging current density was varied between cycles. The voltage was held for 5 min at 2.2 and 2.8 V, at the end of discharge and charge, respectively (see Fig. S12 for the XRD intensity from β-S₈, ESI†). Fig. 5b presents the XRM images of the cathode at 85%, 90% and 100% SOCs for different cycles (see Fig. S13 for voltage profiles and corresponding XRM images at the same capacity, ESI†), together with the corresponding histogram of cluster sizes at 100% SOC in Fig. 5c. In order to better observe the effects of current density on the formation of the sulfur clusters, the absorption contrast experimental configuration was selected, since it reduces the signal from the carbon fibers, thus enhancing the signal from the sulfur clusters. As is evident in Fig. 5b, even with the polysulfide as the starting material, the formation of sulfur clusters can be clearly observed during the charging process. Increasing the current to 0.2 and 0.5 mA for the 2nd and 3rd cycles, respectively, produced sulfur clusters that were smaller than those formed at the lower current density of 0.1 mA. In the 4th cycle, in which the current was 0.05 mA (lowest current density employed), much larger sulfur clusters were formed. It is worth noting that the capacity delivered at the 4th cycle was comparable to that of the other cycles, indicating that the dependency of sulfur morphology on current density was not due to capacity fade (Fig. S13, ESI†). Our results suggest that the larger overpotentials, induced by the higher current densities, lead to a higher nucleation density of sulfur clusters and, therefore, the nuclei grow more uniformly on the carbon fiber, as illustrated in Fig. 5d. After adjusting the charging current density back to 0.1 mA, at the 5th cycle, the morphology of the resulting sulfur clusters was similar to that of the 1st cycle, establishing that the size of the sulfur clusters was not influenced by the specific sequence of our experiments.

Fig. 5 Operando X-ray microscopy of a lithium/polysulfide battery at different charging rates. (a) Voltage profile of lithium/polysulfide battery. The discharge rate was held constant at 0.1 mA, and charging rates were varied from 0.05 to 0.5 mA. (b) Sequential operando X-ray microscopy images of the cathode at different charging rates. (c) Sulfur cluster size histograms of cathode at 100% of SOC, charged at different rates, as shown in the last column in (b). (d) Schematic picture of the morphology of sulfur clusters deposited on the carbon fibers at high and low current densities.

4. Conclusions

We have directly observed the dissolution and reformation of sulfur and lithium sulfide in real time during battery operation, with operando XRD and XRM. The initial and final three-dimensional structure of the sulfur cathode was imaged using X-ray tomography. We find excellent agreement between crystal structure information from operando XRD and morphology information from XRM. The trends from XRM and XRD for sulfur dissolution and reformation also closely match each other.

We have also found that the location of reformed sulfur clusters, while independent of cycle number, is different from the initial distribution, likely reflecting that sulfur particles are totally dissolved during the discharge, so that the sulfur nucleation sites are refreshed in every cycle. Moreover, we have shown, for the first time, by comparing results from an elemental sulfur cathode and a polysulfide catholyte as the starting materials, that two factors govern the size distribution of the sulfur clusters: current density and the operating history of the cell. Higher current densities generate larger overpotentials, which lead to a higher nucleation density of sulfur clusters and, therefore, the nuclei grow more uniformly with smaller particle size, on the carbon fiber current collector. Similar behavior was also observed in the formation of Li₂S during discharge. In addition, we have also found that temperature affects the size of the Li₂S clusters, with smaller particles formed at lower temperatures. Our results expand the understanding of the reaction mechanism of Li–S batteries and demonstrate the potential of operando studies to unravel the complex reaction mechanisms of advanced electrode materials for electrical energy storage.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is based upon research conducted at the Cornell High Energy Synchrotron Source (CHESS) which is supported by the National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award DMR-1332208. S.-H. Y. acknowledges the financial support from the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2015R1A6A3A03020354). S.-H. Y. and X. H. acknowledge support from CHESS and the Energy Materials Center at Cornell (emc²).

References

1. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–29.
2. J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 16013.
3. B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935.
4. D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29.
5. Y.-X. Yin, S. Xin, Y.-G. Guo and L.-J. Wan, Angew. Chem., Int. Ed., 2013, 52, 13186–13200.
6. S. Evers and L. F. Nazar, Acc. Chem. Res., 2013, 46, 1135–1143.
7. Y. Yang, G. Zheng and Y. Cui, Chem. Soc. Rev., 2013, 42, 3018–3032.
8. A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2013, 46, 1125–1134.
9. A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787.
10. X. Ji, K. T. Lee and L. F. Nazar, Nat. Mater., 2009, 8, 500–506.
11. W. Zhou, Y. Yu, H. Chen, F. J. DiSalvo and H. D. Abruña, J. Am. Chem. Soc., 2013, 135, 16736–16743.
12. S. Xin, L. Gu, N.-H. Zhao, Y.-X. Yin, L.-J. Zhou, Y.-G. Guo and L.-J. Wan, J. Am. Chem. Soc., 2012, 134, 18510–18513.
13. L. Suo, Y.-S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481.
14. W. J. Chung, J. J. Griebel, E. T. Kim, H. Yoon, A. G. Simmonds, H. J. Ji, P. T. Dirlam, R. S. Glass, J. J. Wie, N. A. Nguyen, B. W. Guralnick, J. Park, Á. Somogyi, P. Theato, M. E. Mackay, Y.-E. Sung, K. Char and J. Pyun, Nat. Chem., 2013, 5, 518–524.
15. S. Waluś, C. Barchasz, R. Bouchet, J.-C. Leprêtre, J.-F. Colin, J.-F. Martin, E. Elkaïm, C. Baehtz and F. Alloin, Adv. Energy Mater., 2015, 5, 1500165.
16. J. Nelson, S. Misra, Y. Yang, A. Jackson, Y. Liu, H. Wang, H. Dai, J. C. Andrews, Y. Cui and M. F. Toney, J. Am. Chem. Soc., 2012, 134, 6337–6343.
17. M. A. Lowe, J. Gao and H. D. Abruña, RSC Adv., 2014, 4, 18347–18353.
18. J. Kulisch, H. Sommer, T. Brezesinski and J. Janek, Phys. Chem. Chem. Phys., 2014, 16, 18765–18771.
19. S. Waluś, C. Barchasz, J.-F. Colin, J.-F. Martin, E. Elkaim, J.-C. Leprêtre and F. Alloin, Chem. Commun., 2013, 49, 7899–7901.
20. N. A. Cañas, S. Wolf, N. Wagner and K. A. Friedrich, J. Power Sources, 2013, 226, 313–319.
21. Y. Gorlin, M. U. M. Patel, A. Freiberg, Q. He, M. Piana, M. Tromp and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A930–A939.
22. H.-L. Wu, L. A. Huff and A. A. Gewirth, ACS Appl. Mater. Interfaces, 2015, 7, 1709–1719.
23. X. Yu, H. Pan, Y. Zhou, P. Northrup, J. Xiao, S. Bak, M. Liu, K.-W. Nam, D. Qu, J. Liu, T. Wu and X.-Q. Yang, Adv. Energy Mater., 2015, 5, 1500072.
24. R. Sundararaman, K. Letchworth-Weaver, D. Gunceler, K. Schwarz and T. A. Arias, 2012, http://jdftx.sourceforge.net.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
26. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
27. D. Gunceler and T. A. Arias, arXiv:1403.6465.
28. K. R. Kim, S.-H. Yu and Y.-E. Sung, Chem. Commun., 2016, 52, 1198–1201.
29. Y. X. Ren, T. S. Zhao, M. Liu, P. Tan and Y. K. Zeng, J. Power Sources, 2016, 336, 115–125.
30. Y. Son, J.-S. Lee, Y. Son, J.-H. Jang and J. Cho, Adv. Energy Mater., 2015, 5, 1500110.
31. Y. Fu, Y.-S. Su and A. Manthiram, Angew. Chem., Int. Ed., 2013, 52, 6930–6935.
32. G. Zhou, E. Paek, G. S. Hwang and A. Manthiram, Nat. Commun., 2015, 6, 7760.

---

Footnotes

† Electronic supplementary information (ESI) available: Unit cell structure of α-S₈, Li₂S and β-S₈. X-ray microscopy of sulfur electrode at different distances between the sample and detector, at different DODs during the second cycle, etc. See DOI: 10.1039/c7ee02874a

‡ These authors equally contributed to this work.

---