Calibration and evaluation of PUF-PAS sampling rates across the Global Atmospheric Passive Sampling (GAPS) network†
Nicholas J.
Herkert
a,
Scott N.
Spak
 b,
Austen
Smith
a,
Jasmin K.
Schuster
c,
Tom
Harner
c,
Andres
Martinez
b,
Austen
Smith
a,
Jasmin K.
Schuster
c,
Tom
Harner
c,
Andres
Martinez
 a and
Keri C.
Hornbuckle
a and
Keri C.
Hornbuckle
 *a
*a
aDepartment of Civil & Environmental Engineering, IIHR-Hydroscience and Engineering, The University of Iowa, 4105 SC, Iowa City, IA 52242, USA. E-mail: keri-hornbuckle@uiowa.edu; Fax: +1-319-335-5660; Tel: +1-319-384-0789
bSchool of Urban and Regional Planning, Public Policy Center, The University of Iowa, IA, USA
cAir Quality Processes Research Section, Environment and Climate Change Canada, 4905 Dufferin St., Toronto, ON M3H 5T4, Canada
First published on 2nd November 2017
Abstract
Passive air samplers equipped with polyurethane foam (PUF-PAS) are frequently used to measure persistent organic pollutants (POPs) in ambient air. Here we present and evaluate a method to determine sampling rates (RS), and the effective sampling volume (Veff), for gas-phase chemical compounds captured by a PUF-PAS sampler deployed anywhere in the world. The method uses a mathematical model that requires only publicly available hourly meteorological data, physical–chemical properties of the target compound, and the deployment dates. The predicted RS is calibrated from sampling rates determined from 5 depuration compounds (13C PCB-9, 13C PCB-15, 13C PCB-32, PCB-30, and d6-γ-HCH) injected in 82 samples from 24 sites deployed by the Global Atmospheric Passive Sampling (GAPS) network around the world. The dimensionless fitting parameter, gamma, was found to be constant at 0.267 when implementing the Integrated Surface Database (ISD) weather observations and 0.315 using the Modern Era Retrospective-Analysis for Research and Applications (MERRA) weather dataset. The model provided acceptable agreement between modelled and depuration determined sampling rates, with 13C PCB-9, 13C PCB-32, and d6-γ-HCH having mean percent bias near zero (±6%) for both weather datasets (ISD and MERRA). The model provides inexpensive and reliable PUF-PAS gas-phase RS and Veff when depuration compounds produce unusual or suspect results and for sites where the use of depuration compounds is impractical, such as sites experiencing low average wind speeds, very cold temperatures, or remote locations.
Environmental significancePassive sampling of semivolatile organic pollutants has a major problem: determination of the effective air volume (Veff). This problem may prohibit passive sampler use in many environments. Depuration compounds are commonly used but they are notoriously unreliable and expensive under the best of circumstances, and useless in very cold environments. We describe a solution – and the model itself – to determine Veff and sampling rates for any location in the world where a PUF-PAS sampler is deployed. We calibrated and tested our model using samples previously collected by the Global Atmospheric Passive Sampling (GAPS) network. The model provides vital information to enable inexpensive and reliable measurements of potentially toxic environmental pollutants at any location on the globe. |
Introduction
Passive air samplers equipped with polyurethane foam (PUF-PAS) are commonly used to measure and assess atmospheric concentrations of persistent organic pollutants (POPs). PUF-PAS samplers have been used to measure regional spatial and temporal trends in urban areas,1–12 estimate the human exposure potential,1,9 and assess the global fate and transport of POPs.6,13–16 Despite their widespread use by researchers, PUF-PAS samplers can be subject to significant human error and uncertainty in interpretation. These challenges are often associated with the determination of sampling rates and effective sampling volumes.The most widely accepted method for determining effective sampling rates for PUF-PAS samplers relies on the loss of depuration compounds.9,13,14,17–25 Harner and colleagues have used this method to determine the sampling rates for thousands of samples deployed by the Global Atmospheric Passive Sampling network (GAPS) and published a widely used spreadsheet for calculating sample effective volume from depuration recoveries.8,9,13–15,22,26–28 This approach has been shown to be effective as long as the depuration compounds are injected and recovered in a consistent and reproducible way. Unfortunately, consistent and reliable use of these compounds requires skilled personnel and reproducible laboratory methods not always available for sample deployment worldwide. They are also expensive to use, prone to human error, unsuitable for sampling in low temperatures, and are only applicable to a narrow range of chemicals.
In the absence of reliable depuration compounds, a constant value (4 m3 d−1 for polychlorinated biphenyls (PCBs), for example) may be assumed for the sampling rate.10,13,24,29 For PCBs, this value was approximated from depuration data and also from other studies that used uptake experiments and calibration with other sampling methods, including low volume and high volume active samplers.7,11–13,18,21,23,24,30,31 This approach fails to resolve variability in local meteorological conditions and is inappropriate for estimating sampling rates for other compounds.21,32–34 In extreme environments, like high mountaintops and remote regions of the world, the inability to consider the effect of local meteorological conditions may negate the benefit of using passive samplers.15,24,28
We have previously shown that sampling rates of gas-phase PCB congeners for a PUF-PAS sample can be modelled as an air-side diffusive mass transfer process, calibrated using flow rates determined from depuration compounds and meteorological measurements (temperature, pressure, wind speed, and humidity) as well as chemical characteristics (octanol–air partitioning coefficient (Koa), molecular weight (MW), and internal energy of transfer).4,35 A model was calibrated from and tested on airborne PCBs collected in Chicago and other locations with local meteorology similar to our calibration sample set.4 However, when we applied the model to a more geographically diverse dataset, our model failed in regions that experienced more extreme weather conditions. At very high and very low wind speeds, the Chicago sampling rate model produced unreasonable results (Fig. S1†).
The central goal of this study was to develop a useful and practical tool to predict sampling rates for specific PUF-PAS deployments without the use of depuration compound recoveries while still resolving the effect of local meteorological conditions. We hypothesized that a recalibrated model using a larger and more diverse dataset of sampling rates would be able to predict sampling rates for deployment of the PUF-PAS samplers anywhere in the world with accuracy comparable to or better than known analytical uncertainties when using depuration compounds. The specific objectives of this study were to (1) calibrate a model from flow rates determined from depuration compounds that were deployed in a wide variety of conditions around the world; and (2) examine the performance and the global spatial distribution of the modelled sampling rates.
Theory
The uptake of semi-volatile organic compounds (SVOCs) on a PUF disk has been represented as a function of a diffusive sampling rate (RS, m3 d−1) and the concentration gradient between the air and PUF sample (eqn. (1)).4,18,20,26,31,33,35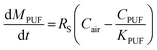 | (1) |
| RS = kvAs | (2) |
Here we describe the mass transfer coefficient using the equation for laminar flow along a flat plate.36 Although we do not expect the flow to be laminar within the sampler, this equation was selected as reasonably representative of the effect of wind speed and air temperature on the diffusion-limited mass transfer coefficient. The equation is as follows
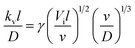 | (3) |
While the focus of this study was the estimation of RS, the final output of the model is an effective sampling volume (Veff, m3) specific for the compound as well as the deployment site and dates. The effective sampling volume accounts for non-linear uptake and the model calculates a compound-specific effective sampling volume integrated at 1 hour time intervals over the deployment period with the following equation,
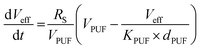 | (4) |
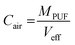 | (5) |
Methods
Data sources
The Global Atmospheric Passive Sampling (GAPS) Network was selected as the global recalibration dataset. The GAPS network was formed in December of 2004 and has included more than 50 sites around the world.19 The GAPS program is operated by a volunteer network that is coordinated through a central laboratory operated by Environment and Climate Change Canada (ECCC), where samples are analyzed.37 Our study considered 290 samples deployed in 2006 and 2007 and spiked with seven depuration compounds [13C labelled PCB congeners 9, 15, 32, 107, and 198, PCB-30, and gamma-hexachlorocyclohexane (d6-γ-HCH)]. The GAPS network is operated with extensive quality assurance and quality control (QA/QC), generally having method recoveries greater than 85% and has instrumental detection limits (IDL) below 1 pg. Both field and lab blanks are analyzed regularly and typically show levels at or below the IDL.14,15We examined two potential sources of meteorological data: local measurements collected at a nearby airport or meteorological station; and meteorological data estimated from a global weather reanalysis. Measurements of local hourly and synoptic meteorological conditions at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active sites are reported through the Integrated Surface Database (ISD) released by the National Oceanic and Atmospheric Administration's (NOAA) National Environmental Information (NCEI).38,39 We acquired ISD weather data from the nearest observations for 38 GAPS sites, at a median distance of 13 km from their respective sampler. Before implementation of the ISD dataset, we ran quality tests to detect any missing or erroneous data and removed them from consideration. Only sites for which the weather data meet the following quality constraints were used: (1) a minimum resolution of 3 hour measurements for each variable, (2) no continuous missing data for any single parameter longer than 72 hours, and (3) site is reasonably close/representative (median distance 13 km) of sampler deployment location conditions. For instances where a weather parameter was not present for a given hour, a persistence policy was used by assigning it the last observed value for that interval.
000 active sites are reported through the Integrated Surface Database (ISD) released by the National Oceanic and Atmospheric Administration's (NOAA) National Environmental Information (NCEI).38,39 We acquired ISD weather data from the nearest observations for 38 GAPS sites, at a median distance of 13 km from their respective sampler. Before implementation of the ISD dataset, we ran quality tests to detect any missing or erroneous data and removed them from consideration. Only sites for which the weather data meet the following quality constraints were used: (1) a minimum resolution of 3 hour measurements for each variable, (2) no continuous missing data for any single parameter longer than 72 hours, and (3) site is reasonably close/representative (median distance 13 km) of sampler deployment location conditions. For instances where a weather parameter was not present for a given hour, a persistence policy was used by assigning it the last observed value for that interval.
The second weather dataset was the Modern Era Retrospective-Analysis for Research and Applications (MERRA) maintained by the National Aeronautics and Space Administration (NASA) agency. The MERRA dataset is a global weather reanalysis that provides hourly two-dimensional data, including surface, fluxes, and vertical integrals, generated using version 5 of the Goddard Earth Observing System Data Assimilation System (GEOS-5 DAS) at one-half by two-thirds degree resolution.40 The MERRA dataset offers meteorological data for temperature, specific humidity, and wind speed at 2 m or 10 m above ground level (AGL), while also offering wind speed at 50 m. The MERRA wind speed used for this study was at 2 m AGL, consistent with the GAPS observational protocol.
Initially, supplying local measurements for weather data (with the ISD dataset) for each sample was preferred for all components of the model. However, upon expanding the scope of applicability and to ensure the model could be used anywhere on the globe, it was necessary to use global modeled or reanalyzed weather data (with the MERRA dataset).
Model calibration
The value of γ was empirically determined using a calibration subset of depuration derived sampling rates reported for 290 samples deployed in 2006 and 2007 by the GAPS program. Sampling rates for all seven depuration compounds (13C labelled PCB congeners 9, 15, 32, 107, and 198, PCB-30, and d6-γ-HCH) were considered for the calibration subset. Depuration compounds are most effective for sampling rate determination if a portion, but not the total, injected mass volatilizes during sample deployment. Therefore, we selected the calibration subset of sampling rates from only samples with acceptable depuration compound recoveries and complete meteorological data. We chose only those sampling rates calculated from depuration compounds with recoveries below 65% to ensure significant loss, consistent with guidelines in Pozo et al.14 This excluded all samples below 0 °C from use in the calibration. The effectively nonvolatile compounds, 13C PCB-107 and 13C PCB-198, were used as a normalizing factor for calculating the recovery of the others. Each of the samples selected had acceptable results for at least one of the five remaining depuration compounds. We further restricted the calibration subset to deployments with nearby meteorological stations and complete meteorological data as described above. This approach produced a calibration subset of sampling rates for 82 samples deployed at 24 locations (Table S2†) from the initial 290 samples. For this calibration subset, γ was calculated for each depuration compound in the 82 samples.Many different forms of multiple linear regressions (MLRs) and regression trees were explored as potential methods for the recalibration of γ. These regression methods were evaluated using the Matlab R2016a software. The MLRs were primarily done with the Curve Fitting Toolbox add-in. MLRs are global models and rely on a single simple relationship explaining the dataset, while a regression tree is a form of decision tree where binary nodes are used to group data in to small, related subgroups that can be simply expressed with real numbers.41 The regression tree approach is often much better for handling large datasets with many inputs (predictors) that interact in very complicated, non-linear ways.42 To avoid over-fitting the data, a leave-one-out cross-validation method was used when creating regression trees.
Results and discussion
A detailed discussion about the recalibration process is available in the ESI.† Briefly, the most reliable γ value was a constant γ for all deployments and compounds. Unsurprisingly, the two different weather datasets produced different calibration factors because they are fundamentally different. The constant γ was determined to be 0.267 for the ISD weather dataset and 0.315 for the MERRA weather dataset. Recall, for laminar flow along a flat plate γ would equal 0.646, therefore our results seem reasonable. The results of the model calibration are evaluated for PUF-PAS deployments in a wide range of conditions, including those with very low wind speeds, gusty environments, polar and other remote locations, and near urban areas and large sources.The 2006–2007 GAPS sample set has the potential to provide 1796 unique depuration determined sampling rates. Of those 1796, 346 were stable depuration compounds used to normalize the other compounds, reducing the usable number to 1450. After removing samples with greater than 65% depuration compound recovery, samples with average temperatures below 0 °C, and other outliers, that number is reduced to 857. Thus, only 48% of the initially available unique depuration values were considered useful for determination of a sampling rate. Of the initial 290 GAPS samples, 41 did not yield any reliable depuration results. The model now allows these samples to be accurately interpreted by providing a deployment specific sampling rate estimate.
Global distribution of sampling rates
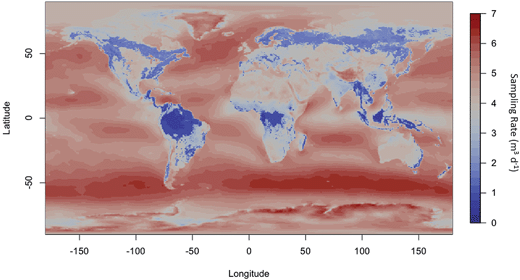
This model provides compound-specific sampling rates for any location across the globe over any current or historical deployment. To illustrate, we calculated an annual sampling rate (for 2006) at a 2 m height above the ground, across the entire global MERRA weather grid (Fig. 1) for a tri-chlorinated PCB congener (MW = 257 g mol−1). The global average sampling rate can be determined for any compound appropriate for PUF-PAS sampling. For example, the average global sampling rate for a tri-chlorinated PCB congener in 2006 was 4.58 ± 1.17 m3 d−1. The sampling rates calculated for all deployments were not strongly correlated to latitude (R2 = 0.157) or temperature (R2 = 0.001), and were primarily a function of wind speed (R2 = 0.910). At the global scale, there is little seasonal variability for a tri-chlorinated PCB congener, and global average for RS varies less than 1% between each quarter of 2006. However, individual locations displayed differences in seasonal averages. For example, in Chicago (latitude: 41.881832; longitude; −87.623177) the sampling rate varied from 4.2 m3 d−1 in quarter 1 to 3.9, 3.5, 4.1 m3 d−1, for quarters 2, 3, and 4, respectively. These quarterly averages for sampling rates are strongly correlated with quarterly average wind speed (R2 = 0.987). As expected, the average global sampling rate for tri-chlorinated PCBs is near 4 m3 d−1. For a tri-chlorinated PCB congener, approximately 50% of the earth's surface would fall in a range of 4 ± 1 m3 d−1, while 88% of the earth's surface would fall in a range of 4 ± 2 m3 d−1. Similarly, for the samples collected by the GAPS Network in 2006 and 2007, approximately 31% of depuration results for tri-chlorinated biphenyls fall in a range of 4 ± 1 m3 d−1, while 62% of depuration results fall in a range of 4 ± 2 m3 d−1.Model performance in low wind speeds
The modeled RS method is a particularly good alternative to depuration compounds for deployments with very low average wind speeds; conditions common at sites with heavy forest cover, such as the boreal forest or Amazon Rainforest. In these conditions, a small percentage (<20%) of the injected depuration compounds are volatilized during deployment, leading to highly uncertain sampling rate determination. Approximately 8.7% of the earth's surface had an annual sampling rate below 3 m3 d−1, while 5.4% was less than 2 m3 d−1 and 1.3% was less than 1 m3 d−1 for trichlorobiphenyls (Table 1 and Fig. 2). Low RS values are expected because the model uses 2 m heights for the meteorological data, consistent with the deployment heights used by GAPS. At this height of 2 m forest cover significantly effects the meteorological conditions. If the sample were deployed in a forest clearing or above the forest canopy, corrections would be required. Fortunately, MERRA provides the capability to directly simulate RS at 10 m or 50 m AGL. It is expected that the calibration described here would be valid for any height, although this was not specifically tested, and may be biased at wind speeds substantially higher than those represented in the calibration dataset.| Homolog | R S (m3 d−1) | St. dev | % surface coverage < 2 m3 d−1 |
|---|---|---|---|
| Mono- | 5.08 | 1.30 | 4.6% |
| Di- | 4.80 | 1.23 | 5.0% |
| Tri- | 4.58 | 1.17 | 5.4% |
| Tetra- | 4.39 | 1.12 | 5.6% |
| Penta- | 4.23 | 1.08 | 5.9% |
| Hexa- | 4.09 | 1.05 | 6.1% |
| Hepta- | 3.97 | 1.02 | 6.3% |
| Octa- | 3.86 | 0.99 | 6.5% |
| Nona- | 3.76 | 0.96 | 6.6% |
| Deca- | 3.67 | 0.94 | 6.8% |
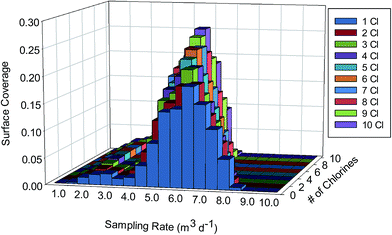 | ||
| Fig. 2 Histogram of the yearly averaged (2006) modelled sampling rates for PCB congeners with percent of global surface coverage as the bin value. | ||
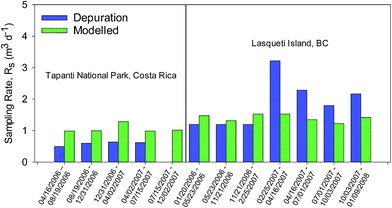
Two GAPS sampling sites from 2006 or 2007 with depuration results (excluded from the recalibration) helped to validate model performance at low sampling rates. One of these sites was Tapanti National Park in Costa Rica and the other was Lasqueti Island, British Columbia, Canada. The comparison between depuration and modelled sampling rates for 13C PCB-9 for these sites is shown in Fig. 3. The depuration results from Tapanti National Park for 2006 and 2007 averaged 0.6 m3 d−1, while the model results averaged 1.1 m3 d−1. At the Lasqueti Island sampling site, the depuration results averaged 2.0 m3 d−1, while the model results averaged 1.4 m3 d−1. Both the predicted RS and the depuration RS values were significantly lower than the global average, with similar values that support the validity of the method. The depuration method is subject to analytical uncertainty, and we expect that uncertainty is the explanation for the differences between the RS values from the two methods illustrated in Fig. 3. Only 23 of 60 depuration compounds measurements in the 12 samples listed in Fig. 3 were considered “reliable”, and 10 of those “reliable” results were for 13C PCB 9, the most volatile of the depuration compounds used. No depuration results were reliable for the Tapanti National Park sample deployed from July 7, 2007 to December 2, 2007. The model presented here is a good substitute should depuration compounds be found questionable in a sample. If a sampling rate of 4 m3 d−1 were assumed for this sample instead of using the modelled value of 1.02 m3 d−1, the estimated airborne concentration would be underestimated be a factor of 4.
Model performance in polar regions
The modeled RS method is a good alternative to depuration compounds for PUF-PAS deployments in the polar regions. Samples collected in extremely cold temperatures typically do not exhibit enough loss of depuration compound to accurately determine a sampling rate. Therefore, there are few measurements in this domain to compare with modelled results. Between 2006 and 2007 there were 22 GAPS samples deployed in the Arctic (above 66.563° latitude). Of the 5 depuration compounds in each sample, only 40% were deemed reliable and only 32% were deemed reliable when the mean temperature was less than 0 °C. The depuration results showed a high variability ranging from 0.9 to 24 m3 d−1 for all compounds, and individual samples often showed disagreement between depuration compounds, averaging a 300% difference between the maximum and minimum. The difficulty of assessing depuration compound results from polar regions is alleviated with the model. The average modelled sampling rate for a tri-chlorinated PCB congener in the Arctic was 4.15 ± 0.61 m3 d−1.Model performance in high wind speeds
The model is less effective for sites with very high average wind speeds. Sampling rates in gusty environments can be difficult to interpret because of the high variability over the deployment period. This effect has been observed in depuration compound results at windy sites.14,15,28 The model calculates a sampling rate from hourly meteorology instead of using average weather parameters, thereby capturing some of the variability but not intense and short term variations. At high wind speeds (>5 m s−1) the PUF-PAS sampler may also behave differently, and experience non-linear aerodynamics.24,43 At high wind speeds, the air side controlled mass transfer assumption is less reliable. It is helpful to note, however, that higher wind speeds often result in a rapid approach to chemical equilibrium. The model corrected for this non-linear uptake and approach to equilibrium through the calculation of effective sampling volume. This feature of the model has been discussed in detail previously.4Independent datasets
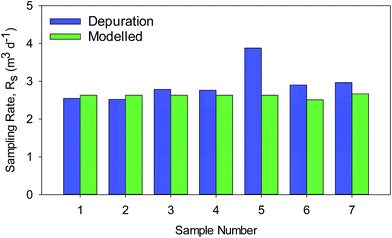
We evaluated the performance of the RS model against independent measurements in three ways. First, as described above, we evaluated the performance for GAPS samples with high quality depuration data that also were not used for calibration (Fig. 3). Second, we evaluated samples deployed near a major PCB source with depuration compounds measured in our laboratory. Third, we calculated and compared RS for deployments reported in the literature.Our laboratory collaborated with Boston University to deploy and measure airborne PCBs near a major source, New Bedford Harbor (NBH), a Superfund site in Massachusetts contaminated with PCBs. Details of the study are provided elsewhere.47 During the summer and fall of 2015, PUF-PAS samples were deployed at 17 or 18 different locations for 3 periods lasting ∼6 weeks, shorter than the typical deployment of 3 months used by GAPS. Prior to deployment, each of the 53 samples were spiked with 3 depuration compounds – one of which was used as a positive control – providing 106 potential values for RS. Only 7 showed depuration compound recovery less the criteria of 65%, rendering the depuration results unreliable – a situation that we now understand is common. These seven values rates compare well to modeled RS values for the same samples (Fig. 4).
The average bias for these 7 samples was 11%, and drops to just 5% if removing one outlier sample deployed at the NBH-15 site from 07/09/2015–08/20/2015. This sample was collected at a site immediately adjacent to the bay and may have experienced different meteorological conditions from the other sites. This highlights the sensitivity of the weather data and the notion that some samplers may experience microclimates within a sampling region that are not all perfectly represented by the weather data, while also highlighting that most samples in a region can be described by a central measurement. However, the modeled and depuration results are still in reasonable agreement and we conclude that the modeled RS method is a particularly good alternative to depuration compounds for PUF-PAS deployments near major sources. Samples collected near major sources require shorter deployment periods to reach analytical detection limits. However, shorter deployment periods reduce the precision and accuracy of the depuration results by not allowing for adequate loss (<65% recovery). In addition, high levels of target compounds on the PUF samples may interfere with the detection of depuration compounds, especially when the ambient concentrations are unexpectedly high or unlabeled depuration compounds are implemented.
We also compared our modelled sampling rates to deployments reported in the literature. We identified a set of studies reporting sampling rates for PCB compounds from either depuration compounds or chemical uptake studies (Fig. 5). These studies report a range of chemical compounds in a range of environmental conditions with varying analytical protocol. In some instances for the comparison the locations/deployments times had to be approximated. Model modifications were made to appropriately account for the nuances of varying sampler designs and PUF substrate where appropriate and possible. However, not everything could be accounted for such as sampler height or wind speed adjustments (based on building/tree interference), because they were not reported. Of the 19 studies examined for this comparison, 5 studies fell within ±10% bias between modelled and measured sampling rate, 9 studies fell within ±20% bias, and 13 studies fell within ±30% bias. It is difficult to determine the reasons for the nuanced differences between modelled and measured sampling rates for these studies due to the wide scope of protocols, samplers, geography, etc. However, in general it appears that studies that cover a larger spatial scale displayed higher mean biases between measured and modelled values, likely due to the influence of more outlier sites/measurements. It also appears that in general sampling rates determined from active sampler calibrations exhibit greater bias when compared to PUF-PAS concentrations that use our sampling rate predictions. They may be due to the other differences in the two approaches – including the collection of air over different time scales. The difference may also be due to particle phase sampling with PUF-PAS.
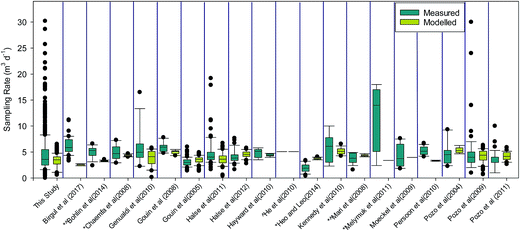 | ||
| Fig. 5 Approximated modelled results for numerous independent studies reporting PUF-PAS sampling rates for a range a different chemicals in a range of different environmental conditions.2,6,9,14,15,17,21–23,28,30,33,34,48–54 The * denotes studies that conducted active sampler comparison (no * indicates DCs were used). The ^ denotes studies with a different sampler design than the default design (24 cm top bowl, 20 cm bottom bowl). | ||
Conclusion
This model (provided in the ESI†) may be used to predict a gas-phase sampling rate for a PUF-PAS sample in any environment on the globe for a “flying saucer” PUF-PAS sampler (24 cm top bowl, 20 cm bottom bowl, 12 cm height, 2 cm gap, 1.5 cm overlay).15,22,26–28,31,43 The model provides a sampling rate in any environment while removing much of the uncertainty involved in the use of depuration compounds. It only requires hourly weather inputs and the molecular weight of the compound of interest to determine a compound specific, deployment specific, and location specific sampling rate based on hourly calculations. With a few additional chemical properties a compound specific, deployment specific, and location specific effective sampling volume can also be determined. The ISD and similar surface observational data can be simply used directly as a weather data source, and the MERRA weather dataset can be used in the absence of local observations. This allows the model to serve as a platform for examining large global datasets with less uncertainty attributed to the sampling rate determination. Although assuming a sampling rate from prior reported field studies has been shown to be reasonable for most locations, it does not account for the effect of local meteorology as the model does. The model also provides a tool to generate information in the pre-deployment stage of the sampling campaign. It can be used to provide insights on length of deployment to stay in linear uptake phase, potential behavior of new chemical contaminants, and location siting.In addition to the RS value predicted by this model for any location on the globe, the model also predicts the effective sampling volume (Veff), as a function of the deployment site, deployment period, and target compound. The model calculates the cumulative effective sampling volume for every hour of deployment. The benefit of calculating the effective sampling volume hourly, instead of using weather parameters averaged over the sample deployment period, has been discussed elsewhere.4
The validity of this model is dependent on the accuracy of the depuration compound method for determining sampling rates: the model assumes that the dynamics of labeled depuration compounds are representative of any compound that can be sampled with PUF-PAS. Similarly, this model is meant for gas-phase compounds only, as it does not consider the uptake processes of particle-phase compounds. To account for particle phase sampling there would need to be consistent globally applicable datasets for total suspended particles, a measure of the gas/particle partitioning, and an estimate of the flow of particles into the sampler housing and onto the PUF. Given the uncertainty in these processes and the ongoing research on the topic,13,21,29,55 sampling of particle-associated POPs are not supported in this version of the model. Some studies have also shown that SVOCs experience a kinetic resistance to chemical transfer from chemicals accumulating in the outer layers of the cylindrical PUF plug sampling media.44,45 This has also been observed in field studies.30,44,46. However, calibration studies of the PUF disk sampler have not revealed a bias of lower sampling rates for high Koa chemicals in PUF disks suggesting that this resistance is less important for the thin-disk geometry of the PUF disk, where air flow and chemical exchange occurs from the top and bottom of the disk, which would enhance chemical movement/dispersion within the disk.13 Due to a lack of complete understanding of this process, the model does not currently account for sample side resistance, however, potential effects of sampler side-resistance, if significant, would be accounted for in the empirical data used to calibrate the model.
Although the model was calibrated and implemented using PCB depuration compounds and lindane (log(Koa) ∼ 7–9), it is applicable to other POPs if the physical–chemical properties are known. However, caution should be exercised towards particle dominated POPs (log(Koa) ≫ 10), and highly volatile (log(Koa) ≪ 6) POPs as they start to drastically deviate from the calibration dataset. Despite these remaining uncertainties, this study provides an accurate unified method of determining sampling rates for large-scale PUF-PAS studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded through the Iowa Superfund Research Program, National Institute of Environmental Health Sciences Grant P42ES013661. We appreciate the support of Madeleine K. Scammell and Wendy Heiger-Bernays at Boston University in deploying samples near New Bedford Harbor thanks to a collaborating project at the Boston University Superfund Research Program Grant P42ES007381. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Karla Pozo and Sum Chi Lee are acknowledged for their contributions to the GAPS Network. The GAPS Network is made possible by a global team of individuals and institutes who volunteer their time and resources. Funding for the GAPS Network is from the Chemicals Management Plan (CMP), United Nations Environment Programme (UNEP), and the Northern Contaminants Program (NCP).Notes and references
- M. D. Ampleman, A. Martinez, J. DeWall, D. F. K. Rawn, K. C. Hornbucke and P. S. Thorne, Inhalation and Dietary Exposure to PCBs in Urban and Rural Cohorts via Congener-Specific Measurements, Environ. Sci. Technol., 2015, 49(2), 1156–1164 CrossRef CAS PubMed.
- C. Persoon, T. M. Peters, N. Kumar and K. C. Hornbuckle, Spatial Distribution of Airborne Polychlorinated Biphenyls in Cleveland, Ohio and Chicago, Illinois, Environ. Sci. Technol., 2010, 44(8), 2797–2802 CrossRef CAS PubMed.
- A. A. Peverly, Y. N. Ma, M. Venier, Z. Rodenburg, S. N. Spak, K. C. Hornbuckle and R. A. Hites, Variations of Flame Retardant, Polycyclic Aromatic Hydrocarbon, and Pesticide Concentrations in Chicago's Atmosphere Measured using Passive Sampling, Environ. Sci. Technol., 2015, 49(9), 5371–5379 CrossRef CAS PubMed.
- N. J. Herkert, A. Martinez and K. C. Hornbuckle, A Model Using Local Weather Data to Determine the Effective Sampling Volume for PCB Congeners Collected on Passive Air Samplers, Environ. Sci. Technol., 2016, 50(13), 6690–6697 CrossRef CAS PubMed.
- D. F. Hu, H. J. Lehmler, A. Martinez, K. Wang and K. C. Hornbuckle, Atmospheric PCB congeners across Chicago, Atmos. Environ., 2010, 44(12), 1550–1557 CrossRef CAS PubMed.
- A. K. Halse, M. Schlabach, A. Sweetman, K. C. Jones and K. Breivik, Using passive air samplers to assess local sources versus long range atmospheric transport of POPs, J. Environ. Monit., 2012, 14(10), 2580–2590 RSC.
- H. Cheng, Z. Deng, P. Chakraborty, D. Liu, R. Zhang, Y. Xu, C. Luo, G. Zhang and J. Li, A comparison study of atmospheric polycyclic aromatic hydrocarbons in three Indian cities using PUF disk passive air samplers, Atmos. Environ., 2013, 73, 16–21 CrossRef CAS.
- A. d. L. Torre, P. Sanz, I. Navarro and M. A. Martinez, Time trends of persistent organic pollutants in spanish air, Environ. Pollut., 2016, 217, 26–32 CrossRef PubMed.
- A. Birgül, P. B. Kurt-Karakus, H. Alegria, E. Gungormus, H. Celik, T. Cicek and E. C. Güven, Polyurethane foam (PUF) disk passive samplers derived polychlorinated biphenyls (PCBs) concentrations in the ambient air of Bursa-Turkey: Spatial and temporal variations and health risk assessment, Chemosphere, 2017, 168, 1345–1355 CrossRef PubMed.
- P. S. Diefenbacher, A. C. Gerecke, C. Bogdal and K. Hungerbühler, Spatial Distribution of Atmospheric PCBs in Zurich, Switzerland: Do Joint Sealants Still Matter?, Environ. Sci. Technol., 2016, 50(1), 232–239 CrossRef CAS PubMed.
- F. M. Jaward, G. Zhang, J. J. Nam, A. J. Sweetman, J. P. Obbard, Y. Kobara and K. C. Jones, Passive Air Sampling of Polychlorinated Biphenyls, Organochlorine Compounds, and Polybrominated Diphenyl Ethers Across Asia, Environ. Sci. Technol., 2005, 39(22), 8638–8645 CrossRef CAS PubMed.
- G. Zhang, P. Chakraborty, J. Li, P. Sampathkumar, T. Balasubramanian, K. Kathiresan, S. Takahashi, A. Subramanian, S. Tanabe and K. C. Jones, Passive Atmospheric Sampling of Organochlorine Pesticides, Polychlorinated Biphenyls, and Polybrominated Diphenyl Ethers in Urban, Rural, and Wetland Sites along the Coastal Length of India, Environ. Sci. Technol., 2008, 42(22), 8218–8223 CrossRef CAS PubMed.
- T. Harner, M. Mitrovic, L. Ahrens and J. Schuster, Characterization of PUF disk passive air samplers for new priority chemicals: a review, Organohalogen Compd., 2014, 76, 11–29 Search PubMed.
- K. Pozo, T. Harner, S. C. Lee, F. Wania, D. C. G. Muir and K. C. Jones, Seasonally Resolved Concentrations of Persistent Organic Pollutants in the Global Atmosphere from the First Year of the GAPS Study, Environ. Sci. Technol., 2009, 43(3), 796–803 CrossRef CAS PubMed.
- K. Pozo, T. Harner, F. Wania, D. C. G. Muir, K. C. Jones and L. A. Barrie, Toward a global network for persistent organic pollutants in air: results from the GAPS study, Environ. Sci. Technol., 2006, 40(16), 4867–4873 CrossRef CAS PubMed.
- C. Bogdal, M. Scheringer, E. Abad, M. Abalos, B. van Bavel, J. Hagberg and H. Fiedler, Worldwide distribution of persistent organic pollutants in air, including results of air monitoring by passive air sampling in five continents, TrAC, Trends Anal. Chem., 2013, 46, 150–161 CrossRef CAS.
- A. K. Halse, M. Schlabach, S. Eckhardt, A. Sweetman, K. C. Jones and K. Breivik, Spatial variability of POPs in European background air, Atmos. Chem. Phys., 2011, 11(4), 1549–1564 CAS.
- C. Persoon and K. C. Hornbuckle, Calculation of passive sampling rates from both native PCBs and depuration compounds in indoor and outdoor environments, Chemosphere, 2009, 74(7), 917–923 CrossRef CAS PubMed.
- T. Harner, K. Pozo, T. Gouin, A. M. Macdonald, H. Hung, J. Cainey and A. Peters, Global pilot study for persistent organic pollutants (POPs) using PUF disk passive air samplers, Environ. Pollut., 2006, 144(2), 445–452 CrossRef CAS PubMed.
- M. E. Bartkow, K. Booij, K. E. Kennedy, J. F. Muller and D. W. Hawker, Passive air sampling theory for semivolatile organic compounds, Chemosphere, 2005, 60(2), 170–176 CrossRef CAS PubMed.
- P. Bohlin, O. Audy, L. Skrdlikova, P. Kukucka, P. Pribylova, R. Prokes, S. Vojta and J. Klanova, Outdoor passive air monitoring of semi volatile organic compounds (SVOCs): a critical evaluation of performance and limitations of polyurethane foam (PUF) disks, Environ. Sci.: Processes Impacts, 2014, 16(3), 433–444 CAS.
- T. Gouin, T. Harner, P. Blanchard and D. Mackay, Passive and active air samplers as complementary methods for investigating persistent organic pollutants in the Great Lakes basin, Environ. Sci. Technol., 2005, 39(23), 9115–9122 CrossRef CAS PubMed.
- S. J. Hayward, T. Gouin and F. Wania, Comparison of Four Active and Passive Sampling Techniques for Pesticides in Air, Environ. Sci. Technol., 2010, 44(9), 3410–3416 CrossRef CAS PubMed.
- L. Melymuk, P. Bohlin, O. Sanka, K. Pozo and J. Klanova, Current Challenges in Air Sampling of Semivolatile Organic Contaminants: Sampling Artifacts and Their Influence on Data Comparability, Environ. Sci. Technol., 2014, 48(24), 14077–14091 CrossRef CAS PubMed.
- W. A. Ockenden, F. M. Jaward and K. C. Jones, Atmospheric sampling of persistent organic pollutants: needs, applications and advances in passive air sampling techniques, Sci. World J., 2001, 1, 557–575 CrossRef CAS PubMed.
- T. Harner, M. Shoeib, M. Diamond, G. Stern and B. Rosenberg, Using passive air samplers to assess urban - Rural trends for persistent organic pollutants. 1. Polychlorinated biphenyls and organochlorine pesticides, Environ. Sci. Technol., 2004, 38(17), 4474–4483 CrossRef CAS PubMed.
- T. Harner, K. Su, S. Genualdi, J. Karpowicz, L. Ahrens, C. Mihele, J. Schuster, J. P. Charland and J. Narayan, Calibration and application of PUF disk passive air samplers for tracking polycyclic aromatic compounds (PACs), Atmos. Environ., 2013, 75, 123–128 CrossRef CAS.
- K. Pozo, T. Harner, M. Shoeib, R. Urrutia, R. Barra, O. Parra and S. Focardi, Passive-sampler derived air concentrations of persistent organic pollutants on a north-south transect in Chile, Environ. Sci. Technol., 2004, 38(24), 6529–6537 CrossRef CAS PubMed.
- M. Z. Markovic, S. Prokop, R. M. Staebler, J. Liggio and T. Harner, Evaluation of the particle infiltration efficiency of three passive samplers and the PS-1 active air sampler, Atmos. Environ., 2015, 112, 289–293 CrossRef CAS.
- C. Chaemfa, J. L. Barber, T. Gocht, T. Harner, I. Holoubek, J. Klanova and K. C. Jones, Field calibration of polyurethane foam (PUF) disk passive air samplers for PCBs and OC pesticides, Environ. Pollut., 2008, 156(3), 1290–1297 CrossRef CAS PubMed.
- M. Shoeib and T. Harner, Characterization and comparison of three passive air samplers for persistent organic pollutants, Environ. Sci. Technol., 2002, 36(19), 4142–4151 CrossRef CAS PubMed.
- S. Hazrati and S. Harrad, Calibration of polyurethane foam (PUF) disk passive air samplers for quantitative measurement of polychlorinated biphenyls (PCBs) and polybrominated diphenyl ethers (PBDEs): Factors influencing sampling rates, Chemosphere, 2007, 67(3), 448–455 CrossRef CAS PubMed.
- L. Melymuk, M. Robson, P. A. Helm and M. L. Diamond, Evaluation of passive air sampler calibrations: Selection of sampling rates and implications for the measurement of persistent organic pollutants in air, Atmos. Environ., 2011, 45(10), 1867–1875 CrossRef CAS.
- J. Heo and G. Lee, Field-measured uptake rates of PCDDs/Fs and dl-PCBs using PUF-disk passive air samplers in Gyeonggi-do, South Korea, Sci. Total Environ., 2014, 491, 42–50 CrossRef PubMed.
- N. T. Petrich, S. N. Spak, G. R. Carmichael, D. F. Hu, A. Martinez and K. C. Hornbuckle, Simulating and Explaining Passive Air Sampling Rates for Semivolatile Compounds on Polyurethane Foam Passive Samplers, Environ. Sci. Technol., 2013, 47(15), 8591–8598 CAS.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, 2nd edn, 1997, p. 600 Search PubMed.
- C. Rauert, T. Harner, J. K. Schuster, K. Quinto, G. Fillmann, L. E. Castillo, O. Fentanes, M. V. Ibarra, K. S. B. Miglioranza, I. M. Rivadeneira, K. Pozo, A. P. Puerta and B. H. A. Zuluaga, Towards a regional passive air sampling network and strategy for new POPs in the GRULAC region: Perspectives from the GAPS Network and first results for organophosphorus flame retardants, Sci. Total Environ., 2016, 573, 1294–1302 CrossRef CAS PubMed.
- National Centers For Environmental Information, Integrated Surface Database (ISD), www.ncdc.noaa.gov/isd, accessed December 3, 2015.
- A. Smith, N. Lott and R. Vose, The Integrated Surface Database Recent Developments and Partnerships, Bull. Am. Meteorol. Soc., 2011, 92(6), 704–708 CrossRef.
- M. M. Rienecker, M. J. Suarez, R. Gelaro, R. Todling, J. Bacmeister, E. Liu, M. G. Bosilovich, S. D. Schubert, L. Takacs, G. K. Kim, S. Bloom, J. Y. Chen, D. Collins, A. Conaty, A. Da Silva, W. Gu, J. Joiner, R. D. Koster, R. Lucchesi, A. Molod, T. Owens, S. Pawson, P. Pegion, C. R. Redder, R. Reichle, F. R. Robertson, A. G. Ruddick, M. Sienkiewicz and J. Woollen, MERRA: NASA's Modern-Era Retrospective Analysis for Research and Applications, J. Clim., 2011, 24(14), 3624–3648 CrossRef.
- W. Mendenhall and T. Sincich, Statistics for Engineering and the Sciences, 2006 Search PubMed.
- L. Breiman, J. Friedman, C. J. Stone and R. A. Olshen, Classification and regression trees, CRC press, 1984 Search PubMed.
- L. Tuduri, T. Harner and H. Hung, Polyurethane foam (PUF) disks passive air samplers: wind effect on sampling rates, Environ. Pollut., 2006, 144(2), 377–383 CrossRef CAS PubMed.
- X. M. Zhang, M. Tsurukawa, T. Nakano, Y. D. Lei and F. Wania, Sampling Medium Side Resistance to Uptake of Semivolatile Organic Compounds in Passive Air Samplers, Environ. Sci. Technol., 2011, 45(24), 10509–10515 CrossRef CAS PubMed.
- X. M. Zhang and F. Wania, Modeling the Uptake of Semivolatile Organic Compounds by Passive Air Samplers: Importance of Mass Transfer Processes within the Porous Sampling Media, Environ. Sci. Technol., 2012, 46(17), 9563–9570 CrossRef CAS PubMed.
- C. Chaemfa, E. Wild, B. Davison, J. L. Barber and K. C. Jones, A study of aerosol entrapment and the influence of wind speed, chamber design and foam density on polyurethane foam passive air samplers used for persistent organic pollutants, J. Environ. Monit., 2009, 11(6), 1135–1139 RSC.
- A. Martinez, B. N. Hadnott, A. M. Awad, N. J. Herkert, K. Tomsho, K. Basra, M. K. Scammell, W. Heiger-Bernays and K. C. Hornbuckle, Release of Airborne Polychlorinated Biphenyls from New Bedford Harbor Results in Elevated Concentrations in the Surrounding Air, Environ. Sci. Technol. Lett., 2017, 4(4), 127–131 CrossRef CAS PubMed.
- J. He and R. Balasubramanian, A comparative evaluation of passive and active samplers for measurements of gaseous semi-volatile organic compounds in the tropical atmosphere, Atmos. Environ., 2010, 44(7), 884–891 CrossRef CAS.
- K. Kennedy, D. W. Hawker, M. E. Bartkow, S. Carter, Y. Ishikawa and J. F. Mueller, The potential effect of differential ambient and deployment chamber temperatures on PRC derived sampling rates with polyurethane foam (PUF) passive air samplers, Environ. Pollut., 2010, 158(1), 142–147 CrossRef CAS PubMed.
- M. Mari, M. Schuhmacher, J. Feliubadaló and J. L. Domingo, Air concentrations of PCDD/Fs, PCBs and PCNs using active and passive air samplers, Chemosphere, 2008, 70(9), 1637–1643 CrossRef CAS PubMed.
- C. Moeckel, T. Harner, L. Nizzetto, B. Strandberg, A. Lindroth and K. C. Jones, Use of depuration compounds in passive air samplers: results from active sampling-supported field deployment, potential uses, and recommendations, Environ. Sci. Technol., 2009, 43(9), 3227–3232 CrossRef CAS PubMed.
- T. Gouin, F. Wania, C. Ruepert and L. E. Castillo, Field Testing Passive Air Samplers for Current Use Pesticides in a Tropical Environment, Environ. Sci. Technol., 2008, 42(17), 6625–6630 CrossRef CAS PubMed.
- K. Pozo, T. Harner, S. C. Lee, R. K. Sinha, B. Sengupta, M. Loewen, V. Geethalakshmi, K. Kannan and V. Volpi, Assessing seasonal and spatial trends of persistent organic pollutants (POPs) in Indian agricultural regions using PUF disk passive air samplers, Environ. Pollut., 2011, 159(2), 646–653 CrossRef CAS PubMed.
- S. Genualdi, S. C. Lee, M. Shoeib, A. Gawor, L. Ahrens and T. Harner, Global Pilot Study of Legacy and Emerging Persistent Organic Pollutants using Sorbent-Impregnated Polyurethane Foam Disk Passive Air Samplers, Environ. Sci. Technol., 2010, 44(14), 5534–5539 CrossRef CAS PubMed.
- J. Klanova, P. Eupr, J. Kohoutek and T. Harner, Assessing the influence of meteorological parameters on the performance of polyurethane foam-based passive air samplers, Environ. Sci. Technol., 2008, 42(2), 550–555 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The Matlab model script, ISD weather data processing script, and the necessary support files for determining Veff as well as information about the quality control and analytical methods. See DOI: 10.1039/c7em00360a |
| This journal is © The Royal Society of Chemistry 2018 |