A novel sample loading method and protocol for monitoring sample fractionation for high precision Ca stable isotope ratio measurements using double-spike TIMS
Surajit
Mondal
and
Ramananda
Chakrabarti
 *
*
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560012, India. E-mail: ramananda@iisc.ac.in; ramananda@gmail.com
First published on 5th December 2017
Abstract
The external reproducibility (2σSD) of Ca stable isotope ratio measurements (δ44/40Ca) using double-spike thermal ionization mass spectrometry (TIMS) shows a large range from <0.1‰ to 0.5‰. We demonstrate that using a 43Ca–48Ca double spike, which allows simultaneous measurements of δ44/40Ca and δ44/42Ca, and analyses at moderate signal strengths (40Ca ranging from 6 to 10 V), high precision δ44/40Ca (external reproducibility better than ±0.08‰, 2σSD) as well as δ44/42Ca can be obtained if samples and standards are analyzed under similar fractionation conditions. To monitor the fractionation conditions, the usage of a parameter β is proposed, which measures the deviation of the 43Ca/48Ca ratio of the sample–double spike mixture from that of the pure double spike. A novel, low-cost sample loading technique using a combination of Re and Ta filaments and a Ta2O5 activator is presented which results in a steady signal. We report the δ44/40Ca and δ44/42Ca values, calculated w.r.t. NIST SRM 915a and reported as deviations in parts per mil (‰), of NIST standards SRM 915a (0.01, −0.02) and SRM 915b (0.73, 0.32), NASS 6 (seawater, 1.80, 0.89), USGS silicate rock standards BHVO-2 (0.86, 0.47) and BCR-2 (0.89, 0.48), Geological Survey of Japan carbonate standards JCp-1 (coral, 0.85, 0.45) and JCt-1 (clam shell, 0.83, 0.46) and ECRM 752-1 (limestone, alternative name BCS-CRM 393) (0.83, 0.46) from the Bureau of Analyzed Samples Ltd. UK. The Ca stable isotopic compositions of JCt-1 and ECRM 752-1 are reported for the first time.
1 Introduction
Calcium is the fifth most abundant element on the Earth with six stable isotopes: 40Ca, 42Ca, 43Ca, 44Ca, 46Ca, and 48Ca. The natural abundance of 40Ca is the highest (96.9%) followed by 44Ca (2.1%), 42Ca (0.65%), 48Ca (0.19%), 43Ca (0.14%) and 46Ca (0.003%). Due to the large mass difference between the isotopes of Ca, significant Ca isotopic fractionation has been observed in various natural reservoirs, which provides insights into understanding diverse processes including early Solar System evolution,1–3 crust–mantle processes,4–7 seawater evolution,8–11 weathering,12,13 and paleotemperature reconstruction.14–19 Even in biological systems, large Ca isotopic fractionations have been observed and these variations have implications for understanding trophic levels20 and forested ecosystems21 and also have biomedical applications.22–24The first successful Ca stable isotopic measurements were performed using a single-collector thermal ionization mass spectrometer (TIMS) where the “double spike” (DS) technique, using a mixture of 42Ca and 48Ca, was used for correcting mass fractionation.25 Improvements in mass spectrometry, particularly the transition from single collector to multi-collector systems, has led to improvements in the internal precision of Ca isotope ratio measurements while the advent of the multi-collector inductively coupled plasma mass spectrometer (MC-ICPMS) has allowed rapid measurements of Ca isotope ratios in samples. While MC-ICPMS allows rapid measurements, isobaric interference of 40Ar+ with 40Ca+ precludes the measurement of the 44Ca/40Ca ratio and hence, only δ44/42Ca is reported for such measurements. Even for δ44/42Ca measurements, molecular isobaric interference of 12C16O2+ with 44Ca+ needs to be minimized. Additionally, MC-ICPMS measurements of δ44/42Ca use sample–standard bracketing to correct for instrumental mass fractionation.26 The use of sample–standard bracketing requires careful monitoring of the yield of Ca (>99%) during ion-exchange chromatography, unlike for TIMS measurements using DS, and minimization of the ‘matrix-effect’ for accurate and precise measurements.
While the internal precision and external reproducibility of δ44/40Ca measurements using DS-TIMS have improved with multi-collection, the external reproducibility of the measurements shows a large range (0.04–0.5‰),27,28 the exact reason for which is not well understood. Several factors might affect the accuracy and the external reproducibility of Ca isotopic measurements using TIMS. These factors include the double spike composition, sample to spike ratio, type of acid and filament used for sample loading, reservoir mixing, choice of the fractionation law to correct for instrumental mass fractionation and changes in detector properties over time.29–36
In this study, we report a method for improving the external reproducibility of δ44/40Ca measurements using TIMS to <0.1‰ using the 43Ca–48Ca double spike, which also allows simultaneous measurements of δ44/42Ca. We propose a novel sample loading protocol that generates a stable Ca signal for several hours resulting in good internal precision and a method to monitor the extent of fractionation in the sample which allows repeated measurements of the same sample to be performed under similar conditions. Improved reproducibility of operational conditions results in external reproducibility of δ44/40Ca to be <0.1‰ for samples with different matrices (seawater, carbonates and silicates). Using the above measurement protocol, we report the Ca isotopic composition of multiple carbonate reference materials, seawater, and silicate rock standards. The Ca isotopic composition of the Geological Survey of Japan (GSJ) carbonate standard JCt-1 (clam shell) and the limestone CRM from the Bureau of Analyzed Samples Ltd. UK (ECRM 752-1, alternative name BCS-CRM 393) is reported for the first time in this study.
2 Experimental methods
2.1 Preparation of the 43Ca–48Ca double spike
The 43Ca–48Ca double spike was prepared using artificially enriched 43Ca and 48Ca single spikes procured from the Oak Ridge National Laboratory with batch numbers NX 169191 and RT 219801, respectively. The single spikes were dissolved separately using 3 M HCl in pre-cleaned Teflon containers. The single spike solutions were mixed gravimetrically to achieve a 43Ca/48Ca ratio of 0.721 ± 0.02 in the double spike, which is close to the natural abundance ratio. The error is estimated based on the precision of our weighing balance. The isotopic composition of the 43Ca–48Ca double spike (Table 3) was estimated using a total evaporation technique on a TIMS (Thermo Fischer Scientific Triton Plus) at the Centre for Earth Sciences, IISc, Bangalore. The double spike with ∼3 μg of Ca was loaded on a Ta filament (evaporation filament) with 5% HNO3 with an additional 0.5 μl of tantalum oxide (Ta2O5) activator on top of the sample. During analysis, the evaporation filament current was slowly increased to 2000 mA at a rate of 200 mA s−1. The ionization filament (zone-refined Re) current was also increased at 200 mA s−1 to 3300 mA. Data acquisition was initiated when the 48Ca signal was ∼10 V. Data were acquired for 500 cycles until the 48Ca signal reduced below 2 V. The total time of analysis was approximately 8 h.2.2 Sample preparation and purification of Ca
Silicate samples were dissolved using a combination of Suprapur grade HF from Merck and Emsure brand (ACS, Reag. Ph. Eur) HNO3 and HCl acids from Merck while carbonate samples were dissolved in 1 M HCl. The human blood sample, which was obtained by our lab in an oxidized form, was dissolved using a combination of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HCl and HNO3. All samples were processed in a class 100 working area using established laboratory protocols.37 Aliquots of sample solutions, with approximately 10 μg of Ca, were mixed with the 43Ca–48Ca double spike in screw cap Teflon vials. Each sample–DS mixture, mixed in optimal proportions as discussed below, was equilibrated at 80 °C on a hot plate for 4 to 6 hours and subsequently, evaporated. The dried mixture was taken up in 2.5 M HCl and processed for the separation of Ca using ion-exchange chromatography. Calcium was separated from the sample matrix using Teflon columns (8 cm long with an inner diameter of 0.4 cm) filled with BioRad AG50W-X8 (200–400 mesh) resin using 2.5 M HCl. Each sample was processed twice using ion-exchange chromatography for better purification. The Ca yield was between 80 and 90% for all the samples. Potential Ca isotopic fractionation due to low yields is also corrected by using the double-spike technique.38 The purified Ca fraction was dried and treated with 50 μl of concentrated, ultra-pure HNO3 to oxidize any resin that may have leaked out of the column. This HNO3 treatment results in better signal stability during the isotope ratio measurements.
1 HCl and HNO3. All samples were processed in a class 100 working area using established laboratory protocols.37 Aliquots of sample solutions, with approximately 10 μg of Ca, were mixed with the 43Ca–48Ca double spike in screw cap Teflon vials. Each sample–DS mixture, mixed in optimal proportions as discussed below, was equilibrated at 80 °C on a hot plate for 4 to 6 hours and subsequently, evaporated. The dried mixture was taken up in 2.5 M HCl and processed for the separation of Ca using ion-exchange chromatography. Calcium was separated from the sample matrix using Teflon columns (8 cm long with an inner diameter of 0.4 cm) filled with BioRad AG50W-X8 (200–400 mesh) resin using 2.5 M HCl. Each sample was processed twice using ion-exchange chromatography for better purification. The Ca yield was between 80 and 90% for all the samples. Potential Ca isotopic fractionation due to low yields is also corrected by using the double-spike technique.38 The purified Ca fraction was dried and treated with 50 μl of concentrated, ultra-pure HNO3 to oxidize any resin that may have leaked out of the column. This HNO3 treatment results in better signal stability during the isotope ratio measurements.
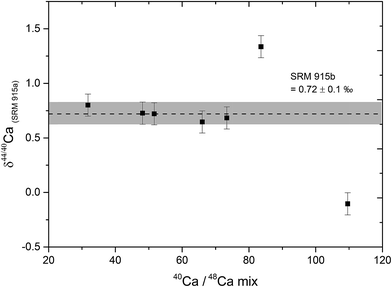
The relative contributions of Ca from the sample and the DS in the sample–DS mixture, referred to as the sample/spike ratio, is a critical parameter which needs to be optimized, failing which, δ44/40Ca measurements can be inaccurate.39 The sample/spike ratio was monitored by measuring the 40Ca/48Ca ratio in the mixture where 40Ca is dominantly derived from the sample and 48Ca from the DS. The optimal range of 40Ca/48Ca in the sample–DS mixtures was determined by mixing different amounts of the DS to a fixed amount (10 μg Ca) of the NIST SRM 915b Ca isotopic standard. Our results indicate that accurate δ44/40Ca can be obtained if the 40Ca/48Ca in the sample–DS mixture is kept between 30 and 70. At higher values of 40Ca/48Ca (under-spiked samples), the δ44/40Ca of the sample deviates from the true value (Fig. 1). The optimal range of 40Ca/48Ca determined in our study is consistent with earlier studies.5 For all the samples and standards analysed in this study, the amount of double spike was added in a manner such that the 40Ca/48Ca ratio of the sample–DS mixture was between 30 and 70 and mostly between 40 and 60.
2.3 Sample loading
In order to test the effects of different sample loading methods on δ44/40Ca measurements, we analysed standards using three different loading techniques, all using a double-filament geometry. Details of these techniques are shown in Table 1. In the first technique (labeled loading #1), 5 μg of Ca was loaded on pre-degassed (kept at 4.5 A for 60 min) zone-refined Re filaments (H. CROSS Co., NJ) with 5% double-distilled HNO3 (Emsure brand, Merck, ACS, Reag. Ph. Eur). This loading technique was adopted from Farkaš et al.8,9 In the second technique (labeled loading #2), 5 μg of Ca was loaded on pre-degassed (kept at 3.5 A for 60 min) Ta filaments with 1.3 M H3PO4. The Ta filaments were degassed seven days prior to loading the samples to allow for mild oxidation of the degassed Ta filament under atmospheric conditions. In a slightly different version of loading #2, the samples were loaded on Ta filaments using 0.03 M H3PO4. No difference in data acquisition or signal stability was observed with change in the molarity of the H3PO4 and hence, we used 1.3 M H3PO4 for our study (Table 1). In the third type of sample loading (labeled loading #3), we loaded approximately ∼3 μg Ca with 5% double distilled HNO3 (Emsure brand, Merck, ACS, Reag. Ph. Eur) on pre-degassed Ta filaments. These Ta filaments, after degassing, were not left for atmospheric oxidation. This step was followed by loading 0.5 μl Ta2O5 on the top of the loaded sample. For all three types of loading, zone-refined Re filaments were used as the ionization filament. The cost of analyses for loading #2 and #3, involving Ta and Re filaments, is lower than that of loading #1, involving double-Re filaments, as Ta filaments are commercially available at cheaper prices compared to zone-refined Re filaments.| Parameters | Loading #1 | Loading #2 | Loading #3 |
|---|---|---|---|
| Amount of Ca loaded | 5 μg | 5 μg | 2.5–3 μg |
| Filament assembly | Double | Double | Double |
| Evaporation filament | Re (zone refined from H. CROSS Co., NJ) | Ta (from H. CROSS Co., NJ) | Ta (from H. CROSS Co., NJ) |
| Ionization filament | Re (zone refined from H. CROSS Co., NJ) | Re (zone refined from H. CROSS Co., NJ) | Re (zone refined from H. CROSS Co., NJ) |
| Loading acid | 5% HNO3 | 1.3 M H3PO4 | 5% HNO3 |
| Activator | None | None (Ta filament allowed to oxidize in air post degassing) | 0.5 μl of tantalum oxide (Ta2O5) added on the top of the sample |
| Ionization current | 2900–3200 mA | 3000–3400 mA | 3000–3400 mA |
| Evaporation current | 225 mA | 1900–2000 mA | 1900–2000 mA |
| Pyrometer reading (°C) | 1400–1500 | 1400–1500 | 1400–1500 |
In all three loading methods, after loading the sample on the filament, the filament current was increased to 0.8 A, until the sample dried. In loading #3, Ta2O5 was added on top of the dried sample and again dried at 0.8 A. The filament current was further increased to 1.8 A and kept for 60 s and then to 2.2 A for 30 s after which the current was slowly reduced to zero. Samples loaded with 5% HNO3 turned greenish white in colour upon drying while samples loaded with H3PO4 looked brownish in colour after drying. Within an hour of loading, the samples were inserted into the TIMS source.
2.4 Calcium isotope ratio measurements
Calcium isotopic measurements were performed using a TIMS at the Centre for Earth Sciences, IISc, Bangalore which was operated in positive ionization mode and is equipped with nine Faraday cups, all with 1011 Ω resistors. For samples loaded with loading #1, the evaporation filament current was increased at 100 mA s−1 and kept at 225 mA while the ionization filament current was increased at 300 mA s−1 and kept between 2900 and 3200 mA. For samples loaded using loading #2 and loading #3, the evaporation filament current was increased at 100 mA s−1 and kept between 1900 and 2000 mA, while the ionization filament current was increased at 300 mA s−1 to a maximum of 3400 mA (Table 1). Data acquisition was performed at a pyrometer reading of 1400–1500 °C although, for double filaments this temperature does not reflect the filament temperature. During analyses, the 40Ca signal was kept between 6 and 10 V during which the 42Ca signal is less than 100 mV. Calcium isotope ratio measurements were performed in a dynamic mode. 40Ca, 41K, 42Ca, 43Ca, and 44Ca signals were measured in the first sequence in cups L3, L1, C, H2, and H4, respectively, while 44Ca, 46Ca, and 48Ca signals were measured in the second sequence using cups L2, C, and H3, respectively (Table 2). Amplifier rotation was not applied. The 41K signal was monitored during the analysis for correcting the contribution of 40K to 40Ca. The intensity of 41K (natural abundance of 6.73%) was <10 mV for the silicate samples and <1 mV for the carbonate samples thereby ruling out any significant contribution of 40K (natural abundance of 0.117%) to 40Ca. Hence, external correction for 40K on 40Ca was not applied. For each analysis, the integration time was set to 16.77 s with 6 s idle time between the two measurement sequences. For focusing and peak centering, 40Ca was used in the first sequence while 44Ca was used for peak centering in the second sequence. Baseline measurements and lens focusing were done after every 4th block. Data acquisition was done for a minimum of 10 blocks with 10 cycles in each block. The TIMS operational conditions are summarised in Table 2.| Parameters | Parameter values |
|---|---|
| 40Ca beam intensity | 6–10 V |
| Accelerating voltage | 10 kV |
| Collectors | Faraday cups with 1011 Ω resistors |
| Source pressure | <1.5 × 10−7 mbar |
| Analyser pressure | <9 × 10−9 mbar |
| Sequence 1 (S1) | 40Ca (L3), 41K (L1), 42Ca (centre), 43Ca (H2), 44Ca (H4) |
| Sequence 2 (S2) | 44Ca (L2), 46Ca (centre), 47Ti (H1), 48Ca (H3) |
| Idle time | 6 s |
| Integration time | 16.7 s |
| Blocks | Minimum 10 |
| Cycles per block | 10 |
| Gain calibration | Once a day before the start of measurements |
| Focus | At the beginning of each analysis |
| Peak centre (control mass) | Every 4 blocks (control mass: 40Ca-S1; 44Ca-S2) |
| Baseline | Every 4 blocks |
| Total analysis time | ∼4 h |
2.5 Data reduction using an iterative algorithm
The 40Ca/44Ca, 42Ca/44Ca, and 43Ca/44Ca ratios measured in the first sequence and the 48Ca/44Ca ratio measured in the second sequence were used to determine the δ44/40Ca values of the samples. Instrumental mass fractionation correction using the double-spike technique was done offline using an iterative algorithm adapted from Heuser et al.30 which was originally proposed by Compston and Oversby40 for lead isotope ratio measurements. The “Russell value”38 was used as the initial value for the iteration (Table 3). The isotopic composition of the “IUPAC value” was not used as the starting value as it results in large errors in δ44/40Ca calculations, as suggested by Heuser et al.30| Isotopes of Ca | Natural isotopic abundance (%) | 43Ca spike isotopic composition (%) | 48Ca spike isotopic composition (%) | 43Ca–48Ca double spike composition | Bulk terrestrial Ca “Russell Values”a |
|---|---|---|---|---|---|
| a Data from Russell et al.38 | |||||
| 40Ca | 96.9 | 10.13 | 2.1 | 40Ca/48Ca = 0.1222561 | 531.54 |
| 42Ca | 0.65 | 0.78 | 0.024 | 42Ca/48Ca = 0.0072123 | 3.5194 |
| 43Ca | 0.14 | 83.93 | >0.01 | 43Ca/48Ca = 0.7210064 | 0.73115 |
| 44Ca | 2.1 | 5.06 | 0.072 | 44Ca/48Ca = 0.0443720 | 11.273 |
| 46Ca | 0.003 | >0.001 | >0.01 | ||
| 48Ca | 0.19 | 0.09 | 97.8 | ||
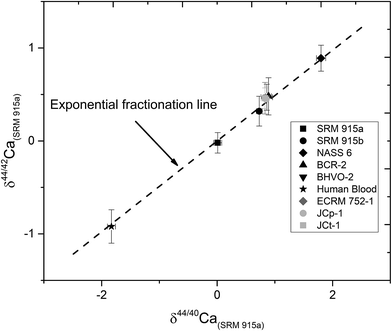
3 Results
In this study, NIST carbonate standards SRM 915a and SRM 915b and a seawater standard NASS 6 were analysed for their Ca isotopic compositions using three different loading techniques (Table 1). The results of these analyses are shown in Table 4 and Fig. 2 and are consistent with previous studies.5,8,21,28,31,32 Calcium isotopic compositions are expressed as deviations in parts per thousand with respect to the NIST standard SRM 915a using the delta notation, where δ44/40Ca = [(44/40Casample/44/40CaSRM 915a) − 1] × 1000 and δ42/44Ca = [(42/44Casample/42/44CaSRM 915a) − 1] × 1000. The 44Ca/40Ca ratio of the SRM 915a standard used for all our measurements is 0.02157692. We have also analysed silicate rock standards from the United States Geological Survey (USGS) which include BCR-2 (Columbia River basalt) and BHVO-2 (Hawaiian basalt), carbonate standards from the Geological Survey of Japan (GSJ) which include JCp-1 (Porites coral),41 JCt-1 (clam shell),41,42 a limestone CRM from the Bureau of Analyzed Samples Ltd. UK, ECRM 752-1 (alternative name BCS-CRM 393),43 and a sample of human blood which was obtained by our lab in an oxidized form (Table 5 and Fig. 5). The data presented in Tables 4 and 5 and plotted in Fig. 5 were obtained using loading #3 (Table 1), which is our preferred loading technique. For loading #3, our internal precision (2σSEM) is better than ±0.03‰ for δ44/40Ca and ranges from ±0.04 to 0.06‰ for δ44/42Ca measurements. The external reproducibility (2σSD) for δ44/40Ca, based on multiple measurements of the standards SRM 915a, SRM 915b and NASS 6 seawater, is better than 0.08‰ (Table 4). Using loading #3, the external reproducibility for δ44/42Ca ranges from ±0.11 to 0.20‰ (Tables 4 and 5). For loading #1 and #2, the external reproducibility for δ44/40Ca is worse and ranges from ±0.16 to 0.26‰ (Table 4 and Fig. 3).| Sample Id | Loading #1 (Re–Re–5% HNO3) | Loading #2 (Re–Ta–4 N H3PO4) | Loading #3 (Re–Ta–Ta2O5) | ||
|---|---|---|---|---|---|
| δ 44/40Ca | δ 44/40Ca | δ 44/42Ca | δ 44/40Ca | δ 44/42Ca | |
| SRM 915a_1 | 0.06 | −0.03 | |||
| SRM 915a_2 | 0.02 | 0.04 | |||
| SRM 915a_3 | 0.00 | −0.06 | |||
| SRM 915a_4 | −0.02 | 0.01 | |||
| SRM 915a_5 | 0.00 | −0.13 | |||
| SRM 915a_6 | 0.00 | 0.13 | |||
| SRM 915a_7 | 0.04 | −0.08 | |||
| SRM 915a_8 | 0.06 | 0.01 | |||
| SRM 915a_9 | −0.03 | −0.03 | |||
| Average | 0.01 | −0.02 | |||
| 2SD | 0.07 | 0.11 | |||
| SRM 915b_1 | 0.78 | 0.72 | 0.40 | 0.71 | 0.21 |
| SRM 915b_2 | 0.62 | 0.74 | 0.45 | 0.73 | 0.34 |
| SRM 915b_3 | 0.74 | 0.77 | 0.39 | 0.72 | 0.31 |
| SRM 915b_4 | 0.69 | 0.76 | 0.49 | 0.72 | 0.2 |
| SRM 915b_5 | 0.70 | 0.61 | 0.49 | 0.74 | 0.4 |
| SRM 915b_6 | 0.71 | 0.59 | 0.56 | 0.69 | 0.34 |
| SRM 915b_7 | 0.75 | 0.43 | 0.78 | 0.43 | |
| SRM 915b_8 | 0.87 | 0.30 | 0.72 | 0.37 | |
| SRM 915b_9 | 0.78 | 0.34 | |||
| SRM915b_10 | 0.77 | 0.41 | |||
| Average | 0.71 | 0.74 | 0.43 | 0.73 | 0.32 |
| 2SD | 0.11 | 0.16 | 0.15 | 0.05 | 0.16 |
| NASS 6_1 | 1.79 | 1.8 | 0.98 | 1.78 | 0.89 |
| NASS 6_2 | 1.96 | 1.82 | 0.93 | 1.76 | 1.02 |
| NASS 6_3 | 1.70 | 1.88 | 0.83 | 1.85 | 0.87 |
| NASS 6_4 | 1.88 | 2.01 | 0.81 | 1.75 | 0.79 |
| NASS 6_5 | 1.70 | 1.72 | 1.15 | 1.78 | 0.88 |
| NASS 6_6 | 1.93 | 0.88 | 1.85 | 0.84 | |
| NASS 6_7 | 1.66 | 0.88 | 1.84 | 0.92 | |
| NASS 6_8 | 2.04 | 1.10 | |||
| NASS 6_9 | 1.78 | 0.96 | |||
| NASS 6_10 | 1.82 | 0.94 | |||
| NASS 6_11 | 2.12 | 0.98 | |||
| NASS 6_12 | 1.94 | 0.86 | |||
| NASS 6_13 | 1.79 | 1.02 | |||
| NASS 6_14 | 1.77 | 0.97 | |||
| Average | 1.81 | 1.86 | 0.95 | 1.80 | 0.89 |
| 2SD | 0.22 | 0.26 | 0.19 | 0.08 | 0.14 |
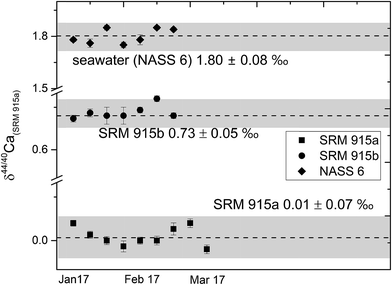 | ||
| Fig. 2 δ 44/40Ca of the NIST standards SRM 915a and SRM 915b and seawater NASS 6 analysed with our preferred sample loading technique (#3, Table 1) using a 43Ca–48Ca double spike. The external reproducibility (2σSD) for δ44/40 Ca was better than ±0.08‰. | ||
| Sample Id | δ 44/40Ca | δ 44/42Ca |
|---|---|---|
| JCt-1_1 | 0.81 | 0.48 |
| JCt-1_2 | 0.85 | 0.46 |
| JCt-1_3 | 0.81 | 0.38 |
| JCt-1_4 | 0.86 | 0.51 |
| Average | 0.83 | 0.46 |
| 2SD | 0.05 | 0.11 |
| JCp-1_1 | 0.80 | 0.41 |
| JCp-1_2 | 0.84 | 0.46 |
| JCp-1_3 | 0.88 | 0.54 |
| JCp-1_4 | 0.83 | 0.39 |
| JCp-1_5 | 0.88 | 0.45 |
| Average | 0.85 | 0.45 |
| 2SD | 0.07 | 0.12 |
| ECRM 752_1 | 0.77 | 0.39 |
| ECRM 752_2 | 0.85 | 0.56 |
| ECRM 752_3 | 0.85 | 0.48 |
| ECRM 752_4 | 0.84 | 0.52 |
| ECRM 752_5 | 0.83 | 0.36 |
| Average | 0.83 | 0.46 |
| 2SD | 0.07 | 0.17 |
| USGS BCR 2_1 | 0.91 | 0.6 |
| USGS BCR 2_2 | 0.93 | 0.42 |
| USGS BCR 2_3 | 0.86 | 0.36 |
| USGS BCR 2_4 | 0.88 | 0.56 |
| USGS BCR 2_5 | 0.89 | 0.45 |
| Average | 0.89 | 0.48 |
| 2SD | 0.05 | 0.20 |
| BCR 2, He et al. (2017) | 0.839 ± 0.145 | 0.423 ± 0.078 |
| USGS BHVO 2_1 | 0.93 | 0.47 |
| USGS BHVO 2_2 | 0.87 | 0.51 |
| USGS BHVO 2_3 | 0.85 | 0.4 |
| USGS BHVO 2_4 | 0.80 | 0.39 |
| USGS BHVO 2_5 | 0.83 | 0.56 |
| Average | 0.86 | 0.47 |
| 2SD | 0.10 | 0.14 |
| USGS BHVO 2, He et al. (2017) | 0.759 ± 0.044 | 0.384 ± 0.055 |
| Human blood | −1.85 | −1.0 |
| Human blood | −1.8 | −0.85 |
| Average | −1.83 | −0.92 |
| 2SD | 0.07 | 0.18 |
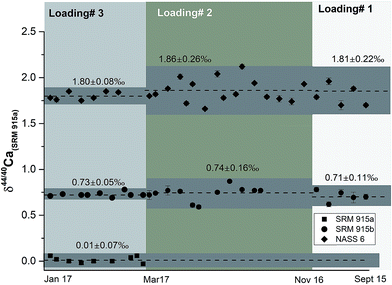 | ||
| Fig. 3 δ 44/40Ca of the NIST standards SRM 915a and SRM 915b and seawater NASS 6 analysed using the three different sample loading techniques. All measurements were done using a 43Ca–48Ca double spike. The external reproducibility of these measurements (2σSD) is the least when loading 3, our preferred technique, is used. See Tables 1 and 4 and the text for more details. | ||
4 Discussion
The external reproducibility of δ44/40Ca measurements is the limiting factor for wider application of Ca stable isotopes.44 We investigate the factors that could hinder the external reproducibility of δ44/40Ca measurements and suggest a new sample loading protocol and a method to monitor the fractionation of the samples, which significantly improves the external reproducibility of δ44/40Ca measurements.4.1 Choice of the double spike
To correct for isotopic fractionation during ion-exchange chromatography as well as mass spectrometry, Russell et al.38 proposed mixing a 42Ca–48Ca DS with the sample prior to ion-exchange chromatography. The authors claimed that the large mass difference between 42Ca and 48Ca reduces the instrumental mass fractionation per amu for 44Ca/40Ca ratio measurements. Other research groups have used different combinations of double spikes like 43Ca–48Ca,5,3042Ca–43Ca31,44 and 43Ca–46Ca45 for δ44/40Ca measurements. As the average mass of 42Ca and 43Ca in the 42Ca–43Ca DS (mean mass 42.5) is close to the average mass of 44Ca and 40Ca (mean mass 42), it was suggested based on the “mean mass law” that the use of the 42Ca–43Ca DS should minimise the error in 44Ca/40Ca measurements compared to when using the 43Ca–48Ca (mean mass 45.5) or 42Ca–48Ca (mean mass 45) double spikes.44 Lehn et al.31,32 argued that the 42Ca–43Ca DS yields better external reproducibility for δ44/40Ca measurements compared to the 43Ca–48Ca DS. For δ44/40Ca measurements using the 43Ca–48Ca DS, Lehn et al.31 reported internal precisions ranging from 0.013 to 0.081‰ and an average external reproducibility of ±0.223‰ for standards with different matrices. In contrast, when using the 42Ca–43Ca DS, the external reproducibility for δ44/40Ca measurements for a silicate standard was 0.033‰ which is only marginally worse than the internal precision of 0.023‰ using the 42Ca–43Ca DS but significantly better than the external reproducibility when using the 43Ca–48Ca DS.31 Additionally, when the 42Ca–43Ca DS is used, only the 40Ca, 42Ca, 43Ca and 44Ca signals have to be measured. This measurement can be done in a single sequence thereby reducing the δ44/40Ca measurement time. However, theoretical studies by Rudge et al.39 have shown that error propagation is approximately half when using the 43Ca–48Ca DS compared to the 42Ca–43Ca DS. In addition, using the 43Ca–48Ca DS allows simultaneous determination of δ44/40Ca and δ44/42Ca values and hence, a direct comparison with δ44/42Ca values from MC-ICPMS measurements is possible.In this study, the Ca isotopic compositions of NIST SRM 915a, NIST SRM 915b, and seawater (NASS 6) were measured multiple times using the 43Ca–48Ca double spike. The measured external reproducibility for δ44/40Ca (2σSD) is ±0.07‰ (n = 9) for SRM 915a, ± 0.05‰ (n = 8) for SRM 915b and ±0.08‰ (n = 7) for seawater (NASS 6) (Table 4). The external reproducibility achieved in the present study for δ44/40Ca measurements using the 43Ca–48Ca double spike is comparable with those reported in studies using the 42Ca–43Ca double spike.16,21,31,32,46 It may be noted that some of the studies using the 42Ca–43Ca double spike analyse the samples at much higher operational voltages compared to those in the present study (6–10 V on 40Ca). The operational voltages in the present study were intentionally kept low as high operational voltages are known to degrade the Faraday cups.47 The external reproducibilities for δ44/42Ca measurements in the present study (0.11–0.2‰) are worse compared to those for δ44/42Ca measurements using MC-ICPMS.26 We believe that the lower precision of δ44/42Ca measurements is due to the low signal (<100 mV) of 42Ca. At higher intensities of 42Ca, the external reproducibility of δ44/42Ca using the proposed protocol is expected to be much better. We believe that the 43Ca–48Ca DS can yield high precision δ44/40Ca and δ44/42Ca values. Instead of the composition of the DS, the sample loading technique and quantitative monitoring of sample fractionation during analysis play a key role in improving the external reproducibility of the δ44/40Ca measurements.
4.2 Sample purification
A pre-requisite for generating a stable ion beam during isotope ratio measurements is the quantitative removal of the sample matrix by using ion-exchange chromatography. Small amounts of impurities (e.g., Fe, Al, and Mg) present in the purified sample being analyzed can suppress Ca ionization in the TIMS source. The presence of potassium (K) in the samples can result in direct isobaric interference of 40K with 40Ca. As K has a low ionization potential (3.43 eV) compared to Ca (6.11 eV), Fletcher et al.48 proposed that rapid heating of the central filament (for a triple filament assembly) or evaporation filament (for a double filament assembly) can reduce the interference from K by evaporating the K on the filament before reaching the optimum 40Ca+ ion beam. During analysis, we monitored the 41K signal for correcting the interference of 40K+ (40K/41K = 0.001738) with 40Ca+. For the samples and standards analysed in this study, the 41K+ signal was less than 1 mV during Ca isotope data acquisition and the typical signal of 40Ca during these measurements was about 6–10 V. Hence, the contribution of 40K to 40Ca was negligible. Some studies8,31 have skipped the ion-chromatographic purification of NIST SRM 915a or SRM 915b carbonate standards because of their pure Ca carbonate matrix. However, the 43Ca spike has a certified value of <100 ppm of K and 5000 ppm of Sr, and hence, the chemical purification of the sample–DS mixture is essential. In the present study, we have chemically purified the samples and standards using cation exchange chromatography after the addition of the double spike.For samples with high K, for e.g., old crustal rocks, variations in 40Ca could also be due to the decay of 40K and this radiogenic 40Ca component can affect the δ44/40Ca values in these samples. The contribution of the radiogenic 40Ca can be corrected using the K/Ca ratio and the age of the samples to yield accurate δ44/40Ca values.26 Additionally, an unspiked aliquot of the sample needs to be analyzed to determine the starting isotopic composition which is used for the iterative procedure to calculate the δ44/40Ca of the rock.
4.3 Sample loading
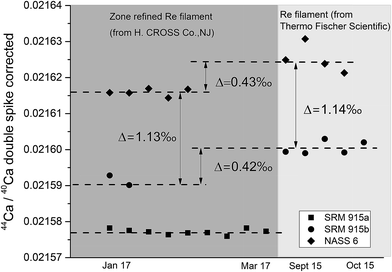
Sample loading on the filament plays a critical role in TIMS measurements as it affects the stability of the signal and the extent of isotopic fractionation, which in turn could affect the accuracy and internal precision of the measurements. For δ44/40Ca measurements, several loading techniques have been proposed. Russell et al.38 loaded 5–10 μg of Ca as a chloride or nitrate salt on a pre-oxidized V-shaped zone refined single Ta filament. Subsequently, different filament assemblies involving single, double and triple filaments on different generations of TIMS manufactured by different companies as well as different loading techniques using HNO3, HCl, and H3PO4 acids21,49,50 have been attempted. The use of activators like Ta2O5 has also been proposed.30 In the last few years, Ca stable isotope data (δ44/40Ca) have mostly been generated using either a GV IsoProbe-T or a Thermo Scientific Triton (Plus) TIMS, with the Triton (Plus) being the more widely used TIMS for Ca isotopic measurements. The IsoProbe-T uses either a single or a triple filament configuration whereas the Triton (Plus) uses either a single or a double filament geometry. In the present study, a double filament geometry has been used.We have tried three different loading techniques in this study as summarized in Table 1. Loading #1 and #2 involve Re double filament configurations. We have tested two types of Re ribbons (synonymously used as filaments) procured from two different commercial sources. Our initial measurements were performed using Re filaments procured from Thermo Fischer Scientific, while most of our measurements were performed using zone-refined Re ribbons procured from H. CROSS, NJ, USA. We have used the same DS for all our experiments. We have noticed that the extent of fractionation of the samples when using the two different Re ribbons was different (Fig. 4). While the exact reason for this difference is unclear, minor differences in the properties of these filaments procured from the two different manufacturers, e.g., their thickness, could affect the heating characteristics and hence, the fractionation of the sample–double spike mixture.
In our preferred loading protocol (#3, Table 1), we used a combination of Re and Ta filaments using a double filament configuration. Calcium was loaded as a nitrate on Ta filaments, followed by the addition of Ta2O5. Zone-refined Re filaments were used as ionization filaments. This sample loading protocol yielded stable Ca signals of 6–10 V which could be sustained for ∼5 hours. While the GV IsoProbe-T TIMS collectors have a dynamic range of 10 V, the Thermo Triton Plus has a higher dynamic range of 50 V, both using the standard 1011 Ω resistors. Most Ca isotope studies using a Triton (Plus) use high operational voltages (e.g., 20 V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31,32) on 40Ca. While high operational voltages yield better counting statistics, the collectors are easily damaged which in turn affects the long-term reproducibility of δ44/40Ca measurements. Low operational voltages, as used in the present study, improve the life-time of the Faraday cups which are expensive to replace. The use of Ta ribbons for loading the samples also reduces the cost of Ca isotopic analyses as Ta ribbons are cheaper than zone-refined Re ribbons. The Ta–Ta double filament configuration was also attempted but the signal stability was poor with this filament combination and hence, not used for further measurements. While stable Ca beams with controlled fractionation improved the internal precision (2σSEM) of our analyses (better than ±0.03‰), the external reproducibility of the data, based on multiple analyses using different filaments, requires reproducible fractionation patterns. We propose a method for ensuring reproducible running conditions which is described in Section 4.4.
31,32) on 40Ca. While high operational voltages yield better counting statistics, the collectors are easily damaged which in turn affects the long-term reproducibility of δ44/40Ca measurements. Low operational voltages, as used in the present study, improve the life-time of the Faraday cups which are expensive to replace. The use of Ta ribbons for loading the samples also reduces the cost of Ca isotopic analyses as Ta ribbons are cheaper than zone-refined Re ribbons. The Ta–Ta double filament configuration was also attempted but the signal stability was poor with this filament combination and hence, not used for further measurements. While stable Ca beams with controlled fractionation improved the internal precision (2σSEM) of our analyses (better than ±0.03‰), the external reproducibility of the data, based on multiple analyses using different filaments, requires reproducible fractionation patterns. We propose a method for ensuring reproducible running conditions which is described in Section 4.4.
4.4 Monitoring isotopic fractionation during analysis
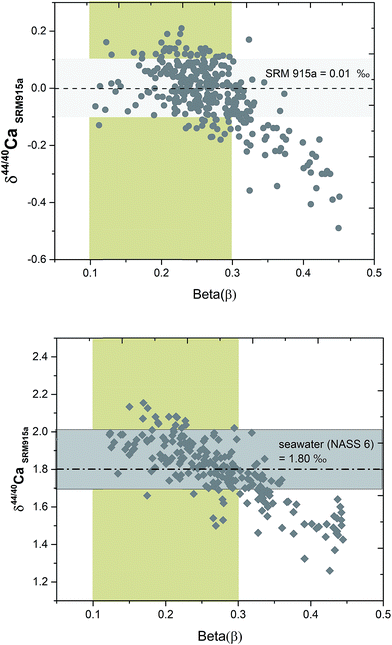
Although, the combination of filaments and sample loading protocols as well as filament heating conditions in the TIMS are kept constant for all the samples, the sample spot size after drying and its exact position on the filament can vary from one filament to another. Due to such differences, the evaporation and ionization pattern of the same sample loaded on different filaments are not reproducible during TIMS measurements. To monitor and compare the fractionation of samples on different filaments, we have introduced a parameter called beta (β) which is defined as:| β = ln[(43Ca/48Ca)DS/(43Ca/48Ca)sample–DS mix]/ln(42.958/47.952) |
The signal of 43Ca and 48Ca in the sample–DS mixture is primarily derived from the DS. So the β value is not affected by the inherent composition of the sample and primarily reflects the extent of fractionation of the sample to DS ratio in the mixture. During the course of analysis of a sample, the β value decreases (Fig. 6). Higher values of β reflect sub-optimal fractionation of the sample–DS mixture whereas very low values of β reflect higher fractionation of the sample–DS mixture at high filament temperatures. For loading #3, using running conditions listed in Table 1, the β values of the samples typically ranged from 0.35 at the beginning of the analyses to 0.1 at the end. By performing repeated analyses of NIST SRM 915a and SRM 915b and seawater (NASS 6), where the 40Ca/48Ca of the sample–DS mixture is kept between 30 and 70, we determined the range of β values during which the δ44/40Ca of these standards and the seawater showed accurate and reproducible values (Fig. 6). This β value range is considered as optimal and is between 0.3 and 0.1. All the other samples were analyzed within the same range of β values. At optimal β values, at least 100 cycles (10 blocks) were measured for each sample and standard. The internal precision (2σSEM) for δ44/40Ca of the samples and standards after 10–15 blocks was better than ±0.03‰. Analysis of all samples and standards at optimal β values resulted in an external reproducibility (2σSD) that is better than ±0.08‰. When β values are higher than optimal, the δ44/40Ca values showed lower values (Fig. 6) and the reason for such deviation is not well understood.
5 Conclusions
We propose a novel sample loading protocol and a method to monitor the fractionation of samples during δ44/40Ca measurements using a TIMS. We demonstrate that high precision Ca isotopic measurements are possible using a 43Ca–48Ca double spike, which allows simultaneous measurements of δ44/40Ca and δ44/42Ca. After ion-exchange chromatography, 2–3 μg of purified Ca from the sample–DS mixture was loaded on degassed Ta filaments using 5% HNO3 followed by addition of a Ta2O5 activator. A zone-refined Re filament was used as the ionization filament. Using this loading technique, a stable signal with 40Ca, intentionally kept between 6 and 10 V, can be sustained for over 5 hours which is essential for the good internal precision of δ44/40Ca measurements. We also propose the usage of a parameter β to monitor the fractionation of the samples in the TIMS source. When all samples and standards are analyzed under similar extents of fractionation (β value), the external reproducibility of δ44/40Ca is better than ±0.08‰. We report δ44/40Ca and δ44/42Ca of USGS rock standards BHVO-2 and BCR-2 as well as carbonate standards JCp-1, JCt-1 and ECRM 752-1 (alternative name BCS-CRM 393). Our preferred loading method using a Ta–Re double filament assembly is more cost effective compared to the commonly used Re–Re double filament assembly, given the lower cost of Ta ribbons compared to zone refined Re ribbons.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Standards and samples for this study were kindly provided by Shichun Huang, Sambuddha Misra, Q.-z. Yin, Stein Jacobsen, Kaustubh Thirumalai and Ravi Rangarajan. This study was supported by DST grants (SR/FTP/ES-72/2012, SR/S4/ES-650/2012) to RC. We thank three anonymous reviewers and the editor for their comments and suggestions.References
- M. Schiller, C. Paton and M. Bizzarro, Geochim. Cosmochim. Acta, 2015, 149, 88–102 CrossRef CAS PubMed.
- M. C. Valdes, M. Moreira, J. Foriel and F. Moynier, Earth Planet. Sci. Lett., 2014, 394, 135–145 CrossRef CAS.
- S. Huang and S. B. Jacobsen, Geochim. Cosmochim. Acta, 2017, 201, 364–376 CrossRef CAS.
- X. Zhao, Z. Zhang, S. Huang, Y. Liu, X. Li and H. Zhang, Geochim. Cosmochim. Acta, 2017, 208, 368–380 CrossRef CAS.
- S. Huang, J. Farkaš and S. B. Jacobsen, Geochim. Cosmochim. Acta, 2011, 75, 4987–4997 CrossRef CAS.
- J.-T. Kang, H.-L. Zhu, Y.-F. Liu, F. Liu, F. Wu, Y.-T. Hao, X.-C. Zhi, Z.-F. Zhang and F. Huang, Geochim. Cosmochim. Acta, 2016, 174, 335–344 CrossRef CAS.
- B. D. Marshall and D. J. DePaolo, Geochim. Cosmochim. Acta, 1989, 53, 917–922 CrossRef CAS.
- J. Farkaš, F. Böhm, K. Wallmann, J. Blenkinsop, A. Eisenhauer, R. Van Geldern, A. Munnecke, S. Voigt and J. Veizer, Geochim. Cosmochim. Acta, 2007, 71, 5117–5134 CrossRef.
- J. Farkaš, D. Buhl, J. Blenkinsop and J. Veizer, Earth Planet. Sci. Lett., 2007, 253, 96–111 CrossRef.
- E. T. Tipper, A. Galy and M. J. Bickle, Earth Planet. Sci. Lett., 2006, 247, 267–279 CrossRef CAS.
- M. S. Fantle and D. J. DePaolo, Earth Planet. Sci. Lett., 2005, 237, 102–117 CrossRef CAS.
- R. S. Hindshaw, B. C. Reynolds, J. G. Wiederhold, R. Kretzschmar and B. Bourdon, Geochim. Cosmochim. Acta, 2011, 75, 106–118 CrossRef CAS.
- J.-S. Ryu, A. D. Jacobson, C. Holmden, C. Lundstrom and Z. Zhang, Geochim. Cosmochim. Acta, 2011, 75, 6004–6026 CrossRef CAS.
- D. Hippler, A. D. Schmitt, N. Gussone, A. Heuser, P. Stille, A. Eisenhauer and T. F. Nägler, Geostand. Newsl., 2003, 27, 13–19 CrossRef CAS.
- X. Chen, W. Deng, H. Zhu, Z. Zhang, G. Wei and M. T. McCulloch, Chem. Geol., 2016, 435, 71–78 CrossRef CAS.
- M. Inoue, N. Gussone, Y. Koga, A. Iwase, A. Suzuki, K. Sakai and H. Kawahata, Geochim. Cosmochim. Acta, 2015, 167, 80–92 CrossRef CAS.
- D. Hippler, A. Eisenhauer and T. F. Nägler, Geochim. Cosmochim. Acta, 2006, 70, 90–100 CrossRef CAS.
- F. Böhm, N. Gussone, A. Eisenhauer, W.-C. Dullo, S. Reynaud and A. Paytan, Geochim. Cosmochim. Acta, 2006, 70, 4452–4462 CrossRef.
- T. F. Nägler, A. Eisenhauer, A. Müller, C. Hemleben and J. Kramers, Geochem., Geophys., Geosyst., 2000, 1 DOI:10.1029/2000GC000091.
- M. Clementz, P. Holden and P. Koch, Int. J. Osteoarchaeol., 2003, 13, 29–36 CrossRef.
- C. Holmden and N. Bélanger, Geochim. Cosmochim. Acta, 2010, 74, 995–1015 CrossRef CAS.
- J. Skulan, D. J. DePaolo and T. L. Owens, Geochim. Cosmochim. Acta, 1997, 61, 2505–2510 CrossRef CAS.
- A. Heuser, A. Eisenhauer, K. E. Scholz-Ahrens and J. Schrezenmeir, Isot. Environ. Health Stud., 2016, 52, 633–648 CrossRef CAS PubMed.
- J. L. Morgan, J. L. Skulan, G. W. Gordon, S. J. Romaniello, S. M. Smith and A. D. Anbar, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9989–9994 CrossRef CAS PubMed.
- W. A. Russell, D. A. Papanastassiou, T. A. Tombrello and S. Epstein, in Lunar and Planetary Science Conference Proceedings, 1977, vol. 8, pp. 3791–3805 Search PubMed.
- M. S. Fantle and E. T. Tipper, Earth-Sci. Rev., 2014, 129, 148–177 CrossRef CAS.
- N. Gussone, A.-D. Schmitt, A. Heuser, F. Wombacher, M. Dietzel, E. Tipper and M. Schiller, Calcium Stable Isotope Geochemistry, Springer, Verlag, Berlin, Heidelberg, 2010, ISBN: 978-3-540-68948-5 Search PubMed.
- Y. He, Y. Wang, C. Zhu, S. Huang and S. Li, Geostand. Geoanal. Res., 2016, 41, 283–302 CrossRef.
- S. F. Boulyga, Mass Spectrom. Rev., 2010, 29, 685–716 CrossRef CAS PubMed.
- A. Heuser, A. Eisenhauer, N. Gussone, B. Bock, B. T. Hansen and T. F. Nägler, Int. J. Mass Spectrom., 2002, 220, 385–397 CrossRef CAS.
- G. O. Lehn and A. D. Jacobson, J. Anal. At. Spectrom., 2015, 30, 1571–1581 RSC.
- G. O. Lehn, A. D. Jacobson and C. Holmden, Int. J. Mass Spectrom., 2013, 351, 69–75 CrossRef CAS.
- M. S. Fantle and T. D. Bullen, Chem. Geol., 2009, 258, 50–64 CrossRef CAS.
- G. Cavazzini, Int. J. Mass Spectrom., 2009, 288, 84–91 CrossRef CAS.
- E. D. Young, A. Galy and H. Nagahara, Geochim. Cosmochim. Acta, 2002, 66, 1095–1104 CrossRef CAS.
- K. Habfast, Int. J. Mass Spectrom., 1998, 176, 133–148 CrossRef CAS.
- A. Banerjee, R. Chakrabarti and S. Mandal, Chem. Geol., 2016, 440, 124–138 CrossRef CAS.
- W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090 CrossRef CAS.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS.
- W. Compston and V. Oversby, J. Geophys. Res., 1969, 74, 4338–4348 CrossRef CAS.
- T. Okai, A. Suzuki, H. Kawahata, S. Terashima and N. Imai, Geostand. Newsl., 2003, 26, 95–99 CrossRef.
- M. Inoue, M. Nohara, T. Okai, A. Suzuki and H. Kawahata, Geostand. Geoanal. Res., 2004, 28, 411–416 CrossRef CAS.
- M. Greaves, S. Barker, C. Daunt and H. Elderfield, Geochem., Geophys., Geosyst., 2005, 6 DOI:10.1029/2004GC000790.
- K. Gopalan, D. Macdougall and C. Macisaac, Int. J. Mass Spectrom., 2006, 248, 9–16 CrossRef CAS.
- K. Gopalan, J. D. Macdougall and C. Macisaac, Geostand. Geoanal. Res., 2007, 31, 227–236 CrossRef CAS.
- A. D. Du Vivier, A. D. Jacobson, G. O. Lehn, D. Selby, M. T. Hurtgen and B. B. Sageman, Earth Planet. Sci. Lett., 2015, 416, 121–131 CrossRef CAS.
- J. I. Simon, D. J. Depaolo and F. Moynier, Astrophys. J., 2009, 702, 707 CrossRef.
- I. R. Fletcher, A. L. Maggi, K. J. R. Rosman and N. J. McNaughton, Int. J. Mass Spectrom. Ion Processes, 1997, 163, 1–17 CrossRef CAS.
- S. Huang, J. Farkaš and S. B. Jacobsen, Earth Planet. Sci. Lett., 2010, 292, 337–344 CrossRef CAS.
- B. D. Marshall and D. J. DePaolo, Geochim. Cosmochim. Acta, 1982, 46, 2537–2545 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |