Loss compensation during subwavelength propagation of enhanced second-harmonic generation signals in a hybrid plasmonic waveguide

Abstract

Ultracompact coherent light sources with broadband wavelength tunability and subwavelength optical waveguiding have attracted extensive attention due to their potential applications ranging from multicolor detection to multiband on-chip photonic communication. Metal–dielectric nonlinear structures, which comprise nonlinear dielectric materials and metal films, have been widely used to generate nanoscale broadband tunable coherent light sources through the second-harmonic generation process below the diffraction limit. However, restricted by high ohmic losses at the metal–dielectric surface, subwavelength propagation of SHG signals with low loss remains a big challenge. Here, a novel strategy is utilized to reduce the propagation loss of SHG signals based on the coupling between the waveguide mode and plasmonic mode in a hybrid plasmonic waveguide (HPW). The generated hybrid plasmonic mode in the HPW exhibits strong optical confinement around the nonlinear dielectric and insulating gap, which is beneficial for minimizing the ohmic losses at the metal–dielectric interface and enhancing the light–matter interaction below the diffraction limit. Moreover, under the phase matching condition, the propagation loss of SHG signals is partially compensated for by the frequency conversion of the fundamental wave (FW) through the SHG process. As a result, low propagation loss of enhanced SHG signals at a subwavelength scale is realized in HPWs.

---

Ultrasmall broadband tunable coherent light sources hold great potential in applications ranging from laser displays and high throughput sensing to multiband on-chip communication.^1–4 Based on the stimulated emission process of gain materials, various miniaturized light sources have been achieved, including plasmon lasers,^5–8 photonic lasers^9–11 and exciton–polariton lasers.^12,13 Unfortunately, because of the interband transition processes, the wavelength variability of coherent light signals is limited by the bandwidth of the gain materials. Second-harmonic generation (SHG),^14,15 which utilizes nonlinear dielectric materials (e.g. ZnO,¹⁶ KNbO₃,¹⁷ ZnS,¹⁸ GaAs,¹⁹ GaP²⁰ nanowires) as media to convert an electromagnetic wave of frequency ω (fundamental wave, FW) into another wave with twice the frequency (2ω), provides an alternative way to generate tunable coherent signals over a wide range. Nevertheless, the small sizes (at a subwavelength scale) of nonlinear dielectric nanomaterials lead to poor field confinement and weak light–matter interaction due to the diffraction limit of light, which results in low nonlinear conversion efficiency.

Surface plasmon polaritons (SPPs), the propagating collective electron oscillations along the metal surface, can tightly confine light in metallic nanostructures.²¹ This makes SPPs a promising candidate for efficient SHG below the diffraction limit. Benefitting from the effective subwavelength confinement of the electric field in a metallic structure, the nonlinear conversion efficiency has been considerably improved in hybrid structures comprising nonlinear dielectric materials and metallic structures.^22–28 However, subwavelength waveguiding of SHG signals with low propagation loss is still inhibited due to the high intrinsic ohmic losses at the metal–dielectric interface, making it impractical for on-chip devices.

In general hybrid structures, dielectrics are usually in direct contact with a metallic surface, which results in a tightly confined electric field within the dissipative metallic region, and thus leads to high optical ohmic losses at the metal–dielectric interface and poor spatial overlap with nonlinear materials.^29,30 A possible solution is to hybridize the tightly confined plasmonic mode with dielectric waveguide mode in a hybrid plasmonic waveguide (HPW), where a semiconductor nanowire is separated from the metallic surface by a nanometer-scale insulating gap.³¹ Strong plasmonic confinement brings about extraordinary localization of the hybrid plasmonic mode around the dielectric, resulting in excellent spatial overlap with nonlinear materials. The small mode area and enhanced light–matter interaction enable intense SHG in a diffraction-unlimited footprint.^7,32 More importantly, the strong overall electric field confinement of the hybrid plasmonic mode in the non-metallic regions lessens the ohmic losses at the metal surface dramatically, which would allow for the loss compensation of SHG signals through the efficient nonlinear process in the HPW.

Herein, we demonstrate the realization of loss-compensated waveguiding of enhanced SHG signals below its diffraction limit by taking advantage of the low-dissipation-loss hybrid plasmonic mode in an HPW. Based on the synergy of the size-dependent in-coupling coefficient and surface plasmon resonances in the HPW, the intensity of the SHG signals was modulated significantly by varying the polarization of the incident laser. Moreover, tuning the coupling between the dielectric waveguide mode and plasmonic mode resulted in a dramatic variation in the intensity of the SHG signals. Meanwhile, by carefully tailoring the hybrid plasmonic mode dispersion in the HPW to fulfill the phase matching condition (PMC), we have successfully achieved loss-compensated subwavelength waveguiding of SHG signals through efficient energy upconversion from the FW to SHG signals. We believe that the results demonstrated here would help in better understanding the loss compensation of hybrid plasmonic modes in the HPW and provide guidance for the development of nonlinear optics below the diffraction limit.

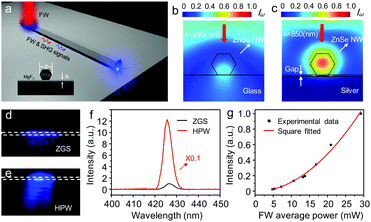
Silver (Ag) was chosen as the plasmonic material owing to the minimal plasmonic damping in the visible and near-infrared ranges,⁷ which is vital for propagation of SPPs with low loss. Single-crystalline ZnSe nanowires (ZnSe NWs) grown along the [111] direction with a zinc blende structure (Fig. S1, ESI†) were selected to obtain efficient SHG due to its significant second-order nonlinear susceptibility.³³ As illustrated in Fig. 1a, the HPW structure consists of a ZnSe NW sitting on top of a Ag film substrate, separated with a thin layer of magnesium fluoride (MgF₂). The simulated electric field distributions of the ZnSe NW on a glass substrate (ZGS, Z stands for ZnSe NW) and a silver substrate (that is, HPW) excited by a transverse magnetic (TM) polarized laser from the top (that is, an FW with a wavelength of 850 nm), calculated by a finite-element method, are demonstrated in Fig. 1b and c (see Fig. S2 in the ESI† for the numerical model). In sharp contrast to the poor electric field confinement of the ZGS (Fig. 1b), the HPW (Fig. 1c) shows much more sufficient electromagnetic field confinement in the ZnSe NW and the gap region between the nanowire and metal surface, which would be helpful to obtain efficient SH radiation. Moreover, the coupling between the dielectric waveguide mode and plasmonic mode of the FW brings about strong overall electric field confinement in non-metallic regions, which would enable subwavelength optical guiding with low mode loss.³¹

Fig. 1 Enhanced second-harmonic generation in a hybrid plasmonic waveguide. (a) Scheme of a hybrid plasmonic waveguide structure, where a single ZnSe NW sits on top of the MgF₂ layer near the Ag film. Under FW excitation, the FW and the generated SHG signals would couple with plasmonics to conduct hybrid plasmonic waveguiding. (b and c) The simulated electric field distributions, calculated with the finite-element method, of the ZGS (b) and HPW (c) excited by a transverse magnetic (TM) polarized laser from the top (that is, the FW with a wavelength of 850 nm). (d and e) Images of SH radiation from the ZGS (d) and HPW (e). The white dashed lines outline the ZnSe NW. (f) Spectra of SHG signals from the ZGS (black) and HPW (red). (g) Measured SHG intensity as a function of FW laser power, which fits to a square dependence.

SHG measurements were carried out on a home-built far-field optical system (Fig. S3, ESI†). An 850 nm wavelength Ti:sapphire laser (150 fs, 80 MHz) was focused onto an individual ZnSe NW laid on a silver substrate and a glass substrate, respectively, with the electric field polarized along the long-axis of the nanowire (transverse magnetic, TM). As shown in Fig. 1d and e, compared with the weak blue spot generated from the ZGS, the ZnSe NW in the HPW exhibits much stronger blue light emission under the 850 nm FW radiation, indicating enhanced SHG in the HPW. Clear interference fringes emerging from the nanowire emission in the HPW suggests coherent radiation of the SHG signals. The spectra collected from the excitation point (Fig. 1f) show that a sharp peak at 425 nm (twice the frequency of the FW at 850 nm, one of the characteristics of SHG) with a full-width at half maximum (FWHM) of 4 nm was acquired. Power-dependent measurements reveal that the signal intensity shows a quadratic response to the excitation power, as illustrated in Fig. 1g, further confirming the second-order nature of the emitted light. A simple estimate of the efficiency of the measured SHG light from the HPW is 5 × 10⁻⁶% at a pumping power of 5 mW (Fig. S4, ESI†), which is much larger than those of most reported metal-related nanostructures (Table S2, ESI†). More than 120 times enhancement of SHG has been realized from the HPW in comparison to the ZGS at the same pumping power (Fig. 1f). Furthermore, while we focused the laser beam directly onto the silver/glass substrate without the ZnSe NW, no measurable SHG signals were obtained, indicating that the SHG signals were generated from the ZnSe NW, and enhanced in the HPW, which agrees well with our early simulation results (Fig. 1b and c). The formation of a Fabry–Pérot cavity in the vertical direction due to the refractive index variation at the surfaces of the ZnSe NW in the HPW,³⁴ along with the plasmonic effect of the silver substrate, brings about strong field confinement in both the ZnSe NW and the gap region of the HPW under the FW excitation and thus results in enhanced SH radiation.

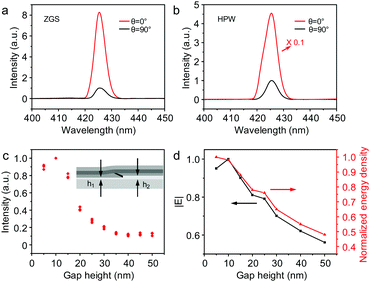
Excitation polarization dependent SHG was performed to further determine the mechanism of SHG enhancement. The polarization orientation (θ) of the FW laser was rotated parallel (θ = 0°) and perpendicular (θ = 90°) to the long-axis of the ZnSe NW with a half wave plate at a fixed pumping power. As shown in Fig. 2a and b, the SH radiation from both the ZGS and HPW reveals obvious polarization anisotropy. The intensity of the SHG signals increased rapidly as the excitation polarization was rotated from perpendicular to parallel with respect to the long-axis of the ZnSe NW. The ratio of the SHG signal intensities (I_SHG(θ = 0°)/I_SHG(θ = 90°)) of the ZGS is about 8 (Fig. 2a), which is in reasonable agreement with previous studies.^35,36 This can be attributed to the anisotropic second-order coefficient of the ZnSe NW and the size-dependent in-coupling coefficient (SDIC) arising from the different dielectric constant between the nanowire and its surrounding environment where the diameter is less than λ/2 (Fig. S5, ESI†).³⁷ In contrast, the I_SHG(θ = 0°)/I_SHG(θ = 90°) ratio of the HPW is 46, nearly 5 times larger than that of the ZGS under the same conditions (Fig. 2b), which indicates that the polarization anisotropy of the SHG signals was enhanced in the HPW due to the highly polarized behavior of the hybrid plasmonic mode. This was further confirmed by the electric field distribution in the HPW under TM- and TE-polarized FW excitation (Fig. S6, ESI†).

Fig. 2 Excitation polarization and gap height dependence of SHG signals. (a and b) Normalized intensity of the SHG signals varied with excitation polarization orientation in the ZGS (a) and HPW (b). (c) Normalized intensity of the SHG signals varied with the gap height (h) of the MgF₂ layer. Inset: Illustration of a single ZnSe NW across two different heights of the MgF₂ layer. (d) Numerically simulated intensities of the confined electric field (black line) in the ZnSe NW with different gap heights and the corresponding energy densities (red line) in the HPW.

Owing to the hybridization of the waveguide mode with plasmonics, the hybrid plasmonic mode can be modulated by tuning the coupling between the plasmonic mode and waveguide mode.⁵ To allow precise comparison, we performed the measurements on the nanowire across the different thicknesses of the MgF₂ layer (Fig. 2c inset, see Fig. S7 in the ESI† for more fabrication details). As shown in Fig. 2c, the SH intensity increases with increasing height of the MgF₂ layer while h < 10 nm, and then exhibits a dramatic decrease upon further increasing the gap height. This can be ascribed to the modulation of the hybrid plasmonic mode in the HPW. The SH intensity is primarily determined by the light–matter interaction between the nonlinear materials and the electromagnetic field,³⁸ including the intensity of the confined electric field interacting with the nonlinear materials and the corresponding energy density (note that it has a reciprocal relationship with mode area).^39,40

With an increase of insulating gap height below 10 nm, the decrease of coupling between the plasmonic mode and waveguide mode leads to an increase in the intensity of the confined electric field interacting with the ZnSe NW on one hand, and a slight decrease of energy density on the other hand (as demonstrated in Fig. 2d). This brings a more dominant increase in the SH intensity. Further increase of insulating gap height while h > 10 nm, resulting in a rapid decrease of the intensity of the confined electric field and the energy density, leads to a dramatic decrease in the interaction between the electric field and the ZnSe NW.³⁸ As a result, there is a rapid monotonic decline in the SH intensity with further gap height increase. It is noteworthy that the SH intensity of the HPW is still stronger than that of the ZGS, even when the coupling between the plasmonic mode and dielectric mode is weak (h = 50 nm). This can be ascribed to the reflection enhancement and Fabry–Pérot cavity resonance in the HPW, where the Ag film substrate functions as a reflecting mirror.³⁴

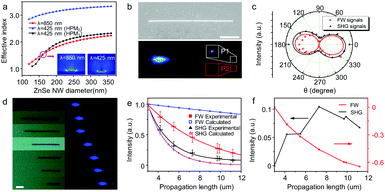
Based on the high optical confinement and strong light–matter interaction, the HPW structure can serve as an ideal candidate for a coherent light source below the diffraction limit. However, suffering from the relatively high propagation loss of the hybrid plasmonic mode at a wavelength of 425 nm, it is difficult to achieve waveguiding of SHG signals at a subwavelength scale. To overcome this drawback, introduction of optical compensation during the waveguiding has been identified as an efficient means of in situ loss compensation for the ohmic loss.^41–44 In addition, coherent loss compensation is needed due to the nature of coherent light of SHG signals. In the HPW, profiting from the coupling between the plasmonic and dielectric waveguide modes, a great enhancement of light–matter interaction is obtained. Furthermore, when the phase matching condition (PMC, where n_FW = n_SH) is satisfied, the SHG signals generated from the interaction between the FW and nonlinear materials during the waveguiding would be in phase with that from the excitation point, which results in a constructive interference between them. Thus, coherent loss compensation can probably be achieved through the efficient energy upconversion of FW,^45,46 which can operate in a broad wavelength range. Fig. 3a shows the effective indices of the guided hybrid plasmonic modes as a function of the diameter of the ZnSe NW for a free space wavelength λ = 850 nm and λ = 425 nm with a fixed gap height (h = 10 nm). We can see that a crossing between the fundamental mode at the FW and the second-order mode at the SH (labeled as HPM₁) occurs when the diameter of the ZnSe NW is around 160 nm, which suggests the possible satisfaction of the PMC in the HPW.^45,47

Fig. 3 Long-range propagation of SHG signals in the HPW with subwavelength confinement. (a) Effective indices of hybrid plasmonic modes of the FW and SHG signals versus the diameter of the ZnSe NW in the HPW, calculated with a finite element method. Inset: Typical hybrid plasmonic mode of the FW and SHG signals when the ZnSe NW diameter is 160 nm. (b) Scanning electron microscopy (top) and SH image (bottom) of a single ZnSe NW in the HPW excited with a pulsed laser (850 nm). Inset: Magnified images of P1 (the distal end of the ZnSe NW) and P2 (the point at the side of the ZnSe NW tip, which has equal distance from the excitation point with P1). The scale bar is 2 μm. (c) Polarization profile of the FW signals (black) and SHG signals (red) collected from the waveguide point (P1). (d) Bright-field and SH images obtained from a single ZnSe NW excited by the FW with the change in nanowire length. The scale bar is 2 μm. (e) Propagation losses (solid symbols: experimental results; void symbols: calculated results) of the FW and SHG signals in the HPW. (f) Propagation losses of the FW and SHG signals after subtracting the intrinsic loss of hybrid plasmonic modes.

Angular FW laser excitation was adopted to produce k-vector components parallel to the surface, which is conducive to obtaining propagating SHG signals (Fig. S8, ESI†).⁴⁸ While a typical 160 nm-diameter ZnSe NW (Fig. 3b, see also the atomic force microscopy (AFM) image shown in Fig. S9, ESI†) was excited at the left distal end, intense SH radiation was achieved at the excitation point (Fig. 3b). Moreover, another weaker visible spot at the waveguide point was obtained, suggesting the waveguiding of SHG signals. Spatially resolved spectra collected from P1 (corresponding to the tip of the ZnSe NW) and P2 (corresponding to the point at the side of the ZnSe NW, which has equal distance from the excitation point with P1) are plotted in Fig. S10 (ESI†). Both FW signals (λ = 850 nm) and SHG signals (λ = 425 nm) can be detected at P1, while there is no measurable signal acquired from P2. These results rule out the possibility of scattering signals from the excited point at high pump power, and provide a direct confirmation of the waveguiding of the FW and SHG signals in the HPW.

Due to the cut-off effect in the HPW (where a lower index hybrid mode cannot exist for effective indices n < 1.44),^31,49 at a wavelength of 425 nm, both TM- (hybrid plasmonic modes) and TE-polarized (dielectric waveguide mode) modes can be supported in the HPW with a 160 nm-diameter ZnSe NW (Fig. S11, ESI†). Further experiments were carried out to check the polarization of the signals acquired at the waveguide point. As demonstrated in Fig. 3c, both FW and SHG signals are parallel polarized to the long-axis of the ZnSe NW (TM-polarized), illustrating the highly polarized behavior of the propagating mode. This is in good agreement with the behavior of hybrid plasmonic modes because the electric field normal to the metal surface binds most strongly to electronic surface charge.⁵ Since the SHG arises from the interaction between the FW and the nonlinear materials, both the dielectric waveguide mode and hybrid plasmonic mode of SHG were generated under the FW excitation. However, affected by the field pulling effects of the substrate, arising from the continuity of the displacement field at the material interface and the electric-field components normal to the material interfaces, the dielectric waveguide mode would couple with the plasmonics during the waveguiding.^31,50 Consequently, hybrid plasmonic waveguiding of SHG signals was achieved.

The propagation losses of the FW and SHG signals were evaluated by looking at the spatially resolved spectra of the emitted light with respect to the distance travelled. A nanofabrication method was used to change the length of the nanowire (Fig. 3d).^51–53 The distance dependent intensities of the FW and SHG signals are shown in Fig. 3e. Due to the wavelength dependent loss of SPPs, where the short wavelength light damps faster than the long wavelength light,⁵⁴ the intensity of the SHG signals decays much more rapidly than the FW signals. This is quite different from that in the dielectric waveguide, which further confirms the hybrid plasmonic waveguiding of FW and SHG signals. The optical-loss coefficient (R), calculated by single exponential fitting I = A exp(−RD) (D is the propagation length),⁵⁵ was 0.51 dB μm⁻¹ at 425 nm, which is smaller than that of the hybrid plasmonic mode in the HPW (i.e., the intrinsic losses of the hybrid plasmonic mode in the HPW arising from absorption in the metal during the waveguiding) obtained by calculating the propagation constant with a finite element method. In sharp contrast, the propagation loss of FW signals is 0.2 dB μm⁻¹, much larger than the calculated result (0.02 dB μm⁻¹), which can be partially ascribed to the scattering losses caused by the roughness of the surfaces. By subtracting the intrinsic loss of the hybrid plasmonic mode of the FW and SHG signals (Fig. 3f), we can see that the intensity of the SHG signals increases at first and then gradually decreases with increase of propagation distance while the intensity of the FW signals decreases monotonically. This indicates that the energy flowing from the FW into SHG signals occurs during the waveguiding in the HPW. As a result, the loss of SHG signals is partially compensated for by the upconversion of the FW. This makes the difference of propagation losses of FW signals between experimental and calculated results larger than that of SHG signals (Fig. 3e). The roughly estimated loss compensation efficiency of SHG signals in the HPW is 0.05 dB μm⁻¹ (see the ESI† for more details).

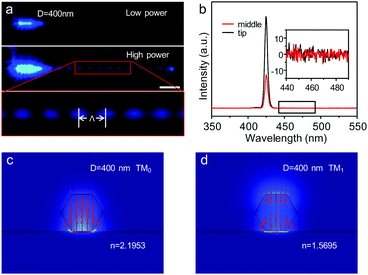
As the hybrid plasmonic modes maintain strong electric field confinement with only a weak dependence on the nanowire diameter,⁵ hybrid plasmonic waveguiding of SHG signals was achieved in an individual ZnSe NW with 400 nm diameter under FW laser radiation (Fig. 4a, see also Fig. S12, ESI†). With an increase of the pump power, periodic blue patterns along the long axis of the ZnSe NW emerged with a periodicity length of 1.87 μm. Spatially resolved spectra collected from the middle and tip of the ZnSe NW (Fig. 4b) show that both signals exhibit a single peak with a wavelength of 425 nm (SHG signals) and no measurable two-photon florescence was obtained (Fig. 4b, inset). This indicates that efficient SHG was achieved along the ZnSe NW during the propagation of FW signals, which provides an experimental confirmation of in situ loss compensation for the SHG signals in the HPW. The polarization orientations of the SHG signals collected from the middle and tip of the ZnSe NW are parallel to the long axis of the ZnSe NW (Fig. S13, ESI†), which is consistent with that obtained in the 160 nm-diameter HPW due to the highly polarized behavior of the hybrid plasmonic mode. These results indicate that the periodic SH radiation should have resulted from the interference of different hybrid plasmonic modes of FW signals during the waveguiding.^56,57

Fig. 4 Long-range propagation of SHG signals based on the in situ propagation loss compensation in the HPW. (a) SH images obtained from an individual ZnSe NW (D = 400 nm) excited with an 850 nm pulsed laser beam at various pump powers: top – low pump power; middle – high pump power; bottom – magnified SH image of periodic patterns generated by high pump power excitation. The scale bar is 3 μm. (b) The corresponding spectra collected from the middle and tip of the ZnSe NW shown in (a) under high pump power. Inset: A close-up spectrum for wavelengths ranging from 440 nm to 490 nm is shown, which shows that no measurable fluorescence of the ZnSe NW was obtained. (c and d) The simulated electric field intensity distributions of the optical mode in the HPW with a 400 nm-diameter ZnSe NW at a wavelength of 850 nm (FW laser), calculated with a finite element method.

As shown in Fig. 4c and d, two TM-polarized modes of FW signals (Fig. 4c and d, marked as TM₀ and TM₁, respectively) are supported in the HPW with a 400 nm-diameter ZnSe NW. The coherent interference of TM₀ and TM₁ modes, arising from their different propagation constants, would result in the periodic beating along the ZnSe NW.⁵⁸ The period of the interference between TM₀ and TM₁ given by Λ = 2π/Re(Δk_‖) (where Δk_‖ is the difference in the propagation constant of the TM₀ and TM₁ modes⁵⁷) is 1.79 μm, in reasonable agreement with our experimental results. That is, under low pump power, the high propagation loss of the TM₁ mode makes it unable to transport along the NW, which results in a short range of periodic patterns. When the pump power of FW enables the waveguiding of the TM₁ mode, a coherent interference of the TM₀ and TM₁ modes would be achieved along the ZnSe NW. As a result, efficient SH radiation was obtained when the interference is constructive.⁵⁹ In other words, the SHG process of FW signals can take place efficiently along the ZnSe NW during the waveguiding, which would result in the compensation for the propagation loss of SHG signals.

Conclusions

In conclusion, loss compensated subwavelength waveguiding of enhanced SHG signals has been realized in an HPW by hybridizing the waveguide mode with plasmonics. Based on the highly polarized behavior of the hybrid plasmonic mode, the intensity of the SHG signals was modulated significantly by changing the polarization of the incident laser. In addition, dramatic variation in the intensity of the SHG signals was obtained by tuning the coupling between the dielectric waveguide mode and plasmonic mode through the thickness of the insulating gap. Furthermore, under the phase matching condition, efficient SHG can be achieved along the ZnSe NW during the propagation of FW signals. This leads to partial compensation for the propagation loss of SHG signals, which in turn favors the realization of waveguiding of SHG signals below the diffraction limit. We anticipate that our results will provide profitable enlightenment for the comprehensive understanding of the optical nonlinear parametric processes at a subwavelength scale, and shed new light on the rational design and fabrication of nanophotonic devices with distinct functionalities.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported financially by the Ministry of Science and Technology of China (2017YFA0204502), the National Natural Science Foundation of China (21533013 and 21373241), the Chinese Academy of Sciences (XDB12020300), and the Youth Innovation Promotion Association of CAS (2014028).

Notes and references

1. R. Yan, D. Gargas and P. Yang, Nat. Photonics, 2009, 3, 569–576.
2. J. Li, C. Meng, Y. Liu, X. Wu, Y. Lu, Y. Ye, L. Dai, L. Tong, X. Liu and Q. Yang, Adv. Mater., 2013, 25, 833–837.
3. F. Fan, S. Turkdogan, Z. Liu, D. Shelhammer and C. Z. Ning, Nat. Nanotechnol., 2015, 10, 796–803.
4. J. Xu, L. Ma, P. Guo, X. Zhuang, X. Zhu, W. Hu, X. Duan and A. Pan, J. Am. Chem. Soc., 2012, 134, 12394–12397.
5. R. F. Oulton, V. J. Sorger, T. Zentgraf, R. M. Ma, C. Gladden, L. Dai, G. Bartal and X. Zhang, Nat. Photonics, 2009, 461, 629–632.
6. M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev, E. E. Narimanov, S. Stout, E. Herz, T. Suteewong and U. Wiesner, Nature, 2009, 460, 1110–1112.
7. Y. J. Lu, J. Kim, H. Y. Chen, C. Wu, N. Dabidian, C. E. Sanders, C. Y. Wang, M. Y. Lu, B. H. Li, X. Qiu, W. H. Chang, L. J. Chen, G. Shvets, C. K. Shih and S. Gwo, Science, 2012, 337, 450–453.
8. Q. Zhang, G. Li, X. Liu, F. Qian, Y. Li, T. C. Sum, C. M. Lieber and Q. Xiong, Nat. Commun., 2014, 5, 4953.
9. M. H. Huang, S. Mao, H. Feick, H. Yan, Y. Wu, H. Kind, E. Weber, R. Russo and P. Yang, Science, 2001, 292, 1897–1899.
10. F. Qian, Y. Li, S. Gradecak, H. G. Park, Y. Dong, Y. Ding, Z. L. Wang and C. M. Lieber, Nat. Mater., 2008, 7, 701–706.
11. W. Zhang, L. Peng, J. Liu, A. Tang, J. S. Hu, J. Yao and Y. S. Zhao, Adv. Mater., 2016, 28, 4040–4046.
12. S. Kéna-Cohen and S. R. Forrest, Nat. Photonics, 2010, 4, 371–375.
13. C. Schneider, A. Rahimi-Iman, N. Y. Kim, J. Fischer, I. G. Savenko, M. Amthor, M. Lermer, A. Wolf, L. Worschech, V. D. Kulakovskii, I. A. Shelykh, M. Kamp, S. Reitzenstein, A. Forchel, Y. Yamamoto and S. Hofling, Nature, 2013, 497, 348–352.
14. J. Gu, Y. Yan, Y. S. Zhao and J. Yao, Adv. Mater., 2012, 24, 2249–2253.
15. H. Yu, W. Fang, X. Wu, X. Lin, L. Tong, W. Liu, A. Wang and Y. R. Shen, Nano Lett., 2014, 14, 3487–3490.
16. J. C. Johnson, H. Yan, R. D. Schaller, P. B. Petersen, P. Yang and R. J. Saykally, Nano Lett., 2002, 2, 279–283.
17. Y. Nakayama, P. J. Pauzauskie, A. Radenovic, R. M. Onorato, R. J. Saykally, J. Liphardt and P. Yang, Nature, 2007, 447, 1098–1101.
18. H. Hu, K. Wang, H. Long, W. Liu, B. Wang and P. Lu, Nano Lett., 2015, 15, 3351–3357.
19. R. Chen, S. Crankshaw, T. Tran, L. C. Chuang, M. Moewe and C. Chang-Hasnain, Appl. Phys. Lett., 2010, 96, 051110.
20. R. Sanatinia, M. Swillo and S. Anand, Nano Lett., 2012, 12, 820–826.
21. A. V. Zayats, I. I. Smolyaninov and A. A. Maradudin, Phys. Rep., 2005, 408, 131–314.
22. M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748.
23. A. Bouhelier, M. Beversluis, A. Hartschuh and L. Novotny, Phys. Rev. Lett., 2003, 90, 013903.
24. A. Nahata, R. A. Linke, T. Ishi and K. Ohashi, Opt. Lett., 2003, 28, 423–425.
25. S. Shen, L. Meng, Y. Zhang, J. Han, Z. Ma, S. Hu, Y. He, J. Li, B. Ren, T. M. Shih, Z. Wang, Z. Yang and Z. Tian, Nano Lett., 2015, 15, 6716–6721.
26. Y. Pu, R. Grange, C. L. Hsieh and D. Psaltis, Phys. Rev. Lett., 2010, 104, 207402.
27. H. Linnenbank, Y. Grynko, J. Forstner and S. Linden, Light: Sci. Appl., 2016, 5, e16013.
28. B. L. Wang, R. Wang, R. J. Liu, X. H. Lu, J. Zhao and Z. Y. Li, Sci. Rep., 2013, 3, 2358.
29. W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830.
30. L. Novotny and C. Hafner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 4094–4106.
31. R. F. Oulton, V. J. Sorger, D. A. Genov, D. F. P. Pile and X. Zhang, Nat. Photonics, 2008, 2, 496–500.
32. M. L. Ren, W. Liu, C. O. Aspetti, L. Sun and R. Agarwal, Nat. Commun., 2014, 5, 5432.
33. R. Cisek, D. Tokarz, N. Hirmiz, A. Saxena, A. Shik, H. E. Ruda and V. Barzda, Nanotechnology, 2014, 25, 505703.
34. X. Liu, Q. Zhang, W. K. Chong, J. N. Yip, X. Wen, Z. Li, F. Wei, G. Yu, Q. Xiong and T. C. Sum, ACS Nano, 2015, 9, 5018–5026.
35. V. Barzda, R. Cisek, T. L. Spencer, U. Philipose, H. E. Ruda and A. Shik, Appl. Phys. Lett., 2008, 92, 113111.
36. M. L. Ren, R. Agarwal, W. Liu and R. Agarwal, Nano Lett., 2015, 15, 7341–7346.
37. J. Wang, M. S. Gudiksen, X. Duan, Y. Cui and C. M. Lieber, Science, 2001, 293, 1455–1457.
38. F. F. Lu, T. Li, X. P. Hu, Q. Q. Cheng, S. N. Zhu and Y. Y. Zhu, Opt. Lett., 2011, 36, 3371–3373.
39. A. E. Neeves and M. H. Birnboim, J. Opt. Soc. Am. B, 1989, 6, 787–796.
40. X. Vidal, A. Fedyanin, A. Molinos-Gómez, S. Rao, J. Martorell and D. Petrov, Opt. Lett., 2008, 33, 699–701.
41. I. De Leon and P. Berini, Nat. Photonics, 2010, 4, 382–387.
42. M. C. Gather, K. Meerholz, N. Danz and K. Leosson, Nat. Photonics, 2010, 4, 457–461.
43. A. Paul, Y. R. Zhen, Y. Wang, W. S. Chang, Y. Xia, P. Nordlander and S. Link, Nano Lett., 2014, 14, 3628–3633.
44. N. Liu, H. Wei, J. Li, Z. Wang, X. Tian, A. Pan and H. Xu, Sci. Rep., 2013, 3, 1967.
45. A. R. Davoyan, I. V. Shadrivov and Y. S. Kivshar, Opt. Express, 2009, 17, 20063–20068.
46. J. Zhang, E. Cassan, D. Gao and X. Zhang, Opt. Express, 2013, 21, 14876–14887.
47. A. Di Falco, C. Conti and G. Assanto, Opt. Lett., 2006, 31, 3146–3148.
48. N. B. Grosse, J. Heckmann and U. Woggon, Phys. Rev. Lett., 2012, 108, 136802.
49. J. Ye, C. Zhang, C. L. Zou, Y. Yan, J. Gu, Y. S. Zhao and J. Yao, Adv. Mater., 2014, 26, 620–624.
50. C. L. Zou, F. W. Sun, Y. F. Xiao, C. H. Dong, X. D. Chen, J. M. Cui, Q. Gong, Z. F. Han and G. C. Guo, Appl. Phys. Lett., 2010, 97, 183102.
51. L. Tong, R. R. Gattass, J. B. Ashcom, S. He, J. Lou, M. Shen, I. Maxwell and E. Mazur, Nature, 2003, 426, 816–819.
52. X. Guo, Y. Ying and L. Tong, Acc. Chem. Res., 2014, 47, 656–666.
53. X. Wu, Y. Xiao, C. Meng, X. Zhang, S. Yu, Y. Wang, C. Yang, X. Guo, C. Z. Ning and L. Tong, Nano Lett., 2013, 13, 5654–5659.
54. R. Yan, P. Pausauskie, J. Huang and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21045–21050.
55. W. Yao, Y. Yan, L. Xue, C. Zhang, G. Li, Q. Zheng, Y. S. Zhao, H. Jiang and J. Yao, Angew. Chem., Int. Ed., 2013, 52, 8713–8717.
56. R. Grange, G. Bronstrup, M. Kiometzis, A. Sergeyev, J. Richter, C. Leiterer, W. Fritzsche, C. Gutsche, A. Lysov, W. Prost, F. J. Tegude, T. Pertsch, A. Tunnermann and S. Christiansen, Nano Lett., 2012, 12, 5412–5417.
57. H. Wei, S. Zhang, X. Tian and H. Xu, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4494–4499.
58. Y. Kou and X. Chen, Opt. Express, 2011, 19, 6042–6047.
59. C. Xin, S. Yu, Q. Bao, X. Wu, B. Chen, Y. Wang, Y. Xu, Z. Yang and L. Tong, Nano Lett., 2016, 16, 4807–4810.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experiments and additional data. See DOI: 10.1039/c7qm00471k

---